"

76 Worked Examples: Propulsion Systems

These worked examples have been fielded as homework problems or exam questions.

Worked Example #1

A static thrust stand is to be designed to test jet engines. The following conditions are expected for a typical test: intake air velocity = 200 m/s, exhaust gas velocity = 500 m/s, intake cross-section area = 1 m{^{2}}, static intake pressure = 78.5 kPa, static intake temperature = 268K, static exhaust pressure = 101 kPa. Estimate the thrust reaction force to design the test stand to withstand, if it must have a structural safety factor of 3.

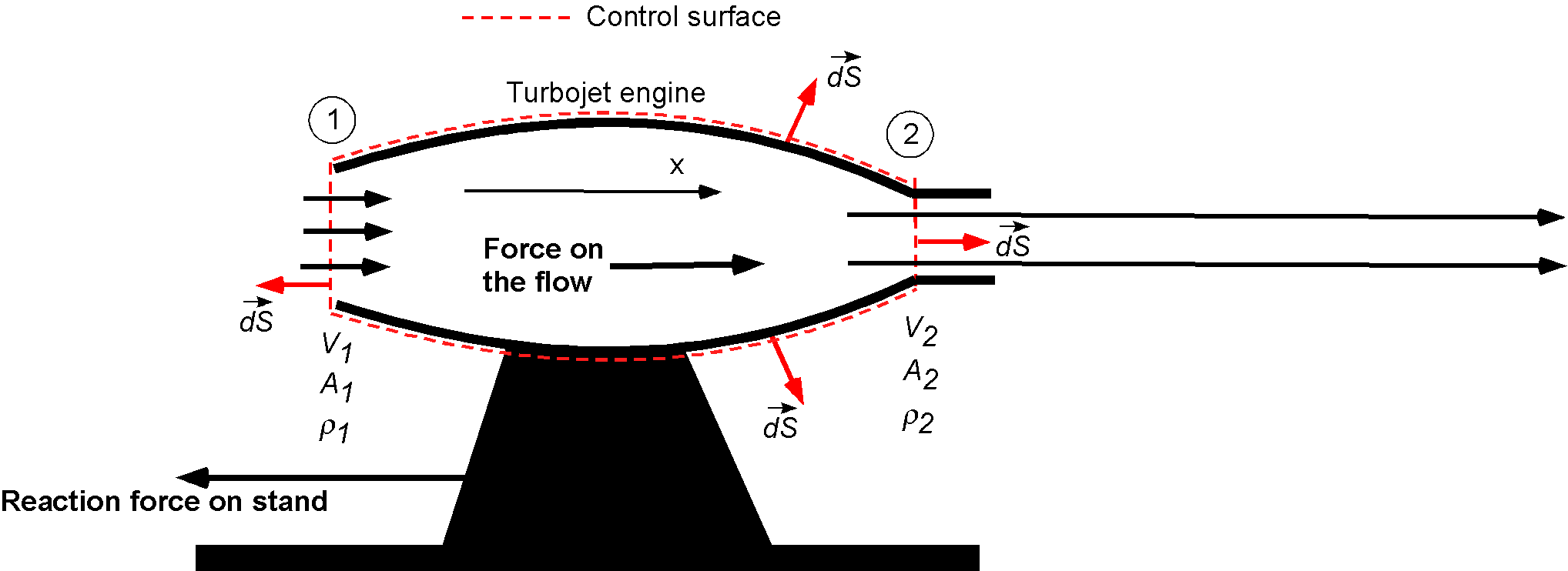
Assume that the inlet condition is identified as station 1 and the outlet as station 2. Assume also that the exit area is equal to the inlet area. The density of the air at the inlet can be found using

    \[ \varrho_1 = \frac{p_1}{R T_1} = \frac{78.5 \times 10^3}{(287)(268)} = 1.0206~\mbox{kg m${^{-3}}$} \]

From continuity considerations (assume 1-dimensional, steady flow), then

    \[ \varrho_1 A_1 V_1 = \varrho_2 A_2 V_2 = \overbigdot{m} = 204.12~\mbox{kg s$^{-1}$} \]

Conservation of momentum (assume 1-dimensional flow) gives the force on the fluid as

    \[ F = -p_1 A_1 + p_2 A_2 + \overbigdot{m} ( V_2 - V_1 ) \]

and substituting the numerical values gives

    \[ F = (-78.5 \times 10^3)(1.0) + (101.0 \times 10^3) \times 1.0 + 204.12 \times (500.0 - 200.0) = 83,736~\mbox{N} \]

For the conditions stated, the residual force on the fluid must be 83,736 N in the direction of fluid flow, and the reaction force on the test stand will be in the opposite direction. Because there is a structural factor of safety requirement of 3, the force to which the stand should be designed is about 251 kN.

Worked Example #2

Consider a turbojet-powered airplane flying at an altitude of 35,000 ft with a true airspeed V_{\infty} of 530 mph; refer to the schematic below. At this altitude, the pressure ratio {\delta = p/p_0} is 0.2353, and the density ratio \sigma = \varrho / \varrho_0 is 0.3099. The inlet and exit areas of the turbojet engine are A_i =13 ft{^{2}} and A_e = 8 ft{^{2}}, respectively. The fuel-to-air ratio by mass injected into the engine is 0.005. The jet exit velocity V_j is 1,510 ft s^{-1} and the pressure at the exit p_e is 450.0 lb ft^{-2}. Assume one-dimensional flow.

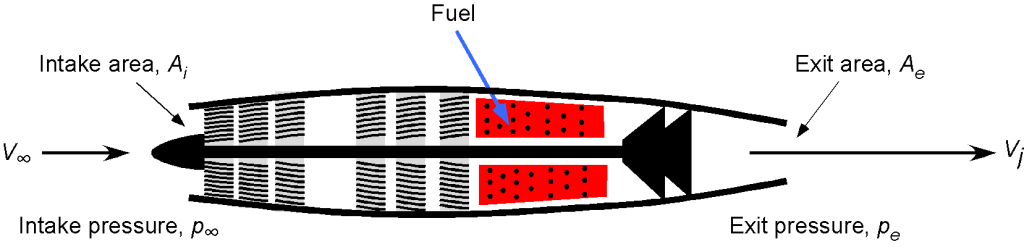
  1. Draw an appropriately annotated control volume to analyze this problem.
  2. Calculate the mass flow rate of air at the inlet to the turbojet.
  3. Calculate the thrust of the turbojet at this flight condition.
  4. Calculate the fuel consumption of the turbojet in units of lb hr^{-1}.
  5. Determine the turbojet’s thrust-specific fuel consumption (TSFC).

1. The control volume is shown in the figure below.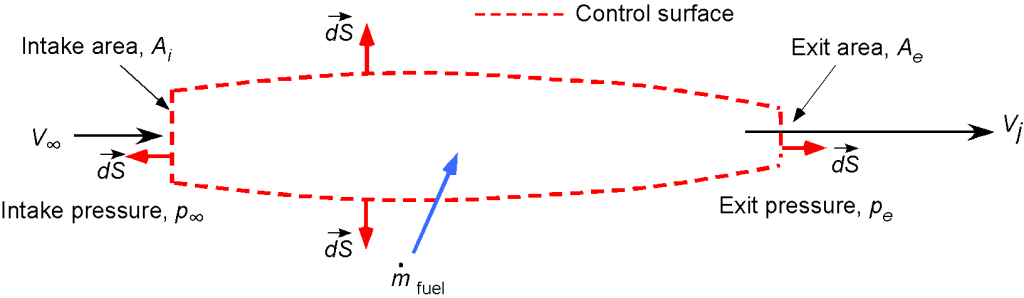

2. The air density at the given altitude is

    \[ \varrho_\infty = \sigma \, \varrho_0 = 0.3099 \times 0.002378 = 0.000737~\mbox{slug ft${^{-3}}$} \]

The corresponding ambient pressure of the air is

    \[ p_\infty = \delta \, p_0 = 0.2353 \times 2116.4 = 498.0~\mbox{lb ft$^{-2}$} \]

3. The air mass flow rate at the inlet of the turbojet engine is

    \[ \overbigdot{m}_{\rm air} = \varrho_{\infty} \, A_i \, V_\infty \]

and substituting the numerical values gives

    \[ \overbigdot{m}_{\rm air} = 0.000737 \times 13.0 \times \left( 530.0 \times 1.46667 \right) = 7.45~\mbox{slug s$^{-1}$} \]

At the exit, the mass flow rate is

    \[ \overbigdot{m}_e = \overbigdot{m}_{\rm air} + \overbigdot{m}_{\rm fuel} = 7.45 + 7.45 \times 0.005 = 7.487~\mbox{slug s$^{-1}$} \]

noting that the mass flow rate of fuel \overbigdot{m}_{\rm fuel} has been. accounted for. With the effects of the pressure on the inlet and outlet, the thrust generated at this flight condition is

    \[ T = \overbigdot{m}_e V_j - \overbigdot{m}_{\rm air} V_\infty + p_e A_e -p_\infty A_{\rm in} \]

Inserting the numerical values gives

    \[ T = 7.487 \times 1,510 - 7.45 \times 777.0 + 450.0 \times 8.0 - 498.0 \times 13.0 = 2,642.7~\mbox{lb} \]

4. The fuel flow rate in terms of the weight of fuel is

    \[ \overbigdot{W}_{\rm fuel} = \overbigdot{m}_{\rm fuel} \, g = 7.45 \times 0.005 \times 3, 600 \times 32.17 = 4,314.0 ~\mbox{lb~hr}^{-1} \]

5. Finally, the TSFC is

    \[ \mbox{TSFC} = \frac{\overbigdot{W}_{\rm fuel}}{T} = \frac{4,314.0}{2,642.7} = 1.63~\mbox{lb lb$^{-1}$ hr$^{-1}$} \]

Worked Example #3

Consider the turbojet in Worked Example #2 with an afterburner. The fuel-to-air ratio by mass injected into the afterburner is 0.016. The jet velocity V_j is 1,510 ft s^{-1}. Consider the flow fully expanded, so there are no pressure difference effects. If the afterburner is ignited, increasing the exit jet velocity to 2,700 ft s^{-1}, what is the extra thrust produced, and what is the new TSFC?

The extra thrust generated with the afterburner is

    \[ T = (\overbigdot{m}_e + \overbigdot{m}_{f_{a}} ) V_{j_{a}} - \overbigdot{m}_e V_j \]

Substituting the numerical values gives

    \[ T = (7.485 + 0.016 \times 7.445) \times 2,700 - 7.485 \times 1,510 = 9,228.77~\mbox{lb} \]

so it gives a massive increase in the thrust from the engine. The new fuel flow rate is

    \[ \overbigdot{W}_f = 4,314.0 + 0.016 \times 7.445 \times 3,600 \, g = 18,113.9~\mbox{lb/hr} \]

and the new TSFC is

    \[ \mbox{TSFC} = \frac{\overbigdot{W}_{\rm fuel}}{T} = \frac{18,113.9}{ 2,642.7 + 9,228.77} = 1.53~\mbox{lb lb$^{-1}$ hr$^{-1}$} \]

Worked Example #4

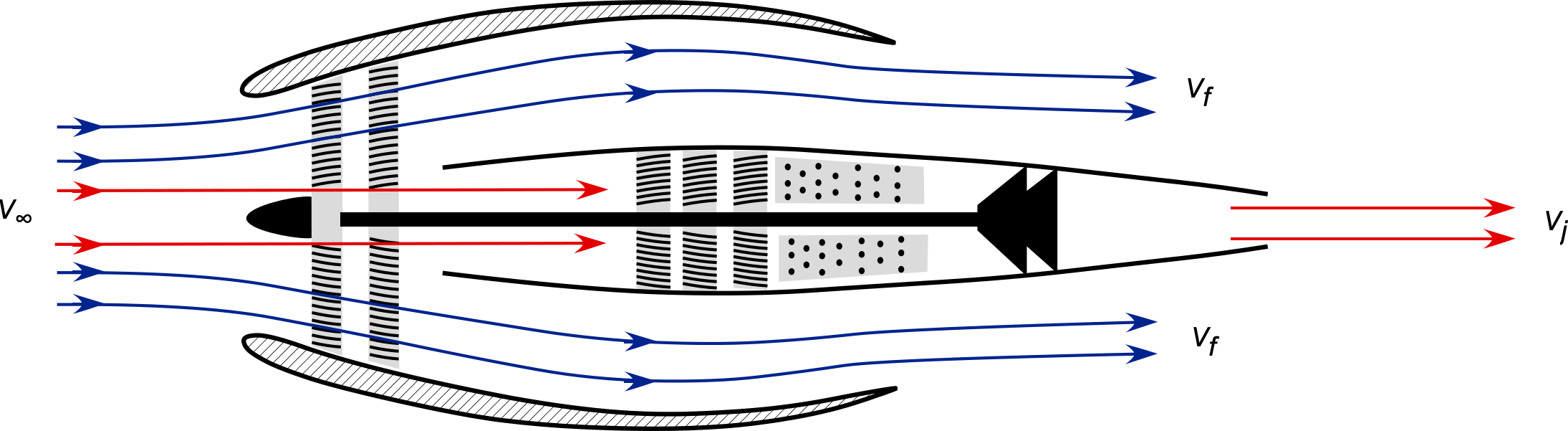
Consider the flow through a turbofan engine, i.e., an engine with a hot jet core of diameter D_j and a cold bypass fan of diameter D_f, as shown in the figure below. Using the flow conservation principles applied to the control volumes, show (using appropriate reduced forms of the conservation equations) how to calculate the net thrust from the engine (i.e., the combined thrust from the core and the fan) in terms of the intake flow velocity V_{\infty} and the jet velocities from the hot core V_j and bypass fan V_f, respectively. Write your result in terms of the bypass ratio and comment on it. State any assumptions that you use. Hints: 1. Consider also the mass of fuel introduced into the engine. 2. Neglect all pressure difference effects.

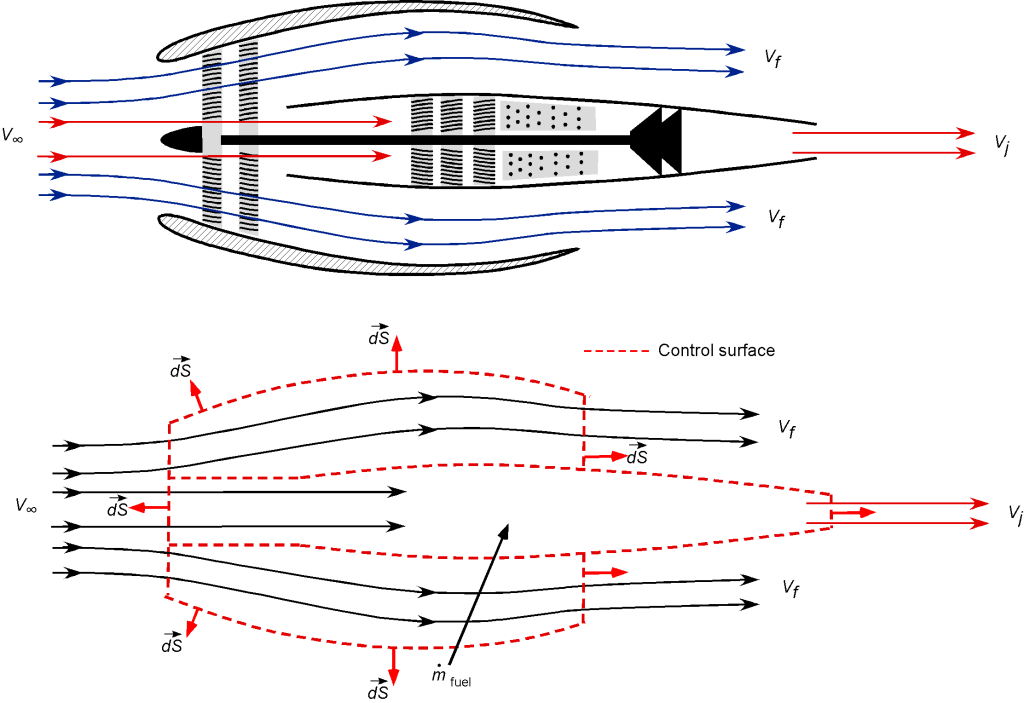
Assume one-dimensional flow throughout the problem. The mass flow through the fan (outer, cold section) is

    \[ \overbigdot{m}_{\rm fan} = \varrho_{\infty} \, A_{\rm fan} V_{\infty} \]

The mass flow through the engine core (inner, hot section) is

    \[ \overbigdot{m}_{\rm core} = \varrho_{\infty} \, A_{\rm core} V_{\infty} \]

Because \overbigdot{m}_{\rm fuel} is much smaller than the mass flow of air into the engine, another assumption is that \overbigdot{m}_{\rm fuel} can be neglected.

Therefore, the application of conservation of momentum gives us that

    \[ T_{\rm fan} = \overbigdot{m}_{\rm fan} \left(V_{f} - V_{\infty}\right) \]

and

    \[ T_{\rm core} = \overbigdot{m}_{\rm core} \left(V_{j} - V_{\infty} \right) \]

where the pressure effects have also been neglected. The bypass ratio (BPR) is given by

    \[ \mbox{BPR} = \frac{\overbigdot{m}_{\rm fan}}{ \overbigdot{m}_{\rm core} } \]

Therefore, the total thrust is

    \[ T = T_{\rm fan} + T_{\rm core} = \overbigdot{m}_{\rm fan} \left(V_{f} - V_{\infty} \right) + \overbigdot{m}_{\rm core} \left(V_{j} - V_{\infty} \right) \]

or in terms of the BPR

    \[ T = \mbox{BPR} \, \overbigdot{m}_{\rm core} \left(V_{f} - V_{\infty} \right) + \overbigdot{m}_{\rm core} \left(V_{j} - V_{\infty} \right) \]

Notice that the higher the BPR, the higher the thrust from the fan stage of the engine. This is also a more efficient way of producing thrust because for a turbofan, the jet velocity for the fan stage, V_f, is less than that of the core, V_j, i.e.,

    \[ \eta_f = \frac{2}{1 + \displaystyle{\frac{V_f}{V_{\infty}}} } \]

and

    \[ \eta_c = \frac{2}{1 + \displaystyle{ \frac{V_j}{V_{\infty}} }} \]

Therefore, the higher the mass flow rate and the lower the jet velocity, the more efficiently the turbojet engine will produce thrust.

Worked Example #5

An aircraft flying at a true airspeed of 200 m/s is powered by a turbofan engine with a bypass ratio of 5:1. The mass flow rate into the engine core is 20 kg/s, and the fuel consumption is 2 kg/s. The average discharge flow velocity from the engine core is V_j = 410 m/s, and from the bypass fan, it is V_f = 270 m/s, both with respect to the engine. Determine the thrust and equivalent power developed by this turbofan engine. Finally, determine the net propulsive efficiency of the turbofan. Neglect all pressure difference effects.

The mass flow of air into the core of the engine is

    \[ \overbigdot{m}_{\rm core} = 20~\mbox{kg/s} \]

and with a bypass ratio of 5:1, the mass flow into the fan will be

    \[ \overbigdot{m}_{\rm fan} = 5 \overbigdot{m}_{\rm core} = 100~\mbox{kg/s} \]

The mass flow rate of fuel is

    \[ \overbigdot{m}_{\rm fuel} = 2~\mbox{kg/s} \]

Therefore, the thrust from the engine core is

    \[ T_{\rm core} = (\overbigdot{m}_{\rm core} + \overbigdot{m}_{\rm fuel} ) V_{\rm core} - \overbigdot{m}_{\rm core} V_{\infty} \]

and from the fan, the thrust is

    \[ T_{\rm fan} = \overbigdot{m}_{\rm fan} V_{\rm fan} - \overbigdot{m}_{\rm fan} V_{\infty} = \overbigdot{m}_{\rm fan} \left( V_{\rm fan} - V_{\infty} \right) = 5 \overbigdot{m}_{\rm core} \left( V_{\rm fan} - V_{\infty} \right) \]

The total thrust is then

    \[ T = T_{\rm core} + T_{\rm fan} \]

In this case we are given that \overbigdot{m}_{\rm core} = 20 kg/s, \overbigdot{m}_{\rm fuel} = 2 kg/s, and also that V_{\rm core} = 410 m/s, V_{\rm fan} = 270 m/s, and V_{\infty} = 200 m/s. Therefore, substituting the numerical values gives

    \[ T_{\rm core} = (20.0 + 2.0 ) \times 410.0 - 20.0 \times 200 = 9,020 - 4,000 = 5.02~\mbox{kN} \]

and

    \[ T_{\rm fan} = 5 (20.0) (270.0 - 200.0) = 7.0~\mbox{kN} \]

The total thrust is then

    \[ T = T_{\rm core} + T_{\rm fan} = 5.02 + 7.0 = 12.02~\mbox{kN} \]

The equivalent net power, P_{\rm eq}, that is developed is

    \[ P_{\rm eq} = T V_{\infty} = 12.02 \times 10^3 \times 200 = 2.4~\mbox{MW} \]

The net propulsive efficiency of the engine is defined as

    \[ \eta_p = \dfrac{\text{Useful power}}{\text{Actual power}} \]

Therefore, for the core and the fan together, then

    \[ \eta_p = \frac{T V_{\infty}}{T V_{\infty} + \frac{1}{2} \overbigdot{m}_{\rm core} \left( V_j^2 - V_{\infty}^2 \right) + \frac{1}{2} \overbigdot{m}_{\rm fan} \left( V_f^2 - V_{\infty}^2 \right)} \]

Substituting all of the numerical values gives

    \[ \eta_p = \frac{ 12.02 \times 10^3 \times 200 }{2.404 \times 10^6 + 1.281 \times 10^6 + 1.645 \times 10^6} = \frac{2.404 \times 10^6}{5.33 \times 10^6} = 45.1\%. \]

Worked Example #6

Refer to the attached propeller charts, which are a standard performance presentation for all propellers. Assume that an actual propeller has a diameter of 7 ft and is a constant-speed propeller with a rotational speed of 2,000 rpm. The propeller operates at an equivalent of 8,000 ft ISA density altitude.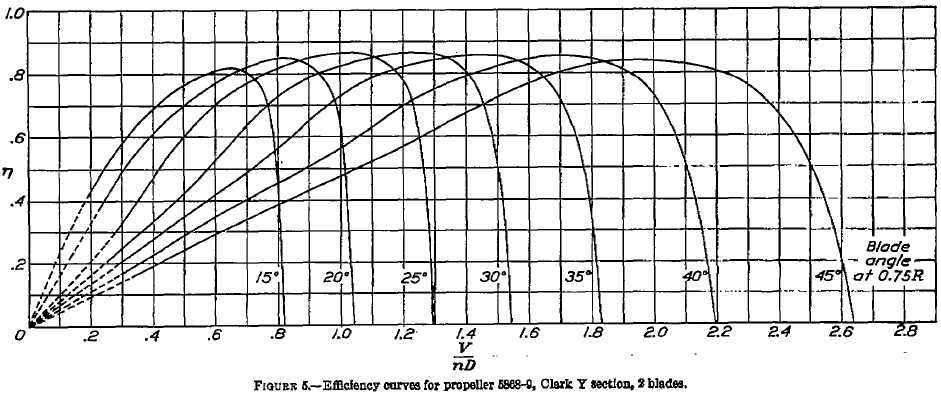

For each blade pitch angle measured at 75% radius and at the point of maximum propulsive efficiency in each case, estimate the following:
(a) What are the advance ratio values and corresponding airspeed values?
(b) What are the propeller thrust coefficient values and the propeller’s corresponding thrust?
(c) What are the values of the propeller power coefficient and the corresponding shaft torque and power required to spin the propeller?
(d) What are the propeller’s helical tip speed values and helical Mach number? Comment on your results. Note: The helical tip speed is the vector sum of the rotational speed at the tip of the propeller and the freestream (airspeed).

(a) At the peak efficiency, the values of the advance ratio can be read off the first chart. We can easily do this to two decimal places; the chart can be digitized for better accuracy. We are also given information about the specific propeller, which is relatively small and would likely be for a general aviation aircraft, so in each case, we can calculate the corresponding airspeed for a given value of J, i.e.,

    \[ J = \frac{V_{\infty} }{n \, d} =\frac{V_{\infty} }{(\text{\small rpm}/60) \, d} \]

so

    \[ V_{\infty} = J \, (\text{\small rpm}/60) \, d = J (2,000/60) \times 7.0 = 233.34 \, J~\mbox{ft/s} \]

It is best to use a table to show the results, i.e.,

Blade pitch (^{\circ}) \eta J V_{\infty} (ft/s)
15 0.82 0.65 151.7
20 0.85 0.82 191.3
25 0.87 1.04 242.7
30 0.87 1.25 292.7
35 0.86 1.45 338.3
40 0.86 1.70 398.7
45 0.84 1.95 455.0

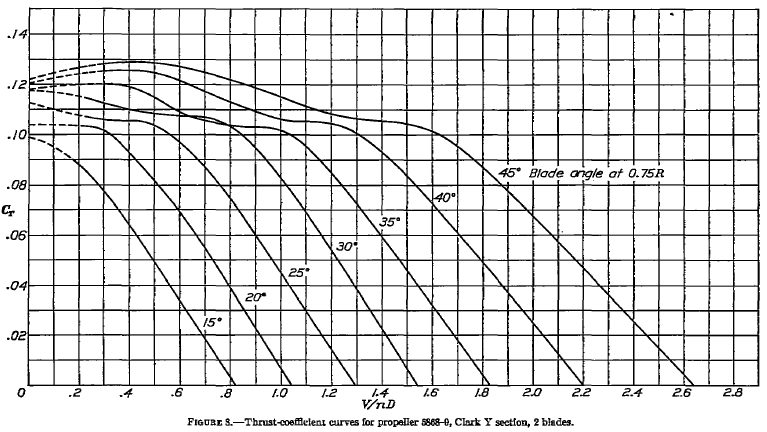
(b) The propeller thrust coefficient can be read off the second chart for each value of the advance ratio, as was identified in the previous part. The thrust coefficient for a propeller is defined as

    \[ C_T = \frac{T}{\varrho n^2 d^4} \]

so the corresponding thrust (in units of force) from the propeller is

    \[ T = \varrho n^2 d^4 C_T \]

We are told that the propeller operates at the equivalent of 8,000 ft ISA density altitude, so according to the ISA equations, the density at this altitude is 0.001869 slugs ft{^{-3}}. Inserting the information gives

    \[ T = \varrho n^2 d^4 C_T = 0.001869 \times \left( \frac{2000}{60} \right)^2 \times 7.0^4 \, C_T = 4986.08 \, C_T \]

Again, it is best to use a table to show the results, i.e.,

Blade pitch (^{\circ}) J C_T T
15 0.65 0.025 124.7
20 0.82 0.038 189.5
25 1.04 0.040 199.4
30 1.25 0.047 234.4
35 1.45 0.052 259.3
40 1.70 0.060 299.2
45 1.95 0.072 359.0

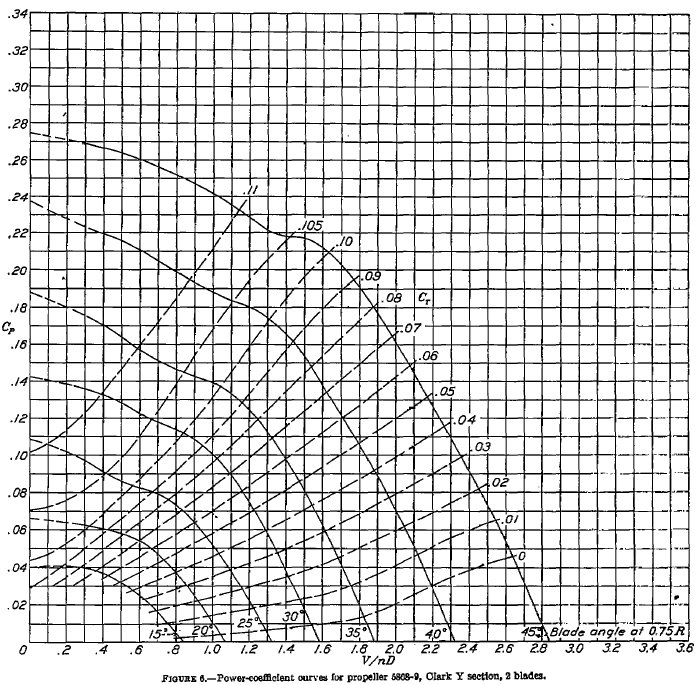
(c) The propeller power coefficient can be read off the third chart for each value of the advance ratio identified in the previous part. The power coefficient for a propeller is defined as

    \[ C_P = \frac{P}{\varrho n^3 d^5} \]

so the corresponding power needed to drive the propeller is

    \[ P = \varrho n^3 d^5 C_P \]

Inserting the known information gives

    \[ P = \varrho n^3 d^5 C_P = 0.001869 \times \left( \frac{2000}{60} \right)^3 \times 7.0^5 \, C_P = 2115.31 \, C_P \]

where we have converted to horsepower (hp) by dividing the result in ft-lb s^{-1} by 550. Again, it is best to use a table to show the results, i.e.,

Blade pitch (^{\circ}) J C_P P (hp)
15 0.65 0.022 46.5
20 0.82 0.035 74.0
25 1.04 0.048 101.3
30 1.25 0.065 137.5
35 1.45 0.09 190.3
40 1.70 0.12 253.8
45 1.95 0.17 359.7

(d) Let V_{\rm hel} be the helical tip velocity based on the vector sum of the rotational and airspeed components. The rotational tip speed of a propeller of diameter {d} is

    \[ V_{\rm tip} = \Omega \left( \frac{d}{2} \right) \]

where \Omega = 2 \pi ( \text{\small rpm}/60 ) and so the helical tip speed of the propeller is

    \[ V_{\rm hel} = \sqrt{ V_{\rm tip}^2 + V_{\infty}^2} \]

where V_{\infty} is the forward airspeed. The helical Mach number M_{\rm hel} will be

    \[ M_{\rm hel} = \frac{V_{\rm hel} }{a} \]

where a is the local speed of sound at the conditions at which the propeller operates. At 8,000 ft ISA density altitude, a = 1085.3 ft/s.As a final table to show the results, the helical tip speed and Mach number are:

Blade pitch (^{\circ}) J V_{\infty} (ft/s) V_{\rm hel} (ft/s) M_{\rm hel}
15 0.65 151.7 748.6 0.69
20 0.82 191.3 757.6 0.70
25 1.04 242.7 772.2 0.71
30 1.25 292.7 788.9 0.73
35 1.45 338.3 807.3 0.74
40 1.70 398.7 833.5 0.77
45 1.95 455.0 862.8 0.79

We notice that for an airspeed above 400 ft/s, the propeller blade tips would likely begin to operate near or just beyond the critical Mach number (i.e., the onset of transonic flow), which for the thin tips of propeller blades is about 0.8. Under these conditions, the propeller will likely lose propulsive efficiency.

Worked Example #7

A rocket engine is to be tested on a test stand. The propellant burns at a steady rate of 150 kg/s, and the specific impulse of the propulsion system is 240 seconds. What thrust does the rocket engine develop?

The equivalent exhaust velocity V_{\rm eq} is given in terms of the specific impulse, i.e.,

    \[ V_{\rm eq} = I_{\rm sp} \, g_0 = 240.0 \times 9.81 = 2,354.4~\mbox{m/s} \]

Therefore, the thrust produced, T, will be

    \[ T = \overbigdot{m}_P \, V_{\rm eq} = 150.0 \times 2,354.4 = 353.16~\mbox{kN} \]

Worked Example #8

A rocket engine generates a thrust of 5,000 N and consumes propellant at a rate of 2 kg/s. Calculate the engine’s specific impulse.

    \[ I_{\rm sp} = \frac{\text{\small Thrust}}{\text{\small Rate of propellant consumption}} = \frac{T}{\overbigdot{m}} \]

Inserting the numerical values gives

    \[ I_{\rm sp} = \frac{5,000.0}{2.0} = 250.0~\mbox{s} \]

Worked Example #9

A small rocket engine has a specific impulse of 300 s and operates in a vacuum. If the engine consumes propellant at a rate of 4 kg/s, what is the thrust produced by the engine?

The thrust is given by

    \[ T = \overbigdot{m} V_{\rm eq} = \overbigdot{m} \, I_{\rm sp} \, g_0 \]

Inserting the numerical values gives

    \[ T = 4.0 \times 300.0 \times 9.81 = 11,772~\mbox{N} = 11.772~\mbox{kN} \]

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Share This Book