"

26 Bluff Body Flows

 Introduction

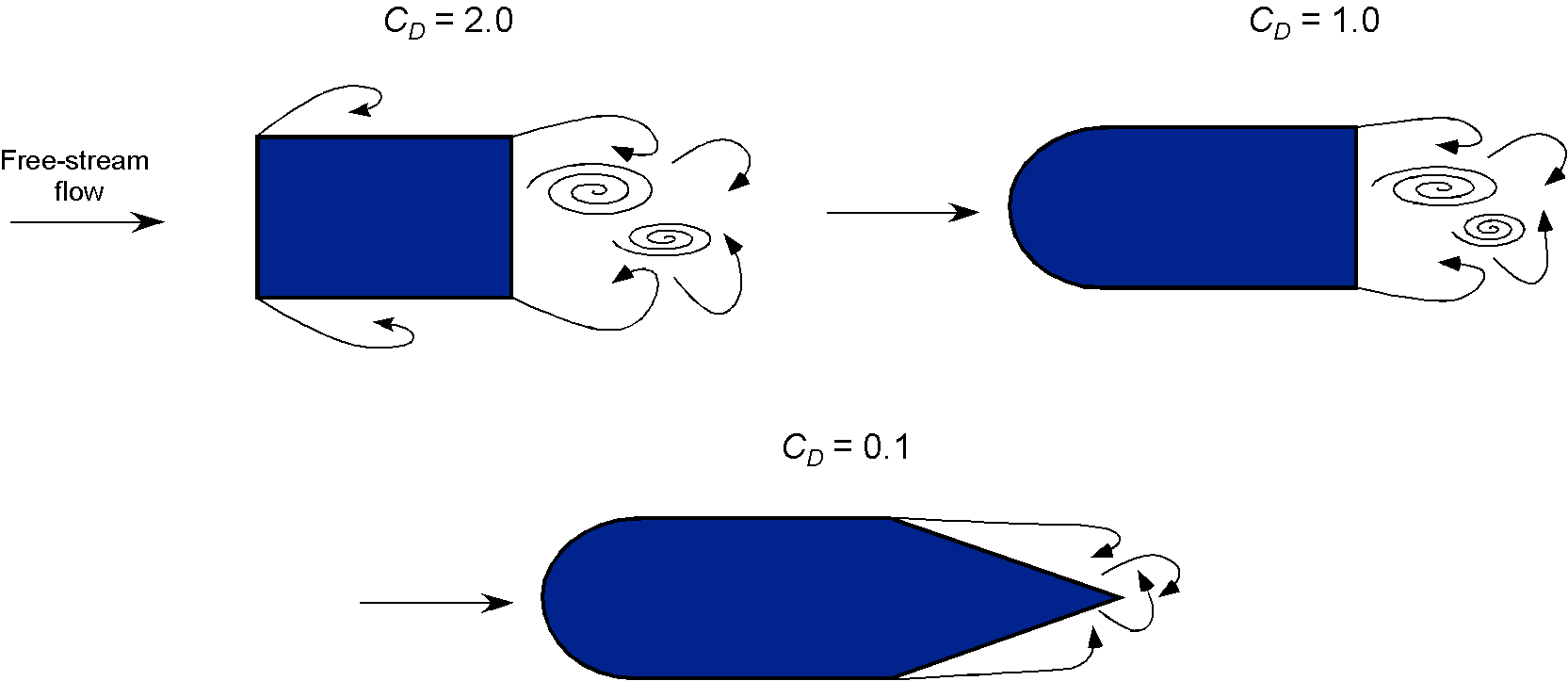
Aerospace engineers are more often than not interested in the aerodynamics of smooth, slender, streamlined shapes that gradually taper to a sharp point at their trailing edges, e.g., airfoils and wings. However, non-streamlined or unstreamlined shapes with blunt front and/or rear faces, called bluff bodies (sometimes they are called blunt bodies, are also encountered in many engineering applications. While the drag force on a body shape comprises the effects of the two primary contributors, skin friction drag and pressure drag, the total drag on bluff bodies is typically dominated by the pressure drag component. This outcome arises because of the effects of the large low-pressure zone produced in the wake at the rear of the body, as illustrated in the diagram below.

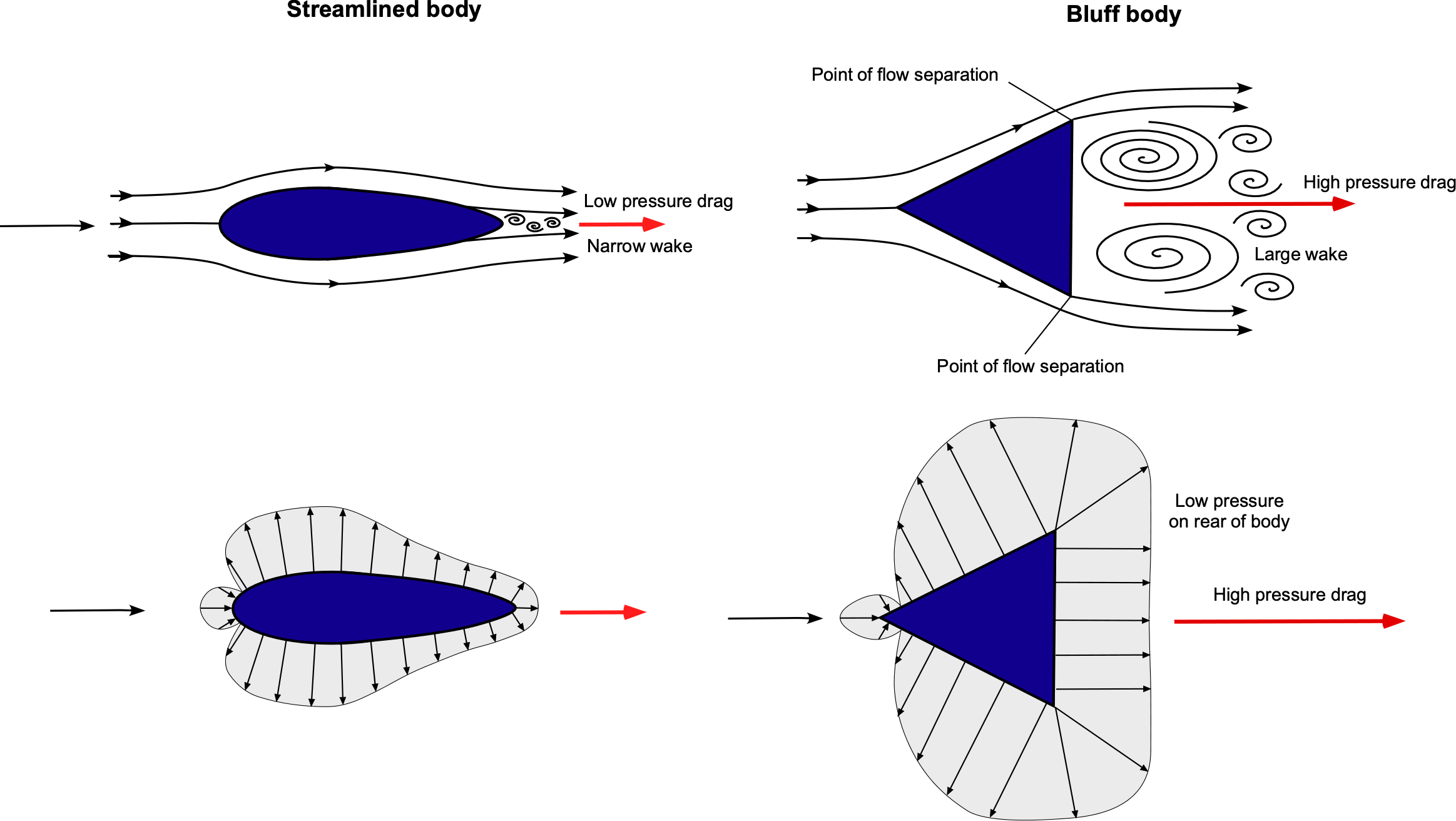
The differences in the flows between a streamlined body and a bluff body. The bluff body produces flow separation and a large, broad wake containing low pressures, producing high drag.

Understanding bluff body aerodynamics is essential because of its wide-ranging applications in various engineering fields. Studying how non-streamlined objects interact with airflows helps design more efficient structures and vehicles. For instance, understanding unsteady wind loads on bluff body shapes such as buildings and bridges ensures aeroelastic stability and prevents failures, while optimizing vehicle shapes reduces drag, improves fuel efficiency, and leads to better performance. The aerodynamics of bluff bodies also comes into consideration in many sports, including golf, tennis, and baseball. For example, the dimples on a golf ball create turbulent flow, reducing drag and allowing the ball to travel further. In tennis, the spin imparted on the ball affects its trajectory and speed. Similarly, in baseball, the stitching on the ball and the way it is thrown, such as with spin, create varying aerodynamic effects based on the players’ skill.

Learning Objectives

  • Distinguish the fundamental differences between the flows of streamlined versus bluff bodies.
  •  Understand the use of reference areas in defining bluff body drag coefficients and the concept of equivalent drag area.
  • Appreciate why the drag of bluff bodies with smooth surfaces, such as circular cylinders and spheres, shows sensitivities to Reynolds number variations.
  • Become familiar with the Magnus effect on spinning cylinders and spheres.

Drag Coefficients

For bluff bodies, the interest is usually in the drag on that body, mainly because experiments have found that drag is the dominant force. This observation, however, does not imply that bluff bodies cannot produce lift because many do. Nevertheless, examining just the drag characteristics of such bodies is convenient in the first instance. Furthermore, bluff bodies may also produce pitching moments, which sometimes need to be known for certain types of engineering work, e.g., to determine torsional loads.

Recall that the two-dimensional drag coefficient is

(1)   \begin{equation*} C_d = \frac{D'}{\frac{1}{2} \varrho_{\infty} \, V_{\infty}^2 \, l} \end{equation*}

where {D'} is the drag per unit span, and {l} is a characteristic length, e.g., for a circular cylinder, l = d, where {d} is its diameter.

In most cases, the drag coefficients for two-dimensional bluff bodies are presented in terms of per length, b, so the drag coefficient is defined as

(2)   \begin{equation*} C_D = \frac{D}{\frac{1}{2} \varrho_{\infty} \, V_{\infty}^2 \, l \, b} \end{equation*}

where the product l\,b is equivalent to an area. In general, for a three-dimensional object, the drag coefficient is defined as

(3)   \begin{equation*} C_D = \frac{D}{\frac{1}{2} \varrho_{\infty} \, V_{\infty}^2 \, A_{\rm ref}} \end{equation*}

where A_{\rm ref} is defined as the reference area, usually the projected frontal area. Using a sphere of diameter {d} as an example, its projected area is {A_{\rm ref} = \pi d^2/4}. Likewise, a cube with side length {l} will have a reference area of A_{\rm ref} = l^2

However, caution must be used when defining drag coefficients for three-dimensional bodies because the drag coefficient always depends on the definition of the body’s reference area, which may not be unique. For example, on the one hand, for specific bodies of revolution, the volumetric drag coefficient is used by convention, in which the reference area is the square of the cube root of the volume. On the other hand, in hydrodynamics, the analysis of submerged streamlined bodies uses the wetted surface area as the reference area. Therefore, to consistently use and compare drag coefficients, adopting the convention used in the particular field of application is imperative.

To avoid ambiguity in the definitions of drag coefficients for different body shapes, drag coefficients per se are not always used. Instead, the equivalent drag area is used, given the symbol {\scriptstyle{f}}. The equivalent drag area is defined as

(4)   \begin{equation*} f = \frac{D}{\frac{1}{2} \varrho_{\infty} \, V_{\infty}^2} \end{equation*}

where {\scriptstyle{f}} would be measured in units of area.

The advantage of using equivalent drag areas is that there is no ambiguity in defining a reference area. This approach is often used when estimating the drag of complex shapes made up of many simpler shapes, e.g., the drag of an entire airplane. In such a case, the equivalent drag area of the complex shape is obtained by a drag synthesis of the equivalent drag areas of N simple shapes, i.e.,

(5)   \begin{equation*} f = f_1 + f_2 + f_3 + ..... + f_N \end{equation*}

However, it would be incorrect to write

(6)   \begin{equation*} { C_D = C_{D_{1}} + C_{D_{2}} + C_{D_{3}} + .... + C_{D_{N}} } \end{equation*}

because the reference areas on which each value of C_D is based could be different, and generally will be. To take into account component interference, i.e., to make some allowance for flow interference effects between the different components, then

(7)   \begin{equation*} f = K \left( f_1 + f_2 + f_3 + ..... + f_N \right) \end{equation*}

where K > 1 and often K = 1.2 will be used for aircraft drag synthesis without any other information, i.e., a 20% drag penalty from component interference effects.

Drag Coefficients of Simple Shapes

There are many bluff body shapes for which the drag (or drag coefficient) may need to be known for engineering purposes. However, in practice, far fewer such shapes are encountered, most of which have been well-studied, and the drag coefficients have been measured in wind tunnels. Furthermore, flows around bluff bodies are often unsteady and can produce various types of vortex shedding, as shown in the animation below. Therefore, the measurement or computation of drag is usually made over a relatively long period, known as an ensemble time average.

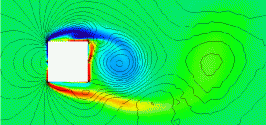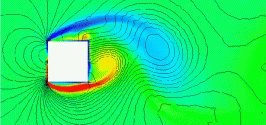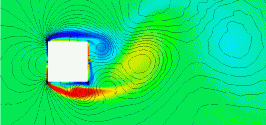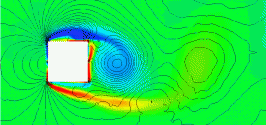
CFD simulation of the unsteady flow and periodic vortex shedding produced by a bluff body shape.

Drag coefficients for standard two-dimensional and three-dimensional bluff body shapes are published in many sources and are a valuable resource for engineers. These shapes can be further categorized into two primary sub-classes of bluff bodies:

  1. Those with sharp angular shapes tend to have fixed points of flow separation and drag coefficients insensitive to the Reynolds number.
  2. Those with smooth contours will have variable flow separation points and can exhibit some sensitivity to the Reynolds number.
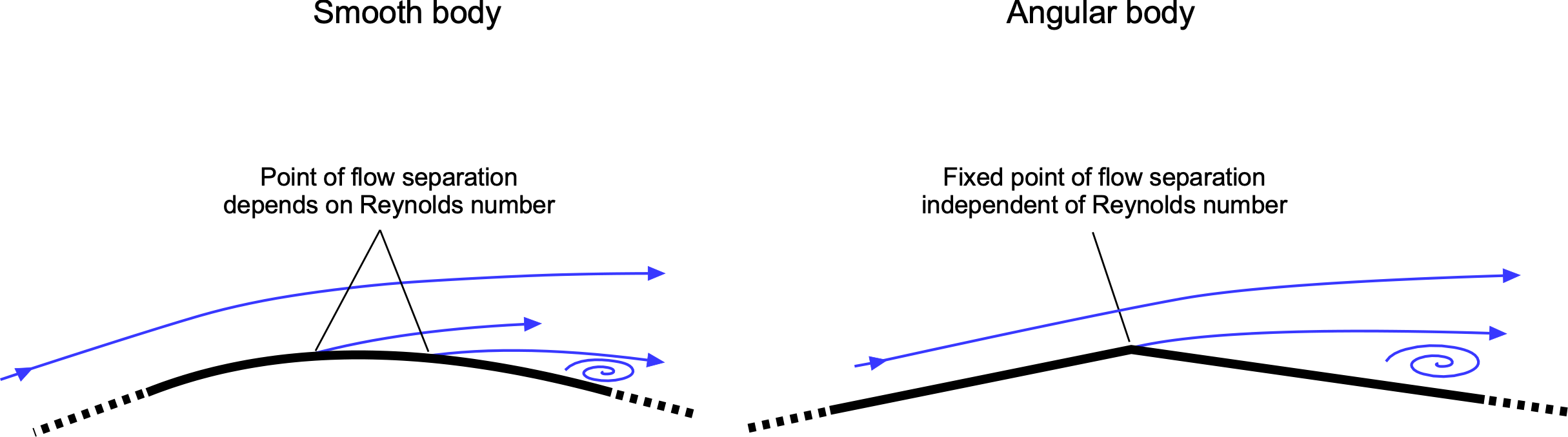
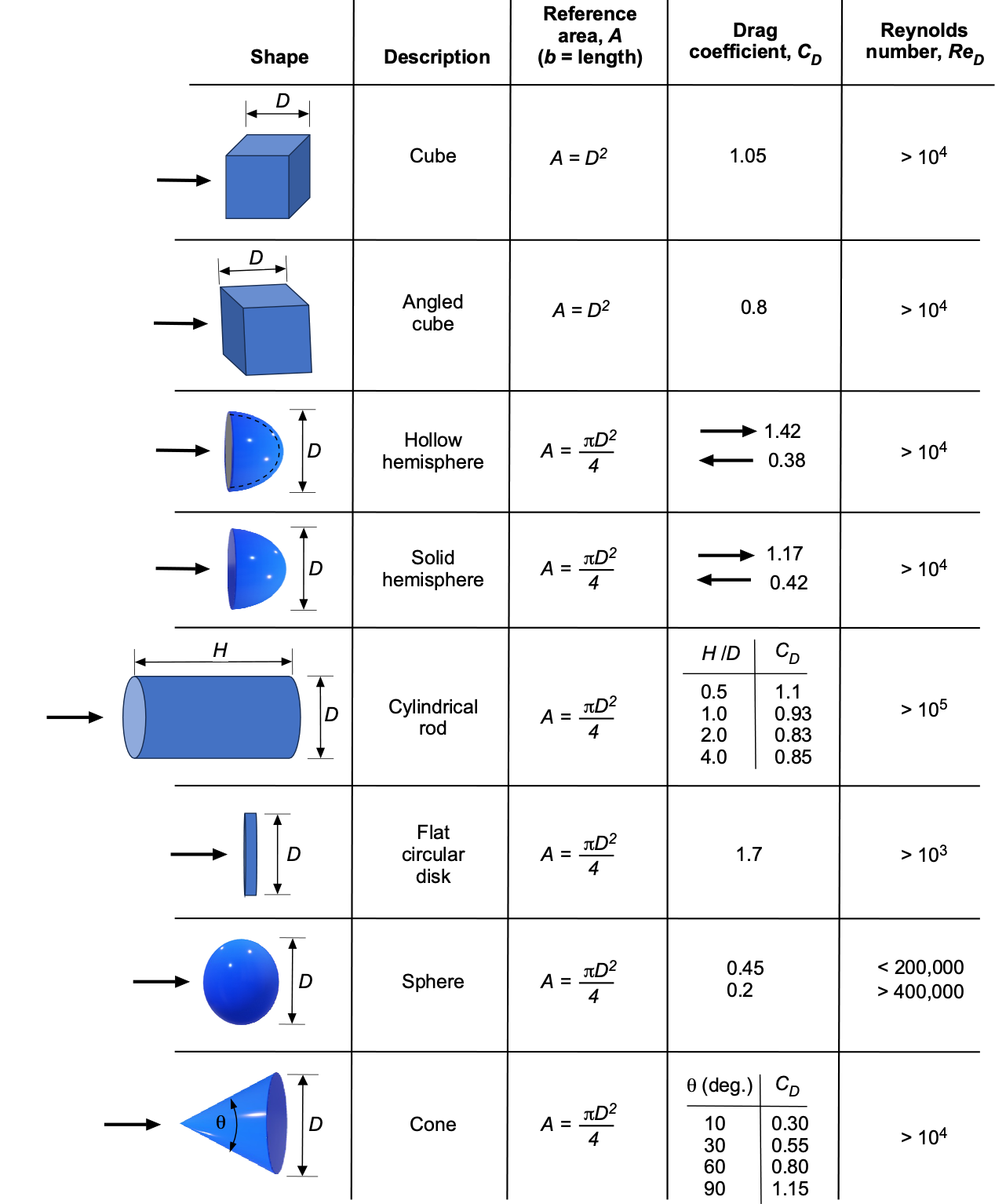
The aerodynamics of smooth bluff bodies depend on the Reynolds number, but angular bodies with sharp corners tend to have fixed flow separation points.

Of course, there is always the possibility that some bluff body shapes combine smooth contours and sharp edges. In this case, determining the drag coefficient and the effects of the Reynolds number may require specific measurements in the wind tunnel to establish the drag coefficients. Values for some common bluff-body shapes are shown in the tables below.

 

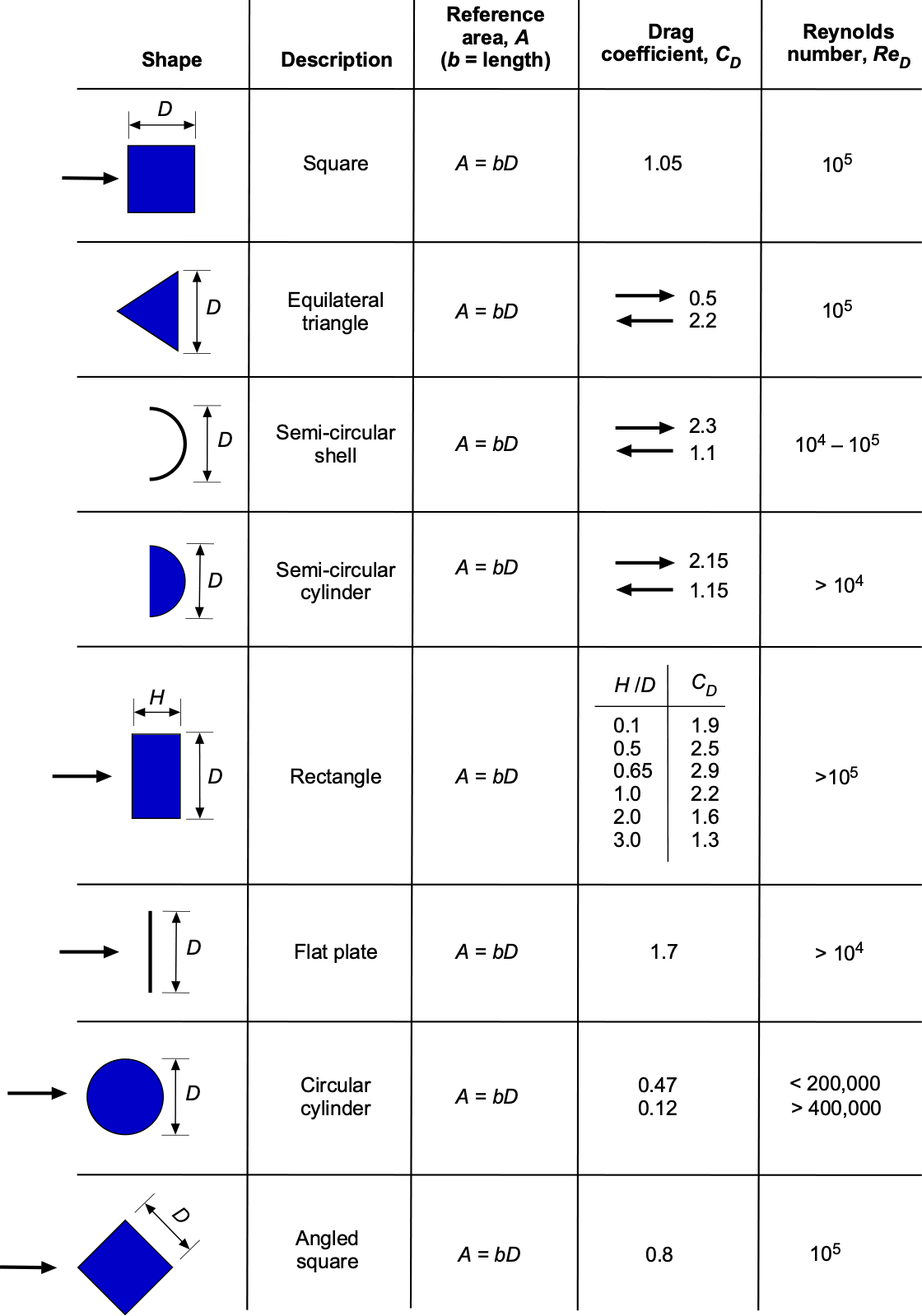
Measured drag coefficients of some simple two-dimensional bluff bodies.

For example, a sphere or a cylinder is smooth, whereas a cube is angular. The flows about smooth bluff bodies or those with rounded corners generally exhibit some sensitivity to the Reynolds number, and their drag coefficients vary as a consequence, as shown in the tables. In contrast, angular shapes show little or no variations with changes in the Reynolds number, at least after reaching a minimum threshold.

 

Measured drag coefficients of some simple three-dimensional bluff bodies.

Check Your Understanding #1 – Calculating the drag on a bluff body

What will be the drag on a solid hemisphere with a frontal area of 0.26 m2 and a flow speed of 100 m/s? Hint: The drag will depend on which side of the hemisphere points into the wind.

Show solution/hide solution.

The drag force on the hemisphere is given by

    \[ D = \frac{1}{2} \varrho V ^2 \, C_D \, A_{\rm ref} \]

where A_{\rm ref} = 0.26 m2 and V = 100 m/s, and if MSL ISA conditions are assumed then \varrho = 1.225 kg/m3. Looking up the value of a solid hemisphere’s drag coefficient in the table above, it can be seen that the C_D value depends on whether the smooth side or the flat side faces the relative wind. In the former case, C_D = 0.42, and in the latter case, C_D = 1.17. Inserting the values for the smooth side facing the flow gives

    \[ D = \frac{1}{2} \varrho V ^2 \, C_D \, A_{\rm ref} = 0.5 \times 1.225 \times 100.0^2 \times 0.42 \times 0.26 = 668.9 \mbox{ N} \]

And for the flat side facing, the flow gives

    \[ D = \frac{1}{2} \varrho V ^2 \, C_D \, A_{\rm ref} = 0.5 \times 1.225 \times 100.0^2 \times 1.17 \times 0.26 = 1,863.2 \mbox{ N} \]

Flow Patterns Around a Circular Cylinder

A classic example of a well-studied two-dimensional bluff body flow is that about a circular cylinder, for which the flow readily separates near its maximum thickness or just downstream, representative examples being shown below. A wake is produced downstream of the cylinder, which usually contains turbulence and various sizes of vortical eddies. As might be expected for a smooth body, the flow about the cylinder and the resulting wake structure and drag are sensitive to variations in Reynolds number, which in this case is defined based on the diameter of the cylinder, {d}.

Various flow states can be produced about a circular cylinder, which will depend primarily on the Reynolds number.

At very low Reynolds numbers near unity, called a “creeping flow” or Stokes flow, the behavior of the flow is influenced much more by viscosity effects than the effects of inertia. At slightly higher Reynolds numbers but for Re < 5, a stable pair of symmetric vortices are formed in the wake of the cylinder; the flow is mainly steady, but a high drag coefficient is produced.

As the Reynolds number is further increased, the drag coefficient decreases to a point. The wake vortices move further downstream of the body in the form of alternative vortex shedding, producing two rows of counter-spinning vortices called a Von Kármán vortex street. This is an unsteady flow, creating an unsteady drag on the cylinder. However, no time-averaged unsteady lift is produced because of the strong asymmetry in the flow with respect to the flow direction. Interestingly, this latter type of periodically alternating flow also creates a periodic pressure field that manifests as a sound or a noise called an Aeolian tone (after Aeolus, the Greek god of the wind). This effect is the source of the buzzing or “singing” sound sometimes heard when the wind blows over high-tension power wires.

As the Reynolds number increases, the periodic flow obtained about the cylinder at the lower Reynolds numbers becomes highly aperiodic, but still with the alternate shedding of vortices. Here, the flow in the wake is more turbulent. However, the boundary layer, which is of the turbulent kind, separates further down the surface, producing a narrower wake. Because the downstream wake is narrower, there is a smaller region of lower pressure on the downstream side, thereby giving lower drag.

As the Reynolds number increases, inertia effects begin to dominate over viscous effects. As a result, the flow becomes attached everywhere with a much smaller wake downstream of the cylinder, i.e., it starts to approach an inviscid flow. Because the flow is symmetric both upstream and downstream, the cylinder has no lift or drag force. This outcome is called d’Alembert’s Paradox, after the mathematician Jean le Rond d’Alembert, who first solved this problem by concluding that his theory for the flow did not agree with experiments made on cylinders in the wind tunnel. The reason was that d’Alembert did not consider the action of viscosity in his solution, i.e., he considered only an inviscid flow. However, as shown in the images above, this flow type does not occur naturally because a real fluid is always viscous to some degree, and the Reynolds number is finite.

Drag of Circular Cylinders & Spheres

The corresponding drag coefficient on a circular cylinder as a function of the Reynolds number is shown in the figure below. Notice that the results are for a “smooth” cylinder, and the effects of surface roughness change the quantitative relationships. The drag coefficient for a sphere is also shown for reference. The drag reduces quickly with increasing Reynolds number Re (notice the logarithmic scales) until Re reaches about 103, after which the drag stays nominally constant. This outcome arises because the point of flow separation (laminar boundary layer separation) is delayed to a greater downstream distance, eventually separating close to the points of maximum thickness.

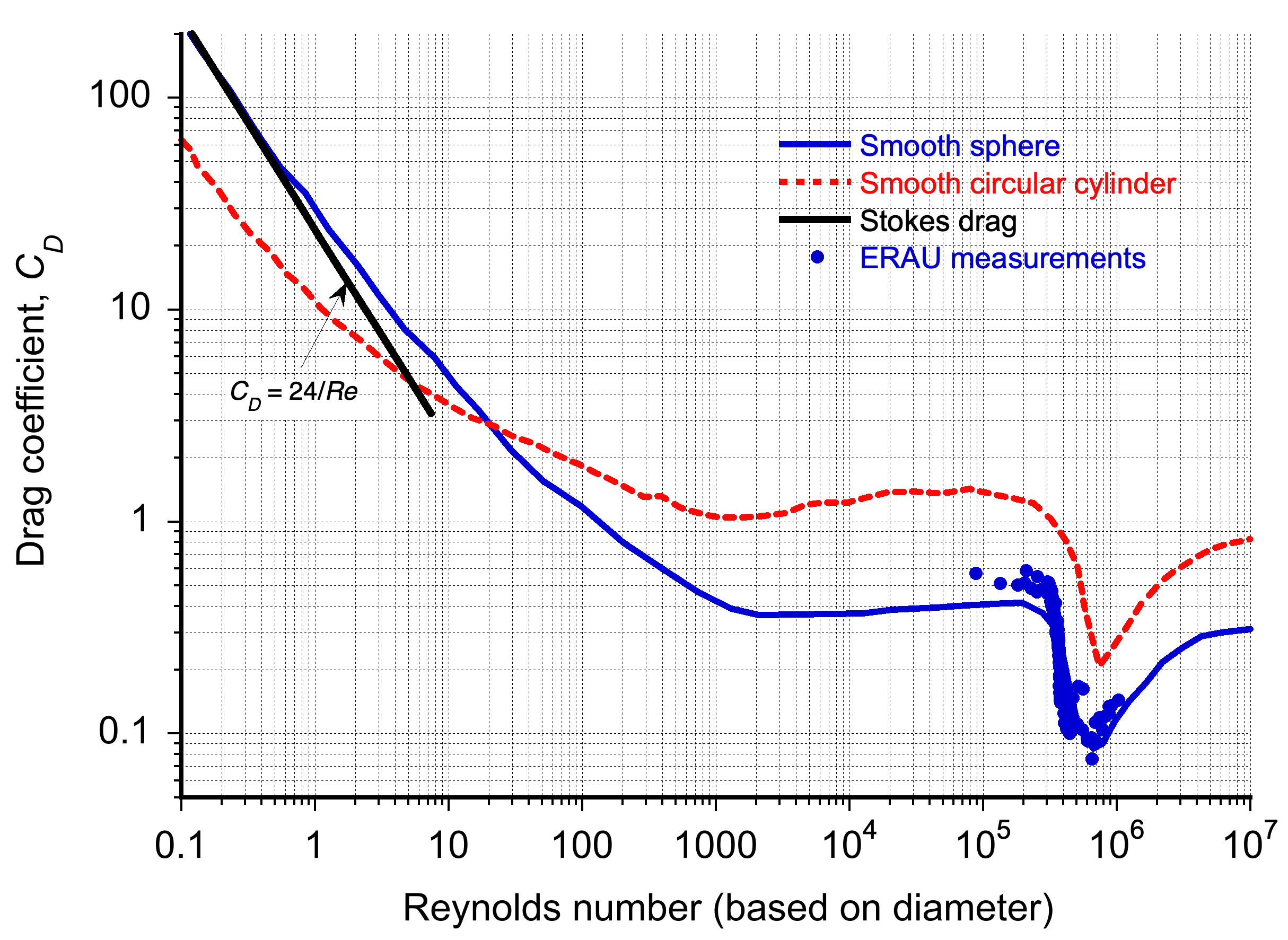
The drag coefficient of a circular cylinder as a function of Reynolds number based on its diameter. Notice the logarithmic scales.

With further increases in Re, it will be apparent that there is a critical value of Re where the drag suddenly decreases by almost an order of magnitude. This condition, called the critical Reynolds number, corresponds to the reattachment of the previously separated laminar boundary layer as a turbulent boundary layer, which finally separates at a further downstream distance on the rear part of the cylinder. The critical Reynolds number for a cylinder is about Re = 2 x 105. The narrower wake subsequently produced leads to a reduction in pressure drag and overall drag. However, notice that with yet further increases in Re, the drag increases again because of the increasingly higher surface shear stresses (i.e., skin friction) produced by the turbulent boundary layer as the flow speed and Reynolds number increase.

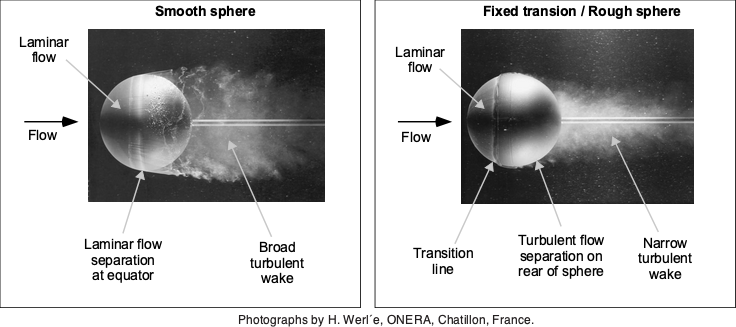
The aerodynamic behavior of a sphere is qualitatively similar to that of a circular cylinder, as shown below. Again, there is a sudden drop in drag as the Reynolds number reaches a critical value because of the change from laminar flow separation to turbulent separation. However, in this case, the surface roughness effects are of some interest, which can cause the drag reduction on the sphere to occur at a lower value of the critical Reynolds number.

The drag coefficient of smooth and rough spheres as a function of Reynolds number. The results for a circular disk are also shown as a reference.

This latter behavior is shown below using flow visualization, the roughness causing a significant reduction in the width and extent of the downstream wake. It explains the reduction in drag, i.e., the roughness manifests as an increase in the effective value of the Reynolds number. The surface roughness causes the laminar boundary layer on the upstream side of the sphere to transition immediately into a turbulent boundary layer, which can remain attached to the sphere’s surface much longer than a laminar boundary layer. The consequence of this behavior is the creation of a narrower low-pressure wake, so there is a lower drag on the sphere.

Flow visualization about a sphere with a smooth surface (left) at a Reynolds number of about Re = 3 \times 10^5, and the same sphere at the same Reynolds number with surface roughness (right).

Check Your Understanding #2 – Drag coefficient of a circular cylinder

Consider the airflow past a circular cylinder with a diameter, {d}, of 0.4 meters. The free-stream velocity, V_{\infty}, is 50 m/s. The properties of air at standard conditions are as follows: \varrho_{\infty} = 1.225 kg/m{^3} and \mu_{\infty} = 1.7894 x 10^{-5} kg m^{-1} s^{-1}.

  1. Determine the Reynolds number for this flow.
  2. Classify the flow regime around the cylinder (laminar or turbulent).
  3. Determine the drag coefficient, C_d, for the cylinder.
Show solution/hide solution.
  1. The Reynolds number is given by

        \[ Re = \frac{\varrho_{\infty} \, V_{\infty} \, d}{\mu_{\infty}} \]

    Inserting the values gives

        \[ Re = \frac{1.225 \times 50.0 \times 0.4}{1.7894 \times 10^{-5} } = 1.369 \times 10^6 \]

  2. The flow regime can be determined based on the Reynolds number. The critical Reynolds number for the transition from laminar to turbulent flow typically occurs at Re about 2 x 10^5 for flow around a circular cylinder. In this case, the Reynolds number is well above this threshold, and the flow regime around the cylinder is turbulent.
  3. The drag coefficient, C_d, for a circular cylinder in turbulent flow can be estimated from the chart, which is approximately 0.12.

Why Do Golf Balls Have Dimples?

Ever wonder why a golf ball has dimples? Did you know that in the earliest days of golf, in the windy, cold links of Scotland, kilted golfers[1] made a remarkable discovery? They found that old, worn, and rough balls traveled further than new ones. This discovery was not just a mere observation but significantly impacted the game. Golfers[2]using these rough balls gained a golfer a considerable competitive edge, requiring much fewer strokes from the tee to the hole.

Scottish golfers discovered after a while that old, beaten-up balls traveled much further than new, smooth balls.

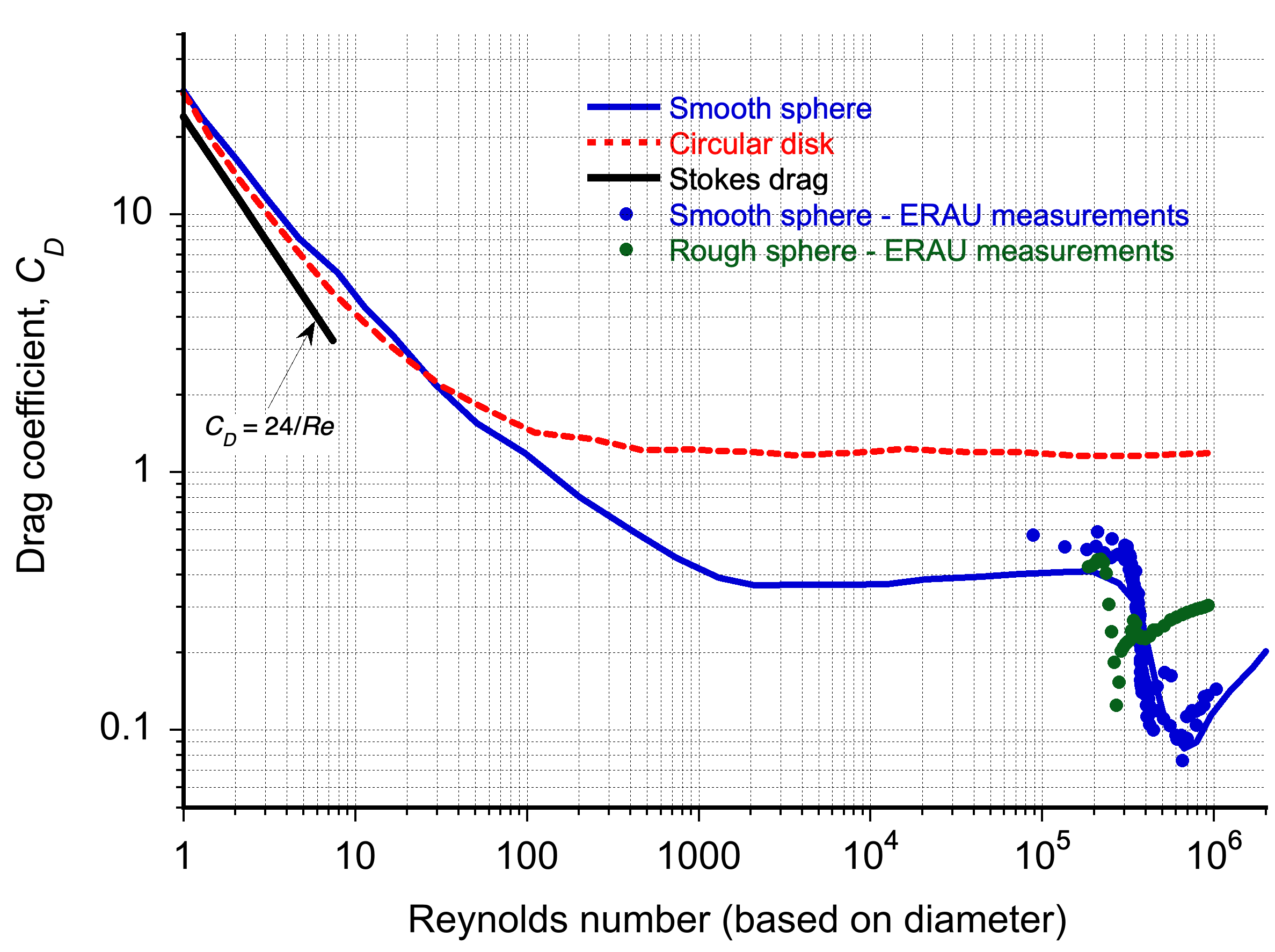
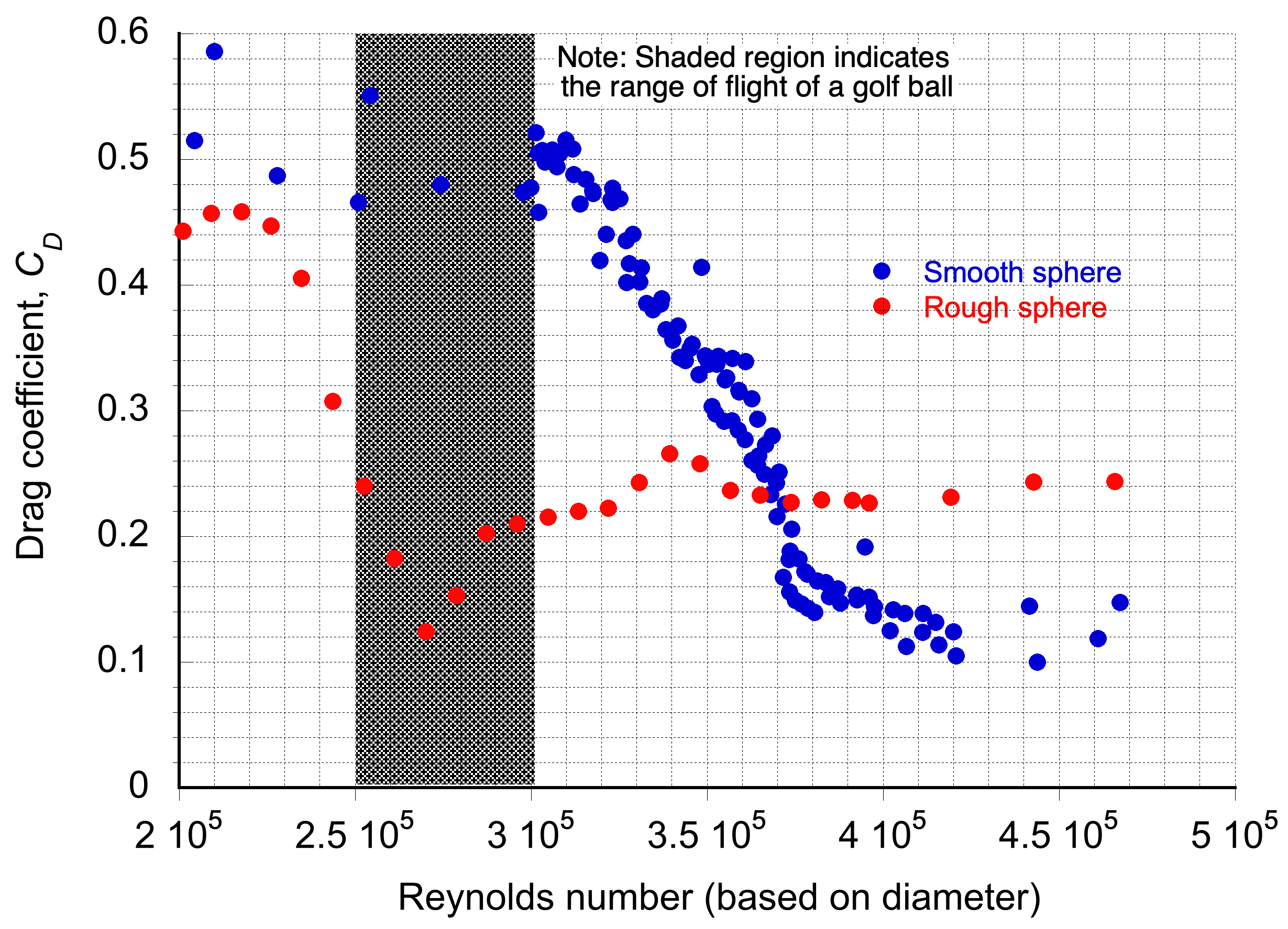
Unsurprisingly, the unique behavior of these rough spheres caught the attention of scientists, who began studying their aerodynamics in wind tunnels. These experiments revealed that rough spheres could have less aerodynamic drag than their smooth counterparts, as shown in the figure below. This discovery also led to the realization that standardizing golf balls was necessary to ensure a fair playing field for all golfers.

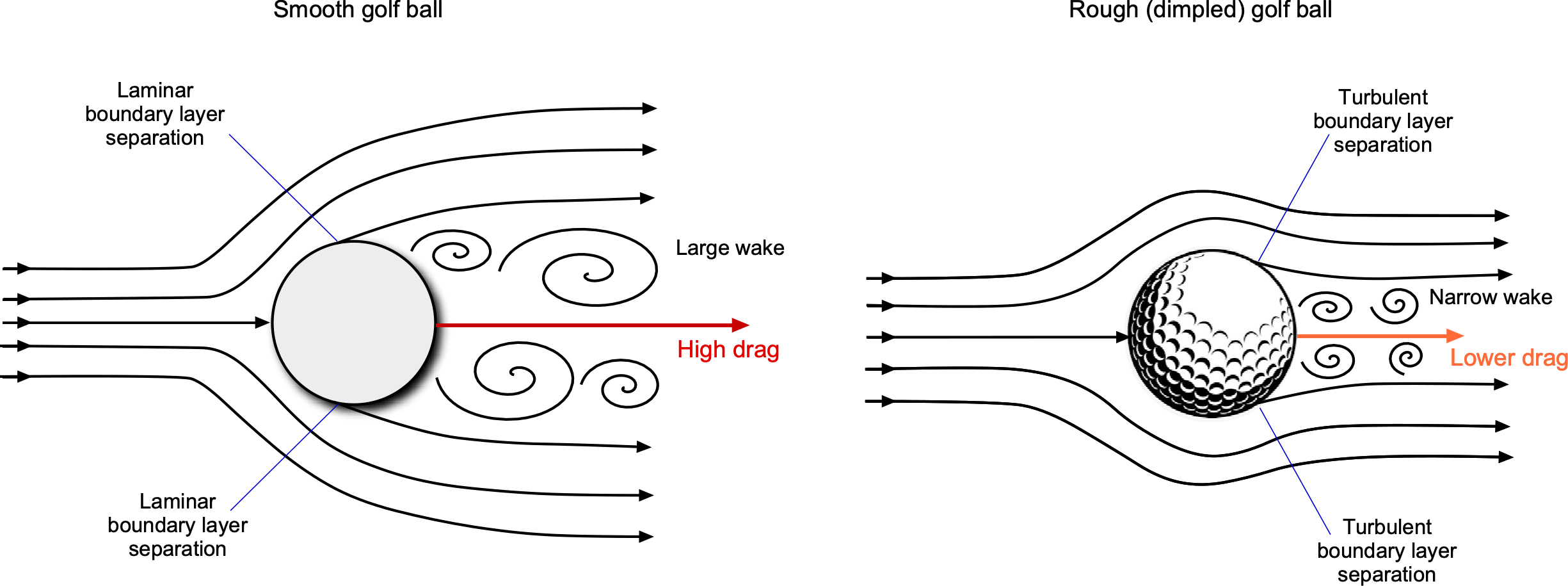
The reduction in drag of the dimpled ball at the Reynolds number of its flight causes it to travel about twice as far as a smooth ball of the same diameter.

A modern golf ball is a machine-dimpled sphere, and the dimples act as surface roughness to deliberately change its aerodynamics. The dimples, a standardized form of roughness, cause the boundary layer on the upstream side of the ball to transition from laminar to turbulent, delaying flow separation and thereby reducing its drag. At the Reynolds numbers corresponding to the ball’s flight, which is about Re = 3 \times 10^5, the flow on a smooth ball would usually be laminar, and the flow would easily separate near the equator and cause higher pressure drag, as shown in the figure below.

However, a turbulent boundary layer, created using surface roughness, will remain attached to the ball’s surface much longer than a laminar boundary layer before it separates. This behavior creates a narrower low-pressure wake and less pressure drag. Interestingly, creating turbulence reduces drag, i.e., the dimples are a form of flow control. However, do not expect dimples to work on streamlined bodies like wings. The objective here is to keep the flow as smooth (laminar) for as long as possible, thereby reducing skin friction drag, which is the dominant drag source at low angles of attack. The addition of dimples can only serve to increase drag on a streamlined body. The upshot of less drag is that a golfer can hit the ball further.

This distance can be calculated using the laws of physics (ballistics) and aerodynamics. One approximation for the range of the ball is given by

(8)   \begin{equation*} { R \approx \frac{{V_0^2 \, \sin(2\theta)}}{g} \left(1 - \frac{{\varrho \, A \, V_0 \, C_D \, \sin\theta}}{{2 \, m \, g}}\right) } \end{equation*}

where V_0 is the initial velocity of the ball, \theta is the initial hit trajectory angle of the ball (\theta = 45^{\circ} for maximum range), A is the projected frontal area of the ball, m is the mass of the ball, \varrho is the air density, and C_D is the Reynolds number dependent drag coefficient based on ball diameter.

Notice that the range, R, is linearly dependent on the drag coefficient. Halving the drag will double the range, all other factors being equal. Does anyone want to try out the theory?

Check Your Understanding #3 – Reynolds number of a golf ball

What is a golf ball’s flight Reynolds number? What is the ball’s drag coefficient under the conditions of flight? Why is this important regarding the flight distance of a golf ball?

To answer this question, the issues to address are:

  1. What is the diameter of a golf ball?
  2. How fast does a golf ball travel?
Show solution/hide solution.

A little research will show that, according to golf rules, a golf ball’s diameter must be at least 1.68 inches or 42.67 mm. Also, an amateur golfer typically hits a ball at an average speed of 135 mph or 217.4 kph with a driver club. However, those speeds can vary significantly with a golfer’s skill level and may range from a low of 110 mph (177 kph) to as high as 160 mph (257.5 kph) for a professional golfer. Therefore, the Reynolds number of a golf ball can only be established within certain bounds.

The Reynolds number of the golf ball based on its diameter is

    \[ Re = \frac{\varrho \, V d}{\mu} \]

where \varrho and \mu can be assumed to take MSL ISA values, i.e., in SI units, then \varrho = 1.225 kg/m3 and \mu = 1.48 x 10-5 kg m-1 s-1. Inserting the values using 257.5 kph or 71.53 m/s gives

    \[ Re = \frac{\varrho \, V d}{\mu} = \frac{1.225 \times 71.53 \times 0.04267}{1.48 \times 10^{-5}} = 2.13 \times 10^5 \]

and for 217.4 kph or 60.39 m/s gives

    \[ Re = \frac{\varrho \, V d}{\mu} = \frac{1.225 \times 60.39 \times 0.04267}{1.48 \times 10^{-5}} = 2.53 \times 10^5 \]

Therefore, the Reynolds number for a golf ball’s flight is approximately 2.2 x 105 to as much as 3 x 105.

Examining the C_D versus Reynolds number for this range, as shown in the graph below, it can be seen that based on measurements then, the drag coefficient of a rough ball in this range will be less than half of a smooth ball, i.e., the dimples act to increase in the effective Reynolds number. Of course, this outcome is supported by experience and other empirical data from golfing.

Aerodynamics of Spinning Balls

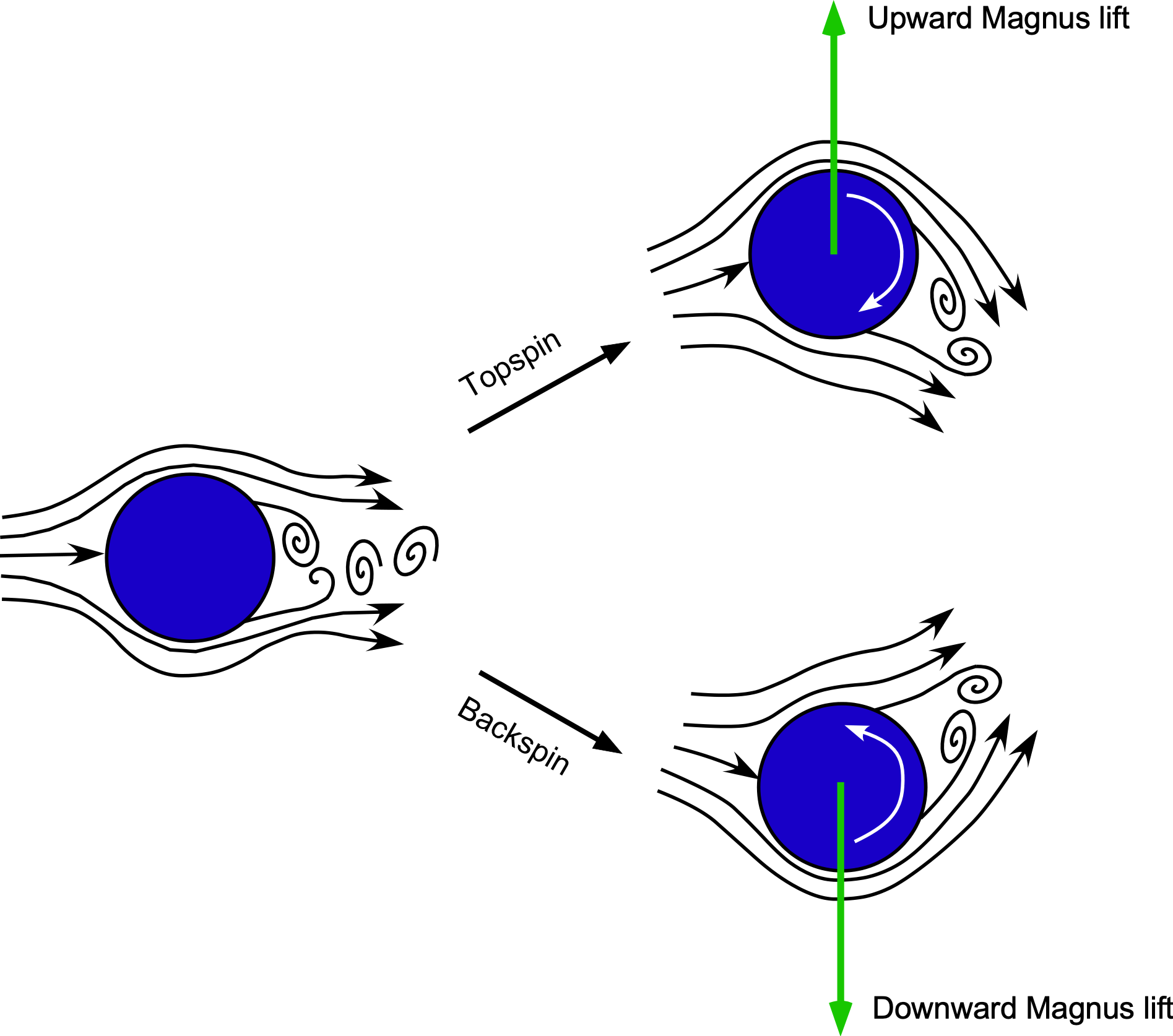
Another effect experienced by golf balls and other balls used in different games and sports is a lift force produced by their spinning motion, e.g., a backspin or topspin. The ball’s spin spoils the flow’s horizontal symmetry, creating differential pressure and producing a lift force. This behavior is called the Magnus effect and is named after Heinrich Magnus, the German scientist who first investigated it in the 19th century, as illustrated in the figure below. In some cases, Magnus observed a tendency of a cannonball to curve or veer significantly away from their expected flight path. He concluded that this behavior was because of their residual spinning motion as the cannonball left the barrel. Isaac Newton also noticed this same behavior while observing people playing tennis.

The spin of a ball (sphere), in this case, a topspin or a backspin, will cause a lift called a Magnus force.

The dependence of the Magnus lift coefficient, C_L, on the translational and rotational speeds of a smooth cylinder of diameter D has been investigated and measured in the wind tunnel, some results being reproduced in the figure below, where V is its translational speed and \Omega is the rotational angular velocity. The results are presented in terms of a non-dimensional spin rate, \Omega D / 2V. Notice the additional dependency on the Reynolds number, as given by Re = \varrho V D / \mu. A negative lift or a so-called “reverse” Magnus effect occurs at or about the critical Reynolds number. This behavior is tied to a “moving wall” effect that affects the boundary layer characteristics over the top and bottom halves of the cylinder, causing premature laminar separation on the upper half and delayed separation on the lower half. This latter behavior is also characteristic of spheres and balls.

Results showing the dependence of the Magnus lift coefficient, C_L, on the translational and rotational speeds of a smooth cylinder.

Therefore, the explanation for the curving behavior of a ball lies in aerodynamics. In the case of a topspin, there is a higher flow velocity (hence a lower pressure) over the ball’s upper surface, thereby producing a positive (upward) lift force. Therefore, a topspin will cause a ball to fly higher but not always further. A backspin will cause a ball to dive more quickly toward the ground. Backspin and topspin effects are used in many other ball games, such as golf, baseball, soccer, etc., which add to the player’s skill and the game’s unpredictability (and fun). The effects of Reynolds number and surface roughness mean that the curving characteristics depend on the size and surface finish of the ball, e.g., a smooth ping pong ball versus the seams found on a baseball or soccer ball.

Complex Three-Dimensional Bluff Bodies

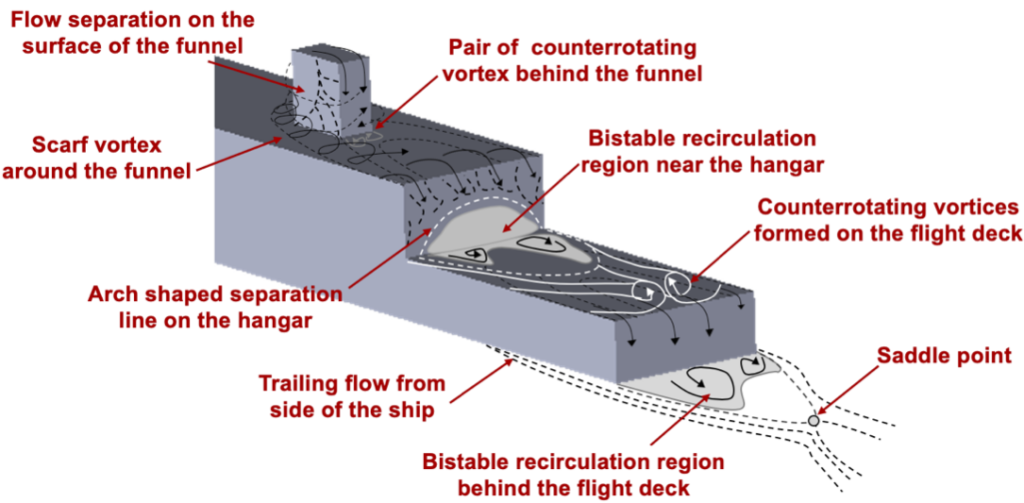
The flows produced about more general three-dimensional bluff body shapes are considerably more complex, and some of the other types of flow phenomena involved are shown in the figure below, which describes the behavior of the so-called “airwake” produced over the surface of a ship. Scarf or horseshoe vortices tend to form and wrap around the base (or foot) of bluff bodies that protrude from a surface (wall), in this case, the funnel. These vortices are, again, another source of drag. In addition, complex flow separation and reattachment regions on the body often make the a priori estimation of drag on such bodies very difficult.

The flow around a complex bluff body, especially those protruding from a surface, is highly complex and three-dimensional. In this case, the flow concerns the rear of a ship with a flight deck for helicopter operations.

Vortex-Induced Vibration

One of the concerns with three-dimensional bluff body flows is that the aerodynamics can produce such high forces to cause excitations of the structure it is made of. One of the most concerning effects in this regard is vortex-induced vibration (VIV), where the aerodynamic excitation produced by vortex shedding causes the structure to vibrate or even flutter. VIV problems can occur in many engineering applications, not just limited to the aerospace field, where flow-induced vortex shedding is possible, particularly with long, slender cantilevered structures such as wires, chimneys, and suspension bridges.

The Strouhal number is usually used to quantify VIV effects, which relates the frequency of shedding to the velocity of the flow and a characteristic dimension of the body (diameter {d} in the case of a cylinder). The Strouhal number St is defined as

(9)   \begin{equation*} St = \frac{f_{\rm st} \, d}{V_{\infty}} \end{equation*}

where f_{\rm st} is the vortex shedding frequency (or the frequency in radians per second), and V_{\infty} is the free-stream flow velocity. The Strouhal number of a cylinder is 0.2 and is constant over a wide range of Reynolds numbers.

The lock-in phenomenon occurs when the vortex-shedding frequency becomes close to a system or structure’s natural vibration frequency, resulting in a severe oscillation or even flutter. Although the onset of flutter will usually always reach a limit cycle in some form, the associated high cyclic stresses produced on a metallic structure can quickly cause fatigue failure.

Wakes Shed from Bridges

In civil engineering, vortex shedding from suspension bridges, which are bluff bodies in cross-section, is a significant cause of concern and can lead to bridge failures. When the Tacoma Narrows Bridge over Puget Sound in Washington state collapsed in 1940 because of a torsional flutter produced in a stiff wind, it was captured on film. The lessons learned have become a textbook example of vortex-induced vibration. However, this bridge is one of many that have suffered from the effects of VIV and flutter.

The figure below shows the essence of the problem. The bluff “H” shape of the bridge’s cross-section causes vortex shedding, leading to periodic unsteady aerodynamic forces. This behavior causes the bridge deck to twist in the wind, as shown in the figure below. Depending on the bridge’s characteristics, such as weight and dynamic frequencies, the deformations can be substantial and may quickly exceed 20 degrees.

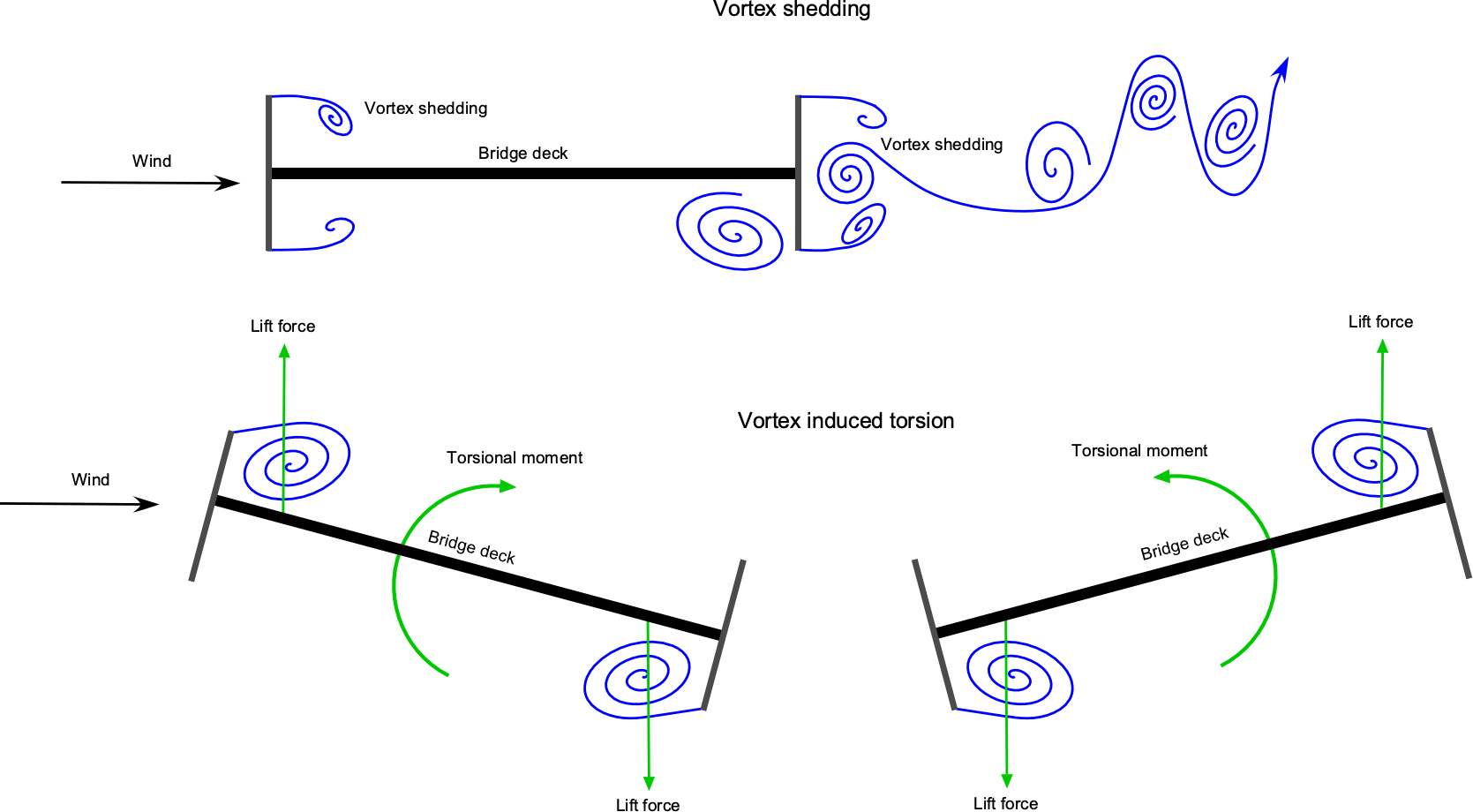
In cross-section, a bridge deck can cause vortex shedding and oscillatory aerodynamic forces.

The twisting of the bridge deck increases the flow separation, forming stronger vortices and higher aerodynamic loads that further twist the deck. While the deck structure resists this lifting and twisting because of its inherent torsional stiffness, this behavior can lead to a “lock-in” event and the development of “torsional flutter.” In some cases, it may be possible to modify the cross-sectional shape of the bridge to reduce the vortex shedding and increase the wind speed for torsional flutter.

Streamlining

Streamlining a bluff or an otherwise unstreamlined body shape is a very effective technique for reducing drag. For example, the basic idea is shown in the figure below. Adding a tail and/or nose fairing can significantly delay flow separation, reducing drag. A consideration, however, for an aircraft is that the fairing adds extra weight.

Streamlining a body can reduce drag, although it is not always a viable design option.

While streamlining may not be a viable engineering option in some cases because of practicality or cost, it is always a worthy effort on an airplane to reduce its overall drag and increase its performance, even at the expense of some increase in overall structural weight. For example, blending a wing carefully to the fuselage using a fairing can eliminate the horseshoe vortex and reduce interference drag from the resulting streamlining achieved, as shown in the photograph below for a general aviation airplane, for an almost negligible increase in airframe weight. For a commercial aircraft, the wing root fairing is designed to reduce interference drag and becomes part of the transonic drag reduction process using Whitcomb’s area rule. The area rule states that the cross-sectional area should change smoothly and continuously rather than abruptly to minimize drag on an aircraft.

A wing root fairing can help reduce the interference drag between the wing and the fuselage, decreasing the total aircraft drag by about 10%.

An airplane with a fixed landing gear can benefit from adding fairings and spats around the landing gear and wheels. Of course, retracting the wheels entirely is the only way of almost eliminating the drag. However, the extra weight and higher cost of a mechanical system to retract the landing gear are not usually viable for a smaller aircraft, e.g., one in the general aviation class.

Other aircraft that can benefit from streamlining include helicopters, which have relatively unstreamlined airframes (for utility). Using fairings in strategic locations on a helicopter’s airframe can reduce drag by 10% to 30%, allowing it to fly faster and/or have better flight range or endurance.

Streamlining of Terrestrial Vehicles

The aerodynamic drag of terrestrial vehicles, such as automobiles, trucks, and trains, increases significantly at higher driving speeds. For a given drag coefficient, C_D, the drag, D, on the vehicle will increase with the square of its speed V, i.e.,

(10)   \begin{equation*} D = \frac{1}{2} \varrho V ^2 \, C_D \, A_{\rm ref} \end{equation*}

So the power required to propel the vehicle P_{\rm req} will increase with the cube of its driving speed over the ground, i.e.,

(11)   \begin{equation*} P_{\rm req} = D V = \frac{1}{2} \varrho \, V ^3 \, C_D \, A_{\rm ref} \end{equation*}

Therefore, it is also apparent that the fuel or energy required will increase with the cube of the speed. Rolling resistance or friction also affects the net resistance on the vehicle and the fuel or energy needed for propulsion, but the aerodynamic effects dominate at higher speeds.

As with flight vehicles, terrestrial vehicles can reduce energy consumption by lowering drag, i.e., by streamlining to reduce the value of C_D as much as possible. Aerospace engineers have the training and expertise to understand the steps needed to make profitable drag reductions. Much of the testing of terrestrial vehicles is done in wind tunnels, although CFD solutions can also be helpful.

Automobiles & Cars

The automotive industry has become proficient in streamlining vehicles to reduce fuel consumption and internal noise, which usually requires extensive wind tunnel testing. Turbulence about the vehicle, such as from rear-view mirrors, can be a significant source of internal noise. The photograph below shows an example of flow visualization. The judicious use of smoke filaments and suitable lighting can provide insight into the flow patterns and where the flow is attached or separated, helping to decide where streamlining may be needed.

Example of smoke flow visualization about an automobile in a wind tunnel.

As shown in the figure below, the careful streamlining of automobile shapes can reduce drag. The result is significant increases in fuel economy and notable reductions in internal noise from corresponding reductions in turbulence. However, streamlining can only be done to a point where compromises in the vehicle’s utility may become problematic. Exposed wheels are a significant drag source, so there has been a trend toward more carefully streamlining the wheel well and the vehicle’s underside.

Streamlining an automobile by rounding off sharp corners can cut drag by half and commensurately improve fuel consumption.

Trucks (Lorries) & Buses

As shown in the figure below, trucks (lorries) and buses are aerodynamically inefficient because of their “boxy” shapes, resulting in high base pressure drag. For most trucks, their average fuel consumption is between 50% and 200% higher than that of automobiles. For example, an 18-wheeler truck, which is used to transport most goods to supermarkets and the like, might get anywhere from 5 to 8 miles per gallon (2.1 to 3.4 km per liter). Still, these values can vary significantly depending on engine size, driving speed, and the load (weight) being carried. The large CONEX rectangular box-like shapes often seen being towed by tractor-trailers are poor aerodynamic shapes with high drag. These boxes are usually called Intermodal Shipping Containers or ISO boxes (ISO 6346).

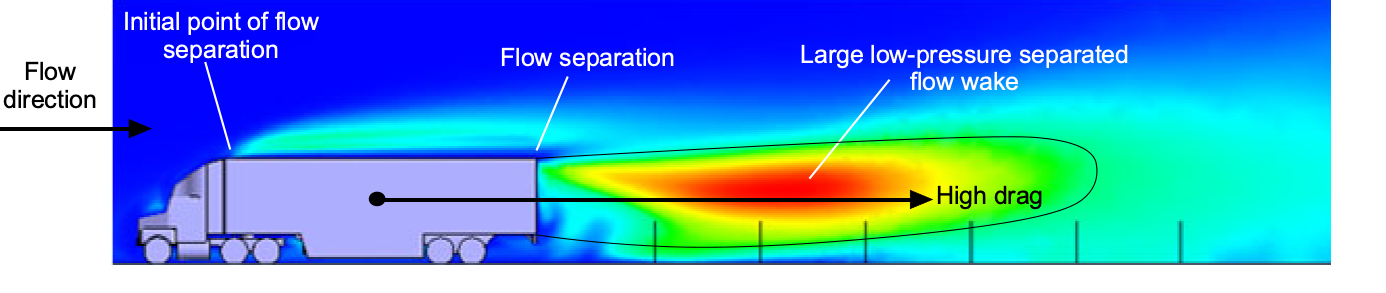
Tractor-trailers are bluff bodies and suffer from high drag and poor fuel economy.

Engineers have four significant areas of interest in obtaining meaningful aerodynamic drag reduction on trucks and lorries. These are:

  1. The frontal shape of the tractor part, which is very unstreamlined, in part for utility (engine access) and cooling requirements.
  2. The gap between the tractor’s end and the trailer’s leading edge (or the front of the CONEX container), which can cause flow separation and turbulence.
  3. The shapes of the sides and underbody of the trailer, which shed turbulence and create drag.
  4. The very back of the trailer, which is a significant source of pressure drag.

Continuous improvements to the aerodynamics of trucks have reduced their drag and saved more fuel. Minimizing the gap between the trailer and the tractor is essential, so fairings on the top of the tractor are often used, as shown in the figure below. In addition, rubber skirts can be placed underneath and along the trailer’s sides, redirecting the higher-speed airflow away from the trailer’s underside and reducing the drag from the wheels, which also act as bluff bodies.

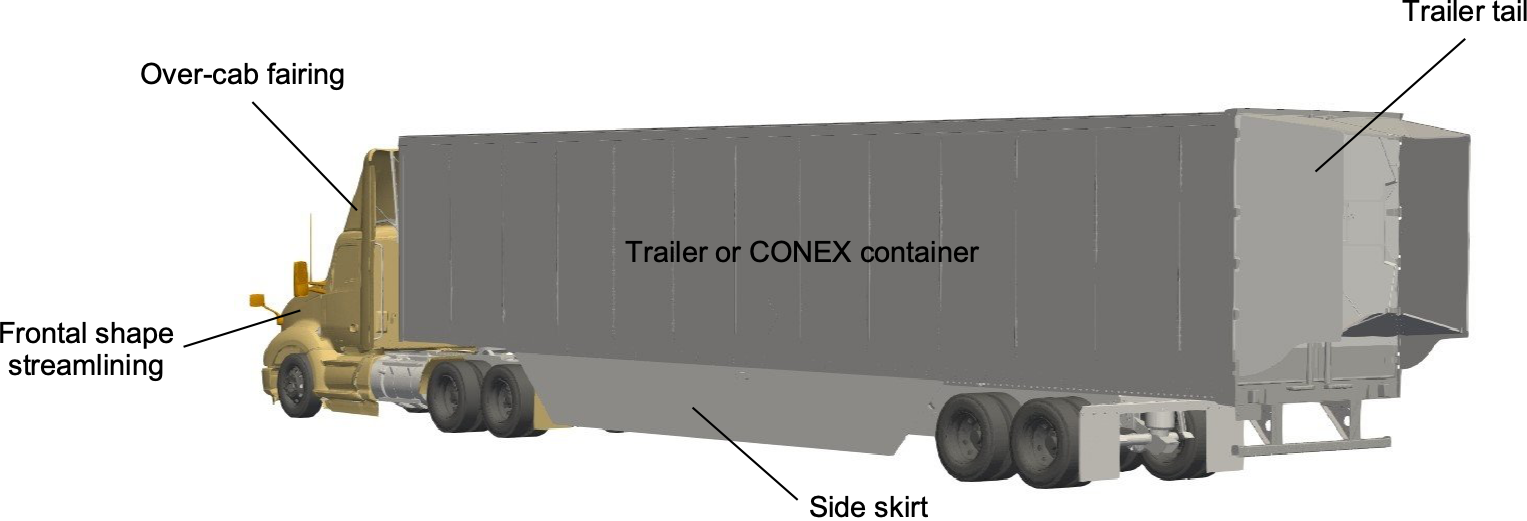
Reductions in drag can be obtained by minimizing the gap between the tractor and trailer, modifying the sides and underbody of the trailer, and adding a fairing at the back.

Trailer tails are increasingly used on trucks, which are pop-out afterbody fairings, as also shown in the figure above. Although relatively crude in shape, they help reduce the drag caused by flow separation and turbulence at the trailer’s rear end. The figure below shows that even a short trailer tail reduces the base pressure drag. The corresponding reduction in fuel consumption makes their use worthwhile when considering the overall fuel costs of the truck fleet. Indeed, a slight decrease in drag can significantly reduce fuel costs when the number of vehicles and the miles traveled are cumulatively considered.

Trailer tails (in this case, the effects of a 2-ft. long trailer tail versus a 4-ft. long tail) can significantly reduce a truck’s drag and, thus, improve its fuel efficiency.

Streamlining the aerodynamics of buses and coaches is also essential in improving fuel efficiency. Manufacturers have begun introducing increasingly more streamlined shapes with minimized frontal areas and curved or tapered roofs. Spoilers, underbody skirts, and wheel covers further improve airflow management, while carefully designing doors, mirrors, and other external components helps reduce turbulence. While employing wind tunnel testing and computational fluid dynamics simulations during the design phase of a bus or coach is a significant investment in time and cost, the improved aerodynamic performance can result in substantial fuel savings and so a lower environmental impact.

Trains

Traveling by train has always been an essential mode of transportation. High-speed railway networks continue to grow, particularly in Europe, China, and Japan. As with all vehicles, the aerodynamic drag of a train increases with the square of the speed, so power and energy requirements to propel the train increase significantly at higher speeds. Related issues for trains include the ability to supply the needed traction from the wheels to the rails and the significant pressure changes (which are felt by the passengers) when trains pass each other at high speeds or travel through tunnels.

Because the length-to-width ratio of a train is much larger than that of any other ground vehicle, the aerodynamic characteristics of trains tend to be more complex than those of cars, trucks, or airplanes. Nevertheless, significant reductions in drag can be achieved by streamlining, an example being shown in the photograph below. The basic principles needed are not unlike those for airplanes, including the need for a streamlined nose shape and rounded corners along the entire length of the train. Again, much of the work on the most effective steps for drag reduction on high-speed trains using types of streamlining is done in wind tunnels.

A high-speed train with a highly streamlined nose and rounded corners on the carriages can significantly reduce aerodynamic drag.

Creating Drag – Parachutes

A parachute slows an object’s motion through the air by creating drag. This situation exemplifies how creating high drag has a good outcome! Parachutes come in many shapes and sizes, but the classic design of a parachute canopy is a hemispherical shell, as shown in the figure below.

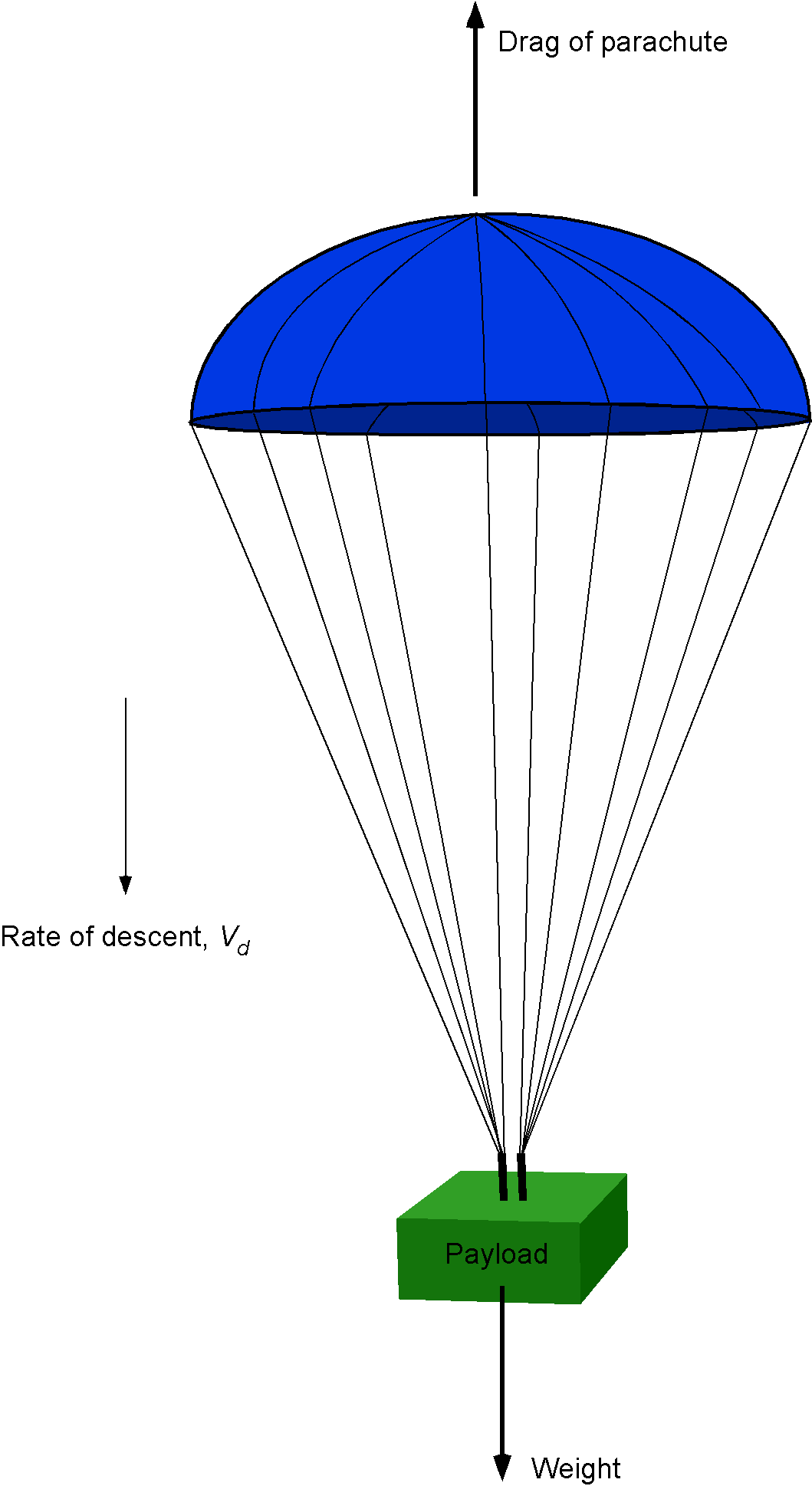
Parachutes are used for various purposes, the classic canopy being hemispherical.

The drag coefficient of a hemispherical shell based on the projected frontal area is about 1.42. Notice that for an open hemispherical shell of diameter {d}, its projected frontal area (i.e., the reference area on which the drag coefficient is based) is just the area of a circle of this diameter. The drag coefficient for most parachutes is close to 1.42, depending on their construction.

If the weight suspended from the parachute is W_p, and if the weight of the parachute itself is neglected, then steady force equilibrium gives

(12)   \begin{equation*} W_p - D = 0 \end{equation*}

where D is the drag of the parachute. The drag is given by

(13)   \begin{equation*} D = \frac{1}{2} \varrho \, A \, C_D \, V_d^2 \end{equation*}

where A is the projected frontal area of the parachute, \varrho is the density of the air, and C_D = 1.42 for an open hemispherical shell. The projected frontal area is A = \pi d^2/4, where {d} is the diameter. Solving for V (the rate of descent) gives

(14)   \begin{equation*} V_d = \sqrt{\frac{2 W_p}{\varrho \, A \, C_D}} \end{equation*}

Notice that the rate of descent increases for a higher weight and/or for a smaller area parachute.

For an average person, parachutes are designed to give a decent speed between 10 and 20 mph (16 and 32 kph). Of course, a more detailed analysis of this problem would consider the weight of the parachute and the backpack, although it would likely only increase the actual rate of descent by a small amount. Holes or vents can be introduced into the canopy to improve the parachute’s stability and give it some forward motion, which aids in the parachutist’s control of the descent; the vents also change the drag coefficient somewhat.

Check Your Understanding #4 – Rate of descent of a mass with a parachute

A general aviation aircraft is fitted with a ballistic parachute recovery system for improved safety in the case of a severe emergency. Consider a scenario where the aircraft’s pilot has to deploy this parachute system. The aircraft has a net mass of 1,200 kg, a projected (horizontal planform) cross-sectional area of 25 m2, and a corresponding drag coefficient of 1.8 based on this reference area. The parachute has an area of 150 m2 and a drag coefficient of 1.5 based on this area. Determine the vertical airspeed at which the aircraft will parachute to a landing. Assume an average air density of 1.01 kg m-3 during the descent. Ignore the parachute’s weight and assume that the aircraft descends in a flat horizontal wings-level attitude.

Show solution/hide solution.

The aircraft’s vertical drag coefficient is two orders of magnitude greater than expected during normal flight. In normal flight, the airplane is streamlined, with minimal pressure drag and boundary layer separation. However, during a vertical descent with a parachute, the airplane behaves as a bluff body with large amounts of flow separation and corresponding pressure drag.

Therefore, the net vertical drag will equal the airplane’s weight during a steady descent. The net drag will be the sum of that produced by the parachute plus that from the airplane itself, i.e.,

    \[ W = M \, g = \frac{1}{2} \varrho \, V_d^2 \, S_a \, C_{D_{a}} + \frac{1}{2} \varrho \, V_d^2 \, S_p \, C_{D_{p}} \]

where V_d is the rate of descent, S_a is the projected cross-sectional area of the airplane, C_{D{a}} is the drag coefficient of the airplane based on this reference, S_p is the projected cross-sectional area of the parachute, C_{D{p}} is the drag coefficient of the parachute based on this reference area. Simplifying gives

    \[ M \, g = \frac{1}{2} \varrho \, V_d^2 \left( S_a \, C_{D_{a}} + S_p \, C_{D_{p}} \right) \]

and rearranging to solve for V_d gives

    \[ V_d = \sqrt{ \frac{2 M \, g}{\varrho \left(S_a \, C_{D_{a}} + S_p \, C_{D_{p}} \right)}} \]

Substituting in the known numerical values gives

    \[ V_d = \sqrt{ \frac{2 \times 1,200.0 \times 9.81 }{1.01 \times \left(25.0 \times 1.8 + 150.0 \times 1.5 \right)} } = 9.29 \mbox{ m/s} \]

which seems reasonable, but it will still be a reasonably firm landing!

Bluff Bodies at Supersonic Speeds

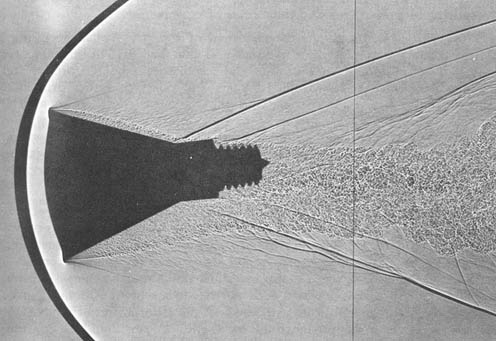
The behavior of bluff bodies at high speeds is also fascinating to aerospace engineers, especially for spacecraft re-entering Earth’s atmosphere. The drag of supersonic projectiles has been studied in wind tunnels. The results show that their drag is comprised of not only a high value of pressure drag from flow separation on the aft part of the body but also wave drag from the formation of shock waves, an example being shown in the figure below for a sphere (ball) flying at supersonic speeds. Notice the strong compression bow shock that stands off from the leading edge of the sphere, as well as the turbulence in the wake behind the sphere.

Schlieren flow visualization image of a sphere flying at a supersonic Mach number of 1.53.

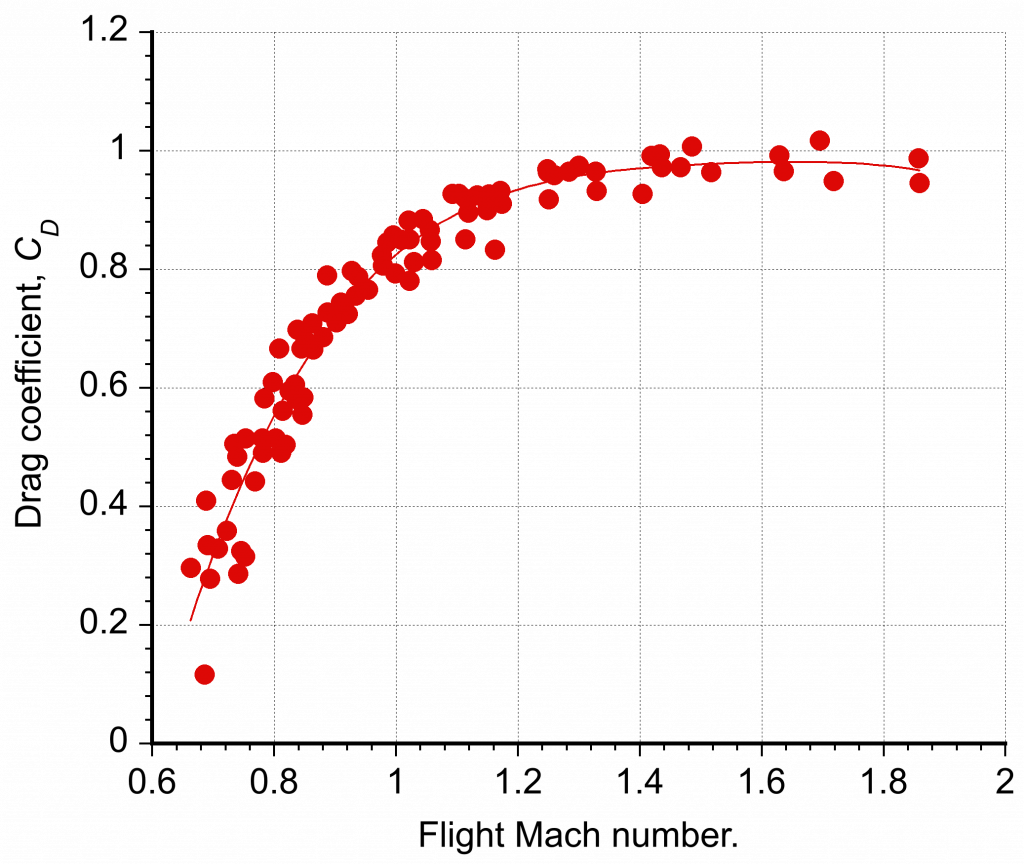
The effects of Reynolds number on the drag of a sphere have been previously discussed, but what about the effects of Mach number? The most accurate high Reynolds number data for spheres flying at Mach numbers between 0.6 and 2.0 date back to the 19th century when Francis Bashforth did drag measurements on supersonically spherical projectiles between 1870 and 1880, which are shown below. Interestingly, it can be seen that the drag coefficient plateaus in value for Mach numbers greater than 1.4.

Francis Bashforth measured the drag coefficient of supersonic traveling spheres, showing that the drag coefficient was independent of the Mach number.

H. Julian “Harvey” Allen, an aeronautical engineer at NASA, designed a spacecraft returning to re-enter the Earth’s atmosphere. His approach recognized that bluff or “blunt” bodies moving at very high supersonic and hypersonic Mach numbers generate strong shock waves that form in front of the body, known as a bow shock, as shown in the image below. Notice that the bow shock is away from the body’s surface, which is called a standoff distance. Because there are significant changes in the temperature of the flows across strong shock waves, shock waves that stand off from the surface allow much more heat to be dissipated into the air rather than into the body itself.

This bluff body at a high supersonic Mach number represents a space capsule during re-entry into the Earth’s atmosphere.

The heat transfer is related to the radius of curvature of the leading edge of the body, R_{\rm le}, by the relationship

(15)   \begin{equation*} \mbox{\small Heat transfer} \, \propto \, \dfrac{1}{\sqrt{R_{\rm le}}} \end{equation*}

Clearly, the larger (blunter) the shape, the lower the heat transfer. Also, notice in this image the significant flow separation and turbulence in the body’s wake. The bluff body shape also creates a lot of pressure drag, helping to slow down the spacecraft as it re-enters the atmosphere until it is slow enough for a parachute to be deployed, which is another example of where the creation of drag on a body can be beneficial.

Summary & Closure

While aerospace engineers are more often than not concerned with minimizing drag using, in part, the principles of streamlining, in other cases, the creation of drag can be beneficial too. The study of bluff body shapes, with its almost infinite number of possibilities, is not just theoretical but has practical applications. Many standard shapes have been studied in the wind tunnel, and their drag characteristics are known and published as functions of Reynolds number and, in some cases, with Mach number, too, e.g., projectiles and re-entry vehicles, which are very important in aerospace engineering.

The flow features and drag characteristics of angular bluff body shapes are primarily independent of variations in Reynolds number, whereas smooth bluff bodies show more sensitivity to Reynolds number. Most smooth bluff bodies (e.g., circular cylinders and spheres) have a critical Reynolds number, below and above which there is a significant change in the flow state and resulting drag behavior. Drag reduction of terrestrial vehicles continues to be a substantial issue in reducing fuel consumption, with conventional streamlining practices being very effective, but are now reaching the point of diminishing returns. However, the future may see more innovative concepts, possibly in the form of active flow control devices, to help further reduce drag.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • Make a list of the parts of an airplane that are potentially bluff-body-producing drag elements. Besides removing them, what steps could be taken to reduce the drag of these elements?
  • A rectangular sensor package is desired to be mounted on the external fuselage of a high-speed aircraft. What are the potential engineering concerns?
  • If dimples can reduce drag on golf balls, then why are dimples not used on the surfaces of airplanes or automobiles?
  • For the nose cone of a rocket, is it best to use a sharply pointed nose or a blunt, rounded nose, and why?

Other Useful Online Resources

For more information on bluff bodies, check out some of these online resources:

  1. They were probably not wearing kilts but trews (trousers), although it still makes a good story. ↵
  2. In Scots, the term is gowfers ↵

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n25

Share This Book