Introduction

Ground Effect Vehicles (GEVs) are designed to operate in proximity to an impervious surface, such as the ground or water, where the interaction between the airflow and the surface produces a rise in static pressure and a reduction in drag. This phenomenon, known as ground effect, enables the vehicle to generate lift more efficiently and support its weight when flying at low altitudes. GEVs are specifically configured to exploit this ground-effect regime and are often referred to as surface skimmers. They can travel efficiently over flat surfaces without fully flying or floating in water, placing them outside conventional classifications of aircraft and marine vessels. As such, they occupy a hybrid category that requires distinct design, operational, and regulatory approaches.

A hovercraft, also known as an air-cushion vehicle (ACV), is one type of ground-effect vehicle (GEV) that creates lift and “flies” using ground effect. The hovercraft rides on a combination of a so-called “cushion” of higher-pressure air below the vehicle inside the inner plenum as well as a jet thrust contribution from a radial “momentum curtain” of downward flow that flows between the inner and outer plenums, as shown in the schematic below. This higher-pressure air and momentum jet originates from an engine driving a fan, for which the excess pressure generated may also be used to direct bleed air through horizontal jets for forward propulsion and control.

The name “hovercraft” is a trademark of Saunders-Roe, an aircraft and maritime engineering company. However, a hovercraft has since become synonymous with all air-cushioned vehicles capable of hovering above the ground. An example of a modern hovercraft is shown in the photograph below, which, in this case, is being propelled over water by two ducted fans with steerable rudder vanes, also known as ruddervators. The name “hovercraft” is also known as “Aeroglisseur” (in France), “Luftkissenboot” (in Germany), and “Ground Effect Machine” (in the U.S.).

Hovercraft are operated by a pilot, much like an aircraft rather than a marine vessel. However, the classification of the vehicle as an aircraft per se is debatable. Nevertheless, a hovercraft can fly free of the ground using aerodynamic lift, so it is technically, on the one hand, an aircraft. On the other hand, it can operate on water as a marine vehicle; therefore, specific additional naval architectural design and seaborne requirements apply, including the need for flotation. Hence, a hybrid vehicle classification for a hovercraft is also appropriate. Hovercraft can travel easily over rough surfaces, including long grass, brush, water, land, mud, and snow, making them unusual yet highly versatile vehicles for many civilian and military applications.

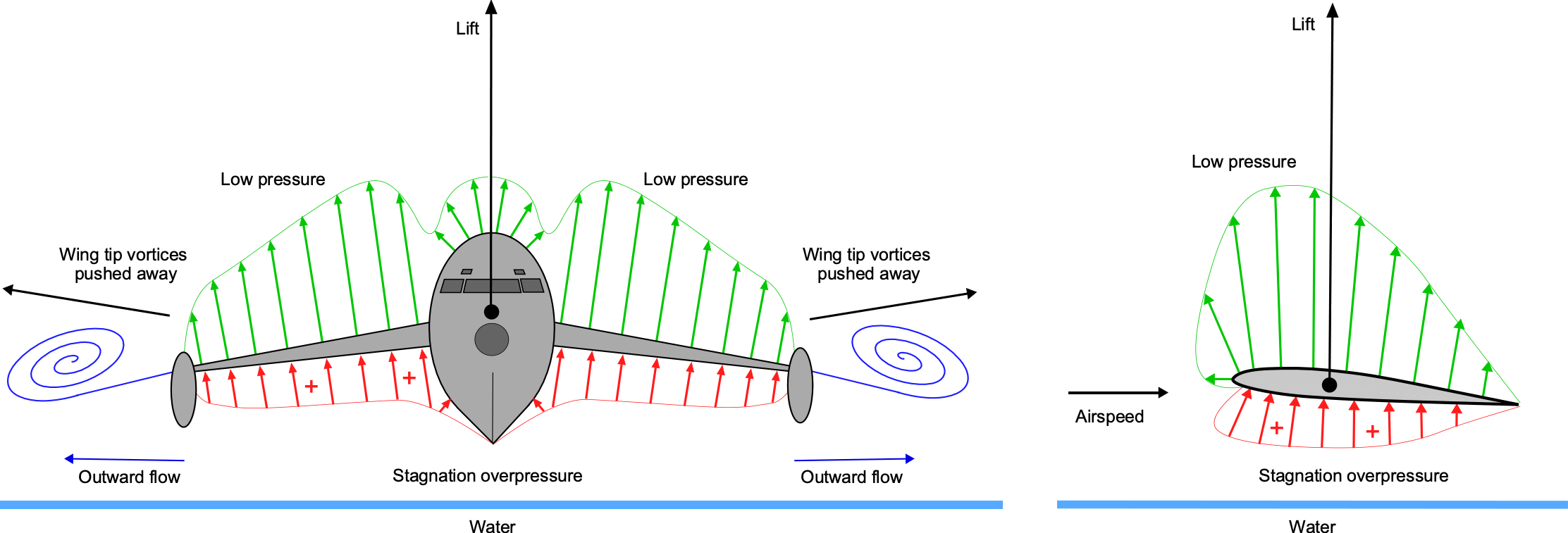
Another type of GEV employs the wing-in-ground-effect (WIGE) concept, which operates by riding on a region of higher-pressure air beneath the vehicle and the ground, generating lift for reasons similar to those of a hovercraft. However, a wing-in-ground-effect (WIGE) vehicle cannot hover and requires forward airspeed to generate lift on its wings; this lift force is significantly increased by the wing’s proximity to the surface, as shown in the schematic below. In addition to the increased stagnation pressure beneath the wings, sometimes referred to as a “ram-air” effect, ground effect pushes the wing-tip vortices laterally farther from the wings, thereby increasing their effective aspect ratio and reducing their drag. The upshot of these beneficial aerodynamic effects is that a WIGE vehicle can skim efficiently over the water at airplane speeds, e.g., more than 100 knots, but only if it maintains relatively low altitudes of less than a wingspan.

The concept of WIGE vehicles is not new, and they continue to be explored for military applications, cargo transportation, and even recreational use. Other names for such vehicles include “surface effect ship” and “surface skimmer.” These rather unusual-looking vehicles perform running takeoffs and landings from the water like a seaplane, but they do not have any contact with the water while in “flight.” Some WIGE concepts may also be able to travel over relatively flat ground, similar to a hovercraft, but they are primarily designed for water operations, such as a seaplane; they cannot take off from any other surface.

A WIGE design utilizing the “reverse-delta wing” concept, which can also fly out of ground effect, is illustrated in the photograph below. This vehicle skims over water at speeds that are four or five times those of most watercraft. It is unsurprising, therefore, that WIGE vehicles must be operated at least partially by maritime regulations. Consequently, the International Maritime Organization (IMO) has issued guidelines for wing-in-ground vehicles (referred to as a “WIG craft”) in the context of other marine vehicles, including safety and navigational requirements. Nevertheless, a WIGE vehicle is still technically classified as an airplane. It is generally piloted like a hovercraft, which is considered more of an aircraft than a marine vehicle.

History

As with most flight vehicles, the concepts of developing “ground effect” and “air-cushioned” vehicles date back over a century. John Thornycroft patented an early concept for an air-cushioned boat in 1877, proposing that the air cushion would reduce the hull’s surface area in contact with the water, thereby reducing drag and increasing speed. He built a catamaran model and used a bellows mechanism driven by a wound-up spring to trap pressurized air between the two hulls. The resulting overpressure partially lifted the boat out of the water, allowing it to glide just above the surface and markedly increase its speed. Thornycroft required a powerful engine to make it practical on a larger scale. Still, it was not until the 1920s, with advancements in internal combustion engines, that proper hovercraft and other GEVs became more viable. In many ways, the availability of engines with high power-to-weight ratios for use in GEVs paralleled the tipping point in the successful development of helicopters.

Hovercraft

In 1915, Dagobert Müller von Thomamühl modified a speedboat by pumping air into the space below its hull. His idea was similar to Thornycroft’s: to reduce hull drag as the boat traveled over the water. Thomamühl’s modified speedboat reportedly achieved a speed of over 32 knots (59.3 kph), more than twice the speed of the original boat. However, although it could partially lift itself out of the water, it could not hover. The availability of suitable engines powerful enough to drive a rotor or fan soon led to designs that created higher-pressure air to form a “cushion” below the vehicle. In 1932, Toivo Kaario is believed to have been the first to develop an air-cushion vehicle (ACV), or hovercraft-type ground-effect vehicle, that utilizes this ground-cushion effect. His prototype, dubbed pintaliitäjä (surface hoverer or hovercraft), shown in the photograph below, used a fan driven by a Harley-Davidson motorcycle engine. It was tested until approximately 1935 with modest success, and although Kaario obtained Finnish patents for the design, further development was halted because of insufficient funding.

In the mid-1930s, Vladimir Levkov developed a series of ACVs capable of hovering above ground or water. The L-1 prototype featured a simple design: a wooden catamaran with two hulls separated by a pressure-filled cavity, following Thornycroft’s ideas and prior work. Further development continued with a series of other prototype machines, each with increasing refinements and performance. One of Levkov’s ACVs, known as the fast-attack L-5 boat or “hover tank,” as depicted in the photograph below, achieved a speed of 70 knots (130 kph); a surviving film of its flights is also available. Levkov led the development of several other ACVs, including the much more capable L-11, but these vehicles were destroyed during WWII. At about the same time, Charles Fletcher in the U.S. designed a hovercraft called a “Glidemobile.” This design also trapped pressurized air within a plenum, thereby lifting it above the surface. However, the U.S. government classified the concept shortly after testing, and the prototype was never developed further.

Significant developments in hovercraft technology occurred after WWII. Christopher Cockerell is widely recognized as the pioneer who developed the modern hovercraft. In 1950, he disclosed his ideas for a hovercraft in British Patent GB854211A, in which a radial air jet generated a reaction “momentum curtain” force and an excess pressure beneath the vehicle, allowing it to hover and travel above ground or water. Cockerell’s design, which added a flexible rubber skirt to trap the air cushion, significantly improved on certain limitations of earlier hovercraft designs. He built a small demonstrator of his hovercraft concept to market it. However, shipbuilding companies claimed his invention was an airplane, and aircraft companies claimed it was a ship, so neither was interested. Nevertheless, a demonstration of the concept before British Government officials led to a grant for further development, but they also declared it top-secret technology.

The first technically successful hovercraft was the SR-N1 (Saunders-Roe Nautical Model 1), a demonstrator built under Cockerell’s design leadership, with its first flights in June 1959. The initial version had a circular structure resembling a “flying saucer,” a term coined by the press. Later versions featured a bow more akin to a boat, designed to facilitate movement over water, as shown in the photograph below. It was primarily made of riveted aluminum stressed skin, similar to an aircraft, with a separate buoyancy tank for flotation. It utilized a 450-hp (336 kW) radial aircraft engine that drove a large fan in a duct positioned below an intake nozzle, generating the air cushion beneath the machine and allowing it to hover in ground effect. Directing some bleed air through ducts to nozzles, rudders, or vanes gave translational speed and directional control. The pilots sat in a small cockpit just forward of the duct. The SR-N1 successfully demonstrated hovercraft technology, including a flight across the English Channel, and paved the way for the rapid development of larger and more capable concepts.

Melville Beardsley developed several hovercraft designs in the 1950s and 1960s and founded the National Research Associates (NRA). NRA developed and tested several ACVs, with the Aqua-GEM being sold in limited numbers. The company also sold several small personal hovercraft, including the “Little Skimmer.” The company was wound up in the late 1960s following patent disputes with the British hovercraft industry. William Bertelsen developed a hovercraft concept, the Aeromobile 35-B, in 1959, followed by a series of prototype designs, including the Aeromobile-200, as shown in the photograph below. There is also a film of one of his hovercraft traveling down the streets of Chicago. None of his concepts, however, was to go into production.

By the early 1970s, the basic hovercraft concept had undergone considerable technical development, and larger, more capable hovercraft began to find several helpful, if niche, roles in both civilian and military applications. The Saunders-Roe company continued to develop a series of hovercraft models with increasing capabilities, including the enormous SR-N4, as shown in the photograph below. The SR-N4 and its variants were used to carry up to 400 passengers and 30 vehicles across the English Channel, operating between Ramsgate and Dover in England and Calais and Boulogne in France. The SR-N4 weighed over 250 tons and was powered by four turboshaft engines, driving variable-pitch propellers that could also swivel by 30 degrees on azipods. It had a cruise speed over the water of 65 knots, making the cross-channel trip in only 30 minutes, about four times as fast as a regular sea ferry. However, such large hovercraft were operationally expensive and not very profitable. With the opening of the Channel Tunnel in 1994, the last two operational SR-N4 hovercraft became obsolete and were retired in October 2000, marking the end of their impressive 30-year continuous service.

Today, various branches of the armed services, particularly the Marine Corps, employ hovercraft or air-cushion vehicles (ACVs) for amphibious operations and search-and-rescue missions. These ACVs mainly transport personnel, weapons, vehicles, equipment, and cargo over diverse terrain. The photograph below shows the Landing Craft Air Cushion Vehicle (LCACV), a high-speed, hovercraft-style, fully amphibious landing craft. It can carry a payload of up to 70 U.S. tons (63.5 tonnes), such as trucks, support vehicles, and even an M-1 tank, and land on almost any shoreline worldwide. These fantastic vehicles have proved their worth to armed forces worldwide for several decades.

The flexibility and speed of hovercraft over water and other terrain also make them suitable for several important service roles, such as patrols and rescue work. Many manufacturers worldwide supply hovercraft for these purposes. Smaller hovercraft are used in Britain as part of the inshore fleet operated by the Royal National Lifeboat Institute. They have been used, with great success, on large areas of tidal mudflats or sand where the surface is too soft to support land vehicles and the water is too shallow for boats.

Smaller hovercraft are used for recreational purposes, including fishing and hunting, across various terrains. Like their larger counterparts, these hovercraft can easily traverse a wide range of terrain, crossing rivers, lakes, snow, and thin ice. They can reach places that are often inaccessible to other vehicles, making them the epitome of amphibious transportation. Some types of single-person sporting hovercraft are used for racing, as shown in the photograph below.

Wing-in-Ground-Effect Vehicles

The first practical application of the wing-in-ground effect (WIGE) phenomenon was demonstrated in 1929 by the enormous Dornier Do X flying boat, which achieved a considerable increase in its flight range by skimming close to the ocean’s surface. In wind tunnel tests, it was also found that the vertical proximity of a lifting wing to a ground surface affected both its lift and drag, with beneficial effects when less than a chord length above the surface. One reason is the reduction in induced drag from the lateral outward movement of the wing-tip vortices near the ground. Pilots also became aware of ground effect during the landing flare, which helped cushion the landings. However, if the airspeeds were too high, they would also “float” down the length of the runway.

Rostislav Alexeyev of the Russian Central Hydrofoil Design Bureau developed the first of a series of specifically designed Wing-in-Ground-Effect (WIGE) vehicles, also known as ekranoplans (meaning “screenplanes”). The SM-1, powered by a single jet engine with two lifting wings, took its first flight in July 1961. The improved SM-2, which flew in March 1962, had a single main wing and large vertical and horizontal stabilizers, shown in the photograph below. This vehicle incorporated a secondary turbojet engine in its nose to direct air toward the main wing, thereby increasing lift at lower speeds, a phenomenon known as power-augmented lift. During the Cold War, several other WIGE vehicles were explored for various military applications, including troop transport and anti-submarine warfare; however, none entered operational service. Nevertheless, development of such ground-effect vehicles continued throughout the 1960s.

The first flight of the massive KM (Korabl Maket) ekranoplan, as depicted in the photograph below, took place in August 1967. The vehicle had a cruise speed of 267 mph (430 km/h) and a maximum speed of 311 mph (500 km/h). The KM had a gross weight of 544,000 kg (1,199,313 lb), with a range of 1,500 km (932 miles). The aircraft first appeared in satellite imagery during its trials in the Caspian Sea, its unusual shape raising many questions about its identity and earning it the moniker “Kaspian Monster” or “Caspian Sea Monster.” It underwent trials, as well as various developments and improvements, throughout the 1980s.

The KM design served as the basis for the Lun-class ekranoplan, developed in the 1980s, which saw one example enter service with the Soviet Navy and later the Russian Navy. This massive missile-carrying S-31 (MD-160) Lun (“Harrier“), as shown in the photograph below, was powered by eight turbojet engines mounted on a foreplane. Although only one vehicle was built, it had a maximum takeoff weight of 380,000 kg (837,756 lb), a payload of up to 137,000 kg (302,000 lb), and a range of 2,000 km (1,243 miles) at a speed exceeding 200 knots. It could launch up to six cruise missiles and was a potentially formidable weapon, capable of evading both sonar and radar; however, it was never used in combat and was retired in the late 1980s.

Alexander Lippisch designed a WIGE vehicle in the late 1960s. Lippisch was an ambitious and forward-thinking aeronautical engineer who had initially worked for the Zeppelin company in Germany. Lippisch became interested in tailless and other unorthodox aircraft, and significantly advanced aircraft designs of the WWII era soon followed. His most famous design was the Messerschmitt Me 163 rocket-powered interceptor, which saw limited use during WWII but paved the way for future swept-wing aircraft designs. Lippisch patented a WIGE design featuring a “reverse-delta” wing shape with an unswept leading edge and a highly swept trailing edge, as illustrated in the figure below. Notably, the pronounced anhedral of the wing also helped capture the air-cushion effect.

Lippisch’s patent was sold to Rhein-Flugzeugbau (RFB), resulting in the X-113, as shown in the photograph below. Anhedral on the wing was found to maintain the benefits of ground effect to a higher cruise altitude over the water, allowing it to operate over rougher seas. It even demonstrated the ability to fly well above ground effect, reaching approximately 1,000 ft (330 m). The wingtips had winglets to increase the effective aspect ratio of the wings and reduce drag, and wing-tip floats to provide stability on the water. A T-tail fin and tail fin were located at the end of a long dorsal fin, the large tail surfaces giving sufficient stability and control. 

One of the adverse characteristics of WIGE aircraft is a relatively significant shift in its center of pressure as it moves in and out of ground effect, leading to pitch instability; therefore, a sizable horizontal tail and good elevator authority are required. The first flight of the X-113 took place in October 1970, and tests continued until 1974; however, the vehicle did not enter production. However, many WIGE vehicles are derivatives of the reverse delta wing concept, such as the Airfish, Eska, and XTW, which have demonstrated that high lift-to-drag ratios of 20:1 are achievable with this configuration.

There has been intermittent interest in WIGE vehicles over the last few decades. DARPA evaluated the Aerocon “Wingship” design as part of a technical study of the WIGE concept for military uses during the 1990s. However, the idea did not progress. In 2002, Boeing’s Phantom Works unveiled a WIGE called the Pelican. It would have been the biggest and heaviest aircraft ever built, but the project seems to have faded into obscurity. However, the WIGE concept has recently received renewed attention from various aerospace companies and government organizations, such as DARPA, which have proposed reconsidering such a surface-skimmer ground-effect vehicle for efficient, long-range, heavy-lift transport over oceans.

The DARPA Liberty Lifter program aims to develop a vehicle similar in size and payload capacity to the C-17 transport aircraft; an artist’s impression of one concept is shown in the figure below. It remains to be seen whether such a vehicle will be realized, although the benefits of it enhancing the long-range and “under the radar” military capabilities remain attractive.

Anatomy of GEVs

The anatomy of GEV vehicles, which encompass various hovercraft and wing-in-ground-effect concepts, is somewhat mysterious to most people, including engineers. Their principle of operation is relatively straightforward/ However, the aerodynamics underlying their performance and handling characteristics require a deeper understanding. Both vehicles operate under the well-known “ground cushion” effect, which results from redistributed air pressure beneath and above the vehicle, thereby increasing lift and helping overcome its weight. It should be noted that even slight pressure differences can generate significant lift forces when acting over large surface areas.

Hovercraft Anatomy

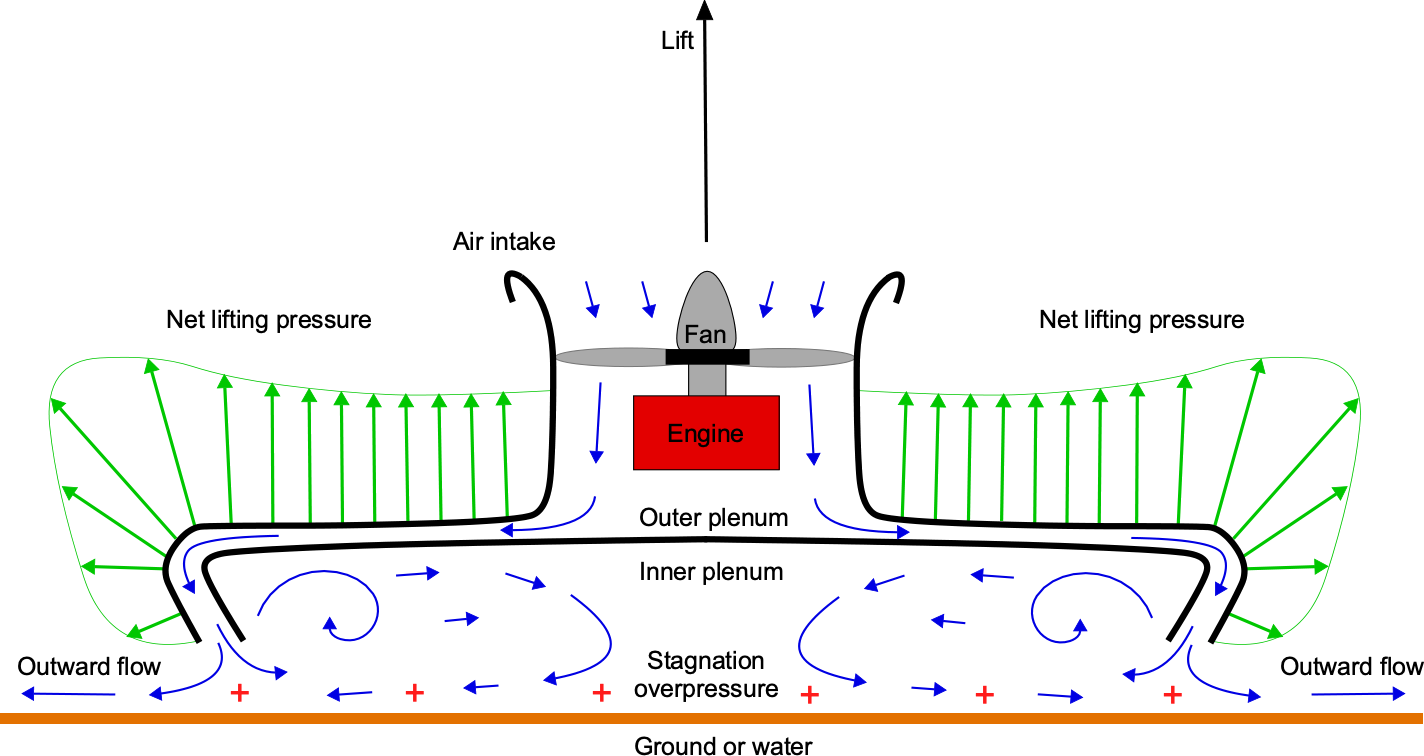
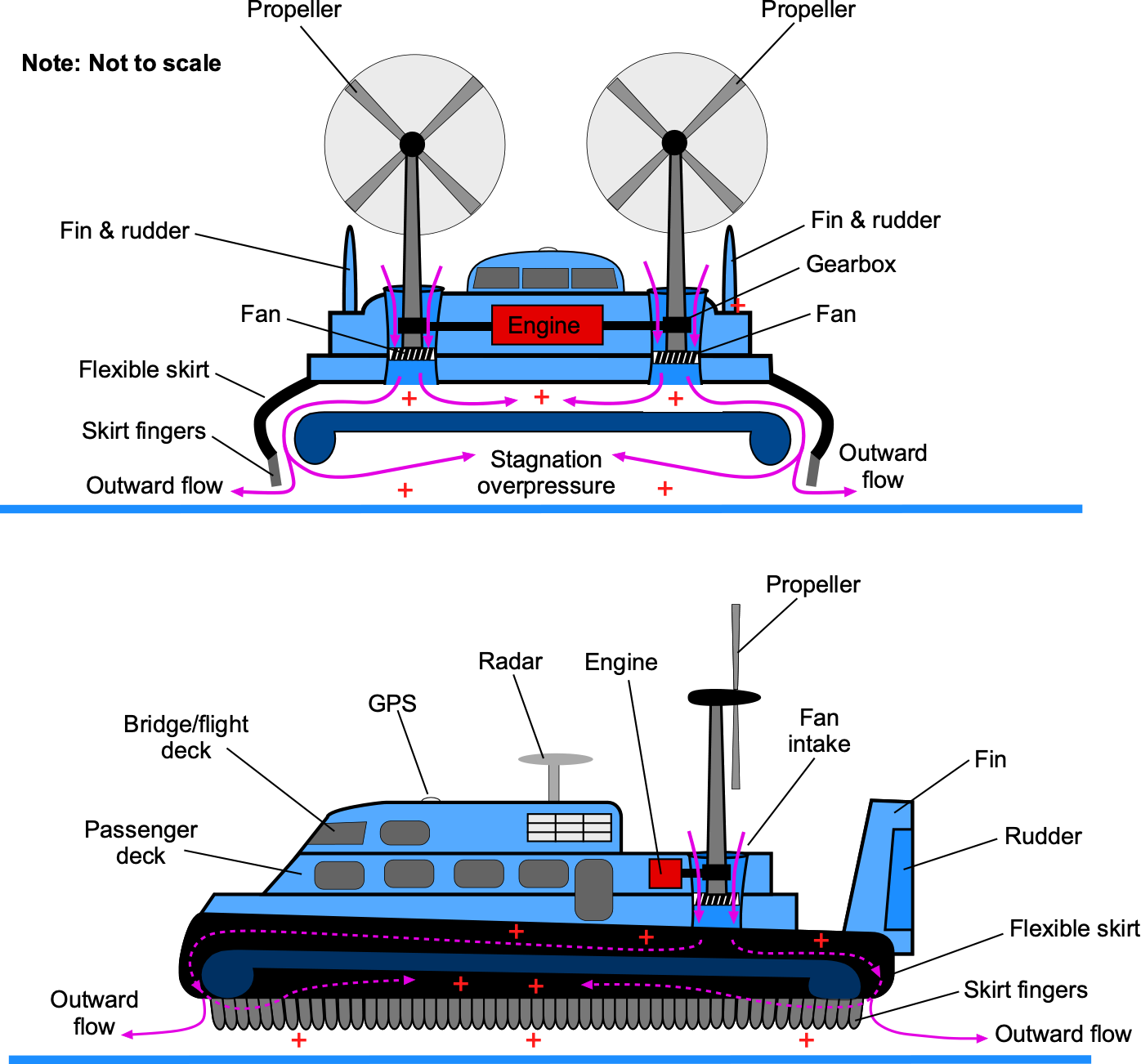
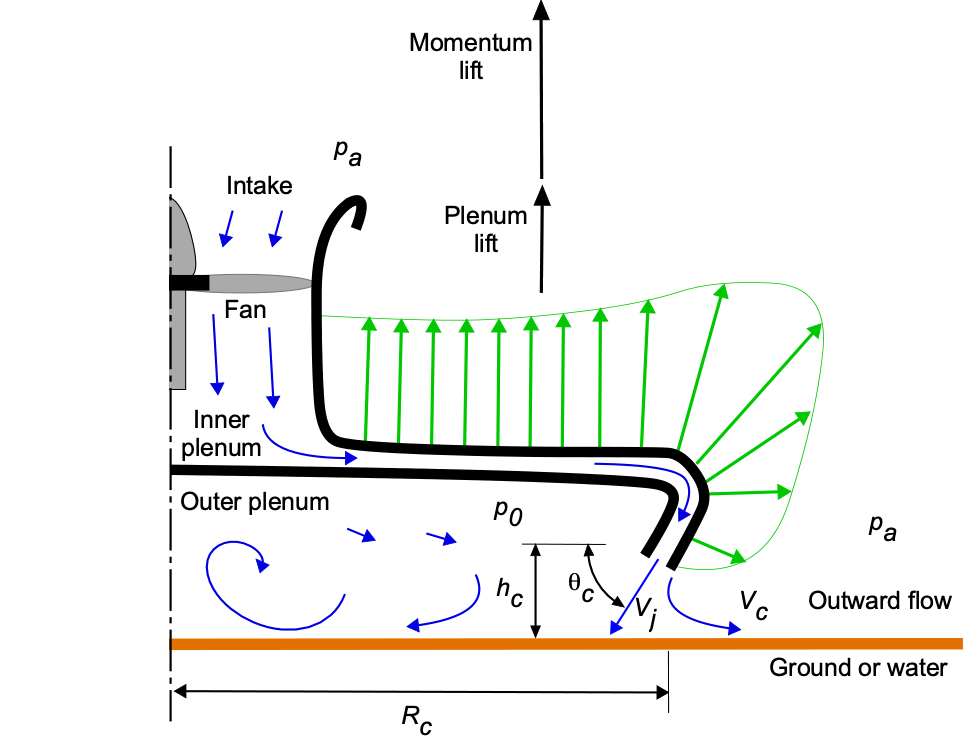
The anatomy of a generic hovercraft is shown in the schematic below. The ground cushion between the vehicle and the surface is created using one or more engine-generated fan combinations. Piston or turboshaft engines can be used, although turbocharged marine diesel engines are also common in modern hovercraft. The fan, sometimes referred to as an impeller, draws in air to increase its static pressure. Either axial or centrifugal fans can be used. The fan must be highly efficient, requiring carefully designed blades with appropriate airfoil sections, blade twist, and planform shape. This higher-pressure air is channeled and distributed in a plenum beneath the vehicle, creating a lift force that helps the vehicle to rise just above the surface, as illustrated in the figure below.

Lift Fan(s)

While the fan may generate some vertical lift, depending on its design (i.e., axial or centrifugal), this is only a fraction of the lift generated by the increased static pressure beneath the vehicle. The flexible skirt or curtain produces the remainder of the lift force, directing airflow as a slightly inwardly angled jet that impinges on the surface. The effect provides an additional momentum lift to the vehicle, exceeding the pressure force generated in the plenum, known as the “momentum curtain,” as proposed by Cockerell.

Increasing the power delivered to the fan increases its rotational speed, thereby increasing the static pressure and the height above the surface. However, more air escapes beneath the skirts when this occurs, thereby diminishing the pressure-cushion effect. The vehicle reaches an equilibrium height when the skirt’s bottom is a short distance above the surface; judicious application of engine power can regulate the ride height.

Engines

One or more engines can power a hovercraft. Smaller hovercraft may use a single engine, with the drive split via a gearbox, delivering power to the lift fan and the remainder to the propulsion system. Other hovercraft may use ducting to enable a single engine to perform both tasks, directing some air to the skirt and the remainder through horizontal ducts for propulsion. On a hovercraft with several engines, one usually drives the lift fan, and the other engines drive propellers or fans. Larger, heavier hovercraft may incorporate variable- and reversing-pitch propellers that can swivel on azipods to improve performance and control.

Propulsion is a vital aspect of hovercraft design, and modulation of the thrust is essential for forward, backward, and lateral movements. To this end, hovercraft may use differential propeller pitch, rudders, and/or vectored thrust to achieve control. Rudders assist with yaw (directional changes). At the same time, vanes located below the fan or within the plenum can be used to control mass flow from the fan, thereby regulating pressure and providing pitch and roll control. Modern hovercraft may also have control systems that augment stability and responsiveness to control inputs.

Skirt

An essential part of the anatomy of a hovercraft is its flexible rubber skirt, which extends around the periphery of the hovercraft and encapsulates the pressure plenum. A secondary skirt or curtain with inward-pointing, independent, flexible extensions, known as fingers, allows the skirt to deform when striking an obstacle or traversing uneven terrain or choppy seas, minimizing pressure loss below the vehicle. While other concepts may be used, skirts must be flexible and adaptive to accommodate changes in surface contours and maintain an effective seal.

Control

A hovercraft has unlimited directional movement over a surface and is more difficult to control than a boat or a terrestrial vehicle. Therefore, this issue presents unique challenges in its control, specifically determining the machine’s center of gravity (CG) and ensuring it moves in the correct direction. Methods used include aerodynamic control surfaces (e.g., rudders), differential thrust, thrust vectoring, differential plenum pressure, and air jets. Control surfaces, such as rudders, provide an effective and responsive means for directional control in the slipstream of a propeller. However, their effectiveness is reduced at lower airspeeds and low thrusts. Adverse coupling between yaw and roll can occur if the center of pressure of these surfaces is high relative to the c.g. of the vehicle. Another method of control is to use pressurized bleed air, which is ejected through nozzles mounted at appropriate locations to generate yawing moments and side forces. However, their response time is relatively long, so pilots must anticipate the vehicle’s behavior well in advance.

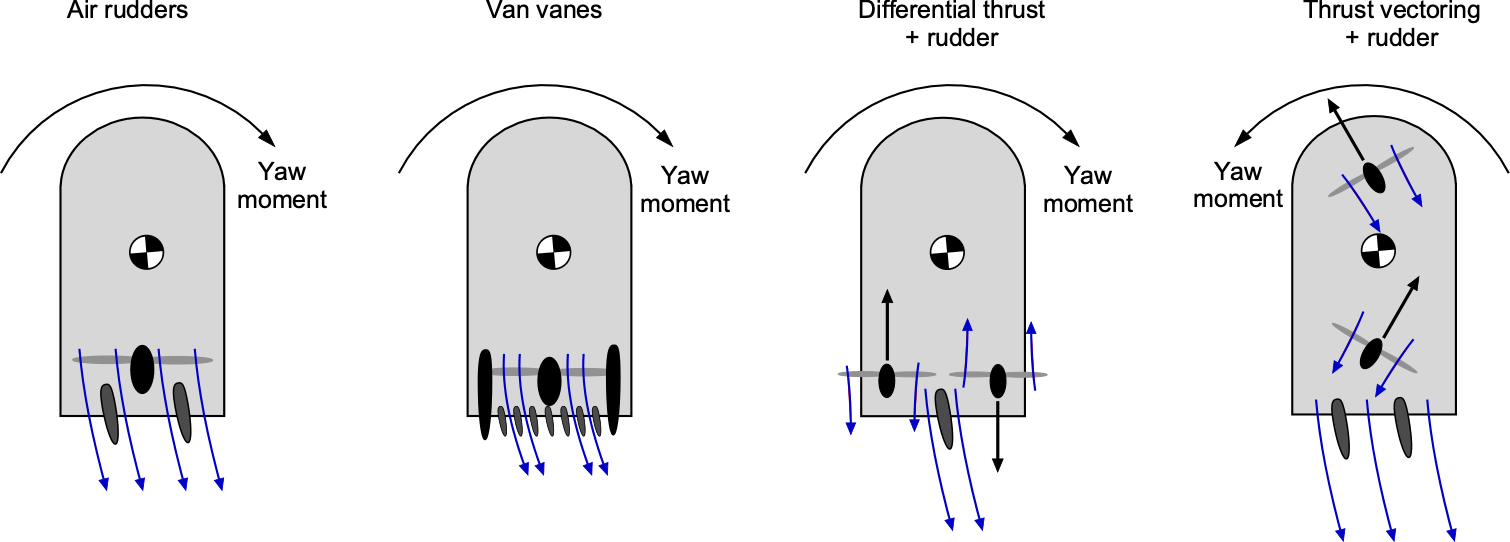
Differential thrust can be produced on twin propellers mounted laterally side by side by controlling the propeller pitch angles and/or rotational speeds. In this fixed, side-by-side propeller configuration, the thrust is parallel to the vehicle’s longitudinal axis, introducing a turning/speed coupling effect. The vehicle must also operate with some yaw angle to generate a lateral force that balances centrifugal forces during a turning maneuver, as illustrated in the figure below. Higher centrifugal forces on larger vehicles during turns mean that thrust vectoring is the most effective method for achieving directional control, which can also be balanced using rudders. Water rudders can also be deployed for over-water operations to provide better control and reduce the turn radius.

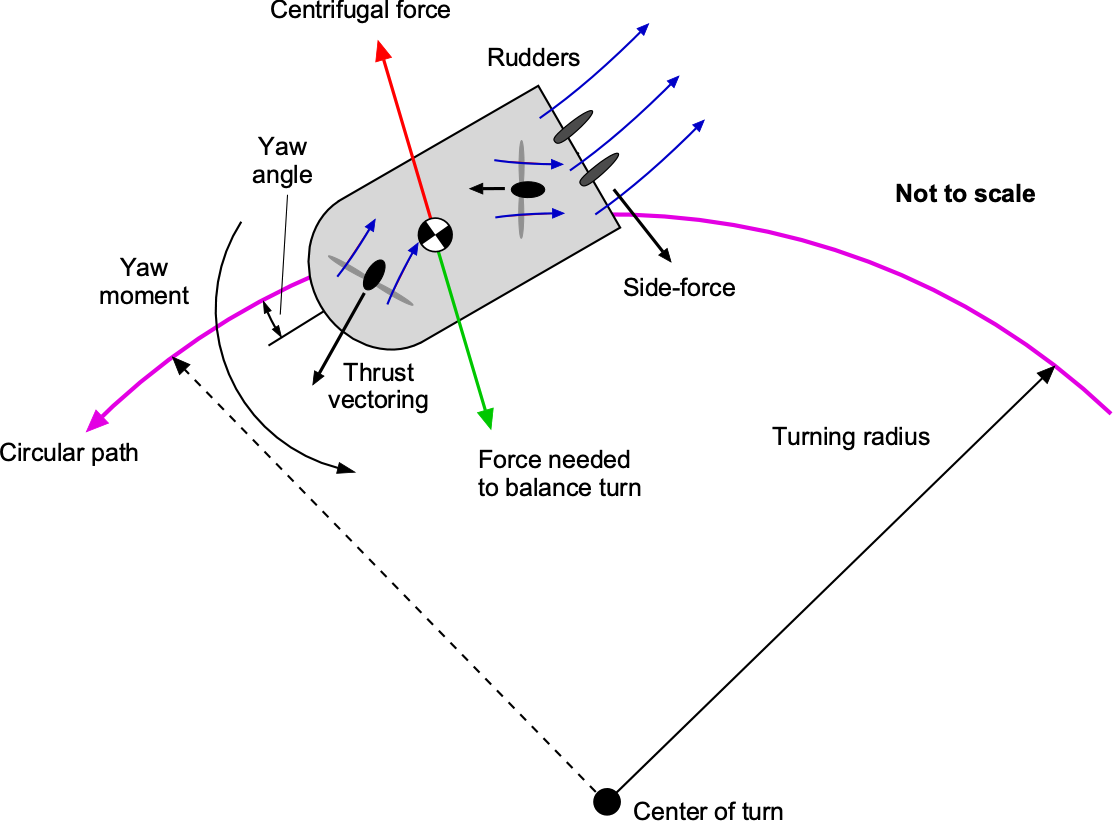
The yawing moment and side force required for directional (yaw) control can also be generated using fore-and-aft swiveling pylon-mounted propellers on azipods. For some designs, the swivel angle must be limited on either side of the longitudinal axis to limit the magnitude of the adverse rolling moment on the hovercraft relative to its c.g. Compared with the fixed side-by-side propeller arrangement, swiveling pylon-mounted propellers can generate a higher yawing moment because the propellers can be mounted further from the vehicle’s c.g., and less forward thrust is lost for a given yawing moment. Aerodynamic rudders can help balance the turn to minimize the yaw angle, which may need cross-controlled inputs.

WIGE Anatomy

By design, this type of flight vehicle leverages ground effect to lift above the water surface. However, it still flies close to the surface, typically at a distance less than half its wingspan. Such WIGE vehicles can achieve high cruise speeds over surfaces like water with good aerodynamic efficiency. Much of the power required by the engines is used during takeoff to overcome hydrodynamic drag from the water. Once airborne and at an equilibrium height in ground-effect conditions, drag decreases substantially, allowing the vehicle to cruise at a relatively high speed with significantly lower power requirements. Cruise speeds of 200 knots or more are entirely possible. There are three types of WIGE vehicles, as shown in the figure below: an ekranoplan, a reverse delta wing, and a tandem wing. They are distinct from conventional subsonic aircraft because of their typically small aspect ratio of the main wing, the addition of endplates and floats, and unique fuselage/hull shapes that enable them to take off and land on water.

The more detailed anatomy of a wing-in-ground-effect (WIGE) vehicle, also known as an ekranoplane (after the Russian concept), is illustrated in the schematic below. Ekranoplans are typically powered by turbojet or turboprop engines, which provide the thrust required for lift and propulsion. The number and placement of engines depend on the ekranoplan’s specific design and size. Placing the engines on a foreplane canard directs the jet exhaust downward toward the wings, thereby increasing their lift. The lift augmentation provided by the propulsive system can be significant, enabling the vehicle to transition from the high drag of seaborne operation to free flight, similar to an airplane. Full-span trailing-edge flaps on the wing help trap higher-pressure air beneath the wings, creating the “ram air” effect and reducing takeoff distance over water.

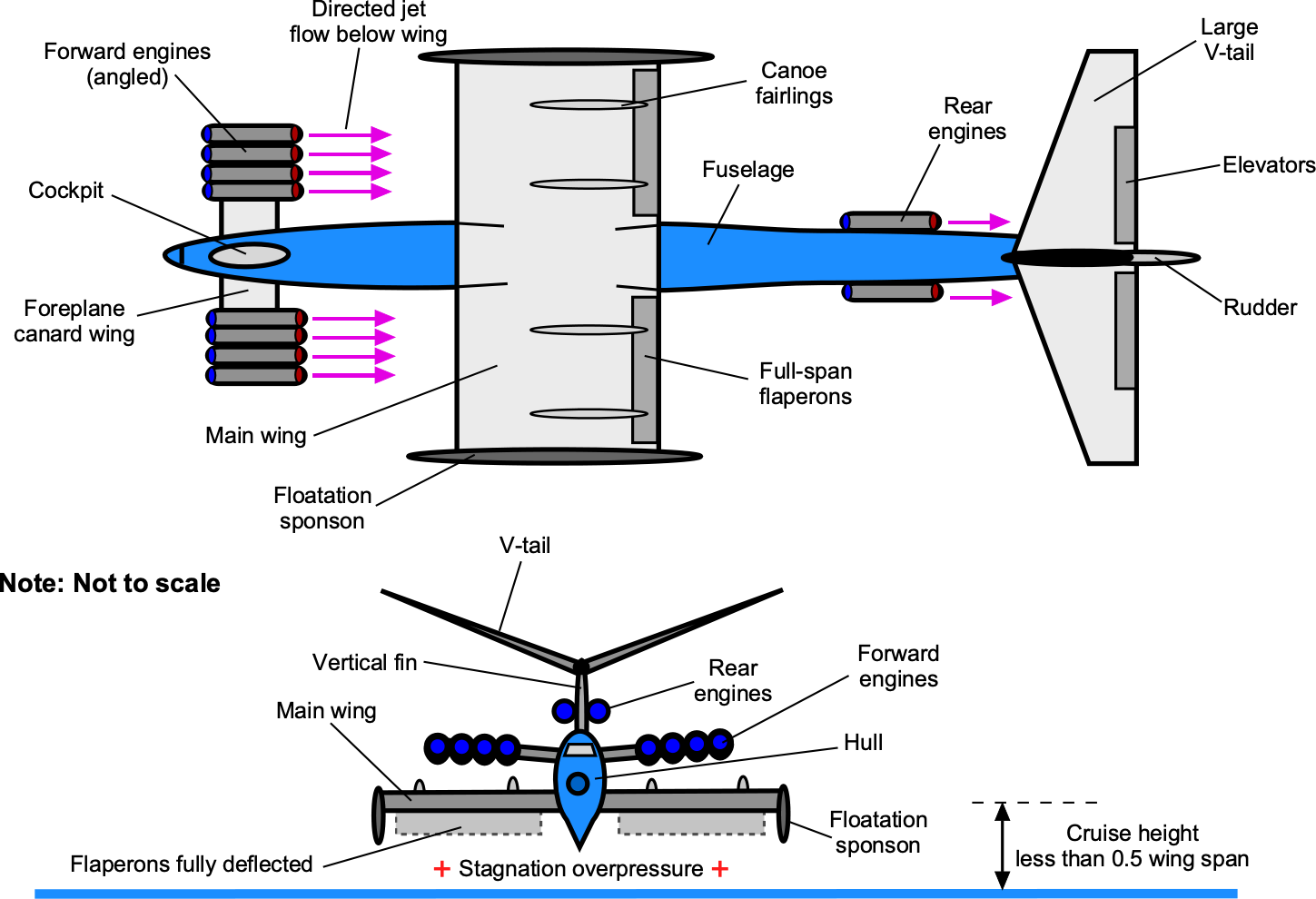
Wings

Like all WIGE vehicles, ekranoplans have large-surface-area wings but are relatively short-winged and have a fairly low aspect ratio, typically between 2 and 3. It is well known that higher-aspect-ratio wings have the lowest induced drag, but at the expense of greater structural weight. However, for a WIGE vehicle, the ground-effect condition increases the stagnation pressure beneath the wing, thereby pushing the wingtip vortices farther from the wing. This effect increases the wing’s effective aspect ratio, providing the benefits of lower induced drag typically associated with a wing of lower aspect ratio, thereby saving structural weight. Flotation sponsons are required at the tips of the wings to provide the vehicle with lateral stability in water.

Fuselage/Hull

Like an airplane, the fuselage of a WIGE vehicle houses the cockpit and other essential flight systems, including volume for a payload. However, unlike an airplane, the fuselage must be designed to be aerodynamic and hydrodynamic. Indeed, hydrodynamic loads on the hull are significant during waterborne operations, and the structure must be designed with increased strength and stiffness relative to an airplane to accommodate these loads, at the expense of structural weight. The design requirements are similar to those of a seaplane.

Empennage

Like all aircraft, WIGE aircraft have an empennage comprising a horizontal and a vertical stabilizer. The horizontal tail must have a significant area and control authority to compensate for changes in pitching moment as the vehicle reaches an altitude that exits ground effect. A large dihedral angle on the horizontal tail can significantly enhance lateral stability. At the same time, the main wing typically has either minimal dihedral or even anhedral characteristics, thereby making no direct contribution to stability. Anhedral can help maintain the benefits of ground effect at greater altitudes over water, thereby benefiting operations in rough seas.

Control

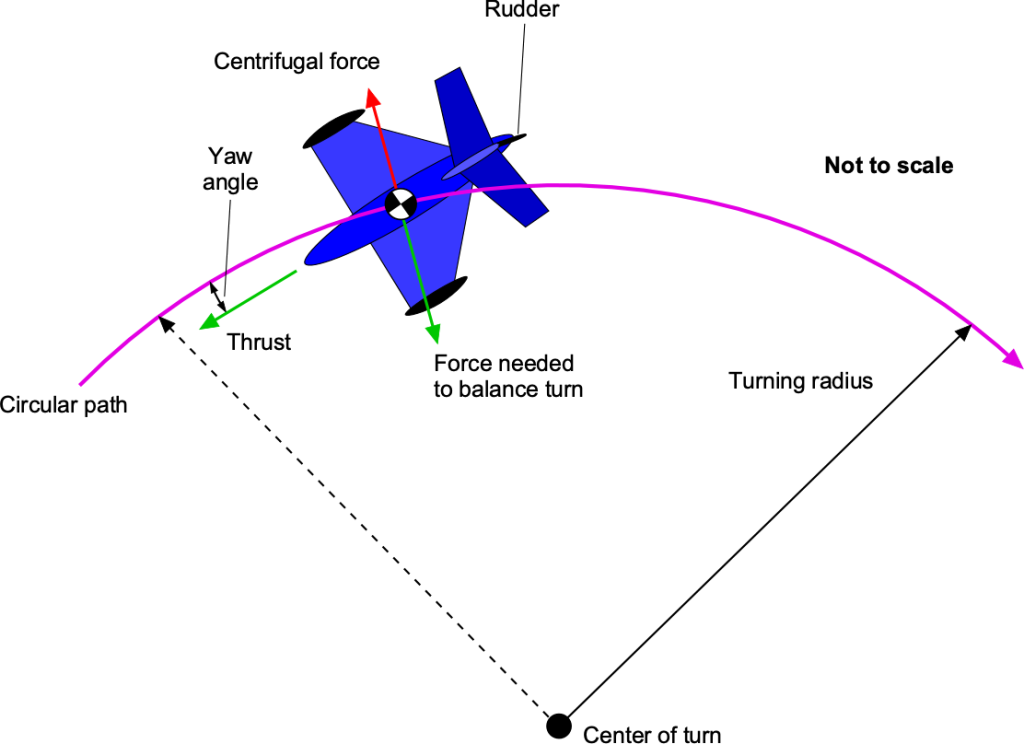
The control of WIGE vehicles is similar to that of hovercraft. Turns are made in a horizontal plane, for which the balance of centrifugal and aerodynamic forces must be considered, as shown in the figure below. Wide-radius skidding turns are the norm, depending on the thrust available and rudder authority. Suppose the vehicle can fly slightly higher above the ground or water. In that case, banking by differentially applying the flaperons can increase the bank angle to control the turn. However, the proximity to the ground may severely limit the bank angle.

Hovercraft Performance

Two types of hovercraft require analysis. The first is the pure plenum type, in which the vehicle is lifted entirely by the fan’s increased pressure differential. The second type is the plenum type, augmented by a “momentum curtain” or peripheral jet, in which a combination of differential plenum pressure and the reaction force of the peripheral jet impinging on the ground contributes to lift production. It is known that the latter type is preferred for a hovercraft, as it creates more lift; however, both types are worthy of analysis to reveal their performance and design characteristics.

Both can be analyzed, at least initially, by applying the conservation principles of mass, momentum, and energy in their integral forms. The published literature shows that the theory of hovercraft comes up in two different fluid dynamic contexts. The first theory is a plenum-discharge analysis derived from internal-flow theory. The second comes from the aerodynamic theory for a lift fan. As will be shown, both theoretical approaches yield the same results for the power required to lift a hovercraft off a surface to a specified hover height.

Fan/Plenum Theory

The figure below shows a cross-section of the control volume of a simple hovercraft that uses a pure plenum-type to lift the vehicle. Assume that the hovercraft has a weight and is of circular airframe shape with an effective pressure-cushion radius . A fan of radius , driven by an engine, draws air from the ambient atmosphere at pressure and does work on the air to raise its static pressure by , producing a stagnation pressure inside the plenum as the flow velocities approach zero. The resulting pressure differential, , acting over the surface of the plenum, becomes the primary source of lift on the hovercraft. The other source of lift is the thrust produced by the fan itself; however, in practice, this contribution is smaller and, in the first instance, can be neglected. It is assumed that air continuously and steadily escapes from beneath the hovercraft around the periphery of the plenum.

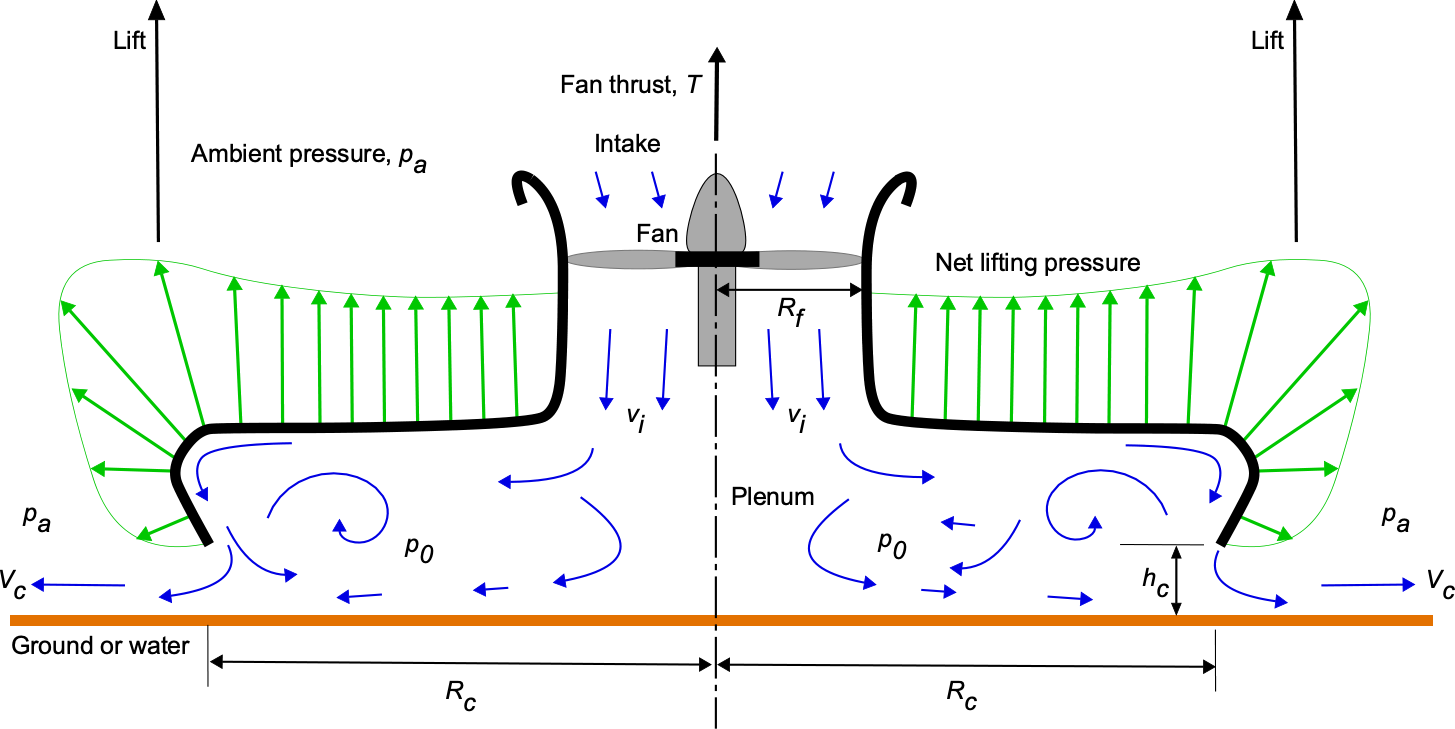
From the conservation of mass, the inlet mass flow rate through the fan must equal the exit mass flow rate around the periphery of the plenum, i.e.,

(1)  

where is the velocity induced through the fan and is the leakage velocity under the skirt. Therefore, the relationship between the fan-induced velocity and the exit velocity can be written as

(2)  

The fan does work on the air to increase its static pressure by the amount

(3)  

where is the fan thrust and is the fan disk area. Lift production from the pressure distribution in the plenum, therefore, depends on the fan disk loading, .

Because the plenum pressure supports the vehicle’s weight, then

(4)  

The fan thrust required to sustain hover is

(5)  

For most hovercraft, the ratio is greater than 10. A critical attribute of the hovercraft is therefore its ability to distribute the pressure increment induced by the fan over a relatively large surface area, producing substantially more lift than the fan disk alone could generate. This illustrates the benefit of low effective surface loading (disk).

The leakage velocity beneath the skirt is related to the cushion overpressure by

(6)  

From the conservation of mass, the induced velocity through the fan must then be

(7)  

Substituting for gives

(8)  

The power required by the fan to sustain hover, obtained from conservation of energy, is

(9)  

Equivalently,

(10)  

Notice that the power required to hover scales with the vehicle weight raised to the power and is linearly proportional to the hover (ride) height . Additional pressure losses in the fan and plenum, as well as frictional losses associated with flow over the ground, are expected to increase the required power by at least 30%. Despite the associated weight penalty, a power margin of at least 100% is advisable to ensure hovercraft operability under a wide range of operating conditions.

Peripheral Jet Theory

The figure below shows the cross-section of a hovercraft that uses the “momentum curtain” type. Again, assume that the hovercraft has a weight and is of the circular “flying saucer” type with an effective pressure cushion of radius . In this case, the fan operates on air flowing through the volume between the inner and outer plenums. The resulting flow provides jet thrust as it exhausts vertically downward through a plenum gap of width , which then impinges on the ground surrounding the vehicle’s periphery. In this case, the momentum jet reaction enhances the lift production on the hovercraft beyond that produced by the stagnation overpressure in the plenum.

The “momentum” lift force from the peripheral momentum curtain, , depends on the time rate of change of momentum of the flow as it is brought to zero at the surface of the ground or the water. The area of the annular flow at the exit, , is given by

(11)  

If , then

(12)  

Conservation of mass means that the mass flow rate out of the jet equals the mass flow rate into and through the fan, i.e.,

(13)  

so that

(14)  

The momentum force (lift) augmentation, , on the hovercraft is then

(15)  

assuming the jet velocity is turned to flow parallel to the ground, and that other momentum losses are negligible. The induced velocity at the fan is

(16)  

so the lift augmentation is

(17)  

The fan does work on the air to increase its static pressure by the amount

(18)  

Finally, a relatively simple result for the momentum thrust augmentation is obtained, i.e.,

(19)  

If it is further assumed, based on the plenum pressure contribution to the lift, that

(20)  

then the final result for the lift from momentum thrust is

(21)  

Note that the fan/plenum and peripheral-jet theories are not competing models but complementary descriptions of the same flow physics, expressed, respectively, through pressure forces and a momentum balance. When applied consistently, both yield the same power requirements and lift scaling, differing only in how the underlying conservation laws are emphasized.

Forward Motion of a Hovercraft

In addition to lifting fans, a hovercraft must have some form of propulsion to overcome aerodynamic drag and other forms of resistance, enabling it to move over land or water. Several drag components, some unique to hovercrafts, must be considered when estimating the performance of such vehicles in forward motion. In addition to the parasitic drag on the hovercraft, there are contributions from momentum drag, trim drag, and skirt contact drag. For overwater operations, wetting drag and other wave-induced hull drag must also be accounted for. Therefore, the drag buildup for a hovercraft is more complex than for an airplane because it must account for both aerodynamic and hydrodynamic effects, as well as interactions among the vehicle, ground, and water, which are difficult to quantify.

The use of flexible skirts of various designs has permitted a considerable reduction in ride height, reducing the power required. However, a lower clearance height may increase contact drag between the skirt and the surface, thereby increasing the drag on the vehicle and the propulsive power required. In hovercraft design, there must be a good balance between the power installed for lift and propulsion, which affects the total power requirements for movement over a given surface at a certain weight and speed. Sufficient thrust and power margins are necessary to prevent overestimating performance, thereby enabling the hovercraft to operate across a broad range of terrain and sea states.

Aerodynamic Parasitic Drag

All vehicles create aerodynamic parasitic drag when moving through the air, denoted as . This drag component can be calculated using the standard drag formula

(22)  

where is the “airspeed” of the hovercraft over the surface, and is the drag coefficient of the specific shape of the hovercraft. Most hovercraft are not particularly streamlined, partly for utility, and they do not need to be because they operate at relatively low speeds compared with airplanes. Drag coefficients for hovercraft shapes have been obtained from wind-tunnel tests and have been found to range in value from 0.25 to 0.4, where is based on the reference of frontal area. However, instead of using drag coefficients and the ambiguity of what is meant by a reference area, it is often useful to represent the drag in terms of equivalent drag area, , where , i.e.,

(23)  

Skirt Contact Drag

While a hovercraft is designed to have a cushion height and a skirt clearance, there can still be some contact between the rubber skirt and the terrain under certain conditions. Therefore, the manifestation of this contact is a drag component known as the skirt contact drag, . Contact primarily occurs when the hovercraft traverses rough terrain, such as tall grass, vegetation, or brush. This source of drag will also depend on the cushion height, which can be represented as

(24)  

where is a drag coefficient at a certain cushion height. Notice that skirt contact drag is analogous to a friction force, which depends on weight, not forward speed.

There are no reliable methods to predict this drag component other than semi-empirical rules derived from experiments. However, available results suggest that for average cushion heights, the value of ranges from approximately 0.01 on smooth surfaces, such as concrete or short grass, to approximately 0.05 on long grass, vegetation, or brush. In some cases, increasing the lifting fan power can increase the cushion height and reduce the drag from skirt contact.

Momentum Drag

When a hovercraft is moving forward over ground or water, the air exiting around the perimeter of the plenum that produces the “momentum curtain” is redirected by the effects of the airspeed, . The upshot of this behavior is an additional form of drag known as momentum drag. The equation used to account for the momentum drag is

(25)  

where is the volume flow rate through the air cushion system, i.e.,

(26)  

However, the creation of momentum drag is offset by the increased dynamic pressure at the intake to the lifting fan. While no rigorous methods exist for calculating such effects, this latter effect may reduce momentum drag by up to 50%. Compared to other sources of drag on a hovercraft, the momentum drag contribution is relatively small, and its explicit contribution can be neglected in preliminary analyses.

Trim Drag

If the bottom of the hovercraft is not horizontal to the surface, i.e., it is tilted forward or backward, then there will be a horizontal component of the lift force (equal to weight) that will contribute to the drag, i.e.,

(27)  

where is the angle between the cushion base and the surface, which could be nose-down or nose-up. Therefore, trim drag can be a thrust or a drag, depending on the trim state. Because the trim state also affects skirt contact drag, the hovercraft’s weight and balance must be properly maintained.

Overwater Drag

For overwater operations, there will be additional drag contributions on the hovercraft, including wetting drag and drag from waves. Wetting drag is similar to skirt drag over the ground, but it depends on the degree of water contact and the volume of water spray striking the skirt. The factors affecting wetting drag will include the cushion height, vehicle size and shape, and vehicle speed. Empirical data are usually used to estimate overwater drag, which is primarily a hydrodynamic problem. Drag on watercraft from waves, for example, depends on the Froude number and the size and length of the waves, so the effects obtained on drag become a nonlinear function of speed over the water.

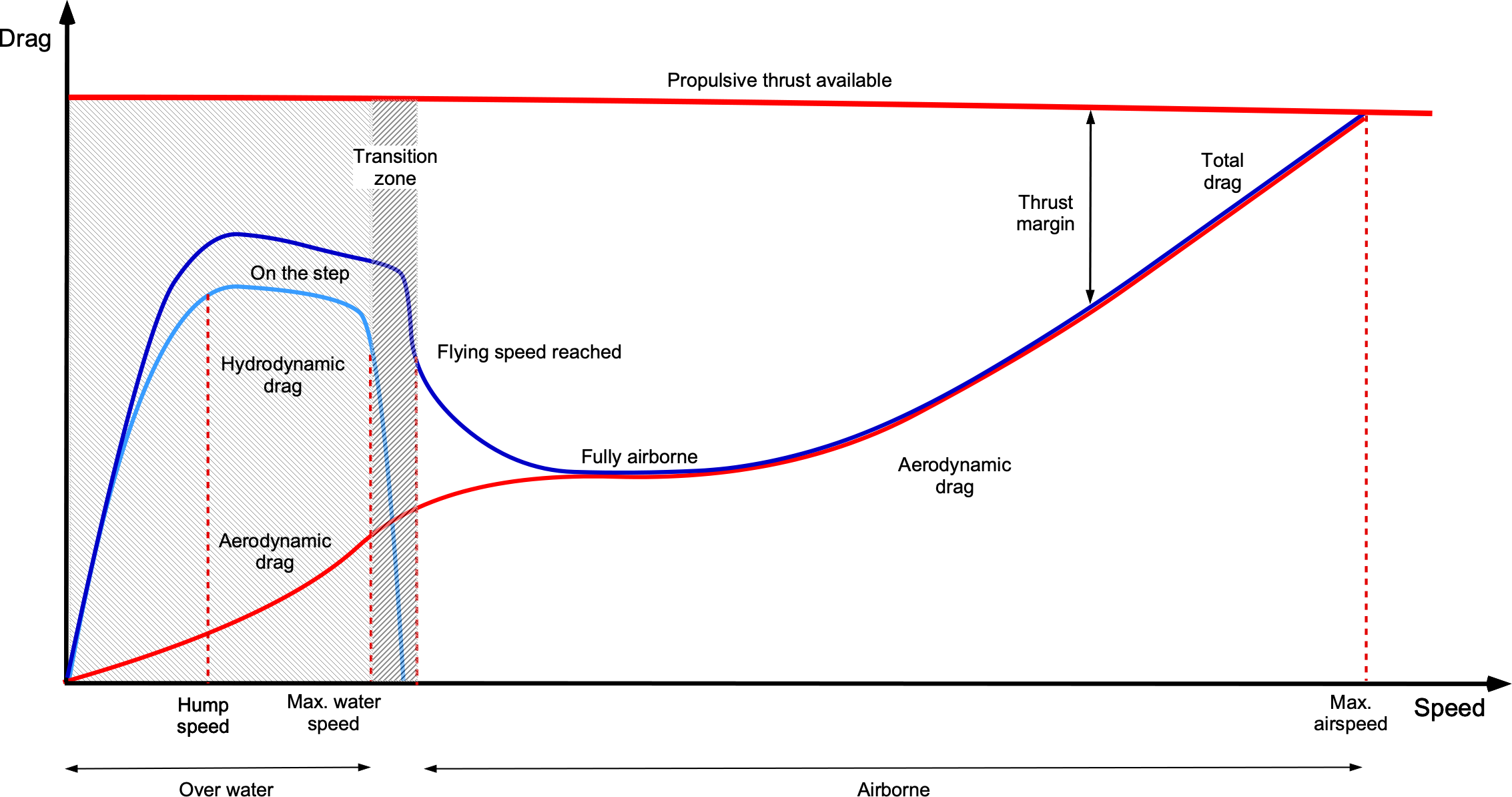
Notice that there is a speed at which the hydrodynamic drag reaches a maximum, often referred to as the “hump” speed. This form of drag is usually referred to as wave-making drag. This condition occurs when the length of the wave created by the bow matches the curtain diameter of the hovercraft, which is equivalent to the hull waterline length for a boat. Significant thrust is required to exceed the hump speed, which pilots usually refer to as “getting on the step,” but after that, the drag will decrease as the hovercraft skims over the waves.

Total Drag

The aggregate contribution of all drag sources is shown qualitatively in the figure below. Notice that power is the product of drag and speed; for example, the parasitic power increases with the cube of speed. Overwater operations significantly increase the vehicle’s drag, thereby increasing the thrust and power required. Therefore, because of the complexity and higher quantitative uncertainties in drag buildup on a hovercraft, significant power margins are typically incorporated into its design, thereby increasing weight and cost. However, any significant underestimation of the required installed power could have a major impact on the hovercraft’s ability to operate in conditions for which it would otherwise be expected to operate.

Hovercraft Stability

The interaction among air-cushion pressure, vehicle geometry, and the dynamic response to external disturbances governs the stability of a hovercraft. The primary modes of motion relevant to stability analysis are similar to those of a flight vehicle: heave (vertical motion), pitch (tilting forward or backward), and roll (tilting side-to-side). Stability in each mode depends on whether the resulting forces and moments act to restore the hovercraft to equilibrium following a disturbance.

The skirt also gives an inherent pitch and roll stability to a hovercraft. For example, suppose a disturbance causes the vehicle to pitch or roll, as shown in the figure below. In that case, the distance from the bottom of the curtain to the ground increases on one side, allowing more air to escape and thereby reducing pressure, while less air escapes on the other side, increasing pressure. The net effect, therefore, is a restoring moment on the vehicle that will cause it to self-right itself. However, there may be a considerable lag in the buildup of the restoring moment because of the vehicle’s inertia.

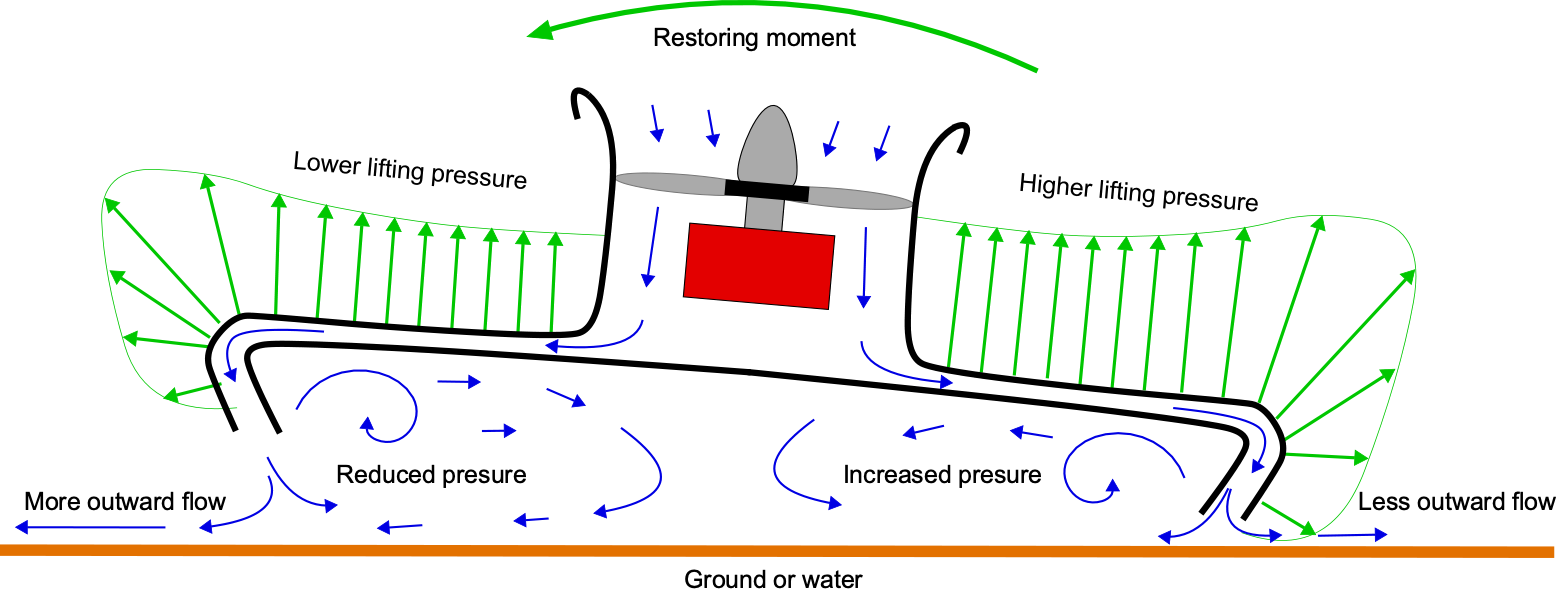
Improved roll and pitch stability, as well as finer control, can also be achieved by inflating compartments that divide the skirt and, consequently, the ground cushion into separate compartments. The air pressure can then be modulated to obtain pitch and roll control. Proper weight distribution is also crucial for stability and control. An evenly distributed load helps prevent tilting or leaning to one side; therefore, pilots must ensure that the vehicle is loaded within its defined weight-and-balance envelope. Sometimes, hovercraft can be equipped with water ballast systems to adjust their weight distribution. Hovercraft designed for maritime use also need to exhibit good sea-keeping abilities, especially in their ability to negotiate waves.

Heave (Vertical) Stability

In the vertical direction, the hovercraft hovers when the cushion pressure , acting over the effective cushion area , generates a lift force equal to the vehicle’s weight, i.e.,

(28)  

To achieve static stability, the lift must decrease with upward displacement, ensuring that any vertical disturbance results in a net restoring force, i.e.,

(29)  

This goal is typically achieved by increasing air leakage as the hovercraft rises, thereby reducing the cushion pressure. Damping forces arising from skirt dynamics or airflow behavior will also oppose rapid vertical oscillations. The vertical equation of motion is then

(30)  

where represents the vertical damping. A design goal is to provide the hovercraft with sufficient heave damping to ensure a smooth ride over most surfaces. To this end, the skirt design is critical for enabling controlled pressure relief and providing damping.

Pitch & Roll Stability

Pitch and roll stability arise from asymmetries in the cushion pressure distribution when the hovercraft tilts. The side of the cushion that moves closer to the ground experiences increased air leakage, resulting in reduced pressure and lift on that side. This imbalance generates a restoring moment that resists further tilting. The rotational dynamics are given by

(31)  

where and are the moments of inertia about the pitch and roll axes, respectively, and and are the corresponding restoring moments. Static stability requires these moments to oppose the motion, i.e.,

(32)  

A low and centrally located c.g. position improves resistance to tipping by minimizing destabilizing moments during pitch or roll. Additionally, the air cushion system must respond smoothly to changes in pressure distribution, such that any disturbance is met with restoring forces and moments. Together, these features contribute to the hovercraft’s ability to maintain a stable hover and consistent orientation during regular operation.

WIGE Vehicle Performance

Flight performance estimates for a WIGE vehicle follow the same fundamental principles as those for an airplane. However, in this case, the challenge lies in quantifying the additional aerodynamic effects arising from flow interactions associated with flying near the ground. While various corrections can be applied, the most representative results are likely to be obtained from wind tunnel tests using scaled models. The diverse types and sizes (flight weights) of WIGE concepts, combined with sparse empirical data, make it challenging to rely on historical trends to establish specific design rules.

A critical issue to consider in predictions is that when a finite wing or lifting surface approaches the ground or another impervious surface, it experiences an increase in lift and a reduction in drag, resulting in improved overall aerodynamic efficiency. There are two causes of the increase in lift. The first source is the change in the flow field around a wing cross-section, which increases the lower-surface pressure and the effective angle of attack, sometimes referred to as the ram air effect. The other impact is caused by the laterally outward movement of the wing tip vortices, which manifests as an increase in the effective aspect ratio of the wing and, hence, a reduction in induced drag. The combined effect of both factors is an increase in lift and a decrease in drag on the wing, thereby enhancing its lift-to-drag ratio and improving the aircraft’s aerodynamic efficiency. Some WIGE vehicles have been estimated to have lift-to-drag ratios exceeding 20, which is higher than those of many aircraft.

Ram Air Effect

The “ram air” effect typically refers to the increase in stagnation pressure on the lower surface of a wing when flying in proximity to the ground. This beneficial effect results from altering airflow patterns around the wing, thereby increasing lift. Further improvements in aerodynamic efficiency arise from the lower suction pressure around the airfoil’s leading edge. These two effects on wing characteristics help enable a WIGE vehicle to maintain flight with improved aerodynamic efficiency, thereby reducing power requirements and fuel consumption. The primary effects are illustrated in the figure below.

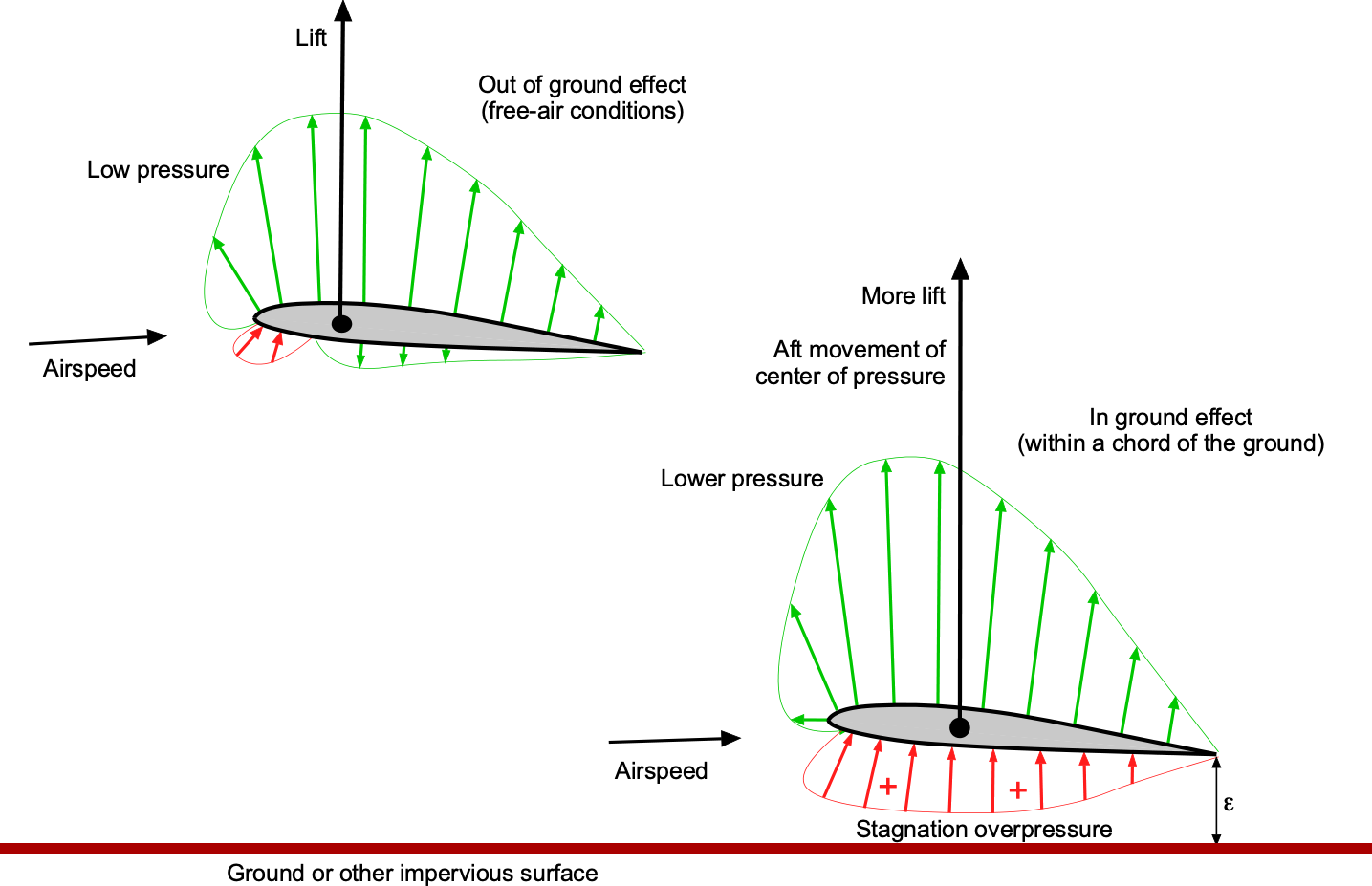
The ram air effect depends primarily on the distance between the trailing edge of the wing and the ground, , so a wing needs to get within one chord length to experience the benefits. Full-span trailing-edge flaps can further reduce , as observed on ekranoplans, thereby enhancing the ram-air effect.

Wing Aspect Ratio Effect

The aspect ratio effect for a wing operating in ground effect pertains to the increase in the effective aspect ratio of the wing by the presence of the ground. Wings with higher aspect ratios (longer and narrower) generally experience less induced drag and are more efficient. Wings with lower aspect ratios can experience a more significant improvement in lift and ground effect efficiency than wings with higher aspect ratios. However, the effects are pronounced for wings of all aspect ratios. The basic principle is illustrated in the figure below, in which a ground or other impervious surface induces lateral outward movement of the wing-tip vortices, thereby increasing the effective aspect ratio of the wing.

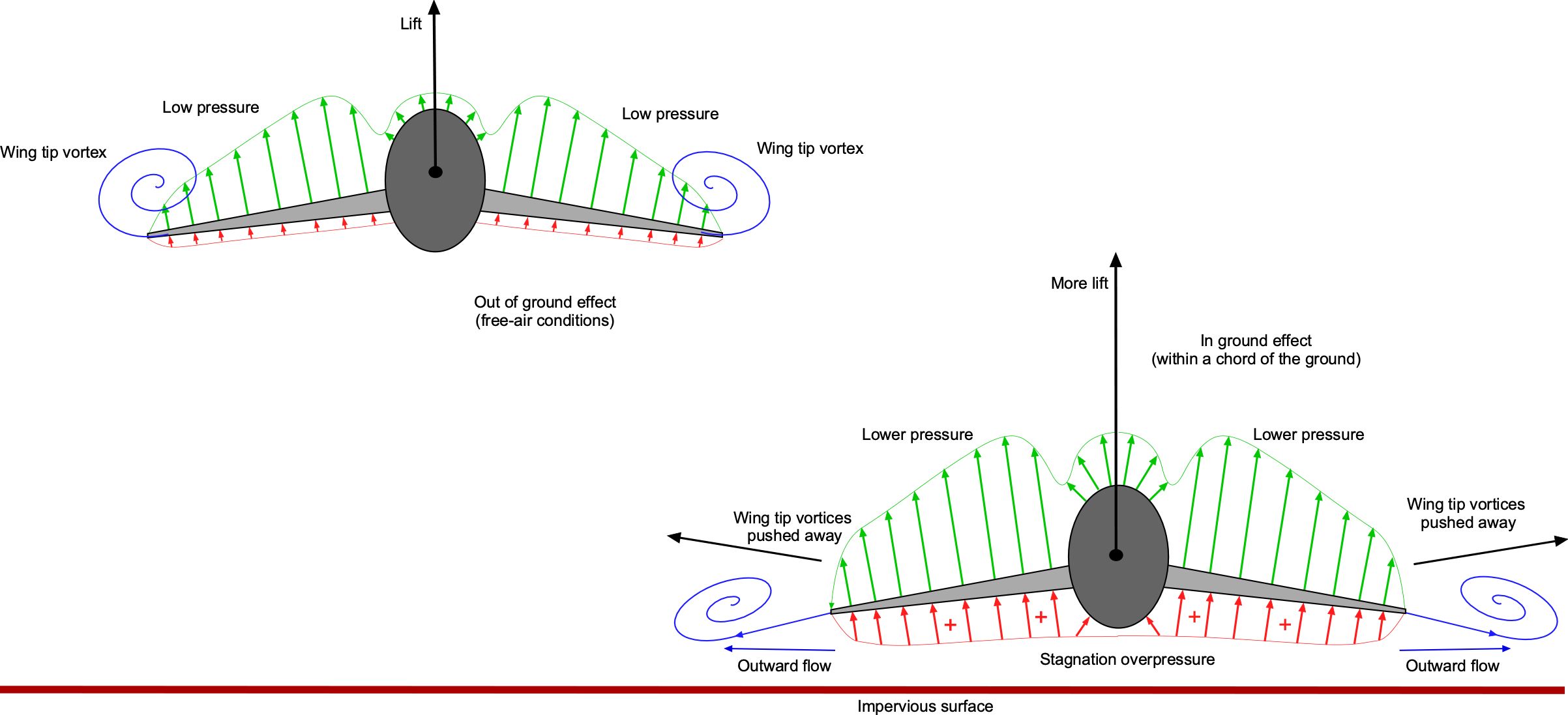
The induced drag on a wing near a surface can be approximated by the equation

(33)  

One equation to account for the benefits of the surface proximity is the aspect ratio correction factor or “ factor” as given by

(34)  

where is the height-to-span ratio of the wing above the surface. Notice that as increases, so the effects are only significant when the wing operates within one wing span. Therefore, the effective aspect ratio of the wing increases in proximity to the surface, as given by

(35)  

Another approximation for the correction factor is that

(36)  

where is the distance between the trailing edge of the wing and the surface. These simple models are supported by the results below, obtained in wind tunnels with wings, suggesting that surface effects can be considered negligible for wing spans greater than one above the ground.

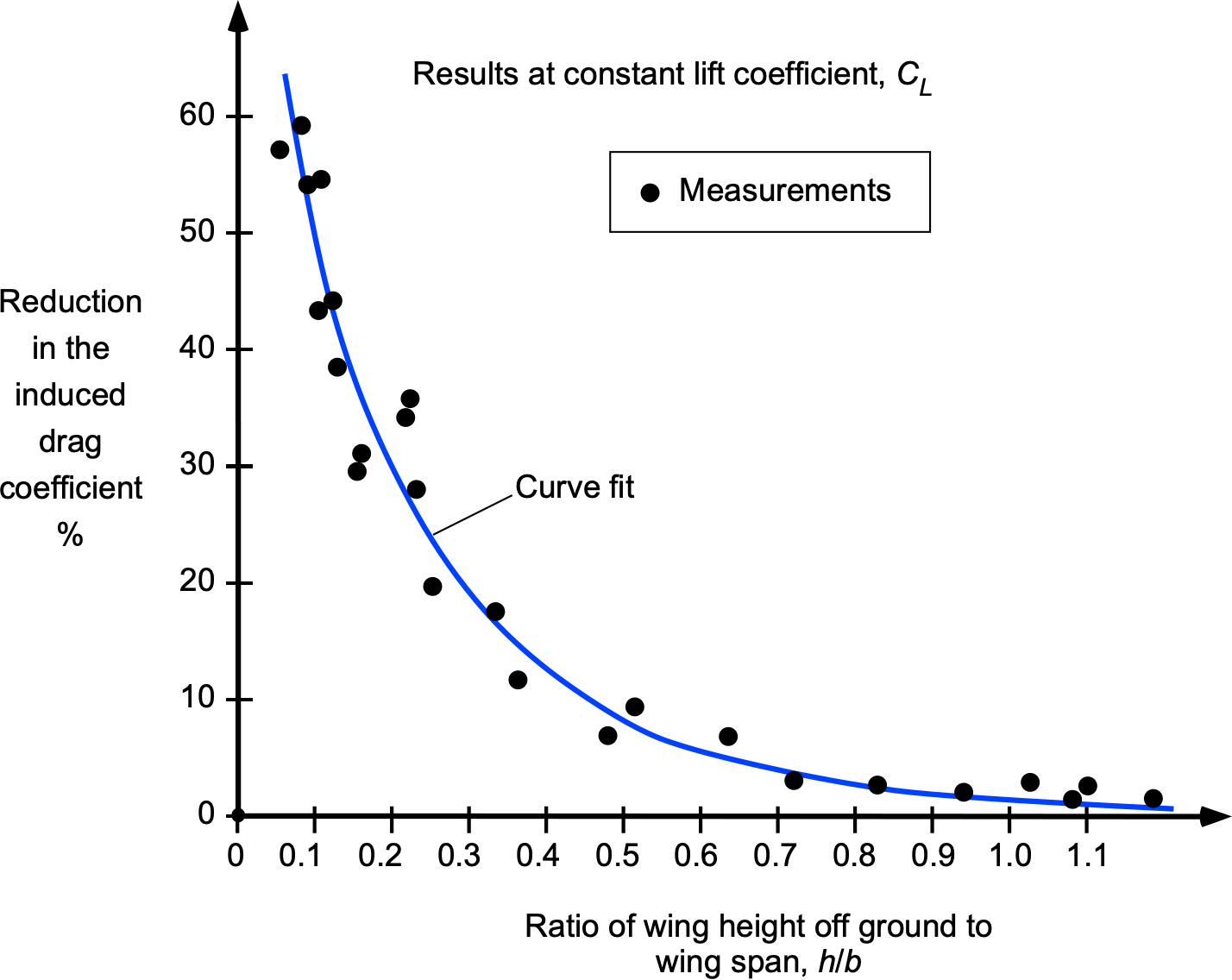
Thrust & Power Requirements

The drag build-up for a WIGE vehicle follows the same principles as those for an airplane when in flight, although hydrodynamic effects must also be considered until the point of takeoff. Hydrodynamic effects associated with wave-making drag are dominant at low speeds and peak at the “hump” speed. A significant thrust is required to exceed this speed and get “on the step,” but the net drag on the vehicle decreases markedly when it becomes airborne, as summarized in the figure below. The initial aerodynamic drag remains relatively high because of induced losses, but quickly decreases to a minimum as airspeed increases. The drag then increases as airspeed rises, and the vehicle eventually reaches its maximum speed at which drag equals available thrust.

For steady-level flight, where thrust equals drag, then

(37)  

The coefficient is given by

(38)  

where is the wing’s aspect ratio and is Oswald’s efficiency factor. Because in steady flight then

(39)  

where is the air density in which the aircraft is flying, is the reference wing area, and is the total wing lift coefficient (the assumption here is that the wings generate all of the lift). Notice that where the value of comes from the ISA model, i.e.,

(40)  

Rearranging this equation, the lift coefficient that needs to be produced on the wing for a given flight speed can be solved for, i.e.,

(41)  

Therefore, the drag becomes

(42)  

and where the corresponding power required, , is given by

(43)  

The first term in this latter equation (the profile or zero-lift power) becomes dominant at higher airspeeds, and the second (induced power) becomes more prominent at lower airspeeds. Of course, the exact quantitative relationships between power and airspeed depend on the vehicle’s detailed aerodynamics, engine characteristics, and overall propulsive and aerodynamic efficiencies. Treating all of a WIGE vehicle’s intricacies must be considered beyond the scope of this introductory exposition.

Limitations of WIGE Vehicles

Several significant limitations of WIGE vehicles must be noted, as with all GEVs. They are specifically designed to operate within half a wingspan above the surface, where the ground effect is most pronounced. Beyond this height, the ground effect quickly diminishes, and the vehicle’s efficiency decreases significantly. This issue can also limit the operational flexibility of WIGE vehicles compared to conventional airplanes, as they cannot use airport runways.

Indeed, WIGE vehicles require large bodies of water or flat surfaces for takeoff and landing, thereby further restricting their operational envelope and increasing their vulnerability to weather conditions such as strong winds and high waves. High sea states, characterized by water spray and large waves, can impose significant loads on the wings and fuselage structure. These loads can manifest as structural limitations during take-off and landing, as in a hovercraft. Large quantities of water ingested into the engines can also cause surging and significantly increase the risk of power loss. Despite these limitations, WIGE vehicles can be viable for maritime surveillance, coastal patrol, and high-speed transportation over limited ranges.

Summary & Closure

Ground Effect (Air) Vehicles (GEVs) offer several operational advancements and potential enhancements to the aviation spectrum. The hovercraft, a type of GEV, continues to offer possibilities for various civil and military applications. The elementary theories and methods discussed in this chapter provide the needed equations to help size hovercraft concepts. Specifically, the results relate fan power to the increase in static pressure required to overcome the hovercraft’s weight and achieve a specified hovering height. The methods can also be used to size the propulsion system. The technical aspects of future hovercraft designs require a balanced integration of aerodynamics, hydrodynamics, and innovative engineering. Despite their versatility, further developments in hovercraft technology are necessary and will leverage ongoing innovations in materials, electric propulsion, and other aerospace technologies. Some future hovercraft designs may incorporate hybrid electric and combustion propulsion systems, paralleling developments in aviation.

In recent years, there has been a resurgence of interest in WIGE vehicles, and renewed technical efforts aim to explore further their potential for civilian and military applications, including transport and maritime patrol. Despite their promising aspects, challenges such as regulatory hurdles and safety concerns continue to temper the adoption of such vehicles for civilian use. Nevertheless, ongoing developments suggest that the technology underlying WIGE vehicles still has much to offer, with potential future applications. However, the substantial technical and financial investments required to realize WIGE vehicles may delay their deployment for military or commercial purposes.