Worked Examples: Fluid Properties & Hydrostatics

J. Gordon Leishman

doi:https://doi.org/10.15394/eaglepub.2022.1066.9

68 Worked Examples: Fluid Properties & Hydrostatics

These worked examples have been fielded as homework problems or exam questions.

Worked Example #1

Convert the following temperature values. Write down the appropriate formulas and show all steps in your calculations. Do not use Google or similar to “convert” these temperature values–use the formulas.

(a) $12 ^{\circ}$ C to units of $^{\circ}$ F.

The conversion is

$Y \, ^{\circ}\mbox{F} = \frac{9}{5} \, X \, ^{\circ}\mbox{C} + 32$

so with $X = 12.0 ^{\circ}$ C, then

$Y \, ^{\circ}\mbox{F} = \frac{9}{5} \, 12.0 \ ^{\circ} \mbox{C} + 32 = 53.6 \, ^{\circ}\mbox{F}$

(b) $67 ^{\circ}$ C to units of $^{\circ}$ K.

The conversion is

$Y \, ^{\circ}\mbox{K} = X \, ^{\circ}\mbox{C} + 273.15$

so with $X = 67.0 ^{\circ}$ C, then

$Y \, ^{\circ}\mbox{K} = 67.0 \, ^{\circ}\mbox{C} + 273.15 = 340.15 \, ^{\circ}\mbox{K}$

(c) $-14 ^{\circ}$ F to units of $^{\circ}$ R.

The conversion is

$Y \, ^{\circ}\mbox{R} = X \, ^{\circ}\mbox{F }+ 459.67$

so with $X = -14.0 ^{\circ}$ F, then

$Y \, ^{\circ}\mbox{R} = -14.0 \, ^{\circ}\mbox{F} + 459.67 = 445.67 \, ^{\circ}\mbox{R}$

(d) $386^{\circ}$ R to units of $^{\circ}$ K.

The conversion is

$Y \, ^{\circ}\mbox{K} = \frac{5}{9} \, X \, ^{\circ}\mbox{R}$

so with $X = 386.0^{\circ}$ R, then

$Y \, ^{\circ}\mbox{K} = \frac{5}{9} \, 386.0 \, ^{\circ}\mbox{R} = 214.44 \, ^{\circ}\mbox{K}$

(e) $-49^{\circ}$ C to units of $^{\circ}$ R.

The conversion is

$Y \, ^{\circ}\mbox{R} = \left( \frac{9}{5} \, X \, ^{\circ}\mbox{C } + 32 \right) + 459.67 \, ^{\circ}\mbox{R}$

so with $X = -49.0^{\circ}$ C, then

$Y \, ^{\circ}\mbox{R} = \left( \frac{9}{5} (-49.0) \, ^{\circ}\mbox{C } + 32 \right) + 459.67 \, ^{\circ}\mbox{R} = 403.47 \, ^{\circ}\mbox{R}$

Worked Example #2

The air in the test section of a wind tunnel has a measured temperature of 82 $^{\circ}$ F and a pressure of 101.1 kPa. Determine the density of the air in both SI and USC units.

SI units:

A temperature of 82 $^{\circ}$ F converted to base units of Kelvin is

$82^{\circ}\mbox{F} = \frac{5}{9} \times ( 82 - 32) = 27.78^{\circ}\mbox{C} = 300.93^{\circ}\mbox{K}$

The equation of state is

$\varrho = \frac{p}{R \ T}$

where $R$ is 286.9 J kg $^{-1}$ K $^{-1}$ in the SI system. Therefore,

$\varrho = \frac{p}{R T} = \frac{101.1 \times 10^3}{286.9 \times 300.93} = 1.171~\mbox{kg m${^{-3}}$}$

USC units:

A temperature of 82 $^{\circ}$ F converted to base units of Rankine is

$82^{\circ}\mbox{F} = 541.67^{\circ}\mbox{R}$

The equation of state is

$\varrho = \frac{p}{R \ T}$

where $R$ is 1716.59 ft lb slug $^{-1}$ R $^{-1}$ in the USC system. A pressure of 101.1 kPa (N/m ${^{2}}$ ) is the same as 2111.52 lb ft $^{-2}$ . Therefore,

$\varrho = \frac{p}{R T} = \frac{2111.52}{1716.59 \times 541.67} = 0.002271~\mbox{slugs ft${^{-3}}$}$

Notice: Raw values (e.g., measurements) in both SI and USC units are common in practice. However, it is critically important that the calculations be conducted in a consistent set of units, i.e., entirely in SI units or entirely in USC units.

Worked Example #3

Starting from the definition of the bulk modulus, i.e., $K_b = -\varrho \dfrac{\partial p}{\partial\varrho}$ , show that for an incompressible flow with a finite change in pressure, $\Delta p$ , then a necessary condition for incompressibility is that

$\Delta p \ll K_b$

The bulk modulus is defined as

$K_b = -\varrho \frac{\partial p}{\partial\varrho}$

For small changes in pressure $\Delta p$ and density $\Delta\varrho$ , then

$K_b \approx -\varrho \frac{\Delta p}{\Delta \varrho}$

Rearranging for the relative density change gives

$\frac{\Delta \varrho}{\varrho} = -\frac{\Delta p}{K_b}$

For an incompressible flow, the relative density change must be negligible, i.e.,

$\frac{\Delta \varrho}{\varrho} \ll 1$

which implies

$\frac{\Delta p}{K_b} \ll 1$

or equivalently

$\Delta p \ll K_b$

Therefore, the pressure change $\Delta p$ must be much smaller than the bulk modulus $K_b$ for the incompressibility assumption to hold.

Worked Example #4

A bed of SAE 10 oil separates two plates that are 20 mm apart. The bottom plate is stationary, but a force $P$ applied to the top plate is such that it moves at a steady speed of 25 mm/s. It is found that the velocity profile of the oil between the plates can be approximated by

$u (y) = 11.822 \ y^{1/4}$

Calculate the shear stress $\tau$ in the oil as a function of ${y}$ (per unit depth or length of the plate) and use MATLAB to plot your results on a graph. Plot also the velocity profile itself. Assume that the dynamic viscosity of the oil is $\mu$ = 0.084 kg m $^{-1}$ s $^{-1}$ .

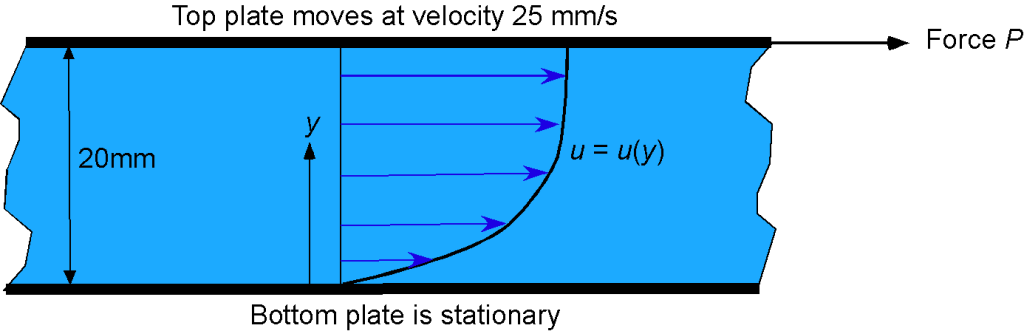
The shear stress $\tau$ can be calculated using Newton’s law of viscosity, i.e.,

$\tau = \mu \left( \frac{\partial u}{\partial y} \right)$

This problem only involves one dimension ( ${y}$ ) so

$\tau = \mu \left( \frac{d u}{d y} \right)$

We are told that

$u (y) = 11.822 \ y^{1/4}$

so

$\frac{d u}{d y} = 11.822 \left( \frac{1}{4} \right) y^{-3/4} = 2.956 y^{-3/4}$

Therefore, the shear stress for this velocity gradient is

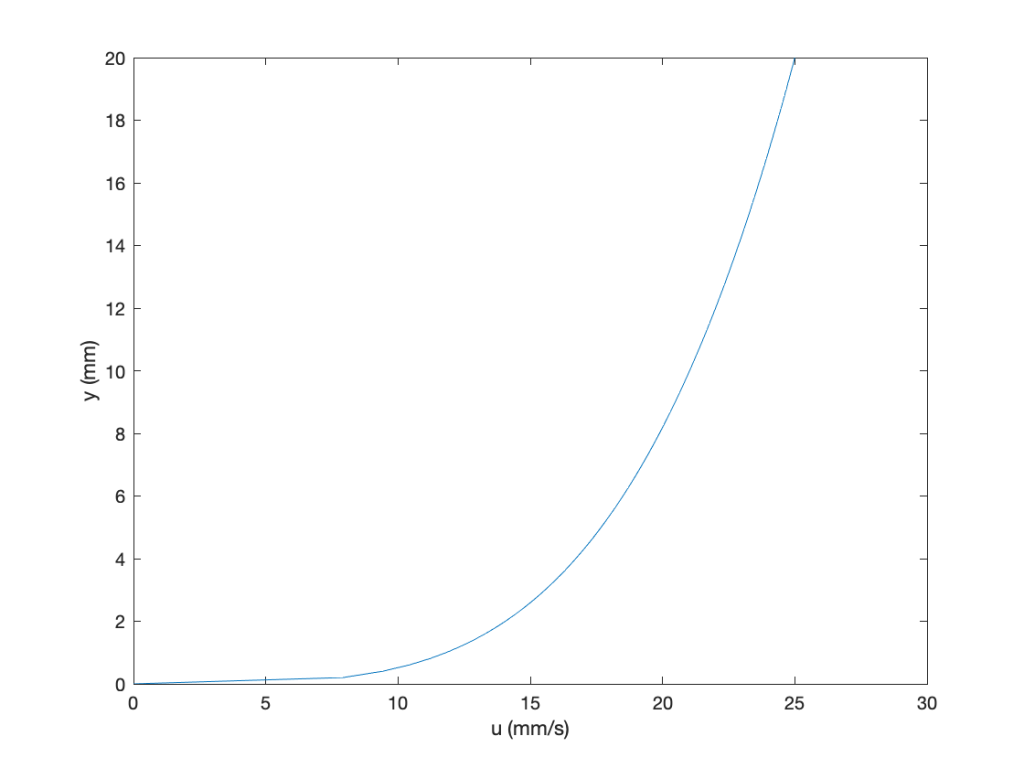
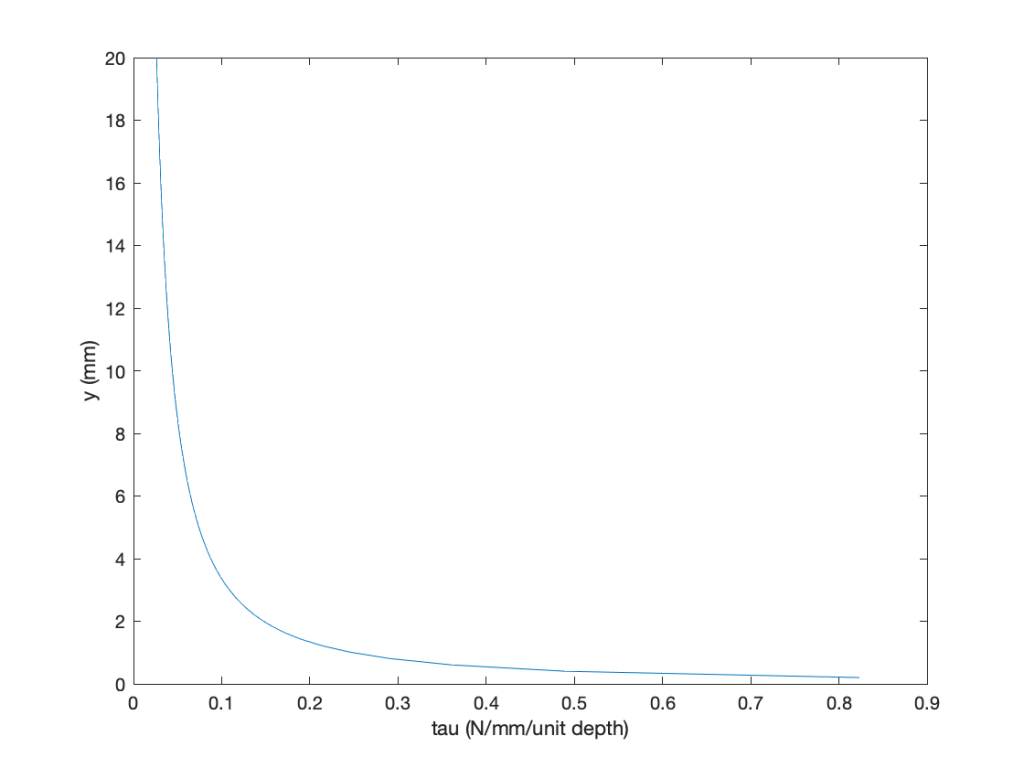
$\tau = \mu \frac{d u}{d y} = 2.956 \times 0.084 \, y^{-3/4} = \frac{0.248}{y^{3/4}}$

Some MATLAB code is given below:

clc
figure
axis([0.0 25 0.0 200])
y = linspace(0.0,20,100); %set the range of values
u = 11.822 * y.^0.25; %velocity profile
tau = 0.248 * y.^-0.75; %shear stress
plot(u,y);hold on
xlabel(‘u (mm/s)’)
ylabel(‘y (mm)’)
clc
figure
plot(tau,y);hold on
xlabel(‘tau (N/mm/unit depth)’)
ylabel(‘y (mm)’)

The results are easily plotted, being sure to pay attention to the units, which would be per unit depth. Notice that the shear stress is high near the surface (wall), where the velocity gradient is higher and drops off quickly when moving away from the wall, typical of a boundary layer flow.

Worked Example #5

Suppose a measurement in the air gives a temperature of 102 $^{\circ}$ F, calculate the dynamic viscosity coefficient. What happens to the viscosity of air as its temperature increases, and why?

Sutherland’s Law can be expressed as

$\mu = \mu_{\rm ref} \left( \frac{T}{T_{\rm ref}} \right)^{1.5} \left( \frac{T_{\rm ref} + S}{T+S} \right)$

where $T_{\rm ref} = 518.67^{\circ}$ R, $S = 198.72^{\circ}$ R and $\mu_{\rm ref} = 3.737 \times 10^{-7}$ slugs s $^{-1}$ ft $^{-1}$ . The absolute temperature is

$102 \ ^{\circ}\mbox{F} \equiv 561.67 \ ^{\circ}\mbox{R}$

Inserting the values gives

$\mu = 3.737 \times 10^{-7} \left( \frac{561.67}{518.67} \right)^{1.5} \left( \frac{518.67 + 198.72}{561.67 + 198.72} \right) = 3.973 \times 10^{-7} \mbox{ slugs s$^{-1}$ ft$^{-1}$}$

Bonding between the molecules in a gas is relatively low compared to a liquid. Therefore, the intermolecular momentum transfer between the molecules increases more with increasing temperature, which manifests as an increase in viscosity.

Worked Example #6

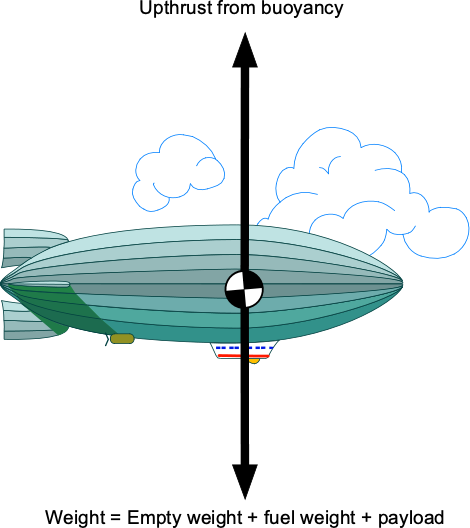
An illusionist floated up to nearly 25,000 feet by hanging from 52 helium-filled balloons. He then detached himself from the balloons, skydived several thousand feet, and parachuted to the ground. Assuming the illusionist weighed 90 kg, determine the volume required for each balloon at the takeoff point. You may assume that the density of the ambient air at takeoff is 1.19 kg m ${^{-3}}$ and that the density of helium at the same conditions is 0.1778 kg m ${^{-3}}$ .

The physics involved in this problem is the buoyancy principle, which Archimedes’ theorem applies. We will ignore the weight of the ropes and the composition of the balloon material itself, which is practically negligible. Archimedes’ principle says that for neutral buoyancy then, the upthrust, $F_u$ , must be equal to the weight of the illusionist, $W$ , plus the weight of the helium, $W_{\rm He}$ , in the balloons, so

$F_u - W - W_{\rm He} = 0$

The air volume displaced by each balloon is $\cal{V}$ , the value to be determined. Let $N_b$ be the number of balloons. The weight of air displaced by the balloons will be

$N_b {\cal{V}} \varrho_{\rm air} g = F_u$

The weight of the helium inside the balloons is

$N_b {\cal{V}} \varrho_{\rm He} g = W_{\rm He}$

Therefore,

$F_u - W - W_{\rm He} = N_b {\cal{V}} \varrho_{\rm air} g - W - N_b {\cal{V}} \varrho_{\rm He} g = 0$

or

$N_b {\cal{V}} \left( \varrho_{\rm air} - \varrho_{\rm He} \right) g = W$

Solving for ${\cal{V}}$ gives

${\cal{V}} = \frac{W}{N_b \left( \varrho_{\rm air} - \varrho_{\rm He} \right) g }$

Using the information given leads to the volume of each balloon, i.e.,

${\cal{V}} = \frac{90.0 g}{N_b ( 1.19 - 0.1778 ) g } = \frac{90}{52 ( 1.19 - 0.1778) } = 1.71~\mbox{m${^3}$}$

which seems reasonable based on the photos we have of the event.

Note: We should be careful about using the term “weight” because we inevitably use units of kg in commonly used SI units. However, a kg is a unit mass, and the unit of weight is a force (Newtons), so in engineering calculations, we need to be careful and much more precise and use Newtons for force (i.e., mass times acceleration under gravity).

Worked Example #7

An airship has a gas envelope with a 296,520 ft ${^3}$ volumetric capacity; helium is used to fill it. If the airship has an empty weight of 14,188 lb and a maximum fuel load of 960 lb, what would be the maximum payload the airship could carry? Assume MSL ISA standard atmospheric conditions. The density of helium can be assumed to be 0.0003192 slugs/ft ${^3}$ .

The hydrostatic principle of buoyancy is applicable here. Using Archimedes’ principle, then the aerostatic upforce (lift), $L$ , on the airship will be equal to the net weight of the fluid displaced minus the weight of the gas inside the envelope, i.e.,

$L = \left( \varrho_{\rm air} - \varrho_{\rm He} \right) g {\cal{V}}$

where ${\cal{V}}$ is the volume of the gas envelope.

The gross weight of the airship will be the sum of the empty weight, $W_e$ , plus the fuel weight, ${W_f}$ , plus the payload, $W_p$ , i.e.,

$W = W_e + W_f + W_p$

For vertical force equilibrium at takeoff, then $L = W$ , so

$W_e + W_f + W_p = \left( \varrho_{\rm air} - \varrho_{\rm He} \right) g {\cal{V}}$

and rearranging for the payload weight gives

$W_p = \left( \varrho_{\rm air} - \varrho_{\rm He} \right) g {\cal{V}} - W_e - W_f$

Using the numerical values supplied gives

$W_p = \left( 0.002378 - 0.0003192 \right) \times 32.17 \times 296,520 - 14,188.0 - 960.0 = 4,491 \mbox{lb}$

Therefore, the maximum payload at the takeoff point would be 4,491 lb.

Worked Example #8

For a class science experiment, the students want to see if they can lift a 10 kg block off the ground using a helium-filled balloon. Determine the balloon volume required for the block to float at ${h}$ = 1,000 m under standard ISA conditions. The helium pressure inside the balloon is 5% greater than the local ambient atmospheric pressure. You can assume that ISA properties are modeled using

$T_{\rm air} = 288.15 \left( 1 - 0.00002256 \, h \right) \mbox{ in units of K}$

$p_{\rm air} = 101325 \left( 1 - 0.00002256 \, h \right) ^{5.25} \mbox{ in units of Pa}$

with $R_{\rm air}$ = 287 and $R_{\rm He}$ = 2077 which are both in units of J Kg $^{-1}$ K $^{-1}$ . Neglect the weight of the balloon itself.

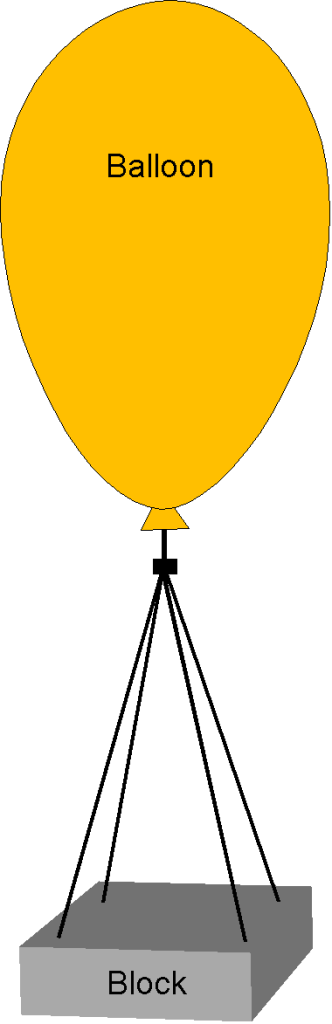
The physics of floatation centers around using Archimedes’ principle, which says that the upthrust on an object (in this case, the balloon) is equal to the weight of the fluid displaced by that object. To ” float,” the upthrust produced by the balloon must equal the weight of the mass plus the weight of the helium inside the balloon. We are told to neglect the weight of the balloon itself. The governing equation to solve, therefore, is

$\mbox{Upthrust~on~balloon} = \rm{Weight~of~block} + \rm{Weight~of~helium~inside~balloon}$

or

$\mbox{Upthrust~on~balloon} - \rm{Weight~of~helium~inside~balloon} = \rm{Weight~of~block}$

To find the upthrust produced by the balloon, we need to find the weight of the air it displaces and the weight of the helium inside the balloon.

$\mbox{Upthrust~on~balloon} = \varrho_{\rm air} {{\cal{V}}} g$

where ${\cal{V}}$ is the volume. Also, we have that

$\mbox{Weight~of~helium~inside~balloon} = \varrho_{\rm He} {\cal{V}} g$

So, the governing equation is

$\left( \varrho_{\rm air} - \varrho_{\rm He} \right) {\cal{V}} g = W$

We are given an altitude of ${h}$ = 1,000 m and two equations to calculate the temperature and pressure at that altitude. It is reasonable to assume that the helium temperature in the balloon will be the same as that of the ambient air. We can then calculate the density of both the air and helium using the equation of state and then find the needed volume of the balloon to obtain the required buoyancy or upthrust.

At 1,000 m, the temperature of the air and the helium will be

$T_{\rm air} = T_{\rm He} = 288.15 \left( 1 - 0.00002256 \, h \right) = 288.15 \left( 1 - 0.00002256 \times 1000 \right) = 281.65~\mbox{K}$

The pressure of the ambient air will be

$p_{\rm air} = 101325 \left( 1 - 0.00002256 \, \times 1000 \right) ^{5.25} = 89885.5~\mbox{Pa}$

and the pressure inside the balloon will be

$p_{\rm He} = 1.05 \times p_{\rm air} = 1.05 \times 89885.5 = 94379.8~\mbox{Pa}$

Using the equation of state $p = \varrho R T$ , the density of the air will be

$\varrho_{\rm air} = \frac{ p_{\rm air} }{R_{\rm air} T_{\rm air} } = \frac{89885.5}{287 \times 281.65} = 1.112~\mbox{kg m${^{-3}}$}$

and the density of helium will be

$\varrho_{\rm He} = \frac{ p_{\rm He} }{R_{\rm He} T_{\rm He} } = \frac{ p_{\rm He} }{R_{\rm He} T_{\rm air} } = \frac{94379.8}{2077 \times 281.65} = 0.161~\mbox{kg m${^{-3}}$}$

We are told that the mass $M$ of the block is 10 kg, so its weight $W$ is

$W = M \, g = 10 \times 9.81 = 98.1 \mbox{N}$

Therefore, the needed volume of the balloon will be

${\cal{V}} = \frac{W}{\left( \varrho_{\rm air} - \varrho_{\rm He} \right) g} = \frac{98.1}{(1.112-0.161) \times 9.81} = 10.52~\mbox{m${^{3}}$}$

Worked Example #9

Write down the engineering form of the equation of state and identify the terms. In what format do we most commonly use the equation of state?

The engineering form of the equation of state is

$p = \varrho R T$

where $p$ is pressure, $\varrho$ is density, $T$ is absolute temperature, and $R$ is the gas constant. In this form of the equation of state, the value of $R$ is gas-specific (i.e., its value depends on the gas). Rearranging for the density, which is the most common use of the equation of state, gives

$\varrho = \frac{p}{R T}$

Worked Example #10

SI Units: During measurements in a wind tunnel, the pressure and temperature of the air in SI units are found to be 102.3 kPa and 15.7 $^{\circ}$ C, respectively. Calculate the density of the air in the wind tunnel. Assume MSL ISA conditions.

The absolute temperature is 15.7 + 273.15 = 288.85 K. The gas constant $R$ for air in SI units is 287.057 J kg $^{-1}$ K $^{-1}$ so the density of the air will be

$\varrho = \frac{p}{R T} = \frac{102.3 \times 10^3}{287.057 \times 288.85} = 1.2304~\mbox{kg m${^{-3}}$}$

USC units: During measurements in a wind tunnel, the pressure and temperature of the air in USC units are 14.61 pounds per square inch (psi) at a temperature of 71.1 $^{\circ}$ F. Calculate the density of the air in the tunnel. Assume MSL ISA conditions.

The absolute temperature is 71.1 $^{\circ}$ F + 459.67 = 530.77 R. The pressure is given in terms of pounds per square inch (psi), so to convert to base units of pounds per square foot (psf or lb/ft ${^{2}}$ ), it is necessary to multiply by 144. The gas constant for air in USC units is 1716.59 ft-lb slug $^{-1}$ R $^{-1}$ so the density of the air will be

$\varrho = \frac{p}{R T} = \frac{14.61 \times 144.0 }{1716.59 \times 530.77} = 0.002309~\mbox{slugs ft${^{-3}}$}$

Worked Example #11

The tires of the main landing gear of an airplane are at a temperature of 40 $^{\circ}$ F and pressure of 40 lb/in ${^{2}}$ just before landing. After landing and braking, the temperature of the tires increases to 165 $^{\circ}$ F. Determine the new pressure in the tires. Hint: Assume that the volume of the tire stays the same.

Because pressure and temperature are involved in this problem, the equation of state is valid, i.e.,

$p = \varrho R T$

Therefore, we can write that

$\frac{p_2}{p_1} = \left( \frac{\varrho_2}{\varrho_1} \right) \frac{T_2}{T_1}$

We are told that the volume of the tire is the same before (condition 1) and after landing (condition 2), so this means that the density of the gas in the tires (usually nitrogen) remains the same (constant volume process) and so the pressure ratio is

$\frac{p_2}{p_1} = \frac{T_2}{T_1}$

We are given that $T_1$ (= 40 $^{\circ}$ F) and $T_2$ (165 $^{\circ}$ F) so that

$\frac{p_2}{p_1} = \frac{165+459.67}{40+459.67} = \frac{624.67}{499.67} = 1.25$

remembering to convert to absolute temperature units, i.e., Rankine. We are also given the pressure in units of lb/in ${^{2}}$ , but we do not need to convert to lb/ft ${^{2}}$ because we are dealing with ratios, so the conversion factor cancels out. Therefore, the pressure in the tires after landing will be

$p_2 = 1.25 p_1 = 1.25 \times 40.0 = 50.0 ~\mbox{lb/in${^{2}}$}$

Worked Example #12

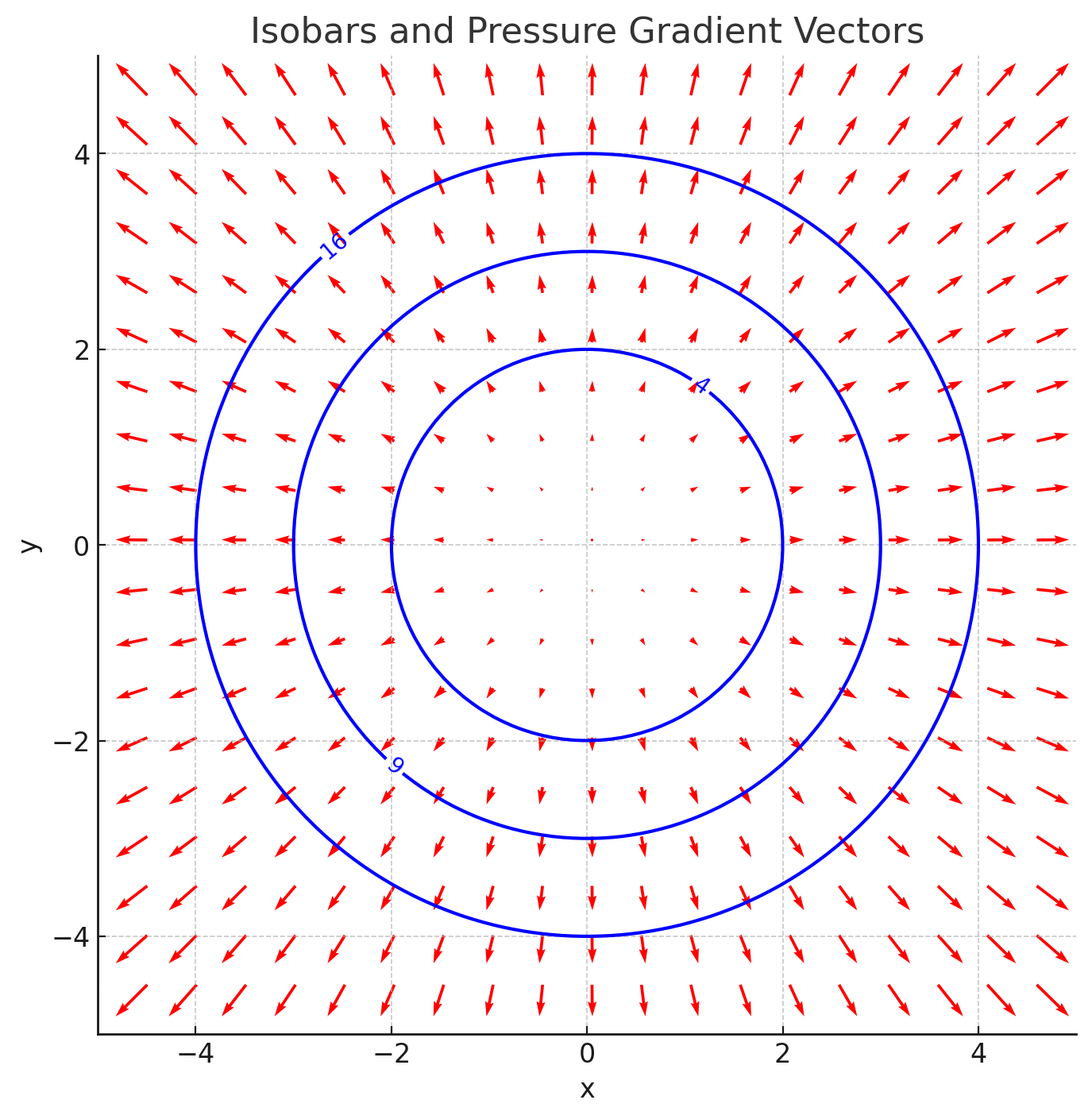
A two-dimensional pressure field is given by

$p(x,y) = x^2 + y^2$

Plot the isobars for $p$ = 4, 9, and 16 and determine the equation of the pressure gradient. Plot the gradient vectors at several points along the isobars.

The given pressure field is

$p(x, y) = x^2 + y^2$

The pressure gradient $\nabla p$ is defined as

$\nabla p = \left( \frac{\partial p}{\partial x}, \frac{\partial p}{\partial y} \right)$

First, we calculate the partial derivatives, i.e.,

$\frac{\partial p}{\partial x} = 2x \quad \text{and} \quad \frac{\partial p}{\partial y} = 2y$

so the pressure gradient is

$\nabla p = (2x, 2y)$

For the isobars, set $p = \text{constant}$ . For $p = 4, 9, 16$ , we get

$x^2 + y^2 = 4, \quad x^2 + y^2 = 9, \quad x^2 + y^2 = 16$

These represent circles with radii $R = 2, 3, 4$ , respectively. The gradient vectors $\nabla p = (2x, 2y)$ point radially outward, and their magnitude increases as the distance from the origin increases. To visualize, we can plot the isobars and overlay the gradient vectors at several points.

Worked Example #13

A well-type manometer filled with water has a leg inclined at an angle of 30 $^{\circ}$ to the horizontal. When pressure $p_a$ is applied on the well side, the water moves along the leg side from level 1 to level 2 by a distance $\Delta l$ equal to 25.25 cm. Find the pressure difference that has been applied.

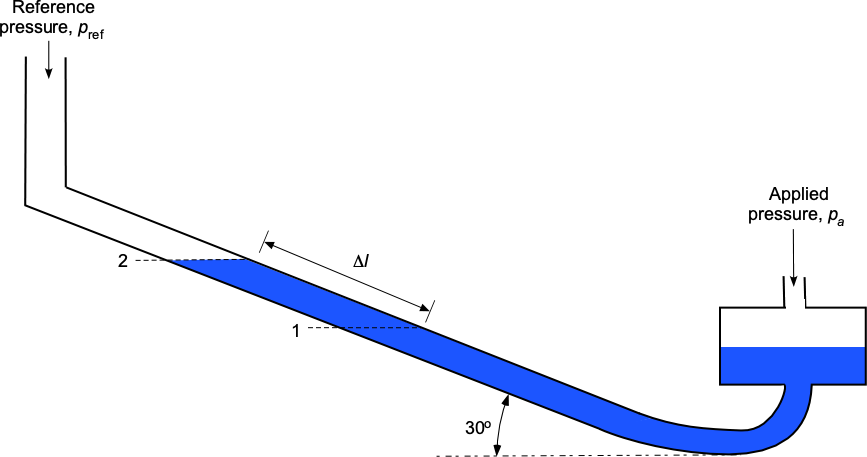
Manometry problems are about hydrostatic balance. The relevant equation is the hydrostatic equation for a constant density fluid, i.e., $p + \varrho g h =$ constant, where ${h}$ is the vertical height. The working fluid is water, so $\varrho =$ 1,000 kg/m ${^3}$ . Remember that the liquid level in the well does not change for a well-type manometer, at least not significantly enough to affect the pressures.

We are told that the manometer is inclined at an angle of 30 $^{\circ}$ to the horizontal. Hence, the relationship between the length of the measured displacement of the water levels in the tube, $\Delta l$ , and the vertical height is $\Delta h = \Delta l \sin 30^{\circ}$ .

Therefore, the difference in the applied pressure will be

$\Delta p = \varrho g \Delta h = \varrho g \Delta l \sin 30^{\circ}$

and substituting the given values leads to

$\Delta p = 1,000 \times 9.81 \times 0.2525 \sin 30^{\circ} = 1.238~\mbox{kPa}$

Worked Example #14

A tank that is vented to the atmosphere is partly filled with fuel. The tank is subject to external vertical and lateral accelerations, $a_z$ and $a_x$ , respectively. Find an expression for the slope (and the angle ${\alpha}$ ) of the free surface of the fuel in the tank in terms of the accelerations.

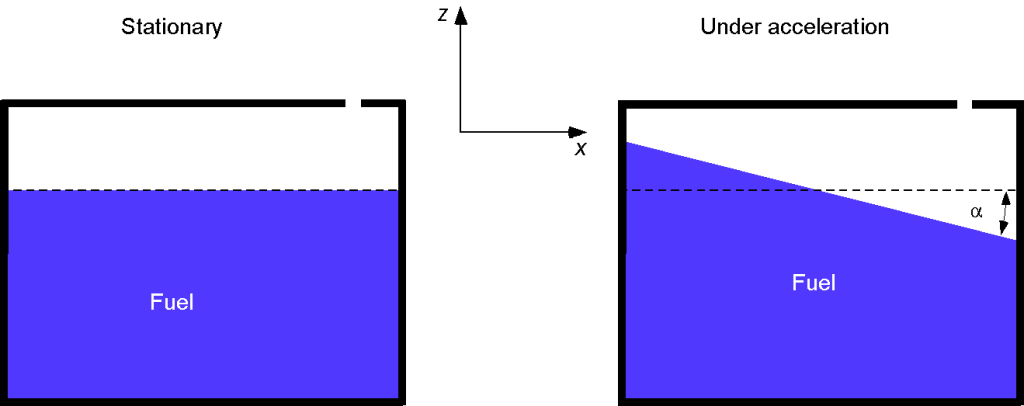
The governing hydrostatic equation for the pressure in the fluid subject to a uniform external acceleration $\vec{a} = a_x \vec{i} + a_y \vec{j} + a_z \vec{k}$ is

$\nabla p = \varrho \vec{a} - \varrho g \vec{k}$

So, for a uniformly accelerating fluid in static equilibrium in the ${x}$ – ${z}$ plane, then

$\begin{eqnarray*} \frac{\partial p}{\partial x} & = & \varrho (-a_x) \nonumber \\ \frac{\partial p}{\partial y} & = & \varrho (-a_y) \nonumber \\ \frac{\partial p}{\partial z} & = & \varrho ((-a_z) - g) \nonumber \end{eqnarray*}$

The minus sign on the acceleration terms appears because these are inertial terms, i.e., in the opposite direction to the accelerations. The relevant subset of equations in this particular two-dimensional case are

$\begin{eqnarray*} \frac{\partial p}{\partial x} & = & -\varrho a_x \nonumber \\ \frac{\partial p}{\partial z} & = & -\varrho (a_z + g) \nonumber \end{eqnarray*}$

Integrating these equations and solving for the pressure $p$ leads to

$p = -\varrho a_x x - \varrho (a_z + g ) z + \mbox{constant}$

The shape of the free surface is obtained by letting $p$ = constant. Therefore, the shape of the free surface becomes a linear function of ${x}$ , i.e.,

$a_x x + (a_z + g) z = \mbox{constant}$

and the angle that the free surface makes with the horizontal will be

$\alpha = \tan^{-1} \left( \frac{-a_x}{a_z + g} \right)$

Worked Example #15

A cylindrical container of radius $R$ is filled with water and then is rotated at an angular velocity of $\Omega$ about a vertical axis to obtain “solid-body rotation” of the container and the water. Find an equation that describes the shape of the free surface of the water. Hints: 1. The body force, in this case, is a centrifugal force, so the body force per unit mass is centripetal acceleration. 2. Even though this is a three-dimensional problem, it is axisymmetric, so it can be solved in two dimensions.

We can assume axisymmetry about the spin axis to define $r$ in the radial direction and ${z}$ in the vertical direction. Using the basic equations for a pressure field (with a body force), the relevant subset of equations in this particular case are

$\begin{eqnarray*} \frac{\partial p}{\partial r} & = & \varrho a_r \nonumber \\ \frac{\partial p}{\partial z} & = & -\varrho g \nonumber \end{eqnarray*}$

The centripetal acceleration (i.e., body force per unit mass) of a fluid element will be

$a_r = \omega^2 r$

so we have

$\begin{eqnarray*} \frac{\partial p}{\partial r} & = & \varrho \omega^2 r \nonumber \\ \frac{\partial p}{\partial z} & = & -\varrho g \nonumber \end{eqnarray*}$

Integrating the first differential equation with respect to $r$ gives

$p = \frac{1}{2} \varrho \omega^2 r^2 + C_1$

Integrating the second differential equation with respect to ${z}$ gives

$p = -\varrho g z + C_2$

Therefore, the solution for the pressure is

$p = \frac{1}{2} \varrho \omega^2 r^2 -\varrho g z + C_3$

for which the pressure $p$ will be constant on the free surface of the water, i.e., the equation of the free surface will be

$p = \frac{1}{2} \varrho \omega^2 r^2 - \varrho g z = \mbox{constant}$

which is a parabola. It can be shown with some further effort that compared to the original free surface (i.e., when the container is not rotating), the free surface dips down at the center of the spin axis by an amount $z = h/2$ equal to the amount the surface rises at the rim of the container at $r = R$ by $z = h/2$ where

$h = \frac{R^2 \omega^2}{2 g}$

where $R$ is the radius. Notice that the density of the fluid does not appear in this equation. Finally, the equation of the free surface is

$z = z_0 - \frac{\omega^2}{4 g} \left( R^2 - 2r^2 \right)$

where $z_0$ is the initial height of the free surface of the non-rotating case. Below is a graph showing the free surface’s shape for increasing rotational rate values.

Worked Example #16

The first stage of a 20 m tall cylindrical rocket fuel tank is filled with liquid RP-1 fuel. This stage experiences a maximum vertical acceleration of 5 g during the launch. Calculate the maximum excess pressure on the bottom of the tank during launch. Assume that the density of RP-1 is 820 kg/m ${^3}$ .

The relevant equation is the hydrostatic equation for a constant density fluid, i.e., $p + \varrho g h =$ constant, where ${h}$ is the vertical height. The working fluid is kerosine with $\varrho =$ 820 kg/m ${^3}$ . The problem can be assumed to be one-dimensional, but the fuel tank is subjected to 5 times the normal acceleration under gravity. Therefore, the excess pressure (over and above any internal pressure) on the bottom of the tank will be

$p = \varrho (5g) h = 820 \times 5 \times 9.81 \times 20 = 804.42 ~\mbox{k Pa}$

Worked Example #17

A U-tube manometer is connected to the inlet and outlet of a water pump as shown below; the left side is connected to the inlet at pressure $p_{\rm in}$ and the right side to the outlet at pressure $p_{\rm out}$ . Assuming that the inlet and outlet conditions are at the same elevation, determine the pressure increase produced by the pump. Remember that specific gravity SG = $\varrho/\varrho_{\rm H_{2}O}$ . The density of water can be assumed to be 1.93 slugs/ft ${^3}$ .

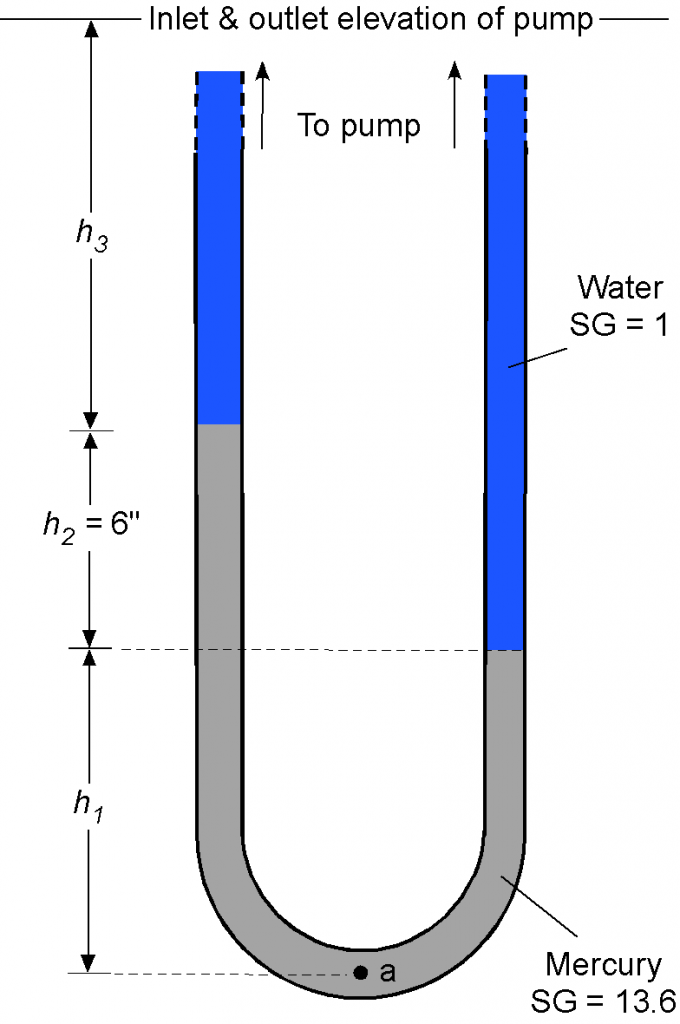
Illustration showing the elevation of a U-tube manometer connected to an inlet and outlet water pump.

Remember that manometry problems are about hydrostatic balance. The pressure at point “a” will equal the pressure produced by each arm of the U-tube manometer. Looking at the left side arm, then we can write

$p_a = \varrho_{\rm Hg} \, g h_1 + \varrho_{\rm Hg} \, g h_2 + \varrho_{\rm H_{2}O} \, g h_3 + p_{\rm in}$

Similarly, for the right side arm, then

$p_a = \varrho_{\rm Hg} \, g h_1 + \varrho_{\rm H_{2}O} \, g h_2 + \varrho_{\rm H_{2}O} \, g h_3 + p_{\rm out}$

Therefore, the difference in pressure becomes

$\Delta p = p_{\rm out} - p_{\rm in} = \varrho_{\rm Hg} \, g h_2 - \varrho_{\rm H_{2}O} \, g h_2 = \left( \varrho_{\rm Hg} - \varrho_{\rm H_{2}O} \right) g h_2$

and substituting the numerical values gives

$\Delta p = \left( 13.6 - 1.0 \right) \times 1.93 \times 32.17 \times (6.0/12) = 391.16 \quad \mbox{lb/ft${^{2}}$}$

Worked Example #18

A manometer contains two liquids of specific weight $\gamma_1$ (Fluid 1 = water) and $\gamma_2$ (Fluid 2 = mercury). Note: Specific weight $\gamma = \varrho g$ . Determine the equation relating the pressure in the spherical reservoir, i.e., $p_0$ , in terms of $p_2$ , $h_1$ , $h_2$ , $\gamma_1$ , and $\gamma_2$ .

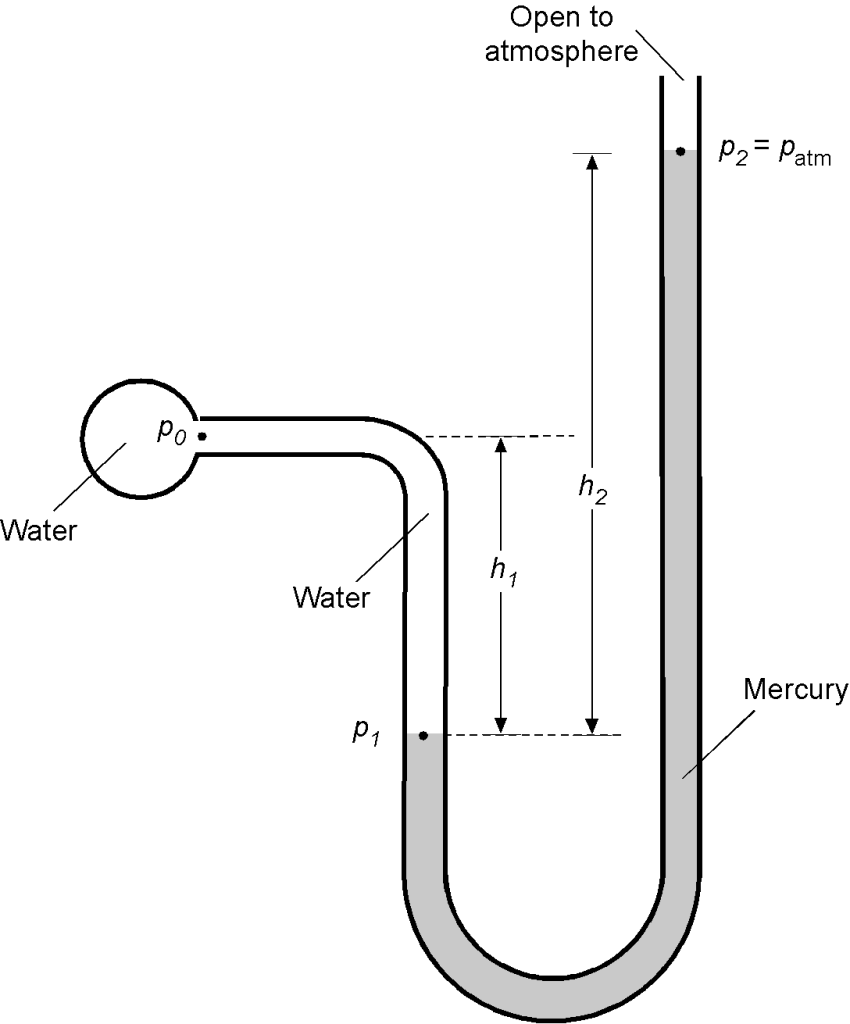
If the open end of the manometer in the above figure is now exposed to the atmosphere and $h_1$ = 5.2 inches and $h_2$ = 18.6 inches, then find the pressure $p_0$ . Assume atmospheric pressure $p_a$ is 14.7 lb/in ${^{2}}$ . The density of water can be assumed to be 1.93 slugs/ft ${^3}$ , and the specific gravity (SG) of mercury is 13.6. Use $g$ = 32.17 ft/s ${^{2}}$ . Note: SG = $\varrho/\varrho_{\rm H_{2}O}$ .

Use the foundational principle that the hydrostatic pressure at the same height in the same fluid will be constant. Using the hydrostatic equation for the left leg

$p_1 = p_0 + \varrho_1 g h_1$

or in terms of specific weight

$p_1 = p_0 + \gamma_1 h_1$

and correspondingly for the right leg

$p_1 = p_2 + \gamma_2 h_2$

Therefore,

$p_0 + \gamma_1 h_1 = p_2 + \gamma_2 h_2$

Solving for $p_0$ in terms of $p_2$ , $h_1$ , $h_2$ , $\gamma_1$ , and $\gamma_2$ , as asked for in the first part of the question, then

$p_0 = p_2 + \gamma_2 h_2 - \gamma_1 h_1$

In the second part of the question, we are then given that $p_2$ is atmospheric pressure = $p_a$ = 14.7 lb/in ${^{2}}$ = 2,116.8 lb/ft ${^{2}}$ . Also, we can calculate $\gamma_1$ and $\gamma_2$ , i.e.,

$\gamma_1 = 1.93 \times 32.17 = 62.09~\mbox{slugs/ft${^{2}}$/s${^{2}}$}$

and

$\gamma_2 = 13.6 \times 1.93 \times 32.17 = 844.40~\mbox{slugs/ft${^{2}}$/s${^{2}}$}$

Therefore, solving for the value of $p_0$ gives

$\begin{eqnarray*} p_0 & = & p_2 + \gamma_2 h_2 - \gamma_1 h_1 \\ & = & 2,116.8 + (844.40 \times 18.6/12) - (62.09 \times 5.2/12) \\ & = & 3,398.71~\mbox{lb/ft${^{2}}$} = 23.6~\mbox{lb/in${^{2}}$} \end{eqnarray*}$

Worked Example #19

A liquid manometer, shown in the figure below, is frequently used to measure small pressure changes. One leg of the manometer is inclined at an angle $\theta$ , and the differential reading of the two heights of the liquid $l_2$ is measured along the inclined tube. The two pipes (which run into the screen) contain gases, the gas in pipe A being of density $\varrho_A$ , and the gas in pipe B being of density $\varrho_B$ . The density of the liquid in the tube is $\varrho_L$ . Determine the equation for the difference in pressure between A and B in terms of the length $l_2$ .

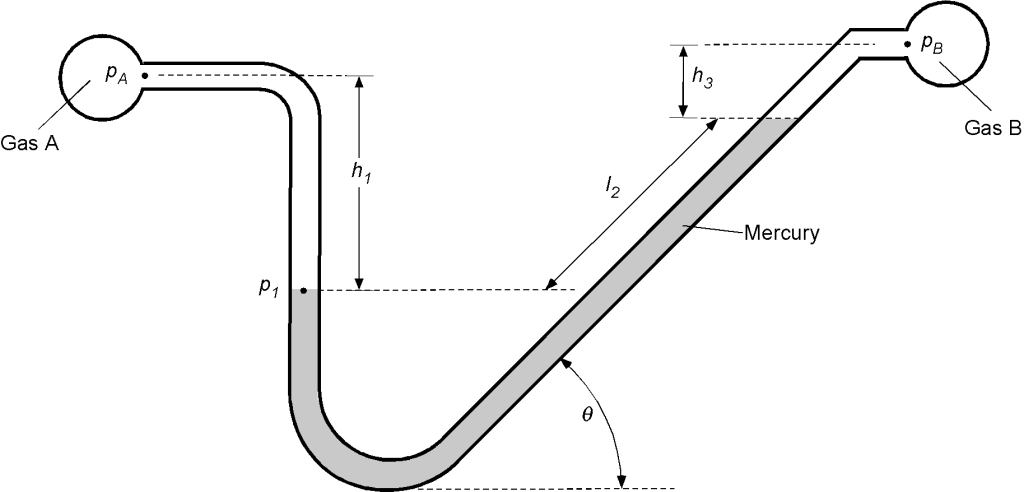
Remember that the pressures at two points in the same fluid at the same vertical height are equal. We will look first at point (1) on the left leg of the manometer. Using the principles of hydrostatics, then pressure there, $p_1$ , will be

$p_1 = p_A + \varrho_A \, g \, h_1$

Looking at the other leg of the manometer, the pressure at the same vertical height will be

$p_B + \varrho_B \, g \, h_3 + \varrho_L \, g \, l_2 \sin \theta$

remembering that it is the vertical height $l_2 \sin \theta$ that matters here. Therefore, equating the two pressures at the same level gives

$p_1 = p_A + \varrho_A g h_1 = p_B + \varrho_B g h_3 + \varrho_L g l_2 \sin \theta$

or that

$p_A - p_B = \varrho_L g l_2 \sin \theta + \left( \varrho_B g h_3 - \varrho_A g h_1 \right)$

which is what we are asked for. But we can take this answer a step further because if A and B are gasses, then their density is very low compared to the density of a liquid, i.e., $\varrho_A \ll \varrho_L$ and $\varrho_B \ll \varrho_L$ and the difference in heights $h_3 - h_1$ is small so that

$\left( \varrho_B g h_3 - \varrho_A g h_1 \right) \ll \varrho_L g l_2 \sin \theta$

Therefore, to a good approximation, if A and B are gasses, then

$p_A - p_B = \varrho_L \, g \, l_2 \sin \theta$

or

$l_2 = \frac{p_A - p_B }{ \varrho_L \, g}$

Worked Example #20

In a particular industrial application, the three-dimensional pressure field $p$ in a stagnant fluid is known to behave according to

$\frac{\partial p}{\partial x} = x$

$\frac{\partial p}{\partial y} = y$

where the ${x}$ – ${y}$ plane is horizontal and ${z}$ is measured positive upwards. Find the equation that describes the pressure field and the isobars, i.e., lines of constant pressure).

We are given two equations for the particular pressure field in stagnant flow, i.e.,

$\frac{\partial p}{\partial x} = x$

and

$\frac{\partial p}{\partial y} = y$

Also, in the ${z}$ direction, we will have

$\frac{\partial p}{\partial z} = -\varrho g$

Integrating the first of the three equations gives

$p = \frac{x^2}{2} + f_1(y) + f_2(z) + C_1$

and integrating the second gives

$p = \frac{y^2}{2} + f_3(x) + f_2(z) + C_2$

Finally, integrating the third gives

$p = -\varrho g z + f_3(x) + f_1(y) + C_3$

Therefore, by inspection we see that $f_1(y) = y^2/2$ and $f_3(x) = x^2/2$ and $f_2(z) = -\varrho g z$ so that the pressure field will be described by

$p(x, y, z) = \frac{x^2}{2} + \frac{y^2}{2} -\varrho g z + C_4$

which are cylindrical isobars. This latter result can be verified using partial differentiation, which will obtain the initial equation for this problem.

Worked Example #21

A hot air balloon becomes neutrally buoyant at an altitude of 1,100 m where the outside air temperature is 10.5 $^{\circ}$ C. With all its cargo, the balloon has a mass of 500 kg (excluding the air in the balloon), displacing a volume of 7,000 m ${^3}$ . Assume that the pressure inside the balloon is the same as that outside. Determine the air temperature inside the balloon to give it neutral buoyancy. Hint: At 1,100 m, the air density can be considered 1.102 kg m ${^{-3}}$ .

The physics of the problem says that for neutral buoyancy, then the weight of hot air inside the balloon $W_{\rm hot}$ + the weight of the balloon itself $W_b$ = the upthrust $F_u$ according to Archimedes’ Principle caused by the weight of displaced cool air. There is no net vertical force on the balloon, so

$F_u - \left( W_b + W_{\rm hot} \right) = 0$

The air volume displaced by the balloon is $\cal{V}$ = 7,000 m ${^3}$ . Therefore, the weight of cool air displaced by the balloon is then

$W_{\rm cool~air} = {\cal{V}} \, \varrho_{1,100} \, g = 7,000 \times 1.102 \times 9.81 = 75,674.3~\mbox{N}$

which is equal to the upward buoyancy force $F_u$ according to Archimedes’ Principle. The mass of the balloon is 500 kg, so its weight, $W_b$ , is 500 $g$ = 500 $\times$ 9.81 = 4905.0 N. Notice $\varrho_{1,100}$ is the density of the displaced air at the height of 1,100 m, which is given as 1.102 kg m ${^{-3}}$ .

Therefore, for neutral buoyancy (i.e., $F_u = W_b + W_{\rm hot}$ if the net vertical force is zero), the weight of the hot air in the balloon must be

$W_{\rm hot} = F_u - W_b = 75,674.3 - 4905.0= 70,769.3~\mbox{N}$

This means that the corresponding density of the hot air inside the balloon must be

${ \varrho_{\rm hot} = \frac{W_{\rm hot} }{g \cal{V}} = \frac{70,769.3}{9.81 \times 7,000} = 1.031~\mbox{kg m${^{-3}}$} }$

which, of course, is less than the density of the surrounding cool air, as expected.

We are asked to determine the corresponding temperature of the hot air, for which we can use the equation of state, i.e.,

$p = \varrho R T$

We are told to assume that the pressure inside the balloon is the same as that outside the balloon so

$p = \varrho_{\rm cool} R T_{\rm cool} = \varrho_{\rm hot} R T_{\rm hot}$

and rearranging gives the ratio of the temperatures as

$\frac{T_{\rm hot}}{T_{\rm cool}} = \frac{\varrho_{\rm cool}}{\varrho_{\rm hot}} = \frac{1.102}{1.1031} = 1.069$

We are told that the outside air temperature at 1,100 m is 10.5 $^{\circ}$ C or 283.65 $^{\circ}$ K. Therefore, the temperature of the hot air needed for neutral buoyancy will be

$T_{\rm hot} = 1.069 \, T_{\rm cool} = 1.069 \times 283.65 = 303.22~\mbox{$^{\circ}$K} = 30.16~\mbox{$^{\circ}$C}$

so a differential balloon internal temperature of about 20 $^{\circ}$ C at this altitude and temperature conditions.

Worked Example #22

A spherical holding tank with a diameter $d =$ 2.7 m stores gaseous helium for a blimp under a pressure of 250 kPa. Determine the total weight of the gas inside the tank. Assume that $R_{\rm He}$ = 2077.1 J kg $^{-1}$ K $^{-1}$ and ISA MSL temperature conditions prevail.

The volume ${\cal{V}}$ of the tank will be

${\cal{V}} = \frac{4}{3} \pi \left(\frac{d}{2}\right)^3 = \frac{4}{3} \pi \left( \frac{2.7}{2} \right)^3 = 10.306~\mbox{m${^3}$}$

To find the weight of helium, we need its density, so use the equation of state $p = \varrho R T$ and so

$\varrho = \frac{p}{R T}$

We are told to use ISA MSL temperature conditions so $T = T_0$ = 15 $^{\circ}$ C = (273.15 + 15) $^{\circ}$ K = 288.15 $^{\circ}$ K, which we can assume as the same temperature as the helium $T_{\rm He}$ . Therefore

$\varrho_{\rm He} = \frac{p_{\rm He} }{R_{\rm He} \ T_{\rm He} } = \frac{250 \times 10^3}{2077.1 \times 288.15} = 0.418~\mbox{kg m${^{-3}}$}$

The weight $W_{\rm He}$ of helium in the tank, therefore, will be

$W_{\rm He} = {\cal{V}} \, \varrho_{\rm He} \, g = 10.306 \times 0.418 \times 9.81 = 42.23~\mbox{N}$

Worked Example #23

Consider a circular cylinder of initial volume $\cal{V}$ = 5 liters whose height ${h}$ = 16 cm. It contains helium gas at ISA MSL pressure and temperature conditions. A weightless (and frictionless) piston seals the top end of the cylinder. A mass is then placed on the piston, which progressively pushes the piston down into the cylinder and compresses the helium gas to half its original volume in an isothermal process.

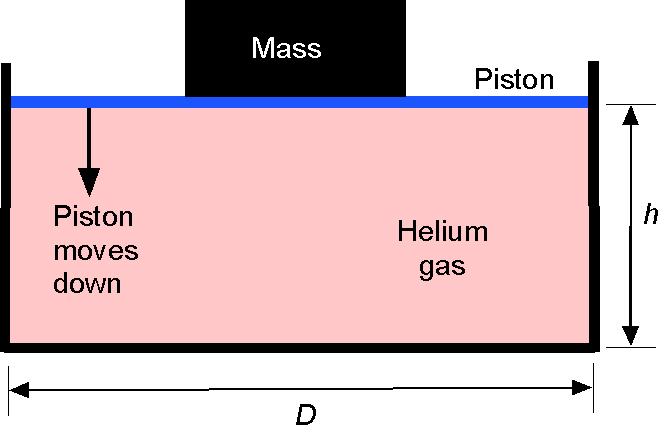
(a) Determine the mass of helium gas (in kg) in the cylinder. (b) What is the new pressure of the helium gas in the cylinder after it is compressed? (c) How large must a mass (in kg) be placed on the top of the piston to compress the gas? Assume that $R_{\rm He}$ = 2,077.0 J Kg $^{-1}$ K $^{-1}$ .

The volume is 5 liters, so ${\cal{V}}$ = 5,000 cm ${^3}$ = 0.005 m ${^3}$ . The conditions are specified as MSL ISA, so $p$ = 1.01325 $\times$ 10 $^{5}$ Pa and temperature $T$ = 15 $^{\circ}$ C = 288.15 $^{\circ}$ K.We see that volume, pressure, and temperature are involved in this question, so the use of the equation of state is appropriate, which can be written as

$p = \varrho R_{\rm He} T = \left( \frac{m}{\cal{V}} \right) R_{\rm He} T$

where $m$ is the mass of gas.

(a) Assume that state 1 refers to the uncompressed state and state 2 refers to the fully compressed state. We can calculate the mass of the gas (in kg) using

$m = \frac{p_1 {{\cal{V}}_1} }{R_{\rm He} T_1} = \frac{ 1.01325 \times 10^{5} \times 0.005}{ 2,077.0 \times 288.15} = 8.47 \times 10^{-4}~\mbox{kg}$

This gas mass is fixed because it is all contained in the volume below the piston.

(b) We have for the initial pressure at state 1

$p_1 = \left( \frac{m}{{\cal{V}}_1} \right) R_{\rm He} T_1$

and for the fully compressed pressure at state 2

$p_2 = \left( \frac{m}{{\cal{V}}_2} \right) R_{\rm He} T_2$

We are told that it is an isothermal process, so $T_1 = T_2$ so we can write for a given mass of gas that

$\frac{p_2}{p_1} = \frac{{\cal{V}}_1}{{\cal{V}}_2} = \frac{{\cal{V}}_1}{{\cal{V}}_1 /2} = \frac{2 {\cal{V}}_1}{{\cal{V}}_1} = 2$

Therefore, we have that

$p_2 = 2 p_1 = 2 \times 1.01325 \times 10^{5} = 2.0265 \times 10^{5}~\mbox{Nm$^{-2}$}$

(c) In this part, we need to find the force on the top of the piston to fully compress the helium to half its volume. Force is a pressure difference between the chamber and ambient times an area, so the area of the piston, using the symbol $A$ , is

$A = \frac{{\cal{V}}_1}{h} = \frac{0.005}{0.16} = 0.03125~\mbox{m${^{2}}$}$

The force, $F_2$ , required to compress the gas fully, therefore, will be

$F_2 = \left(p_2-p_1\right) A = \left(2.0265 - 1.01325\right) \times 10^{5} \times 0.03125 = 3.166 \times 10^3~\mbox{N}$

and the mass $M$ that needs to be placed on top of the piston will be

$M = \frac{F_2}{g} = \frac{3.166 \times 10^3}{9.81} = 322.73~\mbox{kg}$

Worked Example #24

Consider a large concrete dam that keeps sea water contained in a dock. The dam has dimensions of $W$ = 20 m wide (in the direction perpendicular to the screen) and is $H$ = 40 m high and $B$ = 30 m thick at its base. The density of seawater can be assumed to vary linearly with depth according to the formula $\varrho = \varrho_0+K \, h$ , where $\varrho_0$ = 1,028 kg m ${^{-3}}$ at ${h}$ = 0 and $K$ = 0.0026 kg m $^{-4}$ .

(a) Find an expression for the hydrostatic water pressure acting on the dam wall below point A at some general depth ${h}$ .
(b) What is the value of the maximum water pressure (in kPa) at the foot of the dam at point B?

(a) Starting from the usual form of the hydrostatic equation

$\displaystyle{\frac{dp}{dz}} = -\varrho g$

gives the differential equation

$\displaystyle{\frac{dp}{dh}} = \varrho g = (\varrho_0+Kh) g$

where the specified density variation has been included. Notice that this equation recognizes that ${h}$ is measured downward, i.e., in the opposite direction to the standard upward definition of ${z}$ .

(b) Separating the variables and integrating downward from the water surface to a general depth ${h}$ gives

$\int_{0}^{p}dp = \int_{0}^{h} (\varrho_0+Kh)g \, dh$

which gives the hydrostatic pressure from the water as

$p = g \left( \varrho_0 h +\frac{1}{2} K h^2 \right)$

When $h = H$ , which is at the foot of the dam, the previous result gives

$p_H = g \left( \varrho_0 H +\frac{1}{2} KH^2 \right)$

and substituting the numbers gives

$p = 9.81 \times \left( 1,028 \times 40 + 0.5 \times 0.0026 \times 40^2 \right) = 403.41~\mbox{kPa}$

Worked Example #25

After the Great Flood, the human race built the Tower of Babel to reach Heaven. A hot-air balloon was made to lift heavy materials from the ground to the tower. Consider a hot-air balloon as a sphere with an inflated diameter $d=50$ ft. The system’s total weight (including the fabric, basket, and payload, but without air inside) is 1,000 lb. You may assume that the local air density $\varrho$ in the ISA relative to MSL $\varrho_0$ is given by

$\frac{\varrho}{\varrho_0} = \left(1 - 6.876\times 10^{-6}h\right)^{4.252}$

where ${h}$ is the altitude in feet. Assume that the balloon’s air mass does not change during the ascent.
(a) Develop the buoyancy equation(s) when the balloon is in static equilibrium.
(b) When the balloon leaves the ground, the air inside is heated to 210 $^\circ$ F, and the pressure is equal to the MSL atmospheric pressure. Determine the maximum potential altitude $h_{\rm max}$ the balloon can achieve when the temperature of the air remains at 210 $^\circ$ F.

(a) The forces acting on the balloon include buoyancy force, the weight of the balloon structure, and the weight of hot air inside. When the balloon reaches the maximum altitude, the forces are in static equilibrium. We have

$F_{\rm up} = W_{\rm air} + W_{\rm balloon}$

(b) At the initial state, the density of the air inside the balloon is

$\varrho_{in,0} = \frac{p_{\rm atm}}{RT} = \frac{2116.4}{1716.59 \times (459.67+210)} = 0. 001841~\mbox{slug/ft}^3$

Assume the balloon is a sphere, so its volume $\mathcal{V}$ is

$\mathcal{V} = \frac{4}{3}\pi(d/2)^3 = 65,450~\mbox{ft}^3$

and the weight of air inside is

$W_{\rm air} = \varrho_{in,0} \, g \, \mathcal{V} = 0.001841 \times 65,450 \times 32.17= 3,876.4~\mbox{lb}$

By using the condition of static equilibrium, when the balloon achieves the maximum altitude, the air density is

$\varrho_{h_{\rm max}} = \frac{W_{\rm air} + W_{\rm balloon}}{g \mathcal{V} } = \frac{3,876.4+1,000}{32.17 \times 65,450} = 0.002316~\mbox{slug/ft}^3$

or the density ratio $\sigma$ is

$\sigma = \frac{\varrho_{h_{\rm max}} }{\varrho_0} = 0.9739$

Substitute this density into the MSL ISA model for the density and solving for ${h}$ gives the maximum potential altitude as

$h_{\rm max} \approx 900 \mbox{ft}$

Worked Example #26

A 6-inch diameter piston is located within a cylinder and connected to an inclined U-tube manometer. The fluid in the cylinder and the manometer is an oil with a density $\varrho_{\rm oil}$ = 1.83 slug ft ${^{-3}}$ . When a weight ${\cal{W}}$ is placed on the top of the piston, the fluid level in the inclined manometer tube moves 6 inches along the tube from points 1 to 2. What is the value of the weight ${\cal{W}}$ ? Assume that the change in the vertical position of the piston is negligible compared to the movement in oil along the tube, and the entire system is open to the atmosphere.

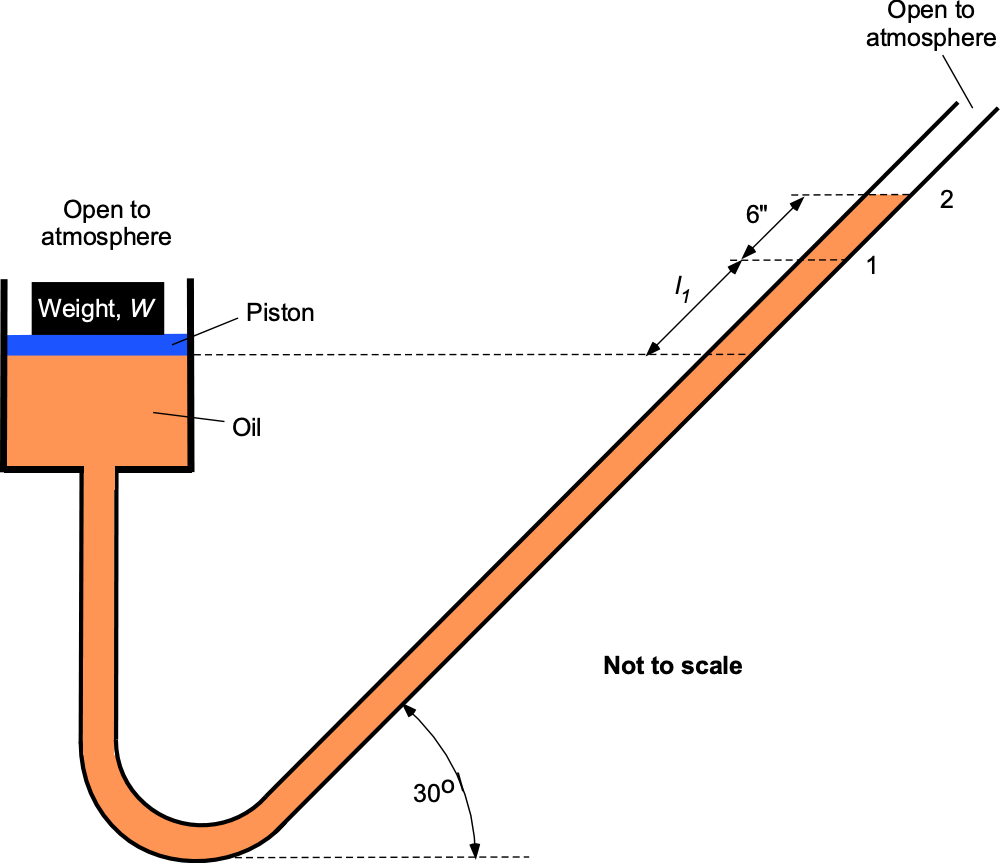
Both sides of the manometer are equally exposed to atmospheric pressure $p_a$ , so it will be apparent there will be no differential effect of $p_a$ on the height of the manometer column, which is initially at level 1.

When the weight ${\cal{W}}$ is placed on the top of the piston, the excess pressure on the oil from the weight (i.e., pressure = weight/area) causes the column to rise to level 2. For pressure equilibrium with the weight applied and recognizing that the pressure at the same height in the same fluid is equal, then

$p_a + \frac{ {\cal{W}} }{A_p} = p_a + \varrho_{\rm oil} \, g \, \left( 6.0/12.0 \right) \sin 30^{\circ}$

where $A_p$ is the cross-sectional area of the piston. Remember that the vertical height of the fluid levels matters in manometry. Hence, the $\sin 30^{\circ}$ term accounts for the inclined leg. The effects of the atmospheric pressure cancel out in the preceding equation, so

$\frac{ {\cal{W}} }{A_p} = \varrho_{\rm oil} \, g \left( 0.5 \right) 0.5 = 0.25 \, \varrho_{\rm oil} \, g$

and rearranging gives

${\cal{W}} = 0.25 \, \varrho_{\rm oil} \, g\, A_p$

The diameter of the piston is ${d}$ = 6-inches = 0.5 ft, so the area of the piston is

$A_p = \frac{\pi d^2}{4} = \frac{\pi 0.5^2}{4} = 0.1964~\mbox{ft${^{2}}$}$

Therefore, the value of the weight to be placed on top of the piston to get the fluid to move along the inclined leg the required 6 inches is

${\cal{W}} = 0.25 \, \varrho_{\rm oil} \, g\, A_p = 0.25 \times 1.83 \times 32.17 \times 0.1964 = 2.89~\mbox{lb}$

Worked Example #27

A fuel tank resides inside a spacecraft and is part of a specialized passive pressure relief valve for an emergency. The hinged gate opens only if subjected to an excess acceleration $n_{\rm max} g$ during a typical launch. To accomplish this, the gate is kept closed during a launch by a preload torque $M_h$ , exerted by a coil spring.

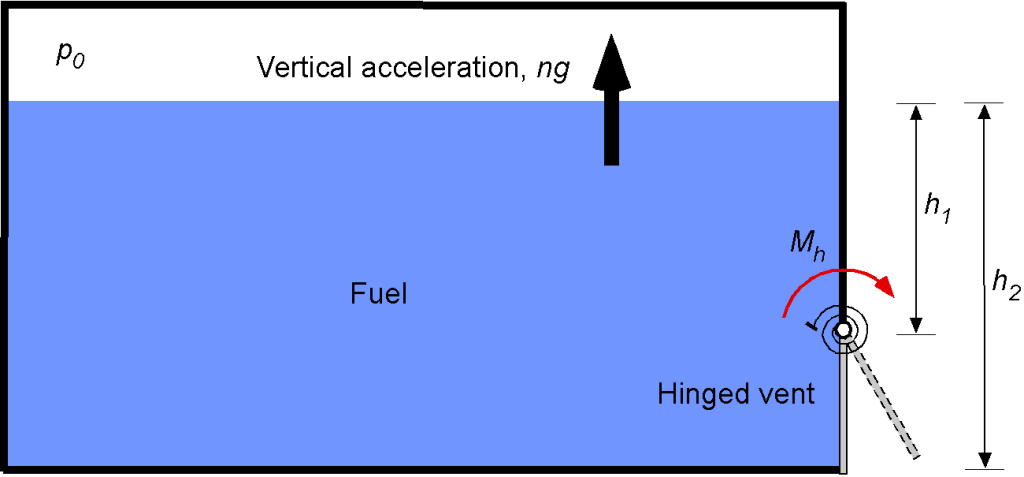
If the door length (normal to screen) is ${w}$ , determine the minimum required preload torque ( $M_h$ ) in terms of the parameters given. When the maximum acceleration is achieved, the spacecraft is in space, and the outside pressure is 0 atm. Calculate the minimum preload torque if $p_0$ = 101,325 Pa, $h_1$ = 45 cm, $h_2$ = 125 cm, $\varrho$ = 820 kg/m ${^3}$ , ${w}$ = 80 cm, and $n_{\rm max}$ = 5.

The pressure, the pressure force, and the moment of the pressure force about the hinge must be determined. This is a hydrostatics problem; the liquid’s pressure varies linearly with depth. Using the hydrostatic equation

$p = p_0 + \varrho n g h$

Where ${h}$ is measured downward from the surface of the liquid and $n$ is the translational acceleration load factor. The pressure variation on the door will produce a force $F$ . Considering a small strip of the door of height $dh$ and width ${w}$ , then the incremental force on that strip is

$dF = p \, w \, dh$

and so the net force on the door is obtained by integration, i.e.,

$F = \int_{h_1}^{h_2} p \, w \, dh = \int_{h_1}^{h_2} (p_0 + \varrho n g h) w \ dh$

To find the moment $M$ , the distance (arm) of the pressure force about the hinge must be determined, i.e., by inspection of the figure, the arm is $h - h_1$ . Therefore, the net moment about the hinge is

$M = \int_{h_1}^{h_2} (p_0 + \varrho n g h) (h - h_1) \, w \, dh$

which must now be solved. Expanding out gives

$M = \int_{h_1}^{h_2} \left( p_0 h - p_0 h_1 + \varrho n g h^2 - \varrho n g h h_1 \right) w \, dh$

Integrating gives

$M = w \left[ \frac{p_0 h^2}{2} - p_0 h_1 h + \frac{\varrho ng h^3}{3} - \frac{ \varrho n g h_1 h^2}{2} \right]_{h_1}^{h_2}$

Therefore

$\begin{eqnarray*} M & = & \left[ \frac{p_0 w h_2^2}{2} - p_0 w h_1 h_2 + \frac{\varrho n g w h_2^3}{3} - \frac{ \varrho n g w h_1 h_2^2}{2} \right] \nonumber \\ & & \quad \quad- \left[ \frac{p_0 w h_1^2}{2} - p_0 w h_1^2 + \frac{\varrho n g w h_1^3}{3} - \frac{ \varrho n g w h_1^3}{2} \right] \end{eqnarray*}$

and simplifying gives

$\begin{eqnarray*} M & = & \frac{1}{2} p_0 w \left( h_2^2 - h_1^2 \right) + p_0 w \left(h_1^2 - h_1 h_2 \right) \nonumber \\ & & \quad \quad- + \frac{1}{3} \varrho n g w \left( h_2^3 - h_1^3 \right) + \frac{1}{2} \varrho n g w \left(h_1^3 - h_1 h_2^2 \right) \end{eqnarray*}$

and so the moment is

$M = \frac{1}{2} p_0 w \left( h_2 - h_1 \right)^2 + \frac{1}{6} \varrho n g w \left( 2 h_2^3 - 3h_1 h_2^2 + h_1^3 \right)$

Substituting the values given leads to

$\begin{eqnarray*} M & = & \frac{1}{2} (101325) (0.8) \left( 1.25 - 0.45 \right)^2 \\ && + \frac{1}{6} (820) (5.0)(9.81) (0.8) \left( 2 (1.25)^3 - 3(0.45) 1.25^2 + 0.45^3 \right) \\ & = & 36.064~\mbox{kN \, m} \end{eqnarray*}$

MATLAB code check
P_0 = 101325; %Pa
h_1 = 45./100; %m
h_2 = 125./100; %m
rho = 820; %kg m-3
w = 80./100; %m
n = 5.0; % load factor
g = 9.81; %m s-2
M = (0.5.*P_0.*w.*((h_2-h_1).^2))+ …
((1./6).*rho.*n.*g.*w.*((2.*(h_2.^3))-(3.*h_1.*(h_2.^2))+(h_1.^3))); %Nm

Worked Example #28

A manometer containing water ( $\varrho_w$ = 1,000 kg m ${^{-3}}$ ) and mercury (SG = 13.6) is connected to a tank containing air at an internal pressure $p$ , the other end being open to atmospheric pressure $p_{\rm atm}$ of 101 $\times 10^3$ Pa.

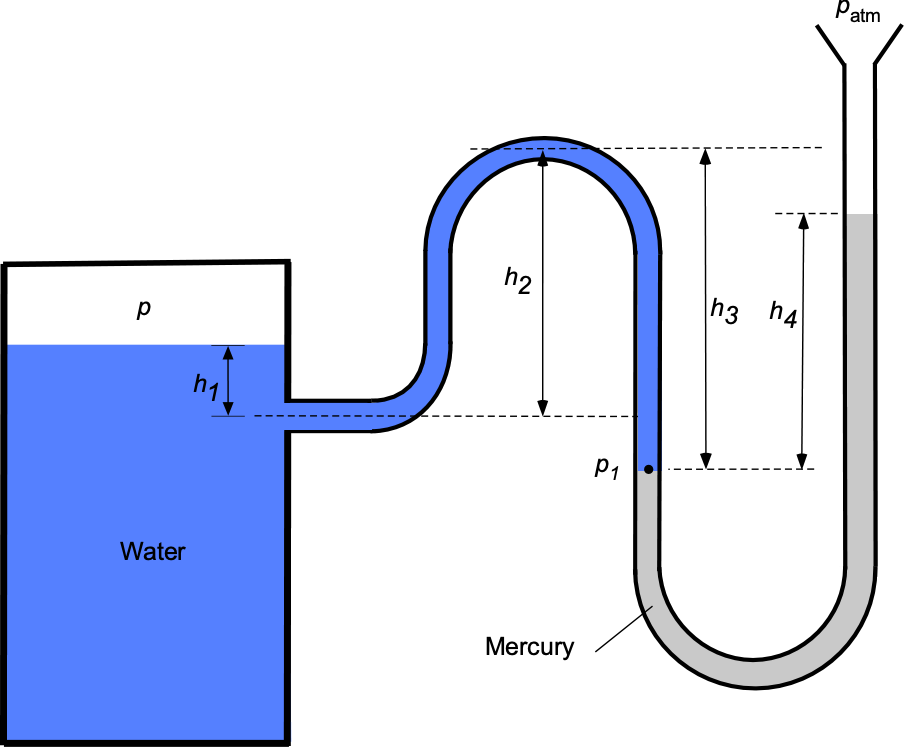
Using hydrostatic principles, derive an expression for the pressure $p_1$ in terms of $p_{\rm atm}$ .
Derive a corresponding expression for the pressure in the tank $p$ in terms of $p_1$ .
Obtain a final expression relating $p$ to $p_{\rm atm}$ .
If $h_1$ = 25 cm, $h_2$ = 50 cm, $h_3$ = 60 cm, and $h_4$ = 40 cm, then determine the internal pressure $p$ in the tank.
If the air temperature in the tank is measured to be 30 $^{\circ}$ C, determine its corresponding density.

1. Let $\varrho_{\rm Hg}$ be the density of mercury. Using the principles of hydrostatics then, the pressure $p_1$ will be

$p_1 = p_{\rm atm} + \varrho_{\rm Hg} g h_4$

2. Continuing to work around the leg in the manometer (and now the fluid is water with density $\varrho_w$ ), then

$p_1 - \varrho_w g h_3 + \varrho_w g h_2 - \varrho_w g h_1 = p$

and rearranging gives

$p_1 = p + \varrho_w g \left( h_3 - h_2 + h_1 \right)$

3. Equating the two previous results from parts (a) and (b) gives

$p_{\rm atm} + \varrho_{\rm Hg} g h_4 = p + \varrho_w g \left( h_3 - h_2 + h_1 \right)$

and rearranging gives

$p = p_{\rm atm} + \varrho_{\rm Hg} g h_4 - \varrho_w g \left( h_3 - h_2 + h_1 \right)$

or in final form as

$p = p_{\rm atm} + \varrho_{w} g \left( SG_{\rm Hg} \, h_4 - h_3 + h_2 - h_1 \right)$

where $SG_{\rm Hg}$ is the specific gravity of mercury, which is 13.6.

4. Now, we can substitute the given numerical values into the prior equation to give

$\begin{eqnarray*} p & = & p_{\rm atm} + \varrho_{w} g \left( SG_{\rm Hg} \, h_4 - h_3 + h_2 - h_1 \right) \\ & = & 101\times 10^3 + 1,000 \times 9.81 \left( 13.6 \times 0.4 - 0.6 + 0.5 - 0.25 \right) \\ & = & 150.9~\mbox{ kPa} \end{eqnarray*}$

5. The temperature $T$ of the air in the tank is given as 30 $^{\circ}$ C, so in units of Kelvin then

$T = 30 + 273.15 = 303.15 \mbox{K}$

The density of the air can be found from the equation of state, i.e.,

$\varrho = \frac{p}{R \, T} = \frac{150.9 \times 10^3} {287.1 \times 303.15} = 1.734~\mbox{kg m${^{-3}}$}$

Worked Example #29

A manometer containing water ( $\varrho_{w}$ = 1,000 kg m ${^{-3}}$ ) and Galinstan (SG = 6.44) is connected to a cylindrical water tank with a piston on top, as shown in the figure below. The diameter of the tank $D$ is 0.45 m. A mass $M$ = 6 kg is placed on top of the piston; the piston can be assumed to be weightless. Both sides of the system are open to an atmospheric pressure $p_{\rm atm}$ = 101.3 kPa. The height values are: $h_1$ = 15.0 cm, $h_2$ = 50.0 cm, $h_3$ = 65.0 cm, and $h_5$ = 95.0 cm.

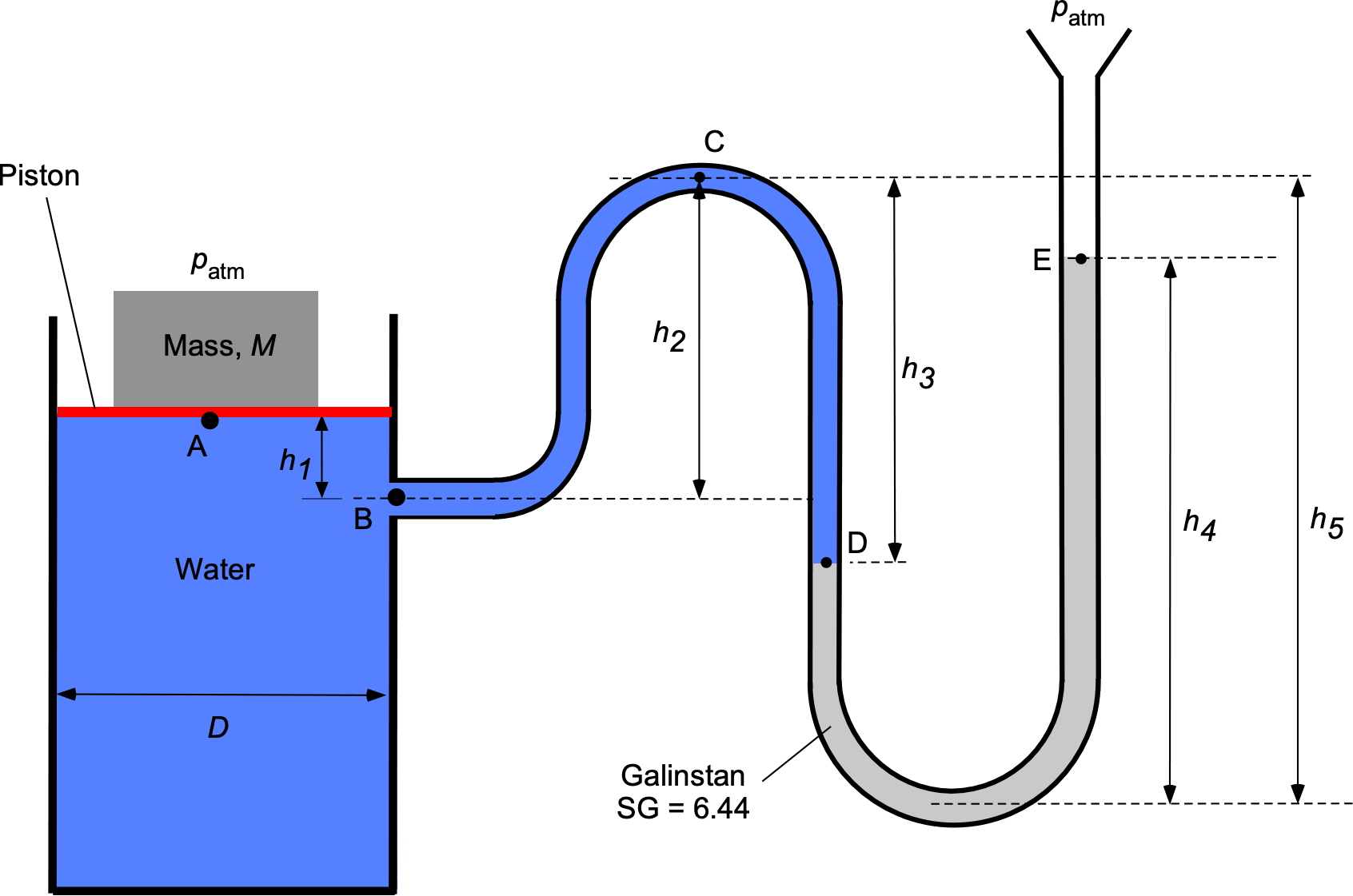
Part 1: Determine an equation for and evaluate the pressure (in kPa) at:

$p_A$ at point A (just below the piston).
$p_B$ at point B.
$p_C$ at point C.
$p_D$ at point D.

Part 2: Answer the following:

What is the relationship (as an equation) between the value of the mass $M$ and the height $h_4$ of the Galinstan column?
For the values of the parameters as given, what will be the value of $h_4$ (in units of cm)?

Part 1:

1. $p_A$ at point A (just below the piston): Pressure is defined as force/area, so the pressure at point A will be

$p_A = p_{\rm atm} + \frac{M \, g}{A} = p_{\rm atm} + \frac{W}{A}$

where $W$ is the weight ( $W = M g)$ and $A$ is the cross-sectional area of the cylinder. Therefore,

$p_A = p_{\rm atm} + \frac{W}{A} = p_{\rm atm} + \frac{4W}{\pi D^2}$

and inserting the values gives

$p_A = 101.3 \times 10^3 + \frac{ 4.0 \times 6.0 \times 9.81}{\pi \, 0.45^2} = 101.67~\mbox{kPa}$

2. $p_B$ at point B: We are going DOWN in the water with an increase in depth $h_1$ , so the pressure at point B will be

$p_B = p_A + \varrho_w \, g \, h_1$

Inserting the values gives

$p_B = p_A + \varrho_w \, g \, h_1 = 101.67 \times 10^3 + 1,000 \times 9.81 \times 0.15 = 103.142~\mbox{kPa}$

3. $p_C$ at point C: We are going UP in the water with a decrease in depth $h_2$ , so the pressure at point C will be

$p_C = p_B - \varrho_w \, g \, h_2$

Inserting the values gives

$p_C = p_B - \varrho_w \, g \, h_2 = 103.142 \times 10^3 - 1,000 \times 9.81 \times 0.50 = 98.237~\mbox{kPa}$

4. $p_D$ at point D: We are going DOWN in the water with an increase in depth $h_3$ , so the pressure at point D will be

$p_D = p_C + \varrho_w \, g \, h_3$

Inserting the values gives

$p_D= p_C + \varrho_w \, g \, h_3 = 98.237 \times 10^3 + 1,000 \times 9.81 \times 0.65 =104.615~\mbox{kPa}$

Part 2:

1. In this problem, we continue the preceding process until we get to point E, i.e.,

$p_{\rm atm} + \frac{W}{A} + \varrho_w \, g \, h_1 - \varrho_w \, g \, h_2 + \varrho_w \, g \, h_3 + \varrho_g \, g \left( h_5 - h_3 \right) - \varrho_g \, g \, h_4 = P_E = p_{\rm atm}$

and noting at the $\varrho_g$ is the density of Galistan and $\varrho_g = 6.44 \varrho_w$ . Collecting terms and also noting that the effects of $p_{\rm atm}$ will balance out on each side of the problem (piston side and open end of U-tube), then

$\frac{W}{A} + \varrho_w \, g \left( h_1 - h_2 + h_3 \right) + \varrho_g \, g \left( h_5 - h_3 - h_4 \right) = 0$

so

$\frac{M \, g}{A} = \varrho_w \, g \left( h_2 - h_1 - h_3 \right) + \varrho_g \, g \left( h_3 - h_5 + h_4 \right)$

which establishes the relationship between $W$ and $h_4$ (the only unknown). Rearranging gives

$\varrho_g \, g \, h_4 = \varrho_w \, g \left( h_1 - h_2 + h_3 \right) + \varrho_g \, g \left( h_5 - h_3 \right) + \frac{M \, g}{A}$

and by canceling out the acceleration under gravity, the “ $g$ ” term gives

$\varrho_g \, h_4 = \varrho_w \left( h_1 - h_2 + h_3 \right) + \varrho_g \left( h_5 - h_3 \right) + \frac{M}{A}$

So the value of $h_4$ is

$h_4 = \frac{\varrho_w}{\varrho_g} \, \left( h_1 - h_2 + h_3 \right) + \left( h_5 - h_3 \right) + \frac{M}{A \, \varrho_g}$

Notice that the grouping $M / (A \, \varrho_g)$ has length dimensions, as it should if the equation is to be dimensionally homogeneous. Also, the ratio of the densities $\varrho_g/\varrho_w$ is the specific gravity of the Galinstan = 6.44.

2. The final step in this question is to insert the numerical values given to us. Therefore, the value of $h_4$ is

$h_4 = \frac{\varrho_w}{\varrho_g} \, \left( h_1 - h_2 + h_3 \right) + \left( h_5 - h_3 \right) + \frac{M}{A \, \varrho_g}$

so

$h_4 = \frac{1.0}{6.44} \left( 0.15 - 0.50 + 0.65 \right) + \left( 0.95 - 0.65 \right) + \frac{ 4.0 \times 6.0 }{\pi \, 0.45^2 \times 6.44 \times 10^3} = 35.24~\mbox{cm}$

Worked Example #30

Consider a cylinder of circular cross-section containing helium gas, initially at MSL ISA pressure and temperature conditions. A frictionless piston seals the top end of the cylinder, as shown in the figure below. The initial volume of helium is 5.2 liters, and the bottom of the piston is at a height $h =$ 16.2 cm. A mass is then placed on the piston, which pushes the piston down into the cylinder to $h =$ 8.3 cm and compresses the helium gas inside. During this process, the temperature of the gas also increases by 23.3 $^{\circ}$ C. Assume that for helium $R_{\rm He}$ = 2,077 J Kg $^{-1}$ K $^{-1}$ .

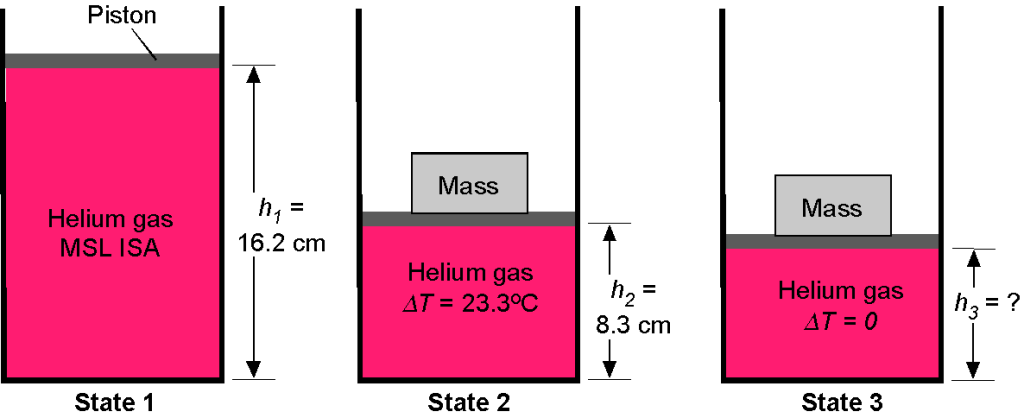
1. Determine the mass of helium gas in the cylinder.
2. What is the new pressure of the helium gas after it is fully compressed?
3. What will be the value of the mass placed on the top of the piston to compress the gas to these conditions?
4. If the helium cools back to ambient conditions, what will be the value of $h_3$ ?

The volume is 5.2 liters, so ${\cal{V}}$ = 5,200 cm ${^3}$ = 0.0052 m ${^3}$ . The conditions are specified as MSL ISA, so the pressure $p = 1.01325 \times 10^{5}$ Nm $^{-2}$ = 1.01325 $\times 10^{5}$ Pa, and temperature $T$ = 15 $^{\circ}$ C = 288.15 $^{\circ}$ K. We see that volume, pressure, density, and temperature are all involved in this question, so the use of the equation of state is appropriate, i.e.,

$p = \varrho \, R \, T = \left( \frac{m}{\cal{V}} \right) R \, T$

where $m$ is the mass of gas inside the cylinder.1. State 1 refers to the uncompressed state, and State 2 refers to the initially compressed state. We can calculate the mass of the gas (in kg) using

$m = \frac{p_1 {{\cal{V}}_1} }{R_{\rm He} \, T_1} = \frac{ 1.01325 \times 10^{5} \times 0.0052}{ 2,077.0 \times 288.15} = 8.804 \times 10^{-4}~\mbox{kg}$

Notice that helium is relatively light. This mass of helium gas is fixed because it is all contained in the volume below the piston. Therefore, the corresponding density of the helium at State 1 is

$\varrho_1 = \frac{m}{{{\cal{V}}_1} } = \frac{8.804 \times 10^{-4}}{ 0.0052} = 0.1693~\mbox{kg m${^{-3}}$}$

2. We have for the initial pressure $p_1$ at State 1

$p_1 = \varrho_1 \, R_{\rm He} \, T_1 = 1.01325 \times 10 ^{5}~\mbox{Pa}$

and for the compressed pressure $p_2$ at State 2

$p_2 = \varrho_2 \, R_{\rm He} \, T_2$

where $T_2$ = 288.15 + 23.3 = 311.45 $^{\circ}$ K. The density $\varrho_2$ is

$\varrho_2 = \varrho_1 \left( \frac{h_1}{h_2} \right) = 0.1693 \left( \frac{16.2}{8.3} \right) = 0.3304~\mbox{kg m${^{-3}}$}$

and so the corresponding pressure $p_2$ is

$p_2 = \varrho_2 \, R_{\rm He} \, T_2 = 0.3304 \times 2,077.0 \times 311.45 = 2.1373 \times 10 ^{5}~\mbox{Pa}$

3. We now need to find the force on the top of the piston to compress the helium. Force is a pressure times an area, so the area of the piston is

$A = \frac{{\cal{V}}}{h_1} = \frac{0.0052}{0.16} = 0.0321~\mbox{m${^{2}}$}$

The weight, $W$ , on the piston that is required to fully compress the gas to State 2 will be

$W = p_2 \, A = 2.1373 \times 10^{5} \times 0.0321 = 6.861 \times 10^3~\mbox{N}$

and the corresponding mass $M$ that needs to be placed on top of the piston will be

$M = \frac{W}{g} = \frac{6.861 \times 10^3}{9.81} = 699.4~\mbox{kg}$

4. If the helium gas now cools down back to ambient temperature $T_1$ = 15 $^{\circ}$ C = 288.15 $^{\circ}$ K at State 3, then the weight will push the piston down a little further to $h_3$ . In this case

$p_3 = \frac{W}{A} = \varrho_3 \, R_{\rm He} \, T_1 = \left( \frac{m}{ A h_3} \right) R_{\rm He} T_1$

where the final compressed volume is just $A h_3$ . Therefore, $h_3$ is given by

$h_3 = \left( \frac{m}{W} \right) \, R_{\rm He} \, T_1 = \frac{8.804 \times 10^{-4}}{6.861 \times 10^3} \times 2,077.0 \times 288.15 = 0.0768~\mbox{m} = 7.68~\mbox{cm}$

Worked Example #31

An oil pipeline and a rigid air tank containing compressed air at an initial pressure of 1.169 MPa and temperature of 80 $^{\circ}$ C are connected by a manometer filled with Gordium, as shown in the figure below. Assume that the hydrostatic effects of the air column inside the tank and the air volume in the manometer are negligible. The specific gravity for the oil is 2.68 and 11.8 for Gordium. Assume that the water density is $\varrho_w =$ 1,000 kg m ${^{-3}}$ .

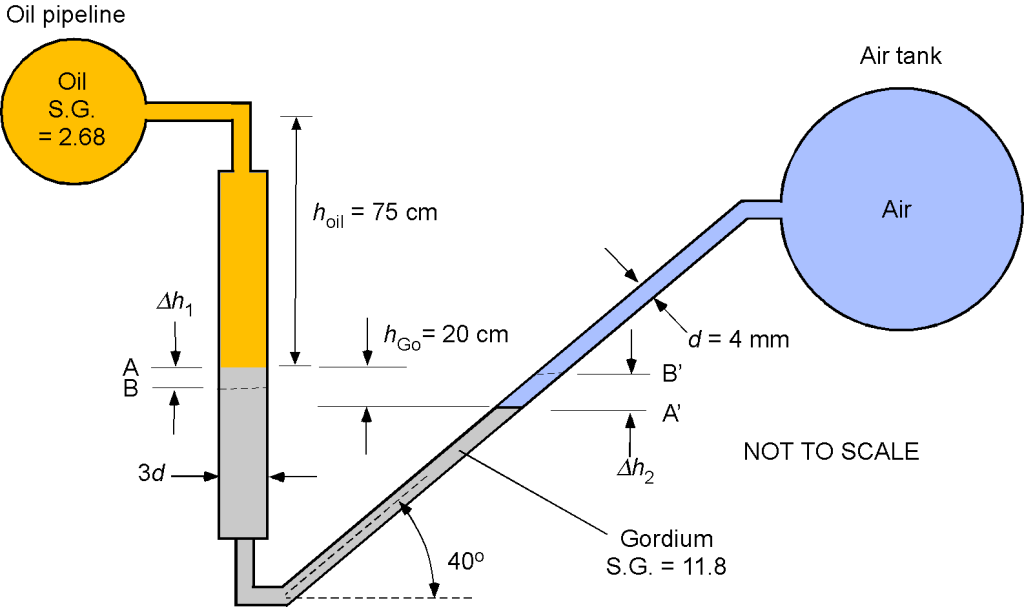
1. Determine the air density in the tank.
2. Determine the oil pressure in the pipe.
3. For a decrease in temperature in the air tank from 80 $^{\circ}$ C to 40 $^{\circ}$ C and assuming that the pressure in the oil pipe remains constant, then determine:
(i) The new pressure in the air tank.
(ii) The changes in the level of the manometer fluid $\Delta h_1$ at the oil/Gordium interface and the manometer fluid $\Delta h_2$ at the air/Gordium interface.

1. We see that pressure, density, and temperature are all involved in this question, so the use of the equation of state is appropriate, i.e.,

$p = \varrho R \,T$

Rearranging for the density gives

$\varrho = \frac{p}{R \, T}$

We are given the pressure and temperature in the compressed air tank, so

$\varrho_{\rm air} = \frac{p_{\rm air}}{R \, T_{\rm air}} = \frac{1.169 \times 10^6}{287.057 \times (273.15 + 80.0)} = 11.531~\mbox{kg m${^{-3}}$}$

2. We need to use hydrostatic principles to find the pressure in the oil pipe over on the manometer’s other leg. Starting at the oil pipe, then adding a hydrostatic pressure increment as we go down and subtracting a hydrostatic pressure increment as we go up, and then

$p_{\rm oil} + \varrho_{\rm oil} \, g \, h_{\rm oil} + \varrho_{\rm Go} \, g \, h_{\rm Go} = p_{\rm air}$

Also, remember that we are told to ignore the (negligible) hydrostatic effects of the air column inside the tank and the air volume in the manometer. Rearranging gives the pressure in the oil pipe as

$p_{\rm oil} = p_{\rm air} - \varrho_{\rm oil} \, g \, h_{\rm oil} - \varrho_{\rm Go} \, g \, h_{\rm Go}$

Inserting the values of the given quantities gives

$p_{\rm oil} = 1.169 \times 10^6 - (2.68 \times 10^3 \times 9.81 \times 0.75) - (11.8 \times 10^3 \times 9.81 \times 0.20)$

noting that $\varrho_{\rm oil} = {\rm SG}_{\rm oil} \, \varrho_w$ and that $\varrho_{\rm Go} = {\rm SG}_{\rm oil} \, \varrho_w$ . Performing the arithmetic gives

$p_{\rm oil} = 1.169 \times 10^6 -1.9718 \times 10^4 - 2.3152 \times 10^4 = 1.126 \times 10^6~\mbox{Pa} = 1.126~\mbox{MPa}$

3. For a decrease in temperature in the air tank from $T_1 =$ 80 $^{\circ}$ C to $T_1 =$ 40 $^{\circ}$ C, then

(i) The new pressure $p_2$ in the air tank will be

$p_2 = \varrho _{\rm air} \, R_{\rm air} \, T_2$

Let $p_{1} = p_{\rm air}$ , and we note that the tank contains the same gas mass, so the density is unchanged. Therefore, the new pressure is

$p_{2} = p_{1} \left( \frac{T_2}{T_1} \right) = 1.169 \times 10^6 \times \left( \frac{273.15 + 40.0}{273.15 + 80.0} \right) = 1.0366~\mbox{MPa}$

(ii) Notice that the left-side leg of the manometer has a larger bore than the right-side leg, in the ratio 3:1. This means that if the level in the left-side leg drops by some amount, say ${x}$ , then it is necessary to determine the change in the fluid length along the right-side leg as well as the corresponding vertical change. The volume of the Gordium is fixed, so the relationship is

$x \left( \frac{\pi (3d)^2}{4} \right) = y \left( \frac{\pi d^2}{4} \right)$

so $y = 9 x$ . Because we need the vertical height change of the Gordium on the right-side leg, then

$y_{\rm vert} = 9 x \sin (40^{\circ}) = 5.785 x$

Returning to the equation for the hydrostatic balance, then

$p_{\rm oil} + \varrho_{\rm oil} \, g \, h_{\rm oil} + \varrho_{\rm Go} \, g \, h_{\rm Go} = p_{\rm air}$

The changes in the heights of the Gordium for a change in air pressure will manifest as

$p_{\rm oil} + \varrho_{\rm oil} \, g \, ( h_{\rm oil} + x) + \varrho_{\rm Go} \, g \, ( h_{\rm Go} - 5.785 x) = p_{\rm air}$

which can be rewritten more simply in terms of the SG, i.e.,

${\rm SG}_{\rm oil} (h_{\rm oil} + x) + {\rm SG}_{\rm Go} \ ( h_{\rm Go} - 5.785 x) = \frac{p_{\rm air} - p_{\rm oil}}{\varrho_w \, g}$

Substituting the numerical values gives

$2.68 \times (0.75 + x) + 11.8 ( 0.20 - 5.785 x) = \frac{( 1.0366- 1.126) \times 10^6}{1,000 \times 9.81}$

so

$x = 0.19~\mbox{m}$

The changes in the level $\Delta h_1$ of the manometer fluid at the oil/Gordium interface will drop 19 cm, and the manometer fluid $\Delta h_2$ at the air/Gordium interface will increase by 1.1 m. Of course, it is noted that the change in the height of the Gordium along the length of the inclined tube is very sensitive to the change in pressure in the air tank.

Worked Example #32

Consider the manometer system below, which taps off and connects two pipes containing fluids A and B, respectively. Fluid A has a specific gravity (S.G.) of 0.9, and fluid B has an S.G. of 3.7. Assume that the density of water is 1.940 slugs/ft ${^3}$ .

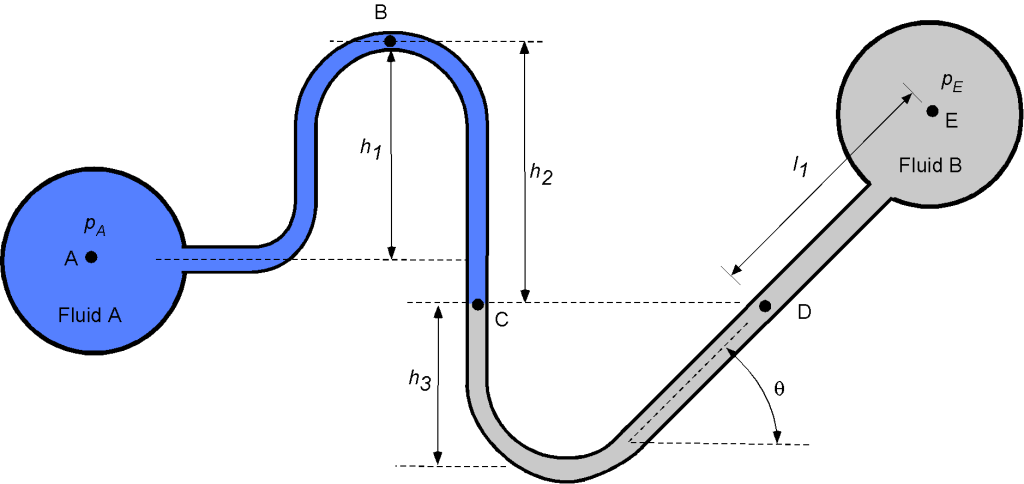
Determine an expression for the pressure at point B.
Determine an expression for the pressure at point C.
Determine an expression for the pressure at point D.
Write down a final expression for the value of $p_A - p_E$ .
If the pressure $p_A$ were to decrease, what would happen to the level at point C?
If $h_1$ = 10 inches, $h_2$ = 13 inches, $h_3$ = 5 inches, $l_1$ = 15 inches, and $\theta$ = 45 $^{\circ}$ , then calculate the pressure difference $p_A - p_E$ in units of lb/in ${^{2}}$ .

1. The pressure at point B will be

$p_B = p_A - \varrho_A \, g \, h_1$

where $\varrho_A$ is the density of fluid A.

2. The pressure at point C will be

$p_C = p_B + \varrho_A \, g \, h_2 = p_A - \varrho_A \, g \, h_1 + \varrho_A \, g \, h_2$

3. Because points C and D are at the same height connected by the same fluid, then the pressure at point D is the same as at point C, i.e.,

$p_D = p_C = p_A - \varrho_A \, g \, h_1 + \varrho_A \, g \, h_2$

4. For the final part of the manometer, we are given a diagonal length $l_1$ in fluid B rather than a vertical height. However, the vertical height between points D and E is just $l_1 \sin \theta$ , so that

$p_E = p_D - \varrho_B \, g \, l_1 \sin \theta$

where $\varrho_B$ is the density of fluid B, and

$p_E = p_A - \varrho_A \, g \, h_1 + \varrho_A \, g \, h_2 - \varrho_B \, g \, l_1 \sin \theta$

Therefore, the final expression for $p_A - p_E$ is

$p_A - p_E = \varrho_A \, g \, h_1 - \varrho_A \, g \, h_2 + \varrho_B \, g \, l_1 \sin \theta$

and collecting terms gives

$p_A - p_E = \varrho_A \, g \left( h_1 - h_2 \right) + \varrho_B \, g \, l_1 \sin \theta$

5. If the pressure $p_A$ were to decrease, then the level at point C would increase, so the level $h_3$ would increase, and the value of $h_2$ would decrease.

6. In the final part, we are asked to substitute some known heights for the various levels and calculate the value of the pressure difference $p_A - p_E$ . We are given the specific gravity of each fluid, so

$p_A - p_E = \varrho_w \, g \bigg( SG_A (h_1 - h_2) + SG_B \, l_1 \sin \theta \bigg)$

Substituting the known values gives

$p_A - p_E = 1.94 \times 32.17 \bigg( 0.9 \times (10.0 - 13.0)/12.0 + 3.7 \times (15.0/12.0) \sin 45^{\circ} \bigg)$

Finally, after doing the arithmetic, then the required pressure difference is

$p_A - p_E = 190.061~\mbox{lb/ft${^{2}}$} = 1.32~\mbox{lb/in${^{2}}$}$

Worked Example #33

The viscosity of an oil is to be determined using a falling ball viscometer, as shown in the figure below. A heavy steel ball of diameter ${d}$ is dropped into the oil and slowly descends at a steady velocity $V_d$ , the time taken for the ball to pass between two reference points being recorded. The forces acting on the ball will be its weight, buoyancy, and fluid drag. The fluid drag force, $D$ , is given by

$D = 3 \, \pi \, \mu \, V_d \, d$

where $\mu$ is the viscosity (coefficient of dynamic viscosity), which is to be determined. The steel ball has a diameter of 2.1 mm and a density of 7,750 kg m ${^{-3}}$ . The oil has a density of 940.2 kg m ${^{-3}}$ . What is the oil’s viscosity if the steel ball falls through a distance of 30 cm in 12.6 s?

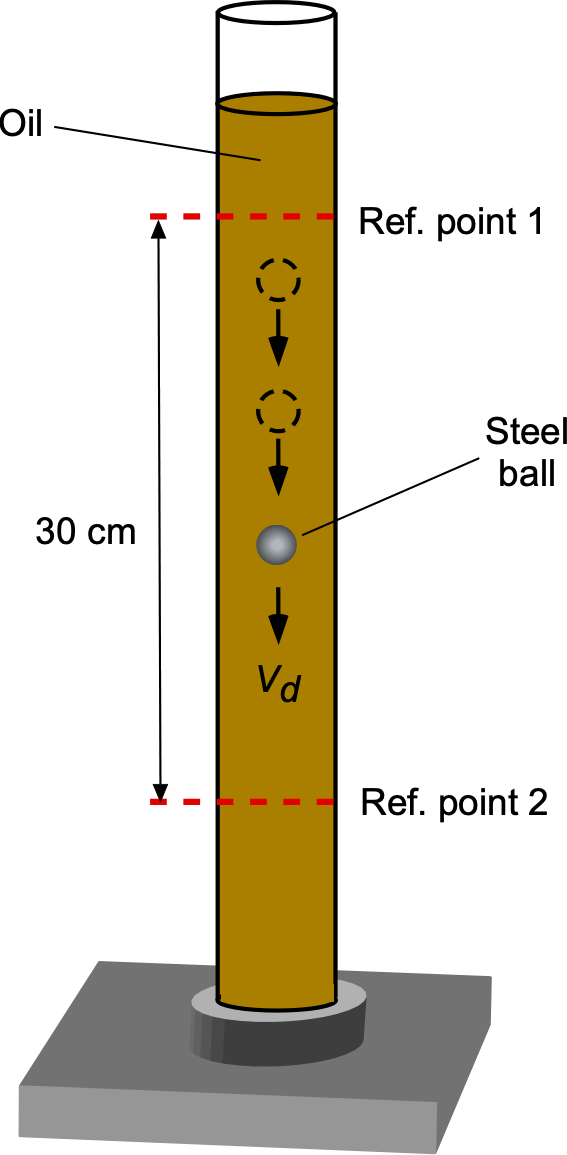
The balance of forces in equilibrium is such that the weight of the ball, $W_b$ , less any buoyancy force, $B_b$ , is equal to the viscous drag on the ball, $D_{\mu}$ . The weight will be density times volume times acceleration under gravity, i.e.,

$W_b = \varrho_b \left( \frac{4}{3} \pi R^3 \right) \,g$

where $\varrho_b$ is the density of the steel ball and $R= d/2$ . The (upward) buoyancy force on the ball (Archimedes’s principle) will be equal to the weight of oil displaced by the ball, i.e.,

$B_b = \varrho_{\rm oil} \left( \frac{4}{3} \pi R^3 \right) \,g$

Therefore, the equilibrium equation is

$W_b - B_b - D_{\mu} = 0 = \frac{4}{3} \pi R^3 \, g \left( \varrho_b -\varrho_{\rm oil} \right) - D_{\mu}$

The drag force $D_{\mu}$ on a sphere of radius $R$ moving through a fluid of high viscosity $\mu$ at low speed $V$ (this is called a creeping flow) is given by Stokes’s law, i.e.,

$D_{\mu} = 3 \, \pi \, \mu \, V_d \, d = 6 \, \pi \, \mu \, V_d \, R$

Therefore, in equilibrium, then

$\frac{4}{3} \pi R^3 \, g \left( \varrho_b -\varrho_{\rm oil} \right) - 6 \pi \mu V_d \, R = 0$

and rearranging to solve for $\mu$ gives

$\mu = \frac{2 ( \varrho_b - \varrho_{\rm oil}) }{9 \, V_d} \, g \, R^2$

The value of $V_d$ can be found using the measured time over the fixed distance, i.e.,

$V_d = \frac{0.30}{12.6} = 0.02381~\mbox{m s$^{-1}$}$

Therefore, introducing all of the numerical values gives

$\mu = \frac{2 \times (7,750 - 940.2) }{9 \times 0.02381} \times 9.81 \times (0.0021/2)^2 = 0.6875~\mbox{Pa s}$

Worked Example #34

The density of an irregularly shaped solid object needs to be determined. The object’s shape is such that it cannot be determined geometrically. Given a container of water, a thin wire, and a load cell to measure force, explain how you would measure the density of this object. Explain all the steps you would take and use equations to support your approach.

This question is about buoyancy and Archimedes’ principle, which states that the buoyancy force on a body immersed in a fluid equals the weight of the fluid displaced. In this case, you should tie the body to the wire, weigh it in the air, and then weigh it when immersed in the water. The difference, then, is the buoyancy force.

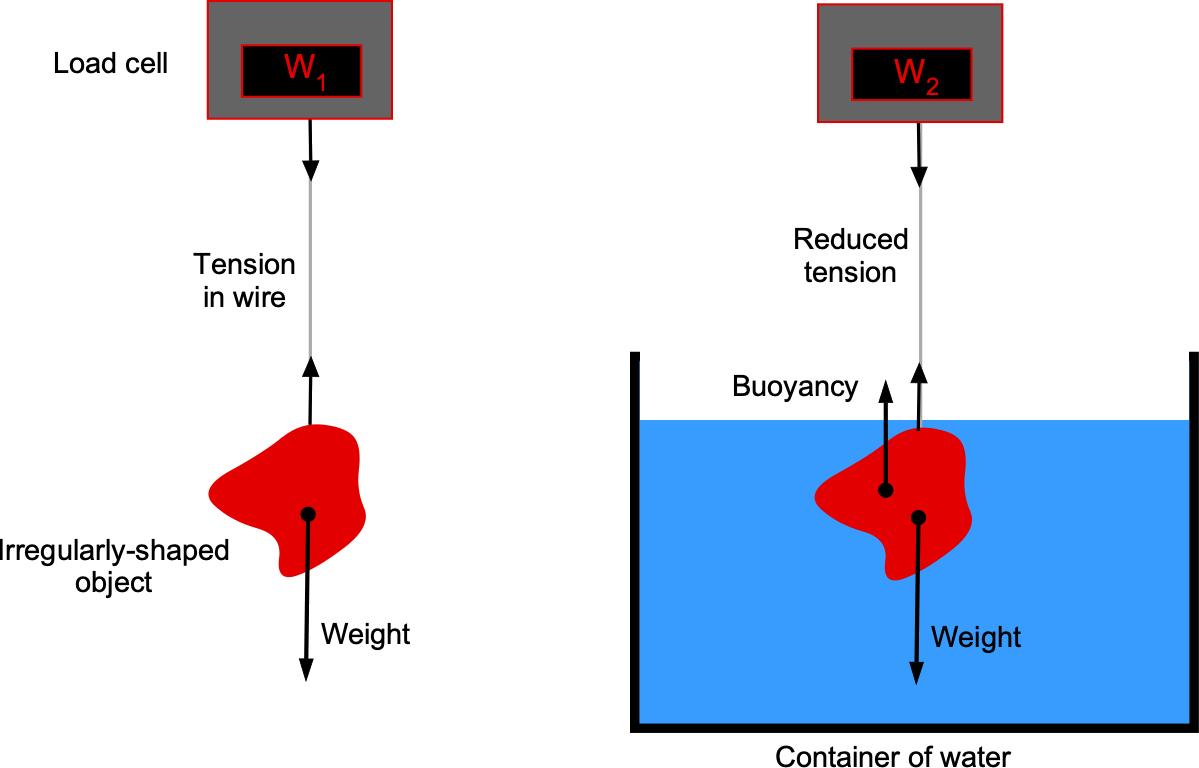
The weight of the body measured on the scale in air is

$W_1 = \varrho_b {\cal{V}} g~\mbox{~(this is the first reading)}$

where ${\cal{V}}$ is the volume of the body. The buoyancy force, according to Archimedes’ principle, is

$F_b = \varrho_w {\cal{V}} g$

The effective weight of the body measured on the scale when immersed in water is

$W_2 = W_1 - F_b = W_1 - \varrho_w {\cal{V}} g~ \mbox{~(this is the second reading)}$

Therefore,

$W_1 - W_2 = \varrho_w {\cal{V}} g$

from which the volume of the body is

${\cal{V}} = \frac{W_1 - W_2}{\varrho_w g}$

The density of water, $\varrho_w$ , is known. And because $\varrho_b {\cal{V}} g = W_1$ then

$\varrho_b = \frac{W_1}{{\cal{V}} g } = \left( \frac{W_1}{W_1 - W_2} \right) \varrho_w$

Therefore, the object’s density can be determined using the two readings on the load cell, $W_1$ and $W_2$ , and the known density of water.

Worked Example #35

Soap bubbles filled with a gas lighter than air (e.g., helium) can cause the bubble to become neutrally buoyant. Determine an equation for the size (radius) of such bubbles. Take into consideration the weight of the soap film of the bubble if its film thickness is $t$ .

The condition for neutral buoyancy (where the bubble neither rises nor falls) is determined by equating the buoyant force to the weight of the gas inside and the soap film. The volume of the bubble is

${\cal{V}} = \frac{4}{3} \pi R^3$

and so the buoyancy force is

$F_b = \varrho_{\rm{air}} \, {\cal{V}} \, g = \varrho_{\rm{air}} \, \frac{4}{3} \pi R^3 g$

The weight of the helium inside the bubble is

$W_{\rm{He}} = \varrho_{\rm{He}} {\cal{V}}g = \varrho_{\rm{He}} \frac{4}{3} \pi R^3 g$

Finally, the weight of the soap film making the bubble is

$W_{\rm{soap}} = 4 \pi R^2 t \varrho_{\rm{soap}} g$

where $t$ is its thickness. Therefore, the neutral buoyancy equilibrium condition is when

$\rm{Buoyancy~force} = \rm{Weight~of~helium} + \rm{Weight~of~soap~film}$

Substituting the preceding expressions gives

$\varrho_{\rm{air}} \frac{4}{3} \pi R^3 g = \varrho_{\rm{He}} \frac{4}{3} \pi R^3 g + 4 \pi R^2 t \varrho_{\rm{soap}} g$

Solving for the radius of the bubble, $R$ , gives

$R = \frac{3 t \, \varrho_{\rm{soap}}}{(\varrho_{\rm{air}} - \varrho_{\rm{He}})}$

Therefore, we see that the surface tension is not directly involved in the calculation of the bubble’s diameter for achieving neutral buoyancy. However, surface tension is fundamentally important in the formation and stability of soap bubbles.

Worked Example #36

Consider a cylindrical tank of radius $R = 2 \, \text{m}$ and height $H = 5 \, \text{m}$ . The tank is filled with water up to a height of $h = 4 \, \text{m}$ . A circular hatch of radius $r = 1 \, \text{m}$ is located at the bottom of the tank. The hatch is hinged along one side and is held closed by a horizontal force $F$ applied at the opposite side. Calculate the total hydrostatic force exerted on the circular hatch by the water. Determine the position of the center of pressure on the hatch. Find the magnitude of the horizontal force $F$ required to keep the hatch closed.

The cylindrical tank has a radius $R = 2 \, \text{m}$ , height $H = 5 \, \text{m}$ , filled with water up to height $h = 4 \, \text{m}$ . A circular hatch of radius $r = 1 \, \text{m}$ is located at the bottom. The pressure at depth ${h}$ is

$p(h) = \varrho \, g \, h = 1,000 \times 9.81 \times 4 = 39,240 \, \text{Pa}$

The area of the hatch is

$A = \pi \, r^2 = \pi \times (1)^2 = \pi \, \text{m}^2$

Therefore, the total force on the hatch is

$F_H = p(h) \, A = 39,240 \times \pi = 123,352 \, \text{N}$

The center of pressure is given by

$z_{cp} = \dfrac{I_G}{A \, h_c} + h_c$

For a circle, then

$I_G = \dfrac{\pi r^4}{4} = \dfrac{\pi (1.0)^2}{4} = \dfrac{\pi}{4} \, \text{m}^4$

Therefore,

$z_{cp} = \dfrac{\dfrac{\pi}{4}}{\pi \times 1 \times 4} + 4 = \dfrac{1}{16} + 4 = 4.0625 \, \text{m}$

The moment from a hydrostatic force about the hinge will be

$M_H = F_H \, r = 123,352 \, \text{N m}$

To balance this moment, then

$F = \dfrac{123,352}{2} = 61,676 \, \text{N}$

Worked Example #37

A submerged object in the shape of a cylinder with a height ${h}$ and radius $r$ is floating in an incompressible fluid of density $\varrho_f$ . The cylinder has a density $\varrho_c$ and is partially submerged such that the height of the submerged portion is $h_s$ . The object is in equilibrium with the fluid. The height of the cylinder is $h = 4 \, \text{m}$ , with a radius $r = 2 \, \text{m}$ . The height of the submerged portion is $h_s = 2 \, \text{m}$ . The density of the fluid is $\varrho_f = 988.0 \, \text{kg/m}^3$ .

Calculate the density of the cylinder $\varrho_c$ needed for the object to be in equilibrium.
The buoyancy force acting on the cylinder.
The position of the center of buoyancy.

The volume of the submerged portion is given by

$V_s = \pi \, r^2 \, h_s = \pi (2)^2 (2) = 8\pi \, \text{m}^3$

The buoyancy force acting on the submerged cylinder is

$F_b = \varrho_f \, V_s = 988.0 \, 8\pi = 24,820.1 \, \text{N}$

The volume of the cylinder is

$V_c = \pi r\, ^2 h = \pi (2)^2 (4) = 16\pi \, \text{m}^3$

Setting the buoyancy force equal to the weight, i.e., $F_b = W$ , means that $\varrho_f \, V_s = \varrho_c \, V_c$
so that

$\varrho_c = \dfrac{988.0 \, 8}{16} = 493.0 \, \text{kg/m}^3$

From previously, then

$F_b = \varrho_f \, t \, V_s = 988.0 \, 8\pi = 77,902.8 \, \text{N}$

The center of buoyancy is located at the centroid of the submerged volume, i.e.,

$z_b = \dfrac{h_s}{2} = \dfrac{2}{2} = 1 \, \text{m}$

Worked Example #38

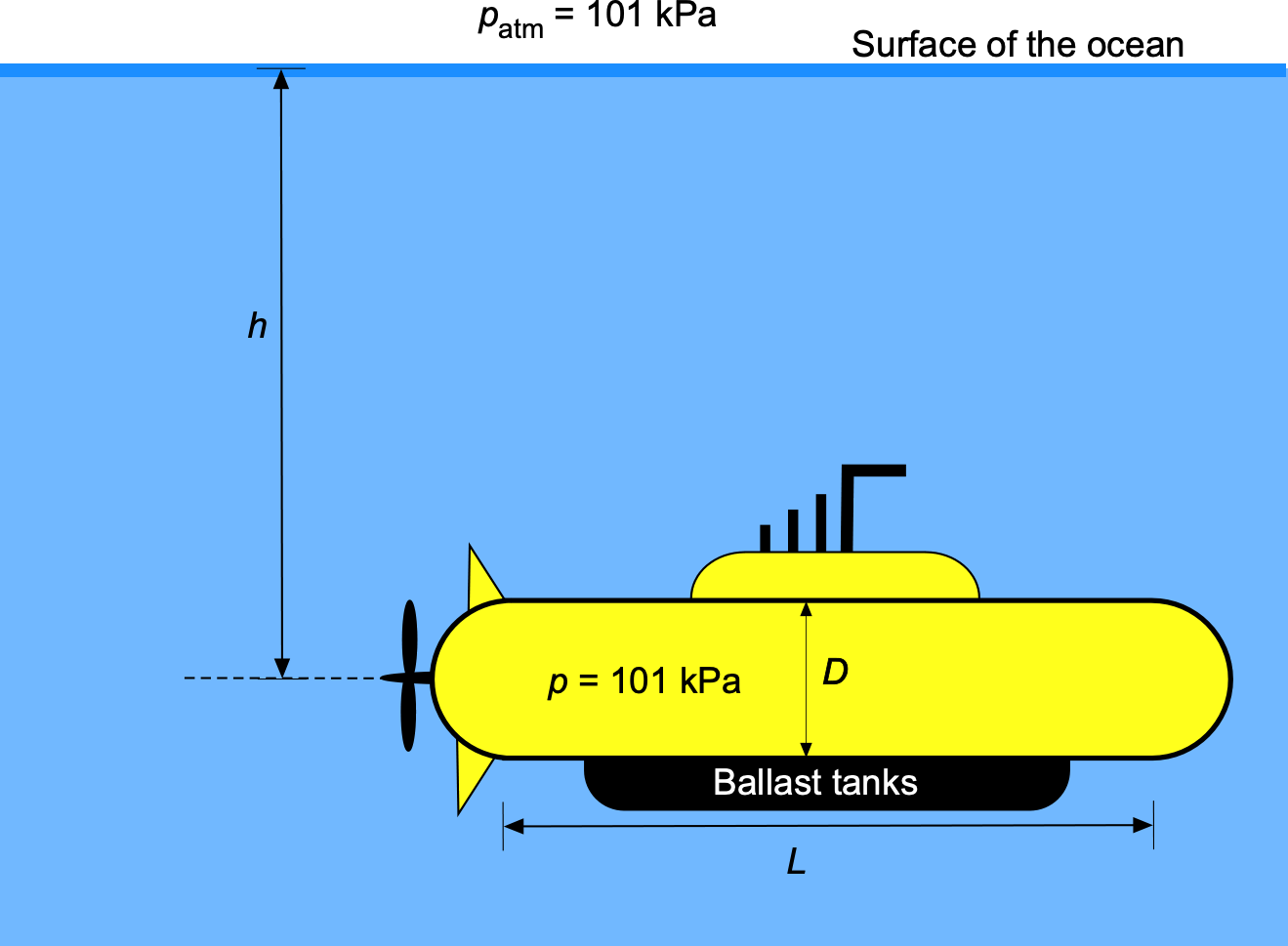
The hull of a big yellow submarine can be assumed to be a cylinder with a circular cross-section and hemispherical ends. The cylinder has a diameter $d =$ 10 m, with the length of the cylindrical part being $L =$ 50 m, as shown in the figure below. The mass of the submarine is $m = 1 \times 10^7$ kg. The submarine has to fill its ballast tanks to dive under the sea to a depth ${h}$ = 300 m. Assume the internal pressure of the submarine is equal to the ambient pressure $p_0$ = 101 kPa, and that the density of water $\varrho_w \,$ = 1,000 kg m $^{-3}$ . Disregard the air mass inside the submarine and any buoyancy from the ballast tanks, which have a much smaller volume than the submarine itself. Explain the balance of forces on the submarine and draw the free-body diagram. What volume of water must the ballast tanks be filled with for the submarine to remain neutrally buoyant at the given depth of 300 m?

For the submarine to be neutrally buoyant, then the upward buoyancy force, ${F_b}$ , must equal the total weight of the system, i.e.,

$F_b = W_s + W_b$

where $W_s$ is the weight of the submarine, and $W_b$ is the weight of the ballast.

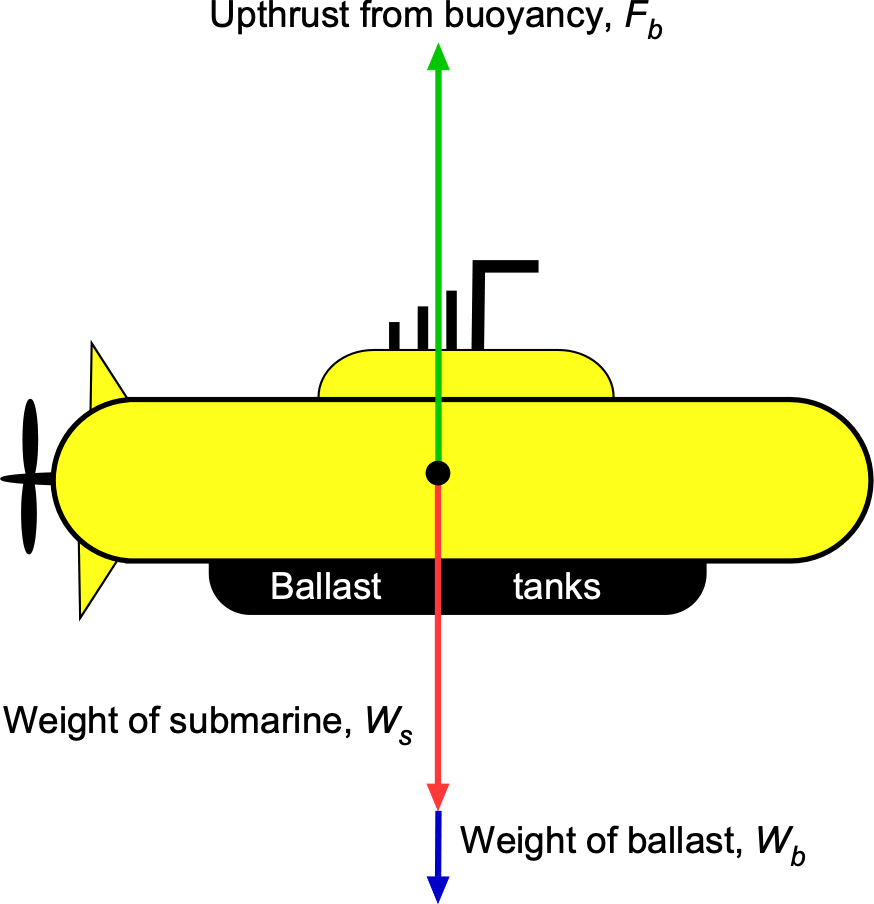The buoyancy force, ${F_b}$ , is equal to the weight of water displaced by the submarine, i.e.,

$F_b = \varrho_w \, g \mathcal{V}$

where $\varrho_w$ is the density of water and $\mathcal{V}$ is the volume of the submarine. From the geometry given, the volume is

$\mathcal{V} = \left( \frac{\pi \, d^2}{4} \right) L + \frac{4 \pi}{3} \left( \frac{d}{2} \right)^3$

Substituting the values gives

$\mathcal{V} = \left( \frac{\pi \times 10.0^2}{4} \right) \times 50.0 + \frac{4 \pi}{3} \left( \frac{10.0}{2} \right)^3 = 3{,}927 + 523.6 = 4{,}450.6~\text{m}^3$

The buoyancy force is then

$F_b = \varrho_w \, g \mathcal{V} = 1{,}000.0 \times 9.81 \times 4{,}450.6 = 43{,}648.086~\text{N}$

The weight of the ballast needed to achieve neutral buoyancy is

$W_b = F_b - W_s = 43{,}648.086 - 10^7 \approx 4.3 \times 10^5~\text{N}$

which is equivalent to

$W_b \approx \frac{4.3 \times 10^5}{9.81} \approx 4.4 \times 10^4~\text{kg}$

Therefore, the volume of water ballast needed will be

$\mathcal{V}_b = \frac{W_b}{\varrho_w \, g} = \frac{4.3 \times 10^5}{9.81 \times 1{,}000.0} \approx 44~\text{m}^3$

Worked Example #39

A double U-tube manometer with three immiscible liquids is used to measure the pressure difference applied between the tops of the first and third tubes, i.e., pressures $p_1$ and $p_3$ , respectively. Tube 1 contains oil of density $\varrho_o$ = 900 kg/m ${^{3}}$ and is open to pressure $p_1$ . Tube 2 is open to standard MSL atmospheric pressure $p_{\text{atm}}$ and is filled with water of density $\varrho_w$ = 1,000 kg/m ${^{3}}$ . Tube 3 contains mercury of density $\varrho_{\text{Hg}}$ = 13,600 kg/m ${^{3}}$ and is open to pressure $p_3$ . Given that the oil column height in the left tube is $h_1$ = 1.5 m, the water column height in Tube 2, $h_2$ , is unknown. and the mercury column height in the right tube is $h_3$ = 0.05 m, then calculate the the pressure, $p_1 - p_3$ , and the height $h_2$ .

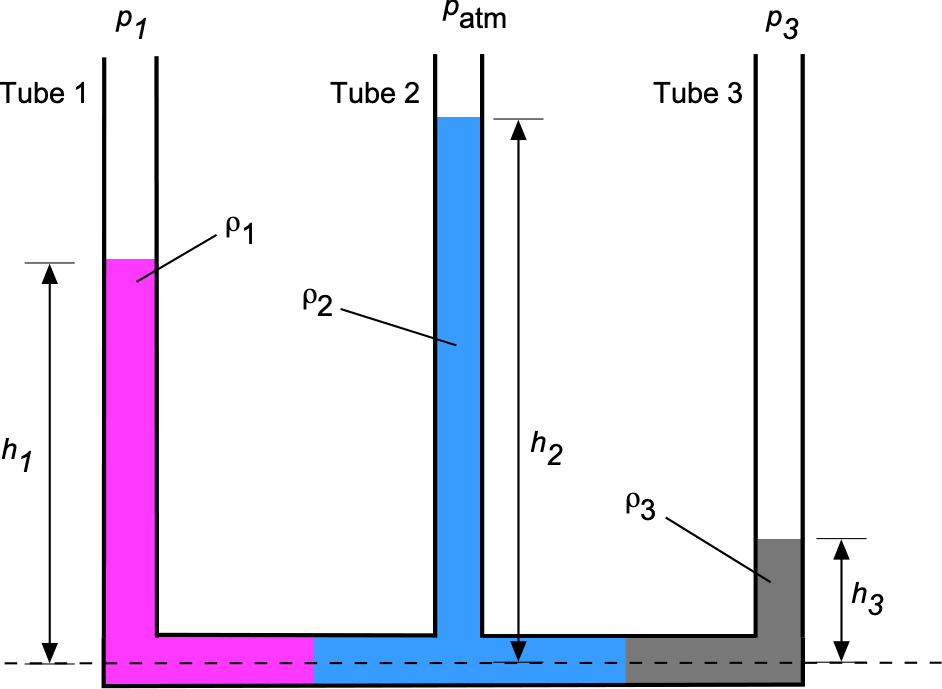
The hydrostatic principle here is that the pressures at the bottom of each tube must be equal; otherwise, fluid would flow along the tubes. The pressure at the bottom of Tube 1 (oil) is

$p_1 + \varrho_0 \, g \, h_1$

The pressure at the bottom of Tube 2 (water) is

$p_{\text{atm}} + \varrho_w \, g \, h_2$

The pressure at the bottom of Tube 3 (mercury) is

$p_3 + \varrho_{\text{Hg}} \, g \, h_3$

Because all three tubes connect at the same depth, the pressures at the bottom must be equal, i.e.,

$p_1 + \varrho_0 \, g \, h_1 = p_{\text{atm}} + \varrho_w \, g \, h_2 = p_3 + \varrho_{\text{Hg}} \, g \, h_3$

From the pressure balance between the water and mercury column, then

$p_{\text{atm}} + \varrho_w \, g \, h_2 = p_3 + \varrho_{\text{Hg}} \, g \, h_3$

Solving for $h_2$ gives

$h_2 = \frac{p_3 - p_{\text{atm}} + \varrho_{\text{Hg}} \, g \, h_3}{\varrho_w g}$

Substituting the known values into the expression for $h_2$ gives

$h_2 = \frac{107{,}400 - 101{,}325 + (13{,}600 \times 9.81 \times 0.05)}{1{,}000 \times 9.81} = \frac{6{,}075 + 6{,}669}{9{,}810} = \frac{12{,}744}{9{,}810} \approx 1.299 \ \text{m}$

Now it is possible to compute $p_1$ from the oil and water side pressure balance, i.e.,

$p_1 = p_{\text{atm}} + \varrho_w \, g \, h_2 - \varrho_0 \, g \, h_1$

and substituting the values gives

$p_1 = 101{,}325 + (1{,}000 \times 9.81 \times 1.299) - (900 \times 9.81 \times 1.50) = 100{,}823.4 \ \text{Pa}$

Therefore, the pressure difference is

$p_1 - p_3 = 100{,}823.4 - 107{,}400 = -6{,}576.6 \ \text{Pa}$

This result indicates that the pressure at the top of the oil column is about $6.58 \ \text{kPa}$ lower than at the top of the mercury column.

Worked Example #40

A manometer containing fluid 1, which is mercury ( $SG_{\rm Hg}$ = 13.6), fluid 2, which is kerosene ( $SG_{\rm k}$ = 0.8), and fluid 3, which is water of density $\varrho_{\rm w}$ = 1,000 kg m $^{-3}$ , is connected to a tank containing water and air, as shown in the figure below.

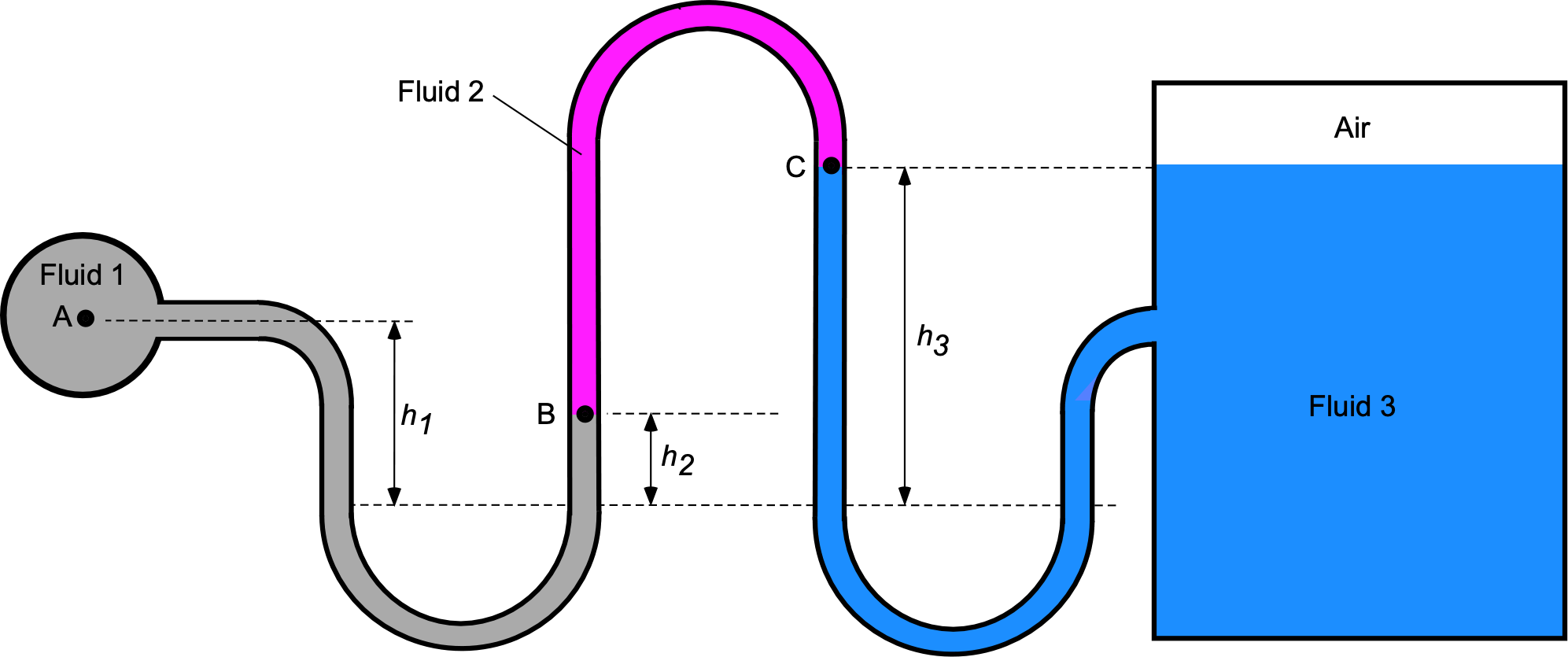
Using hydrostatic principles, obtain an expression for the pressure value $p_B$ in terms of the pressure value $p_A$ .
Obtain a corresponding expression for the pressure value $p_C$ in terms of $p_A$ .
If $p_A$ = 100 kPa, $h_1$ = 20 cm, $h_2$ = 8 cm, and $h_3$ = 40 cm, then calculate the pressure of the air in the tank in units of kPa.
Calculate the pressure at the bottom of the water tank in units of kPa.
If the air temperature in the tank is measured to be $40^{\circ}$ C, determine its corresponding density in units of kg/m ${^{3}}$ . Assume $R_{\rm air} = 287.057$ J kg $^{-1}$ K $^{-1}$ .

1. The fluid between points A and B is mercury (Hg). The pressure at point B, $p_B$ , is given by

$p_B = p_A + SG_{\rm Hg} \, \varrho_{\rm w} \, g \, h_1 - SG_{\rm Hg} \, \varrho_{\rm w} \, g \, h_2 = p_A + SG_{\rm Hg} \, \varrho_{\rm w} \, g \, (h_1 - h_2)$

remembering that $\varrho_{\rm Hg} = SG_{\rm Hg} \, \varrho_{\rm w}$ .

2. The fluid between points B and C is kerosine (k). The corresponding expression for the pressure value $p_C$ in terms of $p_A$ is

$p_C = p_B - SG_{\rm k} \, \varrho_{\rm w} \, g (h_3 - h_2)$

which gives on substituting for $p_B$

$p_C = p_A + SG_{\rm Hg} \, \varrho_{\rm w} \, g \, (h_1 - h_2) - SG_{\rm k} \, \varrho_{\rm w} \, g (h_3 - h_2)$

After reaarangement, then

$p_C = p_A + \varrho_{\rm w} \, g \big( SG_{\text{Hg}} (h_1 - h_2) - SG_{\rm k} (h_3 - h_2) \big)$

Notice that because point C is level with the top of the water in the tank, then the pressure of the air in the tank will be equal to the pressure at point, i.e., $p_{\rm air} = p_C$ .

3. If $p_A$ = 100 kPa, $h_1$ = 20 cm, $h_2$ = 8 cm, and $h_3$ = 40 cm, then the pressure of the air in the tank will be

$p_{\rm air} = p_B = 100,000 + 1,000 \times 9.81 \big( 13.6 \times (0.2 - 0.08) - 0.8 \times (0.40 - 0.08) \big)$

so that

$p_{\rm air} = 113,498.56 \text{ Pa} = 113.499 \text{ kPa}$

4. The pressure at the bottom of the water tank, $p_b$ , is obtained by adding the hydrostatic head of water, i.e.,

$p_b = p_{\rm air} + \varrho_{\rm w} \, g \, h_3 = 113,498.56 + 1,000 \times 9.81 \times 0.40$

so that

$p_b = 117,423.56 \text{ Pa} = 117.424 \text{ kPa}$

5. If the temperature in the air pocket at the top of the tank is measured to be $40^{\circ}$ C, and if $R_{\rm air} = 287.057$ J kg $^{-1}$ K $^{-1}$ , then using the equation of state the density of the air in the tank will be

$\varrho_{\rm air} = \frac{p_{\rm air}}{R_{\rm air} \, T_{\rm air}} = \frac{113,498.56}{287.057 \times (40 + 273.15)} = 1.263 \text{ kg m$^{-3}$}$

Remember to convert into absolute temperature units when using the equation of state.

Worked Example #41

A U-tube manometer contains three liquids, as shown in the figure below. Both legs of the manometer are open to the atmosphere. The liquids are in static equilibrium and do not mix. The heights are $h_1 = 3$ cm and $h_2 = 10$ cm. If liquid 1 has a specific gravity of 0.73 and liquid 2 has a specific gravity of 0.88, what is the value of the height $h_3$ ? Ignore the hydrostatic effects of air.

Manometry problems are about hydrostatic balance. Using the principles of hydrostatics, the pressure at the bottom of liquid 2 on the left side leg (at the water interface) will be

$p = p_{\rm atm} + \varrho_1 g h_1 + \varrho_2 g h_2$

The pressure at the same height in the same fluid is equal, so on the right side (inclined leg) in the water, then working down from the top of this leg gives

$p = p_{\rm atm} + \varrho_w g \left( h_1 + h_2 - h_3 \right)$

where $\varrho_w$ is the density of water. Remember that hydrostatic pressure or “head” depends only on the vertical height. Therefore, equating the pressures (for hydrostatic balance) gives

$p_{\rm atm} + \varrho_1 \, g \, h_1 + \varrho_2 \, g \, h_2 = p_{\rm atm} + \varrho_w \, g \left( h_1 + h_2 - h_3 \right)$

or

$\varrho_1 \, h_1 + \varrho_2 \, h_2 = \varrho_w \left( h_1 + h_2 - h_3 \right)$

In terms of specific gravity, then

$SG_1 \, h_1 + SG_2 \, h_2 = \left( h_1 + h_2 - h_3 \right)$

noting that the specific gravity of water is 1. Rearranging to solve for $h_3$ gives

$h_3 = \left( h_1 + h_2 \right) - SG_1 \, h_1 - SG_2 \, h_2 = \left( 0.03 + 0.1 \right) - 0.73 \times 0.03 - 0.88 \times 0.10 = 0.0201~\mbox{m} = 2.01~\mbox{cm}$

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.9

License

Digital Object Identifier (DOI)

Share This Book