"

43 Turbojet Engines

Introduction

The turbojet is the name used for a gas turbine engine designed to produce thrust by discharging exhaust gases at high speed out of the rear of the engine, i.e., the “jet,” which is done through a suitably shaped propelling nozzle. The turbojet engine, a cutaway example shown in the photograph below, is used on many aircraft types, particularly those designed to fly at higher airspeeds, including in supersonic flight. Unfortunately, turbojets have relatively poor propulsive efficiency at lower airspeeds, limiting their usefulness to high-speed aircraft. Nevertheless, the turbojet has been, and still is, an essential form of propulsion system for various aircraft.

Cutaway of the General Electric J85-GE-17A turbojet engine, circa 1970, which produced a thrust of up to 2,950 lb (13.1 kN). More than 12,000 engines were made until the end of production in 1988.

Today, turbojet engines are primarily used in military aviation, powering high-speed fighter jets. Turbojets have also been employed in cruise missiles and certain high-speed unoccupied aerial vehicles (UAVs), providing the necessary thrust for rapid deployment and long-range missions. Experimental and supersonic aircraft, including some research and prototype models, continue to utilize turbojet engines to explore advanced aerodynamics and propulsion technologies.

Learning Objectives

  • Know about a turbojet engine’s essential components and characteristics, and how it works.
  • Understand the essential characteristics of a turbojet engine in terms of its thrust production and specific fuel consumption as a function of flight Mach number and operational altitude.
  • Appreciate the technique of “afterburning” in a turbojet engine and the various trades in using afterburning engines on an aircraft.
  • Know what a ramjet engine is and how it works.

Design of a Turbojet

The basic design of a turbojet engine is shown in the schematic below. The gas turbine has an air inlet, a compressor stage (driven by the high-pressure turbine), a combustion chamber, and high-pressure and low-pressure turbines. The compressed air that passes through the compressor stage mixes with the fuel in the combustion chamber, where it is ignited, and then hot gases flow to drive the main power turbine stages. The exhaust is then expanded in the propelling nozzle; it is accelerated to a relatively high jet velocity to provide the propulsive thrust by increasing the time change in momentum of the net flow, i.e., the momentum of the air and hot gases that are a combustion product.

 

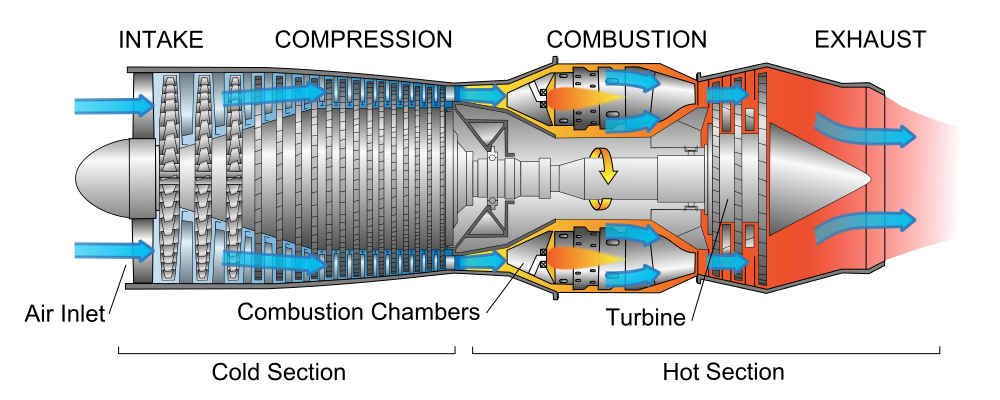
Schematic of a turbojet engine, which has five stages: 1. Air inlet or intake stage; 2. Compressor stage; 3. Combustion stage; 4. Gas generator turbine stage; 5. Exhaust stage through a nozzle.

Operational Principle

The operational principle of a turbojet engine is straightforward to understand, as shown in the figure below. The thermodynamic operation of a turbojet is based on the Brayton cycle.

 

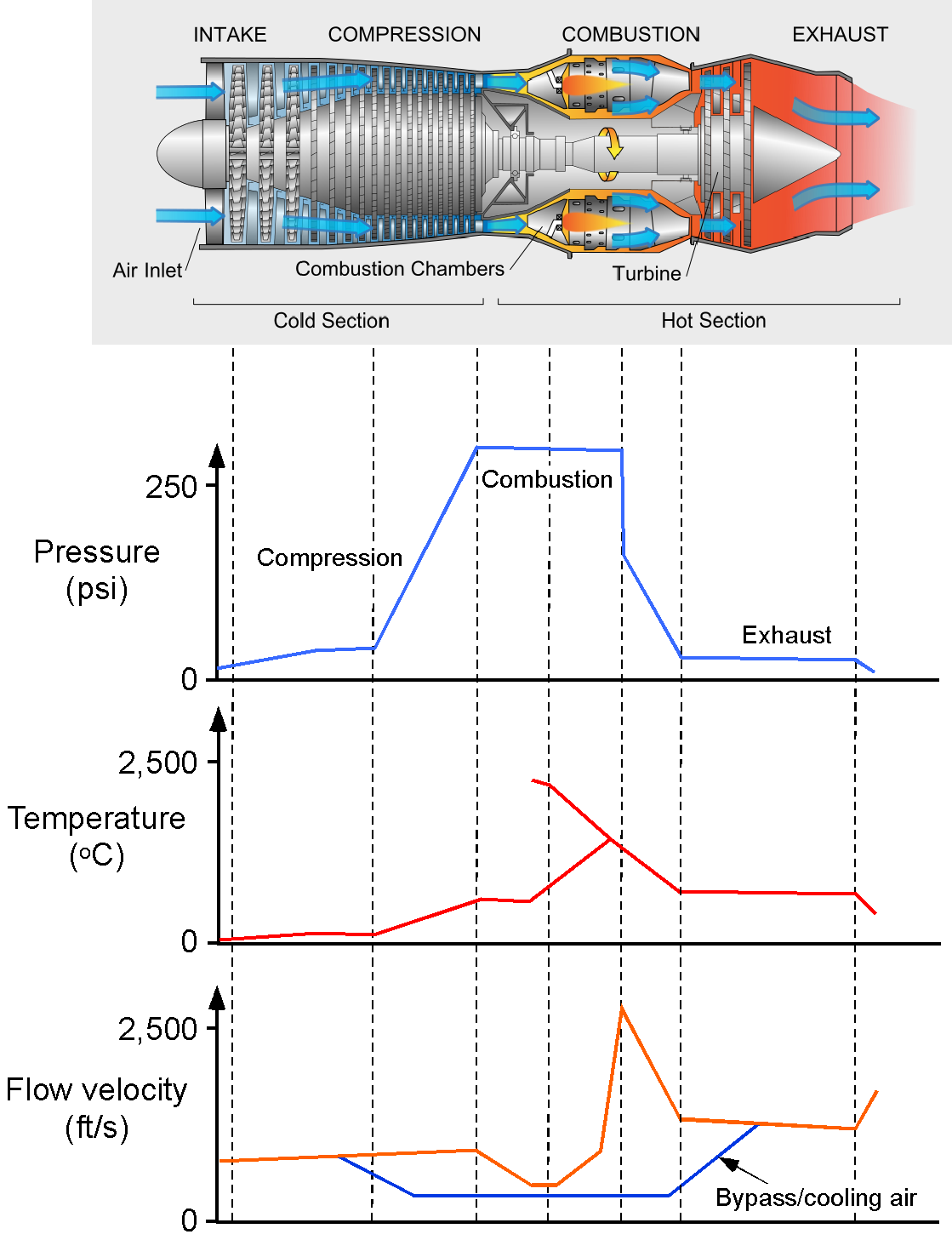
Representative pressure, temperature, and flow velocity variations through a turbojet engine.

There are five primary stages:

1. Air intake stage. The intake stage in front of the compressor slows the air down, slightly increasing its static pressure. By design, the airflow speed into a turbojet engine’s compressor must be subsonic, regardless of the aircraft’s airspeed. In the case of supersonic flight, a diverging duct with doors and/or baffles can reduce the incoming flow to subsonic conditions.

2. Compressor stage. The flow is then directed onto vanes and the spinning compressor blades, where progressively more significant pressure increases are produced. Older turbojet engines had fixed vanes (stators) before the moving blades. However, modern engines have stators with variable pitch to direct the oncoming air onto the compressor blades at the appropriate angles based on the engine’s operating state and flight speed. Notice that the high-pressure turbine drives the compressor through a forward-facing shaft in the hot stage.

3. Combustion stage. The burning of the fuel occurs in the combustor to produce a gas flow at a much higher temperature. This process is a continuous, almost constant-pressure process, which is different from the combustion process in a piston engine. As the fuel burns, the pressure increases quickly in the confined region on top of a piston. This flow then passes into the gas generator turbine.

4. Gas generator turbine stage. This stage rotates relatively faster than the compressor stage, significantly adding a lot of kinetic energy to the airflow. Notice that the process of compressing the air increases both its pressure and its temperature. Additional air from the compressor is bled into the region downstream of the combustion chambers through a bypass circuit to reduce the temperature of the hot gases so that turbine blades in the power stage can safely tolerate these gases without burning or melting. The hot-stage high-pressure and low-pressure turbine blades are made of special steel alloys that can sustain extremely high temperatures. Nevertheless, the turbine vanes and blades need internal cooling passages to keep the material temperatures at acceptable levels.

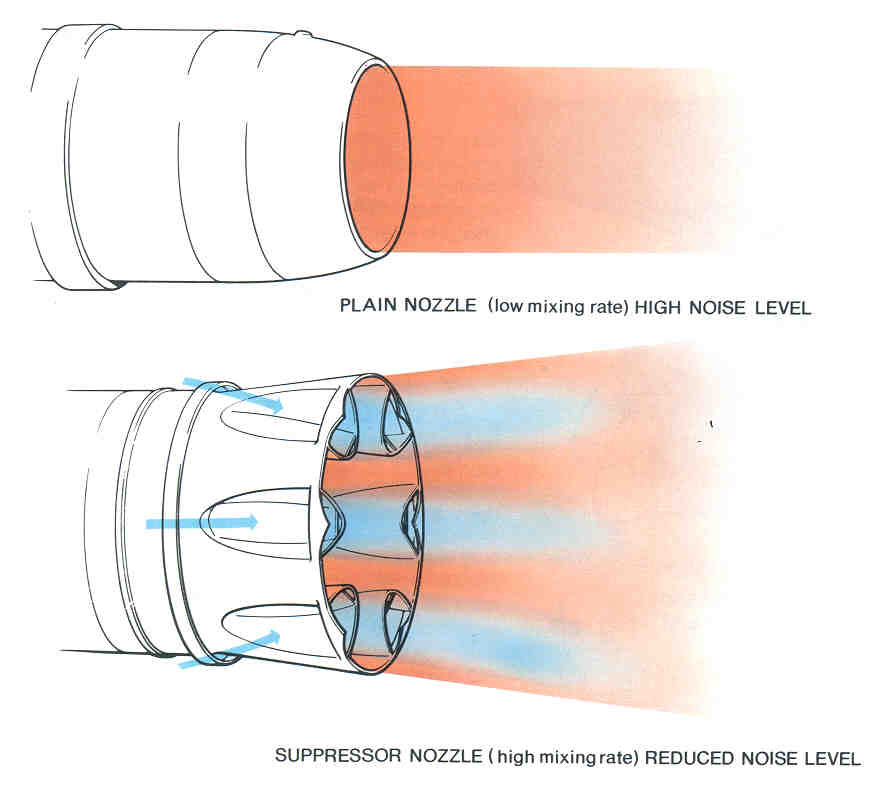
5. Exhaust stage through a nozzle. After the turbine, the gases expand through the exhaust nozzle, producing a high-velocity jet, which is the thrust source. One problem with this high-speed flow from a turbojet engine is that it creates significant noise. Research has shown that the increase in noise is approximately proportional to the fully expanded exit velocity, V_j, i.e.,

(1)   \begin{equation*} \text{Noise} \ \propto \ V_j^{\, n} \end{equation*}

where n = 8 for subsonic jet conditions is called the eighth-power law, and n = 3 for supersonic jet conditions is called the third-power law. These are both empirical laws, i.e., based on actual measurements of jet noise. As shown in the figure below, most turbojet engines use noise suppression devices such as corrugated or lobe-type suppressors. Such devices alter the turbulent mixing in the jet so that the resulting jet flow sounds quieter to an external observer.

The principle of a jet noise suppressor nozzle is to encourage mixing the jet exhaust, which reduces noise.

Basis of Thrust Production

The thrust produced by a turbojet engine can be examined using conservation principles of fluid dynamics applied to a control volume surrounding the engine, as shown in the figure below. The basic principle of operation is that air comes in and is then compressed to a level to support combustion, the energy being used to drive the compressor, and the exhaust gases exiting at high speed to produce the thrust.

 

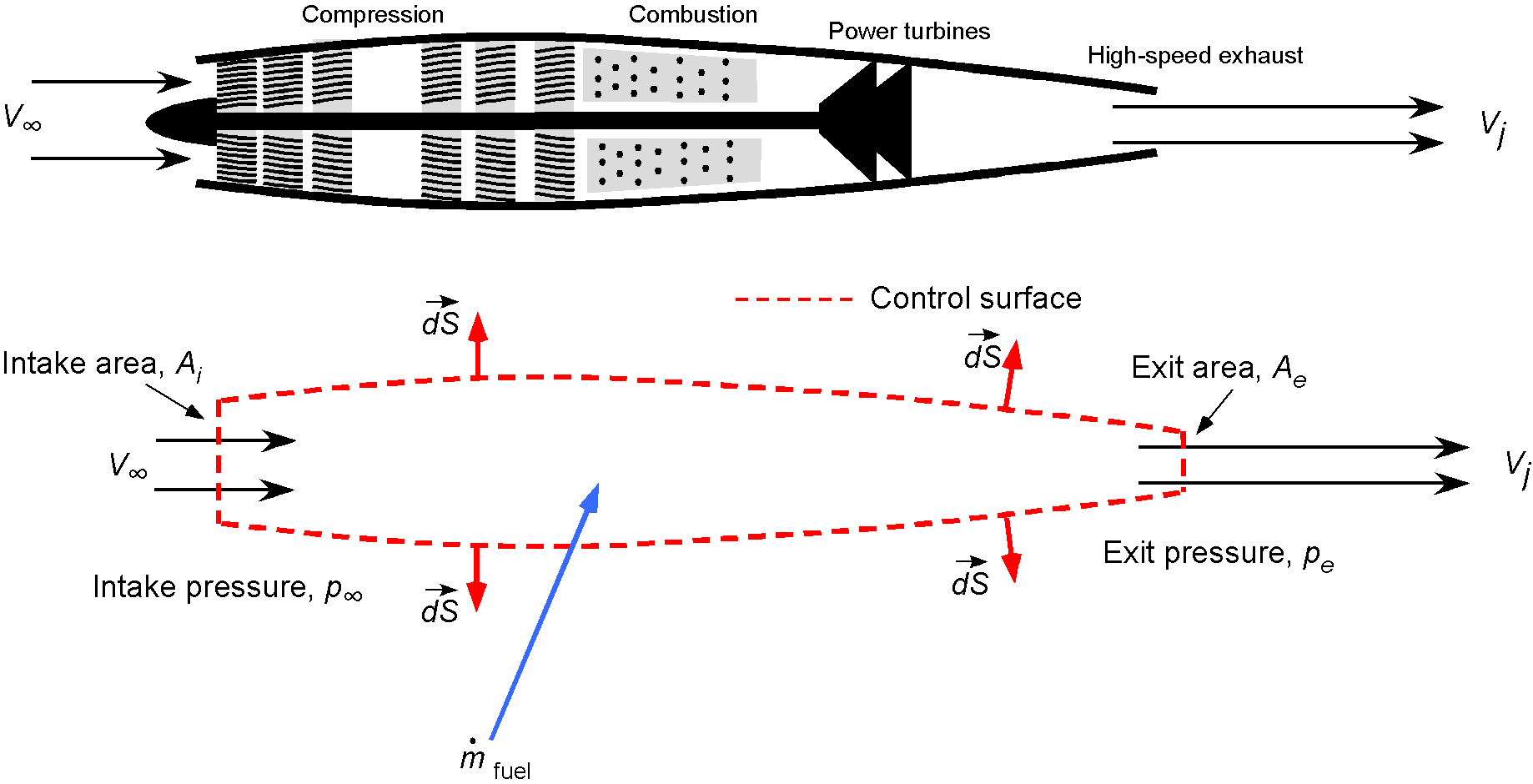
Control volume for analyzing a turbojet engine, which works on the air to increase its momentum in the downstream direction and produce a reaction force directed in the upstream direction.

The mass flow of air into the intake of the engine will be

(2)   \begin{equation*} \overbigdot{m}_{\rm air} = \varrho_{\infty} V_{\infty} A_i \end{equation*}

where A_i is the inlet area, and the mass flow rate of fuel is \overbigdot{m}_{\rm fuel}. Therefore, using conservation of momentum, the thrust produced T is

(3)   \begin{equation*} T = \left( \overbigdot{m}_{\rm air} + \overbigdot{m}_{\rm fuel} \right) V_e - \overbigdot{m}_{\rm air} V_{\infty} + \left( p_e A_ e - p_{\infty} A_i \right) \end{equation*}

where A_e is the exit area and V_e is the exit or “jet” velocity, usually given the symbol V_j. The pressure (second) term in Eq. 3 is relatively small compared to the change in momentum of the flow, and so in practice, it may be neglected, i.e.,

(4)   \begin{equation*} T = \left( \overbigdot{m}_{\rm air} + \overbigdot{m}_{\rm fuel} \right) V_j - \overbigdot{m}_{\rm air} V_{\infty} \end{equation*}

Notice that the thrust decreases when V_{\infty} increases because V_j depends on both the compression and the combustion, so the difference V_j - V_{\infty} decreases. However, \overbigdot{m}_{\rm air} increases with increasing V_{\infty}, and so the value of thrust depends weakly on V_{\infty} at low Mach numbers but more so at higher Mach numbers.

For a turbojet engine at subsonic Mach numbers, it is found that T stays relatively constant with V_{\infty}. Thrust increases with Mach number at higher flight Mach numbers but lapses with altitude, as shown in the figure below. A jet engine’s “Uninstalled Thrust” is typically determined during static tests on a test stand. The engine is calibrated to relate parameters such as speed, pressure ratio, and exhaust gas temperature to thrust. These parameters are also available to the pilot on the cockpit instrument panel. Together with information in the airplane flight manual, it can be used to calculate the anticipated aircraft performance.

Representative variations in thrust produced by an advanced turbojet engine as functions of flight Mach number and operational altitude.

The overall thrust characteristics of a turbojet depend significantly on the flight Mach number and the operational altitude at which the engine operates. Again, remember that when speaking of “altitude,” it is generally density altitude, i.e., the altitude corresponding to the local ambient density when measured according to the ISA. In particular, the maximum thrust is influenced by ambient temperature, with thrust decreasing as temperature increases. This means that on hot days, an airplane may require a longer runway for takeoff than on cooler days. Engine manufacturers provide a rated thrust value guaranteed for use in the airplane flight manual. This rated thrust is often “flat-rated,” meaning it is a single value based on the highest ambient temperature. It is determined by analyzing static engine test data and possibly flight test data.

One approximation for the thrust produced by a turbojet engine is that it increases linearly with flight Mach number according to

(5)   \begin{equation*} T \approx T\big|_{\tiny M = M_{0}} + k_1 M_{\infty} \end{equation*}

where {M_0} is the lowest Mach number for which the thrust is known, and k_1 is a constant. The thrust will also decrease with altitude according to

(6)   \begin{equation*} \frac{T}{T_{\rm MSL}} \approx \frac{\varrho}{\varrho_0} = \sigma \end{equation*}

where T_{\rm MSL} is the thrust produced at MSL conditions, and the density ratio \varrho / \varrho_0 is the density at altitude relative to the density at MSL. The air density can be estimated using the ISA equations based on the local ambient pressure (i.e., pressure altitude) and outside air temperature.

Check Your Understanding #1 – Estimating the thrust produced by a turbojet

Consider a turbojet-powered airplane flying at a pressure altitude of 30,000 ft at ISA standard conditions. The true airspeed of the airplane is 500 kts. The engine has an inlet area, A_i, of 0.7 m{^2}. The velocity at the exit, V_e, is 463 m/s. All velocities are measured relative to the engine. Estimate the thrust of the turbojet and the equivalent power it produces. Neglect the mass of fuel into the engine and all pressure difference effects.

Show solution/hide solution.

The thrust, T, of the engine can be expressed as

    \[ T = \overbigdot{m} \left( V_e - V_{\infty} \right) + \left(p_e \, A_e - p_i \, A_i \right) \]

where

    \[ \overbigdot{m} = \varrho_{\infty} \, A_i \, V_{\infty} \]

At 30,000 ISA standard conditions, \varrho_{\infty} = 0.4583 kg/m{^3}. The flight velocity is 500 kts, which is equivalent to 257.2 m/s. Hence, the mass flow into the engine is

    \[ \overbigdot{m} = \varrho_{\infty} \, A_i \, V_{\infty} = 0.4583 \times 0.7 \times 257.2 = 82.51~\mbox{kg/s} \]

In this case, we are told to neglect the pressure difference effects, so the thrust, T, from the engine is equal to the time rate of change of the momentum of the flow as it goes through the engine, i.e.,

    \[ T = \overbigdot{m} \Delta V = \overbigdot{m} \left( V_e - V_{\infty} \right) \]

Inserting the numerical values gives

    \[ T = 82.51 \left( 463.0 - 257.2 \right) = 16.98~\mbox{kN} \]

The equivalent power produced by the engine, P_{\rm eq}, is given by

    \[ P_{\rm eq} = T V_{\infty} = 16.98 \times 10^3 \times 257.2 = 4.27~\mbox{MW} \]

Thrust-Specific Fuel Consumption (TSFC)

The output from a turbojet is the thrust, so the specific fuel consumption is based on thrust production. Recall that the specific fuel consumption is based on the shaft or brake power for engines that primarily produce shaft power (e.g., a piston engine or a turboshaft engine). The thrust-specific fuel consumption or TSFC is a measure of the weight of fuel consumed per unit thrust produced per unit time, i.e.,

(7)   \begin{equation*} {\rm TSFC} = c_t = \frac{ \mbox{Weight of fuel consumed}}{\mbox{(Unit thrust output) (Unit time)}} \end{equation*}

Usually, the TSFC is measured in terms of units of lb lb^{-1} hr^{-1} in the USC system or units of kg kN^{-1} hr^{-1} in the SI system. Again, note the anomaly of the SI system where mass units are used instead of weight. Further caution should be exercised because publications may use other units for TSFC. Published values of TSFC for different turbojet engines are often quoted at the maximum-rated thrust at sea level on a standard day.

A turbojet engine’s overall propulsive efficiency increases with increasing Mach number because of the more significant increase in thrust and relatively small change in TSFC. This reason is why this engine type is more suitable for higher-speed aircraft. Representative variations of the TSFC of a turbojet engine are shown in the figure below. Notice that the TSFC of a turbojet engine generally gets slightly worse with increasing flight Mach number.

 

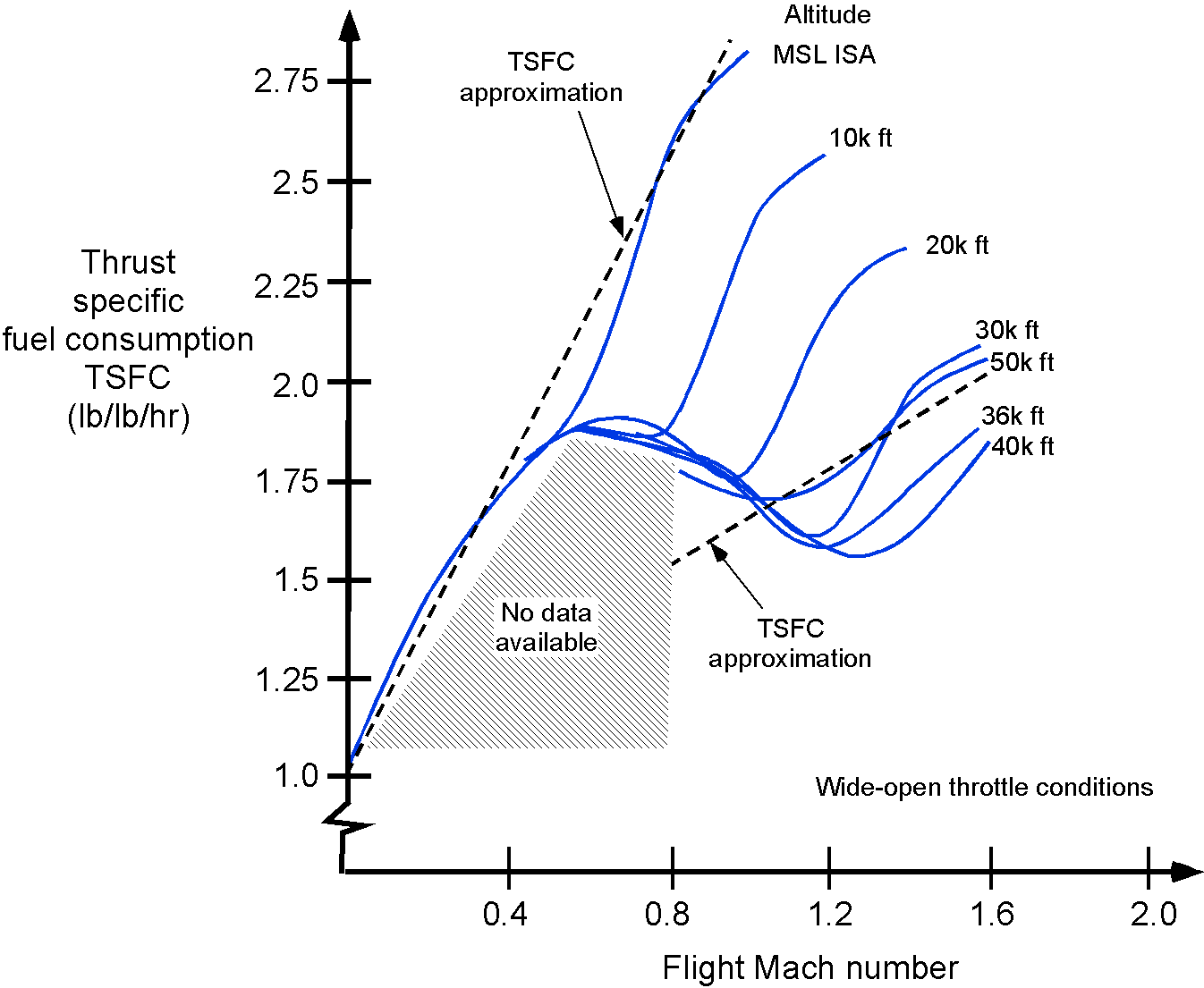
Representative variations in TSFC for an advanced turbojet engine as functions of flight Mach number and operational altitude.

In performance analyses, one linear approximation that can be used for the TSFC in the subsonic regime is

(8)   \begin{equation*} {\rm TSFC} = c_t \approx 1.0 + k_2 M_{\infty} \end{equation*}

which is measured in units of weight of fuel per unit of thrust per hour. The value of k_2 is engine-specific and also depends on the throttle setting of the engine. However, a turbojet engine will run at or near wide-open throttle settings for most flight operations. Remember that air density is lower at higher flight altitudes, so the mass flow of air \overbigdot{m}_{\rm air} into the engine decreases.

In supersonic flight, the inlet to a turbojet engine must be designed so that the intake to the compressor occurs at subsonic speeds. This is done using a duct and/or doors or baffles in which the total pressure p_T increases according to the thermodynamic relationship

(9)   \begin{equation*} \frac{p_{T}}{p_{\rm static}} = \left[ 1 + \frac{\gamma-1}{2} M_{\infty}^2 \right]^\frac{\gamma}{(\gamma - 1)} \end{equation*}

This duct provides total pressure recovery at the end of the inlet diffuser before the compressor stage. Therefore, thrust from a turbojet engine tends to increase linearly with supersonic flight Mach number according to the approximate relationship

(10)   \begin{equation*} \frac{T}{T_{\text{(for $M_{\infty}=1$)}} }\approx 1 + 1.18 (M_{\infty} - 1) \end{equation*}

These characteristics are obtained because as p_{T} increases and \overbigdot{m}_{\rm air} increases and then V_j increases and eventually becomes supersonic, which all combine to increase the thrust T. Also, as shown in the figure above, the TSFC remains relatively constant or gets slightly worse with M_{\infty} in the supersonic regime, but the overall propulsive efficiency still increases.

Check Your Understanding #2 – Using the TSFC in a calculation

Two turbojet engines power a military airplane. It has the following characteristics:

In-flight mass = 37,991 kg.
Engine inlet area, A_i = 0.6 m{^{2}}.
Engine thrust specific fuel consumption (TSFC) = 231.84 kg/kN/hr
Cruise speed, V_{\infty} = 245.0 m/s.
Pressure altitude = 34,000 ft, ISA standard conditions.
Aircraft lift-to-drag ratio = 15.

Determine the thrust required from each engine, the mass flow rate through each engine, as well as the fuel mass flow rate and the jet velocity. All velocities are measured relative to the engine. Neglect all pressure difference effects.

Show solution/hide solution.

In level flight, L = W and {T = D}. Therefore, the net thrust required for flight will be

    \[ T = \frac{W}{L/D} = \frac{37,991 \times 9.81}{15} = 24.846~\mbox{kN} \]

so the thrust per engine, T_e, will be 12.423 kN.

At 34,000 ft ISA standard, the air density is 0.3953 kg/m{^3}. See here for a handy ISA calculator. Therefore, the mass flow rate into the engine is

    \[ \overbigdot{m}_i = \varrho_{\infty} \, A_i V_{\infty} = 0.3953 \times 0.6 \times 245.0 = 58.11~\mbox{kg/s} \]

In this case, we are given the engine TSFC, and the fuel flow rate, \overbigdot{m}_f, must be determined to get the mass flow rate exiting the engine. Notice that the units of the TSFC are given in kg of fuel per kN of thrust per hour. Converting to base units gives the TSFC as 231.84/10{^3}/3,600 = 6.44\times 10^{-5} kg/N/s. Therefore, the fuel flow rate per engine is

    \[ \overbigdot{m}_f = \mbox{TSFC} \ T_e = 6.44 \times 10^{-5}\times 12.423 \times 10^3 = 0.8~\mbox{kg/s} \]

Therefore, the mass flow exiting the engine is

    \[ \overbigdot{m}_e = \overbigdot{m}_i + \overbigdot{m}_f = 58.11 + 0.8 = 58.91~\mbox{kg/s} \]

The thrust per engine, T_e, is given by the momentum equation, i.e.,

    \[ T_e = \left( \overbigdot{m}_i + \overbigdot{m}_f \right) V_e - \overbigdot{m}_{\rm air} V_{\infty} + \left( p_e A_ e - p_{\infty} A_i \right) \]

and with no pressure effects, it becomes

    \[ T_e = \overbigdot{m}_e V_e - \overbigdot{m}_i V_{\infty} = \left( \overbigdot{m}_i +\overbigdot{m}_f \right) V_e - \overbigdot{m}_i V_{\infty} = 12.423~\mbox{kN} \]

To solve for the exit velocity, V_e, the previous equation can be rearranged to give

    \[ V_e = \frac{T_e + \overbigdot{m}_i V_{\infty}}{ \overbigdot{m}_i +\overbigdot{m}_f} \]

Inserting the numerical values gives

    \[ V_e = \frac{ 12.423 \times 10^3 + 58.11 \times 245.0}{58.91} = 452.55~\mbox{m/s} \]

Afterburning

Military aircraft often require a significant increase in engine thrust for a relatively short time, such as during takeoff, climb, acceleration into supersonic flight, or some combat maneuvers. This thrust is achieved using an afterburner, as shown schematically in the figure below. An afterburner injects additional fuel into the engine exhaust and burns in an extended tailpipe. Afterburning is sometimes referred to as reheat.

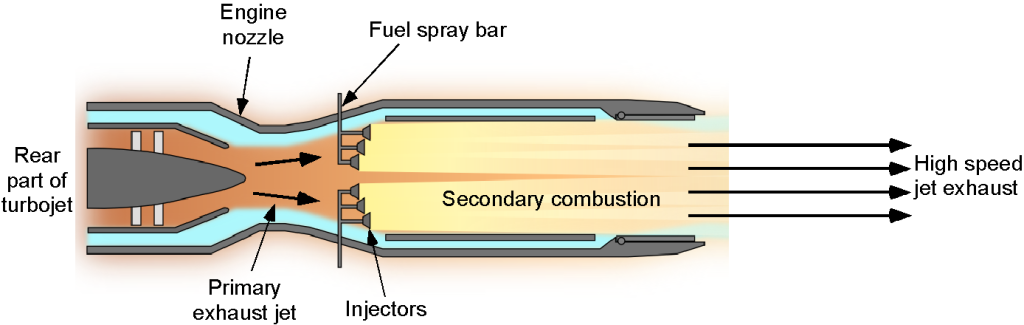
The principle of an afterburner is relatively simple: Inject and ignite large quantities of fuel in the tailpipe to generate large amounts of extra thrust.

Fuel spray bars, flame holders, and an adjustable nozzle are in the afterburner tube. An adjustable exhaust nozzle is necessary for an afterburning engine; two or three-position nozzles are usually used. Raw fuel is injected into the exhaust from the engine core by the fuel spray bars, and the flame holders stabilize the resulting combustion process as it develops down the tube and into the tailpipe. The engine’s core exhaust contains enough excess oxygen to allow for afterburner operation, so no additional inlets are needed. The resulting exhaust flame from an afterburner is usually rather spectacular, partly because the flow speeds are supersonic, and the hot gases contain diamond-shaped shock waves, as shown in the photograph below.

Photograph of a fighter jet aircraft taking off with the afterburner lit.

 

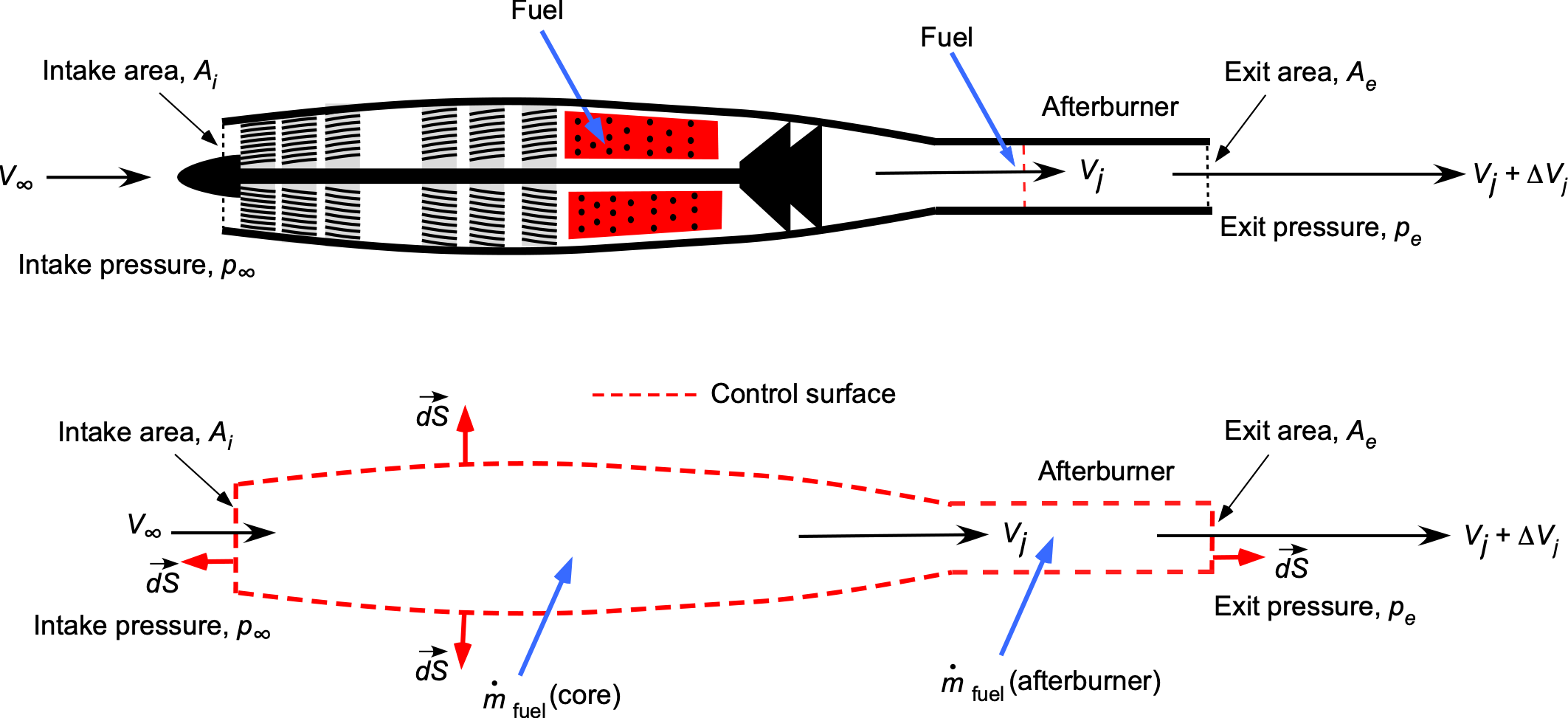
The thrust produced by a turbojet engine with an afterburner can be examined using conservation principles of fluid dynamics applied to a control volume surrounding the engine, as shown in the figure below. The secondary combustion in the afterburner significantly increases the exhaust velocity from V_j to V_j + \Delta V_j, which raises the net thrust from T to T + \Delta T, as described by the momentum thrust relation

(11)   \begin{equation*} T + \Delta T = \left( \overbigdot{m}_{\rm air} + \overbigdot{m}_{\rm fuel} + \Delta \overbigdot{m}_{\rm fuel} \right) \left( V_j + \Delta V_j \right) - \overbigdot{m}_{\rm air} V_\infty \end{equation*}

where \overbigdot{m} denotes the mass flow rate and V_\infty is the freestream velocity. If the increase in fuel mass flow rate is neglected compared to the air mass flow rate, so that \overbigdot{m} \approx \overbigdot{m}_{\rm air}, the thrust equation simplifies to

(12)   \begin{equation*} T + \Delta T = \overbigdot{m} \left( V_j + \Delta V_j - V_\infty \right) = \overbigdot{m} \left( V_j - V_\infty \right) + \overbigdot{m} \, \Delta V_j \end{equation*}

This shows that the additional thrust produced by the afterburner is approximately equal to \overbigdot{m} \Delta V_j, representing the extra momentum gained from the increase in jet exhaust velocity.

Control volume for analyzing a turbojet engine with an afterburner.

While the engine thrust may increase nearly twice when the afterburner is lit, the net engine TSFC increases markedly and proportionally more than the thrust, so the corresponding fuel burn increases quickly. For example, published values for the Pratt & Whitney F100-PW-220, as used on the F-15 and F-16, are 0.76 lb lb^{-1}hr^{-1} without the afterburner and 1.94 lb lb^{-1}hr^{-1} with the afterburner. Because of the higher jet velocities out of the tailpipe, engine noise increases dramatically, i.e., according to Eq. 1. Afterburning is usually used by military fighter aircraft for takeoff and initial climb. In this case, the high noise levels produced using an afterburner are particularly noticeable to an observer on the ground. Concorde used afterburning turbojet engines.

Afterburning is also possible with a turbofan engine. Afterburning turbofans are usually found on military aircraft designed to reach transonic and low-supersonic cruise speed ranges. When performance requirements encompass these speed ranges and subsonic flight under various conditions, selecting a low-bypass-ratio turbofan engine usually becomes the best design compromise to meet the flight requirements. In all cases, however, matching an engine to an aircraft requires careful consideration of not only the requirements for the aircraft but also weight, cost, and installation issues.

Check Your Understanding #3 – Performance of a turbojet engine with an afterburner

Consider a turbojet with an afterburner on an airplane flying at an altitude of 35,000 ft with a true airspeed V_{\infty} = 530 mph; refer to the figure below. The inlet area is 13 ft^2. At this altitude, p_{\infty}/p_0 = 0.2353, and \varrho_{\infty} / \varrho_0 = 0.3099. The fuel-to-air ratio by mass injected into the engine core is 0.005, and the fuel-to-air ratio by mass injected into the afterburner is 0.016. The jet velocity V_j is 1,510 ft s^{-1} without afterburner, and V_j = V_{j_{a}} = 2,700 ft s^{-1} with the afterburner ignited. The flow is fully expanded, so there are no pressure difference effects. Assume a one-dimensional, steady flow.

  1. Calculate the thrust produced at this flight condition without the afterburner.
  2. Determine the equivalent propulsive power produced without the afterburner.
  3. Calculate the fuel consumption (in units of lb hr^{-1}) and the thrust-specific fuel consumption (TSFC) without the afterburner.
  4. Determine the propulsive efficiency without the afterburner.
  5. If the afterburner is ignited, what is the new thrust produced?
  6. What is the new TSFC with the afterburner? Comment on your result compared to without the afterburner.
Show solution/hide solution.
  1. The thrust is found from the momentum equation for steady one-dimensional flow, neglecting pressure differences, which gives

        \[ T = \overbigdot{m}_{\text{air}} (V_j - V_{\infty}) + \overbigdot{m}_{\text{fuel}} V_j \]

    The mass flow rate of air is

        \[ \overbigdot{m}_{\text{air}} = \varrho_{\infty} V_{\infty} A_{\infty} \]

    Convert V_{\infty} to ft/s to get

        \[ V_{\infty} = 530 \times \frac{5,280}{3,600} = 777.0~\text{ft/s} \]

    The standard sea-level density is \varrho_0 = 0.002377 slug/ft^{3},  so

        \[ \varrho_{\infty} = 0.3099 \times 0.002377 = 0.000736~\text{slug/ft}^3 \]

    Therefore,

        \[ \overbigdot{m}_{\text{air}} = 0.000736 \times 777 \times 13 = 7.41~\text{slug/s} \]

    The core fuel-to-air ratio is f = 0.005, so

        \[ \overbigdot{m}_{\text{fuel}} = f \, \overbigdot{m}_{\text{air}} = 0.005 \times 7.41 = 0.03705~\text{slug/s} \]

    Therefore, the thrust is

        \[ T = 7.41 (1,510 - 777) + 0.03705 \times 1,510 = 5,486~\text{lb} \]

  2. The equivalent propulsive power is

        \[\]

        \[ P_{\text{eq}} = T V_{\infty} = 5,486 \times 777 = 4,263,222~\text{ft-lb/s} \approx 7,751~\text{hp} \]

  3. The fuel mass flow rate in lb/s is

        \[ \overbigdot{W}_{\text{fuel}} = 0.03705 \times 32.17 = 1.19~\text{lb/s} \]

    Converting to lb/hr gives

        \[ \overbigdot{W}_{\text{fuel}} = 1.19 \times 3,600 = 4,290~\text{lb/hr} \]

    The thrust-specific fuel consumption (TSFC) is

        \[ \text{TSFC} = \frac{\overbigdot{W}_{\text{fuel}}}{T} \]

    so that

        \[ \text{TSFC} = \frac{4,290}{5,486} = 0.782~\text{lb/hr/lb} \]

  4. The propulsive efficiency is

        \[ \eta_p = \frac{2V_{\infty}}{V_j + V_{\infty}} = \frac{2 \times 777}{1,510 + 777.0} = 0.68 \]

  5. With the afterburner, the exit velocity is V_{j_a} = 2,700~\text{ft/s}, and the afterburner adds additional fuel mass, i.e.,

        \[\]

        \[ f_{\text{total}} = 0.005 + 0.016 = 0.021 \]

    so that

        \[ \overbigdot{m}_{\text{fuel total}} = 0.021 \times 7.41 = 0.1556~\text{slug/s} \]

    The new thrust is

        \[ T_a = 7.41 (2,700 - 777) + 0.1556 \times 2,700 = 14,670~\text{lb} \]

  6. The fuel mass flow in lb/hr is

        \[ \overbigdot{m}_{\text{fuel total}} = 0.1556~\text{slug/s} \times 32.17 = 5.004~\text{lb/s}= 5.004 \times 3,600 = 18,015~\text{lb/hr} \]

    so that

        \[ \text{TSFC}_{\text{afterburner}} = \frac{18,015}{14,670} = 1.228~\text{lb/hr/lb} \]

    The TSFC with the afterburner is significantly higher than without the afterburner, indicating that afterburners greatly increase fuel consumption for a given amount of thrust.

Ramjets

Finally, a description of a ramjet engine is appropriate in that engine category. A ramjet is a straightforward air-breathing jet engine with no rotating or moving parts, much like an afterburner. Ramjets employ a continuous combustion process where fuel is injected and burned in a flame holder as a circular ring, as shown in the schematic below. A ramjet cannot produce thrust when it is stationary, so it has to be accelerated to a high airspeed where it begins to produce thrust. Ramjets work best at supersonic conditions from Mach 3 and upward. Ramjets have been used for supersonic missiles and other types of weapon technology. However, the Fairey Rotodyne gyroplane used ramjets to power its rotor in what is called a reaction-drive rotor system.

A schematic of a ramjet engine.

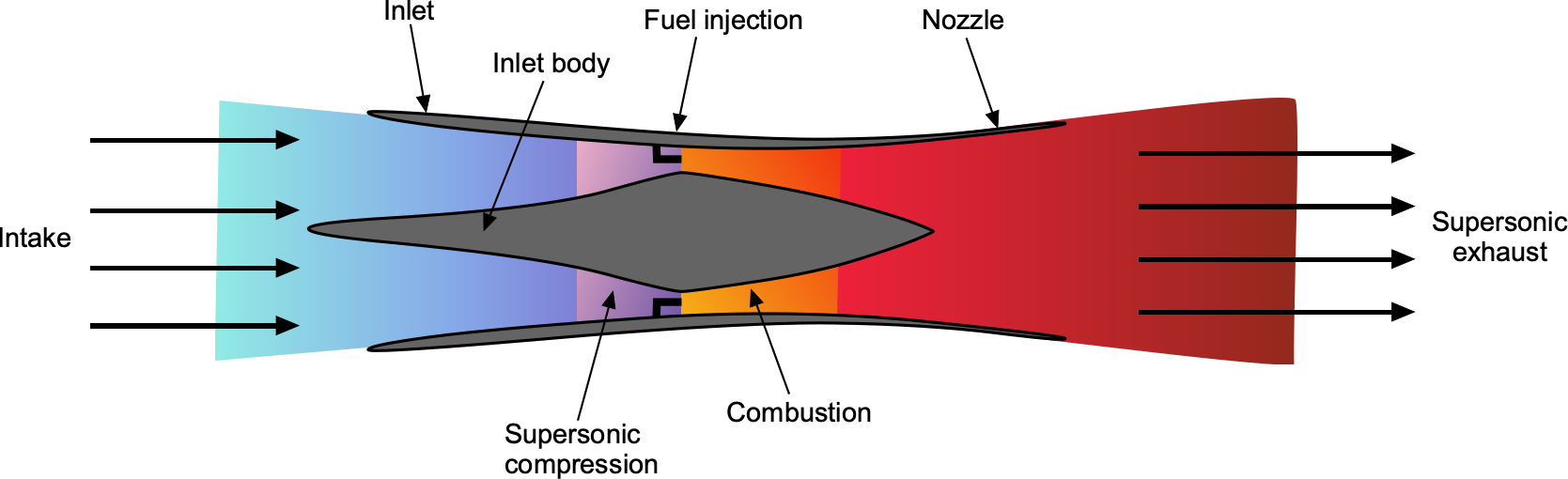
Ramjets, despite their simplicity, have various limitations. One is that they cannot produce thrust at zero airspeeds; they must be accelerated to some minimum airspeed by another means. Second, they are very inefficient at low flight Mach numbers. Consequently, the TSFC of a ramjet is very poor at low Mach numbers and may be nearly an order of magnitude worse than a turbojet. Furthermore, as the Mach number increases, the efficiency of a ramjet improves markedly and may exceed that of a turbojet, but then starts to decrease again as the inlet temperature increases from the effects of compression. However, its TSFC is reasonably good at supersonic Mach numbers above 3.0. Therefore, it is an attractive propulsion system for a hypersonic aircraft, which is called a scramjet (supersonic ramjet).

To understand ramjet performance, consider an idealized model based on steady, one-dimensional, isentropic flow, neglecting friction and shock losses except across the combustor where heat is added. The total temperature at the inlet is given by

(13)   \begin{equation*} \frac{T_0}{T_{\infty}} = 1 + \frac{\gamma - 1}{2} M_0^2 \end{equation*}

where T_0 is the total (stagnation) temperature at the inlet, T_{\infty} is the freestream static temperature, {M_0} = M_{\infty} is the freestream Mach number, and \gamma is the ratio of specific heats, usually 1.4 for air. Fuel is burned at constant pressure, raising the total temperature to T_3, and the resulting hot gas is expanded through the nozzle. Assuming full expansion to ambient pressure, the exhaust velocity is given by

(14)   \begin{equation*} V_j = \sqrt{2 c_p (T_3 - T_0)} \end{equation*}

where c_p is the specific heat at constant pressure. The net thrust per unit mass flow is then

(15)   \begin{equation*} \frac{T}{\overbigdot{m}} = V_j - V_0 \end{equation*}

where V_0 = M_{\infty} is the freestream velocity and \overbigdot{m} is the incoming air mass flow rate. Recall that the thrust-specific fuel consumption is defined as

(16)   \begin{equation*} \text{TSFC} = \frac{\overbigdot{m}_f}{T} = \frac{f \, \overbigdot{m}}{T} \end{equation*}

where {f} is the fuel-to-air mass ratio. The small difference between {V_j} and V_0 at low Mach numbers leads to low thrust and high TSFC. The increased inlet stagnation temperature and greater heat addition capability improve the thrust and reduce the TSFC at moderate supersonic Mach numbers. At high Mach numbers, the growing inlet temperature limits further increases in T_3, which reduces the thermal efficiency and causes TSFC to rise again. This behavior defines the useful performance envelope of the ramjet engine.

Fuels for Turbojet Engines

Turbojet and other gas turbine engines require fuels that are chemically stable, energy-dense, and capable of reliable performance under extreme operating conditions, including high altitudes and wide temperature variations. Jet fuels are refined to meet these criteria, emphasizing combustion properties, thermal stability, and safety characteristics such as flash point.

The most widely used jet fuels in aviation are categorized into standard types. The two principal grades are Jet A and Jet A-1. Jet A is primarily used in the United States, while Jet A-1 is the international standard. Both fuels are kerosene-based, with Jet A-1 having a slightly lower freezing point of -47^\circ\text{C} compared to Jet A’s -40^\circ\text{C}, enhancing its suitability for long-haul international flights at high altitudes. These fuels are characterized by high energy content, approximately 43 MJ/kg, and densities near 0.80 kg/L at standard conditions.

Jet fuels must have a sufficiently high flash point to minimize fire hazards. Jet A and Jet A-1 have minimum flash points of approximately 38^\circ\text{C}, ensuring that the fuels do not vaporize excessively at ground temperatures. In addition to flash point, freezing point is critical, as turbine aircraft routinely operate at stratospheric altitudes where ambient air temperatures can fall below -50^\circ\text{C}.

Another important aviation fuel is JP-8, a military-grade kerosene similar to Jet A-1 but containing additional additives to enhance thermal stability, reduce the risk of icing, and improve lubrication. Historically, JP-4, a wide-cut fuel blending gasoline and kerosene fractions, was used extensively in military aviation. Still, it has largely been replaced due to its lower flash point and greater volatility, which posed increased fire risks. Jet B, a wide-cut fuel containing a higher proportion of lighter hydrocarbons, is limited in very cold climates because of its good low-temperature properties. However, its higher volatility and handling risks have limited its adoption in civil aviation.

The combustion of jet fuel in a turbojet engine releases thermal energy that drives the turbine and produces high-velocity exhaust to generate thrust. The basic energy balance can be expressed by the relationship

    \[ \overbigdot{Q}_{\text{in}} = \overbigdot{m}_{\text{fuel}} \, h_{\text{comb}} \]

where \overbigdot{m}_{\text{fuel}} is the mass flow rate of the fuel and h_{\text{comb}} is the lower heating value of the fuel, typically around 43 MJ/kg for kerosene-based fuels.

Because turbojets operate continuously at high temperatures and pressures, fuel properties such as thermal oxidative stability are also critical. Fuel degradation under heat, known as coking, can lead to deposits in fuel nozzles and afterburners, reducing engine performance and reliability. The proper selection, certification, and management of jet fuels are essential to ensure the safe and efficient operation of turbine-powered aircraft. Understanding the physical and chemical characteristics of these fuels forms a fundamental part of aerospace engineering education.

Summary & Closure

The turbojet engine is a classic solution to jet propulsion and is ideally suited for high subsonic or supersonic flight. Today, turbojets are used more on military aircraft. For supersonic flight, the turbojet will be fitted with an afterburner, which may give the engine twice the thrust, but it can only be used for short periods because of the high fuel consumption. For the most part, choosing a turbojet for an aircraft that cruises at less than Mach 0.5 is inappropriate, and a turboprop should be used here because they have much better specific fuel consumption. Using a turbofan at higher airspeeds is better than a turbojet because it has a better specific fuel consumption. A turbofan also has much lower noise because of the lower jet velocity. With increasingly stringent aircraft engine noise constraints, the pure turbojet may eventually be relegated to aeronautical history, even for military aircraft.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • Explain why increasing the flight Mach number improves a turbojet’s overall propulsive efficiency.
  • Study the SR-71 and Concorde supersonic aircraft. What kinds of engines did they use? Did they use afterburning (reheat)?
  • How does the afterburner affect the performance of a turbojet engine, and under what conditions is it typically used?
  • Explain the concept of thrust-to-weight ratio and its significance in determining the performance characteristics of a turbojet engine.
  • What are the primary factors that influence the efficiency of a turbojet engine, and how can these factors be optimized?
  • Discuss the typical applications of turbojet engines and provide examples of aircraft that utilize this type of propulsion system.
  • Describe any recent advancements or technological developments in turbojet engine design that have improved performance or fuel efficiency.

Other Useful Online Resources

  • A great video on how jet engines work.
  • A video on World War 2 Jet Power.
  • How jet engines transformed our world: A History Channel video.
  • An excellent early film on the history of the gas turbine engine.
  • To learn more about afterburning and turbojets, check out these articles from science.gov.
  • You can learn more about turbojets from the NASA website.
  • A good video shows the internals of a turbojet engine as well as its running.
  • A fun video on a turbojet-powered scooter!
  • Video explaining the detailed design and inner workings of a jet engine.

 

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n32

Share This Book