Stalling & Spinning

J. Gordon Leishman

doi:https://doi.org/10.15394/eaglepub.2022.1066.n41

55 Stalling & Spinning

Introduction

The wings generate the lift on an airplane to overcome the airplane’s weight. Lift production depends on the airplane’s airspeed, the air’s density, the wing’s size (i.e., area), and the wing’s angle of attack. The angle of attack is of particular interest because a wing can only produce lift with good aerodynamic efficiency over a relatively small range of angles of attack before the flow separates from the upper surface and the wing stalls. At low angles of attack, the flow will pass smoothly over a wing, as shown in the image below; this aerodynamic condition is the normal mode of flight operations. The highest angle of attack that a wing can operate is called the stall angle of attack (or the stall angle) and corresponds to the angle to the flow when flow separation progresses to the point that it causes a loss of lift.

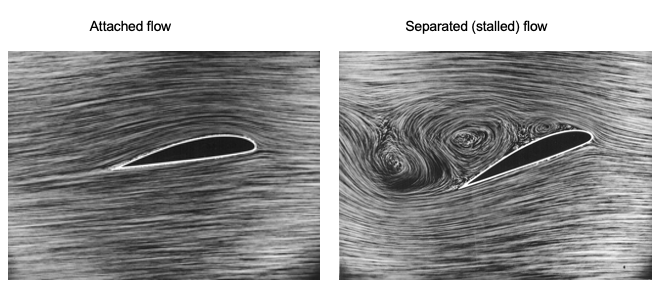
Flow visualization images show the smooth streamlines typical of attached flow (left image) and the detached or separated flow and turbulence characteristic of stall onset (right image).

The onset of flow separation anywhere on a wing will limit its maximum lifting capability; this behavior is also commensurate with increased drag. When a wing fully stalls, there is also a pronounced nose-down pitching moment associated with an aft movement of the center of pressure produced by the effects of the separated flow, as well as significant unsteady flow and buffeting from the creation of turbulence. Therefore, the onset of a stall on a wing usually represents a limiting factor in the operational flight envelope of an airplane and generally sets its lowest controllable airspeed. In some cases, the onset of stall may precipitate a spin where the airplane enters into a rapid downward spiral with the wing in the stalled state. Therefore, it is crucial to understand what stall is on a wing, how it occurs, and the factors that can affect the onset of the stall.

Learning Objectives

Understand the fundamental flow physics associated with the onset of flow separation and stall on an airfoil and a finite wing, as well as its implications.
Know how to calculate an airplane’s stall airspeed under different weight and density altitude conditions and for different maximum lift coefficients.
Understand the importance of various “high-lift” devices, such as flaps on airplane wings, to raise the maximum lift coefficients and reduce stall airspeeds.
Appreciate the significance of a spin and why the onset of a stall is a prerequisite to developing a spin.

Stalling Airspeeds & Angles of Attack

In terms of aerodynamics, for vertical equilibrium on an airplane in straight-and-level flight, then

(1) $\begin{equation*} L = \frac{1}{2} \varrho_{\infty} V_{\infty}^2 \, S \, C_L = q_{\infty} \, S \, C_L = W \end{equation*}$

where $\varrho_{\infty}$ is the air density in which the airplane flies, $S$ is the wing area, and $C_L$ is the total wing lift coefficient. The assumption is that the main wings generate all lift to overcome the weight $W$ , even though the horizontal tail may carry some small lift (positive or negative).

Stall Airspeeds

For estimating the stall airspeeds of an airplane, i.e., before verification by flight testing, it is normal to assume that only the main wings carry the lift of the entire airplane. For the density of the air, recall that $\varrho = \varrho_0 \, \sigma$ where the value of the density ratio, $\sigma$ , comes from the ISA model, so an alternative variant of Eq. 1 is that

(2) $\begin{equation*} L = W = \frac{1}{2} (\varrho_0 \, \sigma ) \, V_{\infty}^2 \, S \, C_L \end{equation*}$

Rearranging this equation gives the lift coefficient needed for the wing at a given flight airspeed, airplane weight, and operational density altitude (i.e., air density), i.e.,

(3) $\begin{equation*} C_L = \frac{2 W}{(\varrho_0 \, \sigma ) S V_{\infty}^2} = \frac{2}{(\varrho_0 \, \sigma ) V_{\infty}^2} \left( \frac{W}{S} \right) \end{equation*}$

The ratio of the airplane’s weight to its lifting wing area, $W/S$ , is called wing loading. Notice also that the lift coefficient is proportional to wing loading but decreases with the square of the airspeed. The lift coefficient also increases with density altitude, i.e., lower values of $\sigma$ , for a given airspeed and flight weight.

The minimum airspeed that would allow for the airplane’s flight is called the stalling airspeed, which corresponds to the angle of attack and lift coefficient at which the wing will stall. To understand why this condition is important, consider the typical relationship between lift coefficient and angle of attack, as shown in the figure below, which also considers the effects of high lift devices such as flaps and leading edge slats. The maximum lift coefficient is $C_{L_{\rm max}}$ , so it is apparent that $C_{L_{\rm max}}$ increases from about 1.4 for the baseline wing in the clean configuration to nearly 3.0 with full flaps and the leading edge slats extended.

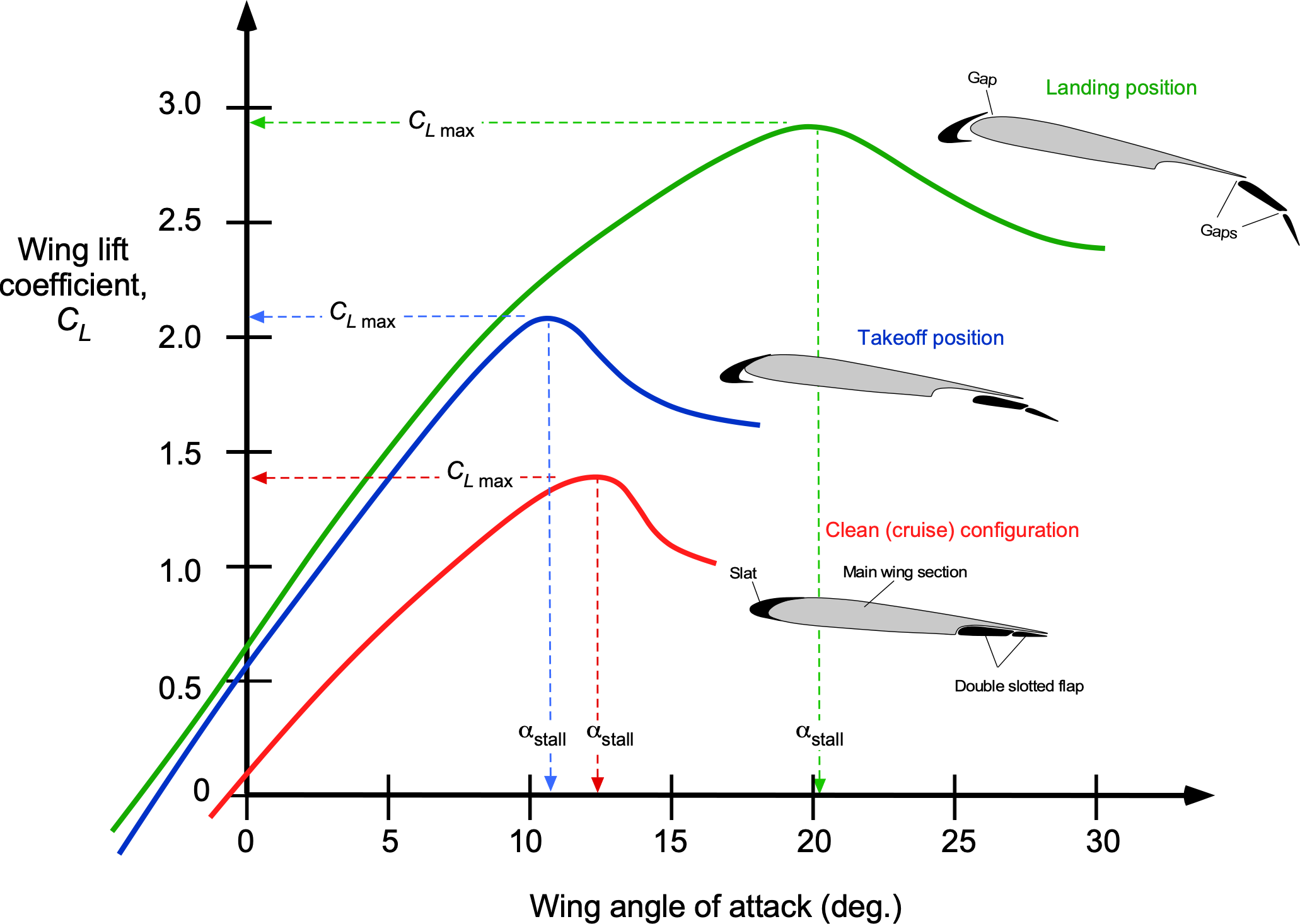
The maximum attainable lift coefficient depends on whether the flaps or slats are retracted or deployed. If retracted, the wing is said to be in its “clean” configuration.

Although the value of $C_{L_{\rm max}}$ may not be exactly known (i.e., predictable) for any wing without a wind tunnel or flight testing, the corresponding stall airspeed in straight and level unaccelerated flight can be solved by using

(4) $\begin{equation*} V_{\rm stall} = \sqrt{ \frac{2}{\varrho_0 \, \sigma } \left( \frac{W}{S} \right) \frac{1}{C_{L_{\rm max}} }} \end{equation*}$

Conversely, if the stall airspeed of the wing is known, which would need a careful measurement of the equivalent and true airspeeds (not the indicated airspeed) at which stall occurs, then it is possible to calculate the corresponding $C_{L_{\rm max}}$ of the wing, i.e.,

(5) $\begin{equation*} C_{L_{\rm max}} = \frac{2 W}{\varrho_0 \, \sigma \, S \, V_{\rm stall}^2} \end{equation*}$

Check Your Understanding #1 – Calculation of stall airspeed

An airplane has a wing with a maximum lift coefficient, $C_{L_{\rm max}}$ , of 1.7. The in-flight weight, $W$ , is 20,000 lb, and the wing area, $S$ , is 340 ft². The aircraft is in steady, unaccelerated flight at an altitude where the density ratio, $\sigma$ , is 0.7385. Calculate the stall airspeed of the airplane.

Show solution/hide solution.

The stall airspeed is given by

$V_{\rm stall} = \sqrt{ \frac{2}{\varrho_0 \, \sigma } \left( \frac{W}{S} \right) \frac{1}{C_{L_{\rm max}} }}$

Inserting the known values gives

$V_{\rm stall} = \sqrt{ \frac{2}{0.002378 \times 0.7385} \left(\frac{20,000}{340.0} \right) \frac{1}{1.7} } = 198.5~\mbox{ft/s} = 117.6~\mbox{kts}$

Stall Angle of Attack

The flow is fully attached to the wing in the linear region of the lift curves shown in the previous figure. In this region, the relationship between the lift coefficient and the angle of attack can be written as

(6) $\begin{equation*} C_L = C_{L_{\alpha}} \left( \alpha - \alpha_0 \right) \end{equation*}$

where $C_{L_{\alpha}}$ is the lift curve (in appropriate units of per degree or radian). The parameter $\alpha_0$ in Eq. 3 is called the zero-lift angle of attack. It reflects that the zero lift coefficient will be obtained when the wing is at a small negative angle of attack, which is typical for a wing with normal amounts of camber. It will be noticed. However, the value of $\alpha_0$ becomes increasingly negative by applying flaps and then with flaps and slats together.

The airspeed in level flight that corresponds to a given lift coefficient can be determined, i.e.,

(7) $\begin{equation*} V_{\infty} = \sqrt{ \frac{2}{\varrho_0 \, \sigma } \left( \frac{W}{S} \right) \frac{1}{C_L} } \end{equation*}$

Further, based on a linear lift-curve slope assumption, i.e., $C_L = C_{L_{\alpha}} \, \alpha$ , then airspeed can also be related to the angle of attack, i.e.,

(8) $\begin{equation*} V_{\infty} = \sqrt{ \frac{2}{\varrho_0 \, \sigma } \left( \frac{W}{S} \right) \frac{1}{C_{L_{\alpha}} \, \alpha} } \end{equation*}$

and so the angle of attack to airspeed, i.e.,

(9) $\begin{equation*} \alpha = \frac{2}{\varrho_0 \, \sigma V_{\infty}^2 } \left( \frac{W}{S} \right) \frac{1}{C_{L_{\alpha}}} \end{equation*}$

This latter result is beneficial for piloting because the pilot generally monitors the airplane’s airspeed, not the wing angle of attack. However, some high-performance airplanes and airliners may have an angle of attack sensor and cockpit indicator to help avoid a stall.

The value of $C_{L_{\alpha}}$ for a high aspect ratio wing at low flight Mach numbers (below 0.3) is typically about 0.1 per degree or 5.7 per radian but somewhat larger at higher subsonic Mach numbers, i.e., according to the Glauert rule. Decreasing the aspect ratio of the wing will also reduce the value of $C_{L_{\alpha}}$ , but the actual value may not be known precisely a priori before the airplane is built and flown, even though it can be estimated based on mathematical aerodynamic models and perhaps with the aid of wind tunnel testing.

At higher angles of attack, the lift coefficient reaches a maximum value and then decreases markedly because of the onset of flow separation and stall. For example, for a plain wing of moderate to high aspect ratio at low Mach numbers (i.e., one without any high lift devices), the maximum lift coefficient, $C_{L_{\rm max}}$ , is typically between 1.4 and 1.6. This result means that the corresponding maximum angle of attack of the wing before stall (based on typical values of lift-curve slope) at the low subsonic Mach numbers typical of takeoff and landing will be between 14 $^{\circ}$ and 16 $^{\circ}$ . However, the figure above shows that for a wing with high-lift devices deployed, values of $C_{L_{\rm max}}$ can be much higher. But also notice that the angle of attack for stall can be lower or higher depending on how the high-lift device(s) modify the wing camber and hence the zero-lift angle of attack, $\alpha_0$ , depending on the wing.

Load Factor

Although airspeed is related to the stall angle of attack, it is important to appreciate that a wing will stall at any airspeed if the angle of attack reaches the stall angle. For example, if the airplane is maneuvering and attains a steady load factor $n >1$ such that now $L = n\, W$ , then the new stall airspeed would be

(10) $\begin{equation*} V_{\rm stall} = \sqrt{ \frac{2}{\varrho_0 \, \sigma } \left( \frac{n \, W}{S} \right) \frac{1}{C_{L_{\rm max}} }} = \sqrt{n} \sqrt{ \frac{2}{\varrho_0 \, \sigma } \left( \frac{W}{S} \right) \frac{1}{C_{L_{\rm max}} }} \end{equation*}$

which shows that the stall airspeed increases with the square root of the load factor, i.e.,

(11) $\begin{equation*} V_{{\rm stall}_{n}} = \sqrt{n} \, V_{{\rm stall}_{n = 1}} \end{equation*}$

where $V_{{\rm stall}_{n}}$ is the stall airspeed for any load factor, $n$ , and $V_{{\rm stall}_{n = 1}}$ is the load factor in level, unaccelerated flight, i.e., $n = 1$ . It will be apparent the stall angle of attack for a given wing in a given configuration, however, is the same regardless of the load factor, and it is not a function of airspeed other than through the effects of Mach number and/or Reynolds number.

Summary of Effects on Stall Airspeed

In summary, from the preceding, it can be concluded that:

Stall airspeed will increase with the increasing weight of the airplane.
Stall airspeed will increase with increasing density altitude, i.e., with a lower air density.
Stall airspeed will decrease with increasing values of wing $C_{L_{\rm max}}$ , which could be achieved by deploying wing flaps and/or leading-edge slats.
Stall airspeed will decrease with increasing wing area.
Stall airspeed will increase with an increasing load factor.

General Flow Physics of Stall

At higher angles of attack before stall, the adverse pressure gradients produced on the wing’s upper surface result in a progressive increase in the thickness of the boundary layer. This causes some deviation from the linear lift versus angle of attack behavior, manifest at first by a “rounding” of the lift curve, as shown previously. With a further increase in the angle of attack, the flow will separate from the upper surface, causing a stall.

On many wings and airfoils, the onset of a stall occurs gradually with an increasing angle of attack, as shown in the figure below, called a trailing edge stall. However, on other wings, particularly those with sharper leading edges found on high-speed aircraft, flow separation may occur quite suddenly up edges, such as on reaching a critical angle of attack, usually referred to as a leading-edge type of stall.

The development of a thickening boundary layer and the onset of flow separation will eventually limit the lift production on an airfoil and will also increase its drag, which is called “stall.”

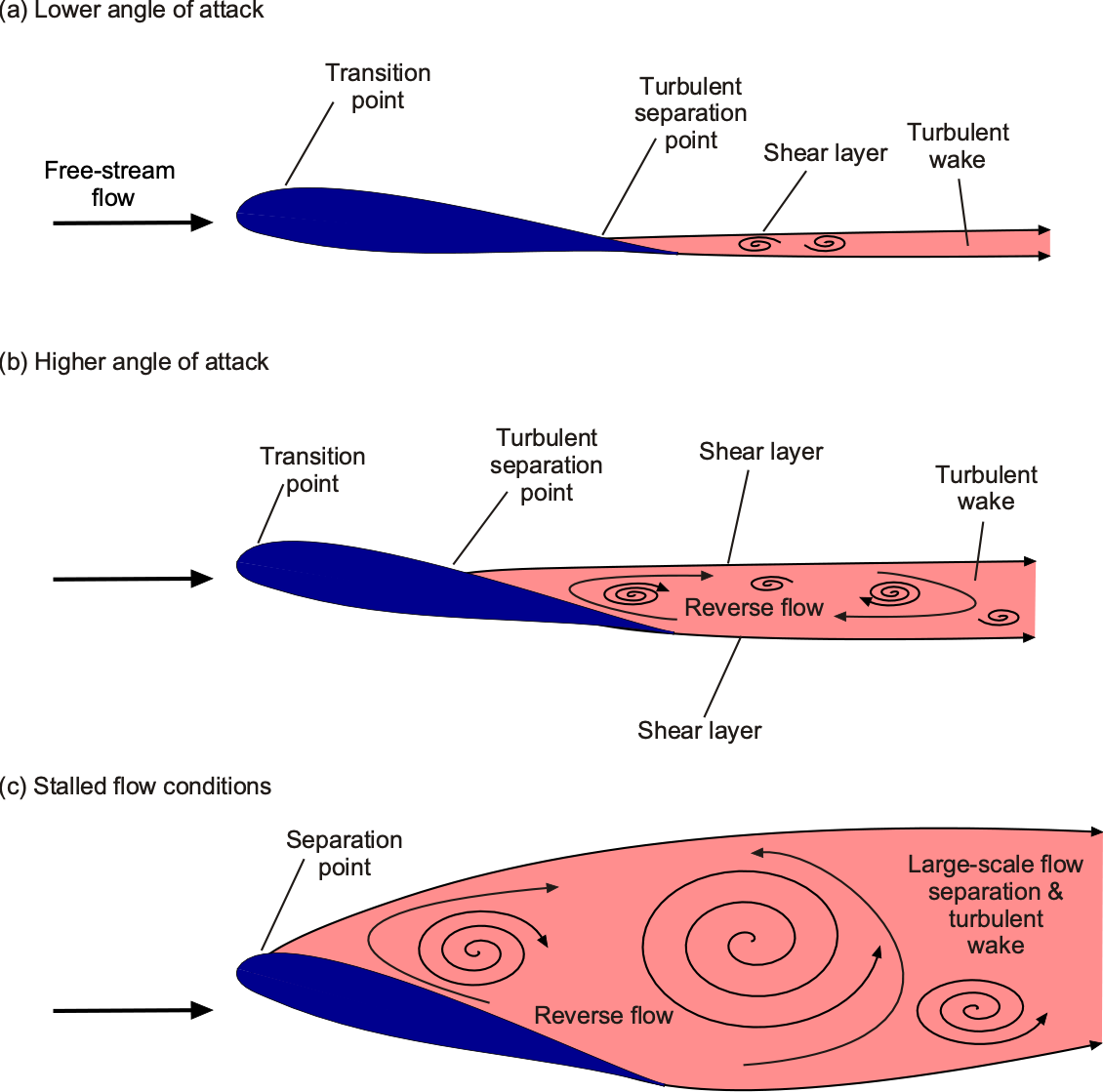
After the stall, much less lift is generated on the wing, and drag is substantially greater. Also, under these separated flow conditions, steady flow no longer prevails, with turbulence being shed into the wake, which manifests as buffeting. For example, measurements on stalled wings in the wind tunnel will generally show large fluctuating forces and pitching moments when the flow separates.

Two-Dimensional Stall Characteristics

Much of the detailed understanding of the aerodynamics of wings and wing sections comes from testing in wind tunnels, the effects of the wing section (i.e., the airfoil shape), wing aspect ratio, and wing planform having the most important effects. In their compendium of measurements, Abbott & von Doenhoff have documented a summary of the characteristics of many airfoil sections made at Reynolds numbers of 3 to 9 million and Mach numbers up to 0.2, which contains a wealth of measurements for the engineer.

It has been found that airfoils generally fall into three static stall categories, namely: thin-airfoil stall, leading-edge stall, and trailing-edge stall. Abbott & von Doenhoff show that thin-airfoil and leading-edge stalls are somewhat abrupt stall types and can be sensitive to changes in airfoil shape, whereas trailing-edge stall is a more gradual type of stall and less sensitive to shape. Most conventional subsonic wings fall into the trailing edge stall category at low to moderate Mach numbers, although the more abrupt form of a leading-edge stall is not uncommon. However, for supersonic wings with relatively sharp leading edges, their stall characteristics at low airspeeds are usually an abrupt leading-edge type of stall.

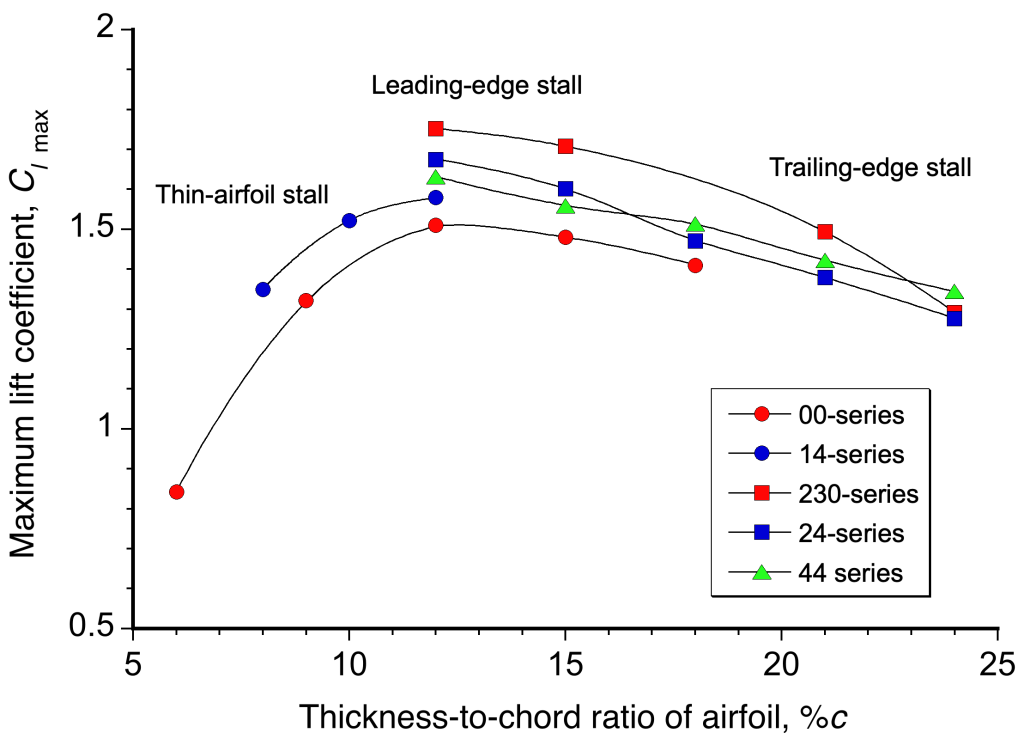
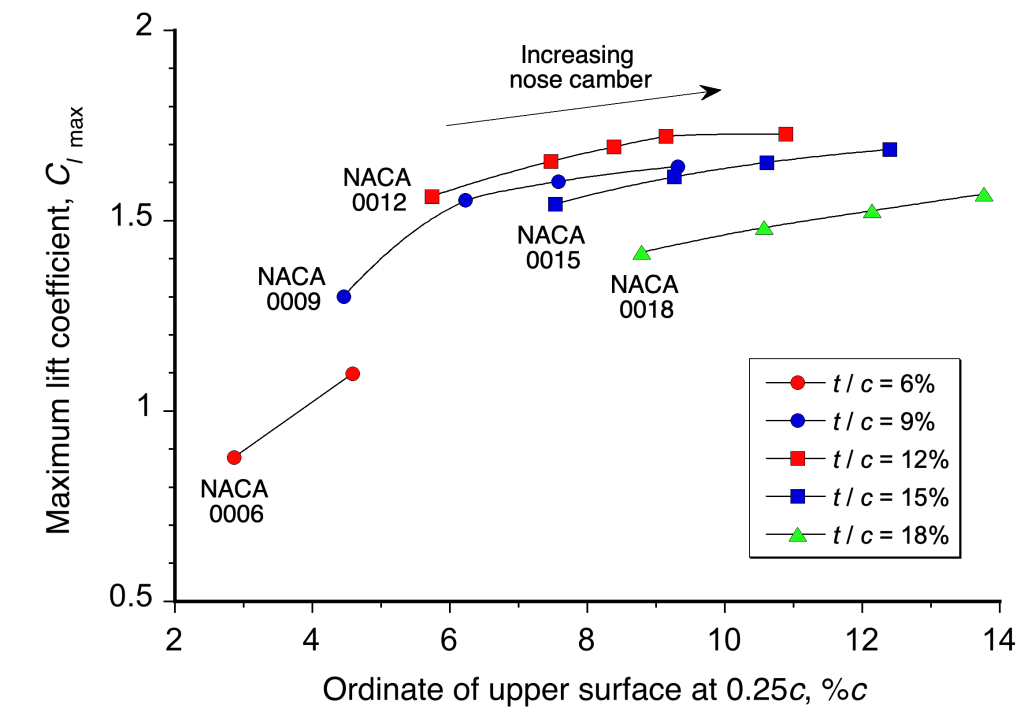
The figure below summarizes measurements showing the combined effect of thickness and camber on the $C_{l_{\rm max}}$ of an airfoil. Clearly, “thin” airfoils (low values of the thickness-to-chord ratio of between 4% and 8%) produce much lower values of $C_{l_{\rm max}}$ . Still, it is interesting to note that increasing thickness above 12% begins to reduce the value of $C_{l_{\rm max}}$ . The best airfoils in terms of attaining the highest $C_{l_{\rm max}}$ have a thickness-to-chord ratio between 12% and 15%, which is common on wings used for airplanes.

Summary of results showing the combined effect of thickness and camber on the $C_{l_{\rm max}}$ of an airfoil.

Using some nose camber for a given thickness-to-chord ratio is also desirable in increasing $C_{l_{\rm max}}$ , as shown in the figure below. However, there is a point of diminishing returns in that some slight camber over the nose region of an airfoil is desirable, but too much gives only minor gains in $C_{l_{\rm max}}$ . Indeed, using significant nose camber is usually undesirable for two reasons. First, large amounts of camber increase the pitching moments on the airfoil section and the wing as a whole, which is not always desirable. Second, too much camber is associated with increased profile drag, which is never a good outcome.

Results showing the effect of nose camber on the $C_{l_{\rm max}}$ of an airfoil.

The $C_{l_{\rm max}}$ of an airfoil section also reduces with increasing free-stream Mach number, as shown in the figure below. This behavior is because increasing the Mach number makes the airfoil’s pressure gradients more adverse, increasing the boundary layer thickness on the upper surface at a lower angle of attack. This effect reduces the value of $C_{l_{\rm max}}$ and the corresponding stall angle with increasing Mach number. Notice also the effects of Reynolds number (chord-based), for which lower Reynolds numbers will result in lower values of $C_{l_{\rm max}}$ for a given Mach number.

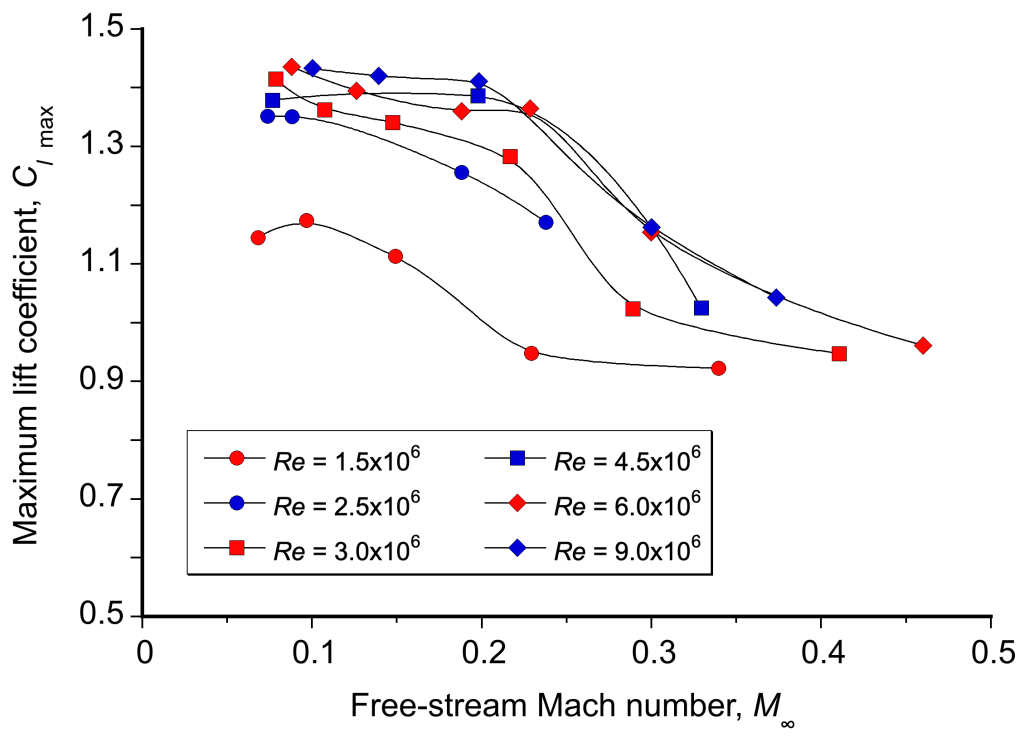
Results showing the effect of increasing free-stream Mach number on the $C_{l_{\rm max}}$ of an airfoil at different chord Reynolds numbers.

Therefore, in addition to the primary factors that have been discussed that will affect the stall airspeed, the stall angle of attack and corresponding airspeed will generally:

Decrease with increasing flight Mach number.
Decrease with decreasing chord-based Reynolds number.

Three-Dimensional Stall

The effects of wing planform (e.g., taper) and twist (washout) also affect the local lift coefficient distribution along the wing (i.e., the distribution of $C_l$ along the span of the wing) and also the total attainable maximum lift coefficient. Therefore, if the local $C_l$ is higher at some point on the wing than another, the wing is more likely to stall at this location.

While no complete generalization of all the possible results is available for wings, it has been found that higher aspect ratio wings tend to reach higher overall maximum lift coefficients. However, too much planform taper can reduce the wing’s maximum lift coefficient. Likewise, too much sweepback also tends to decrease the maximum attainable lift. Both effects are predictable using various types of aerodynamic theories.

The main problem in wing design is that at the point of stall, a finite wing often develops somewhat complicated three-dimensional flow patterns, an example being shown in the images below based on wind tunnel flow visualization. Sometimes, the pattern is not symmetrical between a wing’s left and right side panels, which in practice produces a rolling moment on the airplane and a departure from controlled flight. In a worst-case scenario, the airplane may develop a spin, taking a significant altitude to recover from (see later).

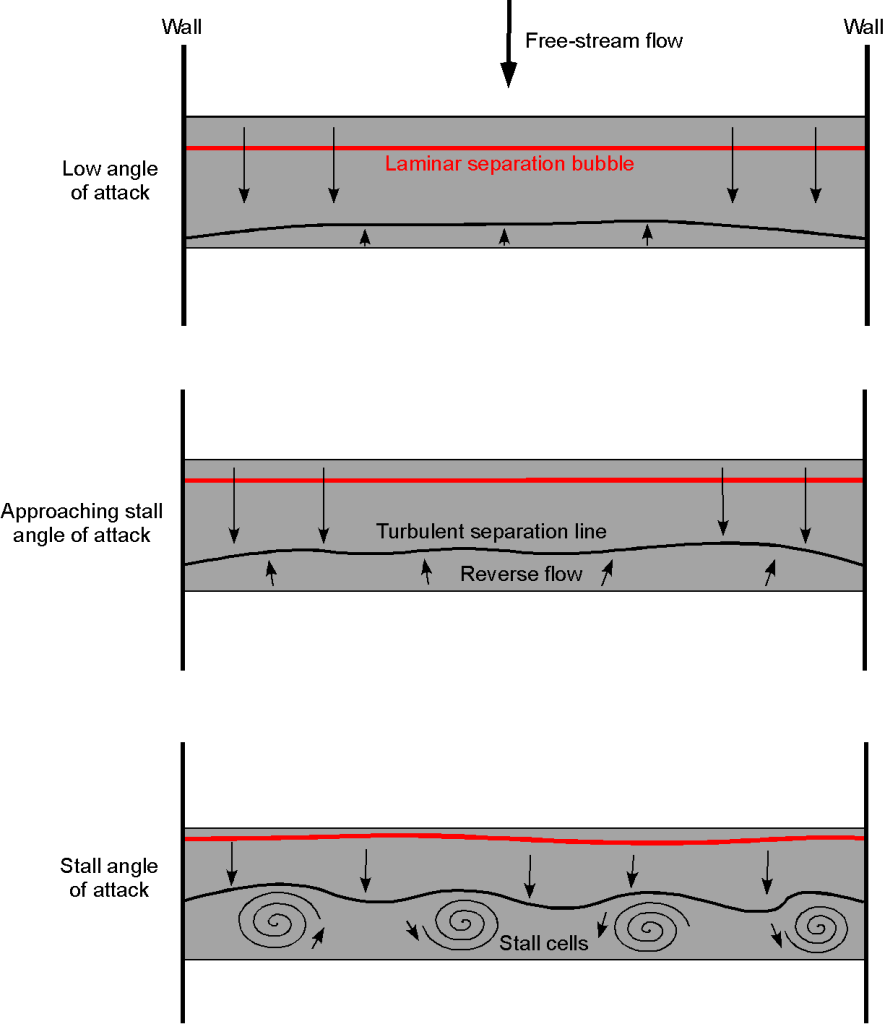
Interpretation of surface oil flow visualization of a wing spanning the walls in a wind tunnel showing the formation of three-dimensional “cells” at stall.

The three-dimensional stall developments on wings can be studied during flight testing by placing strips of yarn called “tufts” all over the wing’s upper surface. The tufts are arranged in orderly rows spanwise and chordwise along the wing, an example being shown in this video. It will be seen that when the tufts are blown straight back, the flow is fully attached. However, suppose the tufts change direction and lift from the surface. In that case, the flow at those locations is inevitably separated, which is likely an indicator of the incipient stall on the entire wing.

The stall patterns that develop on any given wing depend on many factors, but some general observations have emerged, as shown in the schematic below. For rectangular wings, the stall will generally start at the root of the wing and work forward and outward toward the mid-span. This behavior is a desirable stall pattern on a wing because the onset of flow separation gives some buffeting, and the pilot will recognize the stall onset before the stall progresses too far. The airplane also tends to pitch down naturally at the stall, reducing the wing’s angle of attack and suppressing further stall developments. Finally, the wing’s outer parts have a fully attached flow, so there will be no tendency for the airplane to roll, and the ailerons will be fully effective.

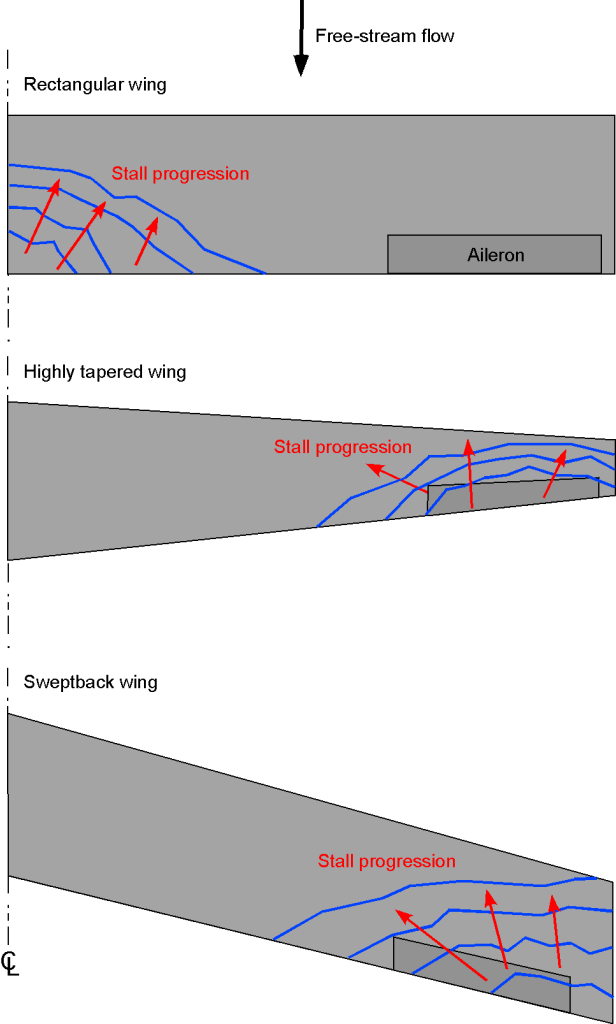
Examples showing the effects of wing planform on the three-dimensional stall developments.

A highly tapered wing has the opposite problem in that the wing tips will tend to stall first. With swept wings, the tips also tend to stall first. In these cases, the aileron effectiveness will be reduced because of the separated flow, and the airplane will often tend to show uncommanded rolls to the left or right. Indeed, in this cases, the application of controls to correct the roll may make the stall worse, and the airplane may experience a control reversal, i.e., if the airplane rolls to the right, for example, the use of normal corrective control inputs make the roll to the right much worse.

As previously mentioned, large amounts of wing sweepback (which is used to delay the onset of compressibility effects to higher cruise airspeeds) are also known to produce stall toward the wing tips, which is a concern in the design of commercial airliners. There are two main reasons why swept wings tend to stall first at their tips. First, sweepback alone produces a spanwise distribution of the local lift coefficient biased toward the wing tips. The second is that the wing taper elevates the lift coefficients at the wing tips.

To establish where a wing will stall first, the product of the local section lift coefficient and the wing chord at that position can be divided by the product of the total wing lift coefficient and the mean aerodynamic chord, as shown in the graphs below. Where the resulting values are highest, then the wing can be expected to stall there first. Using too much planform taper only exacerbates this effect of increasing the lift coefficients at the wing tip, making the wing more likely to stall there. However, the consequences can be mitigated to some extent by using wing twist (washout) and careful use of leading-edge camber.

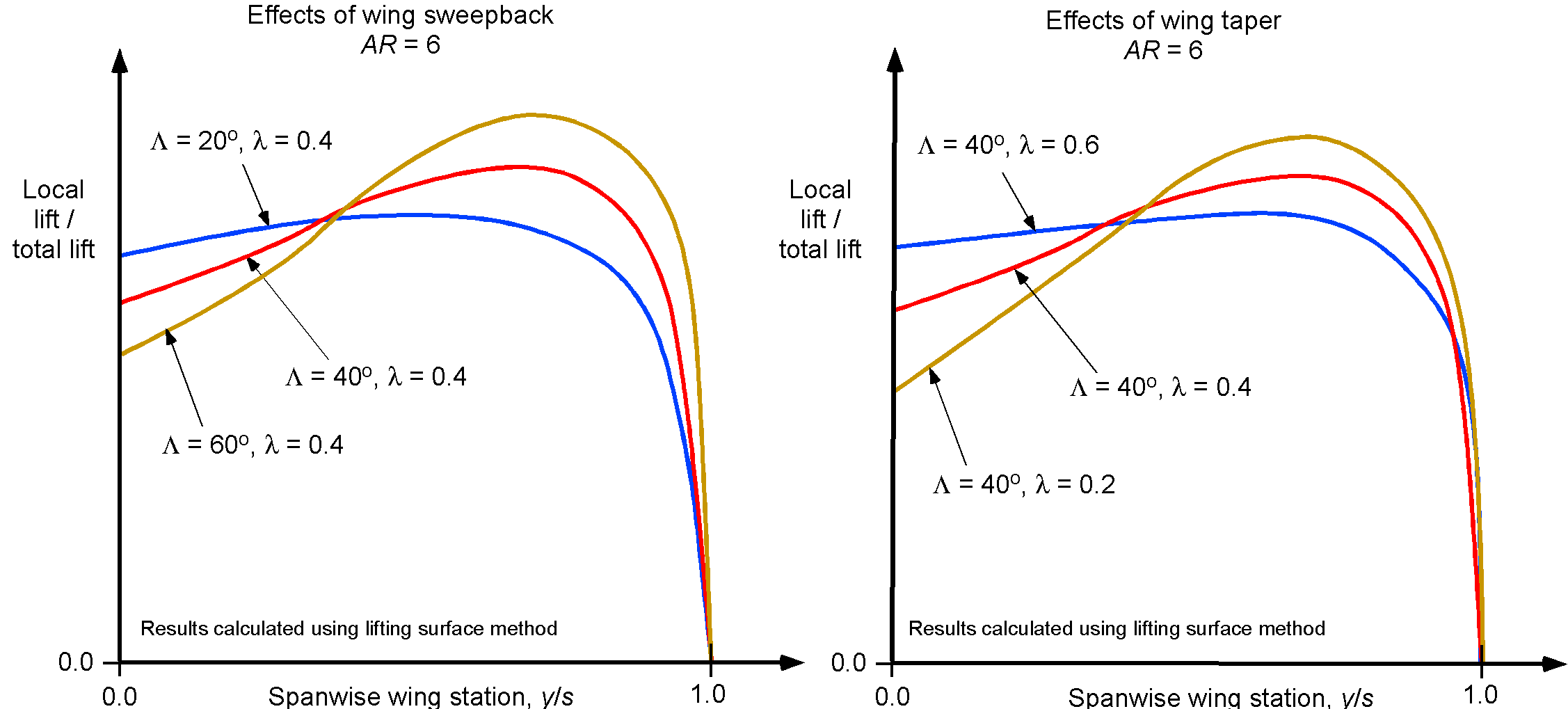
The effects of sweepback on the spanwise distribution of local lift coefficient.

At higher angles of attack, sweepback tends to encourage the boundary layer to grow thicker in the spanwise direction, thus making it more susceptible to separating at the wing tips. Usually, the wing is carefully designed to minimize such tendencies, but other steps are generally necessary. For example, various fences and vortex generators are often used to help keep the flow attached. In addition, some commercial airplanes have “auto-slats” so that if the wing approaches the stall, the slats automatically extend to prevent the stall from developing.

Importance of High-Lift Devices

Airplane wings are usually designed for the best efficiency in cruising flight conditions. In fact, on commercial transport airplanes, the supercritical wing is explicitly designed to be efficient at transonic flight conditions. However, relatively thin, swept wings tend to have much poorer aerodynamic performance at lower airspeeds and Mach numbers. In the “clean” condition, the airplane tends to exhibit relatively high stalling airspeeds and is susceptible to adverse stall qualities.

However, as previously explained, it is possible to increase the maximum lift coefficient of a wing and reduce the stall airspeed by using high-lift devices such as trailing-edge flaps and leading-edge slats. The photo below shows the triple-slotted trailing edge flap system in the fully deflected landing configuration. Notice also the condensation trails marking the locations of trailing vortices from the side edges of the flaps and the inboard aileron. The main advantage of reducing stall airspeeds is that the airplane can fly at lower airspeeds, significantly reducing takeoff and landing distances. Of course, nearly every type of airplane can benefit from using high lift devices to lower its stall airspeed and reduce its takeoff and landing distances.

The triple-slotted trailing edge flap system of a Boeing 747 in the fully deflected landing configuration.

The figure below shows a schematic of a wing section with high-lift devices. Usually, the flaps operate in conjunction with the leading-edge slats if they are available. In many cases, the flaps are designed to deflect rearward and downward (called Fowler flaps), which increases the effective area of the wing and its camber in the region of the flaps.

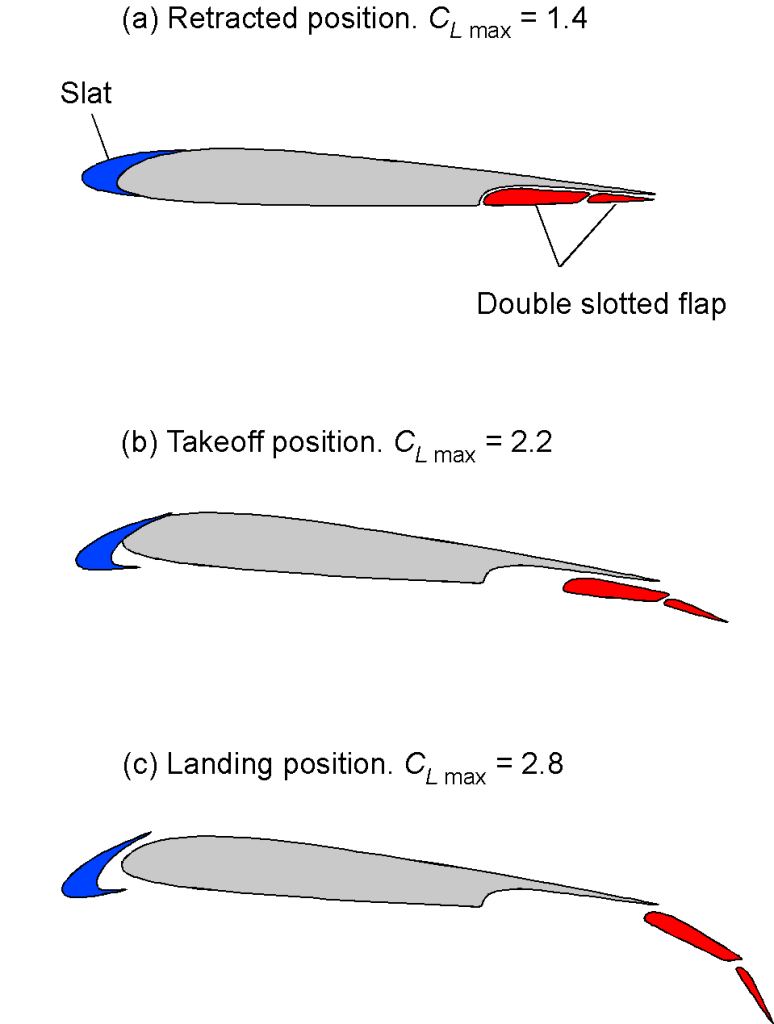
The flaps and leading edge slats work together to increase the maximum lift coefficient of the wing for takeoff and landing.

The flaps and slats are partly deflected for takeoff to reduce the takeoff airspeed and takeoff distance. After takeoff, the flaps on the airplane are progressively retracted as airspeed builds and the slats retracted. For landing, the flaps are fully deflected; they are gradually extended in stages as the airplane descends from altitude and slows down to its final landing approach airspeed. The extra drag from full flap deflection helps to slow the airplane down to landing airspeeds and steepens its final approach angle to the runway, both of which help the pilot successfully land the airplane.

Leading-edge slats usually work in synchronization with the flaps. Like the trailing edge flaps, their purpose is to increase the wing’s maximum lift and angle of attack capability before it stalls and allow the airplane to fly at lower airspeeds. The usual types of slats initially move forward and downward and increase the camber of the wing section. When fully deployed, they also open up a small gap between the slat and the leading edge of the main wing. This gap is critical because it helps to energize the boundary layer on the wing’s top surface. Other leading-edge devices include Kruger flaps, which rotate forward to increase the leading-edge camber of the wing; such devices are often found on the inboard parts of wings, such as on the Boeing 747. Such devices are highly effective in increasing the attainable maximum lift coefficient and angle of attack before the wing stalls.

While flaps by themselves are effective in increasing $C_{L_{\rm max}}$ , the use of flaps and slats together may increase $C_{L_{\rm max}}$ to values of over 3.0. Consequently, if the slats and flaps are both fully deployed, the airplane can typically fly at airspeeds that may be 50% less than without them, i.e., compared to flying in the clean condition with flaps and slats retracted. In addition, using flaps and slats substantially changes the wing’s camber, which modifies the zero-lift angle of attack and the nature of the lift curve. In some cases, the system’s lift-curve slope may change, especially with the highly effective wing camber introduced by the slats.

Check Your Understanding #2 – Calculation of stall airspeeds with flaps

Calculate the stall speeds for a Cessna 402 in knots for flap deflection angles of 0, 15, and 30 degrees. The lift characteristics of the wing are shown in the graph below. The airplane has a wing area, $S$ , of 255.8 ft^2, and weight, $W$ , of 6,300 lb. Assume standard MSL ISA conditions.

Show solution/hide solution.

The stall speed is determined using

$V_{\rm stall} = \sqrt{ \frac{2}{\varrho_0 \, \sigma } \left( \frac{W}{S} \right) \frac{1}{C_{L_{\rm max}} }}$

In this case,

$V_{\rm stall} = \sqrt{ \frac{2}{0.002378} \left( \frac{6,300}{255.8} \right) \frac{1}{C_{L_{\rm max}} }} = \sqrt{\frac{20713.7}{C_{L_{\rm max}}} }$

The values of $C_{L_{\rm max}}$ now must be estimated by reading the graph.

For the plain wing with the flaps up, $C_{L_{\rm max}}\approx 1.26$ . Therefore,
$V_{\rm stall} = \sqrt{\frac{20713.7}{C_{L_{\rm max}} }} = \sqrt{\frac{20713.7}{1.26} }= 128.2~\mbox{ft/s} = 76.0~\mbox{kts}$
For 15 $^{\circ}$ of flaps, then $C_{L_{\rm max}}\approx 1.45$ . Therefore,
$V_{\rm stall} = \sqrt{\frac{20713.7}{C_{L_{\rm max}} }} = \sqrt{\frac{20713.7}{1.45}} = 119.5~\mbox{ft/s} = 70.8~\mbox{kts}$
For 30 $^{\circ}$ of flaps, then $C_{L_{\rm max}}\approx 1.61$ . Therefore,
$V_{\rm stall} = \sqrt{\frac{20713.7}{C_{L_{\rm max}} } }= \sqrt{\frac{20713.7}{1.61}} = 113.4~\mbox{ft/s} = 67.2~\mbox{kts}$

Stall Control Devices

Because the effects of a stall on a new airplane are not entirely predictable in advance of the first flight, the stall is carefully examined during flight testing. This is done to determine the stall airspeeds and the stall qualities, which is how the aircraft feels or “handles” to the pilot at the point of stall. Unfortunately, not all aircraft are created equal in this regard.

Some aircraft have been found to experience undesirable flight characteristics near stalls, such as uncommanded rolling to the left or the right. What is desired for flight safety is a recognizable and repeatable stall with no adverse characteristics; this outcome would be considered good or acceptable handling qualities at the point of a stall for aircraft certification. In some cases, “stall fixes” are needed to give the airplane predictable and repeatable stall characteristics.

Vortex Generators

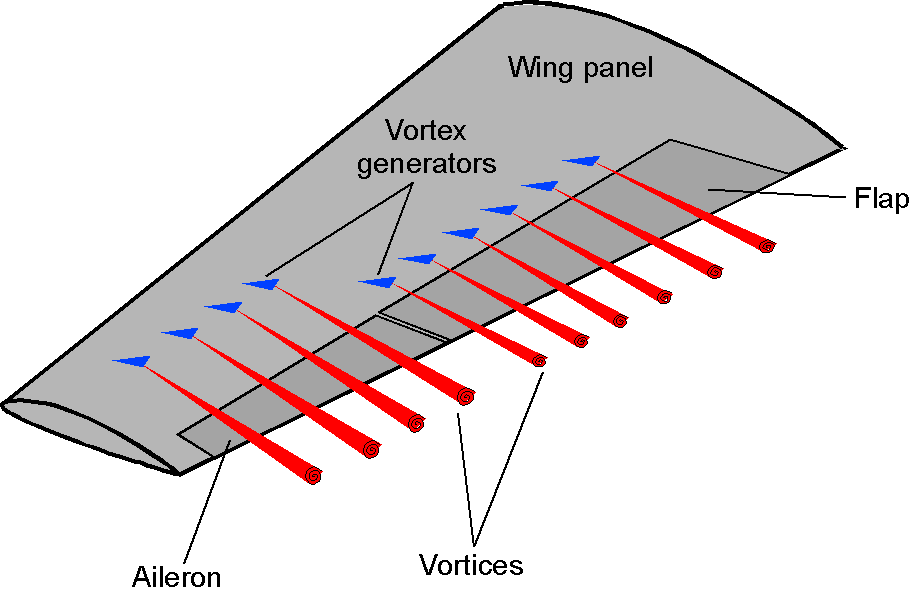
Even a casual observation of the wing on a modern airliner will show numerous regions where little “vanes” are attached to the wing surface, as shown in the photograph below. These devices are called vortex generators or VGs. They are designed to create small vortices to energize the boundary layer flow and keep the flow attached to the wing to higher angles of attack. While the VGs create some drag, the drag is more than offset by the maximum lift benefits.

The VGs are usually just small angled plates set at a steep angle to the flow, often looking like little delta half-wings, which generate flow separation that rolls up into a concentrated vortex, as shown in the schematic below. This vortex is like a tip vortex but is much smaller and mixes with the thickened boundary layer. The consequence is that the boundary layer profile, on average, becomes “energized” and is less susceptible to flow separation. The penalty, however, is a slight increase in drag.

Vortex generators help energize the flow and keep it attached at higher angles of attack, at the expense of some drag at lower angles.

Stall Strips

It may seem odd to force a wing to stall, but that is precisely the purpose of stall strips or airflow disruptors. A photograph of a stall strip is shown below, and they are relatively common on many types of aircraft, from small general aviation airplanes to commercial jets to fighter aircraft. The strips are usually a few inches long and perhaps 1/4 inch (6 mm) in height.

A stall strip mounted on the inboard leading edge of a wing.

Stall strips are used to promote flow separation at specific locations on the wing during high-angle of attack flight to improve the stall qualities of the airplane. They are typically employed in pairs symmetrically distributed on the inboard sections of both the left and right wings, but not always. The usual approach in flight testing is to place the stall strips on the wing’s leading edge, where the desired outcomes are realized, i.e., to force stall to occur at that point on the wing, as suggested in the figure below. On many propeller-driven airplanes, the stall strips are placed at different locations to account for the asymmetric flow produced on the wing by the propeller(s) wake swirl.

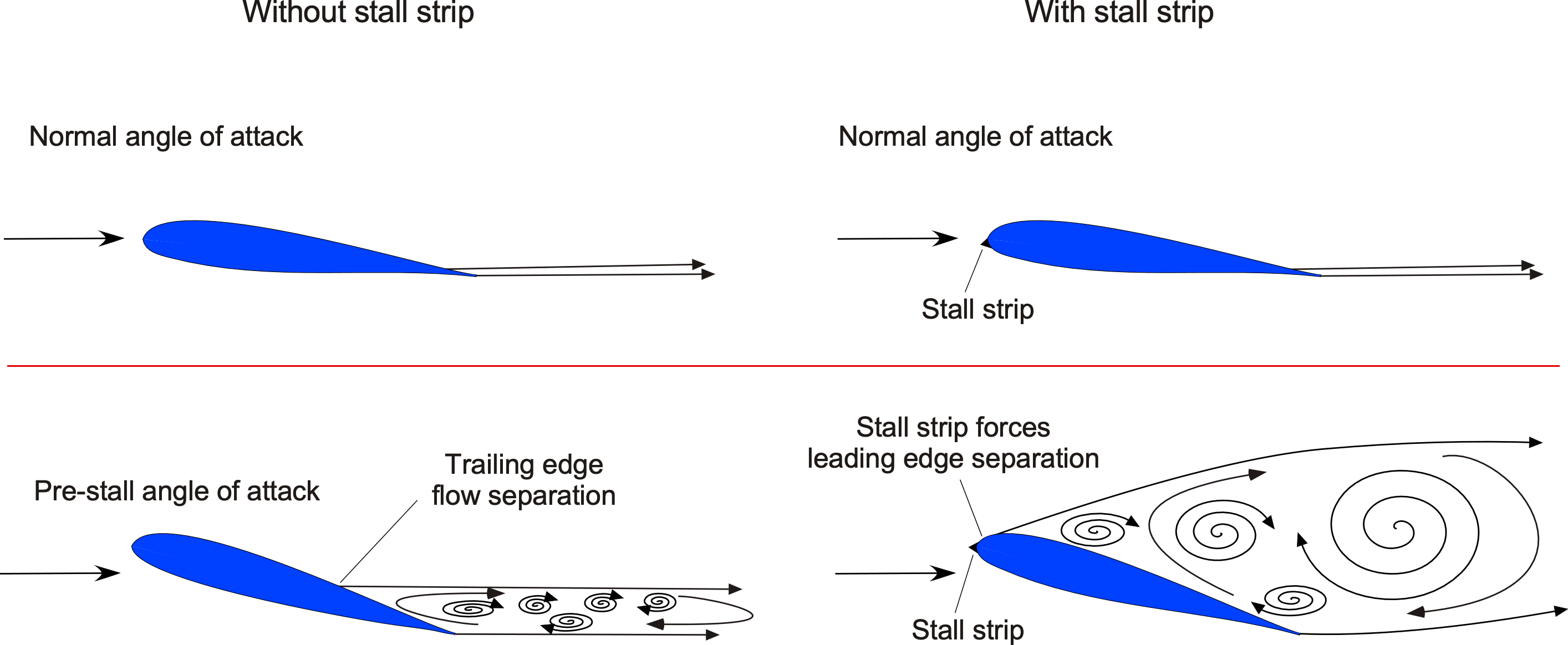
Stall strips can promote flow separation on a wing as the stall is approached, thereby leading to more noticeable and repeatable stall characteristics.

Many aircraft have been built and flown to find that their stall qualities and high angle of attack flight characteristics need to be revised. The solution usually combines stall strips and vortex generators, although more drastic action may sometimes be required. Stall strips are usually employed near the root of the wing to force flow separation to occur there first. Then, with the simultaneous application of vortex generators over the outboard wing panels, the airplane’s stall characteristics are usually improved.

Wing Fences

Wing fences, also known as boundary layer fences or stall fences, are fixed aerodynamic devices that project perpendicular to aircraft wings and wrap around the leading edge, as shown in the schematic below. With their highly swept wings, many early jet aircraft used fences to control wing stalls, often leading to undesirable flight characteristics. Some wings may have several fences, which reflects the difficulties in correcting the stall qualities of some swept wing designs.

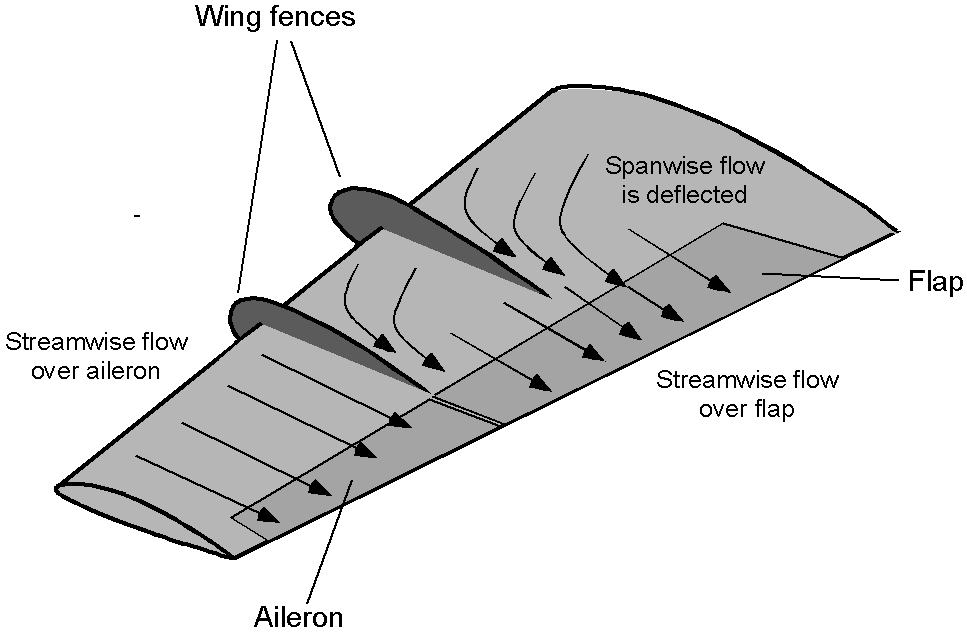
If there is any significant spanwise flow along the wing, the boundary layer thickness can grow toward the wing tips without the fences. The consequence is reduced aileron effectiveness, increased tendency for the wing tips to stall first, and susceptibility to control reversal and spins. The fences limit the spanwise airflow along the wing, directing the flow over the control surfaces and preventing premature boundary layer growth and stall.

Spinning

A spin can develop as a consequence of an asymmetric stall, which causes the airplane to rotate about a vertical axis and create a steep, spiraling, nose-down flight path, as shown in the figure below. While spins can be provoked on airplanes, such for flight demonstrations and pilot training, inadvertent spins are usually dangerous.

A spin can result from an asymmetric stall and cause the airplane to develop into a steep, spiraling downward path in a stalled condition.

In a spin, the wings are stalled and operate at a high angle of attack, even though the airplane’s attitude is distinctly nosed downward. Recovery from a spin requires counterintuitive control inputs from the pilot, which includes pushing forward on the control stick to lower the angle of attack and un-stall the wing, with simultaneous use of the opposite rudder (to the direction of spin) to stop the rotational motion. The rapid rotation about the vertical axis and the nose-down attitude can disorient a pilot, and many “stall/spin” accidents have occurred.

Stall development is a prerequisite to a spin, so stall avoidance will generally prevent an airplane from spinning. Modern commercial airplanes have sophisticated stall warning and stall avoidance systems, so the likelihood of such airplanes inadvertently developing a stall or a spin is exceptionally remote. Nevertheless, their stall characteristics are always carefully explored during flight testing.

Smaller airplanes, however, generally do not have such stall avoidance systems. Therefore, FAA certification standards for smaller civil airplanes with up to a 12,500 lb maximum takeoff weight require that they demonstrate stalls and spins. Such airplanes need to show a full recovery from stalls and a one-turn spin with the regular use of flight controls. If intentional spins are to be allowed by certification, then the airplane must demonstrate a six-turn spin. Many GA airplanes are certified for spins if operated in the utility category, which usually means reduced gross weight and forward center of gravity position. Spin testing for certification is a potentially dangerous activity, so the test airplane will usually be equipped with some secondary spin-recovery device, such as a tail parachute.

Summary & Closure

Determining the stall characteristics of an airplane is critically important because the airplane will be flown near stalled conditions during takeoff and landing. While much can be done at the design stage to estimate stall airspeeds, both in the “clean” condition (with flaps and slats retracted) and in the “dirty” state (with flaps and slats deployed along with the undercarriage), the stall airspeeds must be confirmed.

In addition to knowing the stall airspeed and onset characteristics, it is essential to understand the recovery characteristics of an airplane during a stall. A well-designed airplane should have a straightforward and uncomplicated stall recovery procedure, which a pilot with appropriate training and skill can execute. The recovery characteristics should be consistent and repeatable regardless of the airplane’s altitude, airspeed, and load factor. Flight test data must demonstrate that the stall recovery procedure is effective and reliable and that the airplane has no dangerous stall-related behavior, such as an uncontrollable spin or an uncommanded roll. Overall, an airplane’s stall characteristics and recovery must be carefully studied and evaluated to ensure that the airplane is safe to fly in all conditions.

Vortex generators and/or stall strips can often improve unacceptable stall qualities. While a spin is not a dangerous maneuver in itself, an inherent tendency for an airplane to spin near the point of the stall is an unacceptable flight characteristic that needs to be mitigated before the airplane could be considered safe to fly by an average pilot, i.e., to meet FAA certification requirements.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

According to published sources, the Helio Courier airplane’s stall airspeed is only 23 kts. Do you think this sounds reasonable, and why?
Another device sometimes used to control an airplane’s stall characteristics is a “wing fence.” Research to find out what these devices are and how they work.
A Boeing 767 loses the ability to lower the leading-edge slats for landing. Wing flaps are not affected. If the reduction in the $C_{L_{\rm max}}$ of the wing is 30% without using the slats, estimate the percentage increase in the landing airspeed of the airplane. Make any reasonable assumptions you feel are needed.
Research the internet and analyze a historical aviation incident involving a stall or spin. What were the contributing factors, and what lessons can be learned from the event?
A new airplane is found to have an undesirable stall characteristic that causes it to roll consistently to the left with a tendency to spin as it approaches the stall. Suggest some options as to how this adverse flight characteristic may be mitigated.
How might flight simulators contribute to pilot training in preventing and recovering from stalls and spins?
What regulatory measures are in place to ensure that pilots receive adequate training in stall and spin recovery? How do aviation authorities enforce compliance with these training requirements?
Do some research on the internet to find out if any advanced technologies or systems could help prevent stalls or spins in modern aircraft. How might fly-by-wire systems contribute to the prevention of stalls and spins?

Other Useful Online Resources

To understand more about stalling and spinning, then follow up with some of these online resources:

A NACA film of the airflow about airfoils with flaps and slats operating in stall.
The use of tufts to examine stall and spin patterns on the wing.
A video about what a spin is.
Stall to spin recovery video.
Video showing the anatomy of a Cirrus stall accident.
An explanation of unsteady stall or dynamic stall.
Video of stalling in a Boeing 747.
Video of stalling in an Airbus A310.
Boeing 737-400 test flight with wing stalls.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n41