Introduction

The earliest practical piston engines were developed in the late 19th century. They were based on the Otto cycle, featuring a stationary crankshaft with pistons moving in cylinders arranged in a straight line (inline) or a “V” configuration. Louis Blériot’s Bleriot XI, which famously crossed the English Channel in 1909, used a 25-horsepower Anzani inline engine. More powerful rotary engines emerged later, primarily during the early 20th century, especially for use in aviation. In a rotary engine, the entire engine, including the cylinders, rotates around a fixed crankshaft. This design was popular in early aircraft engines because of its high power-to-weight ratio and compactness, making it suitable for the lightweight requirements of early aircraft.

The rotary and radial types, once the workhorses of aviation, have given way to the “flat,” horizontally opposed “boxer” engines. These reciprocating piston internal combustion engines, which drive a propeller, continue to be the powerhouses of modern general aviation. Their use in relatively low to moderate-performance airplane types is a testament to their relatively low cost, decent performance, and reliability. An example of a Piper Cherokee airplane is shown in the photograph below, which has a Lycoming 4-cylinder O-320, 160 hp (119.3 kW), horizontally opposed “boxer” piston engine driving a Sensenich fixed-pitch propeller. The advantages of this propulsion system are that it is reliable, affordable, and provides reasonable propulsive efficiency. However, the system is not readily scalable because the power-to-weight ratio of a piston engine decreases rapidly with increased power output, making it unattractive for larger and heavier aircraft; a turboprop engine will be preferred if a propeller is used in such cases.

Piston engines, including the higher efficiency afforded by types of diesel, may also be suitable for certain classes of drones and UAVs where the required flight range and/or endurance cannot be achieved using batteries alone, e.g., by using hybrid propulsion systems. One of the most common systems combines a gasoline (petrol) engine or a diesel engine with electric motors, which can be operated purely on diesel or electrical power but using both when needed. To this end, engineers must understand the basic principles of aircraft piston engine operation, including the effects of density altitude on their power output and specific fuel consumption, as well as the associated propeller performance under the conditions of flight.

Piston Engine Types

The first common type of piston engine used for aircraft was a rotary engine, which saw extensive use up through the 1920s. In this type of arrangement, the cylinders are arranged in a radial configuration that “radiate” outward from a central crankshaft like the spokes of a wheel, as shown in the figure below. It also resembles a star when viewed from the front, so the type is sometimes called a star engine. In a rotary engine, the entire crankcase and its attached cylinders rotate around it as a unit along with the propeller. The pistons are connected to the crankshaft using a primary rod assembly, and the remaining pistons and their connecting rods are attached to rings around the primary rod. The air/fuel inlets are connected to a carburation system, and the exhaust outlets are connected to a radial manifold. The inlet and outlet valves are opened and closed using a cam. In some versions, a carburetor delivers the fuel/air mix into the crankcase, reaching the cylinders through transfer ports, so only exhaust valves are needed.

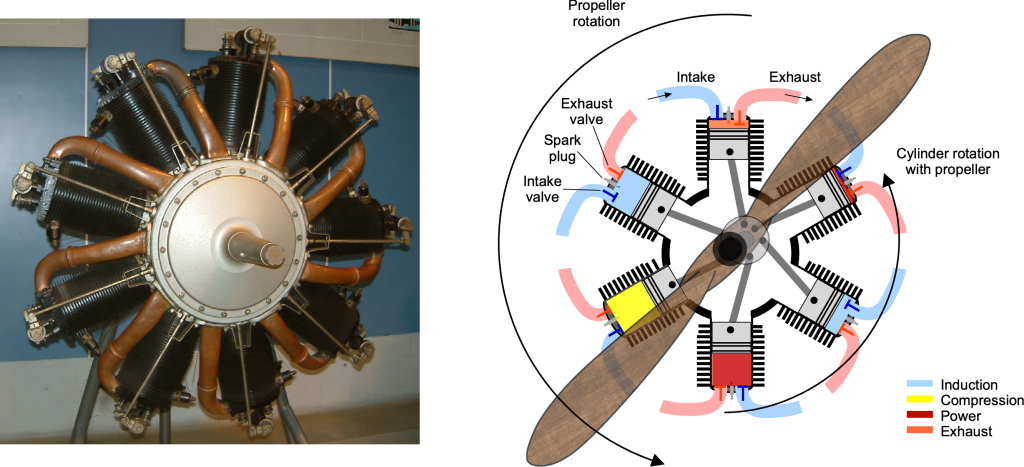
One advantage of the rotary engine design is good cooling because the cylinders rotate. However, a significant disadvantage is the large gyroscopic moments caused by the rotating engine mass. This characteristic led to several serious issues with the flight-handling qualities of early aircraft, namely, the ability to turn only in one direction.

The radial engine is another early reciprocating piston engine used to power many pre-1950 airplanes, as shown in the photograph below. The radial engine has fixed (non-rotating) cylinders, and the propeller is connected to the crankshaft. The inlets are connected to a carburation system, and the exhaust outlets are connected to a system of pipes. In the radial engine, the gyroscopic effects on the airplane are much lower than for the rotary style of the engine, in which the cylinders rotate with the propeller. Consequently, radial engines were much preferred over the rotary type, which became obsolete for aircraft use after WWI.

Powerful radial engines with 12 or more cylinders have been built for aviation use, mainly for airplanes constructed through the 1950s, raising power output levels from about 2,000 hp (1,491 kW) to about 4,000 hp (2,983 kW). In addition, extra rows of radial cylinders can be added to increase the engine’s power. However, this approach rapidly drives up the engine’s weight and also results in cooling challenges for the downstream rows of cylinders. The most powerful piston aircraft engine ever built was the Lycoming XR-7755, which had 36 cylinders and a shaft power output of 5,000 hp (3,700 kW). However, with the advent of jet engines, which offered better performance and efficiency, the XR-7755 project was eventually discontinued, and no aircraft were ever powered by this engine in operational service.

Modern piston aero-engines for aircraft are usually flat and horizontally opposed, as shown in the figure below. The horizontally opposed engine configuration is also known as a “boxer” or “flat” engine. In this design, the cylinders are arranged in two banks on opposite sides of the crankshaft, forming a flat and wide configuration, which allows for a more streamlined and aerodynamic profile. This is important for minimizing drag and also allows for efficient air cooling. Several manufacturers, including Lycoming, Teledyne Continental, and Rotax, produce piston engines suitable for aircraft use. They are manufactured with 4, 6, or 8 cylinders with power ratings from about 125 hp (147 kW) to 600 hp (441 kW). They also come in normally aspirated and supercharged (i.e., forced induction) forms and carbureted or fuel-injected variants; fuel injection is used for higher-performance engines.

Superchargers and turbochargers are forced induction systems used in aircraft engines to increase the intake air pressure, allowing for better combustion and improved engine performance. Supercharging or turbocharging (or both) may be used to increase the power of a piston engine and maintain its power output to higher flight altitudes; this is a good solution for higher-performance aircraft despite the penalty of some extra engine weight and maintenance costs.

While modern piston aero-engines are mechanically reliable and robust, one concern is that they are relatively heavy compared to their power output. Their power-to-weight ratios are relatively low, only about 0.2 hp/lb (0.33 kW/kg) to 0.4 hp/lb (0.66 kW/kg). Therefore, when such engines are required to produce higher power levels, they can become prohibitively heavy for use on an aircraft. This reason is why a turboshaft engine is usually necessary to drive a propeller (i.e., a turboprop) after a specific power requirement for flight is reached. A turboprop has a much better power-to-weight ratio of about 0.8 hp/lb (1.32 kW/kg) to 1.2 hp/lb (1.97 kW/kg). While turboshaft engines have a higher capital and maintenance cost per power unit, their better specific fuel consumption and reliability make them very attractive for larger propeller-driven aircraft.

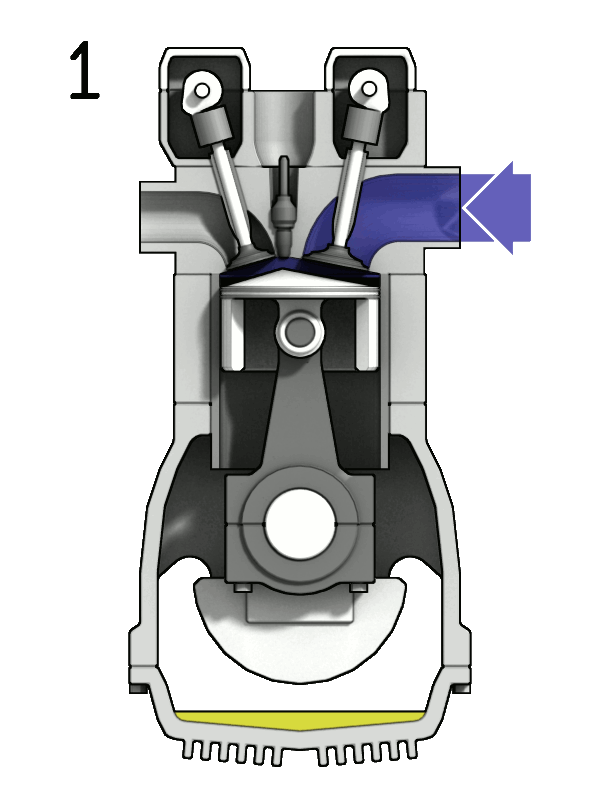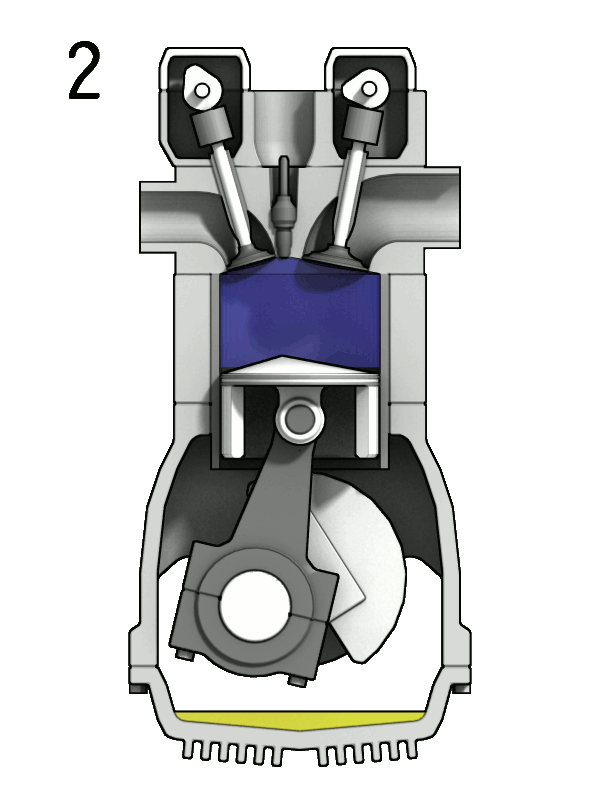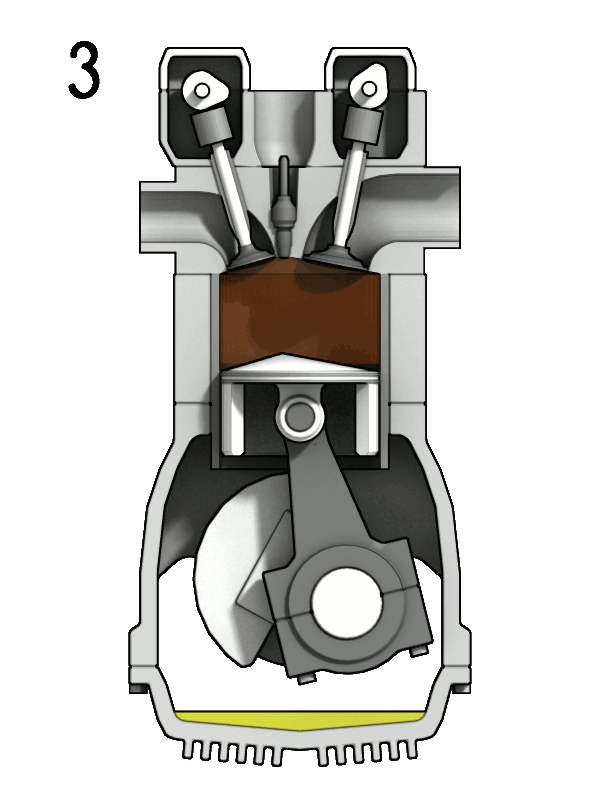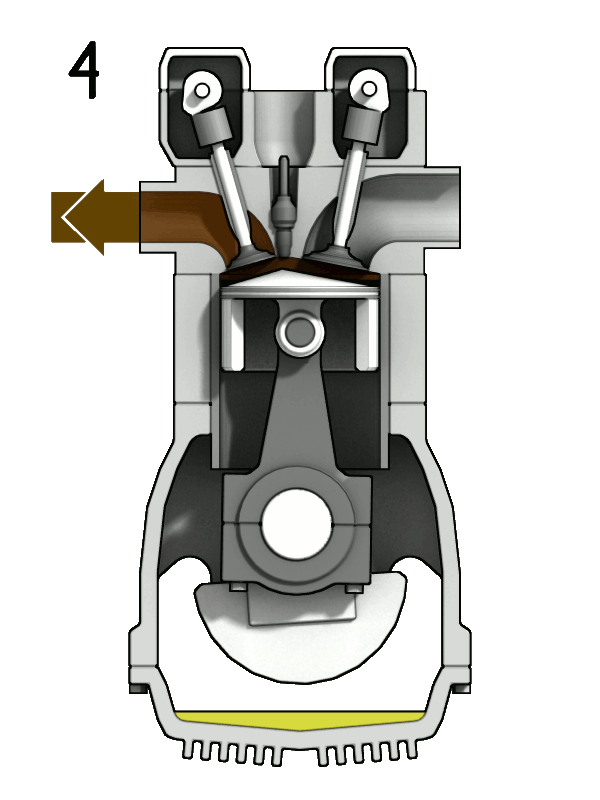
The principle of operation of a reciprocating piston internal combustion engine is based on the Otto cycle, as shown in the figure below. A cam synchronizes the piston’s up-and-down movement with the opening and closing of the two valves (intake and exhaust), allowing the sequential entry of the fuel/air mixture, followed by the compression and combustion process, and then the exit of the exhaust gases.

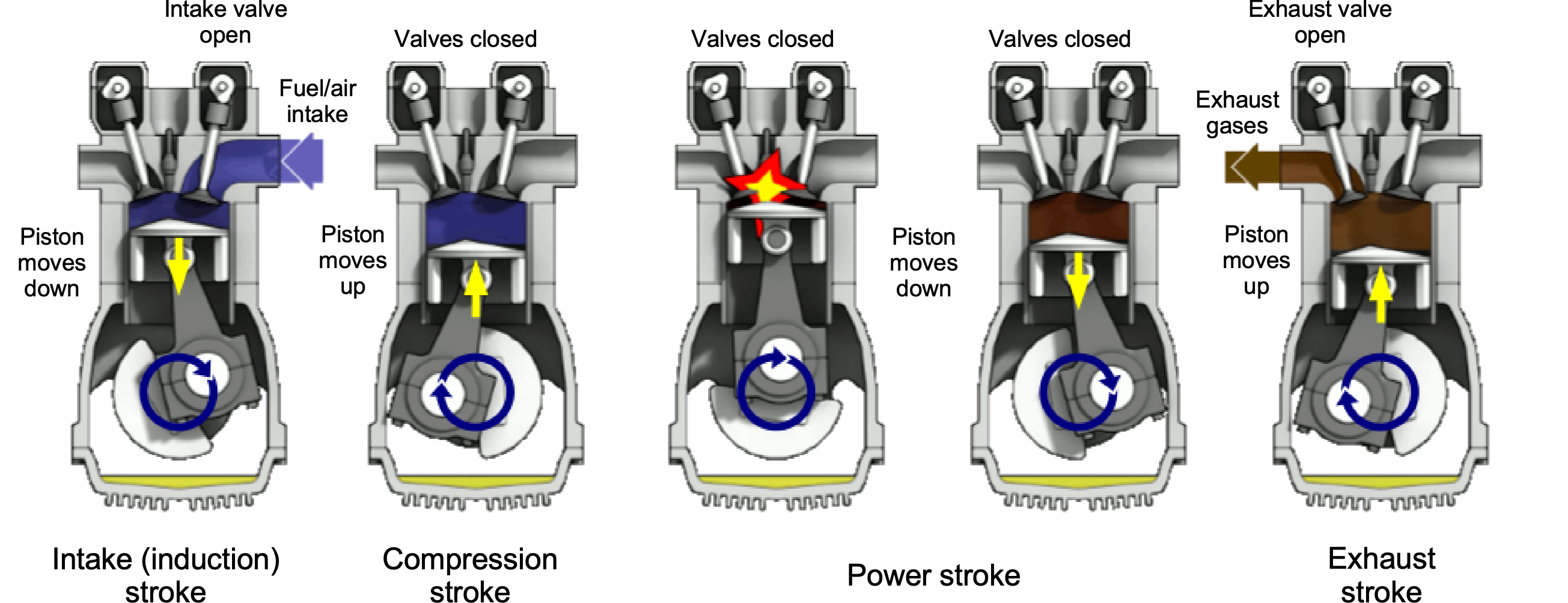
In summary, the operation of the engine consists of four cycles (or strokes), as shown in the animation below, namely:

1. In the intake stroke, the piston moves down the cylinder, and the cam opens the intake valve. A carburetor or fuel injection system draws the air and fuel mixture into the cylinder.
2. The compression stroke is where the intake and exhaust valves are shut. The upward-moving piston then compresses the fuel/air mixture to the point that it will support combustion.
3. The power stroke is where a spark plug ignites the compressed mixture. The resulting flame front and expanding gases (called deflagration) progressively force the piston downward in the cylinder to drive the crankshaft.
4. The exhaust stroke is where the exhaust valve opens, and the upward-moving piston forces the combustion products out from the cylinder before the entire four-stroke process starts again.

A piston engine may also work on the principle of the Diesel cycle, where the much higher compression in the cylinder raises the temperatures sufficiently to cause the fuel to burn without using a spark plug. Another advantage of a diesel engine is its better thermal efficiency and lower specific fuel consumption. In many countries, diesel fuel is also less expensive than gasoline.

Effects on Power

For a piston engine, the power from the engine to the crankshaft (the so-called shaft brake power) is given by

(1)  

where is the total displacement or swept volume, is the mean effective pressure (pressure in the cylinders), and rpm is the crankshaft revolutions per minute. The swept volume by the piston as it moves up and down inside the cylinder equals the displacement of one cylinder, so the total engine displacement is that value times the number of cylinders, e.g., 5.9 liters (5,900 cc) or 360 cubic inches.

Detailed dynamometer testing is typically conducted to assess an engine’s performance accurately, considering various parameters and conditions. Also, the specific configuration and characteristics of the engine, as well as any forced induction systems (like superchargers or turbochargers), can influence the overall power output. The name “brake” power comes from the fact that the power is measured using a brake-type dynamometer, which provides a resistance or braking torque at the engine shaft. Remember that a torque, , is the product of a force times a distance, so it has units of work. Power is the rate of doing work, so the power, , at the shaft is the product of the torque and angular velocity of the shaft, i.e., .

Power Limitations

It will be apparent from Eq. 1 that the power out from the engine can be increased by:

1. Increasing the swept volume, i.e., by increasing the cylinder bore, stroke, number of cylinders, or all of these things.
2. Increasing the pressure in the cylinder by the appropriate design of the combustion chamber and/or the piston shape, or by turbocharging the air entering the cylinders.
3. Running the engine at a higher rpm. However, in part, rpm will be limited by keeping the propeller’s tip Mach number below the speed of sound.

There is a practical limit to all of these things, partly by the allowable mechanical stresses and temperatures in the engine to prevent failure. To a large extent, the design of a piston engine comes down to the selection of high-strength and/or high-temperature metals and appropriate metallurgy to give the engine good operational reliability and durability, especially for the exhaust valves. On aviation engines, which run at high power settings and high average temperatures, the exhaust valves are often sodium-filled, which improves thermal conduction away from the valve stems and seats and keeps the engine cooler. The maximum attainable rpm of the engine will also be limited by the propeller tip speed, which should be kept below the speed of sound (Mach 1) to maintain its propulsive efficiency and keep noise levels down. Propellers with high tip speeds that approach the speed of sound are also always very noisy.

Altitude Effects

As the flight altitude of the airplane changes, so does the engine power available, as shown in the figure below.  Lower air density affects the amount of oxygen available for combustion in the engine cylinders. Because the power output of an engine is directly related to the amount of oxygen available for combustion, a decrease in air density leads to reduced engine performance. Engines also rely on the pressure difference between the outside air and the combustion chamber to facilitate the intake of air and the expulsion of exhaust gases. Reduced atmospheric pressure at higher altitudes can impact the efficiency of these processes, affecting engine performance. While lower temperatures can be beneficial for engine cooling, they also influence combustion efficiency. Cooler air can result in better air-fuel mixture density, but it may also affect fuel vaporization, potentially impacting combustion efficiency. So, the power output decreases or lapses with increasing density altitude.

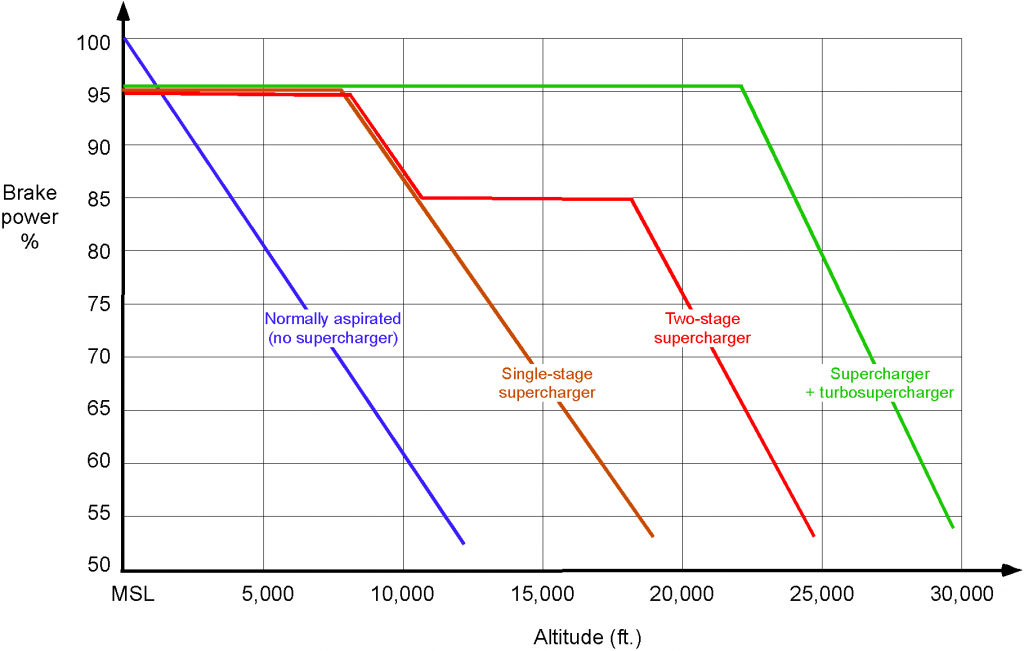
An approximation for the effects of density altitude on the power output of a normally aspirated (non-supercharged) piston engine is to assume that

(2)  

where is the power available at altitude and is the power available at mean sea level conditions. Remember that the density ratio, , of the air, which is a surrogate measure of the oxygen content, can be calculated using the ISA model from measurements of pressure altitude and outside air temperature at that altitude. An empirical correction for a normally aspirated engine that is often used in practice is

(3)  

Supercharging

It can also be seen that supercharging can maintain the rated power of a piston engine at much higher altitudes. This outcome is obtained because a supercharger increases the pressure and density of the air supplied to the engine intake, i.e., boosting the manifold pressure and the oxygen content of the inducted air. The consequence is that more fuel can be burned, thereby increasing the power available from the engine at lower altitudes as well as maintaining that power at higher altitudes.

Superchargers and turbochargers have been used extensively to maintain the power output from aero-engines. Some of the earlier high-powered radial engines employed a combined system known as a “turbo-supercharger,” where both a supercharger and a turbocharger were incorporated to maximize performance over a broad range of altitudes. As shown in the figure below, the engine mechanically drives superchargers, typically through a belt connected to an accessory drive from the crankshaft. The engine’s exhaust gases drive turbochargers, consisting of a turbine and a compressor connected by a shaft. The exhaust gas spins the turbine, which, in turn, rotates the compressor and forces more air into the engine and, hence, into the fuel management system. Turbochargers are generally more efficient than superchargers because they harness waste energy from the exhaust gases, rather than drawing mechanical power directly from the engine.

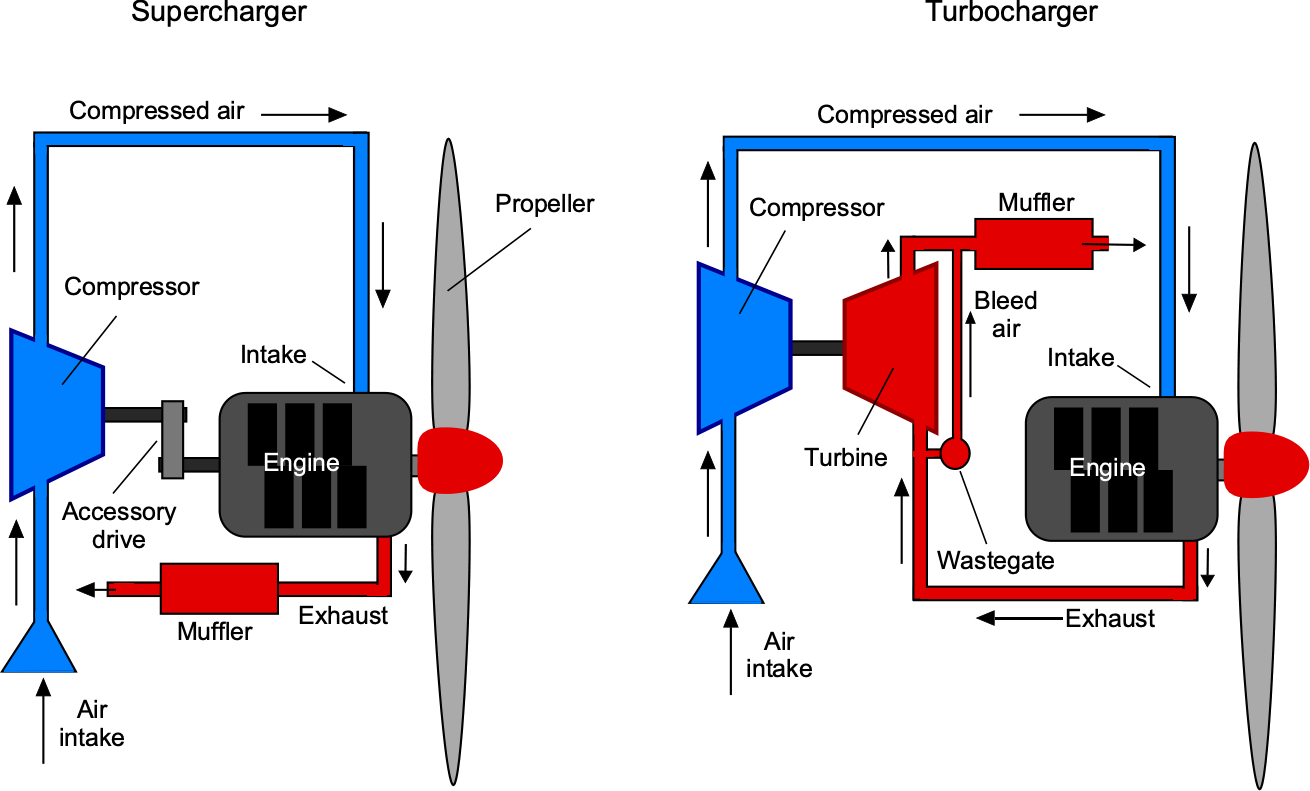
The mass flow rate of air into the engine is proportional to the air density and the engine displacement volume, so increasing intake density increases the available mass flow rate, i.e.,

(4)  

where is the mass flow rate of air into the cylinders, is the ambient intake air density, and is the engine displacement volume per cycle.

Assuming a roughly constant air-fuel ratio (AFR), increasing permits a proportional increase in the fuel flow rate , and hence, a proportional increase in power output. The ideal power increase from boosting can be estimated as

(5)  

where is the new power output, is the rated power at sea level ambient conditions, is the boosted intake manifold pressure above the ambient atmospheric pressure, .

The efficiency of a turbocharger compared to a mechanically driven supercharger can be illustrated by considering that the mechanical load imposed by a supercharger reduces the net power output, i.e.,

(6)  

whereas a turbocharger does not directly extract power from the crankshaft, relying instead on exhaust energy that would otherwise be wasted.

Compressing the intake air through supercharging or turbocharging not only increases its pressure but also raises its temperature. According to the ideal gas law, an increase in temperature at constant pressure reduces air density, which can partially offset the benefits of compression. The temperature rise through an ideal isentropic compression process is given by

(7)  

where and are the inlet and outlet temperatures across the intercooler, and are the inlet and outlet pressures, and is the ratio of specific heats = 1.4 for air.

Intercoolers are employed to mitigate the temperature rise and maximize the density of the intake air. An intercooler is a heat exchanger placed between stages of compression (in multi-stage supercharging) or between the compressor and the engine intake (in turbocharged systems). The function of the intercooler is to cool the compressed air before it enters the engine cylinders, thereby increasing the air’s density and improving the mass flow rate into the engine.

The benefit of intercooling can be quantified by considering the reduction in intake temperature, which leads to a denser charge and greater available oxygen mass per cycle. The net effect is an improvement in engine power output, better fuel efficiency, and reduced tendency for detonation (engine knock) at high manifold pressures. Aircraft engines that employed two-stage supercharging often incorporated intercoolers or aftercoolers between stages. In turbocharged systems, such as those used on high-altitude bombers during WW2, intercoolers were critical for maintaining engine performance and reliability at altitudes above 25,000 feet.

There may be a further boost in engine power as the flight speed increases. The pressure of the air entering the engine will generally increase by an amount proportional to the dynamic pressure, i.e., . Therefore, the power from the engine increases somewhat from a ram air effect. Ram air can be significant for some aircraft, especially those flying at airspeeds above 250 kts. However, pressure losses in the ducting between the air intake and the engine tend to reduce the significance of this potentially beneficial effect. Nowadays, reciprocating engines are used for lower-speed general aviation aircraft, so the ram air effect can usually be ignored as far as it might affect the engine performance. From a design perspective, relying on ram air effects at any airspeed would be inadvisable when sizing an engine to an airframe.

Engine Performance Charts

The engine manufacturers provide detailed charts to allow engineers to calculate shaft power available at any combination of altitude and temperature, an example being shown in the figure below. Notice that there are two sides to this chart, the left side being the mean sea-level (MSL) power output performance and the right being the performance at altitude.

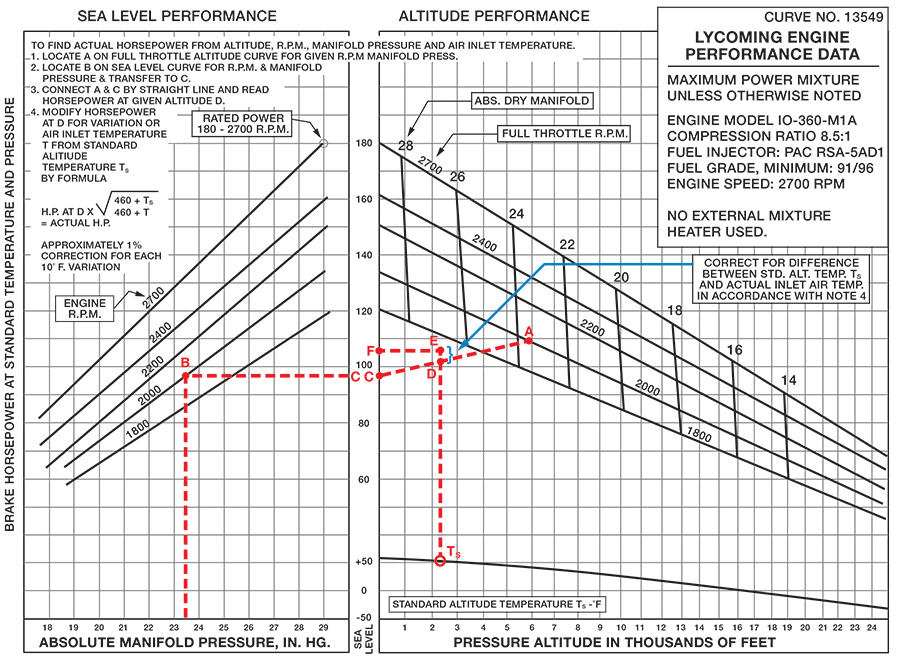
The instructions on the chart explain how it is used to determine the engine’s brake power. This chart differs from what pilots would use in flight, but engineers use it to estimate the available engine power under different flight conditions. The chart can be used to make all of the needed measurements to determine power output. Standard cockpit instruments can be used to measure the pressure altitude, engine rpm, manifold pressure, and outside air temperature, which is very useful from a flight test perspective.

The power available at the engine shaft (the brake horsepower or bhp) can be determined given measurements of the following:

1. Pressure altitude can be measured directly on the altimeter by setting the reference pressure in the Kollsman window to the MSL standard conditions of 29.92 inches of Hg.
2. Air temperature would be measured in flight using an appropriately calibrated outside air temperature (OAT) gauge.
3. Engine rpm, which would be measured using a tachometer. While a tachometer is part of the standard cockpit instruments, an optical tachometer that counts the passage of the propeller blades is more accurate.
4. Manifold pressure can be measured on the manifold pressure gauge, which is also part of the standard cockpit instruments.

The process starts by entering the left chart (MSL performance) at the bottom using the manifold pressure measurement, then reading up to point B on the lines of constant engine rpm. Notice that interpolation will generally be required. Reading across to the right to the axis and to point C gives the engine brake power at MSL standard conditions.

The next part of the process is establishing the engine performance at altitude, which is done using the right-side chart. After carrying point C onto the left chart, a straight line is connected between points C and A, point A being at the appropriate point on the rpm and manifold pressure map. To find the power available for a given pressure altitude, it is necessary to move along the line AC. Reading to the left axis will give the brake power output at altitude under standard temperature conditions. Finally, there is a minor correction for non-standard temperatures (the formula is shown on the chart) to give the final brake power output at point F. Notice again that interpolation will be required throughout this process.

Brake Specific Fuel Consumption (BSFC)

The efficiency of a piston engine is measured in terms of its power-specific or brake-specific fuel consumption (BSFC), which is often given the symbol . The BSFC measures the fuel used (in units of mass or weight) per unit of power supplied (in hp or kW) per unit time of engine operation (usually one hour). BSFC is used as a measure of the fuel efficiency of any engine that burns fuel and produces rotational or shaft power.

The BSFC is defined as

(8)  

The units of BSFC are typically in lb hp hr in the U.S. customary system, or kg kW hr or grams per kilowatt-hour (g/kWh) in the SI system. Notice that the unit of mass (kilogram or grams) is used in the SI units of BSFC, an anomaly of the SI system. However, the time unit is hours in both cases.

For a piston engine used on an aircraft, the values of BSFC are typically in the range of 0.4 to 0.6 lb hp hr (0.24 to 0.37 kg/kWh), as shown in the figure below. These values are approximate and can vary based on factors such as engine design, operating conditions (e.g., cruising, takeoff, climb), and the specific model of the engine. Additionally, advancements in engine technology may lead to improved fuel efficiency compared to older engines.

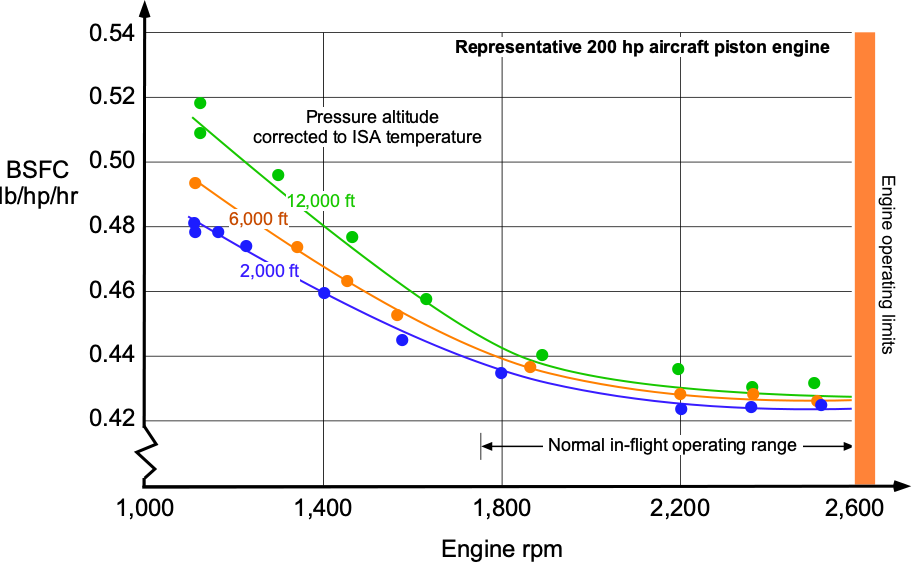
There is usually some dependence of BSFC on flight altitude, with the values increasing somewhat. Notice that the best (lowest) BSFC is obtained when the engine operates at or near its rated rpm and power output. Today, the best-performing and most efficient piston engines are supercharged types of diesel, which have better thermal efficiencies and BSFC values in the 0.45 to 0.7 lb hp hr range (0.27 to 0.43 kg/kWh).

Turbocharging generally improves brake-specific fuel consumption (BSFC) compared to a naturally aspirated engine, particularly at higher altitudes. Turbocharging increases the intake air pressure and density, allowing more complete combustion and improving the engine’s volumetric efficiency. Because turbochargers harness waste energy from the exhaust gases rather than imposing a mechanical load on the crankshaft, they boost engine power output without significantly increasing fuel consumption. As a result, the BSFC tends to decrease, meaning that less fuel is needed per unit of useful power output.

For example, consider a naturally aspirated piston engine producing 200 hp with a fuel mass flow rate of 60 lb/h. Its BSFC is

(9)  

Now, assume the same engine is equipped with a turbocharger, producing 270 hp at a slightly increased fuel mass flow rate of 75 lb/h. The turbocharged BSFC is

(10)  

Therefore, while the fuel consumption increased, the power output increased proportionally more, resulting in a lower BSFC. The engine becomes more fuel-efficient on a per-horsepower basis after turbocharging.

While turbocharging improves BSFC and altitude performance, several tradeoffs must be considered. At very high boost pressures, the intake air temperature increases significantly, potentially requiring enrichment of the fuel-air mixture to prevent engine knock, which can partially degrade the BSFC benefits. Additionally, turbochargers introduce thermal management challenges due to the high temperatures encountered in the exhaust turbine and the compressed intake air. Proper intercooling is necessary to maintain high efficiency and reliability. Finally, turbochargers may exhibit a phenomenon known as turbo lag, where a delay occurs between throttle application and boost generation, although this is generally less critical in aircraft applications than in automotive use.

Fuel Types for Piston Aeroengines

Piston aeroengines rely on specialized fuels to ensure reliable combustion, efficient power output, and safe operation across various altitudes and atmospheric conditions. The most widely used fuel for aviation piston engines is aviation gasoline, or AVGAS, which is specifically formulated to meet the demanding requirements of flight. Aviation gasoline is characterized by high chemical stability, a high energy content, and a controlled vapor pressure to prevent vapor lock during altitude changes. Today’s most common grade is AVGAS 100LL, where “100” denotes the fuel’s octane rating under aviation testing conditions and “LL” indicates low lead content. Despite the “low lead” designation, AVGAS 100LL contains tetraethyl lead (TEL), a chemical additive that significantly improves knock resistance by inhibiting premature combustion, or detonation, inside the engine cylinders. AVGAS 100LL is dyed blue for easy identification. Historically, grades such as AVGAS 100/130 and 80/87 were also used, but these have largely been phased out.

The octane rating is a measure of a fuel’s resistance to detonation. Aircraft engines, particularly those operating at high compression ratios or under high manifold pressures, require fuels with high knock resistance to avoid engine damage. In aviation fuels, two octane ratings are often given, such as 100/130, where the first number represents the octane rating under lean mixture conditions and the second number under rich mixture conditions. Detonation is particularly dangerous in aircraft engines because it can cause rapid mechanical failure, so properly formulated and rated fuel is essential.

The industry continues to rely heavily on leaded fuels, but environmental and health concerns have accelerated the development of unleaded alternatives, such as G100UL, a 100-octane unleaded aviation fuel. Although G100UL has completed certification testing for some engine types, AVGAS 100LL remains the dominant fuel in current use. In some cases, aircraft engines are certified to use automotive gasoline, or mogas. While mogas is widely available and often less expensive, it is not a direct substitute for aviation gasoline. Its higher vapor pressure can cause vapor lock at altitude, and the absence of lead additives reduces its knock resistance, making it unsuitable for high-performance aviation engines unless properly certified. Additionally, mogas formulations can include ethanol blends, which present risks of water absorption and corrosion within the aircraft’s fuel system.

The energy content of aviation gasoline is approximately 43 MJ/kg, and its density at standard conditions ranges from about 0.68 to 0.74 kg/L. For proper combustion, piston aeroengines typically operate near a stoichiometric air–fuel ratio of about 14.7:1 by mass, corresponding to a fuel–air ratio of approximately 0.067. Deviations from this ratio are often used to control engine temperature and performance: rich mixtures provide additional cooling by increasing the latent heat absorption of the fuel vaporization process, while lean mixtures improve fuel economy but carry an increased risk of detonation if not carefully managed.

Summary & Closure

The reciprocating piston engine remains a cornerstone for propelling low to moderate-performance aircraft. Its robustness and affordability ensure that it remains accessible and reliable, particularly for general aviation and certain classes of UAVs. The engine’s good propulsive efficiency, relatively low fuel consumption, and overall mechanical reliability contribute to its continued use in various applications, providing an economical and effective solution for many aviation needs. However, as aircraft size and performance demands increase, the limitations of the reciprocating piston engine become more apparent. Its lower power-to-weight ratio constrains its applicability in larger, more demanding aircraft operations.

This limitation has driven the adoption of turboprop engines, which offer a higher power output and better scalability for larger airplanes. Turboprops also bridge the gap between piston and jet engines, providing an optimal balance of power, efficiency, and operational flexibility for larger airplanes. While reciprocating piston engines will continue to play a vital role in aviation, particularly in general aviation and specialized applications, the progression to more advanced propulsion systems like turboprops ensures that the aviation industry can meet the growing demands for higher performance and greater efficiency in larger airplanes. The correct selection and handling of fuel are critical aspects of piston aeroengine operation, directly affecting performance, efficiency, and safety. Knowledge of the properties of different aviation fuels, as well as the operational consequences of fuel mixture control, is an essential part of basic aerospace engineering practice.