45 Flight Range & Endurance

Introduction

There are flight profiles and missions where there is a requirement for an aircraft to fly as far as possible (i.e., for the maximum flight range) or to stay in the air for as long as possible (i.e., for maximum flight endurance). The critical issue in both cases is the amount of fuel (i.e., allowable tankage volume or allowable weight) that can be carried on board the aircraft relative to how quickly the fuel is consumed, i.e., the fuel being burned per unit of time. For example, transporting passengers and cargo across the Atlantic Ocean requires an airliner to have sufficient non-stop range (over 3,000 nautical miles); in this case, flight range is more important than endurance. Good flight range at a high airspeed (to minimize total transportation time) is also essential.

However, other types of missions, especially those that the military might use, may require that the aircraft be flown in such a way as to maximize its total time in the air, i.e., its endurance. An example could be a surveillance mission that requires a significant loiter time at a given geographic location. There are also possible missions where a military aircraft needs to be flown in such a way as to maximize both its range and endurance during different phases of the same flight, a maritime search and rescue mission being just one. The P3-K2 Orion, for example, has an endurance of more than 15 hours, with two of its engines shut down to conserve fuel.

Learning Objectives

  • Appreciate the importance of specific fuel consumption in determining fuel burn, flight endurance, and flight range.
  • Understand the flight conditions an airplane needs for its best range or endurance.
  • Use the appropriate versions of the Breguet equations to estimate flight endurance and range for propeller and jet aircraft.
  • Know how to estimate total fuel burn and the significance of payload-range diagrams.

Fuel Flow & Specific Fuel Consumption

Flight range and endurance depend on the amount of fuel that can be carried and the fuel flow rate, which depends on the thrust or power produced by the engine(s) and its other characteristics (e.g., thermodynamic and mechanical). The fuel flow or fuel burn rate is the volume (or, more typically, the mass or weight) of fuel burned by the engine(s) per unit of time. Remember that one quantity used to measure an engine’s efficiency is its specific fuel consumption.

For engines that deliver power to drive a propeller, power-specific fuel consumption or the “brake” power-specific fuel consumption (BSFC) is defined as the weight of fuel burned per unit power produced per unit time of operation, i.e.,

(1)   \begin{equation*} \mbox{BSFC} = \frac{\text{Weight~of~fuel~burned}}{ (\text{Unit power})\text{(Unit time~=~hour)}} = c_b \end{equation*}

When delivering a certain amount of power, an engine with a lower value of BSFC will be more efficient because it will burn less fuel per unit time.

In USC, then c_b has units of lb bhp^{-1} hr^{-1}, where “bhp” means “brake horsepower,” so this is the power in hp that can be delivered at the engine’s shaft. In SI units, BSFC is often measured in kg kW^{-1} hr^{-1}; remember that in aviation, weight is usually calculated in units of kg although it is strictly a unit of mass – be sure to convert to Newtons (if needed) by multiplying by acceleration under gravity, g, where g = 9.81 m/s2 = 32.17 ft/s2.

When dealing with jet thrust-producing engines, the specific fuel consumption is defined in terms of the engine’s thrust or the thrust-specific fuel consumption (TSFC). The TSFC is

(2)   \begin{equation*} \mbox{TSFC} = \frac{\text{Weight of fuel burned}}{ \text{(Unit thrust)(Unit time~=~hour)}} = c_t \end{equation*}

Notice that TSFC is also a measure of engine efficiency in converting the energy in the fuel, in this case, into useful thrust; the lower the value of TSFC, the more efficient the engine. For example, in USC units, then the TSFC has units of lb lb^{-1} hr^{-1}; in SI units, then TSFC would be measured in units of kg kg^{-1} hr^{-1} or just hr^{-1}.

Although TSFC can be interpreted to have units of “per hour” (hr^{-1}) or “per second” (s^{-1}), it is generally always quoted in units of lb lb^{-1} hr^{-1} or kg kg^{-1} hr^{-1}. Using the kg as a unit of weight is an anomaly in the SI system.

A complication when dealing with engines (reciprocating or jet engines) is that the value of BSFC or TSFC is generally not constant, and it depends on the throttle setting for the engine. In the case of jet engines, the TSFC also depends on the flight Mach number it operates at. Piston engine performance (at least for normally aspirated engines) does not depend substantially on airspeed. All engines are typically designed to have their best (lowest) BSFC or TSFC when operating at wide-open throttle and at or close to their rated power or thrust appropriate to the airplane they are selected to power. For lower throttle settings, the BSFC or TSFC tends to increase somewhat, i.e., the engine becomes less efficient because it burns more fuel per unit or power or thrust produced; this latter behavior is an artifact of their design.

The BSFC or TSFC curves for aircraft engines are often relatively flat over the range of almost wide-open throttle settings used in flight. Therefore, it is a reasonable assumption for an aircraft engine to assume that the BSFC or TSFC is constant. This latter assumption helps estimate net fuel burn during flight at different airspeeds, weights, and operating altitudes, at least in the first iteration, where detailed engine performance characteristics may not be available. However, the BSFC or TSFC characteristics must be known (or estimated) to determine actual fuel burn properly. More detailed performance calculations always require that the specific engine performance characteristics are carefully modeled, which will require engine charts or engine decks; such detailed information about engine performance is usually only made available to aircraft manufacturers who plan to use the engine on their aircraft.

Therefore, if the BSFC or the TSFC is known, then the corresponding fuel flow rate curves can be determined (estimated) because they are proportional to the power required for a propeller-driven airplane and the thrust for a jet-driven airplane. A generic fuel flow example is shown in the figure below. Notice that there is an airspeed on the fuel flow curve at which the minimum fuel flow is required for flight (point A) and also an airspeed where the ratio of the airspeed/fuel flow is a maximum (point B), both operating points being significant in terms of flight operations.

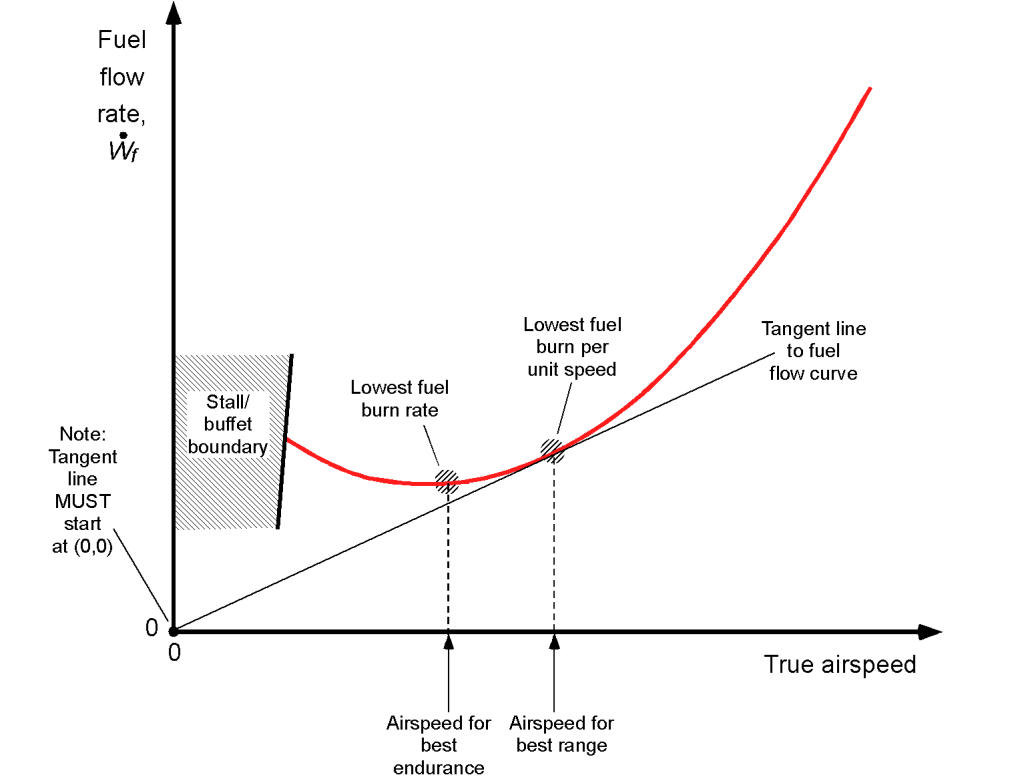
An airplane’s generic fuel flow curve will mimic the shape of a jet aircraft’s thrust and propeller aircraft’s power-required curves.

For a given quantity of fuel carried on the airplane, the airspeed to fly for minimum fuel flow (point A) will correspond to the flight conditions to achieve the longest flight time, i.e., the maximum flight endurance. The tangent of the straight line from (0,0) to the fuel flow curve (point B) corresponds to the condition that the airspeed ratio to fuel flow is at a maximum. Because distance (in still air or zero winds) is the product of airspeed and a given flight time, point A corresponds to the furthest still air distance covered for a given quantity of fuel, i.e., this will be the airspeed to fly to achieve the best range.

Fuel Flow Curves – Propeller Airplanes

The power required, P_{\rm req}, for a propeller-driven airplane is assumed to be the brake power required (i.e., the brake power at the shaft, P_{\rm bp}), which will also reflect the effects of the propeller efficiency, i.e.,

(3)   \begin{equation*} P_{\rm req} = P_{\rm bp} = \frac{T V_{\infty}}{\eta_p} = \frac{D V_{\infty}}{\eta_p} = \frac{1}{\eta_p} \left( \frac{1}{2} \varrho_0 \, \sigma \, V_{\infty}^3 \, S \left( C_{D_{0}} + k {C_L}^2 \right) \right) \end{equation*}

A constant-speed propeller will have a propulsive efficiency, \eta_p, that will be reasonably constant over the normal range of flight speeds. This assumption is a reasonable one for analyzing turboprops and high-performance piston-engine aircraft. A fixed-pitch propeller’s propulsive efficiency is not constant; it can vary significantly as a function of airspeed. So, the aircraft performance analysis requires that the propeller charts be considered so that \eta_p can be determined at the actual flight conditions. Notice that in most cases, the density of the air has been referenced to ISA conditions, where \varrho_{\infty} = \varrho_0 \, \sigma, and the value of \sigma comes from the ISA equations.

If it is assumed that the engine BSFC is constant (this is a reasonable but not a general assumption), then the fuel flow (in appropriate units of time) will be

(4)   \begin{equation*} \frac{dW_f}{dt} = \overbigdot{W}_{\!f} = ({\rm BSFC}) P_{\rm bp} = c_b \, P_{\rm bp} \end{equation*}

where the BSFC is now given the symbol c_b. The fuel flow is, therefore,

(5)   \begin{equation*} \overbigdot{W}_{\!f} = \left( \frac{1}{2} \varrho_0 \, \sigma \, V_{\infty}^3 \, c_b \, S \right) \frac{1}{\eta_p} C_{D_{0}} + \left( \frac{k \, c_b }{\eta_p} \right) \frac{2 W^2}{\varrho_0 \, \sigma \, S \, V_{\infty} } \end{equation*}

which is of the form

(6)   \begin{equation*} \overbigdot{W}_{\!f} = A V_{\infty}^3 + \frac{B}{V_{\infty}} \end{equation*}

for a constant weight and/or altitude.

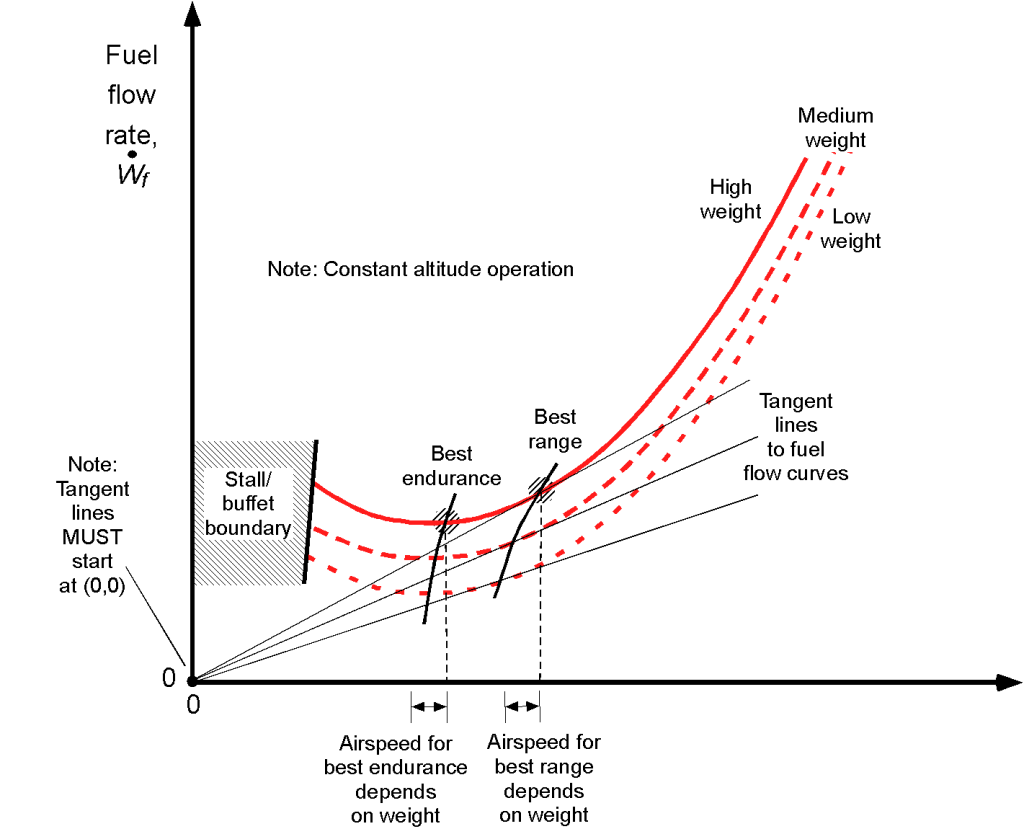
Remember the general “U” shaped characteristic of the power required for a propeller-driven airplane flight curve; these power curves are a function of airspeed and depend on the weight of the airplane and the equivalent density altitude at which it is flying. Therefore, the fuel flow curves will mimic the shapes of the power curves. For example, the effects of the in-flight weight of the airplane on the fuel flow characteristics are shown in the figure below. Notice that a higher flight weight increases the power and corresponding fuel required. In addition, the points for best endurance (lowest fuel flow) and best range (lowest fuel flow per unit speed or distance) are indicated; these speeds are not constant and depend on weight.

Representative fuel flow curves for a propeller-driven airplane as a function of airspeed and in-flight weight.

The speed to fly for the lowest fuel burn (hence maximum flight endurance) can be determined by finding when \overbigdot{W}_{\!f} is a minimum. Differentiating the fuel flow result given by Eq. 6 with respect to V_{\infty} gives

(7)   \begin{equation*} \frac{d \overbigdot{W}_{\!f}}{d V_{\infty}} = 3 A V_{\infty}^2 - \frac{B}{V_{\infty}^2} \end{equation*}

which is zero for a minimum, i.e.,

(8)   \begin{equation*} 3 A V_{\infty}^2 - \frac{B}{V_{\infty}^2} = 0 \end{equation*}

and so the speed to fly for the best endurance will be

(9)   \begin{equation*} V_{\infty} = V_x = \left( \frac{B}{3A} \right)^{1/4} \end{equation*}

confirming that V_x will depend on both weight and altitude.

The best range is obtained when the ratio \overbigdot{W}_{\!f}/V_{\infty} is a minimum. In this case

(10)   \begin{equation*} \frac{\overbigdot{W}_{\!f}}{V_{\infty}} = A V_{\infty}^2 + \frac{B}{V_{\infty}^2} \end{equation*}

so that

(11)   \begin{equation*} \frac{d(\overbigdot{W}_{\!f}/V_{\infty})}{dV_{\infty}} = 2 A V_{\infty} - 2\frac{B}{V_{\infty}^3} \end{equation*}

which is zero for a minimum, i.e.,

(12)   \begin{equation*} 2 A V_{\infty} - \frac{2B}{V_{\infty}^3} = 0 \end{equation*}

and so

(13)   \begin{equation*} V_{\infty} = V_y = \left( \frac{B}{A} \right)^{1/4} \end{equation*}

also confirming that V_y will depend on both weight and altitude.

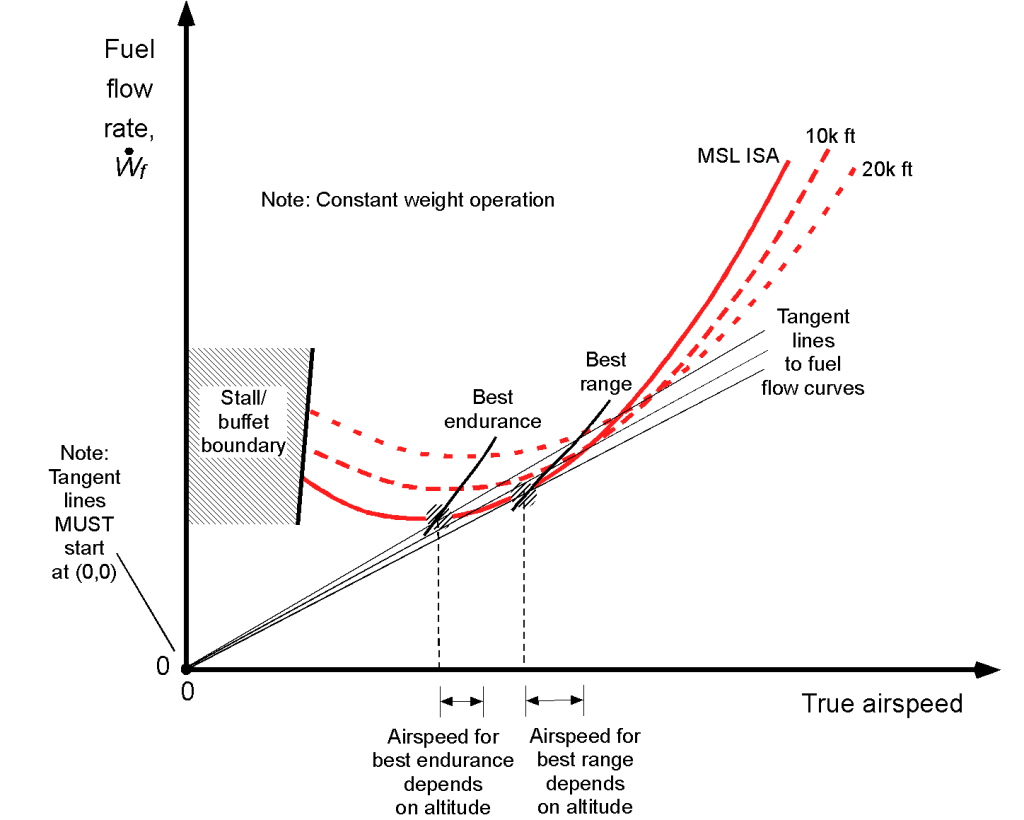
The corresponding effects of altitude on the fuel flow characteristics are shown in the figure below. Notice that at lower airspeeds, the effects of altitude increase the power required, increasing the fuel flow. This outcome is because it can be deduced that at low airspeeds, the power required is dominated by the induced component (see Eq. 6). Again, the points for best endurance (lowest fuel flow) and best range (lowest fuel flow per unit speed or distance) are indicated; these speeds are not constant and depend on the weight and can be calculated using Eqs. 9 and 13, respectively.

Representative fuel flow curves for a propeller-driven airplane as a function of airspeed and operational altitude.

Fuel Flow Curves – Jet Airplanes

As for propeller-driven airplanes, the fuel flow for a jet aircraft will be a function of airspeed, in-flight weight, and operating altitude. While the shapes of the fuel flow curves are different because they depend on thrust, they retain the qualitative U-shapes described by the thrust-required equation, i.e.,

(14)   \begin{equation*} T = \frac{1}{2} \varrho_0 \, \sigma V_{\infty}^2 \, S \, C_D = \frac{1}{2} \varrho_0 \, \sigma V_{\infty}^2 S \left( C_{D_{0}} + k {C_L}^2 \right) \end{equation*}

If it is assumed that the TSFC is constant (again, this is a reasonable assumption), then the fuel flow (in appropriate units of time) will be

(15)   \begin{equation*} \frac{dW_f}{dt} = \overbigdot{W}_{\!f} = ({\rm TSFC}) T_{\rm req} = c_t \, T_{\rm req} \end{equation*}

where the TSFC is now given the symbol c_t. The fuel flow is, therefore,

(16)   \begin{equation*} \overbigdot{W}_{\!f} = \frac{1}{2} \varrho_0 \, \sigma V_{\infty}^2 \, S \, c_t \, C_{D_{0}} + \frac{2 k \, c_t \, W^2}{\varrho_0 \, \sigma \, S \, V_{\infty}^2} \end{equation*}

which, in this case, is of the form

(17)   \begin{equation*} \overbigdot{W}_{\!f} = A V_{\infty}^2 + \frac{B}{V_{\infty}^2} \end{equation*}

for a constant weight and/or altitude.

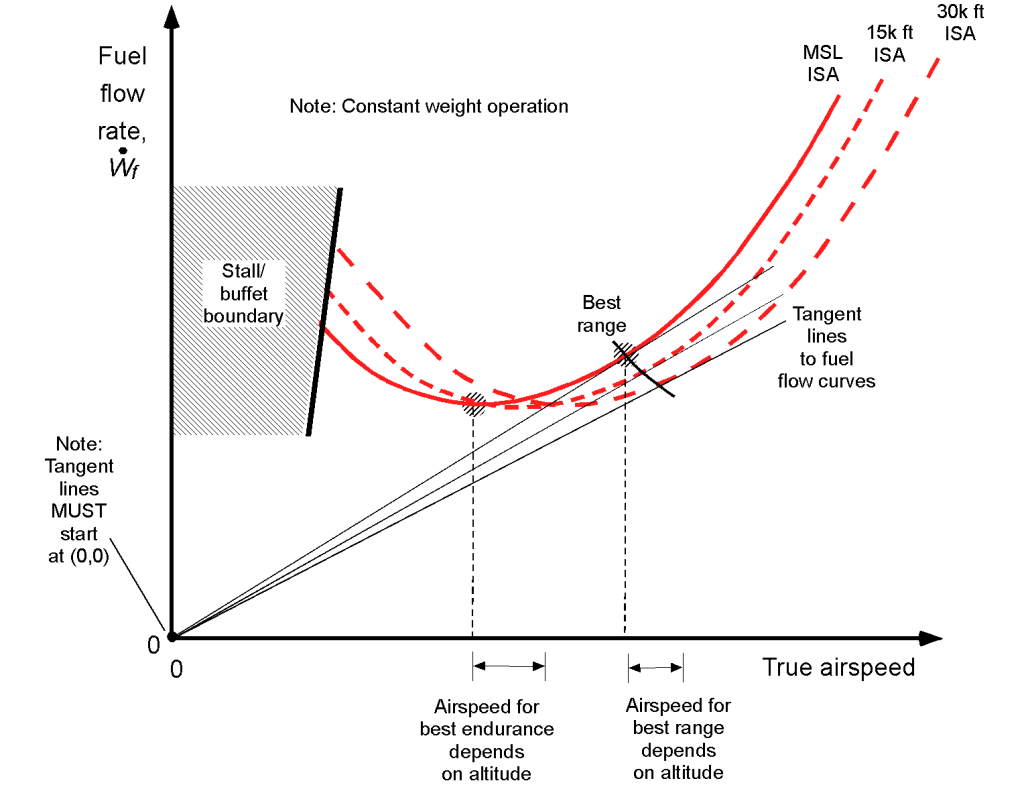
The effects of the jet airplane’s in-flight weight on the fuel flow characteristics are shown in the figure below. Notice again that a higher flight weight increases the power and fuel required. The points for best endurance (lowest fuel flow) and best range (lowest fuel flow per unit speed or distance) are indicated; these speeds depend on the airplane’s weight.

Representative fuel flow curves for a jet airplane as a function of airspeed and in-flight weight.

The speed to fly for the lowest fuel burn (hence maximum flight endurance) can be determined by finding when \overbigdot{W}_{\!f} is a minimum. Differentiating the fuel flow result given by Eq. 17 with respect to V_{\infty} gives

(18)   \begin{equation*} \frac{d\overbigdot{W}_{\!f}}{d V_{\infty}} = 2A V_{\infty} - \frac{2B}{V_{\infty}^3} \end{equation*}

which is zero for a minimum, i.e.,

(19)   \begin{equation*} 2 A V_{\infty} - \frac{2 B}{V_{\infty}^3} = 0 \end{equation*}

and so the speed to fly for the best endurance for a jet aircraft will be

(20)   \begin{equation*} V_{\infty} = V_x = \left( \frac{B}{A} \right)^{1/4} \end{equation*}

confirming that V_x will depend on both the weight of the airplane and its operating altitude.

As previously discussed, the best range is obtained when the ratio \overbigdot{W}_{\!f}/V_{\infty} is a minimum. In this case, for a jet, then

(21)   \begin{equation*} \frac{\overbigdot{W}_{\!f}}{V_{\infty}} = A V_{\infty} + \frac{B}{V_{\infty}^3} \end{equation*}

so that

(22)   \begin{equation*} \frac{d(\overbigdot{W}_{\!f}/V_{\infty})}{dV_{\infty}} = A - 3\frac{B}{V_{\infty}^4} \end{equation*}

which is zero for a minimum, i.e.,

(23)   \begin{equation*} A - \frac{3B}{V_{\infty}^4} = 0 \end{equation*}

and so

(24)   \begin{equation*} V_{\infty} = V_y = \left( \frac{3B}{A} \right)^{1/4} \end{equation*}

also confirming that V_y will depend on both weight and altitude for a jet.

The corresponding effects of altitude on the fuel flow characteristics are shown in the figure below. Notice that at lower airspeeds, the effects of altitude increase the power required, increasing the fuel flow. Again, the points for best endurance (lowest fuel flow) and best range (lowest fuel flow per unit speed or distance) are indicated; these speeds are not constant and depend on the weight and can be calculated using Eqs. 20 and 24, respectively.

Representative fuel flow curves for a jet airplane as a function of airspeed and altitude.

Total Fuel Burn

Determining the total fuel burn of the aircraft over the intended flight or mission requires that the fuel flow is known as a function of aircraft weight, operating altitude, and true airspeed (or Mach number). While the fuel flow curves have been previously delineated for the separate effects of weight and altitude, the aircraft weight, altitude, and airspeed can vary continuously during flight. In addition, there are also the climb and descent phases of the flight to consider. Therefore, the net fuel burn is a summation performed numerically by adding up the fuel burned for each flight segment. An estimated fuel burn will be used for flight planning so sufficient fuel for the flight (plus reserve fuel) can be loaded onboard the aircraft.

A representative fuel flow rate versus time is shown in the figure below for a typical civil flight, i.e., takeoff, climb, and cruise to a destination, followed by a landing. By integration over time, the total fuel burned can be determined in units of weight, i.e., for the interval between t = t_1 and t = t_2, then

(25)   \begin{equation*} W_f = \int_{t_1}^{t_2} \overbigdot{W_f} \, dt \end{equation*}

which is just the area under the fuel flow curve between t_1 and t_2. The total fuel burn, therefore, is the total area under the fuel flow curve from takeoff to landing.

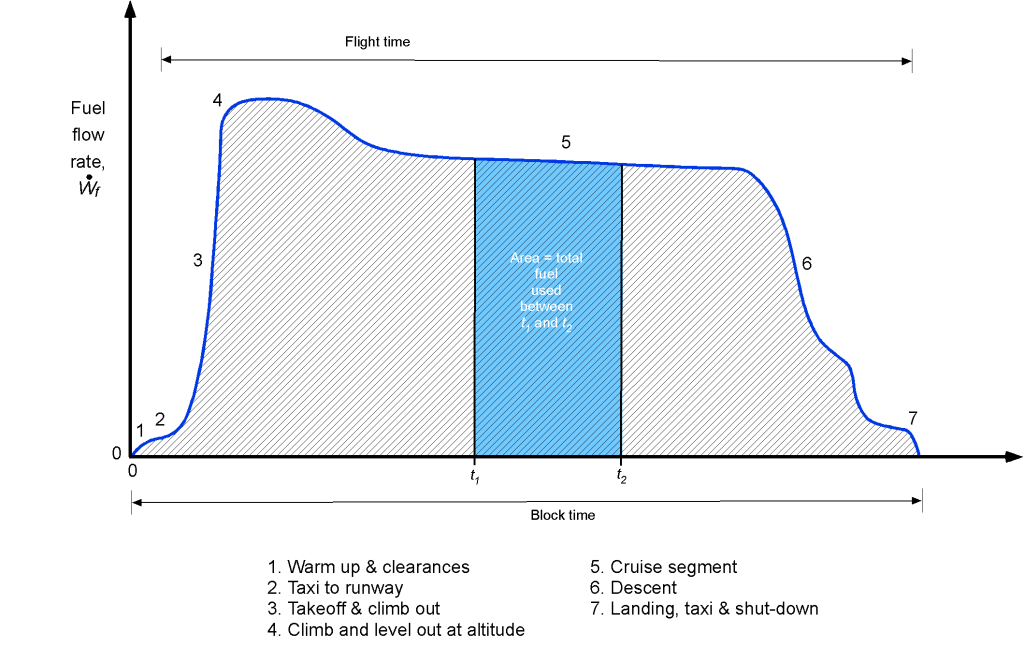
A representative fuel burn profile (fuel flow rate versus time) for a commercial airliner. The area under the fuel flow rate curve between two values of time will be the total fuel burned in that interval.

As a special case, if \overbigdot{W}_{\!f} is assumed to be constant (which is reasonable over relatively short flight times in the cruise segment of flight), then the weight of fuel weight burned W_f would be

(26)   \begin{equation*} W_f \approx \overbigdot{W}_{\!f} \left( t_1 - t_2 \right) \end{equation*}

In general, however, the total fuel burn for each flight segment must be obtained by integration.

If the initial weight of the airplane at t_0 is W_0 and the fuel available is W_f then, when all of this fuel is burned, the new weight of the airplane at t_1 will be W_0 - W_f = W_1. Using a propeller-driven airplane as an example, the change in weight of the airplane with time will be

(27)   \begin{equation*} \frac{dW}{dt} = c_b \, P_{\rm bp} \end{equation*}

so rearranging and integrating gives

(28)   \begin{equation*} \int_{t_1}^{t_2} dt = - \int_{W_0}^{W_1} \frac{ \, dW}{c_b \, P_{\rm bp}} = \int_{W_1}^{W_0} \frac{ \, dW}{c_b \, P_{\rm bp}} \end{equation*}

the minus sign indicates that the weight of the airplane W decreases with time, rectified by reversing the limits of integration. Therefore, the flight time corresponding to the fuel burned will be

(29)   \begin{equation*} t_2 - t_1 = \Delta t = \int_{W_1}^{W_0} \frac{ \, dW}{c_b \, P_{\rm bp}} \end{equation*}

If W_f is further assumed to be the total fuel available, then \Delta t, in this case, becomes the endurance E, i.e.,

(30)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{ \, dW}{c_b \, P_{\rm bp}} \end{equation*}

which would use all the available fuel. Again, as a special case, P_{\rm bp} and c_b are assumed to be constant, then the flight endurance for a given fuel weight would just be

(31)   \begin{equation*} E \approx \frac{W_f}{c_b \, P_{\rm bp} } \end{equation*}

Regarding range, the interest here is in the distance covered for a given quantity of fuel. Multiplying both sides of Eq. 27 by V_{\infty} gives

(32)   \begin{equation*} V_{\infty} \frac{\, dW}{dt} = V_{\infty} \, c_b \, P_{\rm bp} \end{equation*}

and then rearranging gives

(33)   \begin{equation*} V_{\infty} \, dt = \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} \end{equation*}

The distance covered in a given time, or the range R, is then

(34)   \begin{equation*} R = \int_{t_0}^{t_1} V_{\infty} \, dt \end{equation*}

so this gives

(35)   \begin{equation*} R = \int_{t_0}^{t_1} V_{\infty} \, dt = -\int_{W_0}^{W_1} \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} = \int_{W_1}^{W_0} \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} \end{equation*}

so that

(36)   \begin{equation*} R = \int_{W_0-W_f}^{W_0} \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} \end{equation*}

where W_1 = W_0 - W_f. The physical meaning of this integral is also related to the area under the fuel flow curve. Again, as a special case, P_{\rm bp} and c_b are assumed to be constant, then the flight range for a given fuel weight would just be

(37)   \begin{equation*} R = \frac{V_{\infty} \, W_f}{c_b \, P_{\rm bp} } \end{equation*}

Reserve Fuel – Why is it needed?

The need for reserve fuel must always be considered when estimating flight range. For example, the flight crew may reach a final destination to find air traffic delays or bad weather preventing landings. The aircraft may also need to enter a holding pattern or divert to an alternative airport. For this reason, reserve fuel is always required. The FAA regulations (FARs) mandate that aircraft carry extra reserve fuel. For VFR (visual flight rules) conditions, the aircraft must carry 30 minutes of reserve fuel over and above what is estimated for the planned flight, and for IFR (instrument flight rules), the FAA requirement is to have 45 minutes of reserve fuel.

Breguet Equations

The preceding principles are formally embodied in what is known as the Breguet equations for airplane endurance and range, which Louis Charles Breguet first developed. These are some of the most famous equations used in aeronautical engineering. How they are derived should be understood, as well as what information they can reveal about the flight performance of an airplane.

Breguet Endurance Equation – Propeller Airplanes

For flight endurance, it has been previously stated that the endurance is given by

(38)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{dW}{c_b \, P_{\rm bp}} \end{equation*}

Assuming lift equals weight (L = W) and P = D \, V_{\infty}, then in level flight the endurance is

(39)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{ \eta_p \, dW}{c_b \, D \, V_{\infty}} = \int_{W_0 - W_f}^{W_0} \frac{ \eta_p \, L}{c_b \, D \, V_{\infty}} \frac{\, dW}{W} \end{equation*}

The lift required (which must equal the weight) is

(40)   \begin{equation*} W = L = \frac{1}{2} \varrho_0 \, \sigma \, V_{\infty}^2 \, S \, C_L \end{equation*}

so solving for the airspeed V_{\infty} gives

(41)   \begin{equation*} V_{\infty} = \sqrt{ \frac{2 W}{\varrho_0 \, \sigma \, S \, C_L}} \end{equation*}

Also, for the drag on the aircraft, then

(42)   \begin{equation*} D = \frac{1}{2} \varrho_0 \, \sigma V_{\infty}^2 \, S \, C_D \end{equation*}

Substituting the previous results means that the endurance equation now becomes

(43)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{ \eta_p}{c_b } \left(\frac{C_L^{\, 3/2}}{C_D}\right) \sqrt{ \frac{\varrho_{\infty} \, S}{2} } \frac{dW}{W^{3/2}} \end{equation*}

Notice that the ratio C_L^{\, 3/2}/C_D appears in this latter equation, not the lift-to-drag ratio C_L/C_D. While the numerical values are similar, the airspeeds at which the maximum values occur are distinctly different, as shown in the figure below.

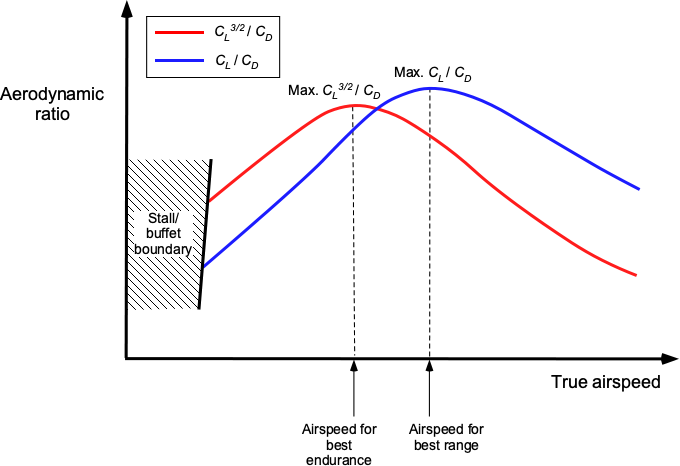
A propeller-driven airplane’s best endurance and airspeed occur at different aerodynamic conditions.

Proceeding further by assuming that the value of C_L^{\, 3/2}/C_D is constant over the flight time, which might be reasonable for shorter flight times where the weight of the airplane does not change by much, as well as assuming that \eta_p, c_b and \varrho_{\infty} = \varrho_0 \, \sigma are constant (i.e., the airplane is flying at a constant altitude), then after integration of Eq. 43 the endurance will be

(44)   \begin{equation*} E = \frac{ \eta_p}{c_b} \left(\frac{C_L^{\, 3/2}}{C_D}\right) \sqrt{2 \varrho_0 \, \sigma \, S} \left( \frac{1}{\sqrt{W_0 - W_f}} - \frac{1}{\sqrt{W_0} } \right) \end{equation*}

which is known as the Breguet endurance equation for a propeller-driven airplane.

This latter equation estimates the flight endurance for a given total fuel weight. If no assumptions were made before the analytic integration, then finding the fuel required and the endurance would usually have to be performed entirely by numerical integration.

Therefore, from the Breguet endurance equation, it becomes clear that to maximize flight endurance, the airplane must be flown in such a way that:

  1. The propeller is operated at (or near to) its best propulsive efficiency; this is typical of a constant speed (variable pitch) propeller.
  2. The engine is operated at (or near to) the power setting to achieve its best BSFC, although this may not be possible at lower power settings, which most likely will be altitude-dependent.
  3. The airplane carries the largest quantity of fuel. Fuel quantity may be limited by other than the volume of the tankage, for example, because of the need to carry a specific payload that must be traded off against the fuel load.
  4. The airplane flies at (or close to) the best aerodynamic ratio of C_L^{\, 3/2}/C_D.

Breguet Range Equation – Propeller Airplanes

Now consider the flight range of the propeller-driven airplane. As was previously established, the range is given by

(45)   \begin{equation*} R = \int_{W_0-W_f}^{W_0} \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} \end{equation*}

After the substitution of the relationships used previously for endurance, then

(46)   \begin{equation*} R = \int_{W_0-W_f}^{W_0} \frac{V_{\infty} \, \eta_p \, dW}{D \, V_{\infty}} = \int_{W_0-W_f}^{W_0} \frac{\eta_p \, dW}{c_b \, D} \end{equation*}

Again, for steady level flight, L = W so

(47)   \begin{equation*} R = \int_{W_0-W_f}^{W_0} \frac{\eta_p}{c_b} \left( \frac{L}{D}\right) \frac{\, dW}{W} = \int_{W_0-W_f}^{W_0} \frac{\eta_p}{c_b} \left(\frac{C_L}{C_D}\right) \frac{\, dW}{W} \end{equation*}

where in this case the lift-to-drag ratio C_L/C_D is involved.

As performed before with the endurance integral, if C_L/C_D, \eta_p and c_b are assumed to be constant then

(48)   \begin{equation*} R = \frac{\eta_p}{c_b} \left( \frac{C_L}{C_D} \right) \int_{W_0-W_f}^{W_0} \frac{dW}{W} \end{equation*}

which, after integration, leads to an estimate for the range as

(49)   \begin{equation*} R = \frac{\eta_p}{c_b} \left( \frac{C_L}{C_D}\right) \ln \left( \frac{W_0}{W_0-W_f}\right) \end{equation*}

which is usually known as the Breguet range equation. Again, if the actual values of C_L/C_D, \eta_p, and c corresponding to a given flight condition were to be used, then the integral would need to be evaluated numerically.

Statute Miles or Nautical Miles?

Nautical miles are used to measure distances in the aeronautical and aviation world. A nautical mile is 1/60th of a degree or one minute of latitude and is 6,076 ft or 1,852 m long. Speed is usually measured in terms of nautical miles per hour or knots (kts), and airspeed indicators on aircraft are calibrated in units of knots. The familiar land mile is a statute mile and is 5,280 ft, based on a Roman measure of 1,000 paces. The statute mile was standardized as exactly 1,609.344 meters by an international agreement in 1959. A nautical mile is abbreviated to “M” or “NM,” but more usually, “nm” is used. The statute mile was previously abbreviated to “m” but is now written as “mi'” to avoid confusion with the SI unit meter (or metre).

Therefore, based on the preceding, it is clear that to maximize the flight range, the airplane must be flown in such a way that:

  1. As previously discussed, the propeller is operated at (or near to) its best propulsive efficiency.
  2. The engine is operated at (or near to) the power setting to achieve its best BSFC, again with the caveats previously discussed.
  3. The airplane carries the largest quantity of fuel.
  4. The airplane flies at or near the best lift-to-drag ratio C_L/C_D.

In summary, when thinking about the design of a propeller-driven airplane, achieving the best flight endurance and/or range is about four things:

  1. Carrying as much fuel as possible.
  2. Getting a high aerodynamic efficiency out of the airframe, i.e., designing the airplane to achieve as low drag as possible.
  3. Striving for high engine efficiency, i.e., obtaining the lowest possible value of BSFC from the engines.
  4. Obtaining high propulsive efficiency, i.e., designing the propeller in this case for good overall aerodynamic efficiency, will inevitably require a variable pitch (i.e., constant speed) propeller.

Check Your Understanding #1 – Finding the range of a propeller-driven airplane

A small propeller-driven aircraft is flying along at an estimated in-flight weight of 2,100 lb and an airspeed of 120 knots at 2,000 ft where the air density is 0.00216 slugs/ft{^3}. The airplane only has 8 gallons of usable fuel (excluding reserves), and the pilot must fly 120 nautical miles to the home airport. Is there enough fuel to do this? Assume no winds. The engineering characteristics of the aircraft are wing span, b = 36 ft, wing area, S = 174 ft^2, non-lifting drag coefficient, C_{D_{0}} = 0.02, propeller efficiency, \eta_p = 0.85, Oswald’s efficiency factor, e = 0.81, and BSFC, c_b = 0.45 lb bhp^{-1} hr^{-1}.

Show solution/hide solution.

There are only 8 gallons of AVGAS fuel, and AVGAS weighs 6.0 lb per gallon, so W_f = 48 lb of fuel. An airspeed of 120 kts is equivalent to 120 \times 1.688 = 202.54 ft/s = V_{\infty}. The initial operating lift coefficient of the wing, C_L, is

    \[ C_L = \frac{2W}{\varrho V^2 S} = \frac{2 \times 2,100}{0.00216 \times 202.54^2 \times 174.0} = 0.272 \]

To find the induced drag coefficient, the aspect ratio of the wing, A\!R, is needed, i.e.,

    \[ A\!R = \frac{b^2}{S} = \frac{(36.0)^2}{174.0} = 7.45 \]

The induced drag coefficient C_{D_{i}} will be

    \[ C_{D_{i}} = \frac{{C_L}^2}{\pi \, A\!R e} = \frac{0.272^2}{\pi \times 7.45 \times 0.81} = 0.0039 \]

Therefore, the total drag coefficient, C_D, is

    \[ C_D = C_{D_0} + C_{D_i} = C_{D_0} + \frac{{C_L}^2}{\pi \, A\!R e} = 0.02 + 0.0039 = 0.0239 \]

and the lift-to-drag ratio of the aircraft at the given conditions of flight is

    \[ \frac{L}{D} = \frac{C_L}{C_D} = \frac{0.272}{0.0239} = 11.38 \]

The Breguet range equation for a propeller-driven airplane is

    \[ R = \frac{\eta_p}{c_b} \left( \frac{C_L}{C_D}\right) \ln \left( \frac{W_0}{W_0-W_f}\right) \]

IMPORTANT: Notice that the value of the brake-specific fuel consumption or BSFC in this problem is given in units of lb bhp^{-1} hr^{-1}, which must be converted to base units before using it in the Breguet equation. One brake horsepower (bhp) is equivalent to 550 ft-lb s^{-1}, and there are 3,600 seconds in an hour, i.e., by dividing the given value by 550 x 3,600.

Therefore, inserting the known values gives the potential approximate range of the aircraft as

    \[ R = \frac{0.85 \times 550 \times 3,600}{0.45} \left( 11.38 \right) \ln \left( \frac{2,100}{2,100 -48}\right) = 984,118~\mbox{ft} \]

which is approximately 162 nautical miles. In conclusion, the aircraft has enough fuel to make it to the home airport with a margin, so the pilot can relax and enjoy the remainder of the flight.

Breguet Endurance Equation – Jet Airplanes

When dealing with the performance of jet airplanes, the thrust required by the engine matters rather than the power required for propeller-driven airplanes. However, the estimation of endurance and range proceeds along a similar path as was previously done for the propeller-driven airplane.

For a jet engine, the thrust-specific fuel consumption (TSFC) is defined as

(50)   \begin{equation*} \mbox{TSFC} = \frac{\text{Weight of fuel burned}}{ \text{(Unit thrust produced)(time~=~hour)}} = \frac{\text{lb of fuel}}{ \text{(lb of thrust)(hr)}} = c_t \end{equation*}

in units of lb lb^{-1} hr^{-1}. Therefore, the fuel flow rate is

(51)   \begin{equation*} \frac{dW_f}{dt} = \overbigdot{W}_{\!f} = T_R \, c_t \end{equation*}

where T_R is the required thrust from the engine. So, in this case, to find the fuel flow rate, the thrust needed from the engine must be determined, and for level flight, this will be equal to the drag of the airplane.

As fuel is burned, the weight of the airplane changes proportionally, so the change in weight of the airplane is

(52)   \begin{equation*} \frac{dW}{dt} = T_R \, c_t \end{equation*}

The airplane’s weight is W_0 at time t = t_0 and W_1 at time t = t_1 where the second weight is the initial weight, less the fuel burned, i.e., W_1 = W_0 - W_f. Therefore,

(53)   \begin{equation*} \int_{t_0}^{t_1} dt = \Delta t = -\int_{W_0}^{W_1} \frac{dW}{c_t \, T_R} = \int_{W_1}^{W_0} \frac{dW}{c_t \, T_R} = \int_{W_0 - W_f}^{W_0} \frac{dW}{c_t \, T_R} \end{equation*}

which gives the time of flight, \Delta t, to burn the fuel weight, W_f. Now, if W_f is the total fuel available then \Delta t is equal to the endurance E so

(54)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{dW}{c_t \, T_R} \end{equation*}

For level flight then T_R = D and L = W and after substitution then

(55)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{1}{c_t} \left( \frac{L}{D} \right) \frac{dW}{W} = \int_{W_0 - W_f}^{W_0} \frac{1}{c_t} \left( \frac{C_L}{C_D} \right) \frac{dW}{W} \end{equation*}

It will be noted immediately that this is a different result to the propeller-driven airplane because, in this case, the endurance depends on C_L/C_D and not C_L^{\, 3/2}/C_D for the propeller airplane.

By assuming that c_t and C_L/C_D are constant, then the forgoing endurance equation integrates out to be

(56)   \begin{equation*} E = \frac{1}{c_t} \left( \frac{C_L}{C_D} \right) \ln \left(\frac{W_0}{W_0 - W_f} \right) \end{equation*}

which is referred to as the Breguet endurance equation for a jet airplane.
Therefore, to maximize the flight endurance of a jet airplane, it must be flown in such a way that:

  1. The engine(s) is/are operated at (or near to) the power setting to achieve its best TSFC. For most jet engines, this condition inevitably occurs at higher altitudes, which is by design.
  2. The airplane carries the largest quantity of fuel, although this may be limited by weight rather than available tankage.
  3. The airplane flies at or near the best lift-to-drag ratio C_L/C_D.

Breguet Range Equation – Jet Airplanes

As before, the differential equation to account for the change in the weight of the airplane as fuel is burned is

(57)   \begin{equation*} \frac{dW}{dt} = T_R \, c_t \end{equation*}

or by rearrangement

(58)   \begin{equation*} dt = \frac{dW}{T_R \, c_t} \end{equation*}

The distance flown is the product of airspeed and time, so multiplying both sides of the preceding equation by V_{\infty} gives

(59)   \begin{equation*} V_{\infty} \, dt = s = \frac{V_{\infty} \, dW}{T_R \, c_t} \end{equation*}

noticing that the term on the left-hand side is just distance, say s. The airplane weight is W_0 at time t = t_0 and W_1 at time t = t_1 where the second weight is the initial weight, less the fuel burned, i.e., W_1 = W_0 - W_f. Integrating Eq. 59 gives

(60)   \begin{equation*} s = \int_{t_0}^{t_1} V_{\infty} \, dt = -\int_{W_0}^{W_1} \frac{V_{\infty} \, dW}{T_R \, c_t} = \int_{W_1}^{W_0} \frac{V_{\infty} \, dW}{T_R \, c_t} \end{equation*}

For level flight, then T_R = D and L = W, and after substitution, the distance traveled on a given weight of fuel W_f is

(61)   \begin{equation*} s = \int_{W_1}^{W_0} \frac{V_{\infty}}{c_t} \left( \frac{L}{D} \right) \frac{dW}{W} = \int_{W_1}^{W_0} \frac{V_{\infty}}{c_t} \left(\frac{C_L}{C_D} \right) \frac{dW}{W} \end{equation*}

which would be the maximum range R if the value of W_f was all the useful fuel. Also

(62)   \begin{equation*} V_{\infty} = \sqrt{ \frac{2 W}{\varrho_0 \, \sigma S C_L}} \end{equation*}

so that after substitution, the range of the airplane becomes

(63)   \begin{equation*} R = \int_{W_1}^{W_0} \frac{1}{c_t} \sqrt{\frac{2}{\varrho_0 \, \sigma \, S}} \left(\frac{C_L^{1/2}}{C_D} \right) \frac{dW}{W^{1/2}} \end{equation*}

which again is a different result to the propeller-driven airplane because it depends on the aerodynamic ratio C_L^{1/2}/C_D rather than C_L/C_D, as shown in the figure below. The airspeed for the best value of C_L^{1/2}/C_D, and so the best range, is generally significantly higher than that for best endurance.

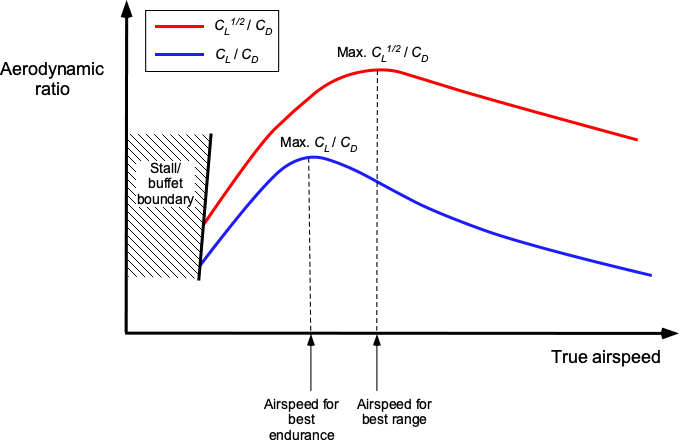
A jet airplane’s best endurance and range airspeeds also occur at distinctly different aerodynamic conditions.

By assuming that c_t and C_L and C_D are constant, then the forgoing endurance equation integrates out to be

(64)   \begin{equation*} R = \frac{1}{c_t} \sqrt{\frac{2}{\varrho_0 \, \sigma \, S}} \left(\frac{C_L^{1/2}}{C_D} \right) \int_{W_1}^{W_0} \frac{dW}{W^{1/2}} = \frac{2}{c_t} \sqrt{ \frac{2}{\varrho_0 \, \sigma \, S}} \left(\frac{C_L^{1/2}}{C_D} \right) \left( W_0^{1/2} - W_1^{1/2} \right) \end{equation*}

which is referred to as the Breguet range equation for a jet airplane.

Therefore, to maximize the flight range of a jet airplane, it must be flown in such a way that:

  1. The engine operates at (or near) the thrust (throttle) setting to achieve its best TSFC.
  2. The airplane carries the largest quantity of fuel.
  3. The airplane flies at or near the best value of the aerodynamic ratio C_L^{1/2}/C_D.

Check Your Understanding #2 – Finding the range of a jet aircraft

A small, single-engine jet-powered aircraft has an initial in-flight weight, W, of 5,000 lbs and carries 1,000 lb of usable fuel. The aircraft is at an altitude of 25,000 ft ISA. Its drag polar can be expressed as C_D = 0.018 + 0.095 \, C_L^ {\,2}. It has a wing area of 180 ft2. The TSFC of the engine is c_t = 1.0 lb/lb/hr. What is the best range of the aircraft in these conditions, and at what airspeed should the pilot fly to reach this range?

Show solution/hide solution.

For a jet aircraft, the conditions for maximum range are achieved when the aerodynamic ratio C_L^{1/2}/C_D is maximized. If the drag polar is

    \[ C_D = C_{D_{0}} + k \, C_L^ {\,2} = 0.018 + 0.095 \, C_L^ {\,2} \]

then

    \[ \frac{C_D}{C_L^{1/2}} = \frac{ C_{D_{0}} + k \, C_L^ {\,2}}{C_L^{1/2}} = \frac{C_{D_{0}}}{C_L^{1/2}} + k C_L^{\, 3/2} \]

To find a maximum (or minimum), the preceding expression is differentiated with respect to C_L and then set to zero, i.e.,

    \[ \frac{ d (C_D/C_L^{1/2})}{d C_L} = -\frac{1}{2} \left( \frac{C_{D_{0}}}{C_L^{1/2}} \right) + \frac{3}{2} k C_L^{1/2} = 0 \]

Therefore, the needed lift coefficient for this best range condition is

    \[ C_L = \sqrt{ \frac{C_{D_{0}}}{K} } = \sqrt{ \frac{0.018}{0.095} } = 0.251 = C_{L_{\rm br}} \]

The corresponding drag coefficient will be

    \[ C_D = 0.018 + 0.095 \, C_L^ {\,2} = 0.018 + 0.095 \times 0.251^2 = 0.024 \]

Therefore,

    \[ \left( \frac{ C_L^{1/2}}{ C_D} \right)_{\rm br} = \frac{ 0.251^{1/2}}{0.024} = 20.875 \]

The Breguet range equation for a jet aircraft is

    \[ R = \frac{2}{c_t} \sqrt{ \frac{2}{\varrho_0 \, \sigma S}} \left(\frac{C_L^{1/2}}{C_D} \right)_{\rm br} \left( W_0^{1/2} - W_1^{1/2} \right) \]

The initial weight is W_0 = 5,000 lb, and the final weight, W_1, is the initial weight, less the fuel weight burned, so W_1 = 4,000 lb. At an altitude of 25,000 ft ISA conditions, \varrho_{\infty} = \varrho_0 \, \sigma = 0.001066 slug/ft3. It is important to be careful here and notice that the value of c_t is in units per hour, so dividing by a factor of 3,600 is needed to convert to units per second. Inserting all the values gives

    \[ R = \frac{2\times 3,600}{1.0} \sqrt{ \frac{2}{0.001066 \times 180.0}} \left( 20.875\right) \left( 5,000^{1/2} - 4,000^{1/2} \right) \]

which gives R = 3,622,400 ft = 596 nautical miles. The airspeed for the best range is obtained using

    \[ V_{\rm br} = \sqrt{ \frac{2 W}{\varrho_{\infty} \, S \, C_{L_{\rm br}}}} = \sqrt{ \frac{2 \times 5,000}{0.001066 \times 180.0 \times 0.251 }} = 455.7~\mbox{ft/s} \]

which is a true airspeed of 270 knots.

Payload-Range & Endurance Charts

The range that an airplane can fly on a given quantity of fuel depends on its weight and operating altitude. The weight of the aircraft is the sum of its empty weight plus the useful load, i.e., the weight of payload and fuel. It takes fuel to carry the payload (i.e., passengers and/or cargo, which is what pays the bills), but fuel is not payload. For most aircraft, because there is a trade between payload and fuel load above a certain flight range, the payload will need to be limited and exchanged for fuel weight.

Airliners

The figure below illustrates a typical payload-range diagram for a commercial airliner. Airliners are point designs because they spend most of their flight time cruising at a constant airspeed (Mach number) and high altitudes. The typical shape of the payload-range diagram is such that the aircraft can carry a maximum payload only over a specified range, i.e., the gray area with the upper bound indicated by the horizontal line between points A and B. When an aircraft operates at maximum payload, the fuel tanks generally cannot be filled to their total capacity.

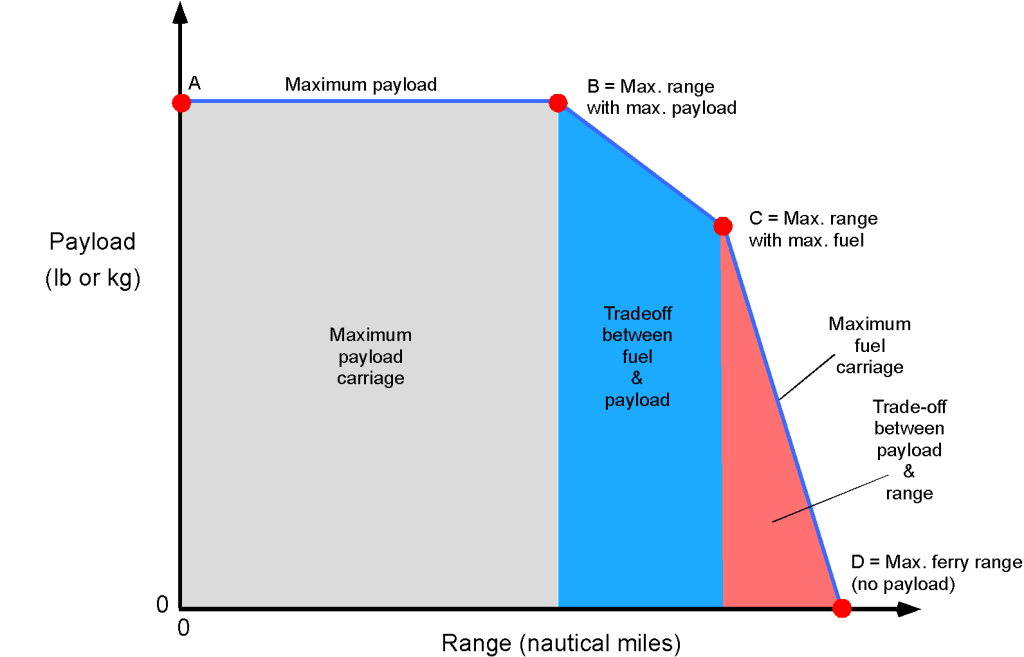
A representative payload-range chart for a commercial airliner. The flight will be flown at a nominally constant cruise altitude and Mach number.

It can be seen from the diagram that longer flight ranges can be flown by reducing payload (i.e., limiting the number of passengers and cargo) in exchange for fuel, i.e., the blue area with the boundary marked between points B and C. Point C would be the maximum range with maximum fuel, i.e., the maximum fuel weight allowed for takeoff. However, for an airline, it would not make as much economic sense to operate in this region because it requires a significant reduction in the payload to achieve a modest increase in range; in this case, the use of another type or model of aircraft might be a better option.

Along the boundary C to D, the payload must be reduced significantly to obtain the needed range; again, this would not be an economical operating condition. Point D would, for example, correspond to a ferry flight or when a technical issue precludes the carrying of passengers, where the aircraft is flown over an extended distance with maximum fuel but without any payload.

As an example, the payload-range chart for the Boeing B-787 Dreamliner is shown in the figure below. Notice that with a maximum payload of passengers and cargo, the aircraft has a range of over 5,000 nautical miles at a cruise Mach number of 0.85. To achieve greater ranges, the payload must be traded off to allow more fuel to be carried. With maximum fuel but a substantially reduced payload, the aircraft can achieve a range of over 8,000 nautical miles. However, as mentioned previously, this is likely not an economically viable operating condition for an airline. Nevertheless, some airlines may opt for ultra-long-range flights with reduced passenger load but introduce higher ticket prices, e.g., operating the entire aircraft in an all-business class configuration.

 

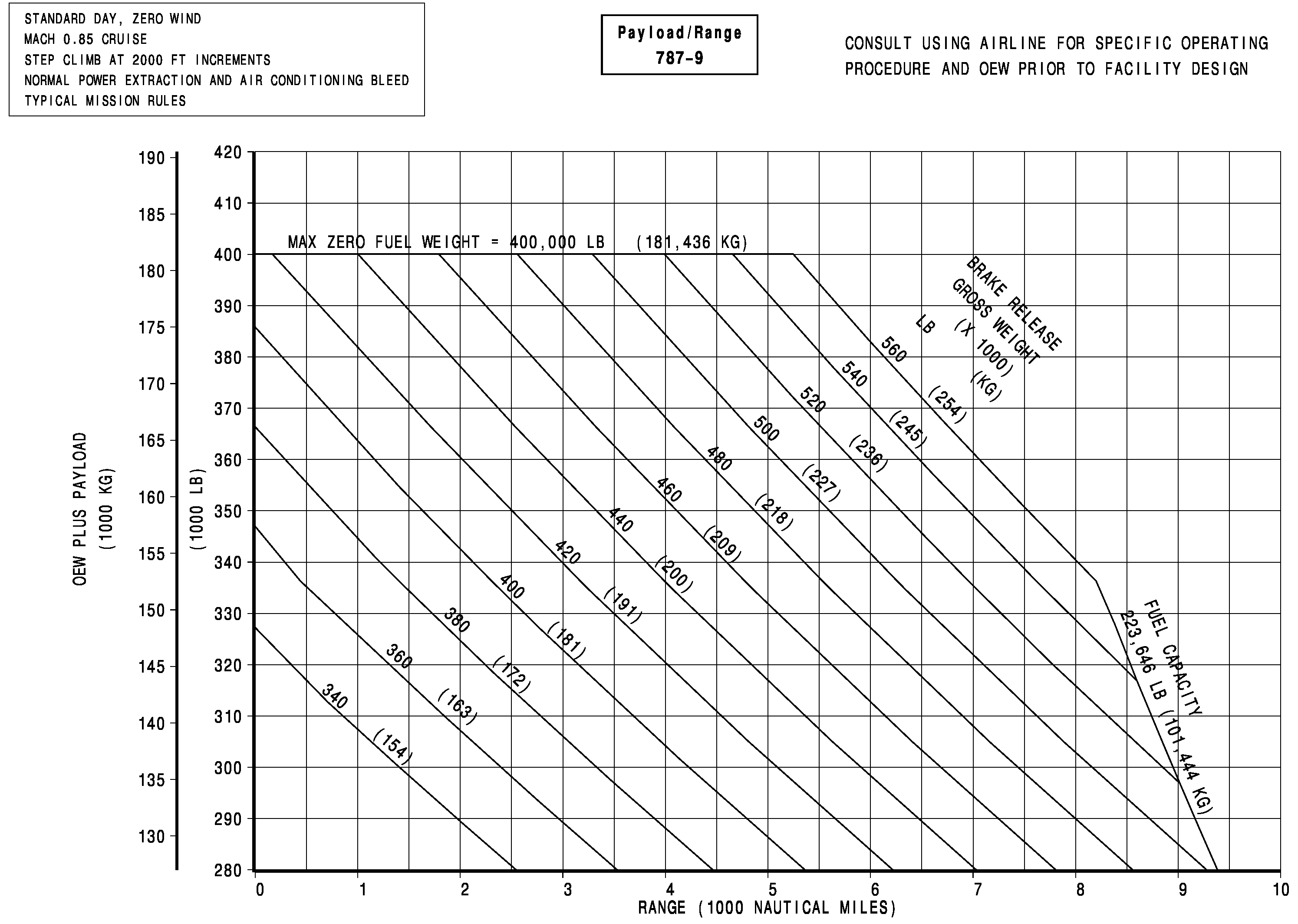
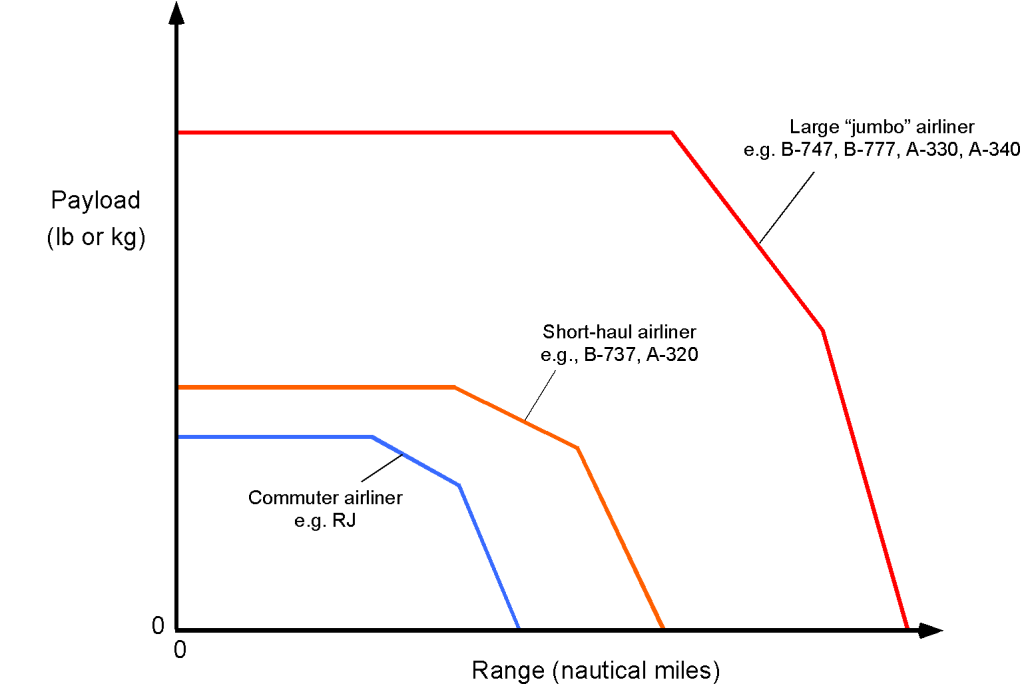
Payload-range chart for a Boeing B-787 Dreamliner. The trade between payload and range becomes necessary for flight ranges greater than 5,000 nautical miles.

Of course, the payload-range chart will vary for each aircraft make and model. The payload and range of commercial airliners are carefully tailored to match specific route requirements, ultimately maximizing profit. Even within the same airliner make, different models will have different range/payload capabilities, e.g., the B-737 family and the A320 series. More generally, however, there is not a “one-size fits all” solution, and airliners are designed for either commuter flights of less than 500 nautical miles, short-haul of between 1,000 to 2,000 miles, and long-haul for transcontinental and transoceanic distances of 4,000 to 5,000 miles, as shown in the payload-range chart below. For example, it would not make sense to operate a B-787 on short-haul segments when carrying only 100 passengers, and an RJ, with its more limited range, would require too many stops to be used for direct transcontinental flights.

Representative payload-range charts for commuter airliners, short-haul airliners like the B-737 or A-320, and long-haul “jumbo” airliners like the B-787 or A-350.

Accessing payload-range and other performance characteristics

The primary open source for airliner payload-range diagrams can be found in the “Airplane Characteristics for Airport Planning” documents. Each airframe manufacturer, including Boeing and Airbus, publishes these documents. These documents are particularly interesting to engineers because they include detailed descriptions of the aircraft, including three-view drawings, passenger, and other loading configurations. Other information included is about flight performance, takeoff and landing performance, ground operations such as taxiway and turning requirements, terminal and gate requirements such as passenger loading and servicing for fuel, etc.

Other Types of Aircraft

Of course, there are many other types of aircraft besides airliners, including general aviation (GA) aircraft, drones, etc., for which payload, range, and endurance are also important. Therefore, pilots need to know for flight planning, for example, the fuel required for a given range or the conditions of flight to maximize range. These aircraft types have relatively low payloads compared to the aircraft’s gross weight, so the payload-range trade is not as severe as for an airliner. However, the range of the aircraft is still affected by altitude and engine power settings.

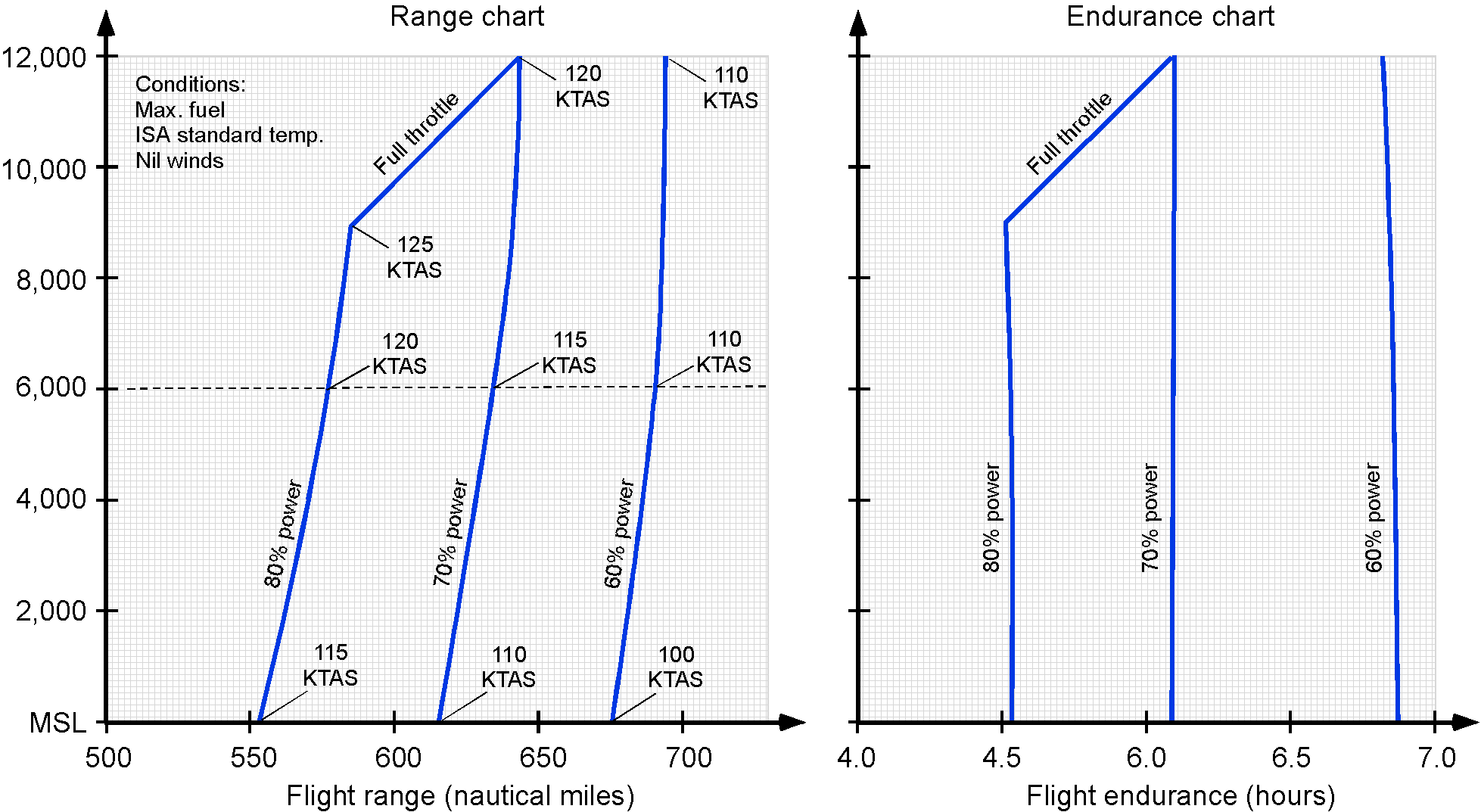
The example below shows a propeller-driven GA aircraft’s range and endurance performance charts. For an airliner, flight endurance is not particularly significant. However, a GA aircraft or drone could be used for reconnaissance, surveillance, or other applications where flight endurance is a primary mission requirement. In this regard, range and endurance charts are available for flight planning.

Representative range and endurance charts for a general aviation aircraft.

Summary & Closure

Estimating flight range (distance) and flight endurance (time) is fundamental to the design process for all aircraft types. In many (most) cases, such as for a commercial airliner, the aircraft’s primary mission is to fly as far as possible on the minimum amount of fuel and with the minimum cost. In this regard, aerodynamic efficiency (good lift-to-drag ratio) and engine efficiency (low specific fuel consumption) are critically important. The maximum flight endurance is irrelevant for an airliner. However, the flight conditions for the best range are usually at a somewhat lower airspeed relative to the top cruise speed. In practice, an aircraft usually flies at an airspeed slightly greater than that for the best range to minimize transportation time. Military missions often include an element of reconnaissance, which means that the airplane is flown in such a way as to maximize its total time in the air, i.e., at the airspeeds for best flight endurance. However, maximizing range and endurance are intrinsically based on engine and aerodynamic efficiency.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • Think of some actual airplane flight profiles or missions where maximum flight range would be essential and where maximum flight endurance would be necessary.
  • For a reconnaissance or search mission in a P3 Orion, should the airplane be flown at the airspeed that provides the best range or the airspeed that provides the best endurance? Explain carefully.
  • For what type(s) of flight profile or mission would an airplane not be flown at its best range or endurance airspeeds?
  • What kind of flight profile (mission) is typically flown by a blimp?
  • Explain why the airspeeds to fly for the best endurance or range depending on the airplane’s weight and altitude. Use any equations and/or graphs you think are needed to make the points of your arguments.
  • Do flight range and the speed to fly for the best range depend on the winds? Explain.
  • Does flight endurance depend on the winds? Explain.
  • In designing a new variant of a jet aircraft, it is desired to increase the airspeed for the best range. What steps might be needed to achieve this? Assume operations at the same flight altitude.

Other Useful Online Resources

To dive deeper into fuel burn, flight range, endurance, payload-range charts, etc., check out some of these online resources:

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2024 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n37