Introduction

Gliders and sailplanes are names often used synonymously to refer to aircraft designed to fly without an engine. However, a sailplane is typically regarded as a high-performance glider that can soar and remain aloft almost indefinitely by relying solely on atmospheric updrafts. A skillful pilot can soar for hours using rising air from thermals, uplifted air when the wind blows against hills and ridges, sea-breeze frontal boundaries, or high-altitude mountain waves. Flights of five or more hours covering hundreds of miles are relatively easy to accomplish in a modern sailplane, even one with modest performance. It is not unusual for sailplanes to soar to altitudes well over 20,000 ft (about 6,000 m), with record altitudes much higher in the stratosphere, and to cover distances of over 1,000 km (621 miles) in a single flight.

Gliders and sailplanes are designed to be lightweight and aerodynamically efficient, featuring long, high-aspect-ratio wings and sleek fuselage shapes, as illustrated in Figure 1. Some sailplanes may also use winglets, which can reduce induced drag by modifying the tip-vortex system, thereby improving the wing’s effective span efficiency. The pilot typically sits in a semi-reclined position, allowing the fuselage to have a minimum cross-section and the lowest possible drag. Early gliders and sailplanes were primarily constructed of steel tubing, wood, and fabric through the 1960s, which gave them glide ratios of about 25:1. This means that for every unit of altitude lost, they would travel horizontally 25 units. Since the 1970s, most sailplanes have been constructed using composite materials such as glass and carbon fiber. These materials offer high strength, low weight, and highly smooth, aerodynamically efficient surfaces, enabling sailplanes to achieve glide ratios exceeding 50:1. Some extreme open-class sailplanes, such as the Nimeta X, have reported glide ratios approaching 70:1.

Gliders and sailplanes offer a unique and exhilarating flying experience. The first step is to launch the engineless aircraft into flight. The most common launch method is aerotow, in which a powered aircraft tows the sailplane behind it using a towline, as shown in Figure 2. The sailplane has relatively low drag compared to many powered aircraft, but the tow still imposes an additional drag load and reduces the towplane’s climb performance. Another technique is winch launching, in which a ground-based winch rapidly reels in a steel cable attached to the sailplane, which then climbs to approximately 1,000 ft (300 m) before the cable is released. Some sailplanes are self-launching and feature a small engine or electric motor driving a propeller, allowing them to take off under their own power. In many designs, the propulsion system is then shut down and retracted or faired to reduce drag after a safe altitude is reached.

Sailplanes are primarily flown for recreation by pilots who enjoy the pure experience of flying without power, as well as the challenges of interpreting weather and understanding atmospheric dynamics. Impressive flights are possible, using only wind currents to stay aloft. Gliding has become a popular sport worldwide, with various competitions held at both national and international levels. These competitions involve flying specific distance courses, achieving the longest flight distance, or staying aloft for the longest time. Other pilots also strive to meet standardized duration, altitude, and distance requirements for FAI certificates or to set records in categories such as altitude gain, distance flown, and speed over a given course. Why not join this experienced pilot and take a flight in a high-performance sailplane to the Matterhorn?

History

Ancient myths speak of humans and gods soaring the skies on giant feathered wings, mimicking those of birds. In Greek mythology, Icarus and Daedalus attempted to escape from the labyrinth of Crete by attaching feathered wings to their arms and soaring like birds. Yet, developing a practical glider design that allowed people to fly and soar in rising air currents took many centuries. In the 18th century, the nobleman George Cayley, often referred to as the “Father of Aeronautics,” conducted extensive research on the principles of gliding flight and flew numerous model gliders to understand their stability and control characteristics. As the story goes, Cayley made his coachman hang from one of his gliders and fly it across a valley, becoming the world’s first glider pilot. After the flight, the coachman resigned, stating that he had been employed to drive, not to fly.

In the late 19th century, Otto Lilienthal, a German aviation pioneer, conducted numerous glider flights, studying aerodynamics and flight characteristics. Lilienthal controlled his gliders by kinesthetic weight shifting, i.e., by using body motion to shift his center of gravity and change the glider’s attitude, much as is done on hang gliders. They were woefully unstable contraptions with tail surfaces that fluttered severely, as evidenced by recent reenactments of his flights. Lilienthal documented his observations in a book published in 1889, “Birdflight As the Basis of Aviation: A Contribution Towards a System of Aviation,” which was to inspire and influence others who would advance the field, including Percy Pilcher in Britain and the Wright brothers in the U.S.

A budding young engineer, Percy Pilcher was a lecturer at the University of Glasgow, and his interest in aviation soon made him a pioneer aviator in his own right. After Cayley, both Lilienthal and Pilcher were the foremost experimenters with gliders at the end of the nineteenth century. Lilienthal’s infatuation with replicating the wings of birds and using weight shifting for flight control was his downfall, and he was killed in a crash in 1896. By this time, Percy Pilcher had made repeated flights with his gliders, including one flight that was recorded. By 1899, Pilcher had constructed a motor-driven triplane, but shortly before its first flight, he was also killed in a crash of one of his gliders.

The Wright brothers had experimented extensively with gliders, flying several variations between 1900 and 1902 and refining their understanding of flight before adding an engine. They initially focused on gliders because, like Lilienthal and Pilcher, they believed that mastering the fundamental principles of aerodynamics, control, and stability was essential before attempting powered flight. However, unlike Lilienthal and Pilcher’s use of bird- and bat-wing shapes, the Wrights conducted wind-tunnel tests and developed wing shapes with high span and slenderness (i.e., high aspect ratio). They also realized that weight-shifting was inadequate, so they created a three-axis control system, including wing warping for roll control, a tail or forward canard for pitch control, and a rudder for yaw control, as shown in Figure 3.

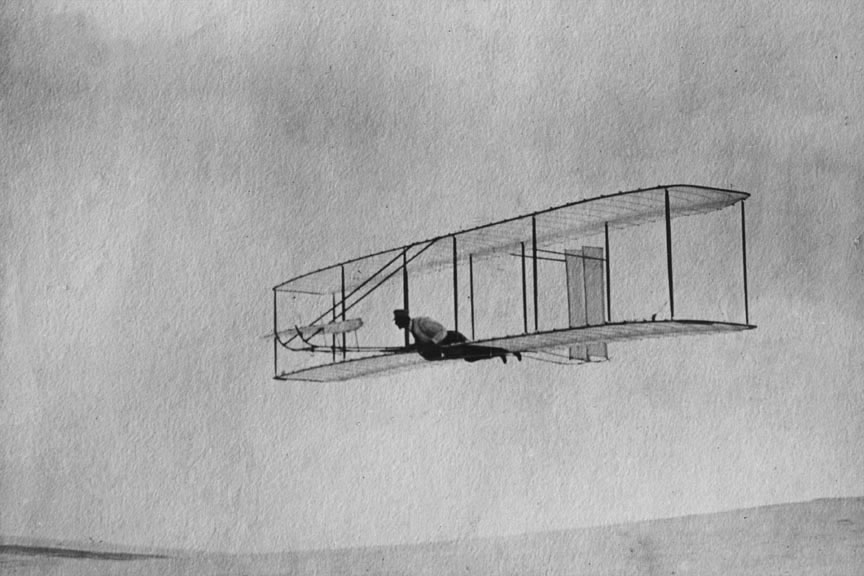
The Wright brothers soon refined their understanding of lift, drag, and the importance of balance and control. They employed three-axis aerodynamic control rather than weight shifting, allowing the aircraft to pitch, roll, and yaw in flight using movable aerodynamic surfaces. This concept was then applied to their powered aircraft, and they quickly achieved success with their “Flyer” in December 1903.

Glider development continued in the early 20th century, driven by aviation enthusiasts in Germany, Great Britain, and the United States. Following WWI, interest in glider flying surged. Countries restricted by treaty limitations on developing powered aircraft then focused on gliders. Gliding clubs were established, and advances were made in aerodynamics, wing design, and launch methods. Simple, open-cockpit designs became popular and could be launched easily from a hill using a tensioned bungee. As shown in Figure 4, the minimalist Elliott EoN open-cockpit glider of 1948 was a British copy of the German SG 38 Schulgleiter, featuring an open-truss framework and a cable-braced wing.

Gliders played a vital role in the military operations of the Allies during WWII. Large gliders were used for transporting troops and equipment, such as the British Airspeed AS.51 Horsa and the American Waco CG-4A. The Horsa was initially designed to transport 30 fully equipped paratroopers or to carry various combinations of troops and equipment, including vehicles. The Horsa glider, as shown in Figure 5, was primarily made of wood to conserve limited aluminum supplies for fighter and bomber production. In contrast, the CG-4A was constructed from welded steel tubing and wooden wings. Over 4,000 Horsas and 14,000 Wacos were built, most seeing a one-way tow over the English Channel before gliding down silently to the battlefield to unload troops and supplies. The most notable use of military gliders was during the D-Day invasion on June 6, 1944.

Since the 1950s, gliding has evolved into a popular sport and recreational activity worldwide. Gliders were also used to train ab initio pilots, including those from the British Royal Air Force (RAF), as shown in Figure 6 of a post-WWII RAF Slingsby T-31 Cadet. While not much of a soaring machine, it was simple, robust, and reliable, and stood up to considerable abuse from ham-fisted student pilots doing “circuits and bumps.” Thousands of future pilots learned to fly in such primary gliders, many of whom later transitioned to the RAF or the airlines. Others became pure gliding enthusiasts, moving on to fly increasingly high-performance sailplanes for sport and recreation.

The pilots of these early sailplanes developed soaring techniques, investigated various aspects of meteorology, including thermals and high-altitude mountain waves, contributed to aeronautical research in low-speed aerodynamics and airfoil design, set numerous altitude and speed records, and provided a sport and recreational activity for subsequent generations of soaring pilots. Wooden gliders, such as the Slingsby Skylark shown in Figure 7, and the Schleicher Ka6E, represented the pinnacle of sailplane performance by the early 1960s. They had smooth laminar-flow wings and glide ratios exceeding 30:1, enabling long cross-country flights of more than 300 km (186 nautical miles).

The transition from the (now!) vintage sailplanes (1970 and before) to modern sailplanes is often equated with the relatively rapid transition from predominantly wooden airframes to composite structures made of glass and carbon fiber. The technology for building composite sailplane airframes advanced rapidly in the 1980s, resulting in significant improvements in gliding and soaring performance. These gains came from smoother, more accurate surfaces, improved laminar-flow airfoils, higher aspect ratios, better sealing, and reduced interference drag, thereby increasing the lift-to-drag ratio by 30% or more compared with many earlier designs. In many ways, sailplane technology has led the aerospace industry in the composite manufacturing of primary airframe structures for at least two decades. Continued technological advancements have led to the development of exceedingly high-performance gliders with lift-to-drag ratios exceeding 50:1, capable of soaring over 1,000 miles in a single flight at average speeds over 100 knots; see Figure 8.

Gliding continues to captivate aviation enthusiasts today, offering a unique and environmentally friendly way to experience the thrill of flight. Gliders are used for recreation, sport, research, and training, contributing to the ongoing exploration and advancement of human flight. It offers people a distinctive perspective on the world from the skies and is another example of humankind’s enduring fascination with flight.

Anatomy of Sailplanes

A sailplane is a highly streamlined aircraft with a slender fuselage and long, high-aspect-ratio wings, as shown in Figure 9. High aerodynamic efficiency is crucial for achieving good gliding performance, so sailplanes possess aerodynamic features not found in other aircraft. The wingspan of sailplanes varies, but the wings are typically long and slender, designed to minimize induced drag and maximize gliding performance. Over the decades, increases in wingspan and aspect ratio have been commensurate with advances in technical design that have employed lightweight composite structures.

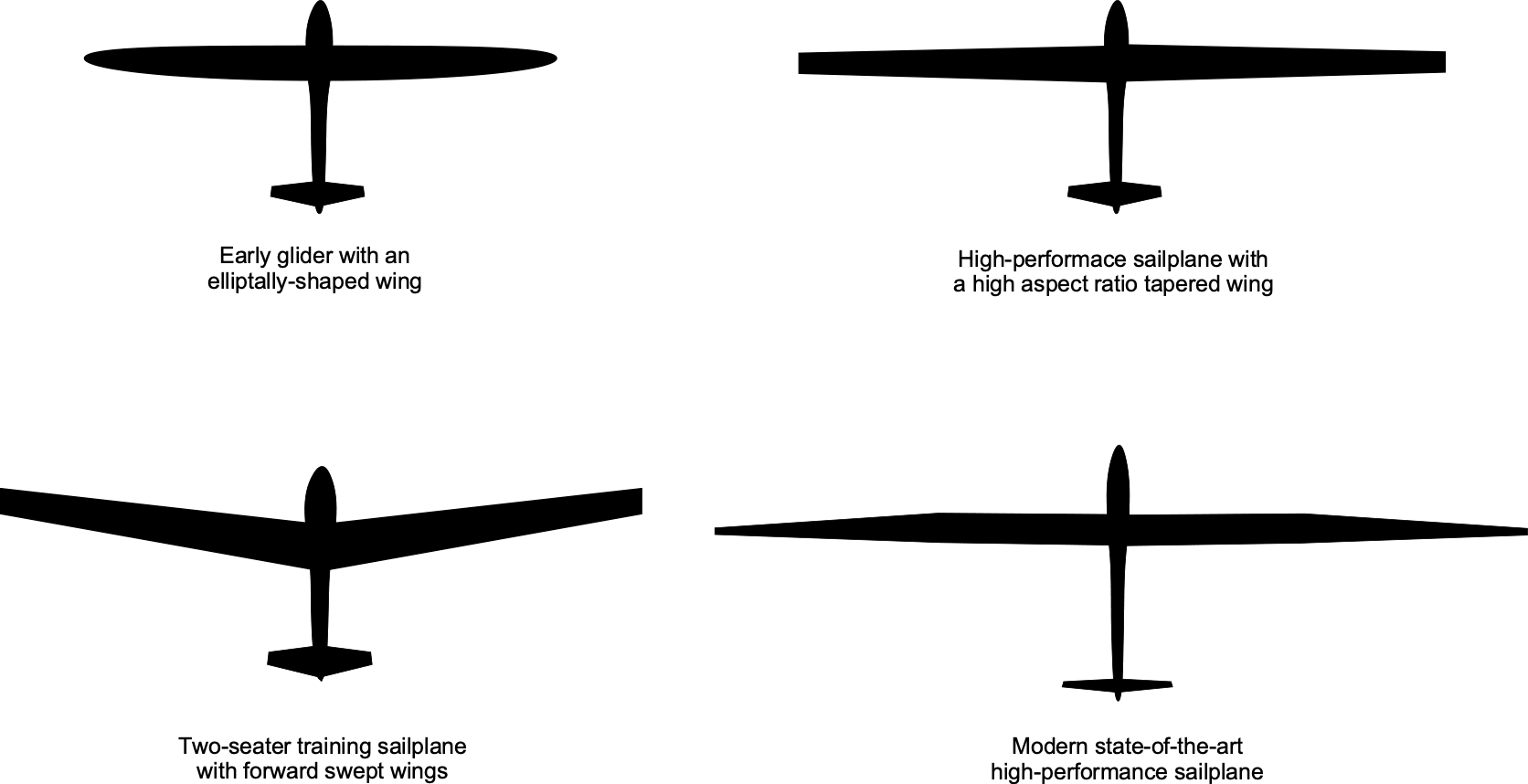
Some early gliders used elliptical wings to minimize induced drag. Still, this wing shape is time-consuming and expensive to build, and there is no significant aerodynamic advantage if the aspect ratio can be modestly larger. Many modern sailplanes feature linearly tapered wings with some washout (wing twist), resulting in very low drag and excellent aerodynamic performance. Forward-swept wings are used on some tandem two-seat sailplanes, not for aerodynamic reasons per se, but because this design feature allows the aircraft’s center of gravity to remain within limits while flying solo or in dual configuration.

As shown in Figure 10, a modern sailplane is likely to be made almost entirely of composite materials, such as glass or carbon fiber, which provide the structure with high strength and low weight. The wings utilize smooth, low-drag laminar airfoil sections, which necessitate precise geometric accuracy in their construction. The surfaces must be rendered glassy smooth through meticulous polishing. Some modern sailplanes may feature winglets at the tips of their wings to further reduce induced drag.

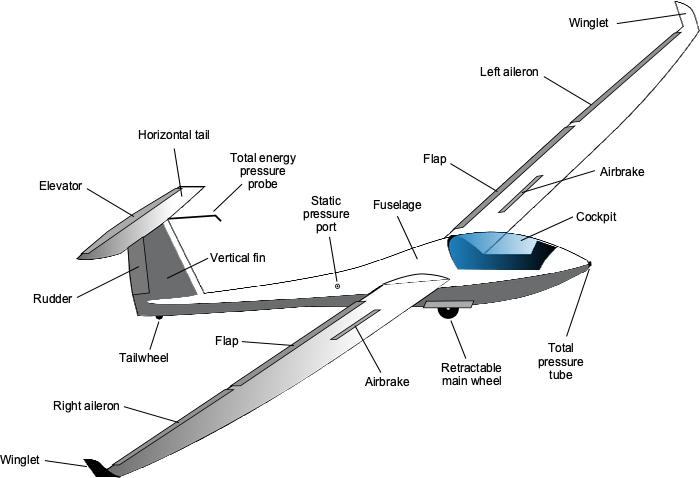
The primary control surfaces on a sailplane’s wings are the ailerons, flaps, and airbrakes. Flaps are used for takeoff and landing, but may also be set to negative angles during flight to maximize glide speed. The airbrakes are like spoilers and can be deployed progressively by the pilot to increase drag and steepen the glide angle, which is especially important for landing; otherwise, the sailplane will tend to “float” too far.

The empennage consists of the horizontal tail and vertical fin, which provide pitch and directional (yaw) stability, respectively. The elevator and rudder give the pilot pitch and yaw control. The hinge gaps of the ailerons, rudder, and elevator must be carefully sealed on sailplanes to minimize drag. Sailplanes may have fixed or retractable landing gear. A retractable landing gear can measurably reduce drag at the expense of some weight and mechanical complexity. The landing gear typically consists of a single central wheel and a tail wheel or a small, hard rubber skid.

The cockpit of a sailplane is minimalistic. It includes a seat, control column, and other flight controls, such as flaps, spoilers, airbrakes, and various instruments, as shown in Figure 11. Pilots typically sit in a semi-reclined position, which allows the fuselage to be slender and minimizes cross-sectional area, thereby reducing drag. The instrument panel will have an airspeed indicator, an altimeter, a sensitive rate of climb indicator (called a variometer), a turn and bank indicator, and a “yaw string,”^[1] and other equipment, such as radios for air-to-ground and air-to-air communications and perhaps a GPS for navigation. Many sailplanes are equipped with an oxygen system for use above 12,000 feet; sailplanes have flown at altitudes well into the stratosphere by exploiting the updrafts produced by mountain waves. Pilots will want to avoid wearing shorts and a T-shirt at these altitudes!

Sailplane Aerodynamics

Sailplanes glide by harnessing gravity; they soar by exploiting the upward-lifting aerodynamics of the atmosphere. Sailplanes are designed with smooth, streamlined shapes to minimize drag. The wings of a sailplane are typically long and slender, with a high aspect ratio, which maximizes lift and minimizes drag. Aerodynamic efficiency depends on the use of laminar-flow airfoils for the wings, reduced surface roughness, and optimized fuselage shape.

Glide Ratio

Consider first a sailplane in steady, unaccelerated, gliding flight in still air, as shown in Figure 12. The glide angle is denoted by and is taken here as a positive descent angle. With the usual pitch angle and angle of attack , this convention gives . The glide ratio measures how far a sailplane can travel horizontally compared to the vertical distance it descends. A high glide ratio means the glider can cover a longer distance for a given altitude loss. Sailplanes are designed to have high glide ratios, typically 30:1 to 50:1 or higher. This means the sailplane can travel 30 to 50 units horizontally for every unit of altitude lost.

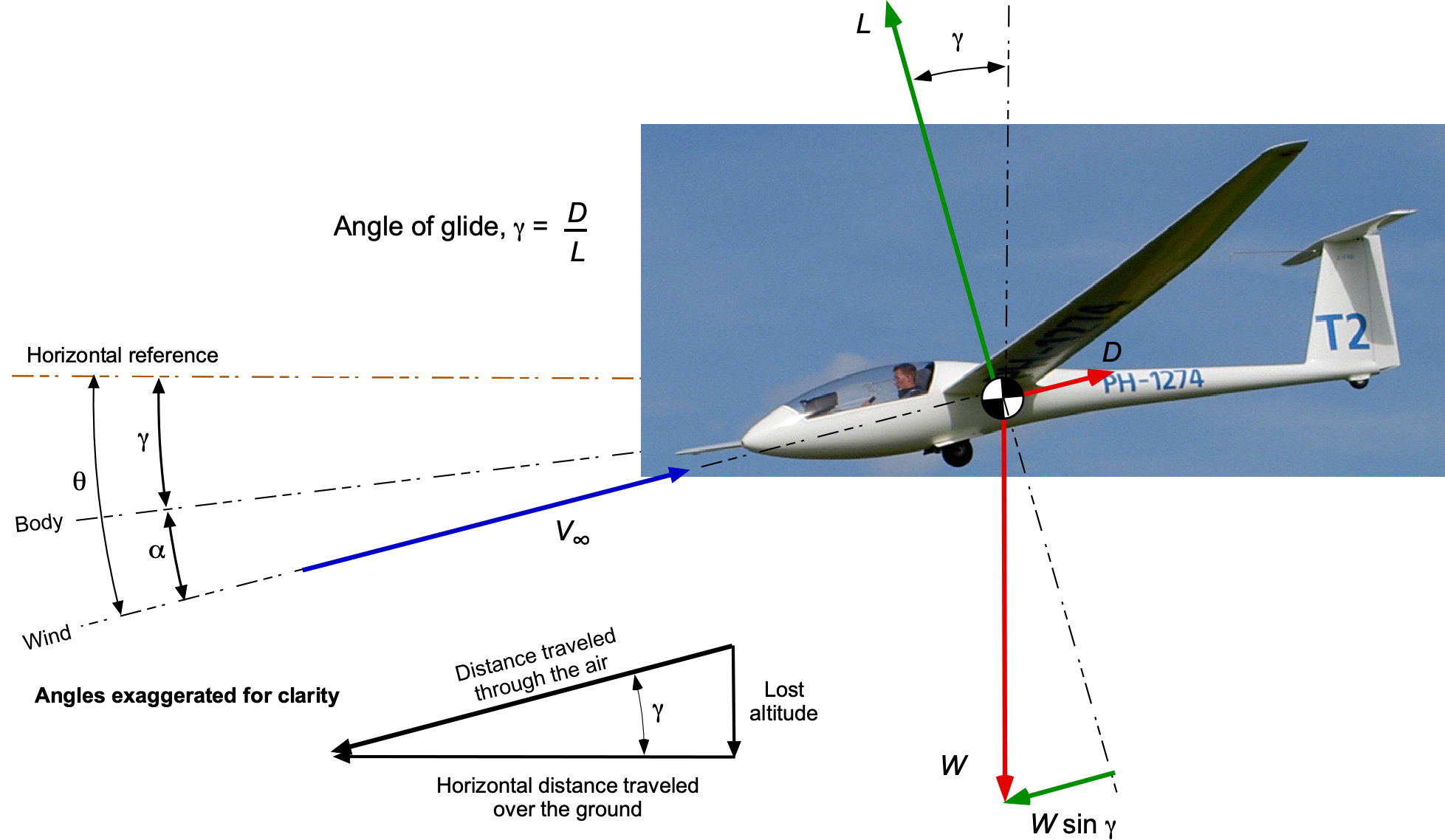
For a steady glide at a constant airspeed, the equations of motion reduce to a simple force equilibrium, i.e.,

(1)  

which shows that the weight component, i.e., the effects of gravity, balances the drag. Therefore,

(2)  

showing that the glide angle will be a function only of the sailplane’s lift-to-drag ratio and not its weight. The higher the , the shallower the glide angle and the further the glide distance from a given height. The shallowest glide angle will be obtained at the maximum value of , i.e.,

(3)  

The airspeed along the flight path can be decomposed into horizontal and vertical components, i.e., , directed downward, and , directed horizontally. Because the distance traveled is equal to velocity times the time in flight, then

(4)  

and the lost altitude is

(5)  

The sailplane’s gliding performance can thus be determined, including gliding range and flight duration.

The steady gliding range, , from a given initial altitude, , is easily calculated because

(6)  

as shown in Figure 13. Therefore, the higher the sailplane’s initial altitude and the better its ratio, the greater its gliding distance. Again, note that the gliding range does not depend on the sailplane’s weight.

Gliding Speed

Proceeding further by considering the aerodynamics in the glide gives the lift

(7)  

A legitimate assumption, which also makes the mathematics easier, is that is small so that . Therefore, solving for the airspeed gives

(8)  

where  is the wing loading. The previous result indicates that higher wing loading is associated with higher expected glide speed, which also depends on air density (i.e., density altitude). The glide angle remains a function of the , but a sailplane with a higher weight will glide under these conditions at a higher airspeed. This means it will cover the same ground distance (i.e., the gliding distance) but arrive at the destination sooner. Such an advantage is important in competitive soaring, where time and speed are essential.

Minimum Sink Condition

For soaring rather than just pure gliding, the minimum sink rate condition is significant. Recall that the airspeed along the flight path can be decomposed into horizontal and vertical components, i.e., , which is downward, and , which is horizontal, where

(9)  

The drag is given by

(10)  

and so eliminating the term gives

(11)  

Alternatively, because

(12)  

then using Eq. 8 gives

(13)  

Therefore,

(14)  

Therefore, the sink rate is proportional to the aerodynamic quantity , so the inverse ratio must be maximized to minimize the sink rate. This flight condition will increase the time to descend or maximize the time aloft in still air. It is also a useful reference condition for soaring in rising air. Interestingly, this aerodynamic operating condition is precisely what is required to maximize flight endurance in a propeller-driven airplane.

Drag Polars

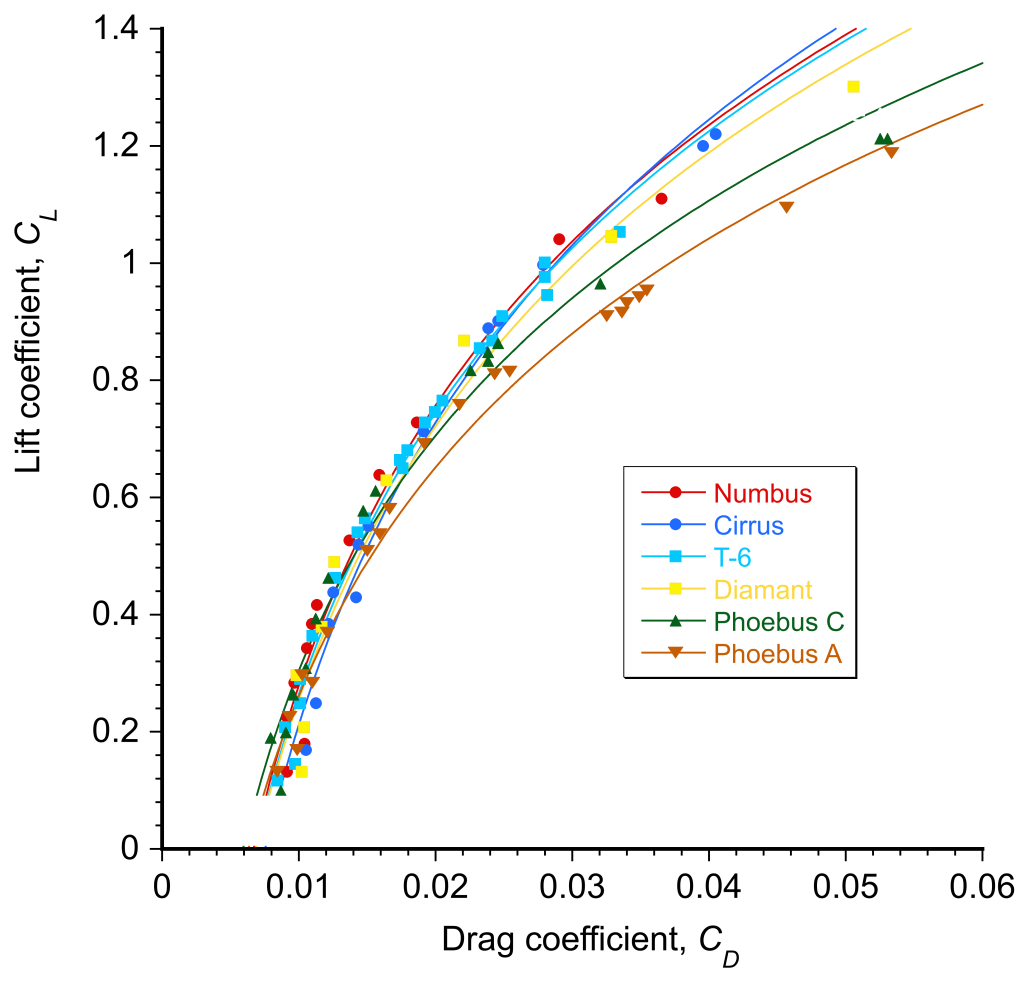
Sailplane performance aerodynamics primarily involves calculating drag on the aircraft and the variation of the drag coefficient with airspeed and lift coefficient. To this end, flight test data have established the drag polars for several sailplanes, as shown in Figure 14. The process of determining these data is lengthy, which is discussed in a technical paper by Paul Bickle.

In the simplest form, a drag polar for a sailplane can be expressed in the same manner as for an airplane, i.e.,

(15)  

where is the net average non-lifting or parasitic drag coefficient, and is the induced drag coefficient. The coefficient depends primarily on the wing and fuselage design. Theoretically, the induced drag coefficient can be expressed as

(16)  

where is the wing’s aspect ratio, and the parameter is Oswald’s efficiency factor. Therefore,

(17)  

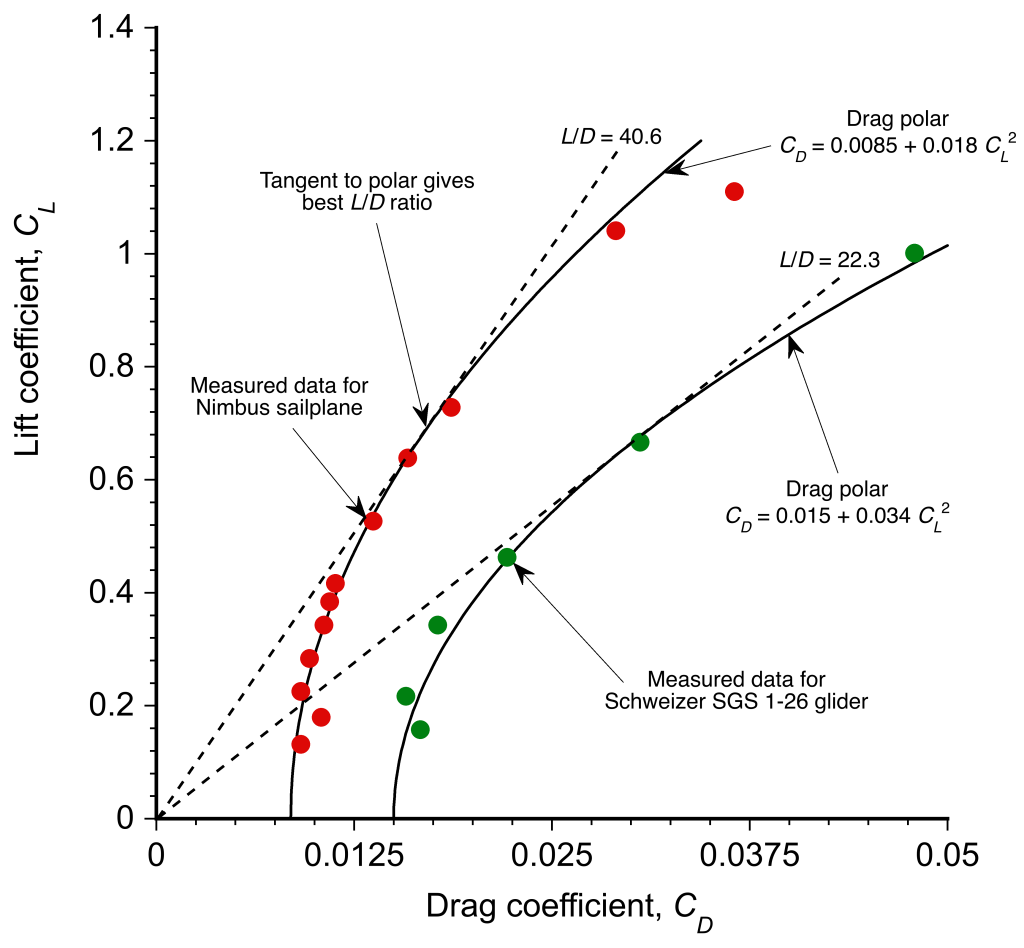
The general validity of Eq. 17 has been established for various categories and classes of airplanes, including gliders and sailplanes, as illustrated in Figure 15. While the fit is imperfect, it is generally sufficiently accurate for sailplane performance calculations in the range , i.e., below the onset of stall.

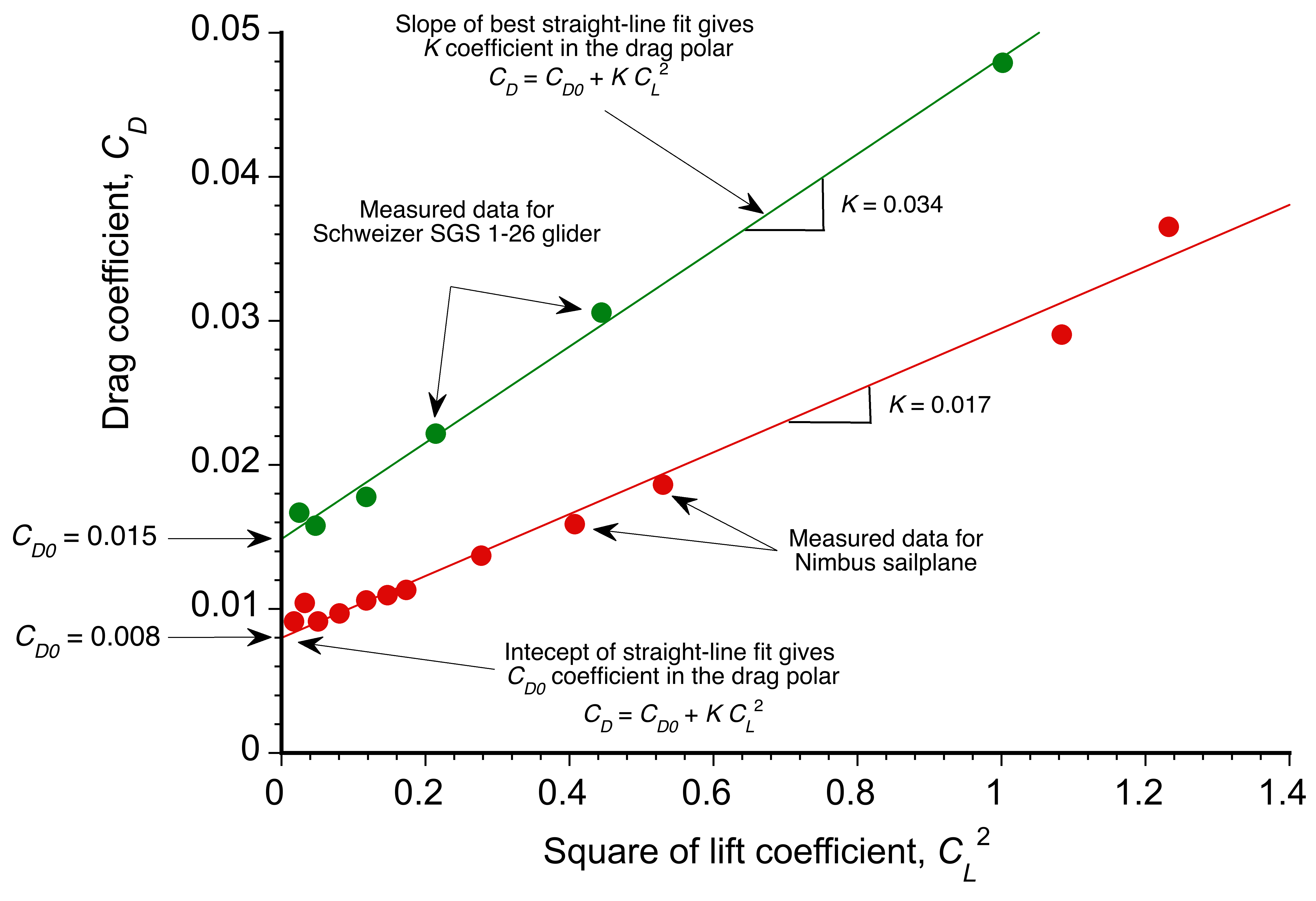
The coefficients of the polars can be obtained by plotting versus , as shown in Figure 16. A straight-line fit to the data yields as the slope and as the intercept on the drag axis.

The parameter , called Oswald’s efficiency factor, is of paramount significance for sailplanes; for conventional airplanes, it is usually less than one, and a design goal is to make it as large as possible. In aggregate, this parameter encompasses several physical effects that can be correlated with details of the wing design, flow interference, and boundary-layer separation. For a sailplane, the value of must be maximized by the careful synergistic aerodynamic design of the wing and the wing/fuselage interface, the fuselage shape, and the empennage, including component interference effects. Values of can reach up to 0.9 for some sailplanes based on flight test results, but the detailed wing design process to reach this value requires much care.

Drag Synthesis

For sailplane design, the total drag coefficient can be expressed more precisely in terms of the contributions from the wing, fuselage, and tailplane, as well as component interference effects. The latter is the most difficult to estimate and can only be approximated. The process of determining an aircraft’s total drag by summing its components is known as drag synthesis.

Wing

The wing drag dominates the performance of a sailplane, as it does on nearly all airplanes. Wing drag arises from two sources: the profile drag at the sectional level and the induced drag, i.e., drag induced by lift. The profile drag comprises skin friction and pressure drag, which can be obtained from two-dimensional airfoil data for the specific wing section. Such data are readily available for many sailplane-specific airfoil sections. A good approximation at the sectional level is

(18)  

where is the non-lifting drag coefficient and is the growth in the drag coefficient with the lift coefficient, .

A representative plot of the drag characteristics of the FX 62-K-131 airfoil is shown in Figure 17. While the fit is imperfect, it reasonably agrees with the actual aerodynamic performance at a Reynolds number of 10⁶. It should be recognized that airfoils used on sailplanes are usually of the “laminar flow” type, so the value of and the coefficient depend on Reynolds number.

Assuming these preceding values can be suitably obtained based on measurements, which are generally available from airfoil data catalogs or other publications, and that each section of the wing operates at the same lift coefficient, , which is a reasonable assumption for an ideal elliptically loaded wing with an elliptical planform, then the profile drag of the entire wing can be expressed as

(19)  

The induced drag of the wing can be expressed as

(20)  

where is the spanwise efficiency factor. For a perfect, elliptically-loaded wing, . For a well-designed sailplane wing with appropriate wing taper and twist, it is reasonable to expect to be in the range. Therefore, the total drag of the wing can be expressed as

(21)  

Fuselage

The fuselage of a sailplane is generally well streamlined but suffers from the same problems as other aircraft, including disturbances caused by cockpit windows, gap leaks at control surfaces, wing-fuselage interference, and the presence of probes and antennas. While the drag caused by any one of these sources is relatively small, the aggregate drag can be significant. The maximum cross-sectional area of the fuselage is generally minimized by having the pilot sit in a semi-reclined position.

The fuselage drag can be expressed as

(22)  

where is determined based on the maximum cross-sectional area, , and slenderness ratio of the fuselage, and is the reference area, which is usually the wing planform area on which all aerodynamic coefficients are based, i.e., . The coefficient accounts for the increased drag of the fuselage when it is operating at an angle of attack.

Empennage

The empennage comprises the horizontal and vertical tail surfaces, along with their respective control surfaces (elevator and rudder). In trimmed, symmetric flight, the vertical tail produces negligible side force because the sideslip angle is essentially zero. The horizontal tail will produce some lift, but it is small enough that its induced drag is usually small and is often neglected in first-order analyses. Therefore, it is reasonable to represent the empennage drag as a profile contribution, i.e.,

(23)  

where is the sum of the projected planform areas of the tail surfaces, and depends on the specific tail design. Values of can be obtained most reliably from wind-tunnel tests on scaled models at or near the Reynolds numbers of flight; historical data derived from flight tests are also useful. A value of is often used for sailplanes.

Total Drag

The total drag on the sailplane is the sum of the preceding area-normalized drag components, i.e.,

(24)  

Note that all individual values of the drag coefficients have now been normalized to the same reference area, allowing them to be added directly without adjustment. Substituting the values gives

(25)  

Notice that it is possible to group the preceding terms into non-lifting and lifting parts for the entire sailplane, i.e.,

(26)  

or

(27)  

where the non-lifting part is

(28)  

and the lift-dependent part is

(29)  

The total drag values obtained by this form of synthesis are typically multiplied by a factor of 1.1 to account for component flow interference effects, i.e.,

(30)  

Values of the Coefficients

Published coefficients for several sailplanes are given in the table below. These values can be used to reconstruct the drag polar for each sailplane, allowing for further analysis of its performance.

Values of published coefficients for several sailplanes, which can be used to reconstruct the drag polars.

Sailplane	Airfoil			(ft2)
Nimbus 2	FX67-K-170	0.0056	0.0031	155.0	28.6	0.12	0.030	0.0117	0.046	0.94
ASW 17	FX62-K-131	0.0047	0.0026	158.0	27.3	0.20	0.029	0.0123	0.054	0.06
ASW 12	FX62-K-131	0.0047	0.0026	140.0	25.0	0.15	0.027	0.0134	0.114	0.09
PIK 20	FX67-K-170	0.0056	0.0031	107.0	22.5	0.20	0.043	0.0149	0.060	0.39
Standard Cirrus	FX66-S-196	0.0068	0.0028	107.0	22.5	0.23	0.043	0.0149	0.038	2.23
ASW 15	FX61-5-161	0.0066	0.0028	118.0	20.5	0.21	0.039	0.0163	0.059	0.048
Standard Libelle	FX62-K-131	0.0070	0.0025	103.0	23.5	0.15	0.036	0.0142	0.068	1.06

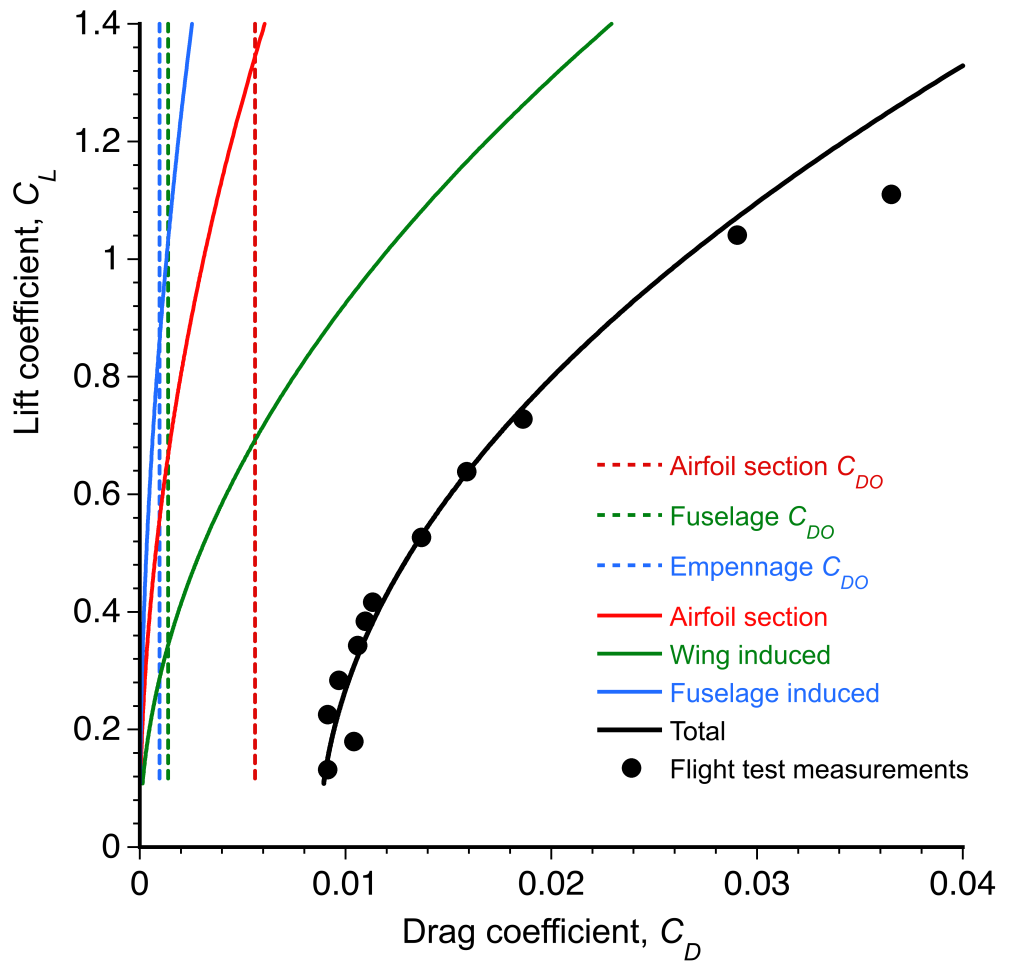
This drag breakdown analysis shows that the wing dominates gliding performance, as shown in Figure 18. The induced drag dominates at lower airspeeds and higher lift coefficients, but the profile contribution is the most important for gliding at higher airspeeds. Hence, a laminar-flow airfoil section is needed for optimal gliding performance. Fuselage drag accounts for about 15% of the total drag and is only weakly dependent on the angle of attack. The empennage drag is about 10% of the total drag, which is relatively small compared to the sailplane’s total drag.

Gliding Polars

Maximizing the of a sailplane is important, and in competitions where both gliding distance and speed are essential, the best must be obtained at relatively high airspeeds. This is where the gliding polar becomes useful, an example being shown in Figure 19.

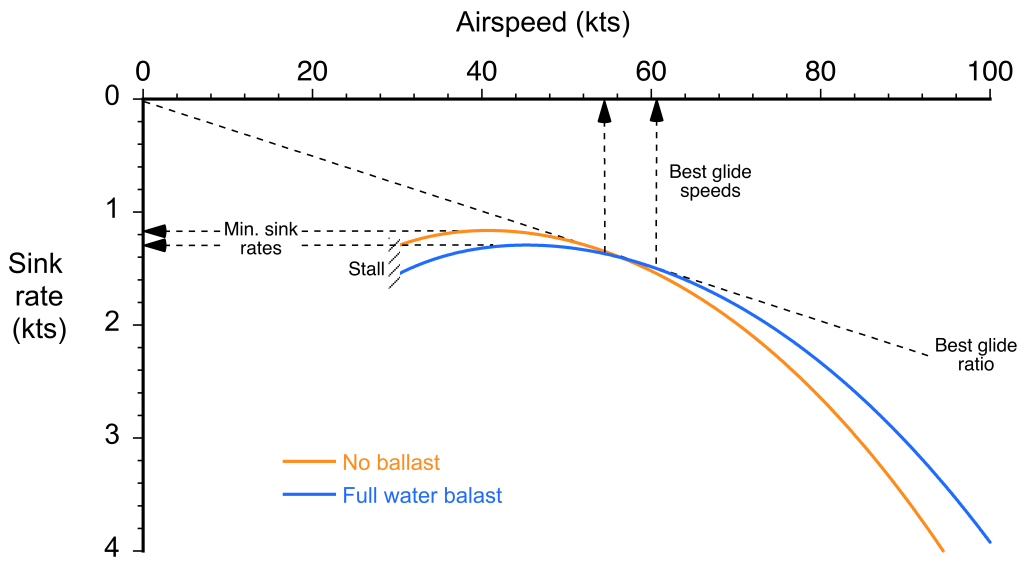
A gliding polar is similar in spirit to a hodograph because it relates velocity components, but it is used specifically as a performance plot for descending flight. It is a dimensional plot in terms of airspeed and rate of descent (sink rate). It can be constructed for any particular sailplane at a given weight and density altitude using essential characteristics such as its flight weight, wing area, and drag polar. The airspeed is the true airspeed, calculated from the indicated airspeed and corrected for density altitude and static position error. The rate of descent can be measured using the variometer.

Significance of the Polar

The gliding polar shows two important flight conditions. The first is the airspeed to fly for the minimum sink rate or rate of descent, . Flying at this airspeed will allow the sailplane to stay in the air for the maximum time, i.e., maximum flight endurance, in still air. It is also a useful reference speed when climbing in rising air, although the actual speed to fly while circling in thermals depends on the thermal structure and the circling flight condition. Notice from the polar that the minimum sink condition occurs on the low-speed side of the polar, so the sailplane must be flown precisely while maintaining an adequate margin above stall. Pilots learn to do this by “feel,” and experienced pilots will not “chase” the reading on the airspeed indicator because it lags what the sailplane is doing aerodynamically.

The airspeed for the second flight condition is the best glide ratio, . A straight line drawn from the origin of the polar at (0, 0) to any point on the polar represents the glide angle, or equivalently, the ratio , which is the inverse of the lift-to-drag ratio. The maximum lift-to-drag ratio, which occurs at a specific airspeed but is independent of weight, is obtained when this line touches the polar at a tangent. Notice from the polar that the best glide ratio is obtained at a higher airspeed when the sailplane is flown at a higher weight. Because the gliding airspeed is proportional to the square root of wing loading, i.e., the ratio of weight to wing area, all things being equal, a sailplane with a higher wing loading can glide at a higher airspeed and travel further in a given time.

In this latter regard, modern competition gliders carry jettisonable water ballast in the wings. The extra weight of water ballast is advantageous when strong thermals and soaring conditions allow sailplanes to climb in rising air. Although heavier gliders have a slight disadvantage when climbing in thermals because they have a higher sink rate, they can achieve a higher airspeed at any given glide angle. This latter characteristic is advantageous in strong updraft conditions when sailplanes spend only a small amount of time climbing in thermals. To minimize landing speeds and loads on the airframe, the pilot can jettison water ballast in flight; it is normally dumped before landing in accordance with the sailplane flight manual and operating conditions.

Dissection of the Gliding Polar

The dissection of the gliding polar exposes a deeper understanding of the underlying aerodynamics of the sailplane. As previously discussed, the airspeed along the flight path of angle can be decomposed into horizontal and vertical components, i.e., , which is downward, and , which is horizontal, i.e.,

(31)  

The small-angle assumption is easily justified for a sailplane, as the glide angles are inevitably less than 5 degrees. The rate of descent or sink speed is

(32)  

From a force equilibrium in a glide, as previously shown, the component of weight balances the drag, i.e.,

(33)  

Eliminating the term gives

(34)  

Best Glide Condition

Because the gliding polar is a dimensional plot, it depends on the sailplane’s weight, . This means that the lift and drag coefficients will have different values at different flight weights because

(35)  

Unlike a powered aircraft, which burns off fuel and so its weight constantly changes, the weight of a sailplane stays constant unless it drops water ballast. Therefore, for a given airspeed and density altitude, the lift coefficient increases linearly with the wing loading, . The corresponding drag coefficient comes from the assumed polar, i.e.,

(36)  

Therefore, the lift-to-drag ratio, , as a function of airspeed, , follows directly, as shown in Figure 20. It is clear that the maximum lift-to-drag ratio is not affected by weight; however, the airspeed at which the maximum lift-to-drag ratio occurs increases with weight, i.e., by carrying water ballast.

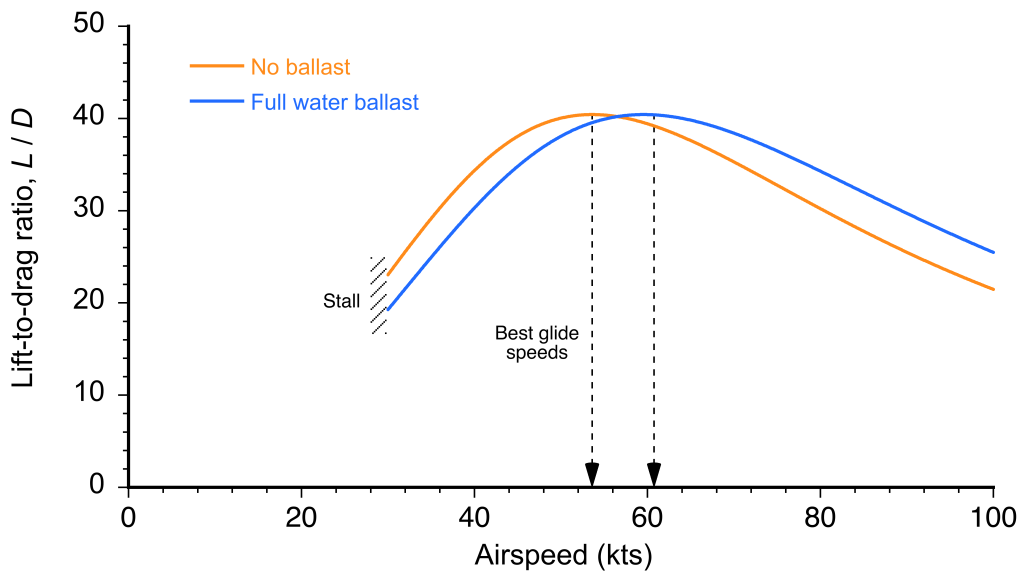
The glide angle, which is inversely proportional to the lift-to-drag ratio, is

(37)  

so the glide angle is

(38)  

This outcome shows that the higher the sailplane’s lift-to-drag ratio, the shallower the glide angle. As with the lift-to-drag ratio, the glide angle is independent of weight and depends only on the lift-to-drag ratio. Therefore, with the addition of water ballast, the same best glide angle is achieved at a higher airspeed, as shown in Figure 21.

The airspeed for the best glide, , can now be established. For best glide, the lift-to-drag ratio must be maximized, or equivalently, the ratio must be minimized. Using the drag polar

(39)  

then

(40)  

Differentiating the previous expression with respect to gives

(41)  

which must be equal to zero for the minimum value of . Therefore, the value of corresponding to the best glide condition is

(42)  

It has been shown previously that

(43)  

and substituting the value of from Eq. 42 gives

(44)  

Minimum Sink Condition

The airspeed for the minimum sink condition can also be established. It was shown previously that

(45)  

Using the drag polar as before gives

(46)  

Differentiating with respect to gives

(47)  

which equals zero for the minimum value of . Therefore, the value of corresponding to the minimum sink rate is

(48)  

Using again that

(49)  

and substituting the value of from Eq. 48 gives

(50)  

The preceding result shows that the airspeed for the minimum rate of descent (minimum sink rate) is proportional to the square root of weight and inversely proportional to the square root of air density, assuming all other factors remain constant. Remember that this flight condition will maximize the time to descend or maximize the time aloft in still air. It also provides a useful reference condition for soaring in rising air. However, when circling in a thermal, the sailplane is banked, so the wing must support an effective load greater than the aircraft’s weight; if this load is written as , then the corresponding speed scale increases approximately as . Therefore, the speed that yields the best climb while circling in a thermal will generally be higher than the straight-flight minimum-sink speed and will also depend on the thermal’s velocity distribution. As noted previously, this airspeed is on the low-speed side of the polar, so the sailplane must be flown with precision while maintaining an adequate margin above stall.

Airfoils for Sailplanes

Sailplanes use laminar flow airfoils, which are designed to maintain an extended laminar boundary layer over a substantial portion of the chord, thereby substantially reducing skin-friction drag, i.e., the value. These airfoils produce low-drag “buckets” over a limited range of lift coefficients near their intended operating conditions. A series of airfoils called the FX-airfoils has been designed specifically for sailplane applications by Franz Xaver “FX” Wortmann, with examples shown in Figure 22. The geometric shapes of these airfoils differ from those used on most airplanes and are designed to have a point of maximum thickness farther aft, often near the half-chord. This shape helps maintain a favorable pressure gradient over much of the forward chord, encouraging the boundary layer to remain laminar for longer. The downside is that such airfoils can be more sensitive to surface roughness and pressure recovery effects, and they may produce lower maximum lift coefficients than more conventional airfoils optimized for high-lift performance.

The Wortmann airfoils have a specific numbering system. The first two digits indicate the year the airfoil was designed. For example, FX 61-163 was designed in 1961 and is notable for its use on many of the first-generation glass-fiber sailplanes. Then, one or two optional letters may follow, which specify the use of the airfoil. For example, the “K” stands for “Klappenprofil” in German, which translates to “flap profile,” so these are airfoils specifically designed for applications involving flaps or ailerons. The “L” stands for “Leitwerk,” the German name for tail surfaces or the empennage, so the FX 71-L-150/30 is a symmetric airfoil. The next three digits denote the relative thickness, so “150” means this airfoil has a 15% thickness-to-chord ratio. The last digits (if present) denote the relative flap or aileron chord as a percent of the chord. For example, the FX 71-L-150/30 is designed to accommodate a flap or aileron over the latter 30% of its chord.

Examples of the drag polars for a few FX airfoils are shown in Figure 23. Notice the extensive laminar flow “bucket” where the drag coefficient is extremely low. Indeed, the laminar flow may prevail over the first 50% of the chord in such regions. However, the wings must be kept perfectly smooth by wiping and polishing, and must always be completely clean and free of bugs, etc., for laminar flow to prevail. Any surface roughness, such as bugs or raindrops, quickly destroys a laminar boundary layer. The resulting increase in skin-friction drag makes the airfoil perform comparably (or sometimes worse) to a conventional airfoil. This is why laminar flow airfoil sections are challenging to use successfully in practice, and sailplane pilots try to avoid flying through rain showers.

Hang Gliders

Hang gliders are perhaps the most primitive form of gliding, but also the purest, an example being shown in the photograph below. It is the closest humans can get to flying like a bird, with flight control achieved through weight-shifting, as used by Lilienthal and Pilcher. Hang gliders were derived from the Rogallo wing concept. Francis Rogallo worked for the NACA, and his patented concept was initially developed for spacecraft recovery systems. A delta-shaped Rogallo wing generates lift from its flexible, cambered, conical wing surfaces, but its low aspect ratio and exposed structure result in relatively high drag compared with a conventional sailplane. A hang glider derived from the Rogallo concept is typically made of several aluminum tubes forming a framework. A flexible fabric wing surface is stretched over this framework to create two partial conic surfaces for lift generation, as shown in Figure 24.

Hang gliders became popular in the 1960s and 1970s because they offered simplicity, affordability, and ease of use. Many enthusiasts experimented with hang gliders and made significant advances in understanding how they fly. During the 1970s, the sport of hang gliding experienced a substantial surge in popularity as advancements in materials and technology made such gliders more accessible, less expensive, and safer.

The introduction of aluminum alloy frames, Dacron coverings, and improved control systems contributed to the development of more efficient and stable hang gliders. Hang gliders are designed to be lightweight and portable. The portability allows pilots to quickly transport and assemble their gliders, enabling them to fly in various locations. Hang gliders are typically launched by foot from a hill or towed into the air by a winch or ground-based vehicle.

The gliding polar for a simple, early Rogallo-type hang glider can be estimated using the same principles and assumptions used for a conventional glider. Recall that the lift coefficient is

(51)  

where is the wing loading. The corresponding drag coefficient comes from the assumed polar, i.e.,

(52)  

which for a first-generation hang glider has representative values of = 0.034 and = 0.07. These values are significantly higher than those for a conventional sailplane, as expected given a hang glider’s relatively low aspect ratio and open configuration. The resulting lift-to-drag ratio of a hang glider is about 10, as shown in Figure 25, so it is quite poor compared to even the lowest-performance sailplanes. Also note that the lift-to-drag ratio is very “peaky,” as performance drops off quickly above a certain airspeed.

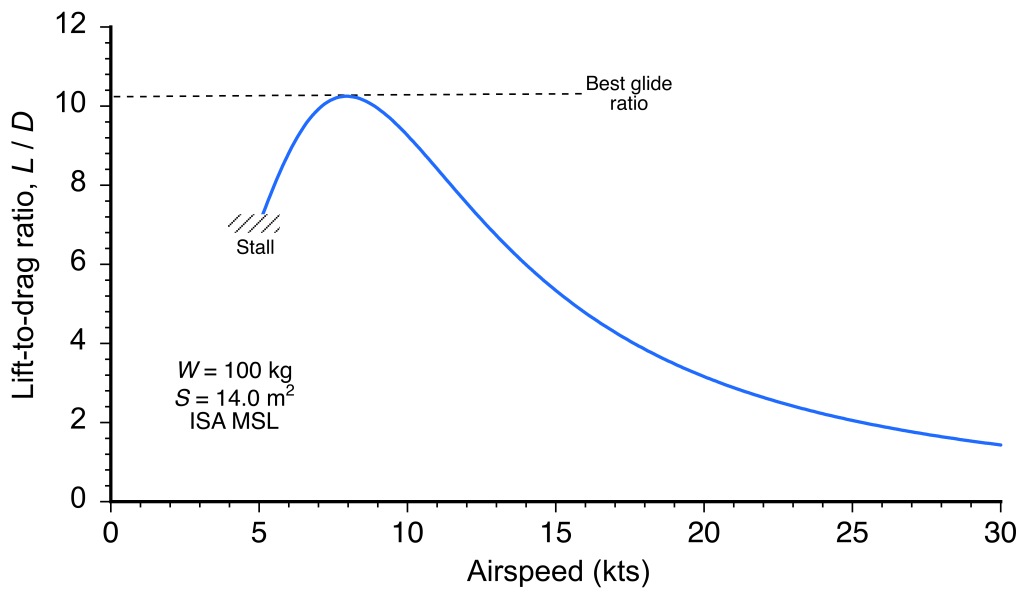
The corresponding gliding polar is shown in Figure 26. The best glide ratio is relatively poor, less than 10, but this is the price to pay for such a basic glider concept. However, hang gliders have relatively low sink rates at low airspeeds because of their lightweight construction. Lower sink rates are desirable because they enable the hang glider to remain airborne in weaker updraft conditions, such as those from thermals or ridge lift. Hang gliders generally have sink rates ranging from 150 to 400 ft/min or 0.75 to 2 m/s.

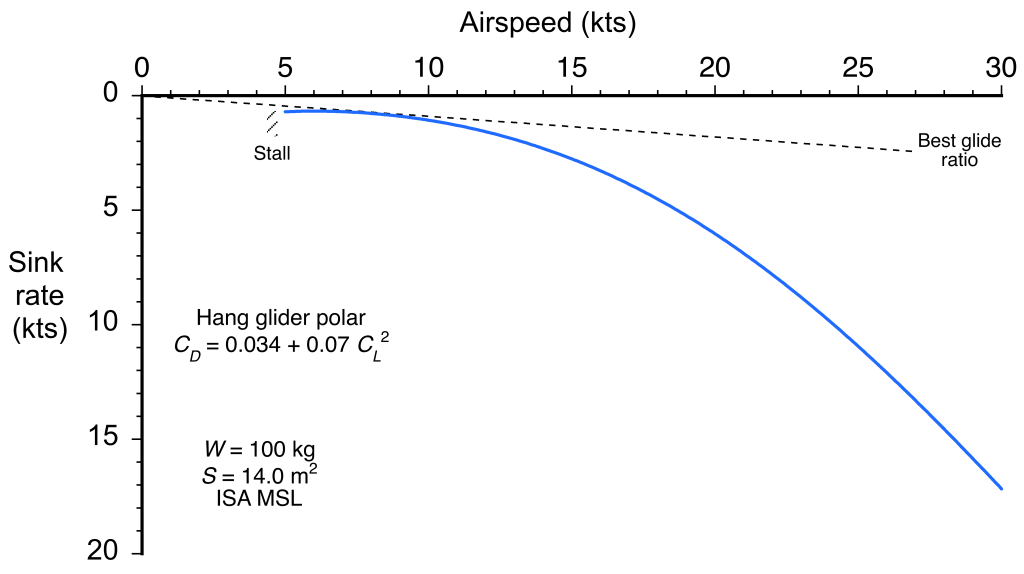
While today’s hang gliders evolved from early Rogallo-type flexible wings, modern designs use more refined, higher-aspect-ratio planforms, battens, improved sail shaping, and stiffer leading-edge structures. Rogallo’s influence on the origins of hang gliding remains significant. Hang gliders have continued to evolve with advancements in materials such as carbon fiber composites, further enhancing performance thanks to their lightweight design. Features such as reserve parachutes and improved harness systems have been introduced, enhancing pilot safety.

Atmospheric Energy Sources for Soaring Flight

Soaring is made possible by pilots flying their gliders skillfully and efficiently to exploit naturally occurring upward motions in the atmosphere. These vertical currents originate from three principal mechanisms: thermal lift, ridge lift, and wave lift. Distinct thermodynamic and aerodynamic principles govern each mechanism. Thermal lift arises from surface heating that generates buoyant plumes in an unstable atmosphere, where rising air parcels cool adiabatically but remain warmer than their surroundings. Ridge lift is created when horizontal winds are deflected upward by sloping terrain, producing a persistent updraft along the windward face of a hill or ridge; its energy source is the interaction between the kinetic energy in the wind flow and the topography rather than thermal gradients. Wave lift, in contrast, occurs in a stably stratified atmosphere when elevated terrain initiates vertically propagating oscillations known as mountain or lee waves. These standing waves store energy and can extend to stratospheric altitudes. All three mechanisms provide usable energy for unpowered flight but differ in spatial structure, duration, and the altitude ranges over which lift is available.

Thermodynamics of Thermals

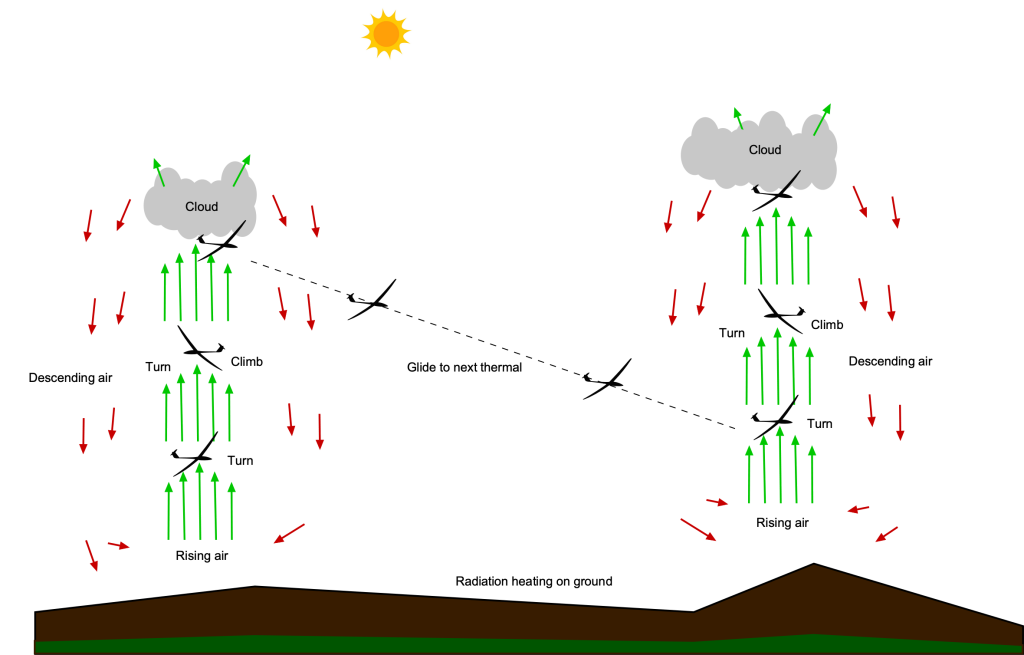
Thermals are buoyant plumes of air arising from localized surface heating and represent the most common means of sustaining soaring flight. Their dynamics are governed by dry atmospheric thermodynamics, hydrostatic balance, and the local stability of the ambient air. When solar radiation heats the ground unevenly, adjacent air warms and may become buoyant enough to rise, as shown in Figure 27. The resulting vertical motion is driven by the temperature contrast between the rising parcel and its environment. Gliders often circle within one thermal to gain altitude and so potential energy, then glide forward using that energy to reach another thermal, repeating the process as long as convective conditions persist.

Assuming a dry, compressible, ideal gas atmosphere in hydrostatic equilibrium, the vertical temperature profile is characterized by the environmental lapse rate, i.e.,

(53)  

A rising unsaturated parcel cools at the dry adiabatic lapse rate based on

(54)  

where is gravitational acceleration and the specific heat at constant pressure. The parcel’s buoyant acceleration per unit mass is approximated by the Boussinesq relation, i.e.,

(55)  

Thermal instability arises when , so that upward-displaced parcels are less dense than their surroundings and continue to rise. The vertical velocity within the thermal evolves from the integrated buoyant acceleration and entrainment losses, i.e.,

(56)  

In practice, entrainment of cooler ambient air reduces the buoyancy with height, limiting the thermal’s vertical extent.

For this simplified soaring-energy balance, written relative to the local air mass, the useful specific energy may be expressed as

(57)  

where is the airspeed relative to the surrounding air and is the altitude. For a shallow, wings-level glide, it can be assumed that . If is the glider’s still-air sink rate and is the thermal’s vertical velocity, then the climb rate relative to the ground is

(58)  

so that the useful specific-energy balance becomes

(59)  

Alternatively, because the still-air sink rate is approximately

(60)  

the balance can be written as

(61)  

where is the weight of the glider and is its lift-to-drag ratio. If is the glider’s sink rate in still air and is the thermal’s vertical velocity, then

(62)  

so that

(63)  

Alternatively, the balance can be expressed as

(64)  

so the higher the lift-to-drag ratio, the more efficiently the glider will use thermal updrafts. To maintain altitude, then . To this end, a nondimensional thermalling efficiency ratio can be defined as

(65)  

where values of indicate a net energy gain.

When a sailplane reaches the cloudbase, this usually represents the practical upper limit of the thermal for normal visual soaring flight; the updraft may continue into the cloud, but cloud flying requires appropriate authorization, equipment, and training. Typical thermals encountered in soaring conditions exhibit core velocities of the order of to ( to ), diameters of 100 to 400 m (about 300 ft to 1,200 ft), and lifespans of several minutes to tens of minutes. Glider pilots will turn tightly to remain near the strongest updraft part of the thermal to maximize the rate of climb. A skilled pilot may be able to stay aloft using thermals for many hours and cover great distances.

Aerodynamics of Ridge Lift

Ridge lift occurs when horizontal wind encounters sloping terrain and is deflected upward, producing a steady updraft along the windward face, as shown in Figure 28. The flow is redirected by the terrain rather than by thermodynamic effects. As a first approximation, if the local flow is deflected to follow a slope of angle , a wind speed produces a vertical velocity scaling as . This lift region is strongest near the slope and extends a few hundred meters outward, depending on terrain geometry and wind speed.

Unlike thermals, ridge lift does not rely on buoyancy; its energy source is the kinetic energy of the horizontal wind. The airmass remains nearly isentropic, and the glider gains altitude by extracting mechanical work from the redirected flow. The glider’s energy balance remains as

(66)  

provided that the flow is steady. In this case, the condition for level flight remains, i.e., , and the minimum required vertical velocity is

(67)  

Therefore, gliders with higher glide ratios can sustain flight in weaker ridge lift. The ridge lift is reliable and easy to exploit near continuous ridgelines when there is a strong wind component blowing toward the slope, but it is limited in vertical extent and dependent on terrain-following flight.

The strength and reliability of ridge lift depend on several factors: wind speed and direction, terrain slope and shape, and atmospheric stability. Stable stratification can help the flow remain attached to the terrain and maintain smooth, organized updrafts favorable for soaring, while unstable conditions may produce turbulence and interfere with coherent updrafts. Orographic clouds may form if the air is sufficiently humid. Ridge lift is usually strongest near the windward slope and generally decreases with height and distance from the terrain. However, its usable vertical extent depends on wind speed, terrain geometry, and atmospheric stability, and when conditions permit, it can serve as an entry point to higher-altitude lift mechanisms, such as wave systems.

Ridge soaring is especially effective in regions with continuous ridgelines and consistent crosswind components. It offers reliable, sustained lift and is often used for long cross-country flights along mountainous terrain. Compared to thermal or wave soaring, ridge lift is more localized but easier to exploit to sustain altitude at low to mid-levels.

Thermodynamics of Wave Soaring

Wave soaring is a flight technique that exploits large-scale, vertically oscillating motions in the atmosphere known as mountain waves or lee waves, as shown in Figure 29. These waves form when stable air is forced over a topographic barrier, such as a mountain ridge, and then undergoes oscillatory vertical displacements downstream that can persist for great distances. Unlike thermals, which depend on atmospheric instability and convective buoyancy, wave systems rely on atmospheric stability to store and propagate energy vertically in the form of standing waves. The crests of lee waves are often marked by smooth lenticular or lens-shaped clouds. In the shear layers, turbulence and rotating flows are produced, often referred to as “rotor.”

Assume a mean wind of speed over terrain in a stably stratified atmosphere. The linearized vertical wave equation (under the Boussinesq approximation) is

(68)  

where is the vertical velocity, is the horizontal wave number, and is the Brunt–Väisälä frequency, i.e.,

(69)  

This expression is valid for statically stable unsaturated air, for which . Here is the dry adiabatic lapse rate, is the environmental lapse rate, which is the actual rate of decrease of temperature with altitude in the atmosphere at a given time and location, and is temperature. When , vertical oscillations in the atmosphere can develop.

Wave lift can offer much smoother, more organized air than ridge or thermal lift and extends to much greater altitudes. The same energy balance applies, i.e.,

(70)  

However, the origin of is different. In ridge soaring, vertical velocity results primarily from terrain-forced deflection of the incoming wind. In wave soaring, it originates from reversible oscillations in stratified air. The energy comes from the kinetic energy of the mean wind and the potential energy associated with vertical displacements in the stably stratified atmosphere. Consequently, wave lift can be much stronger and longer-lasting, enabling gliders to achieve record-setting altitudes of over 30,000 ft.

Dynamic Soaring

Dynamic soaring is a flight technique that enables a glider to extract energy from atmospheric wind gradients, particularly vertical shear in horizontal wind velocity. Unlike traditional soaring, which relies on thermals or rising air, dynamic soaring exploits differences in wind speed with altitude to sustain or increase energy without propulsion. This mechanism is famously used by seabirds such as the albatross, which can travel vast distances over the ocean with minimal flapping by repeatedly crossing the wind shear in the atmospheric boundary layer near the sea surface. Lord Rayleigh first described dynamic soaring in 1883 in the British journal Nature.

The principle behind dynamic soaring in a glider or sailplane is that it can gain or retain kinetic energy by repeatedly crossing a wind-speed gradient and turning so that the change in wind velocity increases the useful air-relative kinetic energy. A typical ocean-boundary-layer maneuver involves climbing into a faster-moving airmass, turning within that layer, and then descending into a slower-moving layer while maintaining a high airspeed, as shown in Figure 30. Such effects can be found close to the ground or in the lee of hills and mountains. Because the wind velocity is different at each level, the glider’s airspeed relative to the surrounding air increases or decreases depending on the direction of the transition. When coordinated correctly, the glider emerges from the cycle with as much, if not more, energy as it started with, allowing it to sustain flight or even climb to a higher altitude.

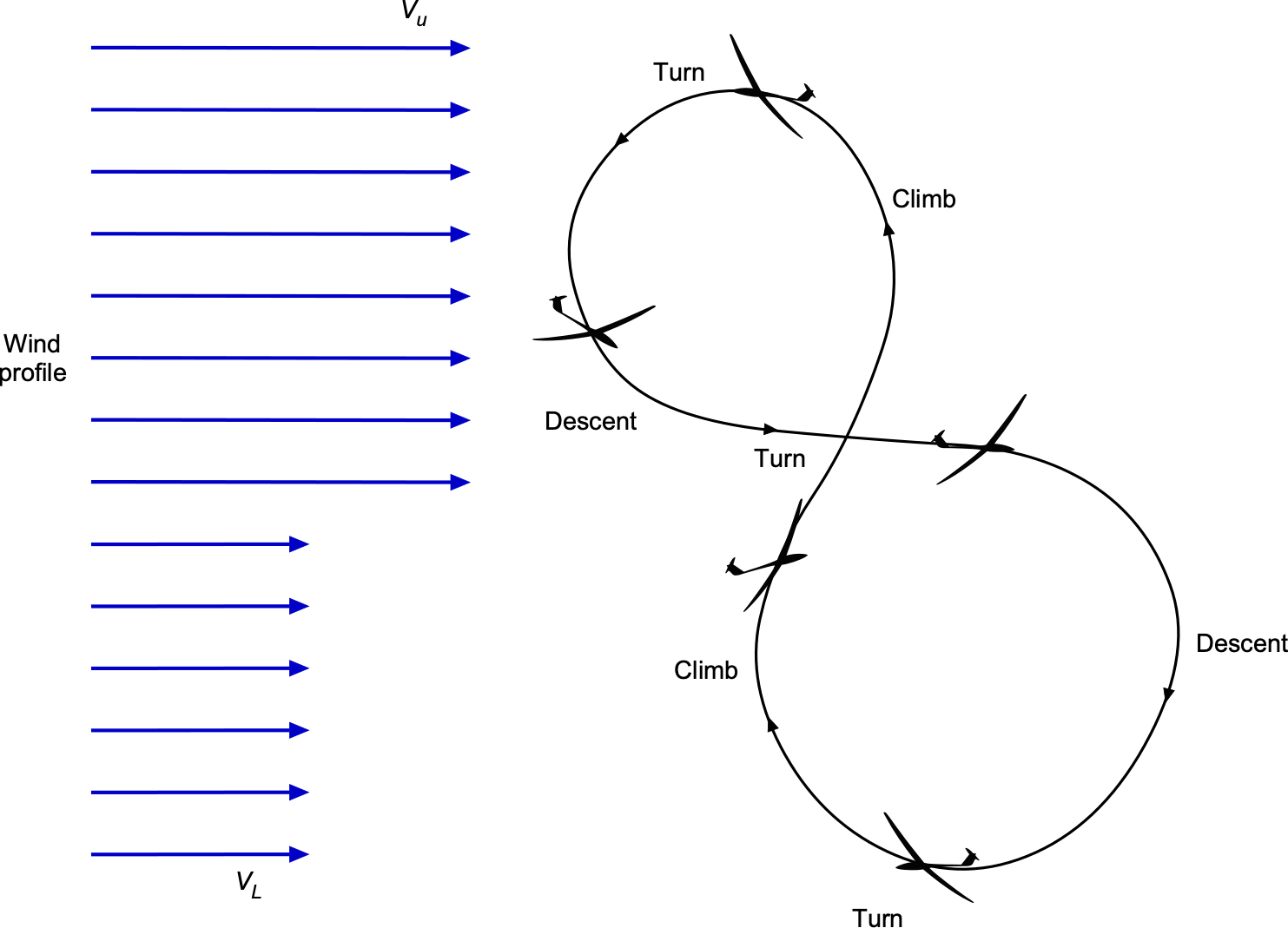
Assuming a wind field that varies only with altitude,

(71)  

or in idealized models, a step change in wind velocity between two layers. When a glider crosses a wind-shear layer, its airspeed changes according to the vector difference between its inertial velocity and the local wind velocity. Depending on the direction of crossing and turn geometry, this change can increase the glider’s airspeed relative to the local airmass. Over a complete dynamic-soaring cycle, the aerodynamic forces associated with the subsequent turns can then produce a net gain in the glider’s inertial mechanical energy if the energy extracted from the wind gradient exceeds the drag losses.

The glider’s mechanical energy is

(72)  

where is the glider’s inertial speed. The airspeed is the speed relative to the local airmass and determines the aerodynamic forces. A crossing through a wind-speed gradient changes the air-relative kinetic energy associated with the glider’s airspeed, i.e.,

(73)  

where and are the wind velocities on the two sides of the gradient. The sign and magnitude of the energy change depend on the direction of crossing and the turn geometry. If the net energy extracted from the wind gradient over a complete maneuver exceeds the aerodynamic drag losses, the maneuver is energetically favorable. Efficient dynamic soaring requires precise control of flight path, bank angle, and timing.

An efficient dynamic soaring maneuver requires careful coordination of turn angles, climb and descent rates, and bank angles to ensure the glider gains more energy from the wind-speed gradient than it loses to drag. The minimum required wind-speed gradient for sustainable soaring depends on the glider’s weight, aerodynamic characteristics, and flight-path geometry. Not all pilots will have the flying skills needed to use the principles of dynamic soaring.

Seabirds such as the albatross execute dynamic soaring maneuvers naturally, flying close to the ocean surface where wind gradients are steep because of the surface boundary layer. Observational data show that their flight paths involve cyclic transitions between layers, forming smooth arcs that match theoretical predictions for optimal energy gain. Inspired by these natural strategies, engineers are developing autonomous UAV systems that use dynamic soaring to extend range and endurance. These systems rely on real-time sensing of wind fields and adaptive trajectory planning to efficiently extract atmospheric energy without propulsion.

Total Energy Probes in Soaring

In soaring flight, the pilot is primarily interested in the vertical motion of the surrounding air mass rather than in the instantaneous climb or sink rate of the sailplane, unlike what is needed with a powered airplane. A conventional variometer is connected to a static source and responds to the rate of change of static pressure. Because static pressure decreases with altitude, the instrument can be calibrated to indicate the aircraft’s vertical velocity. However, this indication is not, by itself, a reliable measure of whether the surrounding air is rising or sinking, because changes in airspeed produced by pilot control inputs can also cause the aircraft to climb or descend temporarily through an exchange of kinetic and potential energy.

For example, if the pilot pulls back on the control stick, the sailplane decelerates and converts kinetic energy into altitude. The aircraft may momentarily climb even in still air so that a conventional variometer will indicate a climb. Conversely, if the pilot lowers the nose and accelerates, the aircraft loses altitude while gaining speed, and the variometer will indicate sink even though the air mass itself may be neither rising nor sinking. These spurious indications arise because the instrument responds only to altitude changes and cannot distinguish between a true gain or loss of energy from the atmosphere and an exchange between the sailplane’s kinetic and potential energy.

For total-energy variometer compensation, the relevant energy-like quantity is the sailplane’s potential energy plus the kinetic energy associated with its airspeed relative to the local air mass, i.e.,

(74)  

Taking the time derivative gives

(75)  

and dividing by gives

(76)  

Therefore, a variometer that could respond to would measure the rate of change of the sailplane’s total mechanical energy per unit weight rather than altitude changes alone. The first term represents vertical velocity, and the second term accounts for the gain or loss of kinetic energy associated with acceleration or deceleration.

To convert this idea into an actual instrument, the analysis must be written in terms of pressure, because a variometer is fundamentally a pressure-rate sensor. Let the ambient static pressure be . In the atmosphere, the hydrostatic relation gives

(77)  

where is the ambient air density. Therefore,

(78)  

or equivalently

(79)  

This equation shows how a conventional variometer infers vertical speed from the rate of change of static pressure.

Now consider the dynamic pressure of the airflow, which is . If the density is assumed approximately constant over the short time scale of the measurement, then differentiation gives

(80)  

Hence

(81)  

Substituting these pressure relations into the total-energy equation gives

(82)  

or

(83)  

This result is the essential pressure form of total energy compensation. It shows that the required instrument signal must be the time derivative of the combination , rather than static pressure alone. In other words, if the pressure source connected to the variometer can be made to behave like , then the variometer will respond to the rate of change of total mechanical energy.

This point is important physically. During a pull-up, the sailplane decelerates so that is negative. The dynamic pressure decreases, so is negative. At the same time, the aircraft may climb, which makes negative. A static variometer responds only to the altitude term and indicates a climb. But if the signal contains the compensating contribution, then the decrease in dynamic pressure offsets the pressure change associated with the climb. Likewise, during a pushover and acceleration, the change in static pressure associated with descent is offset by the increase in dynamic pressure. The result is that the instrument no longer responds strongly to changes in speed alone.

A total energy probe is designed to produce precisely this compensated pressure. It is not a Pitot tube, and it does not simply measure total pressure. Rather, it is an aerodynamic pressure source whose local pressure varies primarily with ambient static pressure and includes a controlled suction term proportional to the dynamic pressure. In idealized form, the probe pressure may be written as

(84)  

where is a coefficient determined by the probe geometry and installation. For perfect compensation, so that . In practice, the geometry of the probe is adjusted so that the pressure developed at the sensing holes produces a value of close to unity over the range of operating speeds and flow angles of interest. This is achieved by using the local flow field around a slender tube, so that the static pressure at the holes is reduced below ambient static pressure by a quantity that scales with the dynamic pressure. The probe, therefore, acts as a pneumatically compensated static pressure source.

The variometer is then connected to this compensated pressure source and responds to

(85)  

For the ideal case with =1, then

(86)  

and the indicated vertical velocity becomes proportional to

(87)  

which is exactly the required total-energy signal.

This derivation also clarifies why the sign matters. The compensation must involve a pressure contribution proportional to , not . A Pitot tube measures stagnation pressure, which is approximately , and that is the wrong combination for total-energy compensation. A TE probe must instead provide a pressure that becomes increasingly negative as speed increases, so that acceleration creates the compensating pressure response needed to cancel the false sink or climb indication associated with altitude changes caused solely by speed variation.

The total energy probe is usually mounted on a short boom behind the vertical tail, as shown in Figure 31, so that it measures a relatively undisturbed flow and is not significantly contaminated by the wing or fuselage pressure field. Common designs use a small vertical or inclined tube with side openings arranged so that the local pressure at the holes is lower than the ambient static pressure by an amount proportional to the dynamic pressure. Although different probe geometries are used in practice, they all seek to produce the same effective relationship between the sensed pressure and the combination .

It should also be recognized that perfect compensation is difficult to achieve under all conditions. The coefficient may deviate from unity because of Reynolds-number effects, sideslip, local flow angularity, interference from the airframe, or imperfections in the probe geometry. For this reason, practical installations are often flight-tested and adjusted to achieve optimal compensation. Nevertheless, when properly installed, a TE probe greatly reduces false indications caused by control-induced speed changes and allows the variometer to respond primarily to gains or losses of energy supplied by the atmosphere.

So You Want to be A Glider Pilot?

Becoming a glider pilot can be a thrilling and rewarding experience, and the best way to learn how to fly; see Figure 32. If you can learn to fly a glider or a sailplane, then learning to fly another aircraft is easier. Engineers make good pilots because they have a technical understanding of the principles and techniques involved. Glider clubs often provide affordable training opportunities and will have experienced instructors who can offer ground school courses on aerodynamics, meteorology, navigation, regulations, and flight planning. Good points of contact are the Soaring Society of America and the British Gliding Association.

The flight training will progress through different stages, starting with basic maneuvers like turns and advancing to more complex skills such as steep turns used in thermalling, as well as stalls and spins. As you gain experience and proficiency, your instructor will determine when you’re ready for your first solo flight. After completing several solo flights and meeting other essential requirements, you’ll undergo a check flight with a flight examiner other than your instructor. The check-flight typically includes oral questions and a comprehensive flight evaluation to assess your knowledge and skills. Subsequent learning and improvement in flying sailplanes is a continuous process, gaining experience by flying in different locations or with other, higher-performance sailplanes.

Summary & Closure

Gliders and sailplanes represent the epitome of human ingenuity in achieving unpowered flight. These remarkable aircraft rely solely on the forces of nature and skillful piloting to soar through the skies. By harnessing rising air currents and exploiting aerodynamic principles, gliders and sailplanes offer a unique and exhilarating flying experience. Gliding and soaring offer an environmentally friendly way to experience flight, aside from the initial launch.

The development of gliders and sailplanes has contributed significantly to aviation. Their growth and technological advancements have influenced other aviation sectors, including commercial and military aircraft. Research conducted on glider aerodynamics and performance has led to advancements in aircraft design, efficiency, and safety. Gliders and sailplanes are designed to have high aspect ratio wings, smooth aerodynamic surfaces, and lightweight structures, allowing them to achieve remarkable glide ratios over 50:1. Pilots participate in various competitions, ranging from local club events to international championships, where they showcase their skill and expertise in exploiting the available thermal updrafts, ridge lift, and wave phenomena to achieve impressive distances and altitudes.