27 Internal Flows

Introduction

Aerospace engineers are more often than not concerned with external fluid flows, e.g., the flow as it develops over the outside surfaces of a body, such as an airfoil, wing, or a complete flight vehicle. However, internal fluid flows are also crucial in many aerospace engineering applications. An internal flow can be defined as a flow in which its downstream development is confined or altered by all of the boundary surfaces inside which it flows. Internal flows may comprise gases (such as air) and liquids. The flow of liquids is often referred to as hydraulics, which is studied extensively and used in all branches of engineering.

Such internal flows are encountered but are not limited to flows inside engines and combustion chambers, engine intake systems, pneumatic and hydraulic systems, fuel systems, heat exchangers and cooling systems, air conditioning systems, fire suppression systems, and wind tunnels. The figure below shows one example of an internal flow through part of a jet engine. Velocity non-uniformities from the wakes behind each blade affect the engine performance and the noise it generates.

Internal flow through part of a jet engine. The blade surfaces are colored by the magnitude of the static pressure, and the flow field is vorticity.

Learning Objectives

  • Appreciate the differences between external flows and internal flows, as well as understand why the action of viscous effects gives pressure losses for internal flows.
  • Distinguish between the different effects caused by laminar and turbulent flows through pipes and ducts.
  • Calculate the frictional losses and pressure drops associated with the flows through pipes and ducts using the Colebrook-White equation and a Moody Chart.
  • Estimate the pumping power requirements to create specific mass flows and flow velocities through pipes and ducts.
  • Understand the design process of producing specific flow velocities in wind tunnels and calculating power requirements.

Internal Versus External Flows

An interesting consequence of all internal flows is that the associated surface boundary layers cannot develop freely, and the flows on each inner surface merge. In this regard, the boundary layer thickness and other properties will not be the same as if the boundary layer formed over an external surface, as illustrated in the figure below. This outcome is obtained because, for external flows, the boundaries or surfaces (often just called walls) introduce viscous effects into the flow that progressively diminish away from the wall. However, for internal flows, all parts of the walls of a duct, tube, or pipe constrain the flow development, so the entire cross-section of the internal flow is affected by the walls.

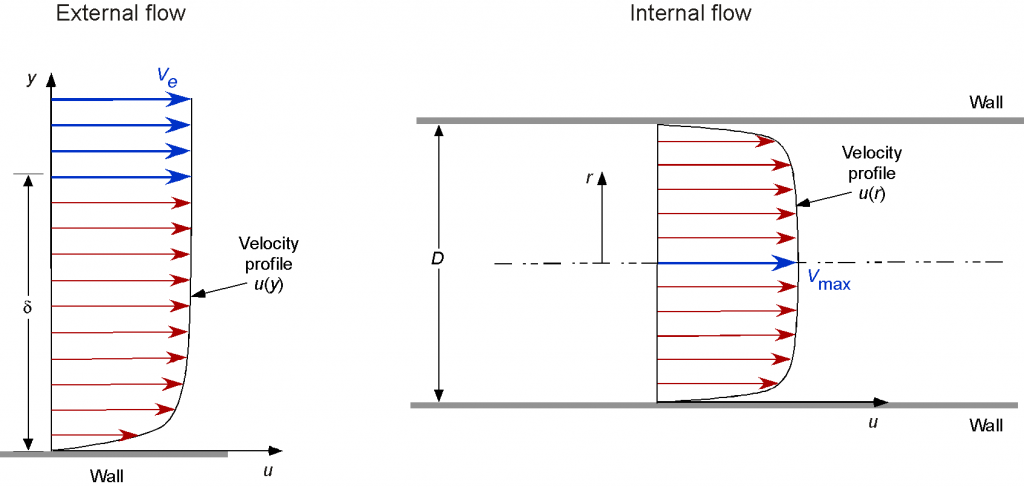
With an external flow, the effects diminish away from the wall, but with an internal flow, all the walls constrain the flow developments.

The forgoing behavior of the surface boundary layers is one reason external and internal flows must be carefully distinguished, i.e., all of the boundaries in an internal flow will affect each other. Because viscous losses (i.e., skin friction) are significant along all flow surfaces, for an internal flow, these effects manifest as significant pressure drops over the length of the interior surfaces where the fluid flows; the friction and the associated energy loss are irrecoverable and appear as heat. Evaluating these pressure drops is essential to understanding internal flows and determining the engineering requirements to move fluids along pipes and ducts.

Internal Flow Problems

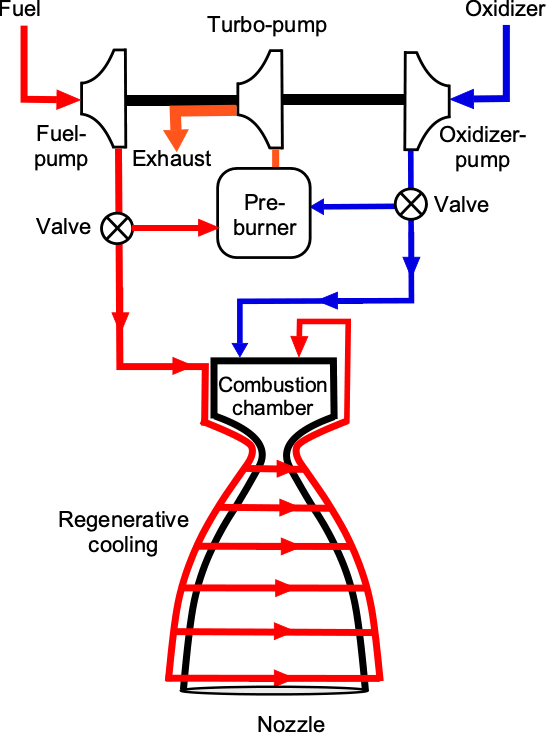
Internal fluid flow problems occur in many aerospace systems, including fuel, hydraulic, and pneumatic systems. A rocket engine, for example, as shown in the schematic below, has many internal flows that require very high mass flow rates of fuel and oxidizer. These fluids must pass through several pumps, pipes, and valves, so significant pressure losses are incurred. Fuel is also pre-circulated in channels or a jacket around the exhaust nozzle to keep it cool, over which considerable pressure drops also occur. Therefore, turbopumps are needed to deliver the fuel and oxidizer to the combustion stage of the rocket engine, which usually involves the flow of cryogenic liquids at extremely high mass flow rates.

Schematic showing the internal flow paths of fuel and oxidizer inside a rocket engine, which has to flow through pipes at high volumetric rates.

For aircraft, their hydraulic systems operate at relatively high pressures. Hence, they require high flow rates to operate the large actuators that power their landing gear, flaps, slats, flight control systems, etc. In addition, the hydraulic lines may stretch through the structure for considerable distances, so pressure drops can be significant. Aircraft usually have multiple hydraulic systems for redundancy in the event of failure, so the systems must be completely independent. Airliners, for example, typically have three parallel hydraulic systems with multiple engine-driven pumps, electrical pumps, air-driven pumps, and hydraulic pumps.

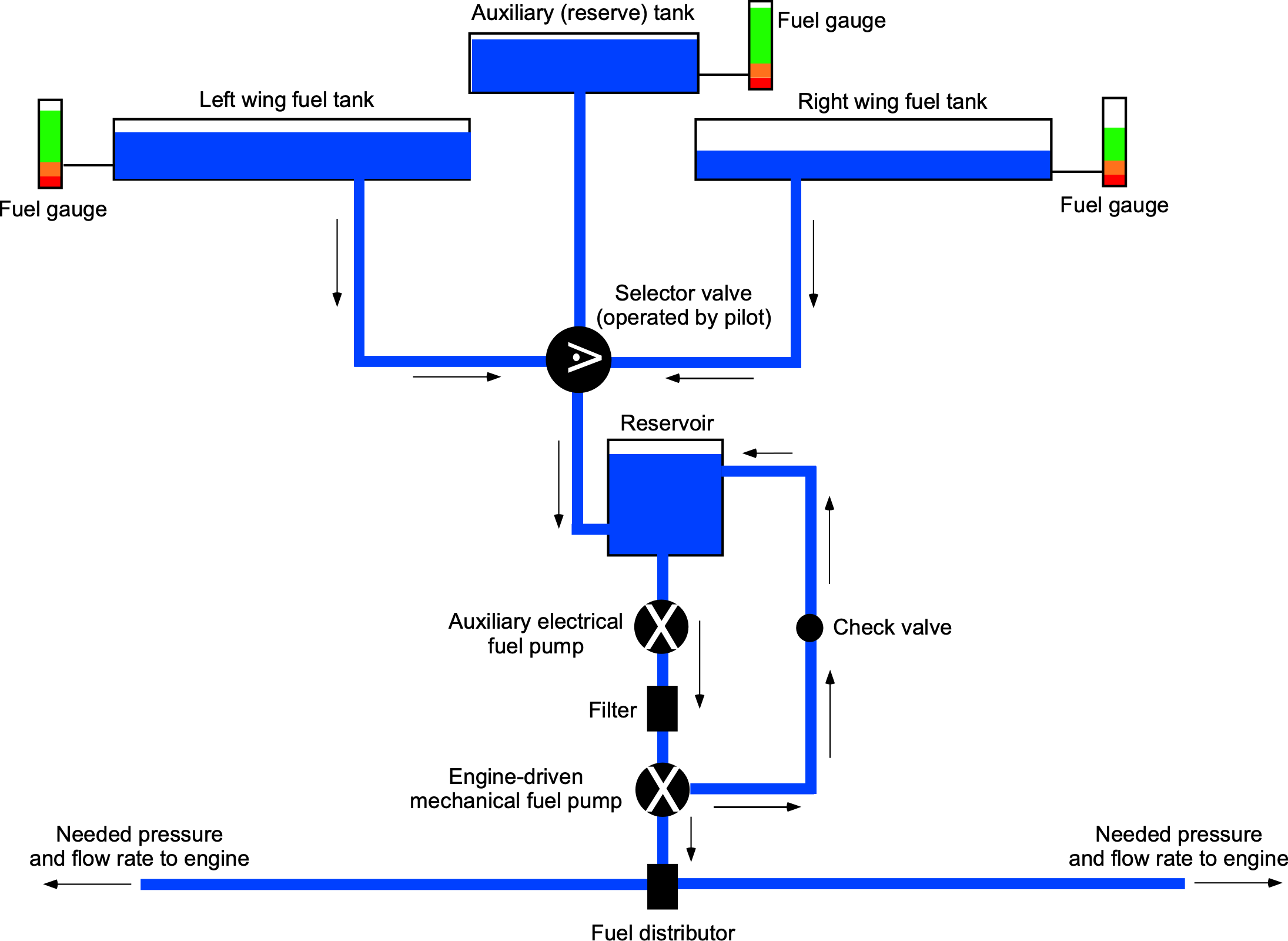
In another example of an internal flow, consider a fuel delivery system on an aircraft where fuel needs to be pumped from one or more fuel tanks (e.g., in the wings) to the engine(s), as shown in the schematic below. The distribution of the fuel lines also involves considerable lengths, often with many twists and turns through the aircraft structure. Therefore, pressure drops, pumping power, and flow rates must be carefully considered so the engines receive the required fuel volumes at the pressures necessary to support the engine’s requirements. Redundancy of the fuel delivery, in this case, is achieved with the use of a mechanical (engine-driven) pump and a completely independent backup electrical pump.

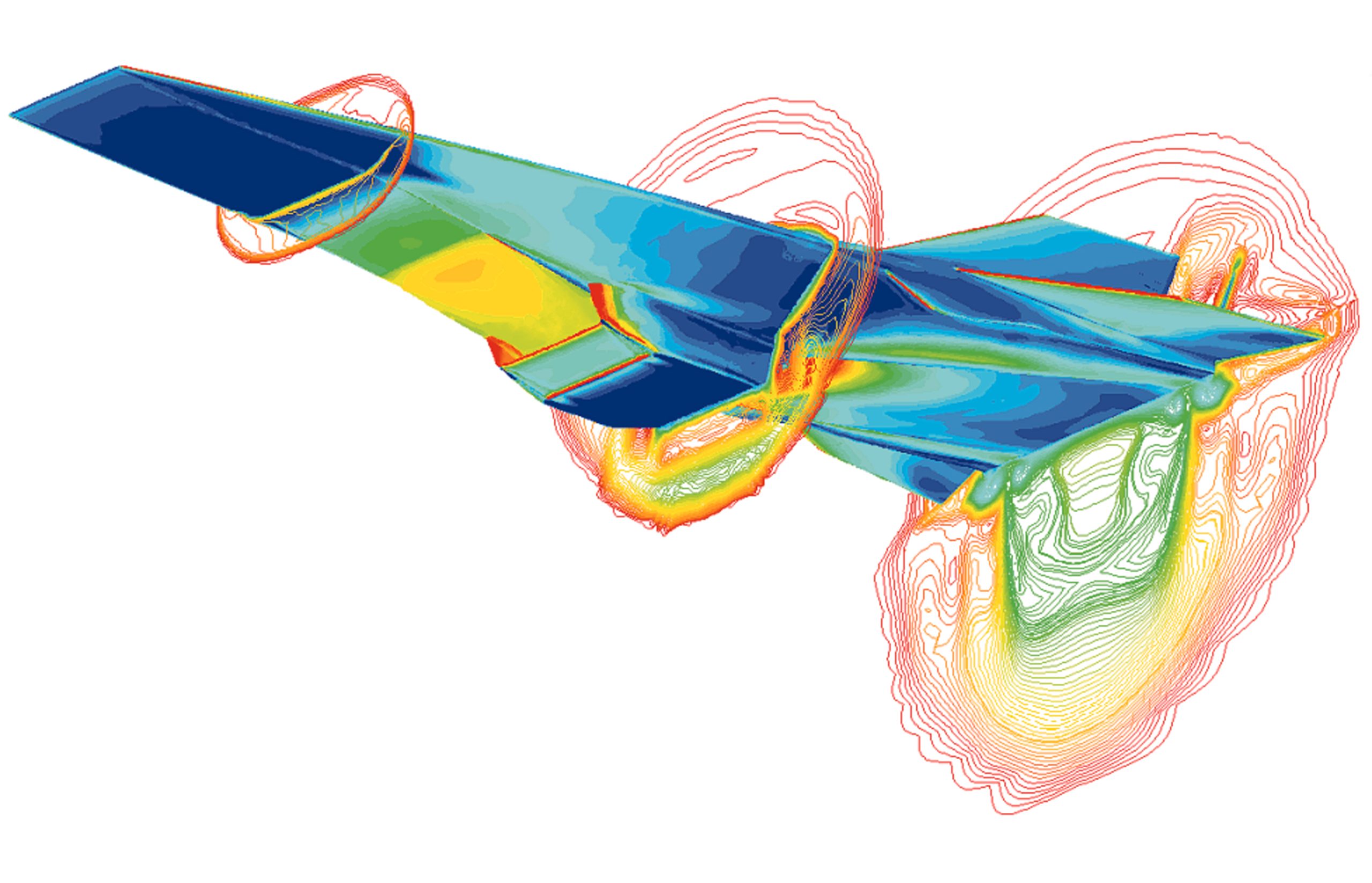
In fuel delivery, even for a relatively simple aircraft, pressure drops, pumping power, and flow rates must be considered to deliver the fuel to the engines at the required pressure.

An interesting aerospace example of a combined external/internal flow interaction problem was encountered with the design of the X-43A, a hypersonic lifting-body research vehicle, and a CFD solution for the flow shown in the figure below. At hypersonic Mach numbers, the shock waves bend back rather steeply and come close to the fuselage. Hence, the design used the lower side of the forward fuselage (an external flow) as part of the engine intake to create the necessary sequence of shock waves to slow down the air and increase the pressure before the flow entered the engine’s intake (an internal flow). Therefore, the external flow forms an upstream (boundary) condition for the internal flow through the engine to make it function.

The X-43A was developed to test a supersonic combustion ramjet (scramjet). External flow about the forebody was an integral part of preconditioning the air intake, an example of an external and internal flow interaction.

Categories of Internal Flow Problems

In general, the types of internal flow problems that often arise for aerospace engineers to solve usually fall into these categories:

1. Determining the pressure drop (or the so-called head loss) when flows move through pipes of a given length and diameter for a required volume or mass flow rate.

2. Determining the volume or mass flow rate when the pipe length and diameter are known for a specified (or allowable) pressure drop, which may be constrained for several possible reasons.

3. Finding the pumping power needed from a mechanical pump to obtain a certain exit pressure and/or flow rate for a pipe of a specific diameter over a certain length.

4. Determining the pipe diameter when the pipe length and flow or mass rate are known for a particular pressure drop. The pipe size needed will also affect its weight and cost, both being significant considerations for aerospace applications.

5. Finding heating effects associated with pumping gases through ducts and pipes, especially at higher flow speeds. Heat is generated because of frictional losses and gas compression, and heat dissipation may need to be considered in some applications.

Not all of these problems can be solved directly, even if most of the relevant information is known. Design purposes sometimes require iterative solutions starting from some initial estimates. However, some fundamental problems illustrating the process of finding pressure drops and determining pumping power through pipes can be introduced.

Fluid Dynamics of Internal Flows

Internal flows are encountered in many shapes and sizes of ducts and pipes, but the flow through a circular pipe is often used as an exemplar, as shown in the figure below. The effects of viscosity cause the fluid in adjacent layers to slow down gradually and progressively develop a velocity gradient in the pipe, i.e., an axisymmetric form of the boundary layer. To make up for this velocity reduction, the fluid’s velocity at the centerline of the pipe has to increase to balance the net mass flow rate through the pipe. Consequently, a significant velocity gradient eventually develops across the entire cross-section of the pipe. The primary manifestation of the viscous friction on the interior walls is a pressure drop along the length of the pipe, which depends on the velocity profile, the volumetric or mass flow rate, and the fluid type.

An internal flow through a pipe will develop a velocity profile, a manifestation of the viscous friction on the walls being a pressure drop along the length of the pipe.

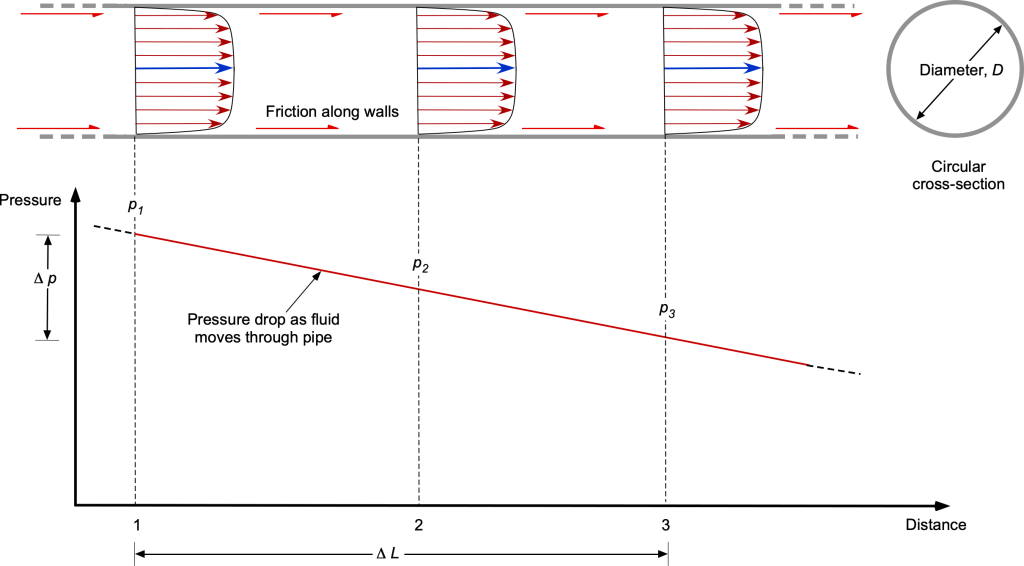
Determining the velocity profile and the corresponding mass (or volume) flow rate is one problem in analyzing internal flows. For example, the average velocity V_{\rm av} at some downstream cross-section of a pipe or duct flow can be determined from the velocity profile using the conservation of mass. The mass flow rate \overbigdot{m} is given by

(1)   \begin{equation*} \overbigdot{m} = \varrho \, V_{\rm av} \, A_c = \int_{A_c} \varrho \, u(r) \, dA_c \end{equation*}

where A_c is the pipe’s cross-sectional area, and {u} represents the velocity profile in the pipe as a function of the distance r from the centerline; notice that the profile is assumed to be axisymmetric.

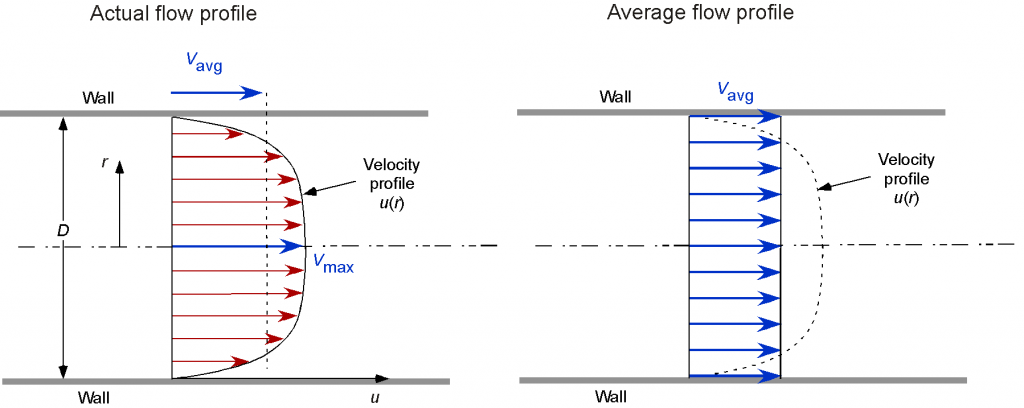
The idea of an average flow velocity in a pipe is obtained by integrating over the cross-section to find the mass (or volume) flow rate and dividing by the pipe’s area.

For the incompressible flow in a circular pipe of diameter D and radius R = D/2, then

(2)   \begin{equation*} V_{\rm av} = \frac{\displaystyle{\int_{A_c} \varrho u(r) \, dA_c}}{\varrho A_c} = \frac{\displaystyle{\int_{A_c} \varrho u(r) \, 2 \pi r dr }}{\varrho \pi R^2 } = \frac{2}{R^2} \int_0^R u(r) r dr \end{equation*}

Therefore, if the velocity profile {u(r)} is known (or the mass flow rate or volume flow rate for an incompressible fluid), then the average velocity in the pipe can be determined.

Entrance Length

At the beginning of any internal flow, there is a transition period as it organizes itself to become a fully developed internal flow. As shown in the schematic diagram below, the entrance region or length in such a flow, L_e, is the length needed to transition to a fully developed internal flow. In the entrance region, the velocity profile changes in the flow direction as it adjusts from some initial profile at the inlet to a fully developed profile where the effects of the walls are felt across the cross-sectional area of the entire pipe, duct, or channel.

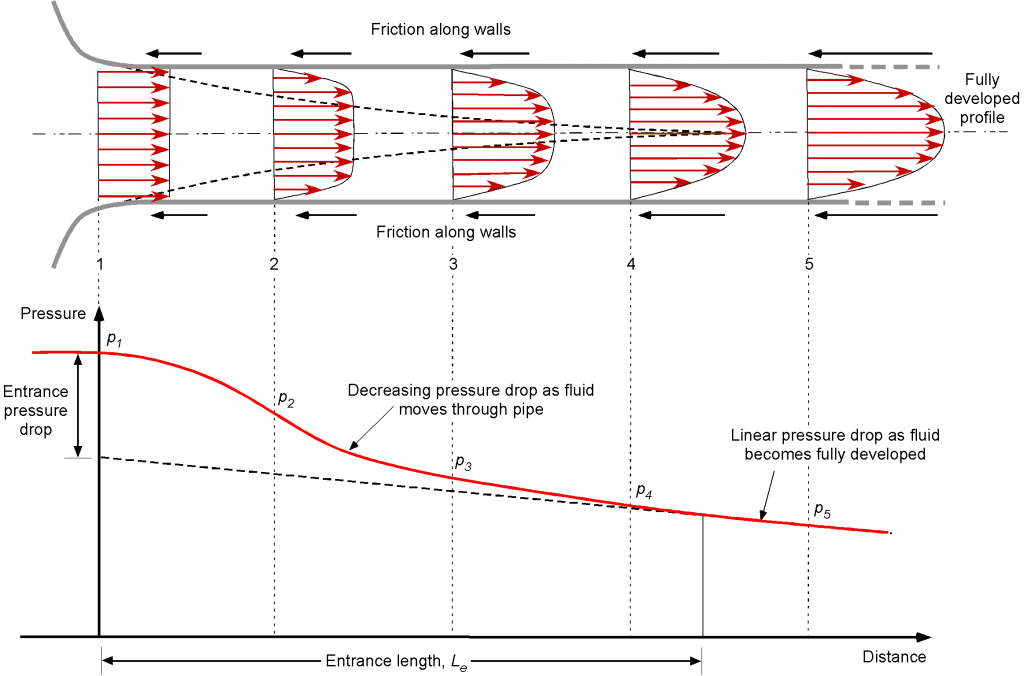
The flow into a pipe or duct takes time to establish a steady-state condition, but the viscous effects produced by the walls play an essential part in determining the final velocity profile. Notice the pressure drop or “loss” as the flow develops along the pipe.

Therefore, a fully developed internal flow is defined as one where the velocity profile does not change along the flow direction, i.e., in the axial downstream direction. When the duct has the same cross-section, sections will have the same velocity profile at successive axial locations. If the pipe changes in cross-section or turns a corner, it will take some distance for the flow to develop again fully.

As might be expected, the entrance length depends on whether the flow is laminar or turbulent and whether the internal surface is smooth or rough. For example, for the laminar flow in a smooth, straight cylindrical pipe of diameter D, the entrance length is known to be

(3)   \begin{equation*} \frac{L_e}{D} \approx 0.05 \, Re_{D} \end{equation*}

where Re_{_{D}} is the Reynolds number based on the diameter of the pipe, i.e.,

(4)   \begin{equation*} Re_{_{D}} = \frac{\varrho \, V_{\rm av} \, D}{\mu} = \frac{V_{\rm av} \, D}{\nu} \end{equation*}

For a fully developed turbulent flow, the entrance length is

(5)   \begin{equation*} \frac{L_e}{D} \approx 4.4 \, Re_{_{D}}^{~1/6} \end{equation*}

this latter result shows that the flow mixing caused by turbulence greatly speeds up the process of reaching a fully developed internal flow.

Under most practical conditions, the flow in a circular pipe is laminar for Re_{\scriptsize D} \le 2,300 and turbulent for Re_{D} > 4,000 and will be transitional intermittent in between, i.e., not entirely one state or another. In practice, the lengths of pipes used are generally many times the entrance length, so for most analyses, the assumption that the entire pipe is turbulent is usually reasonable. Of course, these preceding results will change somewhat for different geometries or if the pipe has a bend, turn, or obstruction, such as a pump, flow meter, etc.

Hydraulic Diameter

For flows through non-circular pipes (for which many types are encountered in engineering practice), the Reynolds number is redefined based on the hydraulic diameter D_h, i.e.,

(6)   \begin{equation*} D_h = \frac{4 A_c}{p} \end{equation*}

where A_c is the cross-sectional area of the pipe, and p is its wetted perimeter. The hydraulic diameter is sometimes called the hydraulic mean diameter. The basic idea is illustrated in the figure below. Naturally, the hydraulic diameter is defined to reduce to the physical diameter for circular pipes, i.e., D_h = D.

The principle of hydraulic diameter is to find an equivalent circular pipe based on the wetted perimeter of the non-circular pipe.

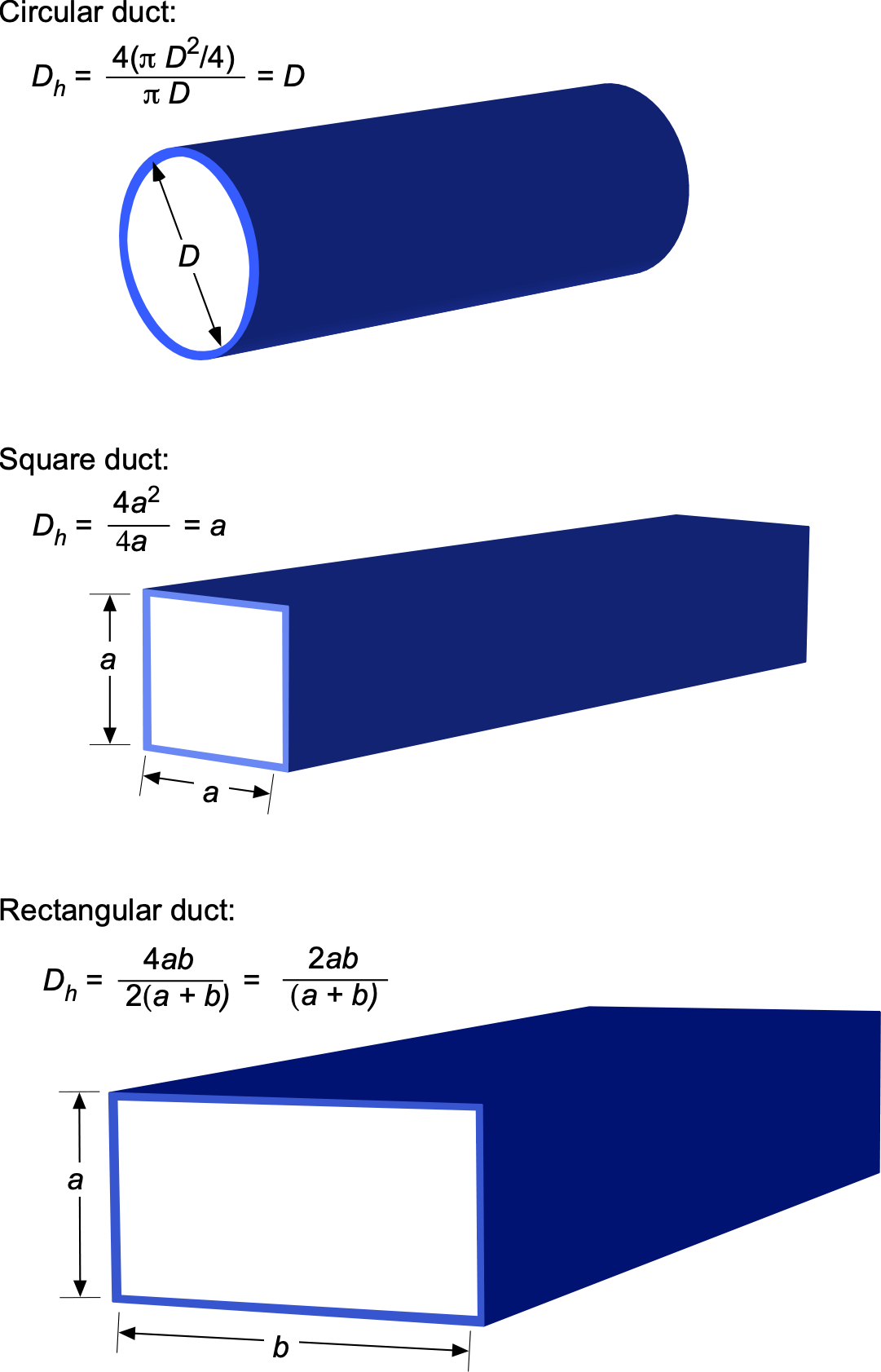
For example, for a pipe with a rectangular cross-section of width a and height b, the area of the duct is A_c = ab, and the perimeter is p = 2a + 2b. Therefore, the equivalent hydraulic diameter for this cross-section is

(7)   \begin{equation*} D_h = \frac{4 A_c}{p} = \frac{4 ab}{2(a + b)} = \frac{2ab}{a+b} \end{equation*}

Notice that in a square duct where b = a, then D_h = a.

The corresponding Reynolds number will now be calculated by using the hydraulic diameter, i.e.,

(8)   \begin{equation*} Re_{D_{h}} = \frac{\varrho \, V_{\rm av} \, D_h}{\mu} = \frac{V_{\rm av} \, D_h}{\nu} \end{equation*}

However, the concept of a hydraulic diameter works well only for fully developed turbulent flows, i.e., for Re_{_{D}} greater than about 2,000, where the effects of the details of the pipe geometry on the flow developments are less critical.

Laminar Flow in Pipes

Consider analyzing a steady laminar flow of an incompressible fluid with constant properties in the fully developed region of a smooth straight pipe of circular cross-section. The following solution, often called a Hagen-Poiseuille flow, is one of the few exact solutions for viscous internal flows. Such laminar flows are also sometimes referred to as Poiseuille or Couette flows. The approach is exceptionally instructive and is a prerequisite to understanding turbulent flows through pipes, which is a more semi-empirically based analysis.

In the fully developed laminar flow, the flow moves at a constant axial velocity. The velocity profile {u(r)} remains unchanged, i.e., self-similar. It can also be assumed that there is no flow in the radial direction, making this a one-dimensional axisymmetric flow problem. In many cases, the assumption that the flow is steady is reasonable, but that must be justified problem by problem.

Consider an area (annular disk) of the flow at a given pipe cross-section. As shown in the figure below, the forces acting on the annular disk arise from pressure and viscous (shear) forces. The area of the annular disk is 2 \pi r dr, and its perimeter is 2\pi r.

Flow model for the flow in a circular pipe that is used to develop the exact laminar solution.

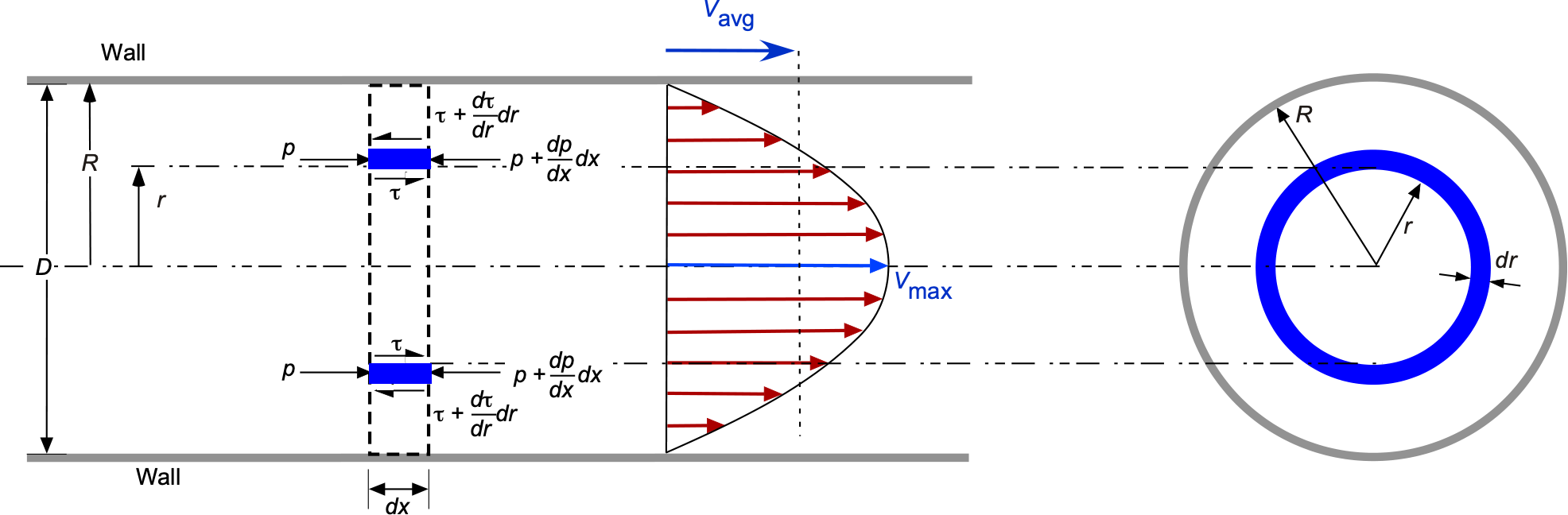
Force equilibrium of the annulus requires a balance of pressure and shear forces such that

(9)   \begin{equation*} p (2\pi r \, dr) - \left( p + \frac{dp}{dx} \right) dx (2\pi r \, dr) + \tau (2 \pi r \, dx) - \left( \tau + \frac{d\tau}{dr} \right) dr \ 2 \pi (r + dr) = 0 \end{equation*}

Expanding out the terms and canceling terms where possible gives

(10)   \begin{equation*} -\frac{dp}{dx} (2 \pi r \, dr \, dx) - \tau (2 \pi \, dr \, dx) - \frac{d\tau}{dr} (2 \pi r \, dx \, dr) - \frac{d\tau}{dr} (2 \pi \, dr^2 \, dx) = 0 \end{equation*}

Because terms involving dr^2 are negligible, then

(11)   \begin{equation*} -\frac{dp}{dx} (2 \pi r \, dr \, dx) - \frac{d\tau}{dr} (2 \pi r \, dx \, dr) = 0 \end{equation*}

which leads to

(12)   \begin{equation*} r\frac{dp}{dx} + \frac{d\tau}{dr} \, r = 0 \end{equation*}

The shear stresses will be given by Newton’s law of viscosity such that

(13)   \begin{equation*} \tau = -\mu \left( \frac{du}{dr} \right) \end{equation*}

where the minus sign reflects that the flow velocity decreases with increasing r away from the radial centerline, i.e., the gradient is negative. Therefore, the governing equation for the internal flow becomes

(14)   \begin{equation*} \frac{\mu}{r} \frac{d}{dr} \left( r \frac{du}{dr} \right) = \frac{dp}{dx} \end{equation*}

It can be seen that the left-hand side of the equation is a function of the radial coordinate r, and the right-hand side is a function of the downstream distance x.The equality in Eq. 14 must hold for any value of r and x, i.e., f (r) = g(x) can be satisfied only if both f(r) and g(x) are equal to the same constant, therefore, dp/dx = constant.

Equation 14 can be solved by rearranging and integrating it twice to give

(15)   \begin{equation*} u(r) = \frac{1}{4 \mu} \left( \frac{dp}{dx} \right) + C_1 \ln r + C_2 \end{equation*}

The velocity profile {u(r)} is obtained by applying the boundary conditions that du/dr = 0 at the centerline where r = 0, and u = 0 at r = R, the latter boundary condition being the classic no-slip condition. These boundary conditions give the result that

(16)   \begin{equation*} u(r) = -\frac{R^2}{4 \mu} \left( \frac{dp}{dx} \right) \left( 1 - \frac{r^2}{R^2} \right) \end{equation*}

which is a parabolic velocity profile. Also, the axial velocity {u} is always positive. Hence, Eq. 16 shows axial pressure gradient dp/dx must be negative, i.e., pressure in the pipe must decrease in the downstream flow direction, which arises because of viscous losses.

For the preceding velocity profile, the average velocity can be determined using

(17)   \begin{equation*} V_{\rm av} = \frac{2}{R^2} \int_0^R u(r) r dr \end{equation*}

which, on substitution, gives

(18)   \begin{equation*} V_{\rm av} = -\frac{2}{R^2} \int_0^R \frac{R^2}{4 \mu} \left( \frac{dp}{dx} \right) \left( 1 - \frac{r^2}{R^2} \right) r dr = \frac{R^2}{8 \mu} \left( \frac{dp}{dx} \right) \end{equation*}

Therefore, in terms of V_{\rm av} then

(19)   \begin{equation*} u(r) = 2 V_{\rm av} \left( 1 - \frac{r^2}{R^2} \right) \end{equation*}

also noticing that the centerline velocity V_{\rm max} = 2 V_{\rm av}, i.e., the average velocity is half the maximum centerline velocity, i.e.,

(20)   \begin{equation*} V_{\rm max} = \frac{R^2}{4 \mu} \left( \frac{dp}{dx} \right) \end{equation*}

but remember that this result applies only to this special case.

Quantifying the Pressure Drop

A quantity of interest in the analysis of internal flows is the pressure drop \Delta p, mainly because this drop is directly related to the power requirements of the pump to maintain a certain flow rate through the pipe. Recall that the pressure gradient dp/dx is constant for a steady flow through a pipe of constant area, so integrating from location 1 where the pressure is p_1 to another point at a distance L downstream where the pressure is p_2 gives

(21)   \begin{equation*} \frac{dp}{dx} = \frac{p_2 - p_1}{L} \end{equation*}

Because V_{\rm av} is given by

(22)   \begin{equation*} V_{\rm av} = \frac{R^2}{8 \mu} \left( \frac{dp}{dx} \right) \end{equation*}

then

(23)   \begin{equation*} \Delta p = p_1 - p_2 = \frac{8 \mu \, L \, V_{\rm av}}{R^2} = \frac{32 \mu \, L \, V_{\rm av}}{D^2} \end{equation*}

Of course, this pressure drop is a direct consequence of the action of viscous effects, so the pressure drop is irrecoverable.

Notice that for a given length of pipe, the pressure drop is proportional to the fluid’s viscosity and flow speed, so the faster a given fluid moves through a pipe or duct, the more significant the pressure drop will be. The pressure drop can also be reduced by using a larger diameter pipe. However, weight and cost are often substantial concerns in aerospace systems, where there will be a trade between the weight and cost of a larger pipe (to reduce the losses) versus a bigger pump (to overcome the existing losses). In practice, this pressure drop will also be different for different pipe cross-sections, surfaces (smooth or rough), etc.

The pressure loss for a laminar flow can be expressed as

(24)   \begin{equation*} \Delta p_L = \frac{1}{2} \varrho \, V_{\rm av}^2 \, f \left( \frac{L}{D} \right) \end{equation*}

where {\scriptstyle{f}} is called the friction factor. For a fully-developed laminar flow in a smooth circular pipe, the friction factor is

(25)   \begin{equation*} f = \frac{64 \mu}{\varrho \, D \, V_{\rm av}} = \frac{64}{Re_{_{D}}} \end{equation*}

which depends on the Reynolds number only. The friction factors for fully developed laminar flow in pipes of other cross-sections, such as square pipes, oval pipes, triangular pipes, etc., are published in various sources. Still, these latter shapes are rarely encountered in aerospace applications.

The head loss, h_L, is frequently used in hydraulics to represent the magnitude of the frictional pressure losses, \Delta p_L. This quantity is equivalent to the additional hydrostatic height that a fluid needs to be raised to overcome the frictional pressure losses. Therefore,

(26)   \begin{equation*} h_L = \frac{\Delta \, p_L}{\varrho\, g} = f \left( \frac{L}{D} \right) \frac{V_{\rm av}^2}{2 g} \end{equation*}

After the pressure or head loss is known, the required power P to overcome the pressure loss can be determined from

(27)   \begin{equation*} P = Q \, \Delta p_L = Q \, \varrho \, g \, h_L = \overbigdot{m} \, g \, h_L \end{equation*}

where Q is the volume flow rate, and h_L is the head loss height, i.e., the hydrostatic height corresponding to the pressure drop \Delta p.

The average velocity for the laminar flow in a horizontal pipe (i.e., no gravitational hydrostatic pressure contributions) is

(28)   \begin{equation*} V_{\rm av} = \frac{\Delta p \, R^2}{8 \mu \, L} = \frac{\Delta p \, D^2}{32 \mu \, L} \end{equation*}

so the volume flow rate for laminar flow through the pipe becomes

(29)   \begin{equation*} Q = V_{\rm av} \, A_c = \frac{\Delta p \, \pi D^4}{128 \mu \, L} \end{equation*}

which is known as Poiseuille’s law.[1]

In terms of the pressure drop, then

(30)   \begin{equation*} \Delta p_L = \dfrac{128 \mu \, L \, Q}{\pi \, D^4} \end{equation*}

This result means that for a specified flow rate, the pressure drop (and the required pumping power to overcome the losses) is proportional to the pipe’s length and the fluid’s viscosity but inversely proportional to the fourth power of the diameter. The consequence of this result is that even relatively modest pipe diameter increases can significantly reduce the pumping power. However, this approach may not always prove practical (or even possible) for other reasons, including higher weight and costs.

Historical Context – Poiseuille’s Original Equation

Poiseuille did not originally derive the equation now known as Poiseuille’s law, which is accepted as

    \[ Q = \frac{\Delta p \, \pi \, D^4}{128 \, \mu \, L} \]

Instead, based on his many meticulous experiments, Poiseuille’s equation for the flow rate in terms of pressure drop was written as

    \[ Q = \frac{K'' \, \Delta p \, D^4}{L} \]

where K'' = 1836.7 (1 + 0.033678 T + 0.00022099 T^2). Poiseuille did not mention viscosity in his work, only indicating that the value of K'' depended on temperature. At that time, the understanding of viscosity was tentative, although Navier and Stokes later (independently) rationalized this physical property. The derivation of Poiseuille’s law from the Navier-Stokes equations came later. Poiseuille’s so-called “constant,” K'', was shown to be

    \[ K'' = \frac{\pi}{128 \, \mu} \]

Measurements of the values of the dynamic viscosity \mu (for water) were later found to match Poiseuille’s results, as expressed by

    \[ \mu = \frac{\pi}{128 \, K''} \]

Check Your Understanding #1 – Using Poiseuille’s law

How many small-diameter pipes of diameter D_1 of length L does it take to discharge the same volume of liquid as a bigger pipe of the same length if the bigger pipe is twice the diameter of the smaller pipes, i.e., D_2 = 2 D_1 \,?

Show solution/hide solution.

Poiseuille’s law can also be expressed in terms of flow rate as

    \[ Q = \dfrac{\pi \, D^4 \, \Delta p_L}{128 \mu \, L} = \dfrac{\pi \, R^4 \, \Delta p_L}{8 \mu \, L} \]

Assume that the hydrostatic pressure is the same at the inlet and outlet (discharge) so that \Delta p_L = constant. For the same flow rate, then

    \[ Q = \dfrac{\pi \, D_2^4 }{128 \mu \, L} = \dfrac{N \pi \, D_1^4 \, \Delta p_L}{8 \mu \, L} \]

where N is the number of smaller pipes. Solving for N gives

    \[ N = \dfrac{D_2^4}{D_1^4} = \dfrac{2^4 D_1^4}{D_1^4} = 16 \]

Therefore, the benefits of using a larger pipe become apparent because the flow rate is proportional to D^4. See the demonstration here.

Recall that the Poiseuille equation (often called the Hagen-Poiseuille equation) is derived under specific assumptions, i.e., laminar, steady, and incompressible flow. When these assumptions are violated, such as in turbulent flow and geometric conditions like wide or short pipes, the Poiseuille equation may no longer accurately describe the flow behavior. A rule of thumb is that the ratio of length to radius of a pipe should be greater than 1/48 of the Reynolds number for the assumption of Poiseuille law to be valid.

Check Your Understanding #2 – Calculating the pressure drop for laminar flow in a pipe

The design of the fuel delivery system requires a flow through a 200 m length of smooth pipe of 15 mm diameter. The required fuel flow rate is 125 kg hr-1. The fluid properties of the fuel are given as \varrho = 800 kg m-3 and \mu = 0.00164 kg m-1 s-1. All entrance effects should be disregarded. Calculate: 1. The pressure drop along the length of the pipe. 2. The pump’s pressure requirements (in terms of head). 3. The pumping power requirements.

Show solution/hide solution.

The cross-sectional area of the pipe is

    \[ A_c = \frac{\pi D^2}{4} = \frac{\pi \times 0.015^2}{4} = 0.0001767~\mbox{ m$^2$} \]

The mass flow rate \overbigdot{m} is given as 125~kg hr^{-1} = 0.0347~kg s^{-1}, i.e.,

    \[ \overbigdot{m} = \varrho \, A_c \, V_{\rm av} = 0.0347~\mbox{ kg s$^{-1}$} \]

The average flow velocity in the pipe is

    \[ V_{\rm av} = \frac{\overbigdot{m}}{\varrho \, A_c} = \frac{0.0347}{800.0 \times 0.0001767} = 0.246~\mbox{m s$^{-1}$} \]

The Reynolds number based on pipe diameter is

    \[ Re = \frac{\varrho V_{\rm av} \, D}{\mu} = \frac{ 800.0 \times 0.246 \times 0.015}{0.00164} = 1,797 \]

Notice that this Reynolds number is the laminar regime, so the friction factor {\scriptstyle{f}} is given by

    \[ f = \frac{64}{Re} = \frac{64}{1,797} = 0.0356 \]

The pressure drop \Delta p is given by

    \[ \Delta p = \frac{1}{2} \varrho \, V_{\rm av}^2 \, f \left( \frac{L}{D} \right) \]

and inserting the given values leads to

    \[ \Delta p = \frac{1}{2} \times 800.0 \times 0.246^2 \times 0.0356 \times \frac{200}{0.015} = 11,490.0~\mbox{ Pa} = 11.46~\mbox{kPa} \]

The equivalent head loss, h, will be

    \[ h = \frac{\Delta p}{\varrho \, g} = \frac{11,490.0}{800.0 \times 9.81} = 1.46~\mbox{ m} \]

Finally, the pumping power P can be determined from

    \[ P = \frac{\overbigdot{m} \, \Delta p}{\varrho} = \frac{0.0347 \times 11,490.0}{800.0} = 0.498~\mbox{W} \]

Turbulent Flows in Pipes

Unlike laminar flows, the expressions for the losses in pipes or ducts containing a turbulent flow are based on analysis and measurements, providing empirical or semi-empirical relationships. In fact, because of the importance of many industrial applications, systematic experiments have been performed with pipe flows to measure pressure losses for different flow rates, Reynolds numbers, and surface roughness values.

Representative relative velocity profiles for fully developed laminar and turbulent flows are shown in the figure below. Remember that the fully laminar velocity profile is parabolic in laminar flow. However, the profile shape is much “fuller” in turbulent flow because of the mixing between fluid layers, with a more uniform centerline velocity and a sharper drop in flow velocity near the pipe wall. Of course, this characteristic is much like a turbulent boundary layer profile as it develops over an external surface.

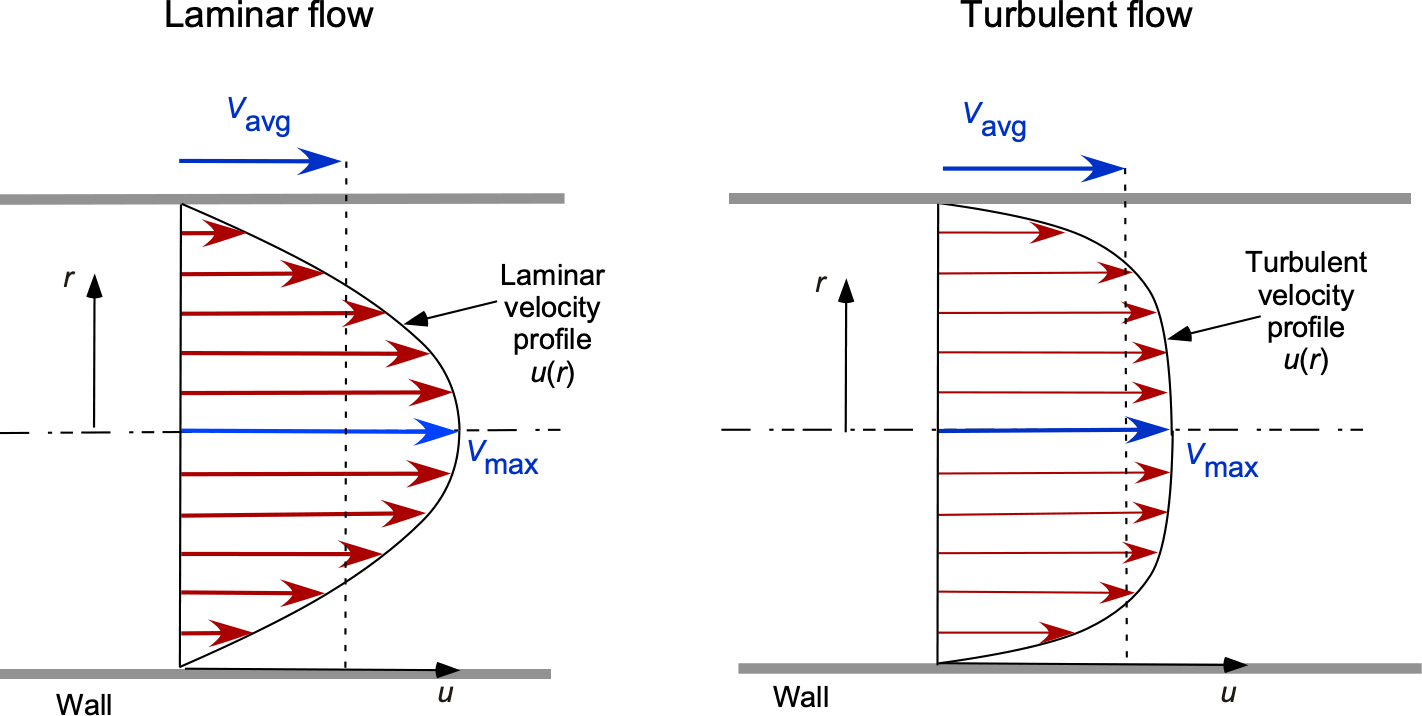
Differences in the fully established velocity profiles for fully laminar and fully- turbulent pipe flows.

Any irregularity or “roughness” on the surface of the pipe, as shown in the figure below, will disturb the development of the boundary layer and create higher wall stresses. Therefore, the friction factor in a pipe flow with turbulence will depend on the internal surface roughness, and pipes with greater roughness will lead to more significant pressure drops. The roughness, \epsilon, is a property of the pipe material.

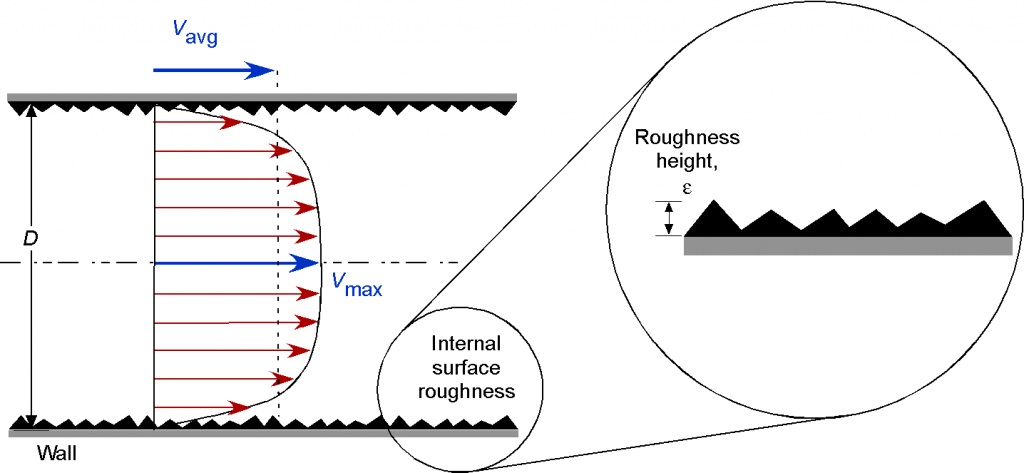
It should be appreciated that “roughness” is a relative concept; in practice, the roughness only starts to become significant when the height of the roughness elements reaches the thickness of the laminar sublayer in the turbulent boundary layer, although this layer is relatively small. Many extruded plastic pipes are generally considered hydrodynamically smooth. However, most other surfaces are rough to some degree, so it will cause the boundary layer to become turbulent quicker, i.e., after a shorter downstream development distance.

The pressure loss with a turbulent flow is still given by

(31)   \begin{equation*} \Delta p_L = \frac{1}{2} \varrho \, V_{\rm av}^2 \, f \left( \frac{L}{D} \right) \end{equation*}

but now, the value of {\scriptstyle{f}} cannot be obtained from theoretical analysis. Indeed, the friction factor in fully developed turbulent pipe flows (sometimes called the Darcy-Welsbach friction factor or just the Darcy friction factor) depends on the Reynolds number and the relative roughness height \epsilon/D, which is the ratio of the mean height of roughness of the pipe \epsilon to the pipe diameter D, i.e., for the friction factor then

(32)   \begin{equation*} f = \mbox{\small function} \left( Re_{_{D}}, \frac{\epsilon}{D} \right) \end{equation*}

which can also be found from the process of dimensional analysis.

All available results for pressure drops and friction factors for turbulent flows through pipes are obtained from experiments using artificially roughened surfaces. These experiments are done by using particle grains of a known size bonded to the inner surfaces of the pipes. Ludwig Prandtl’s students conducted the first such experiments in the 1930s, but generations of hydraulic engineers have performed many more experiments since then. The resulting friction factor {\scriptstyle{f}} is then calculated from the flow rate measurements and the pressure drop.

Pipe friction factors can be presented in tabular, graphical, or functional forms, which are obtained by curve-fitting the measured data. Commercially available pipes are assessed with equivalent roughness values so that engineers can make appropriate calculations for design and installations. However, the relative roughness of the pipe may increase with everyday use because of corrosion or abrasion (depending on the fluid), so friction factors may change over time. Good engineering practice would always make allowances for such effects so that the needed pressure at the end of the pipe can be maintained for its expected service life.

Colebrook-White Equation

The most widely used equation to find the friction factor for turbulent flows in pipes is the Colebrook-White equation. This equation has no theoretical basis and is based on a curve fitting to measurements. The equation is given by

(33)   \begin{equation*} \frac{1}{\sqrt{f}} = -2 \log_{10}\left( \displaystyle{ \frac{\epsilon}{3.7 \, D_h}} + \frac{2.51}{Re_{D_{h}} \, \sqrt{f}} \right) \end{equation*}

where \epsilon is the pipe roughness, D_h is the hydraulic diameter, and Re_{D_{h}} is the Reynolds number based on D_h. Notice that the Colebrook-White equation is an implicit function of {\scriptstyle{f}} (i.e., the value of {\scriptstyle{f}} appears on both the left- and right-hand sides), requiring an iterative numerical solution. The procedure is easily programmed in MATLAB, and convergence is rapid.

Moody Chart

Most of the available results for turbulent flows through common types of rough pipes have been summarized in the form of a Moody Chart, an example being shown below. Engineers can use this chart to calculate the friction factor for a given internal flow along a pipe. The friction factor is then used to calculate the pressure (or head) loss, pumping power, etc. Lewis Moody solved the Colebrook-White equation to create this type of chart, combining the dimensional terms of roughness, \epsilon, and pipe diameter, D_h, into a non-dimensional relative roughness, \epsilon/D_h, and the Reynolds number to find the friction factor.

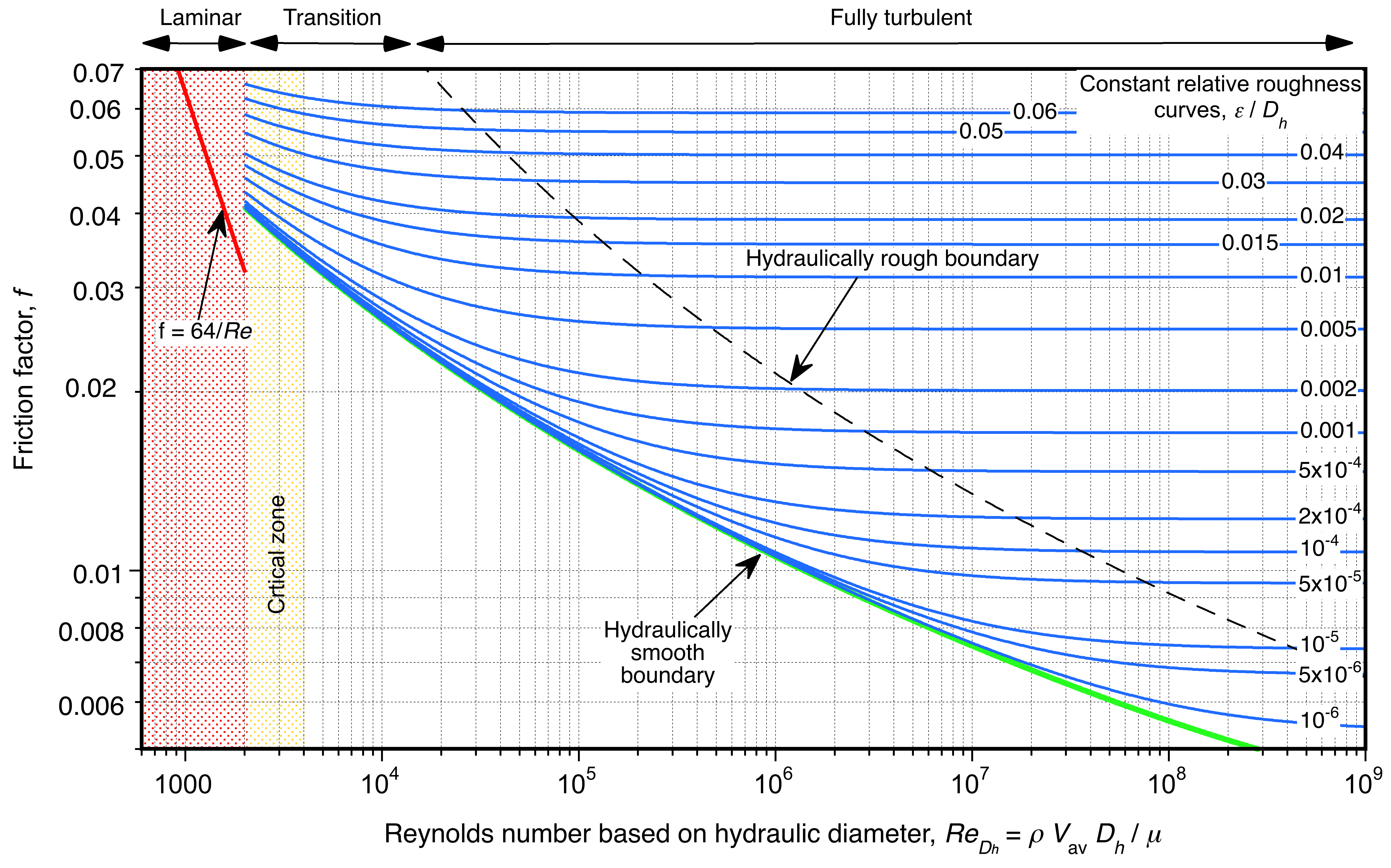
A standard Moody chart for estimating the Darcy-Weisbach friction factor in pipes and ducts. It is essential to recognize that careful interpolation on the chart will be required to find the needed values.

On the Moody Chart, the friction factor, {\scriptstyle{f}}, is on the left-hand side ordinate, the Reynolds number based on diameter (or hydraulic diameter), and the average flow velocity, Re_{D_{h}}, is on the abscissa. Notice that the chart has a log-log scale. Curves of constant values of relative roughness, \epsilon/D_h, are then plotted, which are the blue lines shown on the chart; the right side of the graph is not a scale. Online calculator versions of the chart are also available, although some may use only approximations to the Colebrook-White equation rather than iteratively solving the actual equation.

Although the Moody Chart was initially developed for flows through circular pipes, it can also be used for non-circular pipes by replacing the circular diameter, D, with the equivalent hydraulic diameter, D_h, as previously discussed. Experience suggests that this approach is sufficiently accurate for calculating the pressure drop along non-circular pipes when the flow is fully turbulent.

Remember that the Reynolds number based on diameter or hydraulic diameter is calculated using

(34)   \begin{equation*} Re_{D_{h}} = \frac{\varrho \, V_{\rm av} \, D_h}{\mu} = \frac{V_{\rm av} \, D_h}{\nu} \end{equation*}

with the fluid properties being represented in terms of density, \varrho, and viscosity, \mu, or the kinematic viscosity, \nu (=\mu / \varrho). The average flow velocity, V_{\rm av}, can be calculated from the volume flow rate, Q, and the area of the cross-section, A_c, i.e.

(35)   \begin{equation*} V_{\rm av} = \frac{Q}{A_c} \end{equation*}

When using the Moody chart, if the values of two of the three parameters are known, i.e., the friction factor, {\scriptstyle{f}} and/or the Reynolds number, Re_{D_{h}}, and/or the relative roughness, \epsilon/D_h, then the third parameter may be determined using this chart. However, in practice, the Reynolds number and the relative roughness are usually known (calculated) values, so the friction factor is the desired output from reading the chart.

MATLAB code to create the Moody chart using the Colebrook-White equation

Show code/hide code

% Moody Chart in MATLAB

clear; clc;

% Define the Reynolds number range
Re = logspace(3, 8, 500); % Reynolds number from 10^3 to 10^8

% Define the relative roughness values (epsilon/D)
rel_roughness = [0, 0.00001, 0.0001, 0.001, 0.01, 0.02, 0.05];

% Preallocate friction factor array
friction_factors = zeros(length(rel_roughness), length(Re));

% Calculate friction factors using the Colebrook equation
for i = 1:length(rel_roughness)
for j = 1:length(Re)
if Re(j) < 2000
% Laminar flow
friction_factors(i, j) = 64/Re(j);
else
% Turbulent flow using Colebrook-White equation
f = 0.02; % Initial guess for f
while true
f_new = 1 / (-2*log10((rel_roughness(i)/3.7) + (2.51/(Re(j)*sqrt(f)))));
if abs(f_new – f) < 1e-6
break;
else
f = f_new;
end
end
friction_factors(i, j) = f_new;
end
end
end

% Plot the Moody chart
figure;
loglog(Re, friction_factors, ‘LineWidth’, 2);
hold on;

% Laminar flow line
Re_laminar = Re(Re < 2000);
friction_laminar = 64 ./ Re_laminar;
loglog(Re_laminar, friction_laminar, ‘k–‘, ‘LineWidth’, 2);

% Annotate plot
grid on;
xlabel(‘Reynolds Number, Re’);
ylabel(‘Friction Factor, f’);
title(‘Moody Chart’);
legend(arrayfun(@(x) sprintf(‘\\epsilon/D = %g’, x), rel_roughness, ‘UniformOutput’, false), ‘Location’, ‘Best’);
set(gca, ‘XScale’, ‘log’, ‘YScale’, ‘log’);
xlim([1e3 1e8]);
ylim([1e-3 1]);

% Add text annotations
text(2e3, 0.08, ‘Laminar Flow’, ‘FontSize’, 12, ‘Rotation’, -45);
text(1e7, 0.008, ‘Turbulent Flow’, ‘FontSize’, 12);

% Add grid lines for guidance
set(gca, ‘MinorGridLineStyle’, ‘-‘, ‘GridAlpha’, 0.5, ‘MinorGridAlpha’, 0.5);

hold off;

Interpretation

The following points should be understood when using and interpreting the curves on the Moody chart:

1. The laminar flow line represents a lower theoretical bound of the friction factor for low Reynolds numbers, i.e.,

(36)   \begin{equation*} f = \frac{64}{Re} \end{equation*}

There are few practical situations where this is a valid assumption other than for very short, smooth pipes and ducts. Nevertheless, the result shows that the friction factor decreases with increasing Reynolds number, and there is no dependency on surface roughness.

2. The shaded area indicates a critical zone. This is where the flow begins to develop turbulence but is unsteady and intermittent in its flow characteristics. The friction factor can show significant changes here, meaning the flow in this region could be laminar or turbulent. Empirical data here are limited in scope and show considerable scatter. Fortunately, having to use this part of the chart is uncommon.

3. The friction factors increase with surface roughness for any given Reynolds number at higher Reynolds numbers, a rather obvious expectation. Notice that even entirely smooth pipes containing a turbulent flow, such as plastic and glass, which have values of \epsilon/D or \epsilon/D_h \rightarrow 0, will still have a friction factor and a pressure drop along their length, but these effects continue to diminish with increasing Reynolds number.

4. At higher Reynolds numbers, which is called the fully turbulent or hydraulically rough zone, the friction factors become nearly independent of the Reynolds number. This behavior happens because the protruding roughness penetrates well into the boundary layer and deeper than any laminar sublayer, so the internal flow will always be fully turbulent. Notice that this zone (boundary) occurs at an increasingly higher Reynolds number with lower roughness factors. Moody defined the boundary of the hydraulically rough zone as

(37)   \begin{equation*} \frac{1}{\sqrt{f}} = \frac{Re_{D_{h}}}{200} \left( \frac{\epsilon}{D_h} \right) \end{equation*}

Using Eq. 33, it can be shown that

(38)   \begin{equation*} \frac{1}{\sqrt{f}} = -2 \log_{10} \left( \frac{57}{Re_{D_{h}} \sqrt{f}} \right) \end{equation*}

Therefore, the hydraulically rough boundary (black dashed line on the Moody chart) can be approximated by the equation

(39)   \begin{equation*} Re_{D_{h}} = \frac{57 \times 10^{\displaystyle{\left(1/(2 \sqrt{f}) \right)}}}{\sqrt{f}} \end{equation*}

5. When the relative roughness becomes even higher, i.e., when \epsilon/D > 0.1, the values of the friction factor become independent of the Reynolds number at any Reynolds number. In such cases, the friction factors become horizontal lines. Because of the large pressure drops associated with flows through pipes with such high roughness levels, they are of no practical significance.

Reading a Moody Chart

Reading a Moody chart is not difficult but requires some practice, recognizing it is a log-log chart and will inevitably involve graphical interpolation. While the friction factor can be calculated numerically using the Colebrook-White equation, it is still essential to understand the visual interpretation of the physical behavior and the process of using the chart, an example being shown below. Reading the chart to three decimal places is more than adequate. Notice that some published Moody charts, such as those found on the internet, may give slightly different friction factor values because they are based on approximations to the Colebrook-White equation.

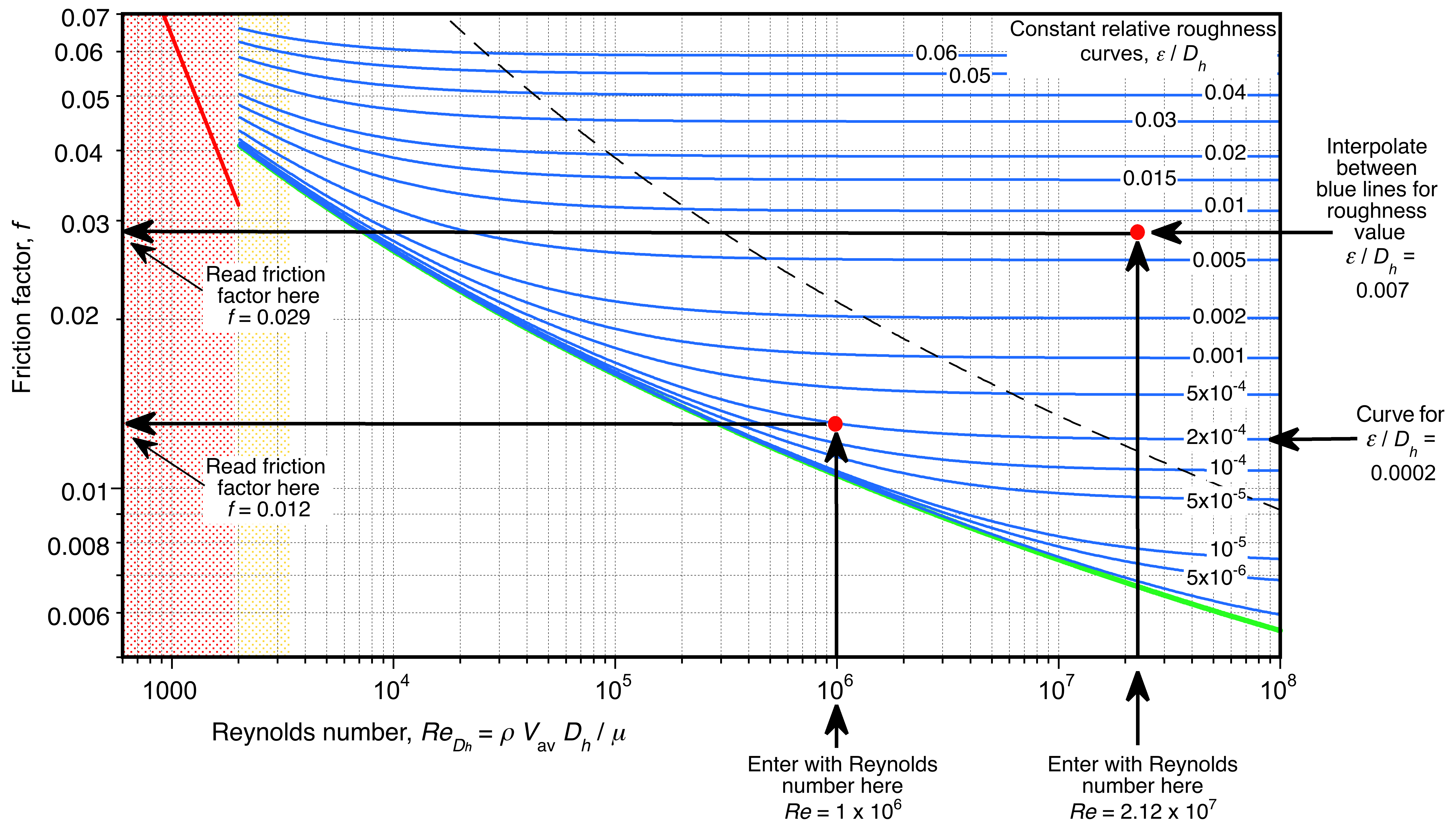
How to read a Moody chart. Remember, it is a log-log scale, so some care is required.

In this case, it is assumed that the information needed to calculate the Reynolds number and the relative roughness is available, and the desired output is the friction factor, {\scriptstyle{f}}.

  1. Determine the Reynolds number based on the average flow velocity, V_{\rm av}, and fluid properties (\varrho and \mu or \nu) using the hydraulic diameter, D_h, of the pipe, i.e.,

        \[ Re_{D_{h}} = \frac{\varrho \, V_{\rm av} \, D_h}{\mu} = \frac{V_{\rm av} \, D_h}{\nu} \]

    where the average flow velocity is determined from the flow rate and cross-sectional area, i.e.,

        \[ V_{\rm av} = \frac{Q}{A_c} \]

  2. Calculate the value of the relative roughness from the actual dimensional roughness, \epsilon, and calculated hydraulic diameter, D_h, i.e.,

        \[ \mbox{\small Relative roughness} = \frac{\epsilon}{D_h} \]

    The roughness value, \epsilon, is often stamped on industrial piping or can be found in standard tables that are widely published.

  3. Find the appropriate (blue) curve for the calculated value of relative roughness on the Moody diagram, recognizing that only a finite number of curves can be shown, and interpolation of the curves on the logarithmic scales will likely be required.
  4. Find where the friction factor curve (or interpolated curve) intersects the Reynolds number (at the red dot).
  5. Estimate the friction factor by reading the value on the vertical scale on the ordinate to the left of the red dot point from where the Reynolds number and relative roughness curve intersect.

Finally, some words of caution are appropriate when using the Moody Chart. First, like all engineering calculations, ensuring that the correct units are consistently used when calculating non-dimensional quantities, such as the Reynolds number and relative roughness, is essential. Be sure that the Reynolds number is calculated based on the pipe’s diameter (or hydraulic diameter), not the pipe’s length. Catastrophic mistakes can occur if the correct units are not used carefully and consistently. Second, because of the numerous lines on the chart, it is essential to interpolate carefully. The human eye/brain combination is a suitable interpolator, but greater accuracy may be required. In this case, the Colebrook-White equation can be solved directly, or an accepted approximation can be used.

Approximations for the Friction Factor

The von Kármán rough pipe law, also known as the von Kármán-Prandtl roughness law, is an empirical relationship used to estimate the friction factor for a fully-developed turbulent fluid flow through a pipe with rough walls. It can be written as

(40)   \begin{equation*} \frac{1}{\sqrt{f}} = -2.0 \, \log_{10}\left[ \left( \displaystyle{\frac{\epsilon}{3.7 D_h}}\right) + \frac{2.51}{Re_{D_{h}}\sqrt{f}}\right] \end{equation*}

which is, again, an implicit equation that must be solved by iteration. While only approximate, it applies to a wide range of Reynolds numbers and roughness factors.

The Swamee-Jain equation, also known as the Swamee-Jain friction factor equation, can also be used to calculate the friction factor, {\scriptstyle{f}}, for internal fluid flow. The equation is a simplified form of the von Kármán rough pipe law and provides an explicit approximation for the friction factor, i.e.,

(41)   \begin{equation*} f = \frac{0.25}{\left[\log_{10}\left( \displaystyle{ \frac{\epsilon}{3.7 D_h} + \frac{5.74}{Re_{D_{h}}^{~0.9}}} \right)\right]^2} \end{equation*}

Roughness Values

In most cases, roughness values cover a range and will depend on the specific surface, as shown in the table below. As manufactured, the roughness values will be on the lower end of the scale, but all types of pipes may develop some roughness over time from oxidation or corrosion. It is always important to consult relevant standards and specifications or obtain specific roughness values for the particular pipe(s) used in a given application.

Roughness factors for different types of internal surfaces. In most cases, roughness values cover a range.
Pipe Material Roughness, ε (mm)
Smooth Plastic (PVC) 0.001 – 0.01
Glass 0.001 – 0.01
Smooth Metal (e.g., SS) 0.001 – 0.03
Concrete 0.2 – 1.5
Galvanized Iron 0.15 – 0.5
Commercial Steel 0.045 – 0.09
Riveted Steel 0.9 – 1.2
Corrugated Metal 3.0 – 8.0
Cast Iron (new) 0.15 – 0.5
Cast Iron (old) 0.6 – 3.0
Smooth Copper 0.001 – 0.01
Polyethylene (PE) 0.001 – 0.01
Polyvinyl Chloride (PVC) 0.001 – 0.01
Fiberglass 0.01 – 0.03
Stainless Steel (welded) 0.025 – 0.05
Stainless Steel (seamless) 0.02 – 0.045
Aluminum 0.05 – 0.1
Brass 0.02 – 0.05
PVC (Corrugated) 1.5 – 3.0
HDPE (Corrugated) 0.4 – 1.5
Ductile Iron 0.025 – 0.05
Polypropylene 0.01 – 0.03
ABS 0.02 – 0.06

Check Your Understanding #3 – Calculating the pressure drop for turbulent flow in a pipe using the Moody chart

Oil with a density \varrho_{\rm oil} = 900 kg/m{^{3}} and kinematic viscosity \nu_{\rm oil} = 10^{-5}m^{2}/s, flows at 0.2 m{^{3}}/s through a 500 m length of 300 mm diameter cast iron pipe. The average roughness of the pipe’s surface is 0.26 mm. Calculate: 1. The average flow velocity in the pipe. 2. The Reynolds number of the flow. 3. Is the flow in the pipe laminar or turbulent? 4. The pressure drop and head loss along the pipe. 5. The minimum power of the pump needed to move the oil.

Show solution/hide solution
  1. The average flow velocity is calculated from the volume flow rate, i.e.,

        \[ V_{\rm av} = \frac{Q}{A }= \frac{4Q}{\pi D^2} = \frac{4 \times 0.2}{\pi \times 0.3^2} = 2.83~\mbox{ m/s} \]

  2. The Reynolds number of the flow in the pipe is

        \[ Re_{_{D}} = \frac{\varrho_{\rm oil} \, V_{\rm av} \, D}{\mu_{\rm oil} } =\frac{V_{\rm av} \, D}{\nu_{\rm oil}} = \frac{2.83\times 0.3 }{10^{-5}} = 84,900 \]

  3. The flow will be turbulent because the Reynolds number is greater than 2,000, and the Moody chart will be needed to find the friction factor {\scriptstyle{f}}.
  4. To find the pressure drop and use the Moody chart, the relative surface roughness is needed, which is

        \[ \frac{\epsilon}{D} = \frac{0.26}{300} = 0.00087 \]

    From the Moody chart for a Reynolds number of 84,900 and a relative roughness of 0.00087 (using interpolation), then f \approx 0.022. Notice: You may get a slightly different number for the friction factor depending on the Moody chart you use. Therefore, the pressure loss over the length of the pipe is

        \[ \Delta p = \frac{1}{2} \varrho_{\rm oil} \, V_{\rm av}^2 \, f \left( \frac{L}{D}\right) = 0.5\times 900\times 2.83^2 \times 0.022\times \frac{500}{0.3} = 132.15~\mbox{ kPa} \]

    The corresponding head loss over this pipe is

        \[ h = \frac{\Delta p}{\varrho_{\rm oil} \, g} = \frac{132.15\times 10^3}{900\times 9.81} = 14.97~\mbox{m} \]

  5. The pumping power required will be

        \[ P_{\rm req} = Q \, \Delta p = 0.2 \times 132.15 \times 10^3 = 26.43~\mbox{kW} \]

Pressure Drop Over a Tapered Pipe

There are no exact solutions for the pressure drop along a tapered pipe; an example of such a shape is shown in the figure below. The main issue is that the flow velocity and Reynolds number vary continuously. However, numerical solutions may be possible where the local losses over short segments are added to determine the local losses in aggregate. In the case of fully turbulent flow with higher Reynolds numbers where the friction factor becomes independent of Reynolds number, the pressure drop can be estimated using the concept of a hydraulic diameter and average flow velocity.

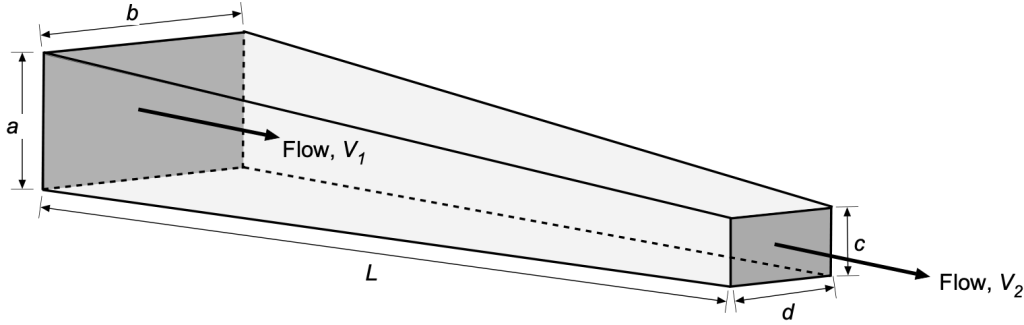
Calculating the pressure drop over a tapered pipe is possible under certain assumptions, including fully turbulent flow at higher Reynolds numbers.

In this case, the average hydraulic diameter D_h is

(42)   \begin{equation*} D_h = \frac{ \displaystyle{\dfrac{4 \, a \,b}{2a + 2 b} }+ \displaystyle{ \dfrac{4 \, c \, d}{2c + 2 d}}}{2} = \dfrac{a\, b}{a + b} + \frac{c \, d}{c + d} \end{equation*}

The average flow velocity, V_{\rm av}, based on continuity considerations is given by

(43)   \begin{equation*} V_{\rm av} = \dfrac{4 \, a \, b \, V_1}{\pi \, D_h^2} = \dfrac{4 \, c \,d \, V_2}{\pi \, D_h^2} \end{equation*}

The Reynolds number based on the average hydraulic diameter and average flow velocity can then be obtained, i.e.,

(44)   \begin{equation*} Re_{D_{h}} = \frac{\varrho \, V_{\rm av} \, D_h}{\mu} = \frac{V_{\rm av} \, D_h}{\nu} \end{equation*}

Then the Moody chart can be used with the relative roughness to get the friction factor, {\scriptstyle{f}}, or the Swamee-Jain equation can also be used, i.e.,

(45)   \begin{equation*} f = \frac{0.25}{\left[\log_{10}\left( \displaystyle{ \frac{\epsilon}{3.7 D_h} + \frac{5.74}{Re_{D_{h}}^{~0.9}}} \right)\right]^2} \end{equation*}

Therefore, the pressure loss over the length of tapered pipe will be

(46)   \begin{equation*} \Delta p = \frac{1}{2} \varrho_{\rm fluid} \, V_{\rm av}^2 \, f \left( \frac{L}{D_h}\right) \end{equation*}

These pressure drop estimates are sufficiently accurate for many practical purposes, including wind tunnel design.

Pumps

Many internal flow problems involve using or designing various types of pumps to move fluid from one place to another. Such pumps include hydraulic pumps, piston pumps, centrifugal pumps, gear-type pumps, vane pumps, axial flow pumps, fans, etc. For aerospace applications, pumps must be lightweight (i.e., high power-to-weight ratio), reliable, and often contend with harsh operating environments, including large temperature swings and vibration. Pumps obtained “off-the-shelf” are usually specified in terms of their volumetric transfer capacity per unit time. It is essential to notice the units in which the volumetric flow rates are given, which will typically not be in base units; e.g., they may be quoted in terms of liters/hr, gallons/minute, or other units. 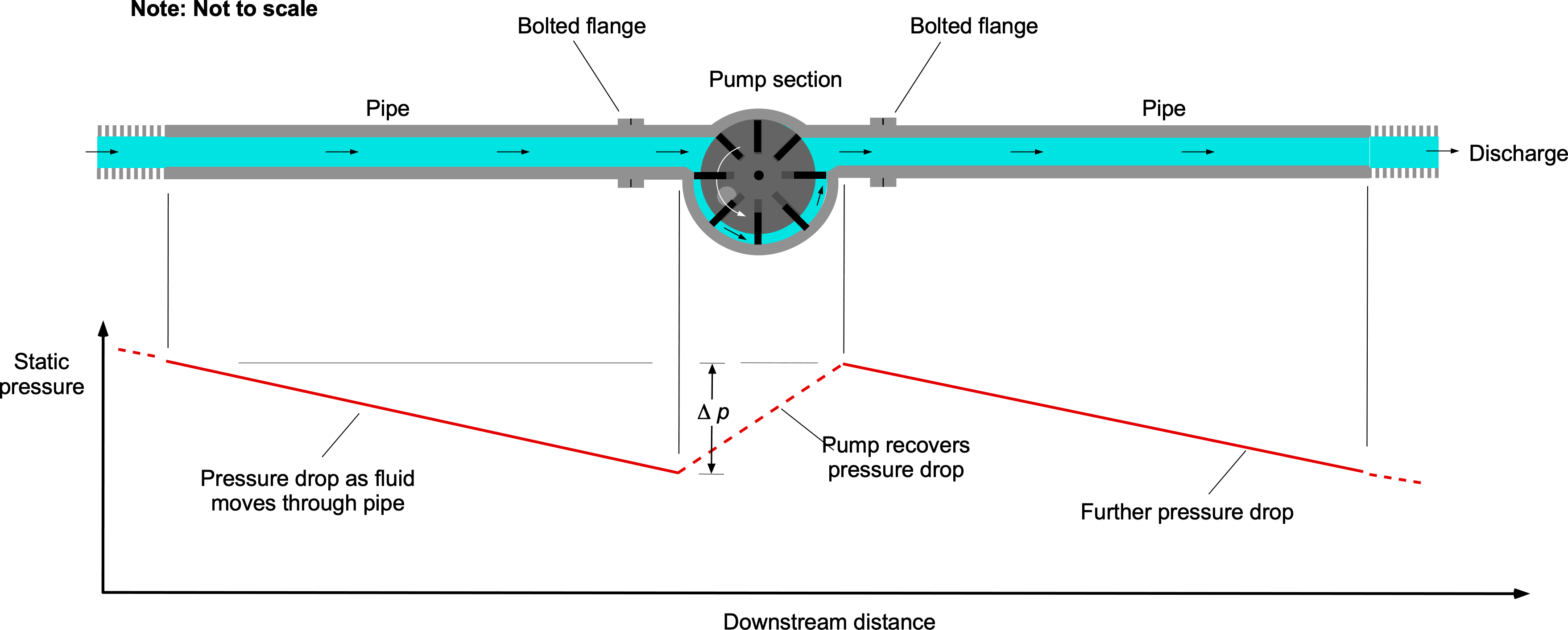In general, pumps recover pressure losses so fluid can be pumped from one location to another, as shown in the figure below. Any pump will produce the same effect of pressure recovery, although with different efficiencies and applicabilities to different types of fluids. Pressure drops depend on several factors, including the flow rate, Reynolds number, and friction factor.

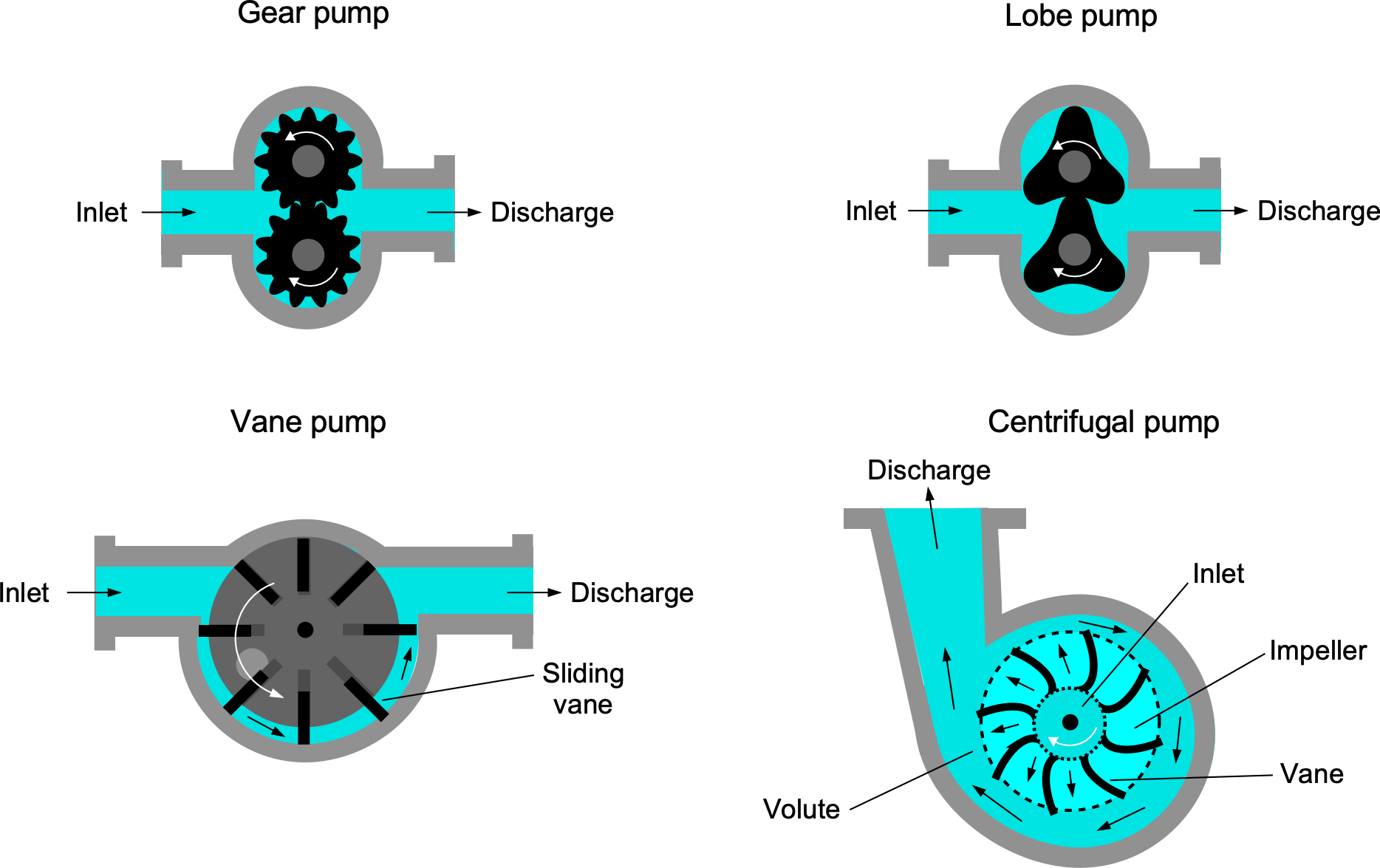
Pumps are usually located in-line with the overall flow and are used to recover the pressure drop and keep the fluid moving through the pipe from one end to the other.

Types of Pumps

The figure below shows four common types of fluid pumps: a gear pump, lobe pump, vane pump, and centrifugal pump. In each case, the pumps must be rotated by a power source. This source could be an accessory drive through a belt or gear system from an engine or propulsion system or a direct drive from a separate source such as an electric motor. Such pumps are usually inserted in series into a pipeline and bolted to the pipe using parallel flanges sealed by a gasket.

There are many different types of pumps, but in each case, their purpose is to move fluid through a pipe to overcome pressure drops.

Gear Pumps

Gear pumps are positive displacement pumps that utilize two meshing gears to transfer fluids by creating chambers between the gear teeth and the pump casing. They come in various types, external and internal, offering specific advantages and applications. Gear pumps are valued for their simplicity, reliability, and ability to handle various viscosities, making them suitable for applications in industries such as hydraulic systems, lubrication systems, and fuel transfer. Lubrication systems in engines often use gear pumps because of their simplicity, low cost, and good reliability.

Lobe Pumps

Lobe pumps are positive displacement pumps characterized by two or more lobes that rotate in synchronized motion within a casing, creating chambers that transport fluid from the inlet to the outlet. Unlike gear pumps, lobe pumps feature smooth meshing lobes instead of gears, offering smoother, more efficient fluid flow with lower losses. They are widely used because they can handle more viscous fluids, such as oils. They are reliable but tend to be more expensive than gear pumps.

Vane Pumps

Vane pumps are positive displacement pumps that employ rotating vanes inside a cylindrical housing to move fluid from the inlet to the outlet. These pumps typically feature an off-center drive to the vanes. The vanes are often made of carbon, causing them to slide in and out of their slots while maintaining close contact with the housing. Vane pumps have a smooth and consistent flow, making them suitable for applications requiring precise and steady fluid delivery, such as hydraulic and pneumatic systems. They offer relatively quiet operation and can handle various viscosities, though they experience reduced efficiency for more viscous fluids. Furthermore, the vanes wear over time and require periodic maintenance to ensure their functionality.

Centrifugal Pumps

Centrifugal pumps utilize centrifugal forces on the fluid to increase the fluid’s rotational kinetic energy. Such pumps consist of an impeller enclosed within a casing, propelling the fluid outward from the center of rotation. The fluid is introduced through a pipe at the center of the pump. As the fluid moves through the pump, it gains velocity and pressure, transferring fluid from the inlet to the outlet. Centrifugal pumps are widely used in applications requiring high flow rates. While efficient, they tend to be better suited for gases rather than more viscous liquids.

Diaphragm pump

The figure below shows a CFD simulation of the internal flow through a diaphragm pump or membrane pump. In this type of pump, which is common in fuel delivery systems, the diaphragm is flexed up and down (by a motor) such that when the volume of the chamber is increased, the pressure decreases, the fluid is drawn from one end of the pipe into the chamber. When the chamber pressure rises from the reduced volume, the fluid previously drawn in is forced through the other pipe. Notice that a pair of butterfly valves prevent reverse fluid flow from the pump.

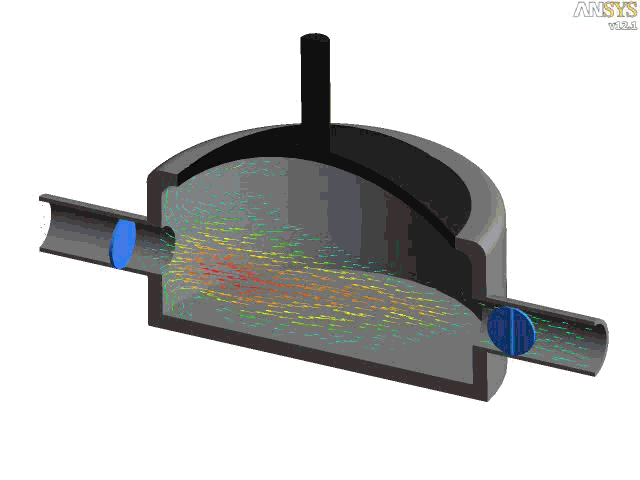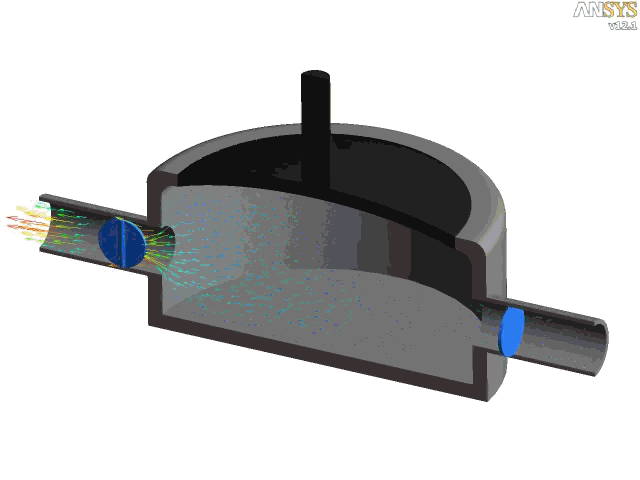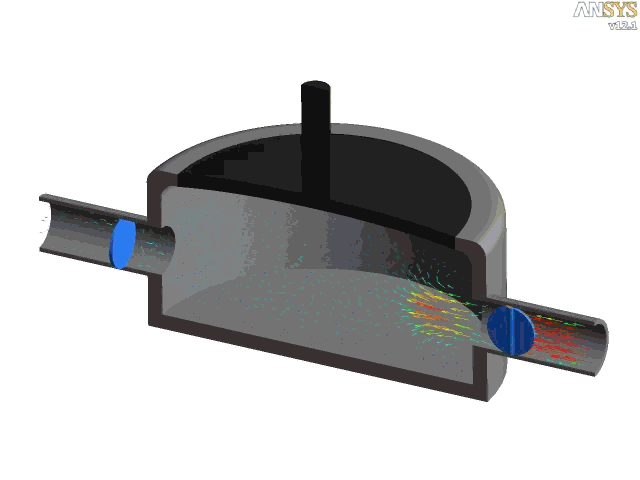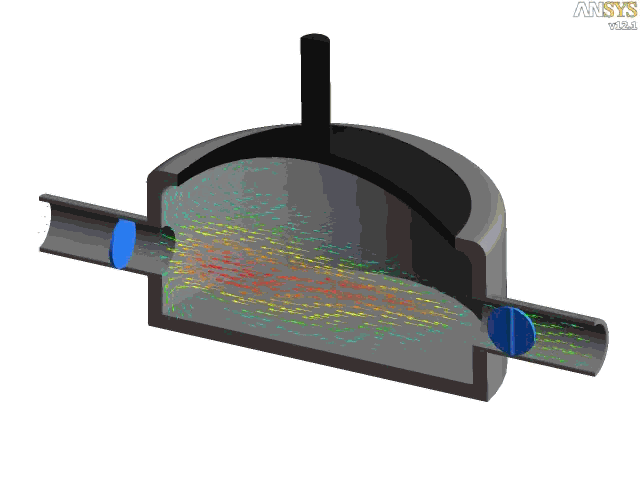
An excellent example of an internal flow is this diaphragm pump, which draws the fluid from a pipe into a chamber and forces it out through the other pipe.

Pressure Drops Over Bends & Corners

When an internal fluid flow encounters a corner or bend, it experiences a pressure drop from the change in direction, as shown in the figure below. Several factors, including centrifugal forces, changes in velocity, and the possibility of flow separation, cause this pressure drop. As the fluid approaches the corner, it tends to move outward under the action of centrifugal forces, which creates a pressure gradient across the cross-section of the corner or bend. If the corner is sharp, the flow separation and higher pressure losses can be expected.

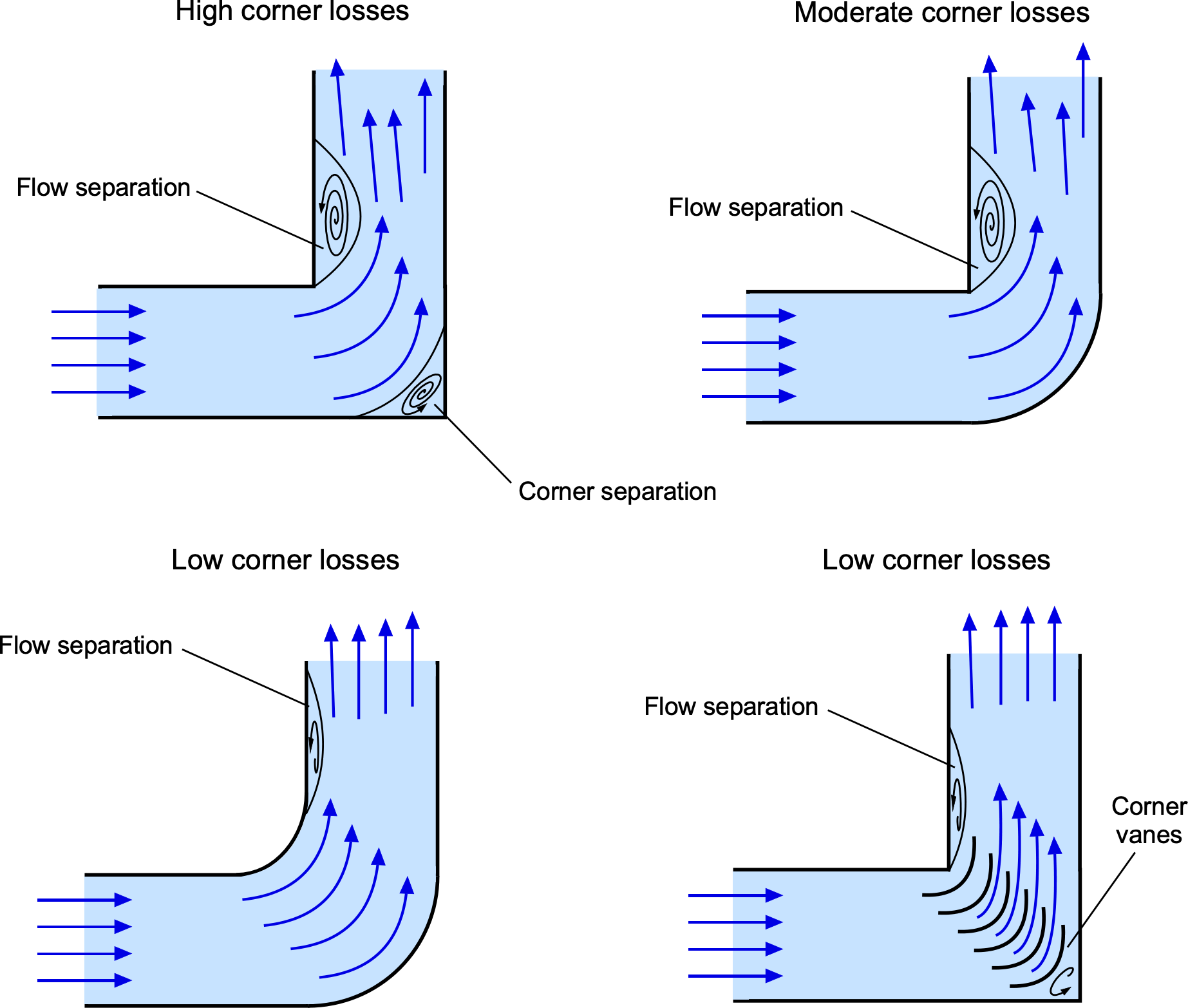
Flow around bends and corners incur additional pressure losses.

The magnitude of the pressure drop around a corner depends on various factors, such as the geometry of the bend, flow rate, fluid viscosity, and Reynolds number. Many studies have been to determine the losses in bends, including by NIST. One way of assessing such pressure losses is by using a local loss coefficient K_L, for which values are published for various corners and bends. The local pressure loss, \Delta p_L, is given by

(47)   \begin{equation*} \Delta p_L = \frac{1}{2} \varrho \, V_{\rm av}^2 \, K_L = \varrho \, g \, h_L \end{equation*}

where h_L is the head loss. The head loss is then

(48)   \begin{equation*} h_L = K_L \left( \frac{\varrho \, V_{\rm av}^2}{2 \, g} \right) \end{equation*}

which is often referred to as a velocity head. For a sharp corner, K_L = 0.3, as shown in the figure above, and for a smooth corner, K_L = 0.1.

Many hydraulic, pneumatic, and other internal fluid flow systems comprise straight sections, turns, and branches. The total pressure losses are the sum of all of the pressure losses incurred by each component of the system, i.e.,

(49)   \begin{equation*} \Delta_{p_{\rm total}} = \Delta_{p_{1}} + \Delta_{p_{2}} + \Delta_{p_{3}} \bigcdot \bigcdot \bigcdot \end{equation*}

Today, computational fluid dynamics (CFD) can better predict and analyze the specific pressure drop for a given internal flow system. In general, the pressure drop around a corner can be minimized by using smooth bends with large radii, which limit the possibilities of flow separation. Additionally, properly designed flow control devices, such as corner vanes or deflectors, can limit the pressure drop.

Wind Tunnels

Wind tunnels are critical tools in the understanding of aerodynamic flows, which enable researchers and engineers to simulate and analyze the effects of airflows over objects such as aircraft, road vehicles, buildings and various other components and types of structures. Wind tunnels are vital to the aerospace engineer’s technical repertoire, and tunnel testing is inevitable when designing a new aircraft. Not everything can be predicted before its first flight, and wind tunnels can help establish high confidence in the aircraft’s design, i.e., that the aircraft, when built, will behave as intended.

The proper design of a wind tunnel, which to a large extent relies on the application of the principles on internal flows, ensures clean, reliable and repeatable measurements, making them invaluable for use in various diverse applications, not just limited to aerospace engineering. Wind tunnels come in all shapes and sizes and can have different flow speed capabilities. However, their fundamental purpose is to allow measurements to be made under controlled flow conditions. Consequently, measurements are often made an airplane models, wings, and other components; geometric scaling is generally required to establish dynamic flow similarity with full-size components. However, because models are usually sub-scale, simultaneously obtaining the correct flight Reynolds and Mach numbers in a wind tunnel environment is often challenging.

Fundamental Components of a Wind Tunnel

A wind tunnel typically comprises five key sections, each with a specific function that contributes to the overall performance and accuracy of the system. A schematic of a ERAU wind tunnel is shown below. This is a closed-return wind tunnel with a 4 ft by 6 ft (1.22 m by 1.83 m) rectangular test section 12 ft (3.66 m) long with tapered corner fillets. This tunnel allows flow speeds of up to 420 ft/s (128 m/s) to be obtained in the test section with exceptional flow quality and low turbulence levels. In addition, the test section has about 70% of its surface area made with optical grade glass, allowing flow measurements using optical methods such as particle image velocimetry (called “PIV”).

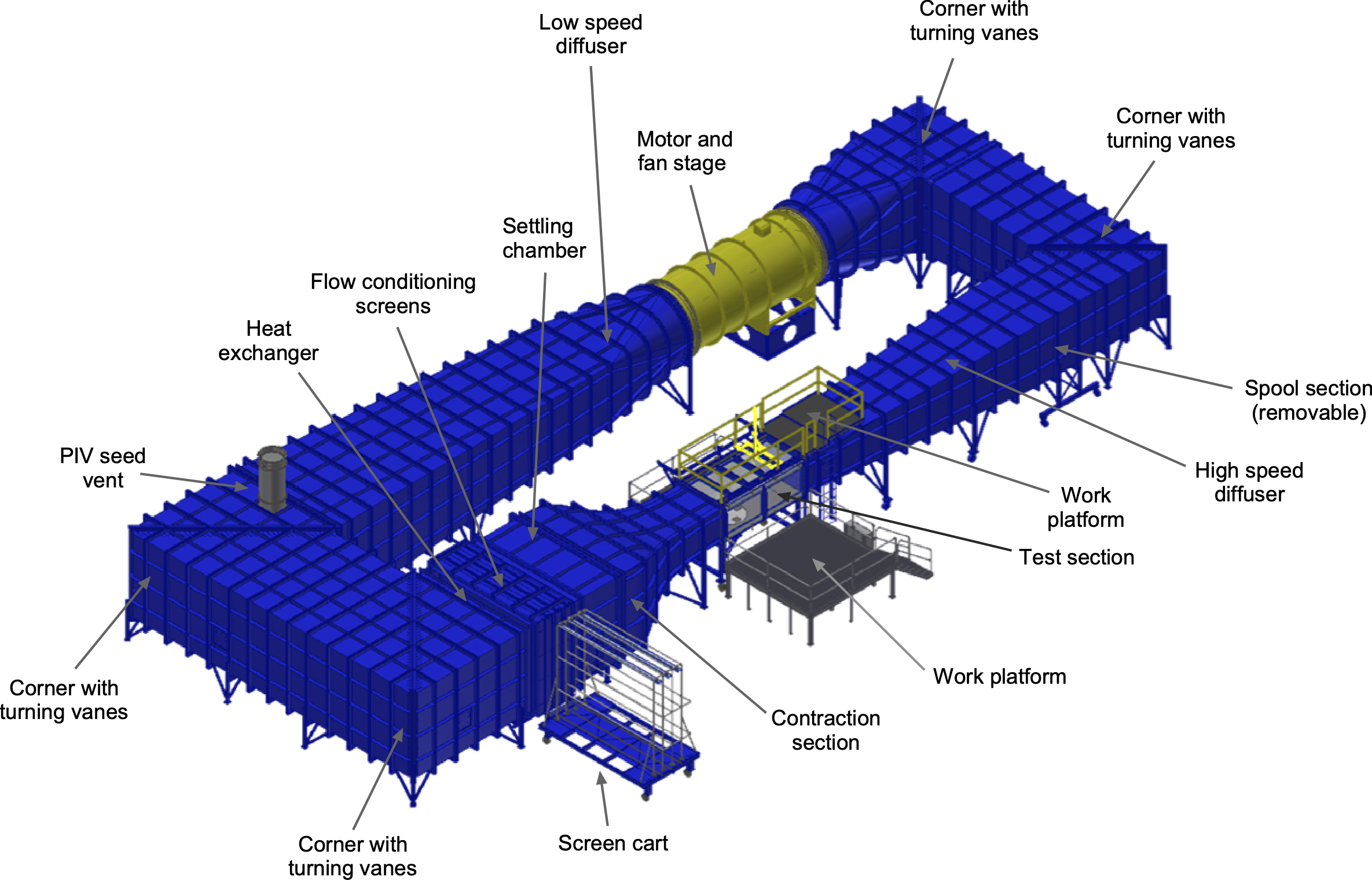
The key features of the ERAU low-speed subsonic wind tunnel.
  • Settling Chamber: The settling or stilling chamber is located at the entrance of the wind tunnel. Its primary purpose is to condition the incoming air and reduce its turbulence levels. This goal is achieved through the use of flow straighteners, such as plates or honeycomb structures and fine mesh screens. These elements remove the turbulent and and angular components of the air flow, and ensure a more uniform velocity profile before the air enters the contraction section.
  • Contraction Section: The contraction section accelerates the airflow and directs it into the test section. The shape of the contraction is typically parabolic or exponential to achieve a smooth and continuous acceleration. The ratio of the inlet area to the outlet area, known as the contraction ratio, is carefully selected based on the desired flow characteristics. While the purpose of the constraction is to speed up the flow before it reaches the test section, it also acts to squeeze out small turbulence eddies and further reduce turbulence levels in the test section.
  • Test Section: The test section is the most important part of the wind tunnel, where the model or object under study is placed. The walls of the test section are designed to minimize boundary layer effects and ensure uniform, almost turbulent free flow conditions. The cross-sectional shape of the test section can be rectangular or circular, depending on the application. Transparent walls are often used for optical measurements, while provisions for instrumentation, such as pressure taps, load cells, and high-speed cameras, are also included.
  • Diffuser: After the test section, the airflow enters the high-speed diffuser, which slows down its velocity to reduce pressure losses from friction. The diffuser gradually expands, allowing the air to decelerate smoothly while preventing flow separation. The design of the diffuser is crucial for maintaining the efficiency of the wind tunnel, as poorly designed diffusers can lead to higher than acceptable pressure losses and turbulence.
  • Drive Section: The drive section houses the fan or blower that generates and maintains airflow through the wind tunnel. High-performance fans are equipped with variable speed control to achieve precise flow conditions. The pitch of the fan may also be adjustable. In closed-circuit wind tunnels, this section or one before the turbulence screens also includes heat exchangers to regulate the temperature of recirculating air.

Types of Wind Tunnels

Wind tunnels are classified based on their speed range and application. The main types include:

  • Subsonic Wind Tunnels: These are designed for low-speed flows (test section Mach number < 0.3) and are commonly used in aeronautical, automotive and architectural testing. Subsonic tunnels typically feature a relatively large test section to accommodate full-scale models.
  • Transonic Wind Tunnels: Operating at speeds close to the speed of sound (Mach number 0.8–1.2), transonic tunnels are used to study phenomena such as shock waves and compressibility effects. They often require special features like slotted walls in the test section to minimize wall interference effects or otherwise manage the flow behavior.
  • Supersonic and Hypersonic Wind Tunnels: These wind tunnels handle speeds beyond Mach 1 and Mach 5, respectively. They are used for aerospace applications, such as missile and spacecraft testing. Supersonic tunnels are pressurized tunnels that use convergent-divergent nozzles to achieve high speed flow in the test section. Hypersonic tunnels also require a proper choice of materials such as high temperatures steels to withstand the associated thermal loads.
  • Open-Circuit vs. Closed-Circuit Wind Tunnels: Open-circuit or Eiffel wind tunnels draw air from the environment and discharge it back, making them simpler but much less energy-efficient. Closed-circuit tunnels recirculate the air, which provides better control over flow conditions and temperature. High speed wind tunnels are usually of the open return type, and are often blow-down tunnels. A blow down tunnel is one where compressed air is stored in a pressure tank, and then a valve is opened to release the air through the test section. Such wind tunnels run for only relatively short time period of the order of seconds.

Key Design Considerations

  • Flow Uniformity and Stability: Ensuring uniform and stable airflow throughout the tunnel is paramount. This goal requires careful design of the settling chamber, contraction, and test section to minimize turbulence and flow angularities.
  • Reynolds Number Scaling: The Reynolds number, a dimensionless parameter that characterizes flow behavior, must be accurately replicated in the wind tunnel. This goal often requires adjusting model size, airspeed, or fluid properties.
  • Pressure and Temperature Control: In high-speed tunnels, maintaining consistent pressure and temperature is critical for replicating actual flight conditions. Closed-circuit designs often incorporate cooling systems to manage heat generated by airflow and the fan system.
  • Acoustic and Vibration Isolation: Noise and vibrations generated by the fan and other mechanical components can interfere with measurements. The force balance, for example, may be situated on an iso-slab that seismically isolates it from the remainder of the wind tunnel and the building. Wind tunnels are usually equipped with acoustic-dampening materials and vibration isolation systems to mitigate these effects. Supersonic and hypersonic wind tunnels are notoriously noisy and are usually located at remote sites.
  • Instrumentation and Data Acquisition: Modern wind tunnels are equipped with a wide range of advanced sensors, such as pressure transducers, force balances, and various types of laser-based optical velocimeters, the latter bing used to capture detailed off-surface flow data. The integration of these instruments into the wind tunnel design process requires considerable attention to detail.

Design of a Wind Tunnel

Consider now an engineering design problem for the internal flow in a wind tunnel. The design of a modern wind tunnel is a complex affair because it is usually customized to meet a set of unique testing requirements, including the test articles themselves and the types of measurements to be made. One of the challenges in wind tunnel design is obtaining uniform flow properties in the test section, i.e., uniform velocities in both magnitude and direction with minimal flow angularity (typically less than 0.1 of a degree) its entire length. This process needs keen attention to the internal flow quality around the whole wind tunnel circuit, including the flow through the fan, and special attention must be paid to the contraction before the test section.

Using CFD and taking into account the thickness of the boundary layer and turbulence, the walls of the contraction of ERAU’s wind tunnel were contoured to ensure the best flow uniformity at the entrance to the test section and along its entire length. Appropriately shaped and tapered corner fillets from the contraction and along the test section length are also part of the design solution.

The ability to design a wind tunnel with uniform flow properties and low flow angularity along its entire test section is essential to the success of the tunnel as an aerodynamic testing resource.

Pressure Losses in Wind Tunnels

While designing a wind tunnel is a specialist activity, one of the design challenges for a new wind tunnel is determining the motor/fan’s power to create a needed flow velocity (or dynamic pressure) in the test section. To this end, estimating (by calculation) the pressure losses as the flow moves around the tunnel circuit is necessary for design.

As previously discussed, wind tunnels are large ducts with different shapes and cross-sections, transition pieces (adapters), etc. As a result, there will be various pressure losses as the flow moves through these different duct elements at different speeds and Reynolds numbers. In addition, corner vanes are used to help turn the flow and are a cascade of thin airfoils of circular arc plates. Significant frictional pressure losses will occur as the flow passes through the four sets of corner vanes.

In the conventional approach to wind tunnel design, the frictional losses can be estimated for the fan and initial sizing of the motor by breaking the tunnel circuit into its primary parts:

  1. Cylindrical sections (even if just transition pieces).
  2. Corners.
  3. Expanding sections, i.e., diffusers.
  4. Contracting sections, i.e., nozzles.
  5. Turbulence screens.
  6. Heat exchangers.
  7. Other miscellaneous parts.

In these sections (and there may be more than one of each), an energy loss occurs in the form of a static pressure loss, \Delta p. This can be written as a coefficient of loss, i.e., K = \Delta p/q, where q is the local dynamic pressure. This loss is then referenced to the test section values (subscript 0) using

(50)   \begin{equation*} K_0 = \frac{\Delta p}{q} \left( \frac{q}{q_0} \right) = K \left( \frac{q}{q_0} \right) \end{equation*}

Because the pressure or head loss depends on the fourth power of the tunnel diameter or equivalent hydraulic diameter for non-circular cross-sections, according to Poiseuille’s law, then

(51)   \begin{equation*} K_0 = K \left(\frac{D_{h_{0}}}{D_h}\right)^4 \end{equation*}

where D_h is the local hydraulic diameter of the tunnel section, and D_{h_{0}} is the hydraulic diameter of the test section. The next step is to refer the energy loss per unit time in the flow \Delta E to the test section, which will be

(52)   \begin{equation*} \Delta E = K \left(\frac{1}{2} \varrho \, A_0 \, V_0^3 \right) \left(\frac{D_{h_{0}}}{D_h}\right)^4 \end{equation*}

where A is the local area, and A_0 is the area of the test section. Therefore, the energy loss per unit time is

(53)   \begin{equation*} \Delta E = K_0 \left(\frac{1}{2} \varrho \, A_0 \, V_0^3 \right) \end{equation*}

and so the so-called Energy ratio ER_t can be determined, which is

(54)   \begin{equation*} \mbox{\small Energy~ratio} = \frac{\mbox{\small Energy at test section}}{\displaystyle{ \sum~ \mbox{\small Circuit losses}}} = ER_t \end{equation*}

the \sum denoting “the sum of.” Therefore,

(55)   \begin{equation*} ER_t = \frac{\frac{1}{2} \varrho \, A_0 \, V_0^3}{\displaystyle{\sum K_0 \, \frac{1}{2} \varrho \, A_0 \, V_0^3}} = \frac{1}{\displaystyle{ \sum K_0}} \end{equation*}

The resulting energy ratio depends on the inverse sum of the equivalent energy losses for each part of the tunnel circuit, i.e., it is, in effect, the reciprocal of the losses. For a closed-return tunnel, the values of ER_t typically range from 4 to 7. This outcome means that the lower the losses, the higher the energy efficiency, so the lower the power required to be delivered to the air by the fan/motor. Corner vanes and diffuser sections typically contribute to the highest source of losses in a wind tunnel, and as such, they must be carefully designed. Minimizing the tunnel circuit’s losses is crucial in reducing the fan’s size and the motor’s power required to drive the flow.

Determining the values of K_0 for each part of the circuit is a straightforward but often lengthy process. As previously discussed, it involves applying the fundamental aerodynamic relationships for turbulent flows through pipes and ducts. In addition, other results are required, such as losses through the corner vanes, turbulence screens, etc. If the losses of the motor and the fan/motor stage were included in the energy ratio, however, it would shed little light on the efficiency of the tunnel design itself. For this reason, it is usually excluded from the pressure loss calculation.

For example, consider determining the fan power required to generate a given flow velocity in the test section of a wind tunnel, an effect often called the pumping power. This approach requires determining all the various pressure losses in the tunnel circuit, including frictional losses and pressure drop over the walls, turning vanes, screens, etc. Unfortunately, not all of these effects may be known other than being estimated until the wind tunnel is built and tested. Therefore, the wind tunnel design may require significant power margins to meet the specifications fully.

Check Your Understanding #4 – Calculating the power required to drive a lo-speed wind tunnel

Estimate the minimum motor power required for a low-speed wind tunnel with a maximum flow speed of 230 mph in the test section. The test section area is 22.5 ft^2, and the energy ratio of ER_t for the tunnel is 5.2. The fan efficiency is 0.74%, and the motor efficiency is 90%.

The specification of the energy ratio gives the cumulative losses in the tunnel, so the first step is to find the energy of the flow in the test section, i.e.,

    \[ \mbox{\small Energy} = \frac{1}{2} \varrho \, A_0 \, V_0^3 \]

The value of A_0 is 22.5 ft^2 and V_0 = 230 mph = 337.33 ft/s. Assume MSL ISA for the air density, so \varrho = 0.002378 slug ft{^{-3}}. This gives

    \[ \mbox{\small Energy} = \frac{1}{2} \varrho \, A_0 \, V_0^3 = 0.5 (0.002378) (22.5) (337.33)^3 = 1.0269 \times 10^6 \]

Therefore, the power required to be delivered to the air at the fan/motor stage would be

    \[ P_{\rm air~power} = \frac{\mbox{\small Energy (at test section)} }{ER_t} = \frac{1.0269 \times 10^6 }{5.2 \times 550} = 359.1~\mbox{ hp} \]

Taking into account the fan and motor efficiency then, the minimum power required would be

    \[ P_{\rm req} = \frac{P_{\rm air~power}}{\eta_p \, \eta_m} = \frac{359.1}{(0.74)(0.90)} = 539.1~\mbox{ hp} \]

This latter result would only be valid for an empty test section, and to get the same flow speed with an article in the test section, more power would be needed to overcome the drag and “blockage'” of the article. This value is generally unknown a priori. However, it is usually considered reasonable to add a margin of power to overcome a winged test article with a wing span of 0.8 of the tunnel diameter (or width), an aspect ratio of 5, and a C_D of 1.0. Furthermore, to account for the potential diversity of test articles (not all will be streamlined shapes), a margin of 50% more power may be needed. The final estimated rated motor power for the tunnel would be about 900 to 1,000 hp.

Summary & Closure

Internal flows are encountered in various aerospace applications, such as engine air intakes, fuel systems, hydraulic systems, air conditioning systems, wind tunnels, and other applications where fluids flow through pipes and ducts. A significant consideration for internal flows is that frictional effects from the action of viscosity produce significant pressure drops along the length of the pipe or duct. These pressure drops require a source of power to pump the fluid along the pipe or duct, and this power required is related to the flow velocity and internal surface finish. Because such flows are inevitably turbulent, a Moody chart must be used to determine the friction factors and estimate the resulting pressure drops for design purposes. Internal flows are critical within the combustion chambers of jet and rocket engines, where combustion produces high-temperature, high-pressure gases to produce thrust. Aircraft and spacecraft have environmental control systems to maintain comfortable conditions for passengers and crew, which also require the analysis of internal flows. Understanding and optimizing internal flows in aerospace applications are essential for improving efficiency, safety, and overall performance.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • For an aircraft’s hydraulic system, discuss some potential design trades in operating the hydraulic system with smaller pipes and higher pressure versus larger pipes and lower pressure.
  • What is the definition of internal flow in fluid dynamics? How does internal flow differ from external flow, and what are some examples of each?
  • Consider the fuel and oxidizer system for a rocket engine, which requires high mass flow rates of cryogenic liquids. What are the internal flow issues to consider regarding the delivery of the fuel and oxidizer to the combustion chamber in this case?
  • The corner or turning vanes in a wind tunnel are a large source of losses. Consider the engineering steps you might take to calculate and minimize such losses.
  • Explain the significance of the Reynolds number in internal flows. How does it affect the flow characteristics? Compare the flow regimes associated with low and high Reynolds numbers in internal flows.
  • Explain the major differences between flow in circular pipes and non-circular conduits. How do these differences impact flow characteristics?

 

Other Useful Online Resources

To learn more about internal flows, take a look at some of these online resources:

  1. See: "The History of Poiseuille's Law," by S. P. Sutera and R. Skalak, Annual Review of Fluid Mechanics, Volume 25, 1993. According to them, the naming of Equation 29  as Poiseuille's law occurs in a publication by Hagenbach (1860), who, after giving the derivation, generously suggested calling it Poiseuille's law.  Jacobson (1860) also calls Equation 29 Poiseuille's law. See: Hagenbach, E. 1860, "Uber die Bestimmung der Zahigkeit einer Fliissigkeit durch den Ausfluss aus R6hren,'' Poggendorf's Annalen der Physik und Chemie, Vol. 108, pp. 38–426, and Jacobson, H. 1860, "Beitriige zur Haemo­ dynamik," Archives of Anatomy and Physiology, Vol. 80, pp. 80–113. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n26