54 Rockets & Launch Vehicles
Introduction
Rockets launch payloads, such as satellites and space probes, into Earth orbit. Launch vehicles are highly specialized and tailored to specific missions and payloads. For example, some launch vehicles are designed to place payloads such as satellites into low Earth orbit, while others are intended to send spacecraft into deep space. The choice of the launch vehicle will depend on various factors, including the desired orbit, payload mass, and size. In addition to military and civilian applications, there is also a growing interest in commercial and tourism-related payloads. Companies like SpaceX and Blue Origin are developing launch vehicles that can be used for both commercial satellite launches and human spaceflight, potentially opening space to a broader range of users and applications.
Solid and liquid propellant rocket engines are commonly used for launch vehicles and can be combined to achieve specific performance characteristics. Solid-fuel rocket boosters can provide high initial thrust at liftoff. In contrast, liquid propellant engines can provide more precise control of the thrust generated and greater efficiency once the vehicle is in flight. In addition, the number of stages in a launch vehicle can vary depending on the mission requirements. Some launch vehicles have only one stage, while others have multiple stages that are separated sequentially during flight. The multi-stage approach enables the payload to achieve higher velocities and altitudes with less propellant than would be possible with a single-stage rocket design.
Learning Objectives
- Appreciate the various types of rockets and launch vehicles, as well as their applications in space missions.
- Know how to derive and use the rocket equation to solve simple problems, such as determining burnout velocities.
- Understand the staging process and its use for launch vehicles.
- Know about missiles and the ballistics of projectiles.
Types of Rockets
There are various types of rockets designed for different purposes and applications. Launch vehicles transport payloads into space. Commercial rockets provide satellite launch services, with some being partially reusable to reduce costs. Crewed spacecraft launch vehicles, like SpaceX’s Falcon 9, can transport humans to orbit. Space probes explore celestial bodies, suborbital rockets facilitate space tourism, and military rockets and missiles serve in defensive and offensive roles. Experimental rockets, such as research and hobbyist rockets, are designed to support scientific experiments and personal projects. The diversity in rocket types reflects the multifaceted nature of space exploration, defense, and scientific research.
Launch Vehicles
A representative launch profile of a rocket designed to send a payload into space is shown in the figure below. At the moment of initial launch, the thrust produced by the engines will be greater than the rocket’s weight, allowing it to accelerate quickly away from the pad. The rocket’s weight rapidly decreases from its high fuel consumption, allowing it to continue accelerating as it gains altitude. As the rocket begins to exit the atmosphere, which is about 60,000 ft (approximately 20,000 m), it will fly at supersonic velocities. It also begins to pitch into a more horizontal flight path, and the rocket gains translational velocity, allowing the payload to reach its initial equilibrium orbital velocity and altitude.
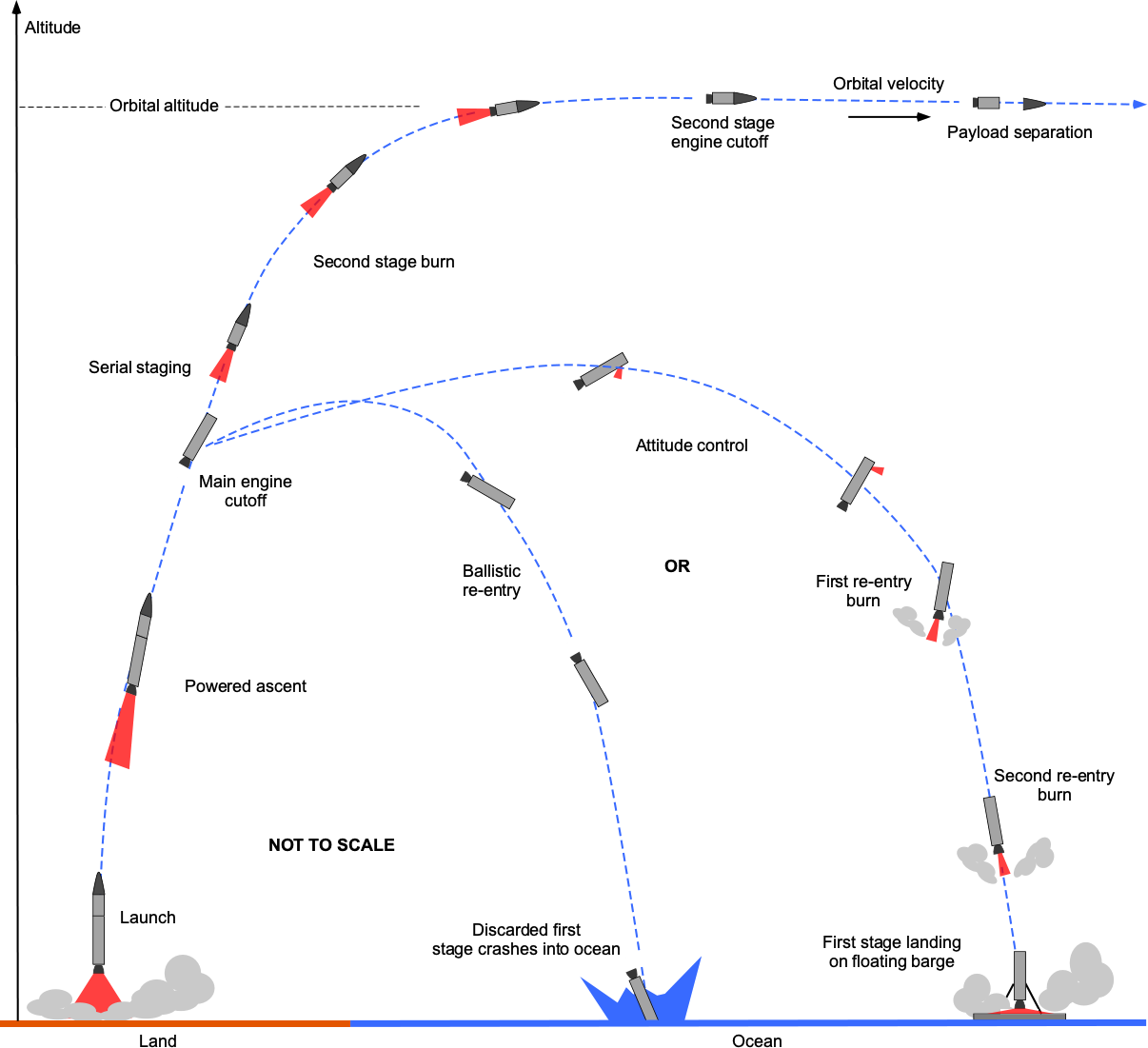
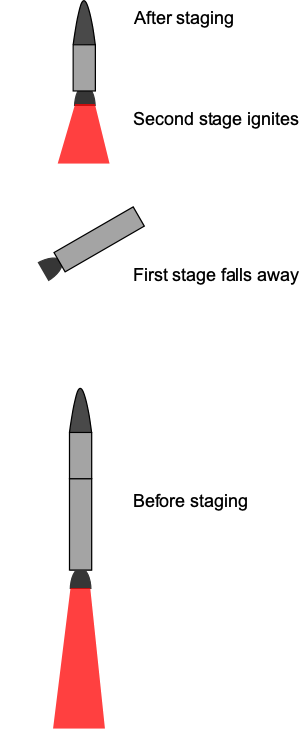
Several minutes into the ascent, staging will occur where the first stage is jettisoned and the rocket engine for the second stage is ignited. The first stage then falls back to the surface and either burns up in the atmosphere (depending on the staging altitude) or breaks apart and crashes into the ocean. In exceptional cases, the first stage may be recovered; solid rocket boosters are usually recovered by parachute and may be reused.
The upper stage (or stages) then continues to accelerate into space. The rocket engines will cut off as the payload reaches the required initial orbital velocity and altitude, which is known as a parking orbit. A second burn is then performed after the orbit has stabilized, placing the spacecraft into its final orbit. At this point, the payload, such as a satellite, is deployed. Rendezvousing a spacecraft with the International Space Station (ISS) involves a series of precise maneuvers to match the ISS’s orbit. The spacecraft gradually approaches the ISS, conducting proximity operations to ensure alignment. During the final approach, automated systems and minor thruster adjustments guide the spacecraft to dock gently with the International Space Station (ISS).
Spacecraft
Spacecraft are utilized in various applications. Some are designed for specialist missions, such as planetary exploration or Earth observation, while others have a more general-purpose application and can be used for multiple tasks. Spacecraft typically consist of numerous sub-systems and components, including a payload (the primary equipment or instruments for the mission), a propulsion system (to maneuver and adjust the spacecraft’s trajectory), communication systems (to transmit and receive data), and power systems (such as solar panels or batteries).
One essential function of a spacecraft is orbit insertion, which involves placing the spacecraft into a specific orbit around a planet or other celestial body. This goal requires a carefully planned trajectory and precise firings of the rocket engines to achieve the desired orbit. However, spacecraft can be highly complex and require extensive testing and development on Earth to ensure their reliability and safety in the space environment. This work involves testing in simulated space environments and rigorous quality control procedures to ensure that all components meet strict performance standards, thereby minimizing the risk of malfunctioning in space, which can be disastrous and result in substantial financial loss.
Missiles
Missiles can be broadly categorized into two main types: ballistic missiles and cruise missiles. Ballistic missiles are used for long-range strikes against threats. They are launched high into the upper atmosphere or the fringes of space, following a parabolic trajectory before reentering the atmosphere and striking their target. Ballistic missiles can be easier to intercept than cruise missiles because they follow a predetermined flight path that is challenging to alter after the launch.
Cruise missiles are designed to fly at low altitudes and follow a more maneuverable flight path to evade threats and defenses. They can be launched from various platforms, including aircraft, ships, and ground-based launchers. Cruise missiles can be more challenging to detect and intercept because they fly at lower altitudes than ballistic missiles and are fast and highly maneuverable.
In addition to their propulsion system, targeting, guidance, and warhead systems, missiles require advanced sensors and communication systems to navigate accurately to their targets and avoid obstacles. Consequently, missiles are highly complex weapons systems that require extensive testing and development to ensure their reliability and effectiveness. In addition, they are subject to strict regulations and controls, and their use is governed by international law.
Miscellaneous Types of Rockets
Sounding rockets gather data on atmospheric conditions, such as temperature, pressure, and wind speed, at altitudes that are difficult to reach with aircraft or balloons. They are typically small, single-stage rockets launched into suborbital trajectories, carrying scientific instruments and sensors to collect various types of data.
Jet-Assisted Takeoff (JATO), also known as Rocket-Assisted Takeoff (RATO), is a technique that utilizes rockets to provide additional thrust during an aircraft’s takeoff, particularly when the aircraft is heavily loaded or operating from a short runway. The rocket engines temporarily boost the aircraft’s acceleration, helping it take off and climb. The most famous RATO aircraft is a modified Lockheed Martin C-130 Hercules. This four-engine turboprop military transport airplane has served as a utility aircraft for the Blue Angels. The RATO system features solid rocket engines mounted on the sides of the aircraft’s fuselage.
Rockets are also used to provide emergency lifelines to ships that are in distress. In this application, a rocket-powered line is fired from shore or another ship to the stranded vessel, enabling rescuers to establish a connection and provide assistance. Rockets could also deliver relief materials to inaccessible areas during natural disasters or humanitarian crises. However, this approach would require the development of reliable and cost-effective rocket delivery systems, as well as appropriate infrastructure and logistical support.
Rocket Equation
The rocket equation is widely used in rocket sizing and estimating propellant loads. The Russian scientist Konstantin Tsiolkovsky, who published it in 1903 in his work on spaceflight theory, is credited with deriving it. However, Robert Goddard and Hermann Oberth also derived the rocket equation independently of Tsiolkovsky (and each other) during the 1920s.
Derivation
Consider an accelerating rocket of mass , where the engine’s thrust is used to propel it, as shown in the figure below. Using Newton’s second law, then
(1)
where is the acceleration of the rocket. The forces from gravity and atmospheric drag have been neglected relative to the rocket’s weight, so the equation is strictly valid for a rocket in space. However, it is not an unreasonable approximation, even when considering flight in the atmosphere.

The thrust produced by the rocket motor is
(2)
where is the mass flow rate of the propellant during the burn, and
is the equivalent exhaust velocity from the rocket motor’s nozzle. Using Eq. 2, then
(3)
which gives the acceleration of the rocket during the burn as
(4)
The change in mass of the rocket is (from the use of propellant), so the time rate of decrease of mass is equal to the mass flow rate, i.e.,
(5)
so that
(6)
Separating the variables and integrating them over the burn time gives
(7)
where and
are the initial mass and velocity of the rocket at
, respectively, and
and
are the final mass and velocity, respectively, at time
.
After integration of the previous equation, the change in the velocity of the rocket is
(8)
This latter equation, known as the rocket equation, is highly useful in mission performance analysis and vehicle sizing. In some ways, it is analogous to the Breguet equations used in aircraft performance analysis. Notice that is given by
(9)
where is the mass of propellant used.
The rocket equation is often written in terms of the initial mass, , and the burnout mass,
, i.e., the mass of the rocket after the propellant is fully expended, as
(10)
where is the initial velocity, and the burnout velocity is
. For a launch vehicle, its initial velocity on the pad is zero (
), so the burnout velocity for the rocket (or the first stage) will be
(11)
Effects of Gravity
If gravity losses are included (but no aerodynamic drag losses) in the case of a pure vertical launch, then the rocket equation in Eq. 10 is modified to
(12)
The second term, , is referred to as the gravity loss. Notice that for a rocket going up vertically, the gravity loss term reduces the attainable velocity of the rocket at the burnout time, i.e.,
(13)
where is standard gravity, which is equal to 9.81 m/s
or 32.17 ft/s
. Therefore, the rocket equation with the gravity loss term becomes
(14)
If the rocket follows a curved trajectory and pitches over at a local trajectory angle (with respect to the horizon) as it increases altitude, then the gravity loss term is
(15)
where when the rocket flies vertically and
when it flies horizontally. However, properly evaluating this latter term requires more specific information about the launch profile, i.e.,
. Neglecting the gravity loss term is usually justified as its value is relatively small compared to the
obtained by burning the propellant.
Burnout Height
For a single-stage rocket, the vertical height achieved at the burnout time, , is
(16)
If the flight velocity, , is given by
(17)
then the height achieved at is
(18)
After integration, then
(19)
Rocket Mass Breakdown
The initial mass of the rocket vehicle can be written as the sum
(20)
where is the mass of the propellant,
is the structural mass of the rocket, and
is the mass of the payload. The burnout mass is reached when all of the propellant is exhausted, which is given by
(21)
As in most engineering fields, it is convenient to use dimensionless quantities. For rockets, the initial mass-to-burnout mass ratio, , is defined as
(22)
Likewise, the payload ratio, , is defined by
(23)
Finally, the structural mass coefficient, , is defined by
(24)
In light of these preceding definitions, it can be shown that the mass ratio is given by
(25)
Therefore, in terms of the mass and payload ratios and the structural mass coefficient, then
(26)
Payload mass ratios can vary significantly depending on the mission objectives, destination, and launch vehicle configuration. However, historical data show that structural mass coefficients are relatively consistent across various rockets and launch vehicles. The structural mass coefficient, denoted by , represents the structural mass ratio to the stage’s initial mass. Its approximate constancy among different vehicle designs is convenient for preliminary design studies, where an estimated value of
can be assumed without requiring a detailed structural analysis. Typical values of
for various launch vehicles are listed in the table below.
| Vehicle Type | Typical Structural Mass Coefficient (ε) |
|---|---|
| Solid rocket stages | 0.09–0.12 |
| Liquid rocket stages (expendable) | 0.07–0.10 |
| Liquid rocket stages (reusable) | 0.10–0.15 |
| Upper stages (lightweight) | 0.04–0.08 |
| Heavy-lift first stages | 0.08–0.12 |
| Reusable boosters (e.g., Falcon 9 first stage) | 0.12–0.18 |
Structural Mass Breakdown
The structural mass of a rocket includes all components of the vehicle that are necessary to support and operate the propulsion and payload systems, excluding the propellant and payload themselves. Structural mass encompasses the mass of the propellant tanks, interstage structures, primary load-bearing frames, thrust mounts, and aerodynamic fairings. It also includes the mass of the propulsion feed systems, pressurization systems, avionics, wiring, thermal protection systems, and, in the case of reusable vehicles, landing gear and recovery hardware. The propellant tanks must withstand internal pressures and dynamic loads during flight, often requiring significant reinforcement, particularly in cryogenic applications where thermal insulation is also necessary. Interstage adapters and bulkheads transfer thrust and aerodynamic loads between different stages while maintaining structural integrity under varying stress conditions.
The thrust structure mounts the engines and transmits the engine loads into the rocket body, often representing a substantial portion of the total structural mass. Aerodynamic fairings protect the payload during ascent through the atmosphere and must be lightweight yet capable of surviving aerodynamic and acoustic loading. Pressurization systems, such as helium tanks for maintaining tank pressure during propellant depletion, add further mass. Avionics and wiring, although individually lightweight, accumulate into a non-negligible fraction of the total structure when distributed throughout the vehicle. Thermal protection systems, particularly for reentry vehicles, contribute to the structural mass through the addition of heat-resistant materials. In modern reusable rockets, additional mass is incurred by structures designed for descent control and landing, such as grid fins, reaction control thrusters, and deployable landing legs. The structural mass must be minimized as much as possible to maximize payload capacity, but it must also meet stringent strength, stiffness, and durability requirements.
Impulse
The total impulse is defined as the integral of the thrust over its burnout time, , i.e., the time for which the rocket engine runs. The total impulse is given by
(27)
as illustrated graphically in the figure below. Notice that the impulse is the area under the thrust/time curve.
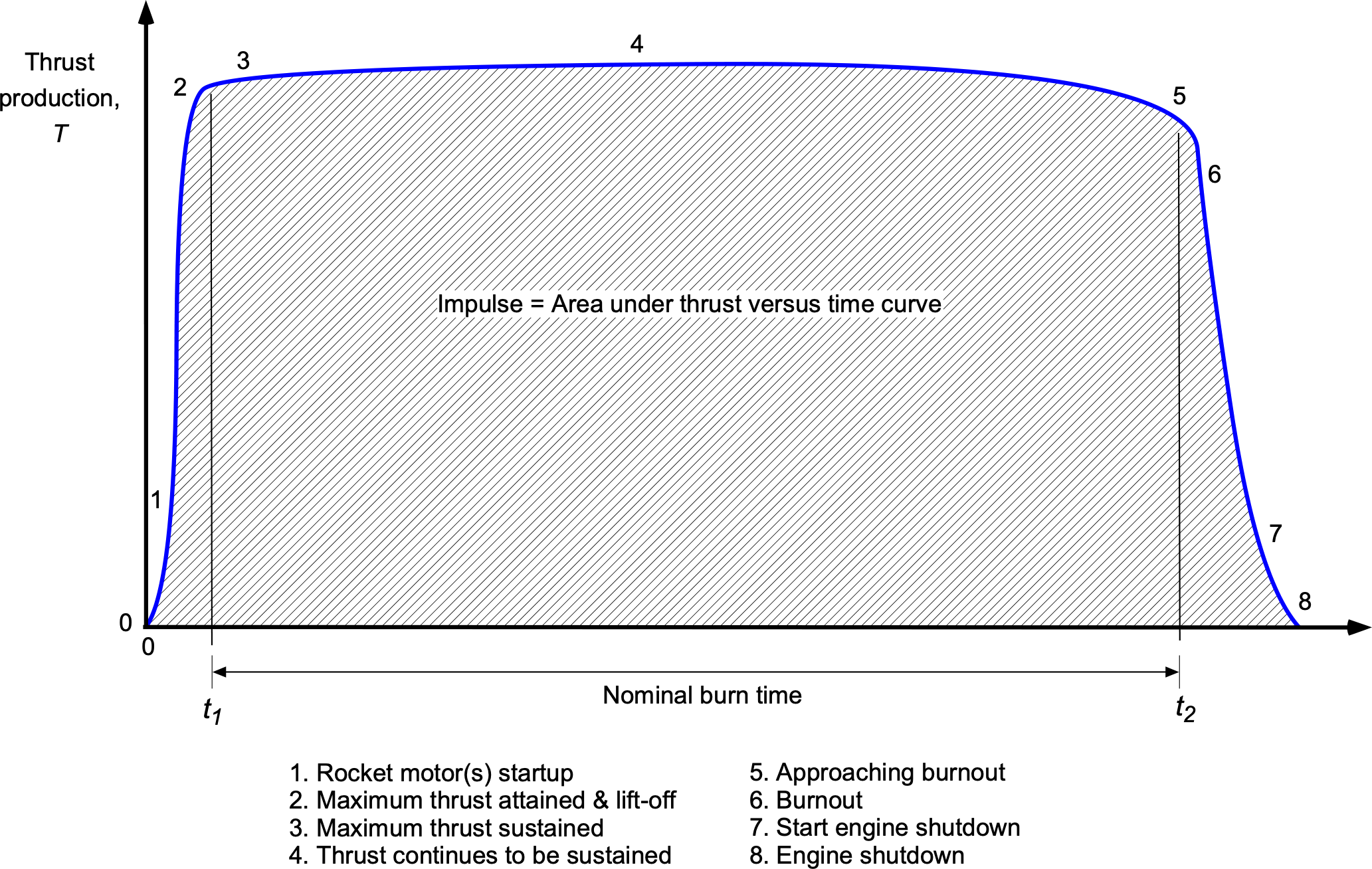
If and
are constant, as is often a good approximation, then
(28)
where is the mass of the propellant burned. The total impulse, therefore, will be equivalent to the net momentum imparted to a rocket by the engine(s) during the burn.
Specific Impulse
The measure of efficiency used in most rocket performance calculations is the specific impulse, which is the total impulse produced divided by the propellant used in terms of its weight. The specific impulse is a property of the propellant’s chemical composition and can be evaluated using a thermodynamic analysis. In general, one wishes to carry as little propellant as possible, so the idea is to have a rocket with a high specific impulse.
The specific impulse, , is defined as
(29)
Therefore, the higher the value of , the more efficient the rocket motor will be in producing thrust. It will be noted that the specific impulse for the rocket motor is analogous to the specific fuel consumption for an air-breathing engine. It is further apparent using Eq. 2 that if the thrust is approximately constant, then
(30)
where it will be noticed that has units of time (seconds).
Therefore, the specific impulse is the total impulse (or change in momentum delivered) per unit weight per unit time of the propellant consumed, which is a measure of the efficiency in producing thrust. The equivalent exhaust velocity, , depends to a large extent on the chemistry and efficiency of the combustion of propellant. High combustion temperatures using propellants of low molecular weight are essential in achieving the highest values of specific impulse. To this end, the best-known propellants are liquid hydrogen (LH2) and liquid oxygen (LO2 or LOX), as summarized in the table below.
| Fuel / Propellant Combination | Rocket Type | Specific Impulse (s) | Conditions |
|---|---|---|---|
| Ammonium perchlorate composite propellant (APCP) | Solid rocket motor | 240–290 | Sea level |
| RP-1 (kerosene) / Liquid oxygen (LOX) | Liquid bipropellant | 280–310 | Sea level |
| Liquid hydrogen (LH₂) / Liquid oxygen (LOX) | Liquid bipropellant | 370–465 | Sea level / Vacuum |
| UDMH / Nitrogen tetroxide (N₂O₄) | Hypergolic bipropellant | 290–320 | Vacuum |
| Hydrazine (monopropellant) | Monopropellant thruster | 220–240 | Vacuum |
| Xenon (electric ion propulsion) | Ion thruster | 2,000–5,000 | Vacuum |
| Liquid methane (CH₄) / Liquid oxygen (LOX) | Liquid bipropellant | 360–380 | Vacuum |
| Graphite-based solid propellant | Solid rocket motor | 200–250 | Sea level |
| Hydrogen / Nuclear thermal propulsion | Nuclear rocket engine | 800–900 | Vacuum |
Check Your Understanding #1 – Burnout velocity of a single-stage rocket
Use the rocket equation to determine the burnout velocity and the maximum achievable height of a simple rocket, assuming that it is launched vertically. Neglect the aerodynamic drag forces. Solve for the burnout velocity and maximum altitude if the burnout time is 60 seconds. The specific impulse is 250 seconds, the initial mass is 12,700 kg, and the propellant mass is 8,610 kg. Assume the launch as vertical, ignoring curvature and drag, and solve for the required velocity, assuming it will be redirected to tangential velocity near apogee (e.g., by a circularization burn).
Show solution/hide solution.
The rocket equation gives the change in the velocity of the vehicle , i.e.,
where is the initial mass of the vehicle and
is the final or burnout mass. If gravity is included (but no aerodynamic drag), then
where is the burnout time, which is 60 seconds in this case.
The equivalent velocity is given in terms of the specific impulse, i.e.,
and the burnout mass is given by
The burnout velocity is given by the rocket equation, i.e.,
Therefore, at the burnout is
which is 2.19 km/s. Assuming the rate of fuel consumption is constant, then the mass of the rocket varies over time as
The velocity of the rocket is
The height achieved at the burnout time, , is
Inserting the values gives
Therefore, the height achieved is
The rocket’s final additional coasting height can then be determined by equating its kinetic energy at its burnout time with its change in potential energy between that point and the maximum obtained height.
Launching into Orbit
Rocket launches are hugely exciting events to watch! The synchronized launch process, the flaming exhaust, and clouds of smoke, followed by the rising spacecraft into the sky, can be awe-inspiring. The technology and engineering behind the launches, the science and exploration they enable, and the thrill of human endeavor all contribute to the excitement. Additionally, watching a rocket launch live or on YouTube can be an educational and inspiring experience, especially for students and younger people interested in science and space. Even those who live in Florida never grow tired of watching rocket launches!

Using the Rocket Equation
Drama and excitement aside, the energy and propellant requirements for a rocket (booster) and its payload with the needed to reach a specific orbital altitude
can be estimated using the principles of energy conservation in conjunction with Tsiolkovsky’s rocket equation. The rocket equation is given as
(31)
where is the equivalent exit velocity from the particular rocket engine,
is the initial mass of the rocket or spacecraft at the beginning of the burn, and
is the final (burnout) mass after the burn at burnout time,
, during which a propellant mass
is consumed. In this case, it is assumed, for simplicity, that it is a single-stage vehicle (i.e., no staging).
The equivalent exit velocity can be written in terms of the specific impulse, , as
(32)
where is the reference value of acceleration under gravity at mean sea-level on Earth, i.e.,
m/s. Therefore, the rocket equation can also be written as
(33)
where the value of depends on the type of rocket engine and its propellant. If the value of
is known, then the rocket equation can be used to determine the propellent mass needed to give a certain
for the satellite or spacecraft to reach an orbit at the required altitude,
, as shown in the figure below.
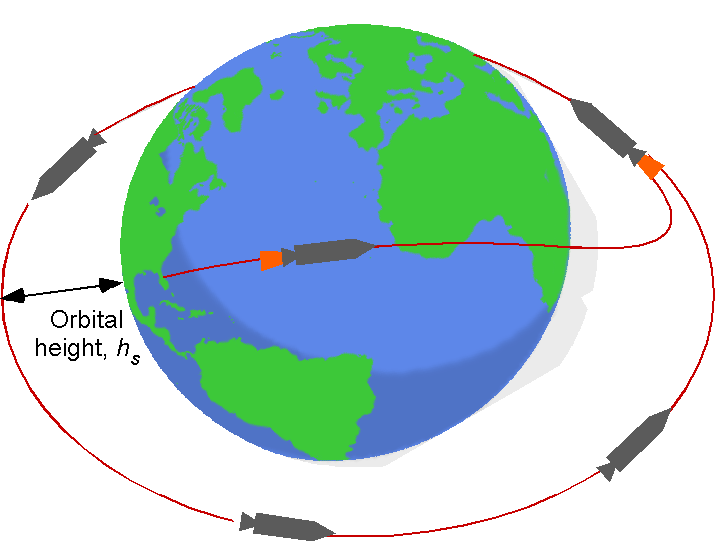
For a launch, several factors can influence the required, i.e.,
- The needed orbital altitude above the surface of the Earth,
.
- The orbital inclination relative to the Earth’s equatorial plane.
- The launch latitude from the Earth (this affects the initial energy).
- The effects of overcoming gravity (when the rocket goes vertically).
- The aerodynamic drag on the rocket in the lower atmosphere.
- Steering losses because of small misalignments of the thrust vector.
Kinetic Energy
For the satellite or spacecraft to reach the required orbital altitude, , the
required for the needed kinetic energy is
(34)
noting that this result does not depend on the mass of the satellite or spacecraft. This latter component is the dominant energy requirement for high orbits.
Potential Energy
The associated with creating the needed potential energy for the same orbit is
(35)
For low orbital altitudes with , then
(36)
which is the dominant term in this case compared to the kinetic energy.
Gravity Loss Effect
A gravitational effect must be added to the total needed , usually called gravity loss. For a rocket going up vertically, then
(37)
where is the burnout time. If the rocket follows a curved trajectory and pitches over at a local trajectory angle
(with respect to the horizon) as it increases altitude, then
(38)
where when the rocket flies vertically and
when it flies horizontally. Therefore, properly evaluating this latter term requires information about the launch profile. Minimizing the gravity loss term means minimizing the burnout time.
Aerodynamic Loss Effect
There is an aerodynamic drag on the rocket as it flies through the lower atmosphere, contributing to the needed propellant requirements to reach a given . This drag force,
, can be expressed as
(39)
where is the dynamic pressure, i.e.,
where
is the local density of the air, and
is the true airspeed, the latter values also requiring information about the launch profile. An ISA model for both the lower troposphere, stratosphere, and extended upper atmosphere can be used to represent the density of the air. The reference area,
, in Eq. 39 is usually taken as the projected frontal area of the rocket. The drag coefficient,
, will also depend on the overall shape of the rocket and its flight Mach number.
The rocket’s drag given by Eq. 39 is proportional to air density and the square of the airspeed. This result shows that to minimize the net aerodynamic effects, the rocket should ascend vertically but as slowly as possible, yet this is contrary to the need to accelerate the rocket as quickly as possible to minimize the cumulative gravitational effects on the net . Nevertheless, the aerodynamic loss on the achievable
is relatively small. More importantly, the dynamic pressure during the launch needs particular emphasis because this quantity affects the aerodynamic-induced structural loads on the rocket.
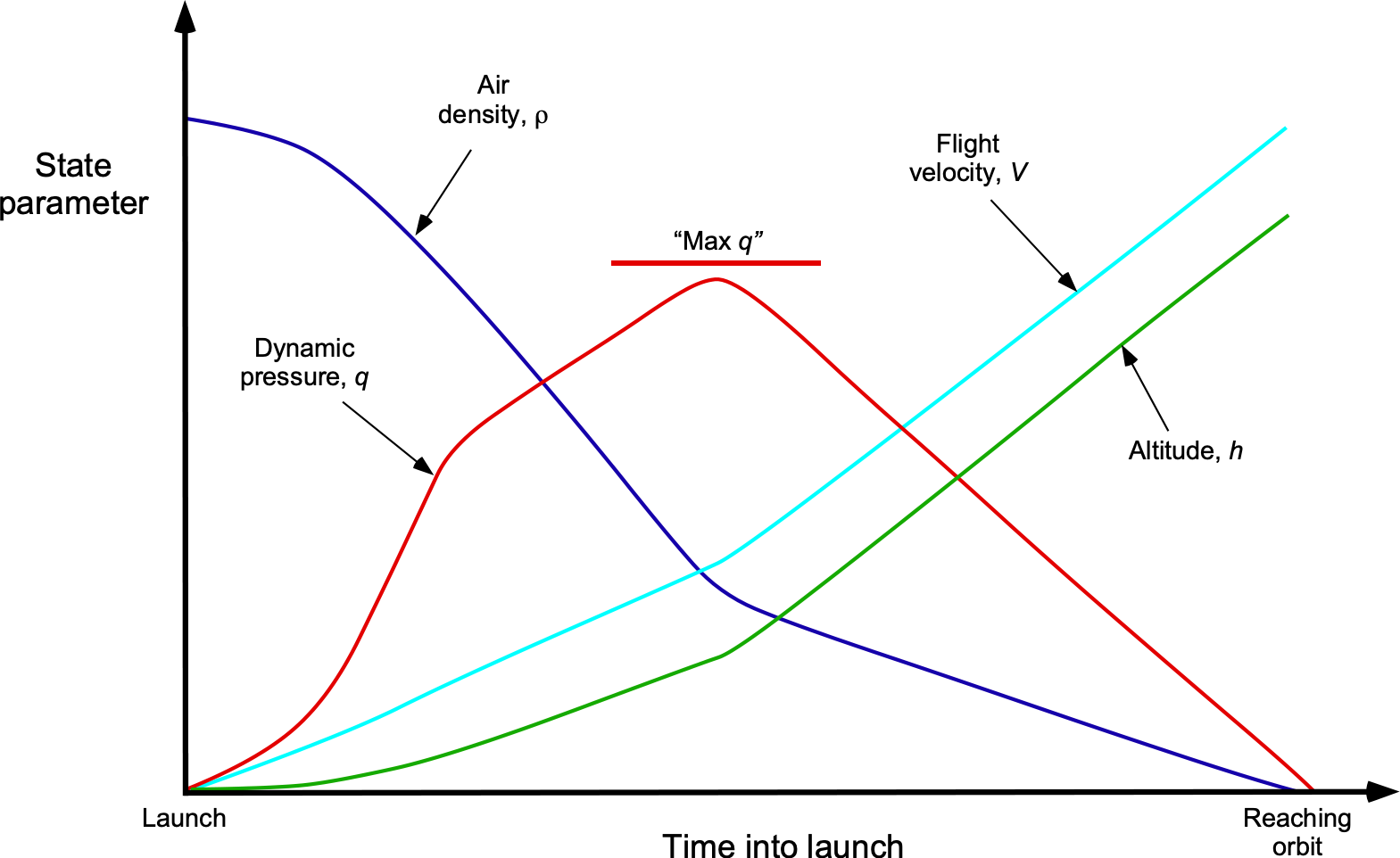
As shown in the representative launch profile below, the value of increases rapidly after launch, reaching a maximum and decreasing quickly as the altitude increases and the density of the air diminishes. In many cases, the “maximum
” value on the rocket will be limited, requiring the rocket engines to be throttled down temporarily to prevent excessive aerodynamic loads on the vehicle.
Aerodynamic drag coefficients for launch vehicles are not generally available. However, some research has been published, including Ballistic Research Laboratories, Memorandum Report No. 545, and NASA TM X-53770. The latter report shows the drag coefficients of the NASA Saturn V launch vehicle as measured in several wind tunnels over a wide range of Mach numbers, a sample of which is shown in the figure below. The reference length used in the results is the diameter of the primary launch vehicle, where = 10.06 meters or 33 feet. The total drag (axial) force is split into forebody drag and base drag. Notice the rapid increase in drag coefficient during the transonic region near Mach = 1, followed by a progressive reduction in drag coefficient in the supersonic regime.
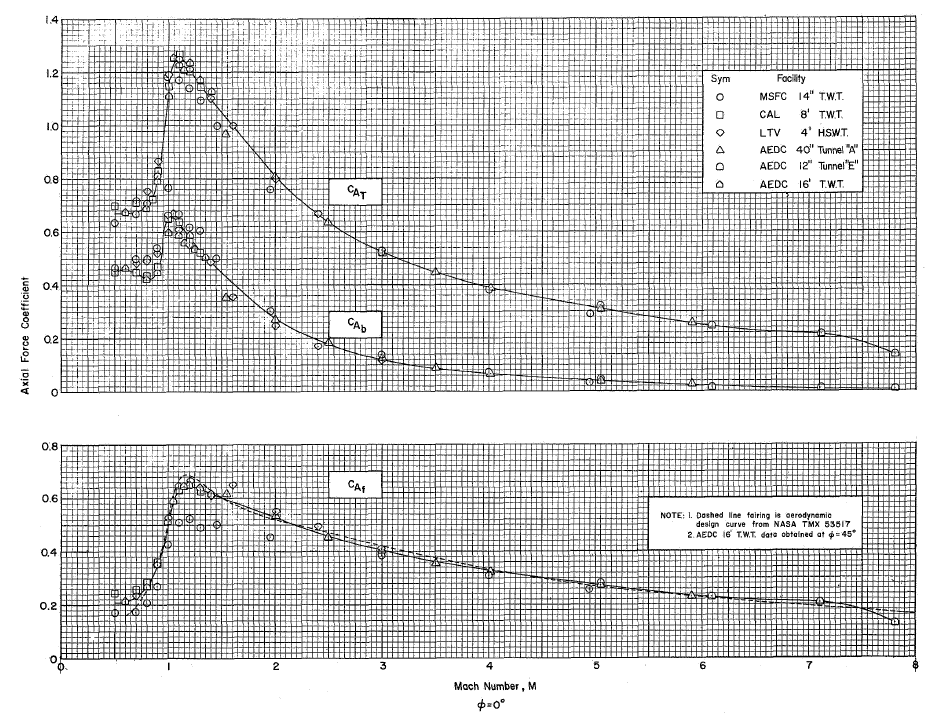
In the absence of any other information, the drag coefficient, , for a rocket is often represented as
(40)
where is the Mach number of the freestream aerodynamic flow. The
increment required to overcome aerodynamic drag (again, using the rocket equation) will be
(41)
where is the instantaneous mass of the rocket and
is the launch time over which aerodynamic forces are considered. However, for most launch vehicles, the
velocity losses from aerodynamic drag are cumulatively small and are typically between 0.05 and 0.15 km/s. In the case of smaller rockets and air-to-air missiles, which reach high flight velocities after a short time, aerodynamic losses will likely need to be considered.
Launch Latitude
The needed also depends on the latitude of the launch. The initial energy given to the rocket from the Earth’s rotation is higher for launch sites closer to the equator. The needed
is lower if the rocket is launched in the direction of the Earth’s rotation (toward the east). For launches from Cape Canaveral, for example, the
boost (i.e., a negative
) is about 0.3 km/s and is certainly not insignificant regarding propellant requirements.
Total Delta-V
Therefore, the total needed is the sum
(42)
The required propellant mass, , can then be estimated from the rocket equation, i.e.,
(43)
again, assuming no staging. Therefore, using the principles of logarithms, then
(44)
If staging is used, the for each stage would be calculated as each stage is depleted of propellant, and the empty stage is discarded.
Estimating the Escape Velocity from Earth
The Earth’s mass, , is 5.97
kg. The radius of an initial orbit will be the radius of the Earth
, which is 6.3781
m, plus the orbital height,
. Also, we know that the universal gravitational constant
= 6.67428
N m
kg
. Assuming that the orbital height relative to the radius of the Earth is small, then it can be shown that the minimum escape velocity is given by
All spacecraft designed to head out into space away from the Earth must be given a velocity larger than 11.2 km/s, which is fast!
Steering a Rocket
A rocket must be steered along a prescribed flight path so the payload can reach the necessary altitude. A modern rocket (e.g., a launch vehicle) is usually steered along its flight path by gimbaling (rotating) the engine(s) to change the direction of the thrust vector. However, as the figure below summarizes, other means may also be used.
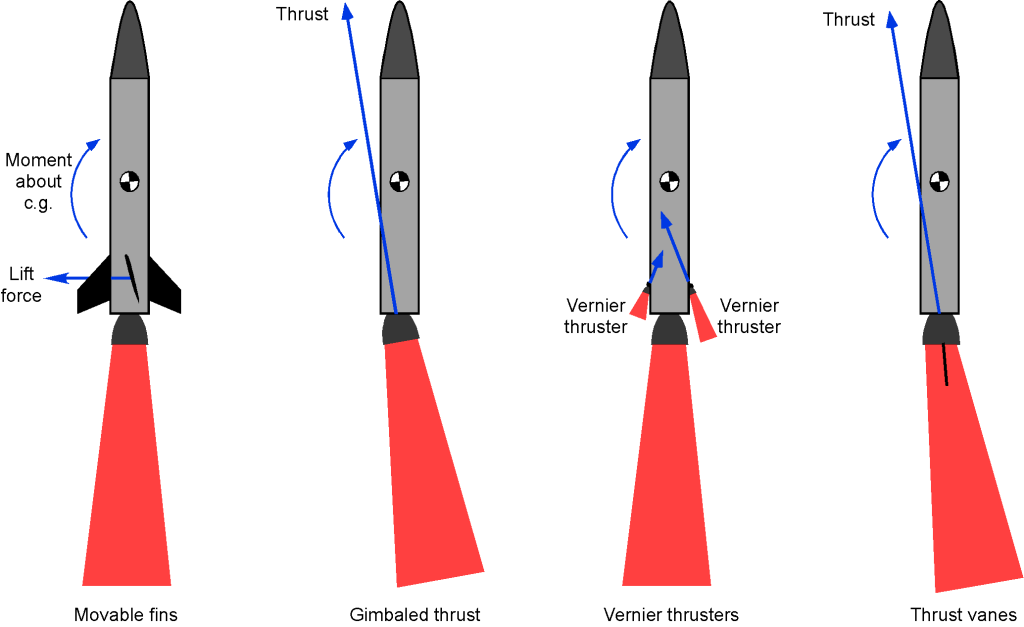
Early rockets used movable aerodynamic surfaces or fins at the rear of the rocket, and this technique is also used on most air-to-air missiles. These surfaces create varying aerodynamic forces and moments on the rocket, which can be used to control its trajectory. Some rockets have used additional vernier rocket engines to give attitude control. However, vernier-steered rockets are not used as much because of this system’s extra weight and the different fuel needed. On some early rockets and ballistic missiles, small thrust vanes were placed directly in the exhaust stream of the rocket’s exhaust to produce forces that could be used for steering.
Steering losses, , also called deviation losses or non-ideal thrust vector losses, arise because the thrust vector cannot always remain perfectly aligned with the velocity vector during a rocket’s ascent. Ideally, thrust would always be directed along the velocity vector to maximize acceleration. However, in practice, the rocket must continually adjust its orientation to follow a curved trajectory, causing a portion of the thrust to be expended in changing the flight path rather than in increasing speed. This misalignment results in a loss of efficiency, which reduces the
, i.e.,
(45)
While steering losses are usually less than gravity and drag losses in magnitude, they can nonetheless become more appreciable for rockets requiring substantial trajectory adjustments.
Staged Rocket Vehicles
Staging a launch vehicle aims to maximize the payload ratio that can be launched into space. The goal is to launch the largest payload to the required burnout velocity using the least non-payload mass (defined as the structural weight of the rocket plus the fuel). As shown in the figure below, there are two types of staging:
- Serial staging, where the stages are ignited, used, and jettisoned in serial sequence.
- Parallel staging, where all stages are ignited and used, but the stages are jettisoned as they burn out, e.g., solid rocket boosters.
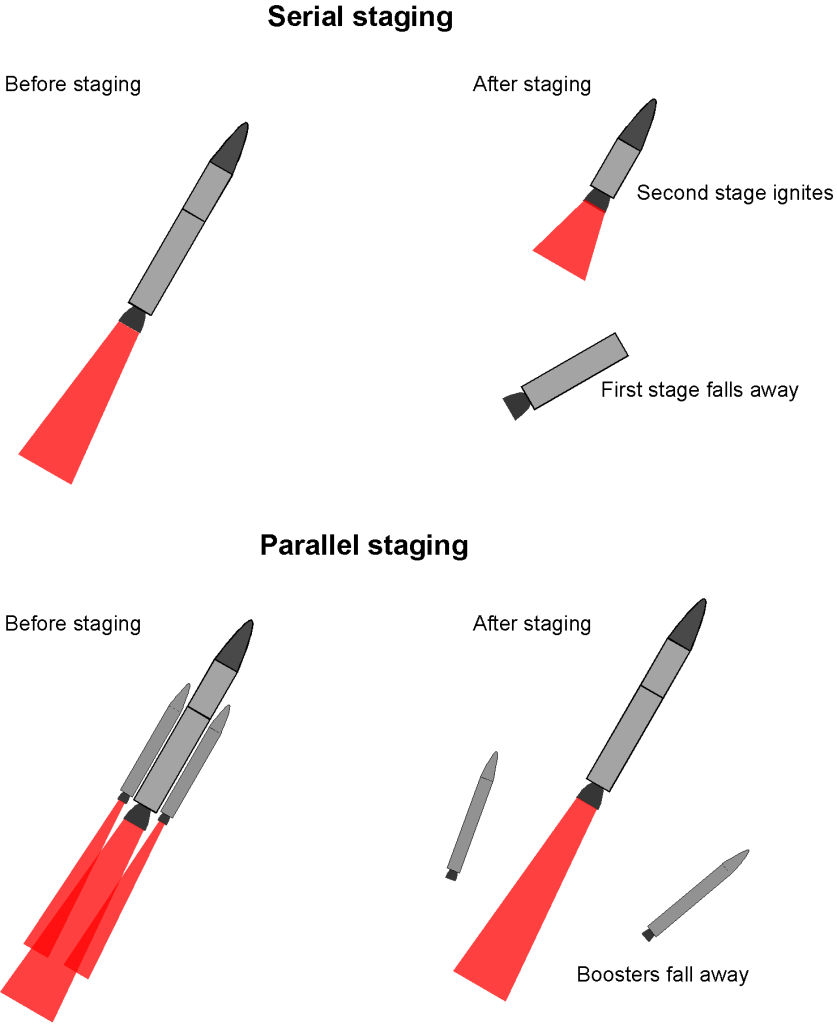
To reach an optimal staging of the launch vehicle, there are four primary considerations:
- The initial stages should have the lowest values of
, and later stages should have the highest
.
- The stages with the lower
should contribute more to
.
- Each successive stage should be smaller than the previous stage.
- Similar stages should provide similar increments to
.
Serial Staged Rocket
For a serial staged launch vehicle, then
(46)
where the index refers to the stage number. Also
(47)
For a staged vehicle overall, the values are added for each stage, i.e.,
(48)
It can be assumed that this velocity is redirected as a tangential velocity for the payload to achieve an orbital path. The structural mass coefficients for a staged launch vehicle are usually similar to those of a single stage. However, payload ratios are generally higher for a staged vehicle. In some cases, finding the maximum allowable structural mass to meet a particular set of payload requirements may be desirable, as well as setting some structural design goals and constraints.
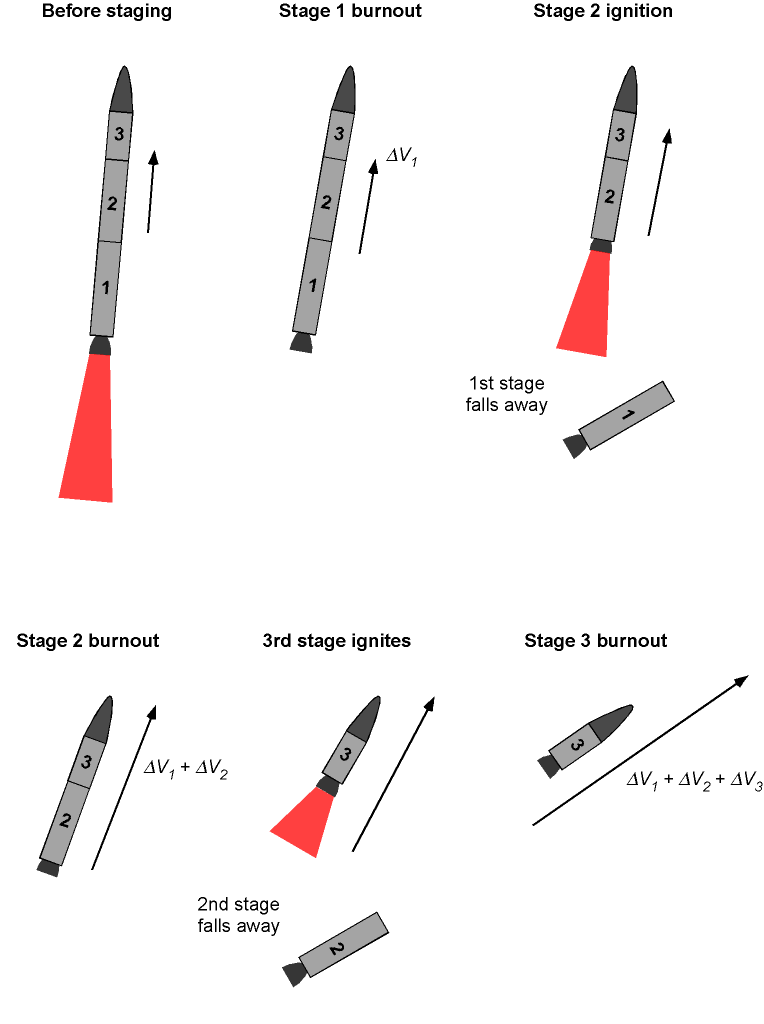
Below is a step-by-step breakdown of the general procedure for calculating the total burnout velocity or time for a multi-stage rocket with serial staging:
-
- Divide the rocket as a system into its stages. A specific propulsion system or engine typically characterizes each stage and will have its own parameters, such as mass, specific impulse, thrust, and fuel weight or burn time.
- For each stage, calculate the initial mass, which is the total mass of the rocket at the beginning of the stage burn, and the final mass, which is the rocket’s mass at the end of the stage burn after the propellant has been burned.
- Calculate the burnout velocity for each stage using the rocket equation. The gravitational force (weight) acting on the rocket must also be considered.
- Add each stage’s burnout velocity to the previous stage’s initial velocity. Assuming that each stage occurs immediately after the previous one, the burnout velocity of one stage becomes the initial velocity for the next stage.
- Repeat steps 2–4 for the final stage of the rocket system until the burnout time and/or burnout velocity have been calculated for the final stage carrying the payload mass.
Check Your Understanding #2 – Two-stage rocket calculation
Consider a two-stage rocket with the following design characteristics. Payload mass = 60 kg. First stage: propellant mass = 7,200 kg, structural mass = 800 kg, and the mass flow rate is = 80.0 kg s
. Second stage: propellant mass = 5,400 kg, structural mass = 600 kg, and the burn time is 100 s. The specific impulse,
, for the first and second stages is 275 s. Assume the launch as vertical, ignoring curvature and drag, and solve for the required velocity, assuming it will be redirected to tangential velocity near apogee (e.g., by a circularization burn). Calculate the following:
For the first stage:
- The equivalent exhaust velocity.
- The thrust produced.
- The total burn time.
- The burnout velocity.
For the second stage:
- The equivalent exhaust velocity.
- The mass flow rate.
- The thrust produced.
- The final burnout velocity.
Show solution/hide solution.
For the first stage:
1. The equivalent exhaust velocity, , is
2. The thrust, , produced is
3. The total burn time, , is
4. The initial mass, , is
and inserting the values gives
The burnout mass, , is
and with the given values leads to the burnout mass of the first stage as
The increment for the first stage is
and inserting the values gives
Therefore, for the first stage, the burnout velocity is
For the second stage:
1. Because the remains the same for stage 2, the equivalent exhaust velocity will also be the same, i.e.,
2. The mass flow rate, , is
3. The thrust produced is
4. For the second stage, the initial mass is
The burnout mass for the second stage is
The for the second stage is
and inserting the values gives
The final value of the burnout velocity, , will be
Launch Height – Two-Stage Serial Rocket
Determining the burnout launch height, , obtained by a two-stage serial launcher, is obtained similarly to a single stage. In this case, the launch heights obtained by each respective stage are added, i.e.,
(49)
For the first stage, the height achieved at will be
(50)
and for the second stage, the height achieved at will be
(51)
Parallel Staged Launcher
With a parallel staged launch vehicle, there are usually dissimilar rockets and rocket engines burning simultaneously, as shown in the figure below. An example would be the NASA Space Shuttle, which used LH2/LOX for the “core” main engines on the Orbiter, with solid propellant rocket boosters being used to significantly augment the initial launch velocity. NASA’s SLS uses the same type of core and booster. Other types of launch vehicles may be configured with different numbers of solid rocket boosters, depending on the payload mass and the desired orbital altitude. An exception is the SpaceX Falcon Heavy, which uses two additional liquid propellant boosters identical to the first (core) stage.

The rocket equation for a core rocket system with one or more boosters can be written as
(52)
where is the initial mass (core plus boosters) and
is the final mass of the launch vehicle after booster burnout. The average or mean equivalent exhaust velocity,
, is given by
(53)
where the subscripts and
refer to the core and the boosters, respectively. The value of
will be the boosters’ net mass flow rate. Alternatively, if
is the mass flow rate of any one identical booster (there is likely to be more than one booster), then
(54)
where is the number of boosters. An illustration of the process for a core rocket system with two boosters is shown in the figure below.
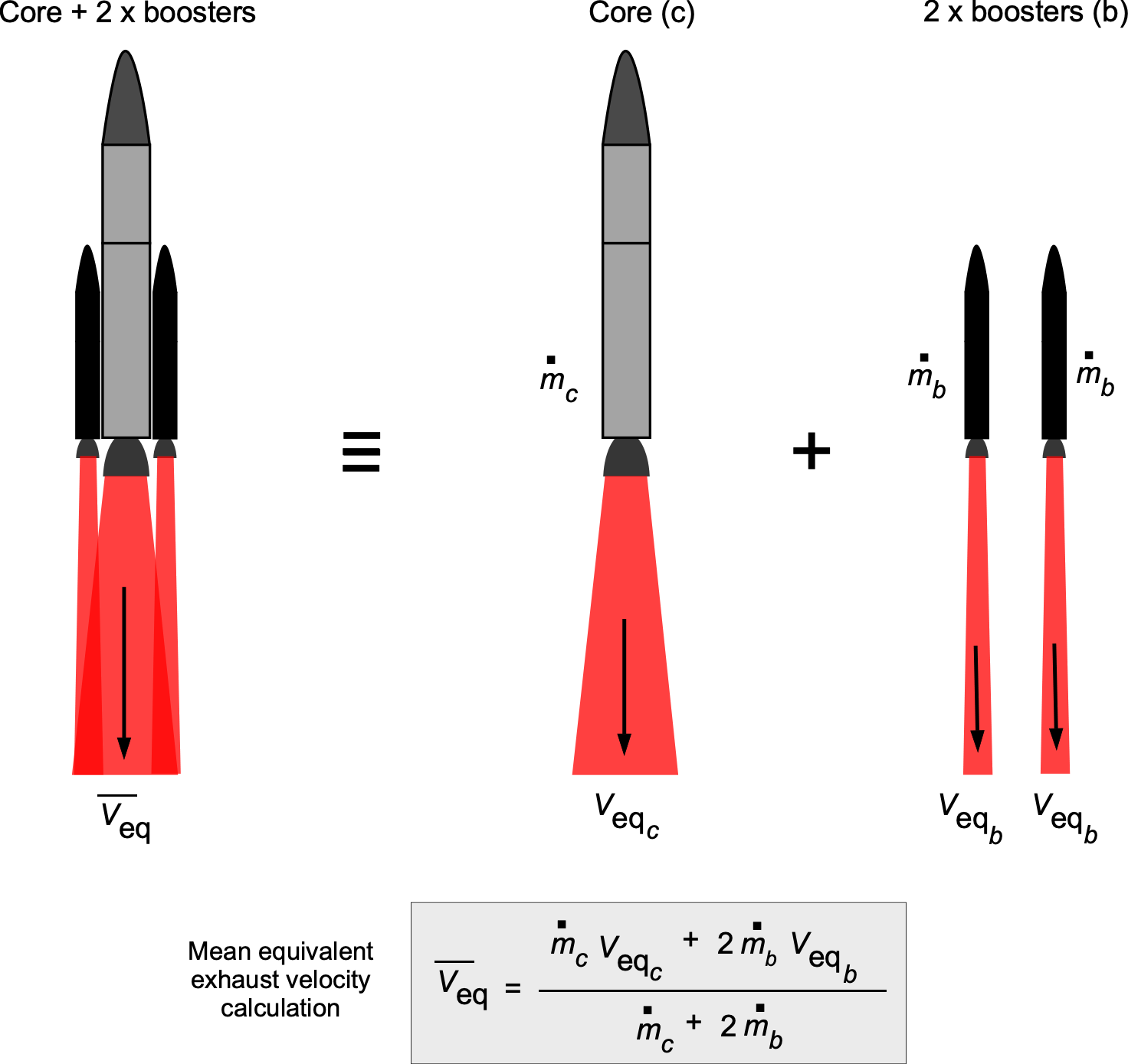
In this case, the initial mass at the launch point is
(55)
where and
are the propellant masses for the core and the boosters, respectively,
and
are the structural masses for the core and the boosters, respectively, and
is the payload mass.
Determining the final burnout mass, , of a launch vehicle with parallel boosters takes further consideration because the core launcher will still have propellant left at booster burnout. Therefore, the final mass at the time of booster burnout, say
, can be written as
(56)
where is the fraction of propellant mass remaining in the core at booster burnout.
Notice that the mass of propellant, , used in a given time,
, is
, so the mean equivalent exhaust velocity,
, can also be written as
(57)
Therefore, the launch of parallel rocket stages can be presented using the sum of pseudo-serial stages, where for stage “0”, with the boosters and the core together, then
(58)
For stage “1” after booster separation, the initial mass will be
(59)
where is the fraction of propellant mass remaining in the core at booster burnout. The final mass after the stage 1 core burns out will be
(60)
where is the fraction of propellant mass remaining in the core at booster burnout.
Therefore, for stage 1, then
(61)
The values of the remaining stages,
, are then calculated as a serial launcher, as before, i.e., the final launch velocity
will be
(62)
Again, it can be assumed that this velocity is redirected as a tangential velocity so that the payload will achieve an orbital path.
Burnout Conditions for Non-Vertical Launch
To place a payload into a stable circular orbit, a launch vehicle must impart sufficient energy to overcome gravity and atmospheric drag, and achieve both the correct altitude and velocity vector. In realistic scenarios, the trajectory is not vertical but gradually transitions from vertical to horizontal flight using what is known as a gravity turn, allowing the vehicle to align its velocity vector with the local horizon at burnout.
For a circular orbit at burnout, the vehicle must travel horizontally at velocity such that the gravitational acceleration provides the necessary centripetal acceleration, i.e., using the universal law of gravitation gives
(63)
where is the gravitational constant,
is the mass of Earth,
is the Earth’s radius, and
is the altitude at burnout. Solving for the required altitude gives
(64)
Notice that this relationship sets a geometric constraint in that orbital velocity and altitude are not independent.
The total velocity increment required from the launch vehicle must equal or exceed the orbital velocity from losses, i.e.,
(65)
In high-altitude ascent, aerodynamic drag is negligible, and steering losses can often be minimized. The dominant loss is from gravity, i.e.,
(66)
where is the pitch angle and
is the burn time. For an approximate analysis, then
(67)
where is the average value of
over the during the thrust phase or burnout time
. Substituting into Eq. 65 gives the approximate required velocity increment as
(68)
The achievable velocity increment is governed by the rocket equation, i.e.,
(69)
where is the effective exhaust velocity of stage
,
is the initial mass, and
is the burnout mass. For a two-stage vehicle, then
(70)
Equating this to Eq. 68 sets the design constraint for orbital insertion.
The altitude gained during thrust is computed by integrating the vertical velocity component, i.e.,
(71)
A simple estimate using average values gives
(72)
where and
are the average velocity and pitch angle, respectively, during
. This approximation captures the tradeoff between thrust direction and vertical altitude gain.
To design an ascent trajectory that leads to orbital insertion, one must determine the orbital altitude using Eq. 64, estimate gravity losses from Eq. 68, compute propulsion performance via Eq. 69, and confirm that the altitude and horizontal velocity at burnout are consistent with orbital conditions. This framework supports preliminary trajectory design, staging analysis, and mission feasibility studies.
Check Your Understanding #3 – Non-vertical launch
A two-stage launch vehicle is designed to place a 300 kg satellite into a circular low Earth orbit (LEO) at an altitude of 200 km. The first stage uses a propulsion system with a specific impulse of = 285 s, and the second stage has
= 326 s. The vehicle consists of a first stage with 8,000 kg of propellant and 80 = kg of structure, and a second stage with 2,500 kg of propellant and 250 kg of structure. The payload mass is 300 kg. Assume standard gravity
= 9.81 m/s2, negligible drag, and an average pitch profile such that
= 0.85. The total powered flight time is estimated to be
= 85 s. Determine whether the rocket can deliver the required velocity increment to achieve orbit, and calculate the burnout altitude.
Show solution/hide solution.
The orbital velocity required for a circular orbit at is computed from
(73)
Using the values m
/kg/s
,
kg,
m, and
m, the orbital radius is
m, then
The total required velocity increment is increased by gravity losses, i.e.,
(74)
Substituting values gives
To determine whether the rocket can deliver this velocity, we can use the rocket equation in terms of the specific impulse. The effective exhaust velocity for each stage is
The initial mass at launch is
For stage 1:
The second stage begins with
Therefore,
The total velocity increment delivered by the two stages is
which exceeds the required by approximately 135 m/s, providing a modest margin for steering corrections or minor unmodeled losses.
To estimate the burnout altitude, assume an average velocity magnitude 4,317 m/s. With
, the average vertical component is
. The burnout altitude is estimated as
(75)
Substituting the values gives
The rocket achieves a burnout altitude of approximately 183 km, which is close to the 200 km target orbit. A brief circularization maneuver at apogee would complete orbital insertion.
Variable Thrust (Throttling) Conditions
The motion of a rocket with variable exhaust velocity and thrust can be analyzed by considering conservation of momentum. Neglecting external forces such as gravity and aerodynamic drag, the governing equation is
(76)
where is the instantaneous mass of the rocket,
is its velocity,
is the mass flow rate (negative), and
is the exhaust velocity, now assumed to vary as a function of mass. Rearranging the force balance gives
. Integrating from an initial mass
to a final mass
, and corresponding velocities
to
, gives
(77)
so that
(78)
This is a more general form of the rocket equation when the exhaust velocity depends on mass. If is constant, the classic form is recovered. Otherwise, the integral must be evaluated based on the specific functional dependence of
on
.
Suppose the rocket is throttled during flight, causing the exhaust velocity to vary with mass according to a power law of the form
(79)
where is the exhaust velocity at the initial mass
and
is a throttling exponent. Substituting into the integral gives
(80)
Evaluating the integral for gives
(81)
so that
(82)
If approaches zero, corresponding to no throttling and constant exhaust velocity, then the classic rocket equation is again recovered as the limiting case. Using a Taylor expansion,
(83)
so that
(84)
This result shows that throttling, by causing the exhaust velocity to vary during the burn, modifies the usual logarithmic dependence of on mass ratio. Throttling down such as at the conditions of maximum dynamic pressure corresponds to small positive values of
. In practice, throttling the rocket engine slightly reduces the achievable
compared to the ideal constant-exhaust-velocity case.
Missiles & Ballistics
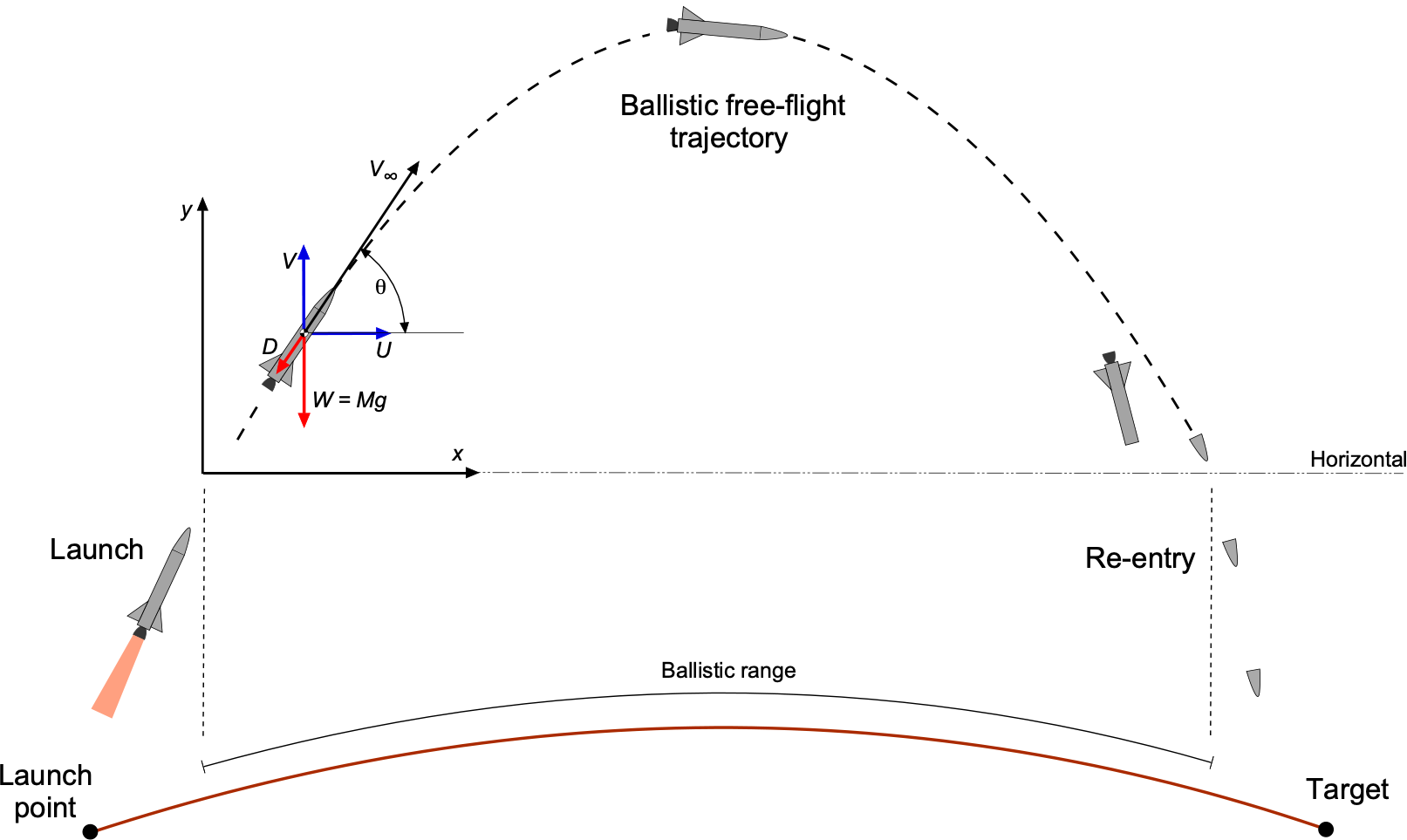
Ballistic trajectories refer to the paths that missiles or artillery projectiles follow from their launch point to their intended targets. Predicting these trajectories is crucial in determining the missile’s flight path, range, and target accuracy. Missile trajectories can vary significantly depending on the type of missile, its intended purpose, the needed range and the altitude it flies to, and the guidance system it uses.
Ballistic missiles follow a trajectory primarily influenced by gravity and the initial launch conditions. They are launched into the atmosphere either vertically or at a steep angle. They then follow a parabolic or elliptical path well into the stratosphere or the edges of space, eventually re-entering the lower atmosphere and impacting their target. Ballistic missiles are known for their high speed and relatively long-range targeting capabilities.
Consider the equations of motion of a missile, as shown in the figure below. For the direction parallel to the flight path, then
(85)
where is the mass of the missile acting at its center of gravity, and
is its acceleration in the direction of the flight path.
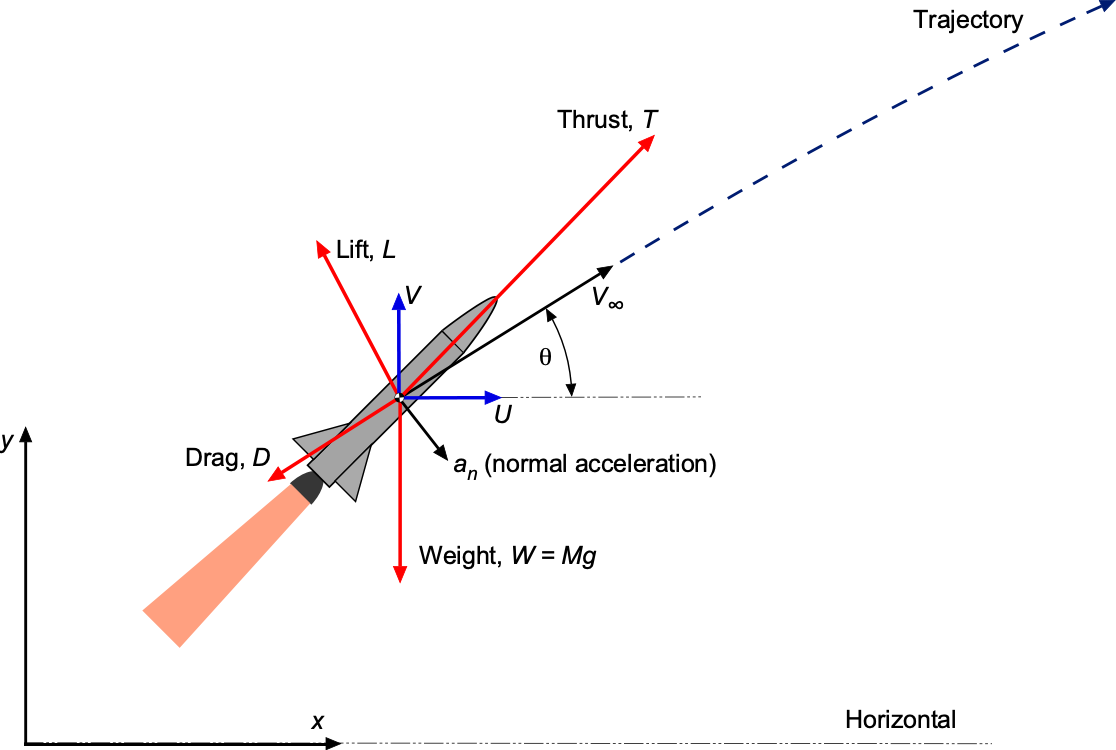
Similarly, the equation of motion perpendicular to the flight path is
(86)
where is the distance along the flight path, i.e.,
, where
is the instantaneous radius of curvature of the flight trajectory. The second equation of motion is then
(87)
In principle, Eqs. 85 and 87 can be solved to predict the launch trajectory of the missile, much in the manner considered previously using the rocket equation. However, the process is much more complicated than this and requires several more assumptions and approximations to obtain any useful results. Likewise, with the re-entry trajectory, there are many variables to consider, not just limited to simple dynamics and aerodynamics.
In the following more elementary exposition, assume that after the initial launch to high altitude, the rocket engine cuts off so that the thrust, , is zero, as shown in the figure below. Also, assume that
, so there is no aerodynamic lift.
The equations of motion now become
(88)
The aerodynamic drag on the missile is given by the standard formula that
(89)
where the drag coefficient, , is based on the reference area,
, which, by convention, is usually the maximum cross-sectional area of the missile. Let the aerodynamic drag be expressed in the form
(90)
where
(91)
where the mean value comprises an average of the aerodynamic drag over the ballistic trajectory. Therefore,
(92)
However,
(93)
so that
(94)
Letting , which seems a reasonable assumption, especially for a long-range ballistic missile, gives
(95)
Separating the variables and integrating them gives
(96)
This equation has the solution
(97)
where is the value of
at
. Therefore,
(98)
(99)
Consider now the equation of motion in the -direction, which becomes
(100)
Therefore,
(101)
and so
(102)
Integrating the preceding equation gives
(103)
noticing that at
. By dividing both sides of the foregoing equation by
, then
(104)
(105)
Therefore, Eqs. 99 and 105 will give the approximate position of the missile’s trajectory in terms of time, .
When the aerodynamic drag is small, i.e., the ballistic trajectory is mostly in the higher atmosphere or in space, then and the equations of motion reduce to
(106)
as well as
(107)
where is the initial velocity. These are the classic equations for the parabolic trajectory of any unpowered projectile, such as an artillery shell.
It can be shown that the total flight time, , of the missile or projectile for level ground, i.e., assuming the launch point and target are at the same height,
, is given by
(108)
where is the initial launch angle of elevation of the projectile. The corresponding range,
, is
(109)
The maximum range occurs when = 45
, i,e.,
.
These preceding equations, collectively, are sometimes referred to as the Laws of Ballistics or the Artilleryman’s Range Equations. However, if the variation of is accounted for during high-altitude flight using the inverse-square law of gravitational attraction, then the trajectory will be elliptic. The effect would be to increase slightly the range of a high-altitude projectile.
Summary & Closure
Payloads launched into space encompass a wide range of missions, including communication satellites, weather satellites, scientific instruments, crewed spacecraft, and planetary exploration probes. Payload mass and size are critical considerations in the design and selection of a launch vehicle. Heavier payloads and missions requiring higher orbital altitudes necessitate larger and more powerful rockets capable of delivering greater amounts of energy. Missions to low Earth orbit (LEO), such as those involving Earth observation or communication satellites, require less total energy than missions to geostationary orbit or interplanetary destinations. Launch vehicle configurations are carefully matched to mission requirements to optimize performance and minimize cost.
Understanding launch vehicle performance requires an appreciation of the fundamental principles governing rocket flight. The rocket equation describes the ideal velocity increment achievable by a rocket, i.e.,
where and
are the initial and final masses, and
is the equivalent exhaust velocity. However, actual missions require greater
than the ideal value because of losses associated with gravity, aerodynamic drag, and steering. Gravity losses, which typically amount to 1.5 to 2.5 km/s, arise from the continuous downward pull of Earth’s gravitational field during ascent. Drag losses, associated with aerodynamic resistance in the atmosphere, typically contribute 0.1 to 0.3 km/s. Steering losses, incurred when the rocket’s thrust vector is not perfectly aligned with its velocity vector, typically range from 0.1 to 0.5 km/s.
Because of the inherent limitations of carrying all propellant in a single stage, launch vehicles often employ multiple stages. Staging allows the vehicle to discard empty structural mass and engines, improving the effective mass ratio and making orbit more attainable. The performance of each stage depends critically on its propellant mass fraction, i.e., the fraction of its initial mass that is usable propellant, and structural mass fraction, i.e., the fraction dedicated to tanks, engines, and support systems.
The efficiency of a rocket engine is characterized by its specific impulse, , which relates directly to the exhaust velocity through the expression
where is the standard gravitational acceleration. Higher values of
enable rockets to achieve a given
with less propellant, increasing mission efficiency. Launch trajectories are carefully shaped to optimize energy use. Rockets perform a gravity turn shortly after liftoff, arcing over gradually to build horizontal velocity while minimizing steering losses.
Commercial companies such as SpaceX and Blue Origin have contributed to the development of new rocket technologies, including reusable launch vehicles and commercially operated crewed spacecraft. SpaceX’s Crew Dragon spacecraft, for example, provides transportation to and from the International Space Station under contract with governmental agencies. Commercial satellite launches for communications, navigation, and Earth observation have also become an established sector of the space industry. In addition, there is active development toward human spaceflight for non-governmental purposes, including space tourism initiatives.
5-Question Self-Assessment Quickquiz
For Further Thought or Discussion
- Consider a staged vehicle for which all
values are the same. How can
be maximized?
- How does a rocket navigate and change its course during flight?
- What is the role of aerodynamics in rocket design?
- How do scientists and engineers calculate the optimal launch trajectory for a rocket?
- What are the challenges of reusing rockets, and why is rocket reusability important?
- Can you name some famous rockets and their notable achievements?
- How has rocket technology evolved, and what are the prospects for rocketry?
Other Useful Online Resources
To learn more about rockets, launch vehicles, and other spacecraft, check out these helpful online resources:
- An article on the history of rockets by NASA
- Great video: The Evolution of Space Rockets.
- The U.S.’s first person in space, Alan Shepard, launches on a Mercury Redstone rocket.
- Saturn V: The rocket that took humans to the Moon – The Saturn V Story.
- Experience the flight of Apollo 11.
- STS-134 – The final launch of the Space Shuttle Endeavour.
- Artemis I Launch to the Moon – Official NASA Broadcast – Nov. 16, 2022.
- First test flight of the SpaceX Falcon Heavy.
- SpaceX Falcon Heavy launches the NASA Psyche – see video here.
- SpaceX Starship SN10 launch and landing – see video here.
- Blastoff! Blue Origin launches 33 payloads.
- Scott Manley’s excellent YouTube channel on everything to do with spaceflight!

