39 Airspeed Definitions & Measurement
pku lkoj0u
Introduction
Knowing how fast an aircraft travels through the air is critical to piloting and engineering. An aircraft’s performance characteristics are generally presented in terms of its airspeed and/or Mach number, as well as a function of its flight altitude and in-flight weight. However, determining an aircraft’s airspeed requires great care, and the process demands a thorough understanding of aerodynamics and other engineering principles.
Pilots are usually concerned more about the indicated airspeed, or IAS, which is read off the airspeed indicator (ASI) or the electronic flight display (EFIS) in the cockpit. When the IAS can be corrected for mechanical (if any) and static pressure reading errors (always present), it is referred to as the equivalent airspeed, or EAS. This particular airspeed is significant because it measures the actual dynamic pressure acting on the aircraft. However, engineers are also concerned with the true airspeed, or TAS, of the aircraft through undisturbed air, which will generally differ from the IAS or the EAS. True airspeed (TAS) and ground speed, which take into account the effects of wind, are also required by pilots for navigation purposes.
Therefore, to avoid confusion and potential misinterpretations of “airspeed,” the proper basis of airspeed measurement and the various definitions of airspeed must be understood, as well as how such measurements are used in engineering and aviation practice.
Learning Objectives
- Understand the aerodynamic principles associated with airspeed measurement.
- Know the difference between indicated, equivalent, calibrated, and true airspeeds.
- Be able to calculate the true airspeed of an aircraft.
- Know how to calculate airspeed at higher Mach numbers.
- Learning about new approaches to airspeed measurement using optical methods.
Airspeed & Mach Number
When a flight vehicle’s performance is addressed, its “airspeed” capabilities are critical. This usually means the speed through the air or airspeed and specifically the true airspeed of the aircraft relative to the air, or what is referred to in engineering terms as the quantity “.” It is often taken for granted that
is known or can be measured by recording a physical distance covered in a given time, as on a terrestrial vehicle, but this is not the case. Instead, the airspeed of an aircraft must be determined using pneumatic measurements such as Pitot probes, and the “true” speed of the aircraft through the air must be obtained by applying the principles of aerodynamics, hydrostatics, and thermodynamics.
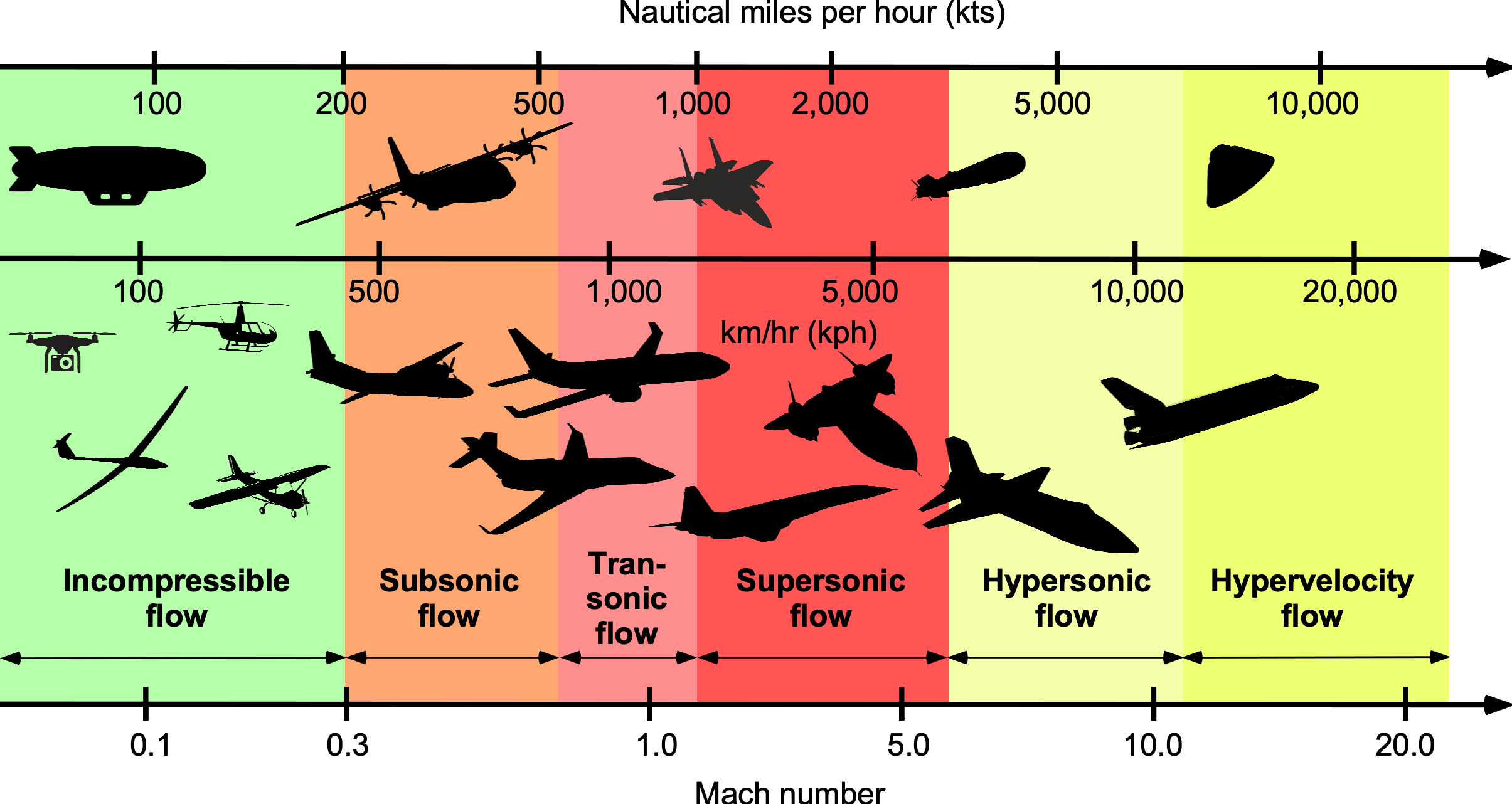
A flight vehicle’s achievable airspeed (or airspeed range) is best classified by its corresponding flight Mach number, as shown in the figure below. Recall that the Mach number is the ratio of airspeed to the speed of sound, so the flight Mach number at any altitude will be given by
(1)
where will be the true airspeed and
is the freestream ambient speed of sound at that altitude and temperature.
Recall that the speed of sound depends on the outside air temperature, , at any altitude, i.e.,
(2)
So, for a given true airspeed, the flight Mach number increases with increasing altitude in the atmosphere. Again, engineers would generally default to using the ISA model for any atmospheric properties needed for calculations unless instructed otherwise. As previously discussed, ISA has the advantage of standardizing definitions, calculations, and measurements because it can serve as a universal basis for instrument calibration, performance standardization, or as an additional atmospheric reference.
A flight vehicle classified as being low subsonic speed capable will cruise in the range up to 0.3 to 0.4, i.e., a predominantly incompressible flow region where the effects of compressibility about the vehicle are minor and would be expected to have a minimal impact on any aspect of the vehicle’s performance. Most general aviation aircraft, rotorcraft, and uncrewed aerial vehicles (UAVs) fly in this range. In this regime, Bernoulli’s equation is helpful in calculating airspeed based on measurements of dynamic pressure using a Pitot probe.
A flight vehicle classified as a high subsonic vehicle will fly at Mach numbers up to to
, which is where many commercial airliners operate, and here compressibility effects are expected to manifest in some form. In subsonic flow, airspeeds are readily measurable, but the effects of compressibility mean that thermodynamic principles are needed to measure airspeed correctly. Recall that the transonic region occurs approximately when
= 0.8 to 1.2, so most airliners begin to intrude into the transonic region of flight, i.e.,
.
Vehicles capable of supersonic flight will fly from = 1 up to as much as three or perhaps higher. Under these conditions, shock waves affect the flow about Pitot probes or other devices used to measure pressure, and so the determination of airspeed. Therefore, thermodynamic principles are necessary to calculate the aircraft’s speed relative to the air.
Definitions of Airspeeds
Several different speeds may be used when dealing with aircraft, which must now be defined. For example, the aircraft’s speed over the ground differs from its true airspeed through the air. This is because the ground speed depends on the relative magnitude and direction of the winds in the air mass in the direction of flight. Additionally, the speed read by an airspeed indicator (or its EFIS equivalent) is not the aircraft’s actual or “true” speed, nor is it its ground speed. This may all sound confusing, and it certainly is to most new engineers, so the various airspeeds used for aircraft must be understood.
What Does an ASI Measure?
It is best to understand precisely what an airspeed indicator (ASI) measures. An ASI, as shown in the figure below, is one of the most fundamental instruments used in flight, and the readings from an ASI are used not only for piloting but also for engineering purposes. An ASI is a pressure-measuring (pneumatic) instrument that responds to dynamic pressure or “” variations with a scale calibrated in speed units. The ASI is calibrated to read airspeed, usually in units of “knots” (kts), which means nautical miles per hour. Units of “knots” are used universally in aviation, but some ASIs may be calibrated in units of kilometers per hour (km/h, or kph).
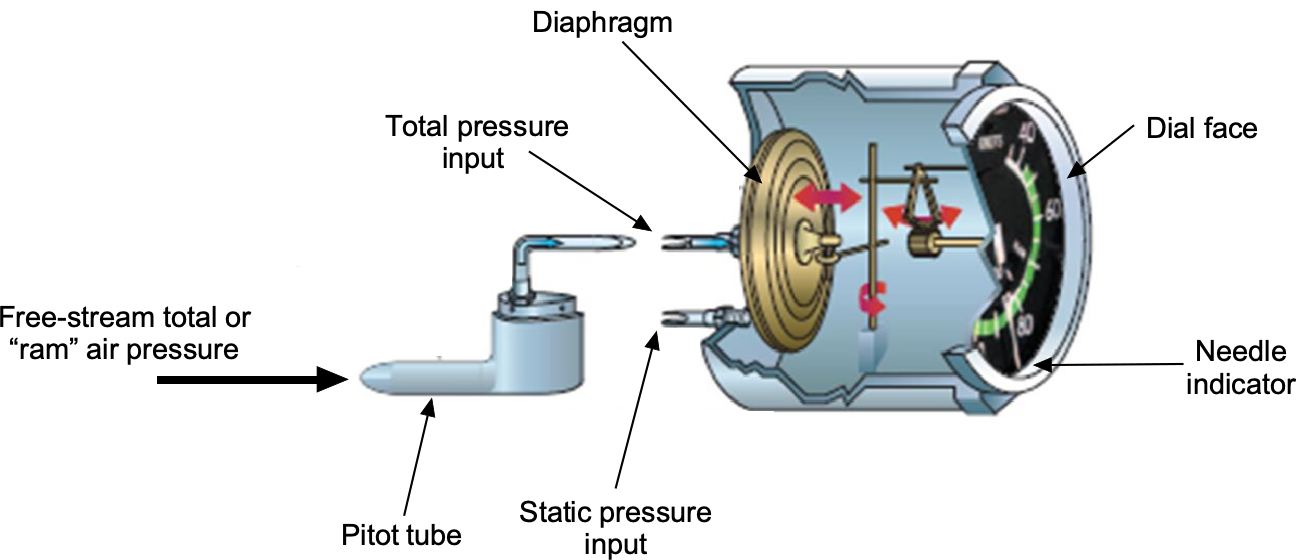
Recall that dynamic pressure is the difference between the total or stagnation pressure (the “ram” pressure) and the static pressure
, i.e.,
. Sometimes, a Pitot-static probe is used to measure dynamic pressure; however, at other times, a separate total pressure probe (which measures
) and a static pressure vent placed on the aircraft’s surface (which measures
) are employed. In either case, the measured pressure difference is the dynamic pressure,
, which the ASI responds to by design.
Analysis
Consider flight at low Mach numbers, where the flow can be assumed to be incompressible. If the total (stagnation) pressure is denoted as , then the use of Bernoulli’s equation (which is valid for incompressible flow) gives that
(3)
Rearranging this latter equation gives the true airspeed (TAS), i.e.,
(4)
which is exact if the density of the air is known and the measured value of
.
Of course, this latter equation is hardly convenient for finding TAS, even if and
are known, because
depends on pressure altitude and temperature. Also, a speed scale on the ASI must be associated with any given
, so a formal calibration is needed against some reference speed. It will also be apparent that the scale required on the ASI will be nonlinear because of the relationship between the value of static pressure and the square of the airspeed (or dynamic pressure) as formalized by the Bernoulli equation.
Basis of Calibration
To resolve these apparent dilemmas, the airspeed measurement on the ASI is referenced to mean sea level (MSL) density conditions by calibrating the speed scale based on the assumption that , the corresponding measured airspeed then being known as the equivalent airspeed or EAS, i.e.,
(5)
In other words, then
(6)
The true airspeed is then obtained from a calculation by using
(7)
which requires the value of to be evaluated.
Finding Air Density
To find first requires a measurement of pressure altitude and the outside air temperature, and then using the equations of the ISA model. Remember that the altimeter is calibrated according to the International Standard Atmosphere (ISA) model. The value of
can be obtained from
(8)
where the local pressure altitude, , is in feet and the local
is in units of Celsius (
C) or using
(9)
where is in feet and
is in units of Fahrenheit (
F). Notice the use of mixed units in some of these equations, which requires care in their proper evaluation. It is convention in international aviation (per ICAO) that altitudes are measured and reported in feet, but temperatures are reported in units of
C.
Summary
The critical point to remember from the preceding is that TAS is not a directly measurable quantity; it requires the measurement of EAS followed by a calculation using the value of to obtain the TAS. Nevertheless, measuring the EAS on the ASI is very convenient from a piloting perspective because the actual dynamic pressure, to which the aircraft responds aerodynamically, is directly proportional to the square of the EAS at a given altitude and temperature. However, it does not solve the problem that engineers generally require TAS, for which a calculation is always needed. Notice that the EAS and TAS will only be equal if the aircraft is flying at MSL and that the EAS measurement is entirely error-free, which is an issue that must now be considered in more detail.
Why is Airspeed Measured in knots?
The “knot” or “knots” is a unit of speed equal to one nautical mile per hour. It is equivalent to 1.15078 mph, 1.852 km/h, or 0.514 m/s. The knot’s standard symbol is “kn.” However, using “kt” or “kts” is common, especially in aviation. The symbol “kt” is the specific form recommended by the International Civil Aviation Organization (ICAO). The term “knot” or “knots” originally derives from pre-19th-century nautical use, when sailors would estimate the speed of a ship by counting the number of knots made on a rope that was unspooled behind the ship during a specific time.
Pitot-Static System
Pitot probes (or tubes) and Pitot-static probes are often used to measure general flow velocities and airspeeds. Consider points 1 and 2, located upstream of the Pitot tube and at the entrance to the tube, respectively, as shown in the figure below. From Bernoulli’s equation it is known that constant along any given streamline, so that
(10)
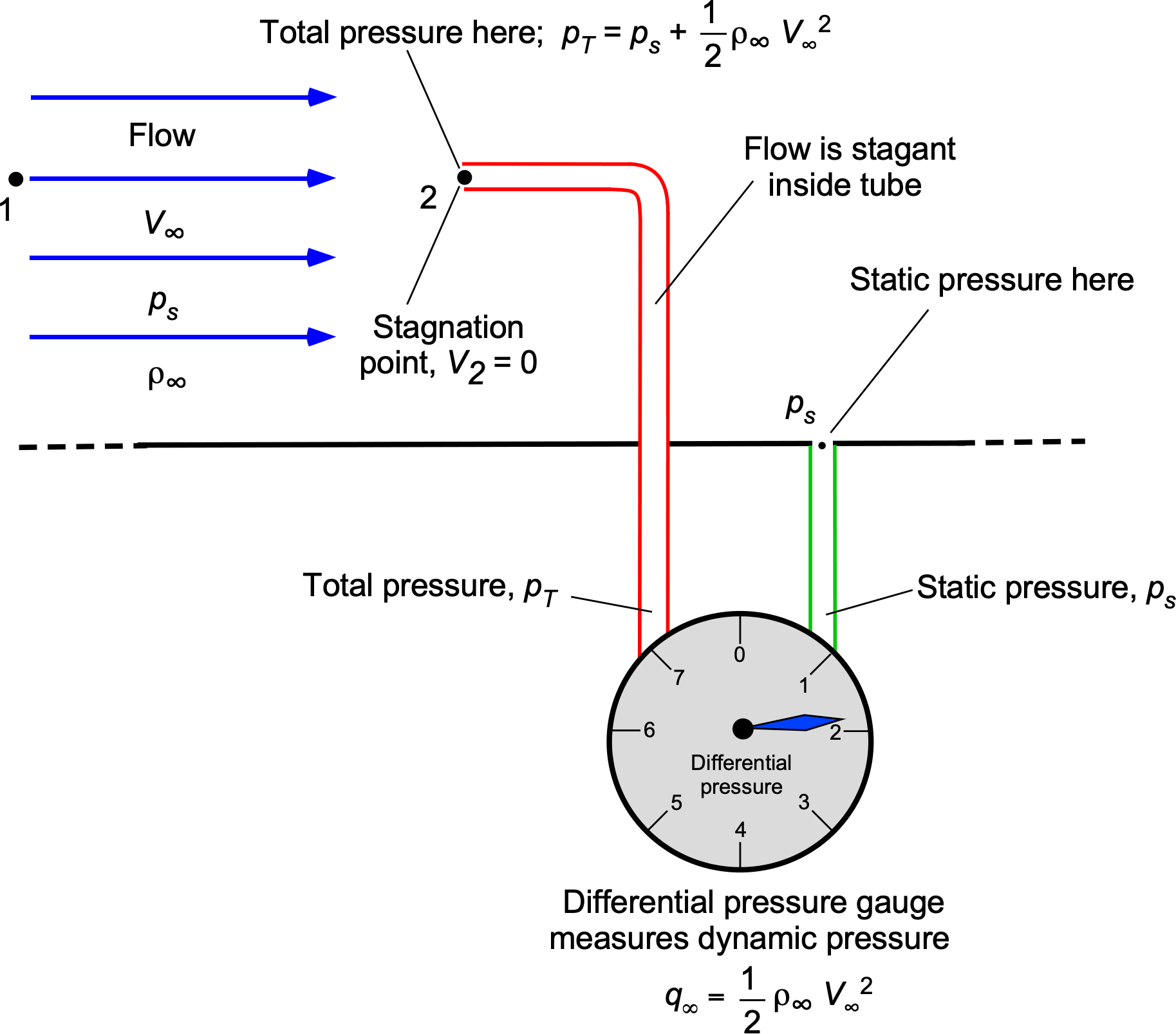
But at point 2 at the entrance to the Pitot tube, the fluid is brought to rest, so , i.e., it is a stagnation point, and
(11)
The static pressure must be measured to obtain the flow velocity from this latter expression. Like the Venturi problem, this static pressure can be measured with a separate static vent or the ports on the outer side of a combined Pitot-static tube. Solving for
gives
(12)
Therefore, the freestream flow velocity, , can be measured by measuring the difference between a flow’s total and static pressure.
While a pitot-static probe is sometimes used to measure dynamic pressure, in practice, it is found that dynamic pressure can be measured somewhat more accurately by using a separate pitot probe and static vent, as shown in the schematic below. On an airplane, the static vent or source is usually located somewhere on the side of the fuselage. There may also be more than one static vent for redundancy. The pitot probe is set off from the aircraft’s surface into the flow; these pitot probes may be mounted on an airplane’s nose or, in some cases, under the wing. The total pressure is connected to the airspeed indicator (ASI), with the static pressure being connected to the altimeter and vertical speed indicator. A heating element is used on the Pitot probe to prevent icing and avoid false ASI readings.

Measuring Total Pressure
The total (ram) pressure can be measured without much error because the probe points directly into the airflow, and the resulting pressure is relatively high compared to the static pressure. The inlet shape of the Pitot tube must be clean and smooth to prevent pressure losses or other pressure disturbances that could affect the reading. The photograph below shows an example of a total pressure probe placed on an airplane’s nose. The probe must be well out of the surface boundary layer, displacing it a short distance from the aircraft’s skin. Such probes must not be located where they could be subject to upstream flow disturbances, such as those caused by propellers, antennas, air scoops, or other probes.

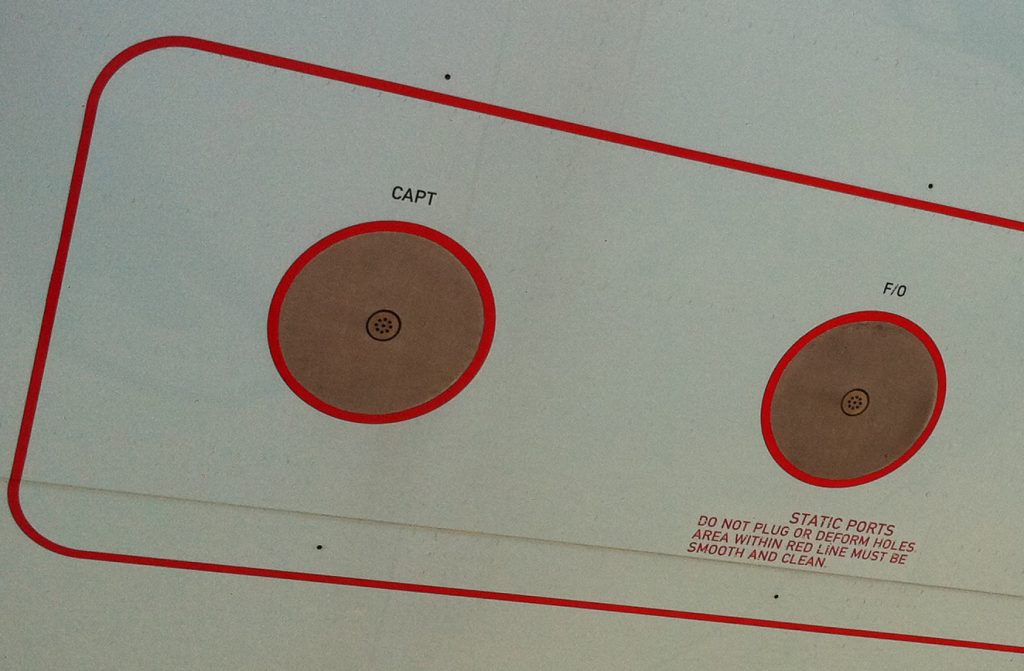
Measuring Static Pressure
Static pressure is often more challenging to measure accurately because of its relatively small value. It is measured on the airplane’s outer skin, usually at a location where the local static pressure is close to the ambient static pressure. However, there can be no point on the surface where the local static pressure exactly equals the static pressure in the freestream flow. Therefore, the static pressure measurement available to the ASI is always in error to some degree, which is referred to as the static position error (SPE).
Static Position Error (SPE)
The “error-free” issue in airspeed measurement mentioned previously requires further elaboration because the preceding arguments are predicated on two major points:
- The total and static pressure can both be measured accurately.
- The ASI can be adequately calibrated against a suitable reference in terms of speed units.
One source of error is the Static Position Error (SPE), which is the error in measuring the local static pressure outside the aircraft relative to the actual static pressure at that altitude and airspeed. If the IAS reading is corrected for the SPE and mechanical errors, the resulting speed is referred to as the calibrated airspeed (CAS). If the SPE and mechanical instrument errors are small, it is sufficient to state that IAS = CAS = EAS. However, it is essential to note that, in general, the IAS differs from the EAS and the TAS.
The effects of SPE must be measured and, in most cases, corrected for use in engineering and piloting. This process uses a formal calibration during flight testing with the specific make and model of the aircraft. The actual static pressure measurements are compared to the local static pressure measured at the pressure tap(s) on the outside skin of the aircraft. As shown in the figure below, there are a few points on the outside skin of the aircraft where the local static pressure equals the true static pressure at which the aircraft is flying. The static pressure port on a prototype aircraft is usually repositioned after flight tests to minimize the SPE as much as possible, ultimately locating it where the SPE is minimized. This location is then used on production versions of the aircraft. However, the SPE will never be precisely zero.
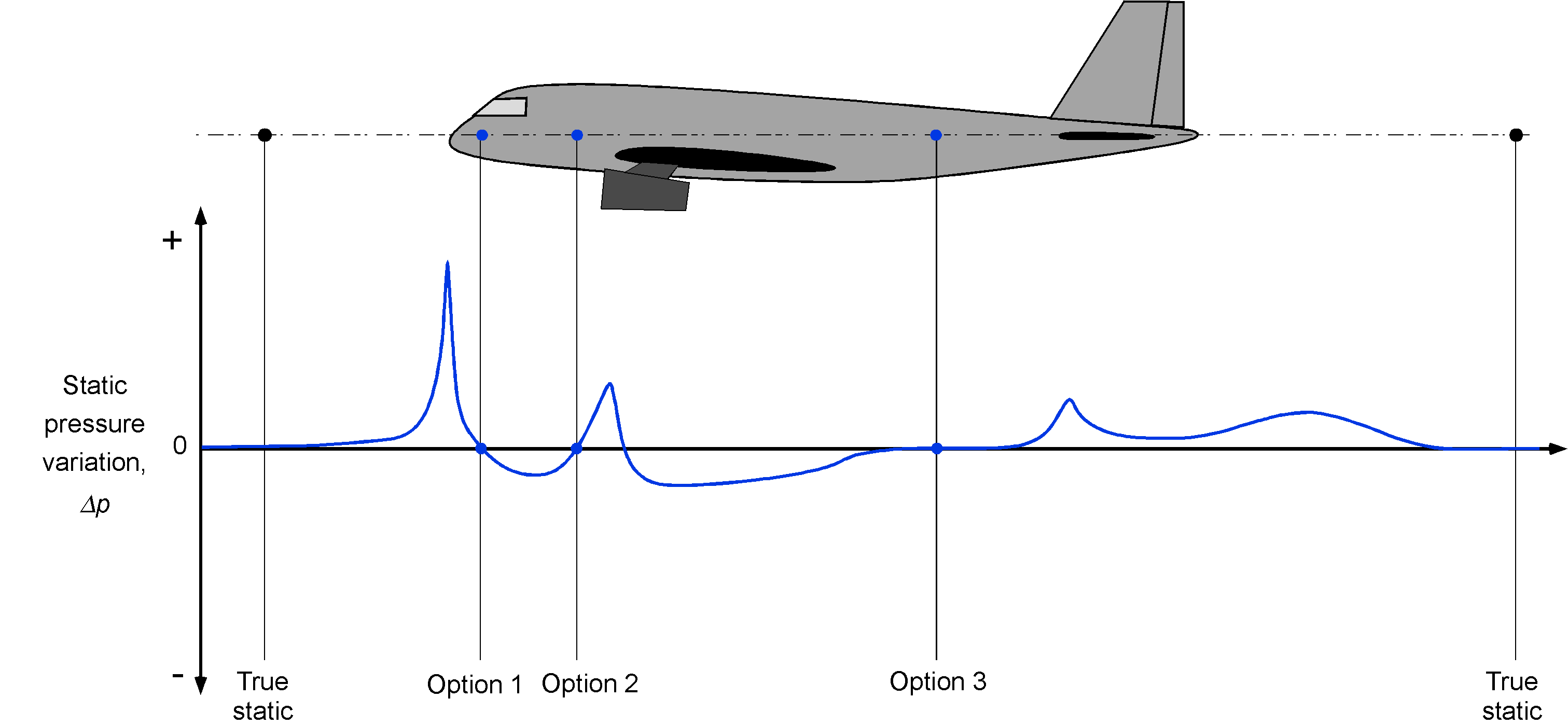
In the SPE calibration process, which is performed during flight testing, the actual or true static pressure is measured well behind the aircraft using a trailing cone apparatus, as shown in the photograph below. The SPE will vary slightly at different airspeeds and altitudes, so it must be mapped out over the entire operating envelope of the aircraft.

The SPE is usually highest at lower airspeeds, lower at higher speeds, and higher at higher altitudes, as shown in the figure below. For higher-performance aircraft such as jets, the SPE is likely to be a function of flight Mach number. The process must also be conducted with the aircraft in both the “clean” configuration (i.e., flaps and landing gear retracted) and the “dirty” configuration (i.e., flaps and landing gear extended, such as for landing).

The results obtained and the corrections subsequently derived as the SPE affects the airspeed readings will apply to all production aircraft of the same make and model. The SPE results (or the corrected airspeed values), as required by FAA or EASA regulations, are always included in the aircraft’s flight manual. In the case of a modern airliner, the correction is incorporated into the EFIS as a software update to the airspeed. For piloting purposes, the SPE and mechanical errors are usually small enough to be ignored on many aircraft (perhaps a couple of kts). However, for engineering purposes, all such errors must be accurately accounted for in all aircraft performance analyses.
Mechanical Errors
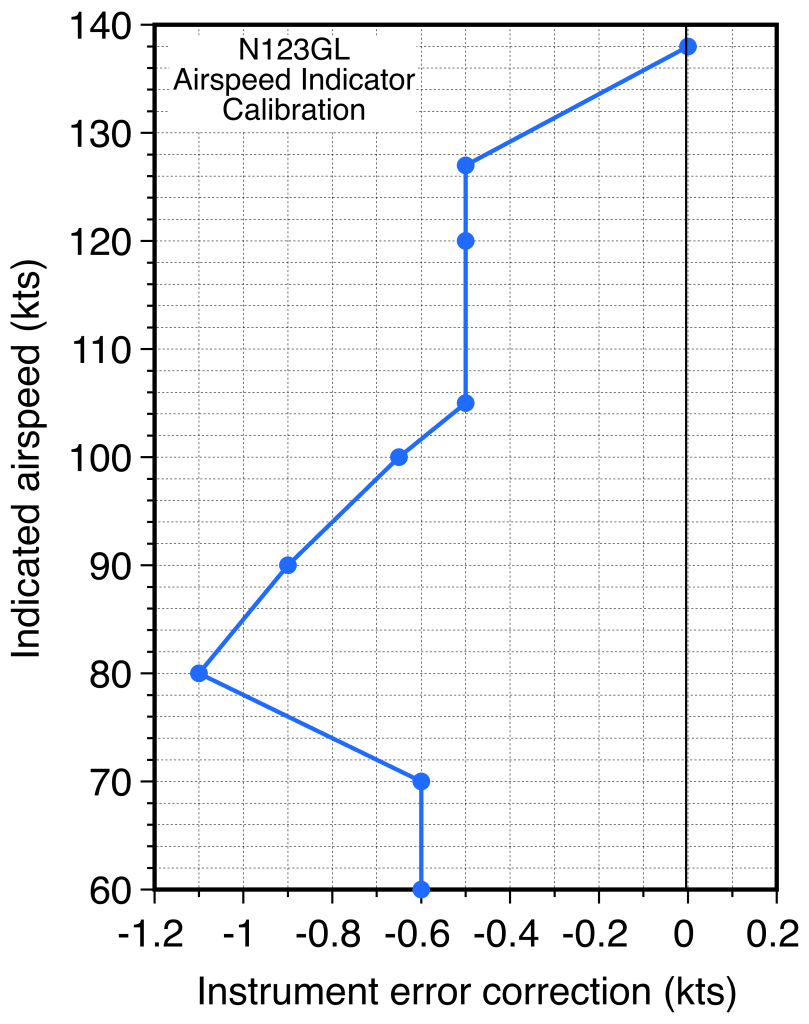
The mechanical error in the ASI can be determined in a laboratory setting by calibrating against a reference ASI, resulting in a standard mechanical error calibration chart or table, as shown in the example below. Each instrument error correction (IEC) calibration is specific to a particular ASI, and a different calibration is required if the ASI is replaced. The errors are usually small enough to be unimportant for piloting purposes, but they should be included in any data reduction process for engineering work.
Check Your Understanding #1 – Correcting an ASI reading
A test aircraft is flying at a pressure altitude of 4,200 ft where the outside air temperature is 68.4F. The airspeed indicator (ASI) reads 134.5 kts. Calibrations available show the mechanical error of the ASI,
, is -0.7 kts, and the static position error,
, is equivalent to +0.3 knots. Calculate the true airspeed of the aircraft.
Show solution/hide solution.
The ISA ambient temperature at this pressure altitude is
Remember that an airspeed indicator (ASI) is calibrated based on sea-level density ( = 0.002378 slugs ft
). The equivalent speed (EAS) is
which also requires (=
) to be evaluated. The actual air temperature is 68.4
F, much warmer than standard by 68.4 – 44.0 = 24.39
F. Calculating the air density using the ISA model at this pressure altitude and temperature gives
= 0.0020 slugs ft
.
In this case, first, we need to correct the for both the instrument error correction (IEC) and for static position error (SPE) to get the calibrated airspeed
so
and from the calibrations, then
Therefore, the true airspeed will be
Airspeed Measurement at Higher Mach Numbers
The issue of airspeed measurement in higher-speed flight, where compressibility issues manifest, must also be addressed. In this case, using the Bernoulli equation would not be appropriate. In practice, compressibility effects on airspeed measurement are negligible below approximately 10,000 feet and 200 knots. At higher altitudes, the lower air temperatures decrease the speed of sound, thereby increasing Mach numbers, so that compressibility thresholds are met at lower airspeeds.
Remember that airspeed values on the ASI are referenced to MSL density conditions by calibrating the speed scale based on the assumption that , so the corresponding equivalent airspeed or EAS is then
(13)
The ASI still responds as a dynamic pressure-measuring instrument. However, the air’s compressibility affects the reading of total pressure from the Pitot tube, which must be taken into account.
Subsonic Flight Speeds
For subsonic Mach numbers above 0.3, the total and static pressures can be related using the isentropic thermodynamic relationships. In this case
(14)
which can be used to solve for the Mach number, , i.e.,
(15)
Therefore, the Pitot system now measures flight Mach numbers.
Not only do the total pressure and static pressure need to be measured in higher-speed flight, but the total temperature must also be measured, from which true airspeed can again be obtained by calculation. To this end, the airspeed is then given by
(16)
which requires either the value of the “static” speed of sound, , or the “stagnation” speed of sound,
, at any given pressure altitude. As previously discussed, the stagnation temperature or total air temperature (TAT), i.e.,
, is usually measured during flight so that
can be obtained by using
(17)
The EAS and the TAS can then be determined by calculation.
Check Your Understanding #2 – Finding the flight Mach number & TAS
An experimental turboprop airplane is flying at a pressure altitude of 25,000 ft. The Pitot-static system monitored by the test engineers measures the total pressure, , as 30.65 kPa, and the corrected static pressure,
, as 23.91 kPa. What are the aircraft’s flight Mach number and true airspeed (TAS)? Assume: 1. ISA standard conditions. 2. No mechanical or SPE errors.
Show solution/hide solution.
Using the compressible flow equations, then
Inserting the measured numerical values gives
giving
Therefore, the flight Mach number of the airplane is
The speed of sound, , at a pressure altitude of 25,000 ft at ISA conditions is 1,016.1 ft/s. Therefore, the TAS is
Note: Determining the actual speed of sound, other than for assumed ISA conditions, requires measuring the outside air temperature.
Supersonic Flight Speeds
For supersonic Mach numbers, a bow shock wave forms ahead of the Pitot probe, as shown in the figure below, further complicating the airspeed measurement issue. Because of this shock wave, the flow does not decelerate isentropically. However, the normal shock equations can be used across a shock wave to find the relationship between the total pressure after the shock, the static pressure, and the Mach number.
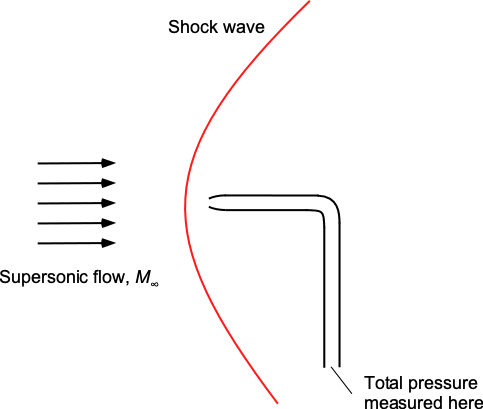
The total pressure is
(18)
and the static pressure is
(19)
Therefore, the ratio of total to static pressure is
(20)
which can be rearranged to give
(21)
This is known as the Rayleigh-Pitot tube formula. Because the flight Mach number is an implicit function of the total and static pressures in the preceding equation, it must be calculated iteratively. Again, the value obtained is predicated on the assumption that the total and static pressures can be measured accurately and that any needed corrections, such as SPE, can be applied.
Summary of Airspeed Definitions
The following definitions of airspeeds in aviation may be encountered:
1. TAS is referred to as “True airspeed,” which is the actual speed of an aircraft through the air relative to an undisturbed air mass. In engineering work, this is referred to as ““.
2. IAS is referred to as “Indicated Airspeed,” which is the speed displayed on an airspeed indicator or ASI. IAS differs from TAS because the ASI is calibrated based on MSL conditions, i.e., .
3. CAS is “Calibrated airspeed,” which is the indicated airspeed corrected for errors such as static position error (i.e., the error in measuring accurate static pressure on the aircraft) and mechanical instrument errors.
4. EAS is the “Equivalent airspeed,” which is the airspeed reading on an error-free ASI corresponding to a given dynamic pressure. The EAS must also be corrected for compressibility effects on the dynamic pressure reading at flight Mach numbers greater than 0.3 to determine the aircraft’s true airspeed (TAS).
Optical Airspeed Measurements
Laser Doppler Velocimetry (LDV) offers a non-intrusive optical method for measuring true airspeed during flight, particularly in conditions where traditional Pitot-static pneumatic systems lose accuracy. Such conditions include flight low airspeeds and low dynamic pressures, or any conditions around the aircraft that cause significant static position error (SPE). This LDV device is beneficial for airspeed measurement during low-speed phases of flight, particularly in helicopters and other types of rotorcraft, such as eVTOLs, where the SPE remains large below airspeeds of approximately 50 kts. In principle, LDV systems can provide free-air measurements at any airspeed, ranging from almost zero or negative to subsonic, supersonic, and hypersonic speeds.
A typical LDV airspeed setup consists of a laser source, beam-splitting optics, and a focusing lens mounted externally on the aircraft, as illustrated in the figure below. The lens has a relatively long focal length to direct two coherent laser beams so they intersect at a fixed point in the undisturbed freestream flow well ahead of the aircraft. The intersection of the laser beams forms a small ellipsoidal measurement volume with a major axis typically on the order of 0.1 mm, where they form an interference fringe pattern.
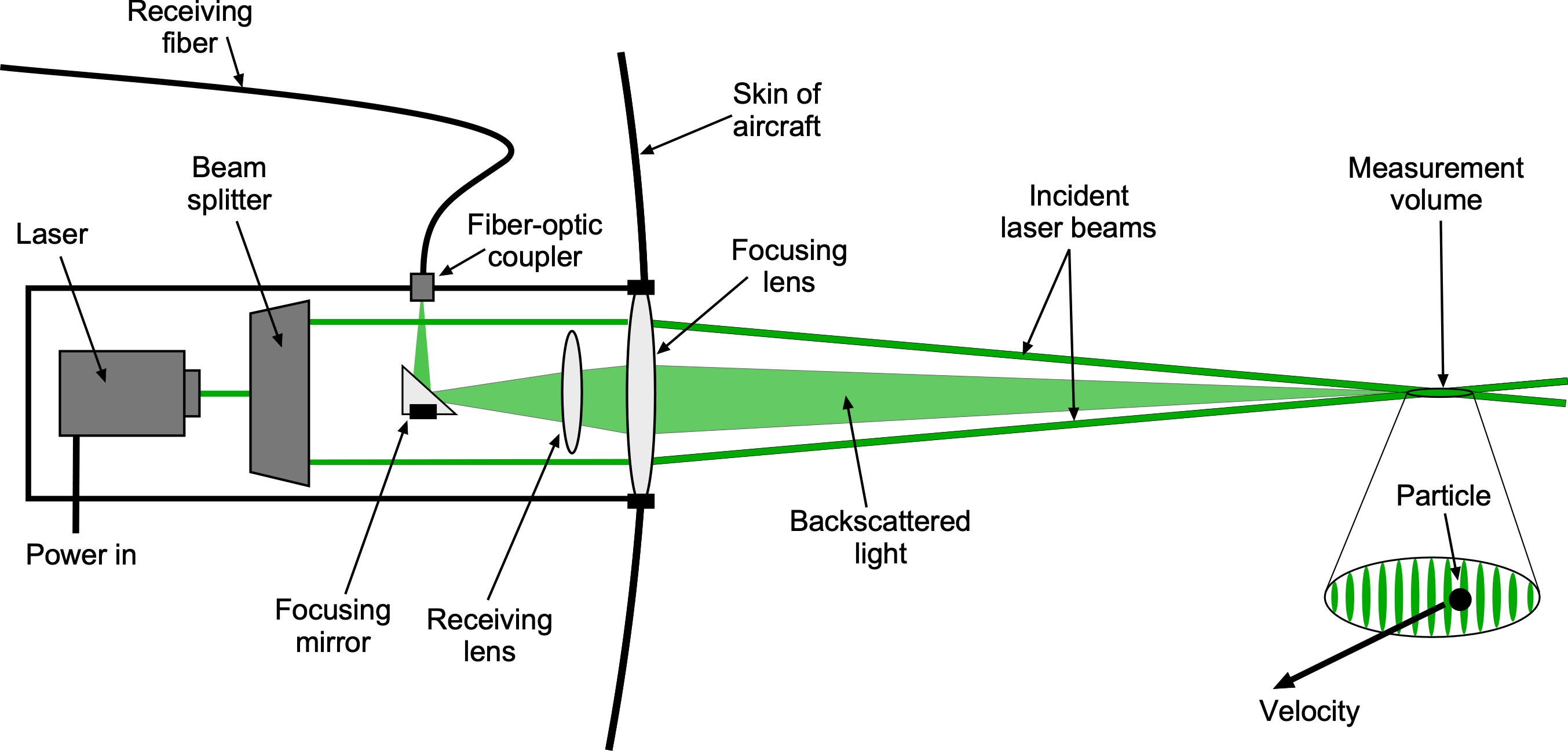
As naturally occurring particles in the atmosphere pass through this fringe pattern, they scatter Doppler-shifted light or “Doppler bursts” based on their velocity. This scattered light is collected and focused onto the end of a fiber-optic cable, which is then connected to a photodetector, followed by signal conditioning. The Doppler frequency is then extracted electronically to determine the instantaneous particle velocity corresponding to the aircraft’s airspeed. Because many bursts arrive in rapid succession, real-time averaging can be used to compute the instantaneous airspeed, that is, its actual speed relative to the surrounding air.
The natural atmosphere typically contains sufficient aerosol-sized particles to scatter light effectively within the measurement volume. Volcanic eruptions, in particular, release significant quantities of fine particulate matter, usually in the micron diameter range, into the upper troposphere and lower stratosphere. These particles can remain suspended over large regions of the Earth’s atmosphere for extended periods, providing ample seeding for in-flight LDV measurements.
The primary advantage of LDV is its independence from SPE, compressibility effects, and boundary layer distortions, all of which can affect the performance of Pitot tubes and static pressure ports. To ensure accurate airspeed measurements, the LDV probe must be calibrated and aligned with the aircraft’s body axes and center of gravity. Misalignment can introduce biases and errors in the measured airspeed. Some systems incorporate inertial measurement units (IMUs) or GPS to provide reference velocity data and to correct for platform motion. In more advanced configurations, differential LDV systems using multiple laser wavelengths are employed to measure airspeed along with the other two components of the aircraft’s velocity vector.
LDV-based airspeed measurement systems have been successfully demonstrated in flight research programs for fixed-wing aircraft and rotorcraft. Pneumatic systems for calibration utilize wingtip booms, nose-mounted probes, or trailing cone systems to provide reference airspeed measurements outside disturbed flow regions. LDV-based airspeed measurement systems focus the laser energy at a measurement volume well upstream of the airplane, ensuring measurements are taken in undisturbed air. However, errors from optical misalignment, beam quality degradation, aircraft vibrations, and aeroelastic deformations can reduce the signal quality. However, such issues can be mitigated with ruggedized fiber-coupled optics, vibration-isolated mounts, and adaptive signal filtering techniques.
Despite its relative complexity compared to conventional pneumatic systems, LDV is currently the most precise method for measuring airspeed. With continued advances in compact and rugged optical hardware, LDV-based airspeed measurement systems will likely see wider adoption, especially for rotorcraft. Companies such as Optical Air Data Systems are at the forefront of this technology. While such systems may never completely replace a conventional pneumatic airspeed measurement system, they will be an essential augmentation for low airspeed measurements on all aircraft types.
Summary & Closure
Airspeed measurement is straightforward using a pitot-static system; however, it is essential to understand precisely what airspeed is being measured, such as equivalent airspeed, calibrated airspeed, or true airspeed. Engineers usually require a measurement of the aircraft’s true airspeed, which must be obtained indirectly by measurement and calculation. True airspeed is not a direct measurement of speed. Pilots, however, require both the equivalent airspeed (to which the aircraft responds aerodynamically) and the true airspeed (for navigation purposes). Static position errors and mechanical errors in airspeed measurement must also be addressed.
One must also remember that the ASI is calibrated based on mean sea-level (MSL) density, i.e., the calibration is performed by assuming that . For higher subsonic and supersonic airspeeds, compressibility effects will impact the total and static pressures measured by the Pitot probe, necessitating appropriate corrections (based on isentropic flow relations) to determine the Mach number and true airspeed. At supersonic airspeeds, other issues arise, including the need to relate total and static pressure measurements to relationships for the flow across shock waves.
5-Question Self-Assessment Quickquiz
For Further Thought or Discussion
- An airplane is flying at a pressure altitude of 10,000 ft with an indicated airspeed of 200 kts. What is its true airspeed? Hint: Assume no SPE and an error-free airspeed indicator.
- In practical aviation, why does a pilot need the indicated airspeed and the ground speed?
- What might be the consequences if an aircraft is found to have a significant static position error? For the pilot? For engineering analysis?
- Research the effects of compressibility on airspeed measurement. What happens to the reading from a pitot probe when an aircraft exceeds the speed of sound?
- Can you explain the concept of airspeed limitations and how they are indicated on the instrument?
- What are the limitations of airspeed indicators and factors that can affect their accuracy?
- Can you describe the effects of airspeed on aircraft performance?
- How are airspeed indicators calibrated and tested for accuracy?
- Air France 447 Accident: Explain how a failed Pitot tube resulted in the loss of control of the aircraft.
Other Useful Online Resources
- Great video on “The Airspeed Indicator & Types of Airspeed.”
- This video explains how a barometric altimeter works and how the readings are interpreted.
- To learn more about the evolution of aircraft instruments, read “70 Years of Flight Instruments and Displays.”
- An excellent discussion on air data measurement and calibration by NASA.

