"

13 Atmospheric Properties & the ISA

Introduction

The performance of any atmospheric flight vehicle is affected by the density of the air in which it is flying. The pressure, temperature, and density of the air in the atmosphere are all functions of altitude. In particular, air density affects the aerodynamic performance of an aircraft in terms of its lift and drag, as well as the thrust and/or power output from its engines. Furthermore, determining the aerodynamic forces on a launch vehicle is crucial during its flight within the lower parts of the atmosphere, as well as spacecraft that fly in the high atmosphere during re-entry. Finally, the readings on aircraft instruments, such as the altimeter and the airspeed indicator, which are pneumatic (i.e., respond to air pressure), also depend on the local properties found in the atmosphere.

The layered shell-like structure of Earth’s atmosphere is visible in the photograph shown below, which was taken at sunset over the Indian Ocean as seen from the International Space Station. The troposphere (orange) is at the bottom, above the darkness of the Earth’s surface. The troposphere, which comprises approximately 80% of the Earth’s atmosphere by mass, is the region where winds and weather phenomena predominantly occur. It is within this layer that all human activity and existence have transpired. Above this lies the pink-to-white colored zone called the stratosphere, which is where the ozone layer resides and protects the Earth from harmful UV radiation.[1] Higher still is the mesosphere, a shell that appears as light blue in this image, and beyond that, it gradually fades into the thermosphere and the darkness of space. Of significance is that the thickness of the majority of the atmosphere is only about 1.6% of the Earth’s radius.

A thin layer of atmosphere surrounds the Earth and protects it from space hazards. (NASA Johnson/ISS image.)

It should also be appreciated that weather and winds cause the properties of the atmosphere to vary from place to place over the Earth, from day to day, and even from hour to hour. Therefore, one problem that arises immediately is developing a means of standardizing the properties of the atmosphere for use in various measurements and for both engineering and aviation purposes. This issue is why defining a standard atmospheric model called the International Standard Atmosphere (ISA) is necessary.

Learning Objectives

  • Know more about the composition and properties of the Earth’s atmosphere as a function of altitude or “height” from the surface.
  • Understand why a “standard” atmospheric model needs to be defined for use in engineering analysis and other areas of practical aviation.
  • Calculate air properties in the International Standard Atmosphere (ISA) using the ISA equations and read the relevant properties from a table.
  • Know how to use the hydrostatic equations to help estimate the atmospheric properties of other planets.

Composition of the Atmosphere

Aeronautical engineers are concerned mainly about the properties of the air in the lower atmosphere where aircraft fly, which is called the troposphere. In this regard, the relevant properties are pressure, temperature, density, viscosity, and the speed of sound. Air represents a mixture of several gases by volume, namely nitrogen (78%), oxygen (21%), noble gases (0.9%), carbon dioxide (less than 0.1%), and other trace gases. The natural winds and turbulence in the lower atmosphere keep these gases well-mixed, as illustrated in the figure below. Other natural atmospheric materials include water vapor, dust particles, smoke, viruses, bacteria, etc. Many dust particles, called aerosol particles or aerosols, are of volcanic origin. Like smoke, they remain suspended for a long time because of their tiny sub-micron size.

Air is a mixture of nitrogen, oxygen, carbon dioxide, water vapor, and other trace gases. In the troposphere, these gases are well-mixed.

The figure below shows that when moving up in the atmosphere away from the surface of the Earth, the atmosphere naturally forms into a series of strata or “shells” where the air has different characteristics and properties. The troposphere is flattened towards the poles because of the centrifugal effects caused by the Earth’s rotation about its orbital axis. Astronautical engineers are concerned more about the atmospheric properties above the tropopause and into the stratosphere and mesosphere. Above the tropopause, the temperature and other properties of the atmosphere change differently compared to those in the troposphere.

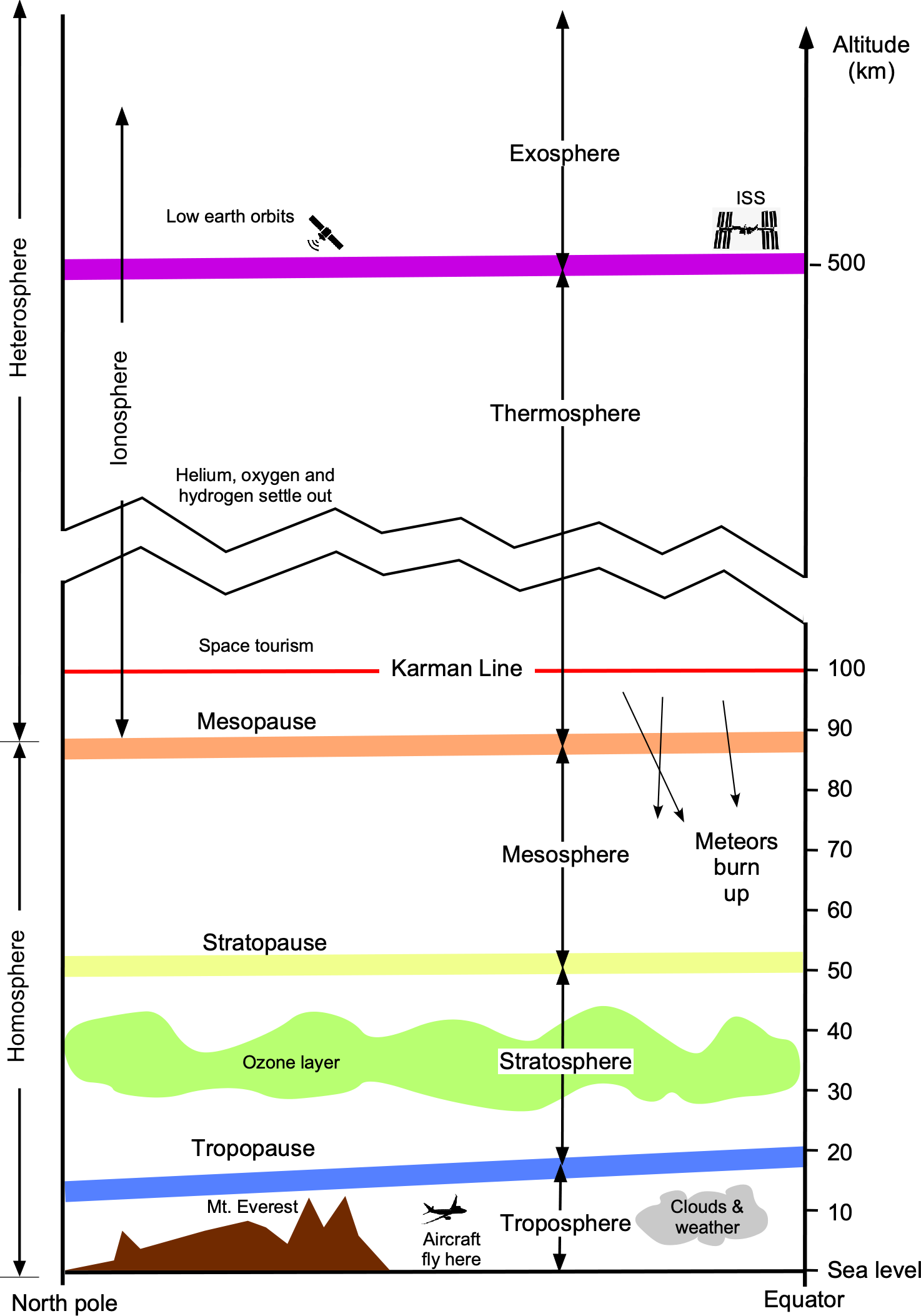
The composition of the Earth’s atmosphere. The atmosphere naturally forms into a series of strata or “shells” with different characteristics and properties.

At higher altitudes above 300,000 ft (90 km), the different gases also begin to settle or separate into shells according to their respective densities, namely oxygen (heaviest), helium, and hydrogen (lightest). The edge of space is usually defined as 100 km (about 62 miles or 328,000 ft), often called the Kármán Line. Although the Kármán line is an arbitrary boundary, it is widely recognized and used as a standard in the aerospace industry. It is also the reference altitude used by the Fédération Aéronautique Internationale (FAI) to define the edge of space.

General Properties of the Atmosphere

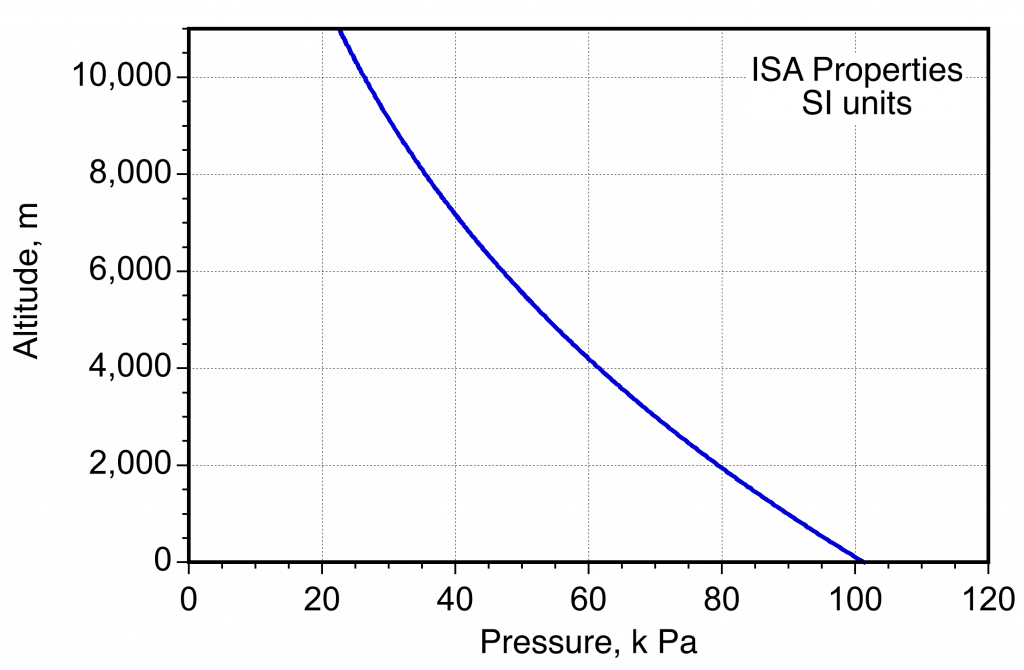
The figure below shows the atmosphere’s temperature, pressure, and density variations. Both pressure and density decrease quickly and asymptotically with height above mean sea level (MSL), which is not surprising because the pressure is related to the weight of air directly above; there is less weight of air above when going higher up into the atmosphere.

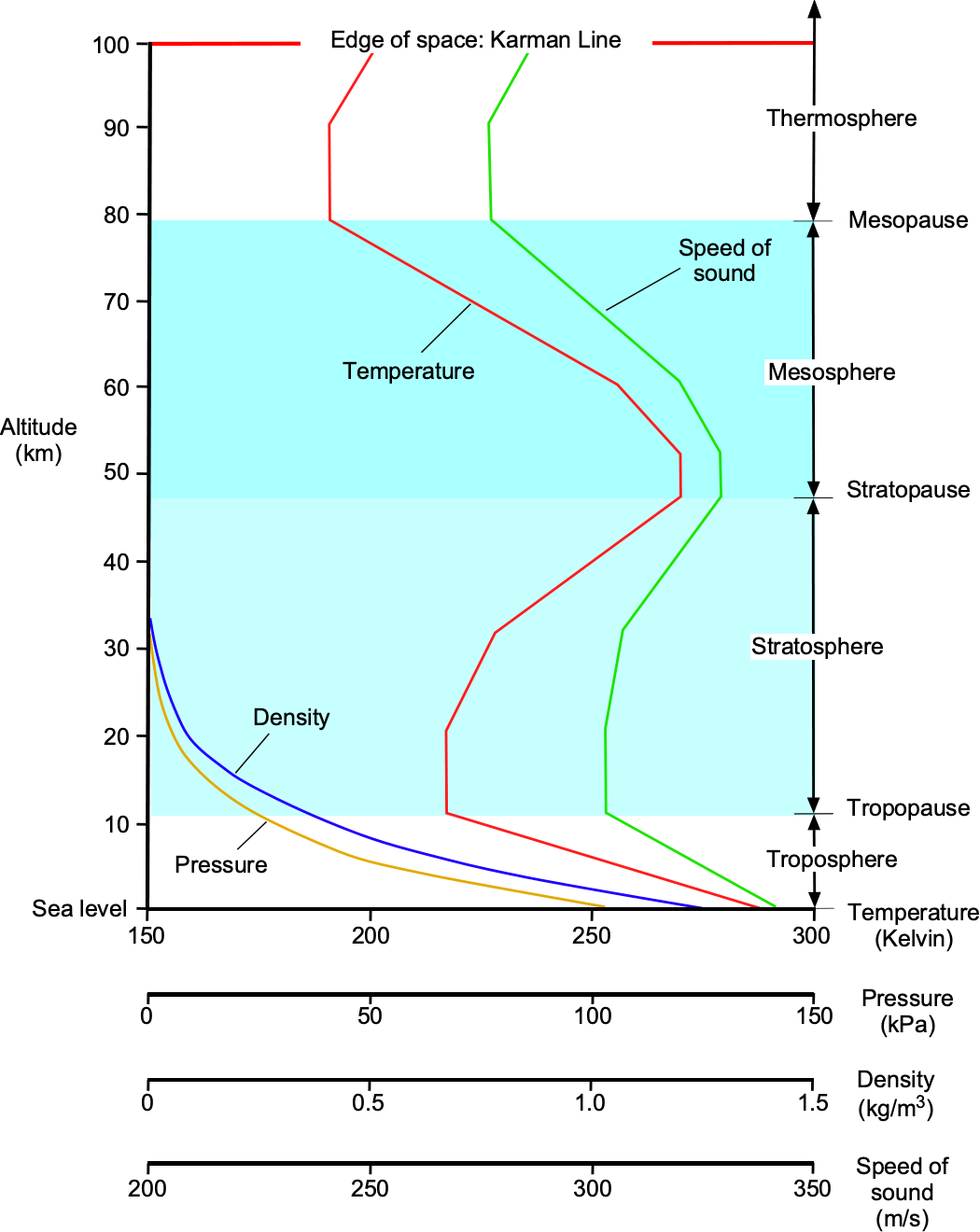
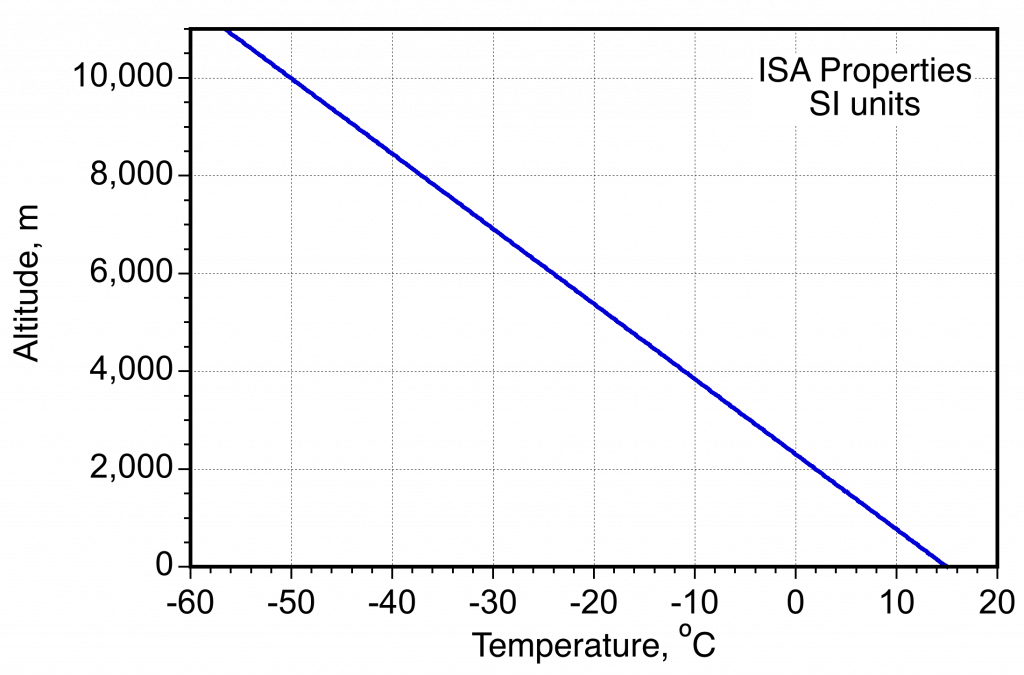
Variations of pressure, temperature, and density in the Earth’s atmosphere. Not to be used for quantitative evaluations.

The temperature in the totality of the atmosphere is more complicated to describe. There are regions where the temperature increases with increasing height and regions where the temperature decreases with increasing height. The temperature decreases or lapses approximately linearly with height in the troposphere (below 36,000 ft or 12,000 m). However, the actual lapse rate can vary daily and from place to place over the Earth. The region above the troposphere is called the stratosphere. In this region, temperature increases with increasing height because solar radiation affects this part of the atmosphere containing the ozone layer.

What is the ozone layer?

The ozone layer is a shell of the Earth’s stratosphere, located approximately 10 to 50 kilometers above the surface. It contains a high concentration of ozone (O3) molecules, which are formed when oxygen (O2) molecules are exposed to ultraviolet (UV) radiation from the Sun. The ozone layer plays a crucial role in protecting life on Earth by absorbing most of the Sun’s harmful UV radiation, particularly the high-energy UV-B and UV-C rays. The discovery of the ozone layer and its significance in the Earth’s climate during the 1970s led to international efforts to reduce the use of ozone-depleting substances, such as chlorofluorocarbons (CFCs), which are now mostly banned.

Development of the ISA model

The International Standard Atmosphere (ISA) model is an average representation of an ideal atmosphere. It is based on thermodynamic relationships (equation of state) and assumes that the atmosphere lacks water vapor, wind, and turbulence. The ISA has been established to provide a common reference standard for the lower atmosphere (i.e., the troposphere) in terms of pressure, temperature, density, and other properties such as viscosity and the speed of sound.

The ISA model is necessary for the aerospace industry because it provides a standardized reference for calculating and testing aircraft and engine performance. With the ISA, engineers can predict and compare the performance of different aircraft designs under the same standard atmospheric conditions, making it easier to compare the performance of other aircraft and engines. In addition to its use in performance calculations, the ISA is also a reference for instrument calibration. By calibrating instruments such as altimeters and airspeed indicators relative to the ISA, all such instruments will show identical readings under the same atmospheric conditions, regardless of the actual conditions on any given day or time.

It is essential to recognize that the ISA model is not a meteorological model of actual atmospheric conditions, e.g., from barometric pressure changes or wind conditions. Neither does it account for humidity effects; the air in the ISA model is assumed to be dry, clean, and of constant composition. However, humidity effects are typically accounted for in the flight vehicle performance or engine analysis by applying a correction factor after obtaining the pressure and density from the ISA model, as discussed later in this chapter.

The International Organization for Standardization (ISO) publishes the ISA model as International Standard ISO 2533:1975. The International Civil Aviation Organization (ICAO) has also adopted the ISA model, which is used universally throughout all aspects of civil aviation. A document on the ISA standard can also be obtained from NOAA. Tables of ISA properties are published for discrete altitude values incremented in a few hundred feet or meters in many sources, including almost every textbook on aerodynamics and aircraft performance. These ISA tables can be used to find appropriate values at intermediate altitudes by using linear interpolation, recognizing that interpolation is a straightforward process but is also approximate. A much better approach, in general, is to calculate the properties for any specified altitude using the equations of the ISA, which will now be determined.

Equations of the ISA in the Troposphere

The equations of the ISA can be established starting from the hydrostatic equation, which has already been introduced, i.e., using

(1)   \begin{equation*} \frac{dp}{dh} = -\varrho g \end{equation*}

Remember that the hydrostatic equation is an ordinary differential equation that relates the change in pressure, dp, in a fluid with respect to a change in vertical height, dh. Usually, when dealing with the atmosphere, the symbol {h} is used instead of {z} to represent “height” or altitude. In this case, the height is measured relative to the mean sea level, or MSL.

Temperature Variation

The temperature T in the standard atmosphere is assumed to be a linearly decreasing function of altitude, which is a good statistical approximation to the actual average temperature variation in the atmosphere and can be expressed by

(2)   \begin{equation*} T = T_0 - B \, h = 59 -\left( \frac{3.57}{1,000} \right) h \quad \hbox{in units of $^{\circ}$F} \end{equation*}

or

(3)   \begin{equation*} T = 59 - 0.00357 h \quad \hbox{in units of $^{\circ}$F} \end{equation*}

In this case, {h} is expressed in feet (ft), and B is a constant known as the standard atmospheric lapse rate. This temperature lapse equation is valid only to the troposphere’s limits, or about 36,000 ft, which is called the tropopause. After that, the temperature stays constant, up to about 65,000 ft.

The value of B is 3.57^{\circ}F per 1,000 ft of altitude or 0.00357^{\circ}F per ft = 0.00357^{\circ}R per ft. In practice, lapse rates will change with the level of humidity. The dry adiabatic lapse rate is about 5.5 ^{\circ}F per 1,000 ft of altitude, and the moist lapse rate ranges varies between 2–3 ^{\circ}F per 1,000 ft of altitude; the ISA model uses an accepted standard value of lapse rate that is between these two other lapse rates.

In SI units, the atmospheric temperature lapse equation can be written as

(4)   \begin{equation*} T = T_0 - B h = 15 - \left( \frac{6.5}{1,000} \right) h\quad \hbox{in units of $^{\circ}$C} \end{equation*}

or

(5)   \begin{equation*} T = 15 - 0.0065 h\quad \hbox{in units of $^{\circ}$C} \end{equation*}

where {h} is expressed in meters (m), and the lapse rate, in this case, is 6.5^{\circ}C per 1,000 m. This lapse rate is equivalent to 1.981^{\circ}C per 1,000 ft, giving

(6)   \begin{equation*} T = 15 - 0.001981 \, h \quad \hbox{in units of $^{\circ}$C} \end{equation*}

with {h} being measured in feet (ft). It is standard practice to measure altitude in feet for aeronautical and aviation purposes, although, if needed, the conversion is 1 meter (m) = 3.28084 feet (ft). It is important to be sure of the value of the lapse rate in the units of interest. Often, the ratio of the ISA temperature at a given altitude to the MSL temperature is used, which is given the symbol \theta, i.e.,

(7)   \begin{equation*} \theta = \frac{T}{T_0} \end{equation*}

Solutions for Pressure & Density

In summary, three equations are now available:

1. The hydrostatic equation, which is an ordinary differential equation, i.e.,

(8)   \begin{equation*} \frac{dp}{dh} = -\varrho g \end{equation*}

2. An equation for the linear temperature variation or lapse with height, i.e.,

(9)   \begin{equation*} T = T_0 - B \, h \end{equation*}

3. The thermodynamic equation of state, i.e.,

(10)   \begin{equation*} p = \varrho R T \end{equation*}

Substituting the latter two equations (Eqs. 9 and 10) into the hydrostatic equation (Eq. 8) gives

(11)   \begin{equation*} \frac{dp}{dh} = -\varrho g = - \frac{p g}{R T} = - \frac{p g}{R (T_0 - B \, h)} \end{equation*}

which is the governing equation that now needs to be solved. Using separation of variables and integrating between MSL (h = 0, p = p_0) and the height of interest, {h} where the pressure is p gives

(12)   \begin{equation*} \int_{p_0}^{p} \frac{dp}{p} = - \int_{0}^{h} \frac{g}{R (T_0 - B \, h)} dh = - \frac{g}{R} \int_{0}^{h} \frac{dh}{T_0 - B \, h} \end{equation*}

Performing the integration gives

(13)   \begin{equation*} \frac{p}{p_0} = \bigg( 1 - \frac{B}{T_0} \, h \bigg)^{\displaystyle{\frac{g}{R B}}} \end{equation*}

The corresponding density ratio is

(14)   \begin{equation*} \frac{\varrho}{\varrho_0}= \bigg( 1 - \frac{B}{T_0} \, h \bigg)^{\left(\displaystyle{\frac{g}{R B}} - 1 \right)} \end{equation*}

ISA Pressure Variations

The resulting pressure in the ISA, p, at any altitude {h} relative to the value at MSL, p_0, becomes

(15)   \begin{equation*} \frac{p}{p_0} = \delta = \left( 1 - 6.883\times 10^{-6} \, h \right)^{g/RB} = \left( 1 - 6.883\times 10^{-6} \, h \right)^{5.256} \end{equation*}

where {h} in this latter equation is measured in feet (ft). Notice that in USC, then

(16)   \begin{equation*} \frac{B}{T_0} = \frac{3.57/1,000}{59.0+ 459.67} = 6.883\times 10^{-6} \end{equation*}

Remember that R is the gas constant for air, which is 1716.49 ft-lb slug^{-1}R^{-1} or 287.057 J kg^{-1} K^{-1}. Therefore, the value of g/RB, which is a non-dimensional grouping, is

(17)   \begin{equation*} \frac{g}{R B} = \frac{32.17}{1716.49 \times 0.00357} = \frac{9.81}{287.057 \times 0.0065} = 5.256 \end{equation*}

so its numerical value does not depend on the unit system. If {h} were to be measured in meters (m), then

(18)   \begin{equation*} \frac{p}{p_0} = \delta = \left( 1 - 2.256\times 10^{-5} \, h \right)^{5.256} \end{equation*}

where, in this case

(19)   \begin{equation*} \frac{B}{T_0} = \frac{6.5/1,000}{15.0+ 273.15} = 2.256\times 10^{-5} \end{equation*}

Under standard MSL conditions, the value of p_0 is 2116.4 lb/ft{^{2}}, 101,325 N/m^{^2}, or 101,325 Pa or 101.325 kPa.

ISA Density Variations

The corresponding density \varrho in the ISA at any altitude can be calculated by invoking the thermodynamic equation of state. The pressure and density are related by using

(20)   \begin{equation*} \frac{\varrho}{\varrho_0} = \frac{p}{p_0} \left( \frac{T_0}{T} \right) \end{equation*}

Therefore, if the local temperature corresponds to the standard local temperature in the ISA, i.e., T_0 - B \, h, then

(21)   \begin{equation*} \frac{\varrho}{\varrho_0} = \frac{p}{p_0} \left( \frac{T_0}{T_0 - B \, h} \right) \end{equation*}

and so the local density in the ISA relative to MSL is

(22)   \begin{equation*} \frac{\varrho}{\varrho_0} = \sigma = \bigg( 1 - 6.883\times 10^{-6}\, h \bigg)^{\left( \displaystyle{\frac{g}{R B} - 1} \right)} = \left( 1 - 6.883\times 10^{-6} \, h \right)^{4.256} \end{equation*}

where {h} is measured in feet (ft). If {h} is measured in meters (m), then

(23)   \begin{equation*} \frac{\varrho}{\varrho_0} = \sigma = \left( 1 - 2.256\times 10^{-5} \, h \right)^{4.256} \end{equation*}

Under standard MSL conditions the value of \varrho_0 is 0.002378 slugs/ft{^{3}} or 1.225 kg/m^{^3}.

Summary of ISA Properties at MSL

Values of the ISA properties at standard MSL conditions are helpful to have on hand and are given in the table below.

Table of ISA Properties at MSL.
Property Symbol SI units USC units
Pressure p_0 1.01325\times10^{5} Nm^{-2} (Pa) 2116.4 lb/ft{^{2}} (29.92 inches of Hg)
Density \varrho_0 1.225 kg m{^{-3}} 0.002378 slugs ft{^{-3}}
Temperature T_0 288.15 K 518.67 R
Dynamic viscosity \mu_0  1.789\times10^{-5} kg m^{-1} s^{-1} 3.737\times10^{-7} slugs ft^{-1} s^{-1}
Speed of sound a_0 340.3 m s^{-1} 1116.47 ft s^{-1}
Gas constant R 287.057 J kg^{-1} K^{-1} 1716.49 ft-lb slug^{-1}R^{-1}

Check Your Understanding #1 – Calculation of the properties of the ISA

Calculate the properties of the ISA using the relevant equations. You may do this in SI or USC units, but it is best to try to calculate the properties in both sets of units.

Show solution/hide solution.

The equations for the ISA are relatively easy to program in MATLAB; below is a short piece of code used to calculate such properties in the troposphere.

g=9.81; % acceleration under gravity in m/s^2
B=-0.0065; % temp lapse rate in ISA in Kelvin/meter
R=287.05; % gas constant for air
T_sl=288.15; % ISA MSL standard temperature in Kelvin
p_sl=1.01325e+5; % standard pressure at sea level in Pascals
rho_sl=p_sl/(R*T_sl) % use ideal gas law to get the density
a_sl=sqrt(1.40*p_sl/rho_sl) % speed of sound at sea level
z=linspace(0,10000,1000); % calculate ISA properties up to the tropopause
T_z=T_sl+B.*z;
p_z=p_sl.*((1+B.*z./T_sl).^(-g/(R*B)));
rho_z=p_z./(R.*T_z);
mu_z=1.458e-6.*sqrt(T_z)./(1.0+0+110.40./T_z); % Sutherland’s law
a_z=sqrt(1.40.*p_z./rho_z); % speed of sound or use a_z=sqrt(1.40.*R*T_z)

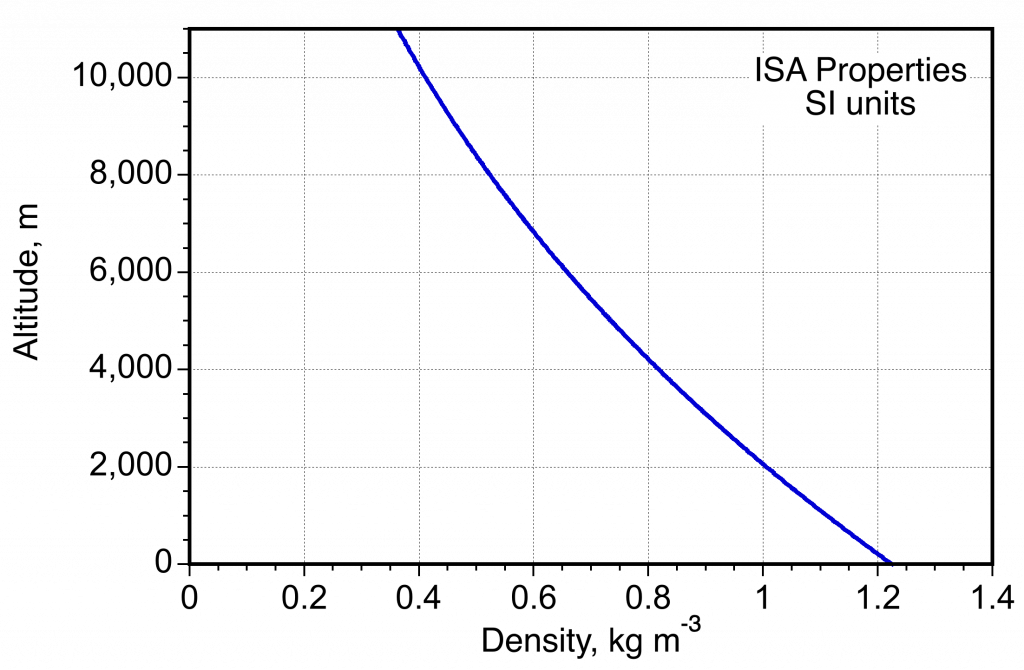
  • Variation of density in the ISA measured in SI units.

  • Variation of pressure in the ISA measured in SI units.

  • Variation of temperature in the ISA measured in SI units.

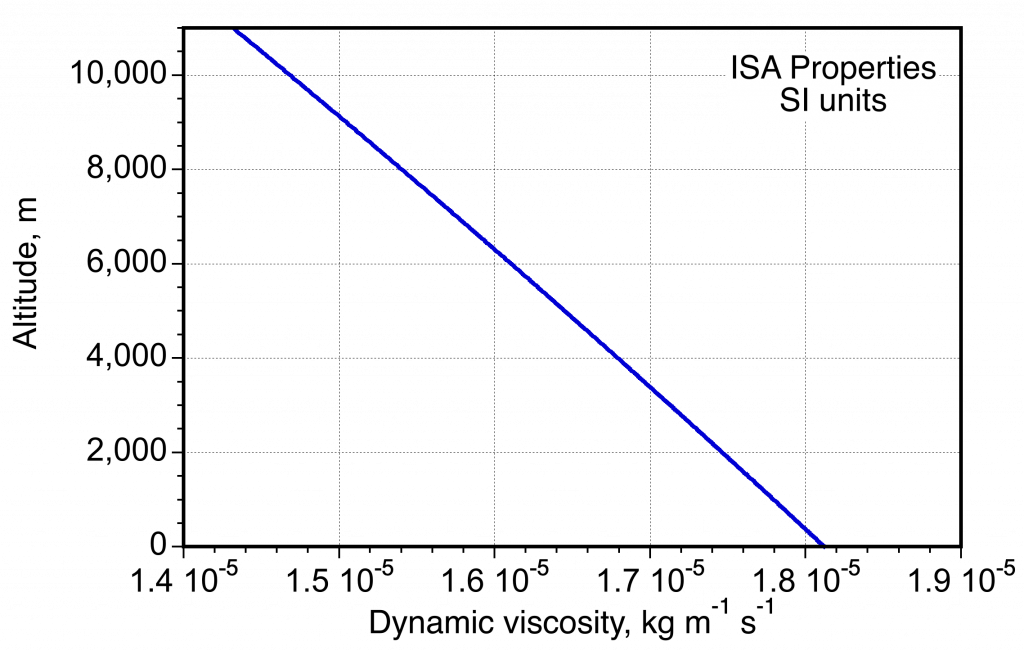
  • Variation of viscosity in the ISA measured in SI units.

Density Corrections for Humidity

The changes in air density from changes in humidity tend to be relatively small, but they can still have an impact in some scientific and engineering applications. To account for these effects, a correction factor is applied to account for the change in air density with varying humidity levels. The magnitude of this correction can range from 1%–2% of the dry air value, so it will be essential to consider in applications where air density plays a more critical role, such as aviation, aerospace engineering, wind tunnel testing, and meteorology.

It should be appreciated that adding humidity (water vapor) to air will decrease its density. The reason is that air comprises mainly diatomic nitrogen molecules and oxygen molecules, i.e., N2 and O2, , with air being composed of 78% nitrogen and 20% oxygen. Nitrogen has an atomic weight of 14, so an N2 molecule has an atomic weight of 28. Oxygen has an atomic weight of 16, so an O2 molecule has an atomic weight of 32. Therefore, the overall atomic weight of air is about 0.78 \times 28 + 0.2 \times 32 \approx 28.2. Water vapor, which is comprised of H2O molecules, has an atomic weight of 2 + 16 = 18; hydrogen has an atomic weight of 1. Therefore, the mass of the air per unit volume (i.e., the density) will decrease as water vapor is added, with the conclusion that moist air will be less dense than dry air.

There are different methods to determine the correction factor for the effects of humidity on air density, such as using wet and dry bulb temperature measurements to find the relative humidity (RH) or finding the dew point, i.e., the temperature at which the air becomes saturated with water vapor and clouds form. These methods allow for the correction of the small but non-negligible impact that humidity can have on air density, hence on the performance of flight vehicles.

For example, the lift force generated by an aircraft’s wings is proportional to air density. Lower air density results in reduced lift for the same airspeed, requiring higher speeds or higher angles of attack to generate the same lift, which can affect fuel efficiency and flight performance. Engines depend on the intake of air to burn fuel and produce thrust. With lower air density, the mass of air entering the engine decreases, reducing the engine’s thrust or power output. In flight test and wind tunnel measurements, correcting the effects of humidity on density can be critical because minor errors in the value of air density can propagate through subsequent steps in the any analysis.

Calculating Relative Humidity

The first step in accounting for the effects of humidity on air density is to either measure the relative humidity (RH) using a hygrometer[2]or to use dry and wet bulb temperature measurements, T_{\rm db} and T_{\rm wb}, respectively, which are usually combined as two thermometers mounted side-by-side known as Mason’s hygrometer. The saturation vapor pressure can then be determined using empirical formulas like Tetens’ equation, i.e.,

(24)   \begin{equation*} p_{\rm vs} = A \, \exp\left(\frac{B \, (T - 273.15)}{T - C}\right) \end{equation*}

where A = 610.78, B = 17.27, and C = 35.85 when in base SI units, i.e., Pa and K. In Eq. 24, the temperature, T, refers to either the dry bulb temperature, i.e., T_{\rm db}, or the wet-bulb temperature, i.e., T_{\rm wb}, as appropriate. If the temperature values are in ^{\circ}C, then the corresponding equation is

(25)   \begin{equation*} p_{\rm vs} = A \, \exp \left( \frac{B \, T}{T + D} \right) \end{equation*}

where D = 237.3. Tetens’ equation has good validity for the saturated vapor pressure from 0^{\circ}C to 35^{\circ}C.

Tetens’ formula predicts that the saturation water vapor pressure changes approximately exponentially with increasing temperature under typical atmospheric conditions. Indeed, the water-holding capacity of the atmosphere increases by about 7% for every 1^{\circ}C rise in temperature. The August-Roche-Magnus formula has the same structure as Eq. 24 but with slightly different values of A, B, C, and D, and provides a somewhat more accurate representation of the saturated vapor pressure over a broader range of temperatures.

The next steps are to calculate the saturation vapor pressure at the dry-bulb temperature, i.e.,
using Eq. 25, then

(26)   \begin{equation*} p_{\text{vs,db}} = A \, \exp \left( \frac{B \, T_{\text{db}}}{T_{\text{db}} + D} \right) = 610.78 \, \exp \left( \frac{17.27 \, T_{\text{db}}}{T_{\text{db}} + 237.3} \right) \end{equation*}

followed by the saturation vapor pressure at the wet-bulb temperature, i.e.,

(27)   \begin{equation*} p_{\text{vs,wb}} = A \, \exp \left( \frac{B \, T_{\text{wb}}}{T_{\text{wb}} + D} \right) = 610.78 \, \exp \left( \frac{17.27 \, T_{\text{wb}}}{T_{\text{wb}} + 237.3} \right) \end{equation*}

The vapor pressure is then

(28)   \begin{equation*} p_v = p_{\text{vs,wb}} - \gamma (T_{\text{db}} - T_{\text{wb}}) \end{equation*}

where {\gamma} is called the psychrometric constant.[3] Finally, the relative humidity, RH, is given by

(29)   \begin{equation*} RH = \frac{p_v}{p_{\text{vs,db}}} \end{equation*}

Using a value of \gamma = 0.65 Pa ^{\circ}C^{-1} (0.00065 kPa ^{\circ}C^{-1}) is usually sufficent in the range of applicability of Tetens’ formula.

Calculating the Density of Humid Air

With the known relative humidity value, the air density, including the effects of humidity, can now be calculated. The partial pressure of water vapor, p_v, depends on the the relative humidity (RH) and the saturation vapor pressure, p_{vs}, at the given temperature, which are related according to

(30)   \begin{equation*} p_v = RH \ p_{\rm vs} \end{equation*}

Again, the saturation vapor pressure can be determined using the Tetens equation given by Eq. 24, i.e.,

(31)   \begin{equation*} p_{\rm vs} = A \exp\left(\frac{B \, (T - 273.15)}{T - C}\right) \end{equation*}

Then the partial pressure of dry air, p_d, can be calculated, i.e.,

(32)   \begin{equation*} p_d = p - p_v = p - RH \ p_{\rm vs} \end{equation*}

where p is the measured (local) atmospheric pressure (including the partial pressure of water vapor). The density of dry air, \varrho_d, can be obtained using the equation of state, i.e.,

(33)   \begin{equation*} \varrho_d = \frac{p_d}{R \, T} \end{equation*}

where p_d is the partial pressure of dry air, R is the specific gas constant for dry air, and T is the absolute temperature. Finally, the density of moist air can be calculated using

(34)   \begin{equation*} \varrho = \frac{p_d}{R \, T} + \frac{RH \, p_{\rm vs}}{R_v T} = \varrho_d + \frac{RH \, p_{\rm vs}}{R_v T} \end{equation*}

where R_v is the specific gas constant for water vapor, where R_v = 461.5 J kg^{-1} K^{-1} = 2,760.0 ft lb slug^{-1} R^{-1}. The humidity corrections to density, however, tend to be small and necessary only for temperatures greater than about 60^{\circ}F or 15^{\circ}C and become much larger for temperatures above 90^{\circ}F or 30^{\circ}C.

Check Your Understanding #2 – Correcting the value of air density for humidity

Calculate the corrected air density for the effects of humidity under “hot and high” conditions. The following conditions are specified: temperature, T = 40^{\circ}C (= 310.15K), local ambient pressure, p = 100.5 kPa, and relative humidity, RH = 75%. Compare the value obtained to the corresponding value of dry air and comment on your results.

Show solution/hide solution.

According to the Tetens formula, the saturation vapor pressure is

    \[ p_{\rm vs} = A \exp\left(\frac{B \, (T - 273.15)}{T - C}\right) = 610.78 \, \exp\left(\frac{17.27 \times (310.15 - 273.15)}{310.15 - 35.85}\right) \approx 6,454.45~\mbox{Pa} \]

Therefore, the partial pressure of water vapor is

    \[ p_v = RH \ p_{\rm vs} = 0.75 \times 3,167.17 \approx 4,836.34~\mbox{Pa} \]

The partial pressure of dry air in the mixture is

    \[ p_d = p - p_v = p - RH \ p_{\rm vs} = 100,500 - 4,836.34 \approx 95,663.66~\mbox{Pa} \]

As a reference, the density of perfectly dry air at T = 310.15 K and p = 100.5 kPa is

    \[ \varrho_{d} = \dfrac{ p}{R \,T} = \dfrac{100,500}{287.05 \times 310.15} = 1.129~\text{kg m}^{-3} \]

where for dry air R = 287.05 \, \text{J kg}^{-1} \text{K}^{-1}. Therefore, the air density with 75% humidity is

    \[ \varrho = \frac{p - p_v}{R \, T} + \frac{p_v}{R_v \, T} = \varrho_d + \varrho_v = \frac{p_d}{R \, T} + \frac{p_v}{R_v \, T} = \varrho_d + \varrho_v \]

where R_v = 461.5 \, \text{J kg}^{-1} \text{K}^{-1}. Substituting the numerical values gives

    \[ \varrho = \frac{100,500 - 4,836.34}{287.05 \times 310.15} + \frac{4,836.34}{461.5 \times 310.15} = 1.075 + 0.0337 = 1.108~\text{kg m}^{-3} \]

Thus, the density of the humid air in this case (1.108 kg m^{-3}) is less than the density of dry air (1.129 kg m^{-3}), as expected. Comment: Although the difference is small, it is still significant enough to have an impact on engine and airplane performance, especially under environmental conditions of high humidity, high altitudes, and high temperatures.

Other Atmospheric Models

Various other extended atmospheric models are used to represent the characteristics of the atmosphere above the tropopause and into space. One purpose of using these models is to help predict the orbital decay of satellites from atmospheric drag.

Approximate Model for the Troposphere

Air density is frequently calculated in aerodynamics to determine aircraft and engine performance. In the lower atmosphere where many general aviation aircraft normally fly (say, below 20,000 ft or 6,000 m), the standard value of air density can be closely approximated by the equation

(35)   \begin{equation*} \frac{\varrho}{\varrho_0} = \exp \left( \frac{-0.0297 \, h}{1000} \right) \end{equation*}

where {h} is expressed in feet (ft) and \varrho_0 = 0.002378 slugs ft{^{-3}}. In SI units, the corresponding equation is

(36)   \begin{equation*} \frac{\varrho}{\varrho_0} = \exp \left( \frac{ -0.0296 \, h}{304.8} \right) \end{equation*}

where {h} is expressed in meters (m) and \varrho_0 = 1.225 kg/m{^3}.

ICAO extended ISA model

The ICAO has published an extended ISA model called “ICAO Standard Atmosphere” (Document 7488-CD). It has the same model as the ISA in the troposphere but extends the altitude coverage to 80 km (262,500 ft). The temperature and pressure values defined by ICAO for the extended model are given in the table below. Notice that one hectoPascal (hPa) is equal to 100 Pascals. Hectopascals are typically used in barometric pressure measurements.

Values used for the ICAO extended ISA model.
Altitude (km) Altitude (ft) Temp. (^{\circ}C) Press. (hPa) Lapse Rate (^{\circ}C/1,000 ft)
0 MSL 15.0 1013.25 -1.98 (Troposphere)
11 36,000 -56.5 226.00 0.00 (Stratosphere)
20 65,000 -56.5 54.70 -0.3 (Stratosphere)
32 105,000 -44.5 8.68 n/a

NLR and Air Force Models

The U.S. Naval Research Laboratory (NLR) has developed a model of the Earth’s atmosphere from Earth’s surface to space. One use of this model is to help engineers predict the orbital decay of satellites from atmospheric drag. The U.S. Air Force Space Command and Space Environment Technologies have also developed a model for the Earth’s atmosphere from 120 km to 2,000 km.

Jacchia/Lineberry 1971 Model

The Jacchia/Lineberry 1971 model is an empirical atmospheric model designed to estimate the density of the Earth’s atmosphere for satellites in Low Earth Orbit (LEO from approximately 50 km to 1,000 km altitude. This model improves upon an earlier model by incorporating updated data and methods for enhanced accuracy. The atmospheric density, \varrho, is calculated based on altitude, {h}, solar activity, and time of year according to

(37)   \begin{equation*} \varrho(h) = \varrho_0 \, \exp\left(-\dfrac{h}{H}\right) \end{equation*}

where \varrho_0 is the MSL ISA density and H is called the scale height. The scale height varies with solar activity and time, as given by

(38)   \begin{equation*} H = H_0 + \Delta H \end{equation*}

where H_0 represents the nominal scale height and \Delta H is the adjustment resulting from solar activity and seasonal variations. The Jacchia/Lineberry 1971 model is often applied in satellite tracking, orbit decay, and spacecraft design to account for atmospheric drag in LEO.

Tables of ISA Properties

The equations of the International Standard Atmosphere (ISA) have now been introduced. All aerospace engineers must understand the ISA properties and how the ISA is used for both engineering and other aviation purposes. In addition, it is necessary to practice applying the equations of the ISA to calculate temperature, pressure, and density (for both standard and non-standard conditions) in appropriate engineering units, i.e., USC and SI. Handy online ISA calculators are also available.

It is also necessary to be able to read values of pressure, temperature, and density from tables of ISA properties, which are listed for discrete values of altitude in almost every aerodynamics textbook; an example is shown below. These tables can be used with linear interpolation methods to find approximate values at intermediate altitudes. For example, the table below gives ISA properties from -1,000 feet to 65,000 feet in 1,000-foot intervals. Recall that \sigma is density divided by MSL density, \delta is the pressure divided by MSL pressure, and \theta is the temperature divided by MSL temperature. Notice that the temperature, T, in the table below is in units of degrees Rankine (^{\circ}R), pressure, p, is in units of pounds per square foot (lb ft^{-2}), the density, \varrho, is in units of slugs per cubic foot (slugs ft{^{-3}}), the speed of sound, a, is in speed of feet per second (ft s^{-1}), and the viscosity, \mu, is in units of slugs per foot-second (slugs ft^{-1}s^{-1}).

Table of ISA values in USC units in steps of 1,000 feet.
Altitude {h} \sigma \delta \theta T p \varrho a \mu \times 10^6
-1 1.0296 1.0367 1.0069 522.2 2193.8 0.0024472 1120.3 0.376
0 1 1 1 518.7 2116.2 0.0023769 1116.5 0.374
1 0.9711 0.9644 0.9931 515.1 2040.9 0.0023081 1112.6 0.372
2 0.9428 0.9298 0.9863 511.5 1967.7 0.0022409 1108.7 0.37
3 0.9151 0.8963 0.9794 508 1896.7 0.0021752 1104.9 0.368
4 0.8881 0.8637 0.9725 504.4 1827.7 0.0021109 1101 0.366
5 0.8617 0.8321 0.9656 500.8 1760.9 0.0020482 1097.1 0.364
6 0.8359 0.8014 0.9588 497.3 1696 0.0019869 1093.2 0.362
7 0.8107 0.7717 0.9519 493.7 1633.1 0.001927 1089.3 0.36
8 0.7861 0.7429 0.945 490.2 1572.1 0.0018685 1085.3 0.358
9 0.7621 0.7149 0.9381 486.6 1512.9 0.0018113 1081.4 0.355
10 0.7386 0.6878 0.9313 483 1455.6 0.0017555 1077.4 0.353
11 0.7157 0.6616 0.9244 479.5 1400.1 0.0017011 1073.4 0.351
12 0.6933 0.6362 0.9175 475.9 1346.2 0.001648 1069.4 0.349
13 0.6715 0.6115 0.9107 472.3 1294.1 0.0015961 1065.4 0.347
14 0.6502 0.5877 0.9038 468.8 1243.6 0.0015455 1061.4 0.345
15 0.6295 0.5646 0.8969 465.2 1194.8 0.0014962 1057.4 0.343
16 0.6092 0.5422 0.8901 461.7 1147.5 0.001448 1053.3 0.341
17 0.5895 0.5206 0.8832 458.1 1101.7 0.0014011 1049.2 0.339
18 0.5702 0.4997 0.8763 454.5 1057.5 0.0013553 1045.1 0.337
19 0.5514 0.4795 0.8695 451 1014.7 0.0013107 1041 0.335
20 0.5332 0.4599 0.8626 447.4 973.3 0.0012673 1036.9 0.332
21 0.5153 0.441 0.8558 443.9 933.3 0.0012249 1032.8 0.33
22 0.498 0.4227 0.8489 440.3 894.6 0.0011836 1028.6 0.328
23 0.4811 0.4051 0.842 436.7 857.2 0.0011435 1024.5 0.326
24 0.4646 0.388 0.8352 433.2 821.2 0.0011043 1020.3 0.324
25 0.4486 0.3716 0.8283 429.6 786.3 0.0010663 1016.1 0.322
26 0.433 0.3557 0.8215 426.1 752.7 0.0010292 1011.9 0.319
27 0.4178 0.3404 0.8146 422.5 720.3 0.0009931 1007.7 0.317
28 0.4031 0.3256 0.8077 419 689 0.000958 1003.4 0.315
29 0.3887 0.3113 0.8009 415.4 658.8 0.0009239 999.1 0.313
30 0.3747 0.2975 0.794 411.8 629.7 0.0008907 994.8 0.311
31 0.3611 0.2843 0.7872 408.3 601.6 0.0008584 990.5 0.308
32 0.348 0.2715 0.7803 404.7 574.6 0.000827 986.2 0.306
33 0.3351 0.2592 0.7735 401.2 548.5 0.0007966 981.9 0.304
34 0.3227 0.2474 0.7666 397.6 523.5 0.000767 977.5 0.302
35 0.3106 0.236 0.7598 394.1 499.3 0.0007382 973.1 0.3
36 0.2988 0.225 0.7529 390.5 476.1 0.0007103 968.7 0.297
37 0.2852 0.2145 0.7519 390 453.9 0.000678 968.1 0.297
38 0.2719 0.2044 0.7519 390 432.6 0.0006463 968.1 0.297
39 0.2592 0.1949 0.7519 390 412.4 0.0006161 968.1 0.297
40 0.2471 0.1858 0.7519 390 393.1 0.0005873 968.1 0.297
41 0.2355 0.1771 0.7519 390 374.7 0.0005598 968.1 0.297
42 0.2245 0.1688 0.7519 390 357.2 0.0005336 968.1 0.297
43 0.214 0.1609 0.7519 390 340.5 0.0005087 968.1 0.297
44 0.204 0.1534 0.7519 390 324.6 0.0004849 968.1 0.297
45 0.1945 0.1462 0.7519 390 309.4 0.0004623 968.1 0.297
46 0.1854 0.1394 0.7519 390 295 0.0004407 968.1 0.297
47 0.1767 0.1329 0.7519 390 281.2 0.0004201 968.1 0.297
48 0.1685 0.1267 0.7519 390 268.1 0.0004005 968.1 0.297
49 0.1606 0.1208 0.7519 390 255.5 0.0003817 968.1 0.297
50 0.1531 0.1151 0.7519 390 243.6 0.0003639 968.1 0.297
51 0.146 0.1097 0.7519 390 232.2 0.0003469 968.1 0.297
52 0.1391 0.1046 0.7519 390 221.4 0.0003307 968.1 0.297
53 0.1326 0.0997 0.7519 390 211 0.0003153 968.1 0.297
54 0.1264 0.0951 0.7519 390 201.2 0.0003006 968.1 0.297
55 0.1205 0.0906 0.7519 390 191.8 0.0002865 968.1 0.297
56 0.1149 0.0864 0.7519 390 182.8 0.0002731 968.1 0.297
57 0.1096 0.0824 0.7519 390 174.3 0.0002604 968.1 0.297
58 0.1044 0.0785 0.7519 390 166.2 0.0002482 968.1 0.297
59 0.0996 0.0749 0.7519 390 158.4 0.0002367 968.1 0.297
60 0.0949 0.0714 0.7519 390 151 0.0002256 968.1 0.297
61 0.0905 0.068 0.7519 390 144 0.0002151 968.1 0.297
62 0.0863 0.0649 0.7519 390 137.3 0.000205 968.1 0.297
63 0.0822 0.0618 0.7519 390 130.9 0.0001955 968.1 0.297
64 0.0784 0.059 0.7519 390 124.8 0.0001864 968.1 0.297
65 0.0747 0.0562 0.7519 390 118.9 0.0001777 968.1 0.297

Check Your Understanding #3 – Estimating the atmospheric properties of Mars

The Viking landers have measured the atmospheric properties of Mars, and engineers have determined that the atmosphere has a linear thermal gradient layer from {z} = 0 to 40 km and an isothermal layer from {z} = 40 km to 80 km. The lapse rate B in the temperature gradient layer is 2^{\circ}K/km. If the pressure and temperature at the surface of Mars are 230^{\circ}K and 750 Pa, respectively, then determine:

  1. The density of the Martian atmosphere at its surface.
  2. The pressure and density of the Martian atmosphere at 20 km and 40 km.
  3. The temperature, pressure, and density of the Martian atmosphere at 60 km.

Hint: The specific gas constant on Mars is 188.92 J kg^{-1} ^{\circ}K^{-1} and the gravitational acceleration is 3.8 ms-2.

Show solution/hide solution.
  1. Assume the validity of an ideal gas and so use the gas-specific equation of state, i.e.,

        \[ p = \varrho R T \quad \mbox{or} \quad \varrho = \frac{p}{R \, T} \]

    where R on Mars is 188.92 J kg^{-1}^{\circ}K^{-1}. At the surface of Mars with T = 230^{\circ}K and p =750 Pa then

        \[ \varrho_0 = \frac{p_0}{R \, T_0} = \frac{750.0}{188.92 \times 230} = 0.01726~\mbox{kg/m${^3}$}\]

  2. In the non-isothermal layer with the constant temperature lapse rate (and so the linearly decreasing temperature), then at 20 km from the surface of Mars, the temperature is

        \[ T_{\rm 20} = T_0 + B z = 230 - (2 \times 20 ) = 190~\mbox{$^{\circ}$K} \]

    The pressure change with a linear thermal gradient with temperature lapse B between two heights {z_1} and {z_2} is

        \[ \frac{p_2}{p_1} = \left|\frac{T_0 - B \, z_2}{T_0 - \alpha z_1}\right|^{g /R B} \]

    The exponent g/RB for Mars is

        \[ \frac{g}{R \, B} = \frac{ 3.8}{188.92 \times 2/1000} = 10.0572 \]

    The pressure at 20 km is

        \[ p_{20} = p_0 \left|\frac{T_0 - B \, z_2}{T_0}\right|^{10.0572} \]

    giving

        \[ p_{20} = 109.79~\mbox{ Pa} \]

    Using the equation of state for the density at 20 km, then

        \[ \varrho_{20} = \frac{p_{20}}{R T_{20}} = \frac{109.79}{188.92 \times 190} = 0.00305~\mbox{ kg/m${^3}$} \]

    At 40 km then

        \[ T_{40}= 230 - 2 \times 40 = 150~\mbox{$^{\circ}$K} \]

    so, the pressure at 40 km on Mars is

        \[ p_{40} = 750.0 \bigg( \frac{150}{230} \bigg)^{-10.0572} = 10.188~\mbox{ Pa} \]

    Using the equation of state for the density at 40 km, then

        \[ \varrho_{40} = \frac{p_{40}}{R \, T_{40}} = \frac{10.188}{188.92 \times 150} = 0.000359~\mbox{kg/m${^3}$} \]

  3.  For the isothermal layer, then

        \[ \frac{p_2}{p_1} = \exp\bigg( \frac{ -g (z_2 - z_1)}{R \, T_0}\bigg) \]

    So, for an altitude of 60 km, then

        \[ T_{60} = T_{40} = 150~\mbox{$^{\circ}$K} \]

    The pressure at 60 km will be

        \[ p_{60} = p_{40} \, \exp\bigg( \frac{ -g (h_{60} - h_{40})}{R \, T_{40}} \bigg) \]

    and inserting the values gives

        \[ p_{60} = 10.188 \, \exp\bigg( \frac{-3.8 \times 1000 (60-40)}{188.92 \times 150}\bigg) = 0.697~\mbox{Pa} \]

    Finally, using the equation of state then, the density at 60 km will be

        \[ \varrho_{60} = \frac{p_{60}}{R \, T_{60}} = \frac{0.697}{188.92 \times 150} = 0.000024~\mbox{kg/m${^3}$} \]

Satellite Drag

The outer fringes of the Earth’s atmosphere, known as the thermosphere and exosphere, extend from about 200 miles (320 km) to 1,200 miles (2,000 km) above the Earth’s surface. In this region, the atmospheric density is significantly lower than in the troposphere and stratosphere. Despite the low density, the residual atmosphere still exerts a drag force on objects in Low Earth Orbit (LEO), typically defined as an orbit within about 2,000 km of the Earth’s surface.

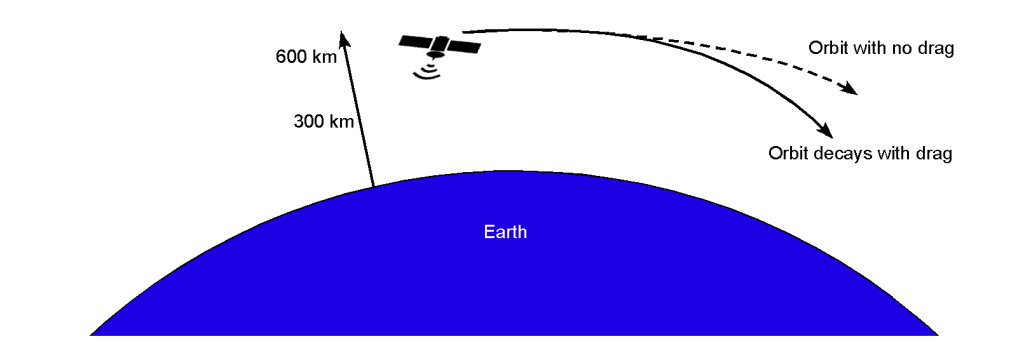
Satellites in low Earth orbit will encounter drag from the residual atmosphere causing their orbits to decay slowly.

LEO is the region closest to Earth, extending from approximately 160 km to 2,000 km in altitude. Objects in LEO travel at very high velocities, typically around 7.8 km/s (17,500 mph), to maintain their orbits. Examples of objects in LEO include the International Space Station (ISS) and the Hubble Space Telescope (HST). Even at the high altitudes of LEO, the low atmospheric density exerts a drag force on satellites and other objects. This drag force causes a gradual loss of altitude, known as orbital decay. The drag force depends on the object’s velocity, cross-sectional area, and atmospheric density at the given altitude.

Orbital decay is a complex process influenced by several factors, including atmospheric density, which varies with altitude, solar activity, and the Earth’s rotation. During periods of high solar activity, the increased solar radiation heats the Earth’s atmosphere, causing it to expand and increase its density at higher altitudes. This results in greater drag on satellites. Semi-empirical models such as the Jacchia/Lineberry 1971 model are used to predict atmospheric density and, consequently, the drag force on objects in LEO. These models combine theoretical calculations with empirical data from satellite observations and other measurements. Satellites in LEO are equipped with thrusters to perform periodic boosts or reboost maneuvers to counteract the effects of drag and maintain their desired orbits. These maneuvers are essential for the operational lifespan of satellites, ensuring they remain in their designated orbits for as long as possible.

The International Space Station (ISS) orbits at an average altitude of about 400 km. Because of atmospheric drag, it loses about 2 km of altitude per month. Regular reboosts are performed to maintain its altitude and ensure continued operation. The Hubble Space Telescope (HST) orbits at an altitude of approximately 540 km. Although it experiences less drag than the ISS, it still requires occasional boosts to maintain its orbit.

Are there aerosol particles in the atmosphere?

Yes! An interesting fact about the atmosphere is that it contains tiny particles known as aerosols, which play a significant role in various atmospheric processes. Aerosols, including dust, pollen, volcanic ash, soot, and pollutants, can be natural or human-made. Despite their small size, aerosols can profoundly impact climate and weather patterns. They can scatter and absorb sunlight, affecting the amount of solar radiation reaching the Earth’s surface. This, in turn, can influence temperature patterns and the formation of clouds. Aerosols also play a crucial role in the formation of cloud droplets. They act as “seeds” around which water vapor can condense, forming tiny droplets that make up clouds. Without aerosols, clouds would not form as quickly or effectively.

Summary & Closure

When dealing with the performance of flight vehicles in the Earth’s atmosphere, it is essential to know (or estimate) the air density in which the vehicle is flying. The power and thrust from air-breathing powerplants are also affected by the air density in which they operate, and their performance generally diminishes with increasing altitude and/or temperature. To address these challenges, aeronautical engineers must have a deep understanding of the properties of the air in the troposphere and how these properties may impact the performance of their aircraft. They use this knowledge to make informed decisions about the design of the aircraft and to conduct tests to ensure that the aircraft meets its performance and safety requirements.

The International Standard Atmosphere (ISA) model forms a basis for standardization. The ISA is used universally in engineering and practical aviation, including as a basis for instrumentation calibration. The International Organization for Standardization (ISO) publishes the ISA model as ISO 2533:1975. The International Civil Aviation Organization (ICAO) has also adopted the ISA model, which is used universally throughout aviation. There are also various extended atmospheric models to represent the characteristics of the atmosphere above the tropopause and into space, which may be needed for multiple reasons, including estimates of the drag on satellites in low Earth orbit. It may also be necessary to know the properties of the atmospheres on other planets, such as for probes or landers.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • Program the ISA equations (use MATLAB or similar) and plot the temperature, pressure, and density as a function of altitude in U.S. customary (USC) units.
  • Use the ISA tables to estimate air density at a pressure altitude of 5,500 ft where the temperature is 10^{\circ}F above standard. Confirm the result using the ISA equations.
  • On a given day, the air temperature at 2,000 feet above mean sea level is 5^{\circ}C. What is this temperature value compared to the ISA temperature?
  • In which atmospheric layer is most of the water vapor contained?
  • Why does the temperature of the atmosphere increase with increasing altitude within the stratosphere?

Additional Online Resources

To improve your understanding of the atmosphere and the ISA, navigate to some of these online resources:

  • High-definition video about the motion of the atmosphere.
  • Take a ride on a U-2 spy-plane through the atmosphere to the edge of space.
  • Try out this handy online ISA calculator.
  • A lecture video on the ISA from Delft University.
  • A YouTube video on the structure of the atmosphere for pilots.
  • A good video summary of the ISA.
  1. UVB radiation has been linked to various harmful effects on human health and the environment. It contributes to global warming and is a significant risk factor for skin cancers such as melanoma. Additionally, excessive exposure to UVB radiation can lead to other human health issues, including cataracts and immune system suppression. ↵
  2. A hygrometer measures relative humidity as distinct from a hydrometer, which measures the specific gravity. Many kinds of analog and digital types are available. ↵
  3. Psychrometry is also called hygrometry, is a field that deals with gas-vapor mixtures. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n10

Share This Book