Worked Examples: Internal Flows

J. Gordon Leishman

72 Worked Examples: Internal Flows

These worked examples have been fielded as homework problems or exam questions.

Worked Example #1

Oil with a density $\varrho_{\rm oil} = 900.0$ kg m ${^{-3}}$ and kinematic viscosity $\nu_{\rm oil}$ = $10^{-5}$ m ${^{2}}$ s $^{-1}$ , flows at 0.2 m ${^3}$ s $^{-1}$ through a 500 m length of 300 mm diameter cast iron pipe. The average roughness of the pipe’s surface is $\epsilon$ = 0.26 mm. Calculate (a) The average flow velocity in the pipe. (b) The Reynolds number of the flow and explain if the flow is laminar or turbulent. (c) The pressure drop and head loss along the pipe. (d) The minimum power of the pump that is needed to move the oil.

(a) The average flow velocity is calculated from the volume flow rate, i.e.,

$V_{\rm av} = \frac{Q}{A}$

so the average flow velocity is given by

$V_{\rm av} = \frac{4Q}{\pi d^2} = \frac{4 \times 0.2}{\pi \times 0.3^2} = 2.83~\mbox{m s$^{-1}$}$

(b) The Reynolds number of the flow in the pipe is

$Re_d = \frac{\varrho_{\rm oil} \, V_{\rm av} \, d}{\mu_{\rm oil} } =\frac{V_{\rm av} \, d}{\nu_{\rm oil}} = \frac{2.83\times 0.3 }{10^{-5}} = 84,900$

so the pipe flow will be turbulent because the Reynolds number is greater than 2,000 and we will need to use the Moody chart to find the friction factor ${\scriptstyle{f}}$ .

(c) We now need the pressure drop and head loss along the pipe. To use the Moody chart, we also need the relative surface roughness, which is

$\frac{\epsilon}{d} = \frac{0.26}{300} = 0.00087$

From the Moody chart for a Reynolds number of 84,900 and a relative roughness of 0.00087 (using interpolation), we have $f$ $\approx 0.022$ . Therefore, the pressure loss over the length of the pipe is

$\Delta p = \frac{1}{2} \varrho_{\rm oil} V_{\rm av}^2 f \left( \frac{L}{d}\right)$

and inserting the values gives

$\Delta p = 0.5\times 900.0\times 2.83^2 \times 0.022\times \left( \frac{500.0}{0.3}\right) = 132.15~\mbox{kPa}$

The corresponding head loss over this pipe is

$h = \frac{\Delta p}{\varrho_{\rm oil} \, g} = \frac{132.15\times 10^3}{900\times 9.81} = 14.97~\mbox{m}$

(d) The pumping power required will be

$P_{\rm req} = Q \, \Delta p_{AB} = 0.2 \times 132.15 \times 10^3 = 26.43~\mbox{kW}$

Worked Example #2

You are tasked with the design of the fuel delivery system. The system requires a flow through a smooth pipe of 200 m in length and 15 mm in diameter. The required fuel flow rate is 125 kg hr $^{-1}$ . The fluid properties of the fuel are given as: $\varrho =$ 800 kg m ${^{-3}}$ and $\mu =$ 0.00164 kg m $^{-1}$ s $^{-1}$ . All entrance effects can be disregarded. (a) What is the pressure drop along the length of the pipe? (b) What pressure capability (in terms of head) is required of the pump? (c) What are the pumping power requirements?

(a) The cross-sectional area of the pipe is

$A_c = \frac{\pi D^2}{4} = \frac{\pi \times 0.015^2}{4} = 0.0001767~\mbox{m${^{2}}$}$

The mass flow rate $\overbigdot{m}$ is given as 125 kg hr $^{-1}$ = 0.0347~kg s $^{-1}$ , i.e.,

$\overbigdot{m} = \varrho \, A_c V_{\rm av} = 0.0347~\mbox{kg s$^{-1}$}$

So, the average flow velocity in the pipe is

$V_{\rm av} = \frac{\overbigdot{m}}{\varrho \, A_c} = \frac{0.0347}{800.0 \times 0.0001767} = 0.246~\mbox{m s$^{-1}$}$

The Reynolds number based on pipe diameter is

$Re = \frac{\varrho V_d \, D}{\mu} = \frac{ 800.0 \times 0.246 \times 0.015}{0.00164} = 1,797$

Notice that this Reynolds number is the laminar regime, so the friction factor $f$ is given by

$f = \frac{64}{Re} = \frac{64}{1,797} = 0.0356$

The pressure drop $\Delta p$ is given by

$\Delta p = \frac{1}{2} \varrho V_{\rm av}^2 \, f \left( \frac{L}{d}\right)$

and inserting the values gives

$\Delta p = \frac{1}{2} \times 800.0 \times 0.246^2 \times 0.0356 \times \left( \frac{200.0}{0.015} \right) = 11,457.4~\mbox{Pa} = 11.46~\mbox{kPa}$

(b) The equivalent head loss ${h}$ will be

$h = \frac{\Delta p}{\varrho \, g} = \frac{11,457.4}{800.0 \times 9.81} = 1.46~\mbox{m}$

(c) The pumping power $P$ can be determined from

$P = \frac{\overbigdot{m} \, \Delta p}{\varrho} = \frac{0.0347 \times 11,457.4}{800.0} = 0.497~\mbox{W}$

Worked Example #3

Oil at 20 $^{\circ}$ C, with density $\varrho$ = 888.0 kg m ${^{-3}}$ and viscosity $\mu$ = 0.800 kg m $^{-1}$ s $^{-1}$ , respectively, is flowing steadily through a 6 cm diameter pipe that is 40 m long. The pressure at the inlet and outlet of the pipe is 745 kPa and 97 kPa, respectively. Determine the flow rate of oil through the pipe.

This pressure drop is a direct consequence of the action of viscous effects. The fluid is oil (dense and thick), so we expect the flow to be at a very low Reynolds number (i.e., laminar). One of the first goals in pipe flow problems is to find the Reynolds number to verify the laminar assumption or to show it is turbulent ( $Re$ > 2,000). Based on the information provided in this problem, the only unknown is $V_{\rm av}$ . From laminar pipe flow theory, we have that

$\Delta p = p_1 - p_2 = \frac{8 \mu \, L \, V_{\rm av}}{R^2} = \frac{32 \, \mu \, L \, V_{\rm av}}{D^2} \label{lam}$

Notice that for a given length of pipe, the pressure drop is proportional to the fluid’s viscosity and flow speed (so the faster we try to move a given fluid, the larger the pressure drop will be) but inversely proportional to the square of the pipe diameter. The average flow velocity is

$V_{\rm av} = \frac{\left( p_1 - p_2 \right) D^2}{32 \, \mu \, L} = \frac{\left(745.0 - 97.0 \right) \times10^3 \times (0.06)^2}{32 \times 0.8 \times 40} = 2.28~\mbox{m s$^{-1}$}$

We can now check to see that the flow is laminar by calculating the pipe Reynolds number, i.e.,

$Re = \frac{\varrho V_{\rm av} \, D}{\mu} = \frac{888.0 \times 2.28 \times 0.06}{0.80} = 151.8$

so it is very low, much less than 2,000, and the expectation of laminar flow is verified, confirming the correct equation (Eq. ??) for the pressure drop. The volume flow rate through the pipe will be

$Q = A \, V_{\rm av} = \frac{\pi D^2}{4} V_{\rm av} = \frac{\pi \left( p_1 - p_2 \right) D^4}{128 \, \mu \, L}$

Substituting in the known values gives

$Q = \frac{\pi \left( p_1 - p_2 \right) D^4}{128 \, \mu \, L} = \frac{\pi \left(745.0 - 97.0 \right) \times10^3 \times (0.06)^4}{128 \times 0.8 \times 40.0} = 0.00644~\mbox{m${^3}$ s$^{-1}$}$

The corresponding mass flow rate of oil will be

$\overbigdot{m} = \varrho \, Q = 888.0 \times 0.00644 = 5.72~\mbox{kg s$^{-1}$}$

Worked Example #4

A coolant type of fluid used in the air-conditioning system of an aircraft is flowing through a smooth 0.12-inch diameter 30 ft long horizontal pipe steadily at an average flow speed of 3 ft s $^{-1}$ . The fluid has a temperature of 40 $^{\circ}$ F, $\varrho$ = 1.93 slug ft ${^{-3}}$ , and $\mu$ = 3.326 $\times$ 10 $^{-5}$ slug ft $^{-1}$ s $^{-1}$ . Determine for this pipe flow: (a) The Reynolds number of the flow based on the pipe diameter and whether the flow is laminar or turbulent; (b) The pressure drop along the length of the pipe; (c) The pumping power required to overcome this pressure drop; (d) Because the pump manufacturer provides pumps measured in pressure units of “head of inches of water,” what is the minimum head needed?

The pressure losses associated with the pipe flow are determined using the equation

$\Delta p_L = \frac{1}{2}\varrho V_{\rm av}^2 \, f \left( \frac{L}{D} \right)$

where ${\scriptstyle{f}}$ is the Darcy-Welsbach friction factor. The friction factor ${\scriptstyle{f}}$ depends on the flow Reynolds number and the roughness of the pipe material. Hence, the pressure loss in a pipe is also a function of the Reynolds number and the roughness of the pipe. Remember that the frictional effects of viscosity cause this pressure loss, which is irrecoverable and subsequently appears as heat.

(a) The Reynolds number of the flow can be calculated using the equation

$Re = \frac{\varrho_{} V_{\rm av} \, D}{\mu_{}} = \frac{1.93 \times 3.0 \times 0.12/12}{3.326 \times 10^{-5}} = 1,740 < 2,300, \mbox{i.e., laminar Flow}$

(b) The pressure loss can be determined using the equation

$\Delta p_L = \frac{1}{2}\varrho V_{\rm av}^2 \, f \left( \frac{L}{D} \right)$

where the friction factor for the laminar flow in a smooth pipe is

$f = \frac{64}{Re}$

Therefore

$\Delta p_L = \frac{1}{2}\varrho V_{\rm av}^2 \frac{64}{Re} \left( \frac{L}{D} \right) = 32\varrho V_{\rm av}^2 \left( \frac{L}{D} \right) \frac{\mu}{\varrho V_{\rm av}D} = \frac{32\mu V_{\rm av} L}{D^2}$

and so

$\Delta p_L = \frac{32 \times (3.326 \times 10^{-5}) \times 3.0 \times 30.0}{(0.01)^2} = 957.89 \mbox{~lb ft$^{-2}$}$

(c) The pumping power required to overcome this pressure drop is

$P = Q \, \Delta p_L$

where the volume flow rate is

$Q = A_pV_{\rm av} = \frac{\pi}{4}D^2V_{\rm av} = \frac{\pi(0.01)^2 \times 3}{4} = 2.356 \times 10^{-4}~\mbox{ft${^3}$ s$^{-1}$}$

Therefore

$P = 2.536 \times 10^{-4} \times 957.89 = 0.2257~\mbox{ft-lb s$^{-1}$}$

(d) The head loss can be determined using

$h_L = \frac{\Delta p_L}{\varrho_{\rm water}g} = \frac{957.89}{1.93 \times 32.17} = 15.43~\mbox{ft} = 185.14~\mbox{inches~of~H}_2\text{O}$

So, we would likely need to specify a pump with a head capability of at least 185 $\mbox{in H}_2\text{O}$ .

Worked Example #5

Write MATLAB code to calculate the friction factor from the Colebrook-White equation.

title(‘Friction Factor vs Reynolds Number’);
function f = frictionFactor(Re, D, epsilon)
% Re: Reynolds number (can be an array)
% D: Pipe diameter
% epsilon: Pipe roughness
% Initial guess for friction factor
f0 = 0.01;
% Iterative solution using the Colebrook-White equation
error = 1e-6;
maxIterations = 100;
f = zeros(size(Re));
for i = 1:length(Re)
f_current = f0;
for iter = 1:maxIterations
leftSide = 1 / sqrt(f_current);
rightSide = -2 * log10((epsilon / D) / 3.7 + 2.51 / (Re(i) * sqrt(f_current)));
f_new = 1 / (leftSide + rightSide^2);
if abs(f_new – f_current) < error
f(i) = f_new;
break;
end
f_current = f_new;
end
end
end

Worked Example #6

In 1865, Van Syckle revolutionized petroleum oil delivery by using an iron oil pipeline. His company transported petroleum oil over a five-statute mile-long pipe with a 4-inch diameter. If the company delivered 200 barrels per hour, what is the minimum power (in horsepower) required to pump the oil along the full length of the pipe? Assume $\varrho_{\rm oil}$ = 1.6046 slug ft ${^{-3}}$ and $\mu_{\rm oil}$ = $8.4627 \times 10^{-5}$ slug ft $^{-1}$ s $^{-1}$ . The roughness $\epsilon$ = 0.09 mm for the pipe. Assume 1 barrel = 5.615 ft ${^3}$ .

We must find the pressure loss $\Delta p_L$ to calculate the power. We need to know whether the flow is turbulent or laminar, and so we need to know the Reynolds number, i.e.,

$Re = \frac{\varrho_{\rm oil} V_{\rm av} \, D}{\mu_{\rm oil}}$

For the above equation, the average flow velocity can be calculated based on the flow rate of the oil. The flow rate of the oil is

$Q = V_{\rm av} \, \rm{Area} = V_{\rm av} \, \frac{\pi}{4} \, D^2 = 200.0 \text{ barrels/hr} = \frac{200\times 5.615}{3,600} = 0.312~\mbox{ft${^{3}}$ s$^{-1}$}$

Therefore,

$V_{\rm av} = \frac{4Q}{\pi D^2} = \frac{4 \times 0.312}{\pi (4/12)^2} = 3.58\mbox{ ft s$^{-1}$}$

Now the Reynolds number can be calculated, i.e.,

$Re = \frac{\varrho_{\rm oil} V_{\rm av} \, D}{\mu_{\rm oil}} = \frac{(1.6046 \times 3.58 \times (4/12)}{8.4627 \times 10^{-5}} = 22,626.6$

This value of the Reynolds number is greater than 2,000. Hence, the flow is turbulent. For a turbulent flow, the pressure loss can be determined using the equation

$\Delta p_L = \frac{1}{2}\varrho_{\rm oil}V_{\rm av}^2 \, f \left( \frac{L}{D} \right)$

Here, the friction factor ${\scriptstyle{f}}$ is a function of relative roughness $\epsilon/D$ and Reynolds number. For the wrought iron pipe, the relative roughness

$\frac{\epsilon}{D} = \frac{0.09}{25.4 \times 4} = 0.00089$

Consulting the Moody chart for $\epsilon/D = 0.00089$ and $Re = 22,626$ , we can find the friction factor, which is about ${\scriptstyle{f}} = 0.0254$ . The pressure drop in the pipe can now be calculated, i.e.,

$\Delta p_L = \frac{1}{2}\varrho_{\rm oil}\, V_{\rm av}^2 \, f \left( \frac{L}{d}\right)$

and inserting the values give

$\Delta p_L = \frac{1}{2}\times 1.6046 \times (3.58)^2 \times 0.0254 \left(\frac{5.0 \times 5,280.0}{(4.0/12)}\right) = 2.069\times 10^4~\mbox{lb ft$^{-2}$}$

The required power to overcome this pressure loss is

$\mbox{Power} = \Delta p_L \, Q$

and inserting the values gives

$\mbox{Power} = \left(2.069\times 10^4\right) (0.312) = 6.63\times 10^4~\mbox{ft-lb s$^{-1}$} = \dfrac{2.718\times 10^4}{550} = 120.5~\mbox{hp}$

Worked Example #7

Air enters a 50 ft long part of an air-conditioning duct made of smooth galvanized steel with a square cross-section of side 2 ft. The equivalent roughness of the duct is $\epsilon$ = 0.00015 ft. The air is pushed through the duct with a fan at a volume flow rate of 1,800 ft ${^3}$ per minute. (a) Determine the pressure drop and head loss along this part of the duct. (b) Determine the power needed to overcome the pressure losses over this part of the duct. Hints: 1. Disregard all entrance effects. 2. Consult the Moody chart.

(a) We are dealing with a duct that has a square cross-section, so we first need to find the hydraulic diameter $D_h$ , which is

$D_h = \frac{4 A_c}{p}$

where $A_c$ is the cross-sectional area, and $p$ is the perimeter of the section. We have a square cross-section of side $a$ , so the equivalent hydraulic diameter is

$D_h = \frac{4 A_c}{p} = \frac{4 a^2}{4a} = a = 2~\mbox{~ft}$

We are given a hint to consult the Moody chart, so the flow through the pipe will likely be turbulent. The equation for the pressure loss through a pipe is

$\Delta p_L = \frac{1}{2} \varrho V_{\rm av}^2 f \left( \frac{L}{D} \right)$

where ${\scriptstyle{f}}$ is the friction factor, which is still to be determined. Its value depends on the Reynolds number and pipe roughness found in the Moody chart.

The average flow velocity $V_{\rm av}$ can be found from the flow rate and cross-sectional area. The pipe area $A_c$ is

$A_c = a^2 = 2^2 = 4.0~\mbox{ft${^{2}}$}$

So, the average flow velocity is

$V_{\rm av} = \frac{Q}{A_c} = \frac{1,800}{60 \times 4.0} = 7.5~\mbox{ft s$^{-1}$}$

To use the Moody chart, we need the corresponding Reynolds number, which is

$Re = \frac{\varrho V_{\rm av} \, D_h}{\mu} = \frac{0.002378 \times 7.5 \times 2}{3.737 \times 10^{-7}} = 95,451$

where we find the density and viscosity of air at ISA conditions.

Because $Re >10^3$ , the flow through the duct will be fully turbulent. We also need the relative pipe roughness, which is

$\frac{\epsilon}{D_h} = \frac{0.00015}{2} = 0.000075 = 7.5 \times 10^{-5}$

Therefore, from the Moody chart, the friction factor is

$f \approx 0.018$

Returning to the calculation of the pressure drop, then

$\begin{eqnarray*} \Delta p & = & \frac{1}{2} \varrho V_{\rm av}^2 \, f \left( \frac{L}{D_h} \right) \\ & = & \frac{1}{2} \times 0.002378 \times 7.5^2 \times 0.018 \times \left( \frac{50.0}{2.0} \right) \\ & = & 0.03~\mbox{lb ft$^{-2}$} \end{eqnarray*}$

which corresponds to a head loss of

$h = \frac{\Delta p}{\varrho \, g} = \frac{0.03}{0.002378 \times 32.17} = 0.39~\mbox{ft}$

(b) The power required to move the air through this part of the duct and overcome this pressure drop is

$P = Q \, \Delta p_L$

so

$P = 1,800/60.0 \times 0.03 = 0.9~\mbox{ft-lb s$^{-1}$}$

which is a minimal amount of power.

Worked Example #8

You are asked to design an irrigation system in which water is pumped through a long horizontal pipe made of smooth plastic tubing. The pipe is 150 m long and has a diameter of 10 cm. The pump output must provide a maximum volume flow rate of 0.09 m ${^3}$ s $^{-1}$ . For satisfactory operation, the sprinklers along the entire length of the pipe must operate at 205.0 kPa or higher pressure. (a) Find the pressure drop along the length of the pipe. (b) Calculate the minimum pressure $p_1$ that needs to be produced at the pump. (c) What pressure capability for the pump (in terms of head) would you specify? Notes: Assume turbulent flow. The density of water $\varrho_{w}$ = 1,000 kg m ${^{-3}}$ and the viscosity of water $\mu_{w} = 1 \times 10^{-3}$ kg m $^{-1}$ s $^{-1}$ .

(a) The volume flow rate, $Q$ , is given by

$Q = V_{\rm av} \, A$

The average flow velocity can be calculated using

$V_{\rm av} = \frac{Q}{A} = \frac{Q}{\displaystyle{\frac{\pi D^2}{4}}} = \frac{4Q}{\pi D^2}$

$V_{\rm av} = \frac{4 \times 0.09}{\pi (0.1)^2} = 11.46~\mbox{m s$^{-1}$}$

Calculating the Reynolds number gives

$Re = \frac{\varrho V_{\rm av} \, D}{\mu} = \frac{1000 \times 11.46 \times 0.1}{0.001} = 1.1 \times 10^6$

For a smooth pipe the roughness factor, $\epsilon = 0.0015$ mm and $\epsilon/D = 1.5 \times 10^{-5}$ . Obtaining the friction factor from the Moody chart gives ${\scriptstyle{f}} = 0.01$ . The pressure drop along the pipe can be calculated using

$\Delta p = p_1 - p_2 = \frac{1}{2} \varrho V_{\rm av}^2 f \left( \frac{L}{d}\right)$

and substituting values gives

$\Delta p = \bigg(\frac{1000 \times 11.46^2}{2}\bigg) \times 0.01 \bigg(\frac{150}{0.1}\bigg) = 984,987~\mbox{Pa} \approx 985.0~\mbox{kPa}$

(b) The pressure at the pump located at point 1 is then the required pressure at the last sprinkler $p_2$ plus the pressure drop

$p_1 = p_2 + \Delta p$

Substituting values in the above equation (notice that both $p_2$ and $\Delta p$ are expressed in kPa) gives

$p_1 = 205.0 + 985.0 = 1,190.0~\mbox{kPa}$

(c) The corresponding head loss can be determined using

$h_L = \frac{\Delta p}{\varrho_{\rm H_2O } \, g} = \frac{1,190 \times 10^3}{1,000 \times 9.81} = 121.3~\mbox{m~of~H}_2\text{O}$

So, we would likely need to specify a pump with a head capability of at least 122 $\mbox{m~of~H}_2\text{O}$ , which would be a reasonably large pump.

Worked Example #9

Cooling water to a wind tunnel heat exchanger flows at a rate of 0.075 m ${^{3}}$ s $^{-1}$ through an asphalted cast-iron pipe 30 m long and 15 cm in diameter. Assume for water that its density $\varrho$ = 1,000 kg m ${^{-3}}$ and its kinematic viscosity $\nu$ = 10 $^{-6}$ m ${^{2}}$ s $^{-1}$ , and the pipe material has an equivalent roughness $\epsilon$ = 0.12 mm. Hint: Consult the Moody Chart. (a) Using the basic principles of pipe flows, show how to calculate the pressure loss and head loss (i.e., frictional losses) along the length of the pipe. (b) Determine the pumping power required.

(a) The general equation for the pressure drop is

$\Delta p = \frac{1}{2} \varrho V_{\rm av}^2 \, f \left( \frac{L}{D} \right)$

where ${\scriptstyle{f}}$ is the friction factor, which depends on the Reynolds number and pipe roughness. The average flow velocity $V_{\rm av}$ can be found from the flow rate and pipe area. The pipe area $A_p$ is

$A_p = \pi \left( \frac{D^2}{4} \right) = \pi \left( \frac{0.15^2}{4} \right) = 0.0177~\mbox{m${^{2}}$}$

so the average flow velocity is

$V_{\rm av} = \frac{Q}{A_p} = \frac{0.075}{0.0177} = 4.24~\mbox{m s$^{-1}$}$

To use the Moody chart, we need the Reynolds number, which is

$Re = \frac{V_{\rm av} \, D}{\nu} = \frac{4.24 \times 0.15}{10^{-6}} = 6.36\times 10^5$

We also need the relative roughness, which is

$\frac{\epsilon}{D} = \frac{0.00012}{0.15} = 0.0008.$

Therefore, from the Moody chart, it can be found that

$f \approx 0.019$

Returning to the calculation of the pressure drop, then

$\begin{eqnarray*} \Delta p & = & \frac{1}{2} \varrho V_{\rm av}^2 \, f \left( \frac{L}{D} \right) \\ & = & \frac{1}{2} \times 1,000 \times 4.24^2 \times 0.019 \times \frac{30}{0.15} \\ & = & 34.157~\mbox{kN m$^{-2}$} \end{eqnarray*}$

The corresponding head loss $h_L$ can be determined using

$h_L = \frac{\Delta p}{\varrho_{w} \, g} = \frac{34.157 \times 10^3}{1,000 \times 9.81} = 3.48~\mbox{m}$

(b) The pumping power required to overcome this pressure drop is

$P = Q \, \Delta p$

where the volume flow rate is

$Q = 0.075~\mbox{m${^{3}}$ s$^{-1}$}$

Therefore

$P = 0.075 \times 34.157 \times 10^3 = 2.562 \times 10^3~\mbox{W} = 2.56~\mbox{kW}$

Worked Example #10

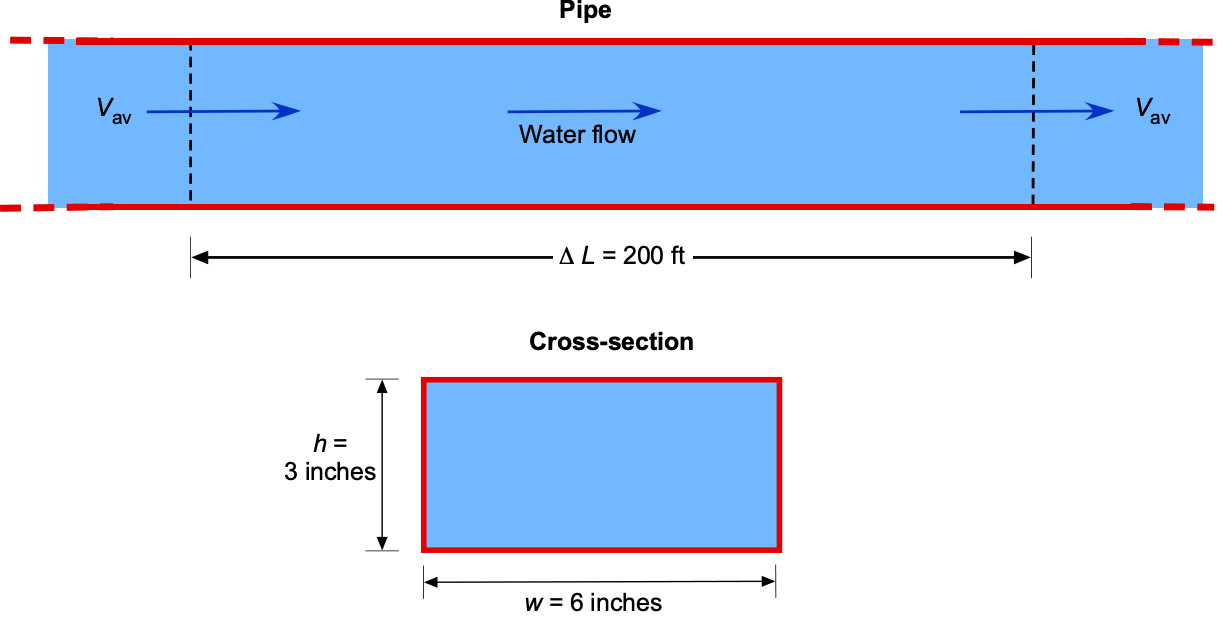
Consider a pump pushing water steadily through a section of cast iron pipe 200 ft long, as shown in the figure below. The rectangular cross-section of the pipe has a height $h =$ 3 in and a width $w =$ 6 in. The internal surface roughness is $\epsilon =$ 0.006 inches. The volumetric flow rate through the pipe is 0.75 ft ${^3}$ s $^{-1}$ . Assume that the density of the water $\varrho_{\rm w}$ is 1.940 slug ft ${^{-3}}$ and its viscosity $\mu$ is 2.1 $\times 10^{-5}$ slug ft $^{-1}$ s $^{-1}$ . Also, assume that entrance effects can be ignored.

1. Determine the hydraulic diameter $D_h$ of the pipe.
2. Determine the average flow velocity $V_{\rm av}$ through the pipe.
3. Determine the Reynolds number $Re_{D_h}$ of the flow in the pipe.
4. Is the flow in the pipe laminar or turbulent? Explain.
5. Determine the pipe’s friction factor ${\scriptstyle{f}}$ .
6. Determine the pressure drop $\Delta p$ and head loss $\Delta h$ through the pipe.

1. The cross-sectional area of the rectangular pipe is

$A = w \times h = (3.0/12.0)(6.0/12.0) = 0.125~\mbox{ft${^{2}}$}$

so the hydraulic diameter is

$D_h = \frac{4 \times \mbox{Area}}{\mbox{Perimeter}} = \frac{4A}{2 (w + h) } = \frac{2A}{(w + h) } = \frac{2.0 \times 0.125}{(3.0/12.0 + 6.0/12.0)} = 0.33~\mbox{ft}$

2. The average flow velocity $V_{\rm av}$ in the pipe is determined from the volumetric flow rate and the cross-sectional area, i.e.,

$V_{\rm av} = \frac{Q}{A} = \frac{0.75}{0.125} = 6.0~\mbox{ft s$^{-1}$}$

3. The Reynolds number based on the hydraulic diameter is

$Re_{D_h} = \frac{\varrho_{\rm w} \, V_{\rm av} \, D_h}{\mu_{\rm w}} = \frac{1.940 \times 6.0 \times 0.33}{2.1\times 10^{-5}} = 184,762 \approx 185,000$

4. Because the Reynolds number is greater than 2,000, the flow in the pipe will be turbulent.

5. The relative surface roughness is

$\frac{\epsilon}{D_h} = \frac{0.006/12.0}{0.33} = 0.0015$

Using the Moody chart, the friction factor for this Reynolds number and relative roughness is about 0.023. Minor errors in reading the chart are acceptable.

6. The pressure drop over a pipe length of 200 ft is

$\Delta p = \frac{1}{2} \varrho_ w \, V_{\rm av}^2 \, f \left(\frac{L}{D_h}\right)$

Inserting the known values gives

$\Delta p = 0.5 \times 1.94 \times 6.0^2 \times 0.023 \left( \frac{200.0}{0.33} \right) = 480.76~\mbox{lb ft$^{-2}$}$

The corresponding head loss is

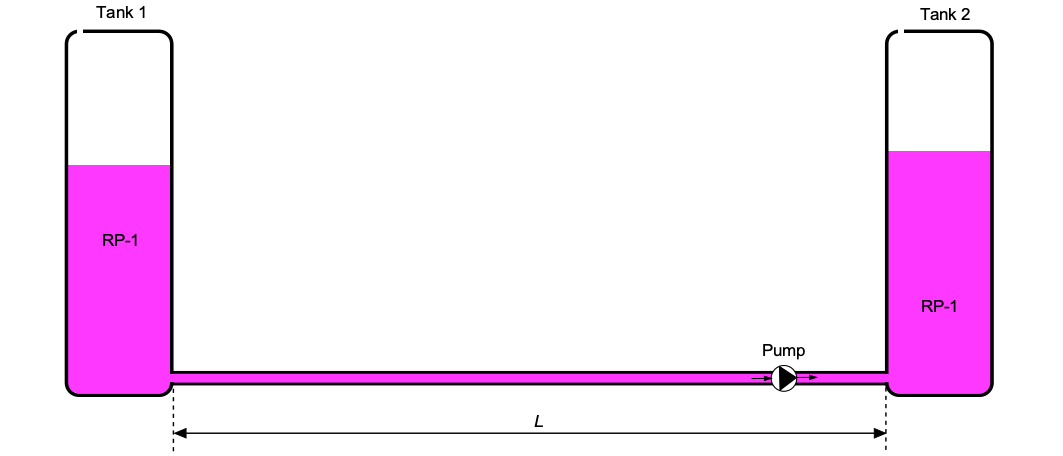
$\Delta h = \frac{\Delta p}{\varrho_w \, g} = \frac{480.76}{1.94 \times 32.17} = 7.79~\mbox{ft}$

Worked Example #11

RP-1 rocket fuel will be transferred from one tank to another using a pump with a flow rate of $Q$ = 52.1 ft ${^3}$ per minute. The fuel passes through a 4-inch diameter steel pipe with a length, $L$ , of 40 ft. The pipe has a roughness, $\epsilon$ = 0.002 inches. Assume the density of RP-1 is 1.746 slug ft ${^{-3}}$ and its viscosity is $7.4 \times 10^{-4}$ slug ft $^{-1}$ s $^{-1}$ . How much pumping power is required to move the RP-1 along the pipe?

The average flow velocity $V_{\rm av}$ in the pipe is

$V_{\rm av} = \frac{Q}{A} = \frac{4 Q}{\pi \, d^2 } = \frac{4 \times 52.1 /60 \times }{\pi (4.0/12.0)^2} = 9.95~\mbox{ft s$^{-1}$}$

The Reynolds number based on the diameter is

$Re_{d} = \frac{\varrho \ V_{\rm av} \, d }{\mu_w} = \frac{1.746 \times 9.95 \times 4.0/12.0}{7.4\times10^{-4}} = 7,825 \approx 8,000$

This result means the pipe flow will be turbulent, so we must refer to the Moody chart to find the friction factor. The relative surface roughness is

$\frac{\epsilon}{d} = \frac{0.002 }{4.0} = 0.0005$

Using the Moody chart, the friction factor is about 0.035. Some minor errors in reading the chart are acceptable. The pressure drop over the 40 ft length of pipe is

$\Delta p = \frac{1}{2} \varrho_ w \ V_{\rm av}^2 \ f \left(\frac{L}{D_h}\right)$

and inserting the values gives

$\Delta p = 0.5 \times 1.746 \times 9.95^2 \times 0.035 \left( \frac{40.0}{4.0/12.0)} \right) = 363.0~\mbox{lb ft$^{-2}$}$

The corresponding pumping power required is

$P = Q \, \Delta p = (52.1/60) \times 363.0 = 0.57~\mbox{hp}$

Worked Example #12

A liquid rocket fuel system utilizes a high-strength nickel alloy pipe with a diameter of $D = 4.0$ cm to transport liquid oxygen (LOX) from the tank to the engine. The LOX has a density $\varrho = 1,140$ kg m ${^{-3}}$ and a viscosity $\mu = 0.0001947$ Pa s. The mass flow rate of the LOX is $\overbigdot{m} = 20.0$ kg s $^{-1}$ . Assume that the average roughness of the pipe $\epsilon$ is 0.04 mm. How much pumping power is required to move the LOX along the pipe?

The average flow velocity in the pipe is

$V_{\rm av} = \frac{\overbigdot{m}}{\varrho \, A_c} = \frac{4 \overbigdot{m}}{\varrho \pi D^2 } = \frac{4 \times 20.0}{1,140.0 \times \pi \times 0.04^2 } = 13.96~\mbox{m s$^{-1}$}$

The Reynolds number of this flow (based on pipe diameter) is

$Re = \frac{\varrho \, V_{\rm av} \, D}{\mu} = \frac{ 1,140 \times 13.96 \times 0.04}{0.0001947} \approx 3,270,000$

This Reynolds number is significantly greater than 2,000, so the flow is in the turbulent regime. The relative roughness is

$\frac{\epsilon}{D} = \frac{0.04}{4.0 \times 10} = 0.001$

Referring to the Moody chart for $Re$ = 3,270,000 and $\epsilon/D$ = 0.001, then ${\scriptstyle{f}} \approx$ 0.02.
The pressure drop along the pipe is

$\Delta p = \frac{1}{2} \varrho V_{\rm av}^2 \, f \left( \frac{L}{D} \right)$

Substituting the numerical values gives

$\Delta p = \frac{1}{2} \times 1,140.0 \times 13.96^2 \times 0.02 \left( \frac{5.0}{0.04} \right) = 277,706.0~\mbox{Pa}$

Therefore, the power required to pump this flow is

$P = Q \, \Delta p = \left( \frac{\overbigdot{m}}{\varrho} \right) \Delta p = \left( \frac{20.0}{1,140.0} \right) \times 277,706.0 \approx 4.87~\mbox{kW}$

Worked Example #13

A steel pipe that is 1,000 ft long has a 15-inch diameter and a 1.5-inch wall thickness. The pipe carries water from a reservoir, and a valve is located downstream. When the valve is fully open, the flow rate through the pipe is 23.3 ft ${^3}$ /s. If the valve is closed completely in 0.15 seconds, determine the water hammer pressure in the pipe. Assume $E_b$ = 3.0 $\times 10^5$ lb/in ${^{2}}$ , and $E_p$ = 2.8 $\times 10^7$ lb/in ${^{2}}$ , and $K$ = 1.0. The density of water is 1.94 slugs/ft ${^{3}}$ .

The relevant equation, in this case, for the water hammer pressure in an elastic pipe is

$\Delta p = \varrho \, a \, V_0 = \varrho \sqrt{ \frac{E_c}{\varrho} } V_0$

where $E_c$ is the effective bulk modulus of the water in the pipe. The average velocity through the pipe, $V_0$ , is related to flow rate, $Q$ , using

$V_0 = \frac{Q}{A} = \frac{4 Q}{\pi \, D^2} = \frac{4 \times 23.3}{\pi (15.0/12.0)^2} = 18.99~\mbox{ft/s}$

The effective bulk modulus is given by

$\frac{1}{E_c} = \frac{1}{E_b} + \frac{D \, K}{E_p \, e} = \frac{1}{3.0 \times 10^5} + \frac{(15.0/12.0) \times 1.0}{2.8 \times 10^7 \times (2.0/12.)} = 3.75 \times 10^{-6}$

so that the value of $E_c$ is $2.67 \times 10^5$ lb/in ${^2}$ . Therefore, the wave propagation speed is

$a = \sqrt{ \frac{E_c}{\varrho} } = \sqrt{ \frac{144 \times 2.67 \times 10^5}{1.94} } = 4,451.8~\mbox{ft/s}$

and the wave reflection time is

$t_t = \frac{2 L}{a} = \frac{2 \times 1,000}{4,451.8} = 0.45~\mbox{s}$

And so with a valve closure time of 0.15 s, then $t_c < t_c$ , this is a sudden closure. Therefore, the water hammer change in pressure will be

$\Delta p = \varrho \, V_0 \, a = 1.94 \times 18.99 \times 4,451.8 = 1.64 \times 10^5~\mbox{lb/ft${^{2}}$} = 1,138.94~\mbox{lb/in${^{2}}$}$

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

License

Share This Book