Units & Conversion Factors

J. Gordon Leishman

5 Units & Conversion Factors

Introduction

To achieve success as an engineer, it is imperative to maintain consistency in unit usage and perform precise unit conversions. This approach ensures that dimensional analysis and dimensional homogeneity corroborate the validity of all equations and calculations. Mastery of these practices will enable accurate and efficient resolution of complex engineering problems.

A unit is a standardized measurement of a parameter (or quantity) that has been adopted by consensus and defined by convention, e.g., the Système International or SI system of units or the United States Customary or USC system of units, also known as the American units or British Imperial units. The expression of quantities measured in standardized units allows their magnitudes and/or numerical values to be evaluated and compared. Adopting a unit system for measuring physical parameters enables engineers and scientists to communicate and work with each other using a common measurement standard. The value of any one particular physical quantity is always given as a number and an accompanying unit (unless unitless), e.g., 12.4 meters per second (m/s or m s^-1) in SI units is equal to 40.68 feet per second (ft/s or ft s^-1) in USC units, where the conversion factor from length units of meters to feet is 3.281. This means that the numerical value of any parameter or quantity depends on the system of units in which it is expressed.

Aerospace engineers in the U.S. routinely use both SI and USC units, so all engineers and students (no matter where they are) must learn to use both unit systems to converse with U.S. engineers effectively. Furthermore, many useful technical reports and legacy publications, such as those from research laborites at NACA in the U.S. and the NPL and the RAE in Britain, will have used English units (i.e., British engineering units) or USC units (as called today) when the documents were published, so engineers need to learn to understand how to use and convert these units, as necessary. Depreciated unit sets include the CGS (centimeter-gram-second) and MKS (meter-kilogram-second) systems. Today, there is generally a preference for SI units because of their widespread adoption and use in engineering and scientific research, as well as compliance with international standards. Conversion factors are available so that numerical values in one unit system can be expressed as equivalent values in another system. Caution is always required to ensure the conversions are conducted properly and accurately.

Learning Objectives

Review SI (metric) and USC (U.S. or British) units of measurement and their proper use.
Understand the differences between base and derived units.
Know how to convert between different units using conversion factors.
Learn about the conventions and accepted practices of using units.
Be aware of the special units used in aviation and aeronautics.

Physical Quantities

Science and engineering involve observations of the physical world; engineers aim to express these observations in the most general and simplest formulations, such as using foundational equations that express specific types of physical behavior. The allowed types of properties are called physical quantities. Physical quantities are divided into two types: base quantities and derived quantities.

Base Quantities

Base quantities are fundamental and independent physical quantities that cannot be defined in terms of other physical quantities. They serve as the foundation for all other quantities of measurement. For example, base quantities such as mass, $M$ , length, $L$ , time, $t$ , and temperature, $T$ , can be readily measured and expressed in appropriate SI or USC units, as shown in the table below. Other base quantities are electrical current, $I$ , amount of substance, $n$ , and luminous intensity, $I_v$ ; notice that the latter three base quantities have the same units in both SI and USC. Notice also that unit symbols are generally not italicized, e.g., the symbol for length is $L$ , but the symbol for the base unit of length is L. Likewise, the symbol for temperature is $T$ , but the symbol for the base unit of temperature is $\theta$ . Confused? It takes time to learn the intricacies.

Base quantities and units used in engineering and science.
Base quantity	Symbol	Base unit	SI unit	USC unit
Mass	$M$ (or $m$ )	M	kilogram (kg)	slug (or slugs or sl)
Length	$L$ (or $l$ )	L	meter or metre (m)	foot (ft)
Time	$t$	T	second (s)	second (s)
Temperature	$T$	$\theta$	Kelvin ( $^{\circ}$ K or K)	Rankine ( $^{\circ}$ R or R)
Electrical current	$I$	Ampere (A)	Ampere (A)	Ampere (A)
Amount of substance	$n$	mole (mol)	mole (mol)^[1]	mole (mol)
Luminous intensity	$I_v$	candela (cd)	candela (cd)^[2]	candela (cd)

Derived Quantities

Derived quantities are physical quantities derived from combinations of base quantities through mathematical expressions. Derived quantities are quantities such as volume, ${\cal{V}}$ , density, $\varrho$ , velocity, $V$ , pressure, $p$ , energy, $E$ , and power, $P$ , all of which are derived from the base quantities. Those encountered in engineering are listed in the table below. Notice that the name of a parameter inside a set of square brackets [ ] means the dimensions of that parameter, i.e.,

(1) $\begin{equation*} \left[ \text{parameter} \right] \equiv \text{dimensions of that parameter} \end{equation*}$

Consider the following examples:

Volume, ${\cal{V}}$ , is a derived quantity because to calculate the volume of something such as a cuboid, then its width (units of L) must be multiplied by its length (units of L) by its height (units of L). Therefore, the derived units for volume are L ${^3}$ , i.e., $[ {\cal{V}}]$ = L ${^{3}}$ .
The density, $\varrho$ , of some substance is its mass ( $M$ ) per unit volume ( ${\cal{V}}$ ). Therefore, the value of density will have units of M L ${^{-3}}$ , i.e., [ $\varrho$ ] = M L ${^{-3}}$ .
A force, $F$ , is equivalent to the product of a mass and acceleration (Newton’s second law), so in terms of its base units, then [ $F$ ] = M LT $^{-2}$ .
Torque, $\tau$ , is a moment, so it is the product of a force times a distance or “arm.” Therefore, [ $\tau$ ] = (M LT $^{-2}$ ) L = M L ${^2}$ T $^{-2}$ .

Obtaining the correct base units of any given parameter takes some practice, but it is essential if any sense is to be made when solving problems. Scientific notation should be used when expressing the units of a parameter to avoid ambiguity, e.g., use the form M L $^{-1}$ T $^{-1}$ and not (M/(LT) and especially not M/L/T.

SI Units

The Système International or International System of Units (SI), sometimes known as the metric system, has become the international standard for measurement units. The SI system is also called the decimal system because it is based on powers of 10. The SI system comprises seven base units with many other derived units that are given unique names and symbols, with a subset being shown in the table below. The SI system is based on the meter (m), or the “metre” if outside the U.S., as the base unit of length, the kilogram (kg) as the base unit of mass, the Newton (N) as the base unit of force, and the second (s) as the base unit of time. Again, notice that unit symbols are generally not italicized.

Definitions for common SI units.
Quantity	Quantity symbol	Base units	SI unit name	Unit symbol
Length	$L$	L	meter or metre	m
Mass	$M$	M	kilogram	kg
Time	$t$	T	second	s
Volume	${\cal{V}}$	L³	meter-cubed	m³
Temperature	$T$	$\theta$	Kelvin	K or ^oK
Velocity	$V$	LT^-1	meter per second	m s^-1
Acceleration	$a$	LT^-2	meter per second²	m s^-2
Force	$F$	MLT^-2	Newton	N
Energy	$E$	ML²T^-2	Joule	J
Power	$P$	ML²T^-3	Joule per second = Watt	W
Pressure	$p$	ML^-1T^-2	Newtons per m² = Pascal	Pa
Density	$\varrho$	ML^-3	Kilograms per meter³	kg m^-3
Viscosity	$\mu$	ML^-1T^-1	Pascal-second	Pa s
Kinematic viscosity	$\nu$	L²T^-1	centiStoke (see CGS system)	cSt

In 1975, the U.S. government declared the international SI system the “preferred” unit system for use in the U.S. but did not require everyone to use it. Indeed, the USC system still prevails in the U.S. as the preferred measurement system, and the U.S. is one of the few countries worldwide that does not exclusively require and use the SI system. However, all countries, including the U.S., have recognized and adopted the SI system to align with international standards. Most products in the U.S. are marketed using SI units, but the use of dual SI and USC units is still commonplace. In the U.S., all government work, including that done by NASA (with some exceptions), uses the SI system. The use of mixed SI and Imperial units in Britain is also common, but less so than in the U.S. The SI unit system is preferred in all engineering and scientific work, and in many situations, it may be required by specification, international code, or regulation. However, in today’s global community, engineers and scientists from all countries must still be conversant in using both SI and USC units.

Metric prefixes are essential components of the metric system, providing a way to express large and small quantities in a concise and standardized manner. These prefixes denote specific powers of ten, allowing for easy conversion and comprehension of various units of measurement. For example, the prefix “kilo-” represents a factor of or 1,000, making 1 kilometer equal to 1,000 meters. Similarly, “milli-” signifies a factor of or 0.001, so 1 millimeter is 0.001 meters. Metric prefixes are used to simplify the expression of numerical values, as summarized in the table below. For example, instead of writing 1.234 $\times$ 10 $^{3}$ Pa (Pascals) the value can be expressed as 1.234 kPa.

Table of the metric prefixes and their symbols.
Prefix	Symbol	Factor
Atto-	a
Femto-	f
Pico-	p
Nano-	n
Micro-	μ
Milli-	m
Centi-	c
Deci-	d
Deca-	da
Hecto-	h
Kilo-	k
Mega-	M
Giga-	G
Tera-	T
Peta-	P
Exa-	E
Zetta-	Z
Yotta-	Y

Why are the designated units of a parameter not italicized?

Unit symbols are written in regular (non-italicized) font to improve readability and prevent misinterpretation. Examples: distance = 10 m not 10 m, time = 5 s not 5 s, and speed = 20 m/s not 20 m/s. Keeping unit symbols in regular font helps distinguish between the symbols used for the parameters (italicized) and their associated units (non-italicized). This convention is widely followed in the scientific and engineering literature to minimize the risk of errors and misunderstandings.

CGS Units

Occasionally, quantities measured in the centimeter–gram–second or CGS system of units will come up. CGS units are an increasingly obsolete variant of the metric system. CGS units are based on the centimeter as the base unit of length, the gram as the base unit of mass, and the second as the base unit of time. SI units have supplanted the CGS system, but sometimes quantities measured in CGS units are still encountered in engineering and scientific practice.

Converting between CGS and SI units is easy because the conversion factors are all powers of 10, as reviewed in the table below. For example, 100 cm = 1 m and 1,000 g = 1 kg. The CGS unit of force is called the dyne, which is 1 g cm s $^{-2}$ , so a Newton (N) in SI units equals 100,000 dynes in CGS units. Some units in the CGS system are considered depreciated or obsolete, such as dyne and erg, but they will still be encountered occasionally in legacy publications. Engineers need to be aware that they exist and how to convert them to SI or USC.

Definitions of CGS units and conversion factors from CGS to SI units.
Quantity	Quantity symbol	Base units	CGS name	Unit symbol	Unit definition	SI units
Length	$L$	L	centimeter	cm	1/100 of a meter	10⁻² m
Mass	$M$	M	gram	g	1/1000 of a kilogram	10⁻³ kg
Time	$t$	T	second	s	1 second	1 s
Volume	${\cal{V}}$	L³	liter (litre)	l (or L)	1/1,000 of a cubic meter	10^-3 m³
Temperature	$T$	$\theta$	Kelvin	K (or ^oK)	–	K or ^oK
Velocity	$V$	LT^-1	centimeter per second	cm/s	cm s^-1	10⁻² m s^-1
Acceleration	$a$	LT^-2	gal (Galileo)	Gal	cm s^-2	10⁻² m s^-2
Force	$F$	MLT^-2	dyne	dyn	g cm s^-2	10⁻⁵ N
Energy	$E$	ML²T^-2	erg	erg	g cm²s^-2	10⁻⁷ J
Power	$P$	ML²T^-3	erg per second	erg/s	g cm²s^-3	10⁻⁷ W
Pressure	$p$	ML^-1T^-2	barye	Ba	g cm^-1 s^-2	10⁻¹ Pa
Density	$\varrho$	ML^-3	grams per cm³	$\varrho$	g cm^-3	10^-6 kg m^-3
Dynamic viscosity	$\mu$	ML^-1T^-1	poise	P	g cm^-1 s^-1	10⁻¹ Pa s
Kinematic viscosity	$\nu$	L²T^-1	Stoke	St	cm²s^-1	10⁻⁴ m²s^-1

USC Units

U.S. customary (USC) units are a system of measurement units most commonly used in the U.S. The USC system was developed from traditional British measurement units. The British measurement system was updated in 1824, which created the so-called Imperial system or British Imperial units of measurement, known in the U.S. as “English” or “British Engineering” units. Interestingly, and perhaps somewhat ironically, British and European engineers call these “American” units today.

For engineering use, the USC or “British system” is based on the foot (ft) as the base unit of length, the slug (slug or sl)^[3] as the base unit of mass, the pound (lb) as the base unit of force, and the second (s) as the base unit of time, as reviewed in the table below. While USC units are primarily similar to British Imperial units, there are some differences regarding specific volumetric measurements.

Definitions for USC units. *Power is commonly measured in horsepower (hp), where 1 hp = 550 ft-lb s^-1.
Quantity	Quantity symbol	Base units	USC unit name	Unit symbol
Length	$L$	L	foot	ft
Mass	$M$	M	slug	slug (or sl)
Time	$t$	T	second	s
Volume	${\cal{V}}$	L³	foot³	ft³
Temperature	$T$	$\theta$	Rankine	R (or ^oR)
Velocity	$V$	LT^-1	feet per second	ft s^-1
Acceleration	$a$	LT^-2	feet per second²	ft s^-2
Force	$F$	MLT^-2	pound	lb
Energy	E	ML²T^-2	foot-pound	ft-lb
Power*	$P$	ML²T^-3	foot-pounds per second	ft-lb s^-1
Pressure	$p$	ML^-1T^-2	pounds per foot²	lb ft^-2
Density	$\varrho$	ML^-3	slugs per foot³	slug ft^-3
Viscosity	$\mu$	ML^-1T^-1	slug per foot per second, or pound seconds per foot	slug ft^-1 s^-1 or (lb s ft^-1)
Kinematic viscosity	$\nu$	L²T^-1	foot² per unit time	ft² s^-1

What is a unit of horsepower?

The mechanical output of an engine is often measured in “horsepower,” which is given the unit symbol “hp” and not “HP” or “Hp” or other such variation. This unit is attributed to the 18th-century Scottish engineer James Watt, whose work on steam engines was fundamental to the changes in society brought about by the Industrial Revolution. James Watt wanted to market his engines by comparing them to the equivalent power produced by a horse, which was a tangible measure to the general public and farmers. Watt did many experiments and determined that a typical Scottish farm horse could, on average, steadily lift a 600 lb weight through a simple pulley system for an average distance of 63.9 ft in an average of 69 seconds; averaging here was important. Therefore, the work done by an average horse is

(2) $\begin{equation*} \mbox{\small Work} = F \, d = 600 \times 63.9 = 38,340~\mbox{\small ft-lb} \end{equation*}$

Power is the rate of doing work, so the work per unit time is

(3) $\begin{equation*} \mbox{\small Power} = \frac{\mbox{\small Work}}{\mbox{\small Time}} = \frac{38,340}{69} = 555.65~\mbox{\small ft-lb s$^{-1}$} \end{equation*}$

James Watt settled on the average result that one horsepower (hp) = 550 ft-lb s $^{-1}$ . This measurement unit of hp made much more sense to farmers and others using horses. For example, for a steam engine of power 10 hp, the purchaser knew precisely what they were buying – an engine with the power equivalent to 10 horses. Marketing genius! Modern usage of horsepower is prevalent in the automotive and industrial fields to describe the power output of engines, motors, and other machinery. The horsepower unit caught on and is still widely used in many countries, even those using SI units exclusively.

Angular Units

In engineering analysis, angles measured in radians are generally always used, which is defined as a ratio of the arc length, $s$ , to the radius of a circle, $r$ , i.e.,

(4) $\begin{equation*} \theta = \dfrac{s}{r} \end{equation*}$

where $\theta$ is the angle in radians, which is sometimes called a natural angle. Notice that one radian is defined when $s = r$ . The dimensions of a radian are 1, i.e., it is unitless.

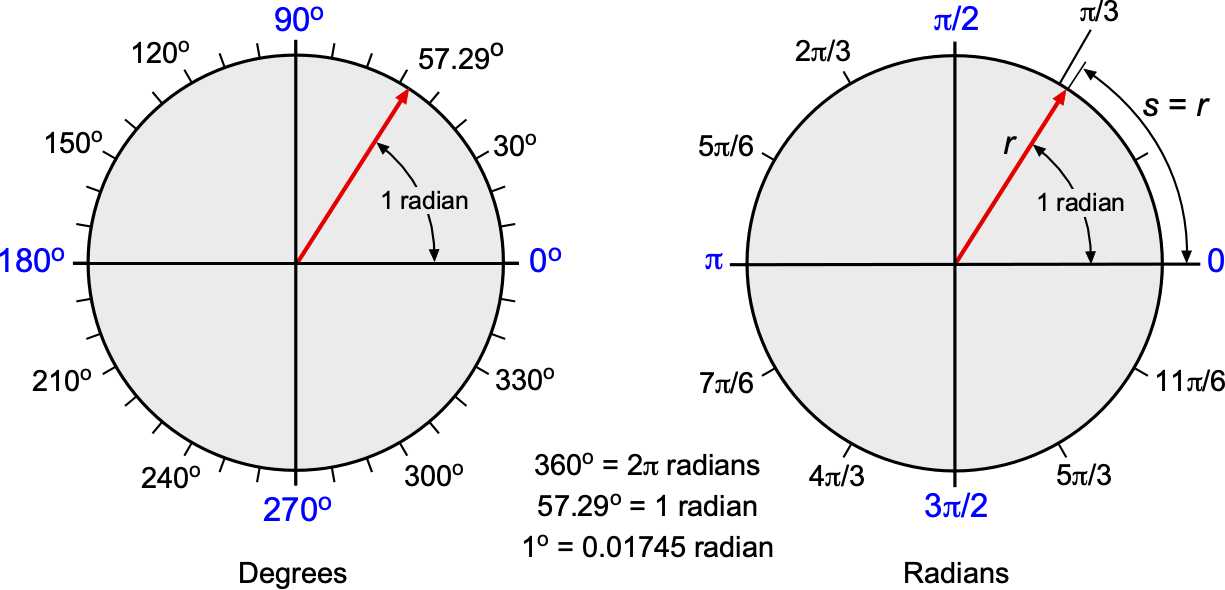
Angular measurements in degrees and radians.

A degree is an ancient unit of angular measurement in which a circle is split into 360 segments. While angles are often measured or otherwise reported in degrees, units of degrees must be converted to radians for most engineering calculations. A complete circle subtends an angle of $2 \pi$ radians, which is equivalent to 360 degrees or 360 $^{\circ}$ , as shown in the figure below. Therefore, the angular conversion is 1 radian = $180/\pi$ = 57.29 degrees, or 1 degree = $\pi/180$ = 0.01745 radians. Notice that radians are used in angular expressions by default in most computer languages.

The same process should also be done with angular rates, which should be converted to radians per second (rad/s) no matter what units the rates are originally given. For example, rates are often measured in units of revolutions per second (rps) or revolutions per minute (rpm), in which case

(5) $\begin{equation*} \dfrac{d \theta}{d t} = \overbigdot{\theta} = 2 \pi \left( \mbox{\small rps} \right) = 2 \pi \left( \dfrac{\mbox{\small rpm}}{60} \right)~\mbox{\small radians per second, i.e., rad/s or rad s$^{-1}$} \end{equation*}$

Because the radian is dimensionless, then the dimensions of the angular rate are time $^{-1}$ , i.e., T $^{-1}$ or s $^{-1}$ . Likewise, [ rps ] = [ rpm ] = T $^{-1}$

Check Your Understanding #1 – Dealing with base dimensions and units

In each case, convert the parameter and units given into their base dimensions (mass, length, and time) and units.

N (Newton)
Pa (Pascal)
lb (pound)
J (Joule)
W (Watt)

Show solution/hide solution

N (Newton) $\equiv$ mass times acceleration $\equiv$ M L T $^{-2}$ $\equiv$ kg m s $^{-2}$
Pa (Pascal) or N m $^{-2}$ $\equiv$ (M L T $^{-2}$ )(L $^{-2}$ ) = M L $^{-1}$ T $^{-2}$ $\equiv$ kg m $^{-1}$ s $^{-2}$
lb (pound) $\equiv$ M L T $^{-2}$ $\equiv$ slug ft s $^{-2}$
J (Joule) or N m $\equiv$ (M L T $^{-2}$ ) L = M L $^{2}$ T $^{-2}$ $\equiv$ kg m $^{2}$ s $^{-2}$
W (Watt) or J s $^{-1}$ $\equiv$ (M L $^{2}$ T $^{-2}$ ) T $^{-1}$ = M L $^{2}$ T ${^{-3}}$ $\equiv$ kg m $^{2}$ s ${^{-3}}$

Note: A Watt (W) is the SI unit of power, which is the rate of doing work. Work is force times distance so that power will have units of MLT $^{-2}$ L T $^{-1}$ or M L $^2$ T ${^{-3}}$ so kg m $^{2}$ s ${^{-3}}$ .

Mass & Weight

Mass and weight are related concepts but have distinct meanings. Mass is a measure of the amount of matter in an object; it is an intrinsic property related to inertia (not gravity) and so independent of its location in the universe. The unit of mass in SI is the kilogram (kg). Other mass units include grams (g), for which there are 1,000 grams in a kilogram, and metric tons or tonnes, which is 1,000 kg.

The base unit of mass in the USC system is the slug (sl). The name “slug” as a unit of mass originates from the concept of mass as a measure of inertia, i.e., “sluggish,” and has been referred to as the “engineer’s mass unit.” The use of “pounds-mass” (lb_m) as a measure of mass is a depreciated unit^[4] and is also considered to be a source of confusion in the engineering and scientific fields, so the use of “pounds-mass” must be avoided in preference of using the “slug” as the base unit of mass.

Weight is the force exerted on an object under gravity. It depends on the object’s mass and the acceleration under gravity at its specific location in the universe. The key difference between mass and weight lies in their definitions and how they are measured. Mass is a scalar quantity, while weight is a force (a vector) that can change based on the gravitational field strength. Newton’s second law relates mass, $M$ , gravitational acceleration, $g$ , and weight, $W$ , i.e.,

(6) $\begin{equation*} W = M \, g \end{equation*}$

However, the proper form of this latter equation would be to write it in vector form, i.e.,

(7) $\begin{equation*} W \, \vec{k} = M \, ( -g \, \vec{k} ) = -M \, g \, \vec{k} \end{equation*}$

where $\vec{k}$ is the unit normal vector in the upward vertical direction, and the minus sign denotes that weight is downward, directed toward the center of the Earth. On the surface of the Earth at mean sea level (MSL), the magnitude of $g$ is approximately 9.81 m/s² or 32.17 ft/s², which is given the symbol $g_0$ . An object will weigh less on the Moon than on Earth because the Moon’s gravitational force is only about one-fifth that on Earth. The unit of weight is the Newton (N) in the SI system and the pound (lb) in USC. However, in everyday use, “weight” is often measured in kilograms (kg), the latter being an anomaly of the SI system that, if used, must be reconciled for engineering calculations by multiplying by the value of $g$ (or $g_0$ if so defined).

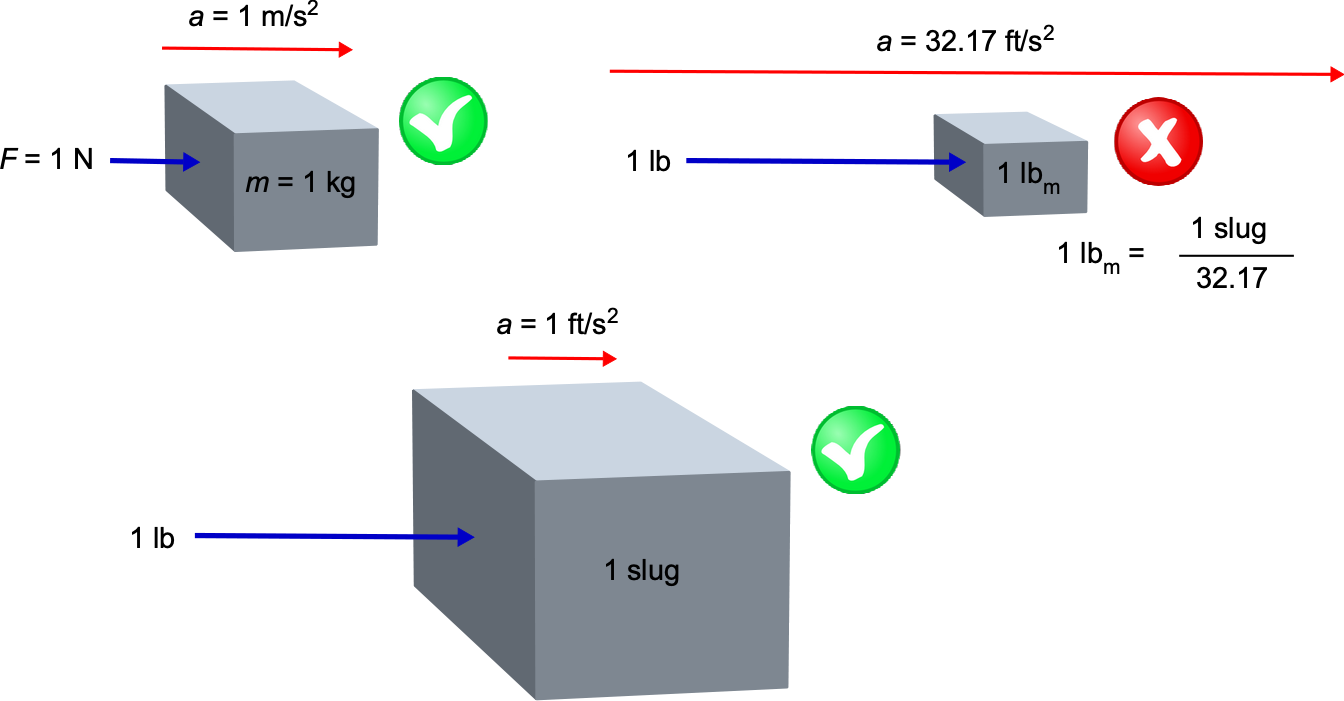
Pound-Force Versus Pound-Mass?

A pound-force (lb) is defined as the product of a pound-mass (lb_m) and acceleration under gravity, g, i.e., F = m g, so that 1 lb = 1 lb_m times g. Therefore, 1 pound-force (lb) = 1 pound-mass (lb_m) times 32.17 ft s $^{-2}$ . Therefore, it can be concluded that a 1 lb force will accelerate 32.17 lb_m (which is the mass equivalent to 1 slug) at 1 ft s $^{-2}$ , or it will accelerate a 1 lb_m at 32.17 ft s $^{-2}$ . Confused? But we see that a 1 lb force will accelerate one slug of mass at 1 ft s $^{-2}$ , which is a more logical outcome that is also consistent with the SI system. Therefore, if using pounds mass in a calculation, there is always a multiplicative factor of “32.17 ” floating around, and most of the time, it causes nothing but problems in calculations. However, the multiplicative factor is always “1” when using slugs. Therefore, the unit of pound-mass is now considered a depreciated unit and the base unit of mass in USC is a slug.

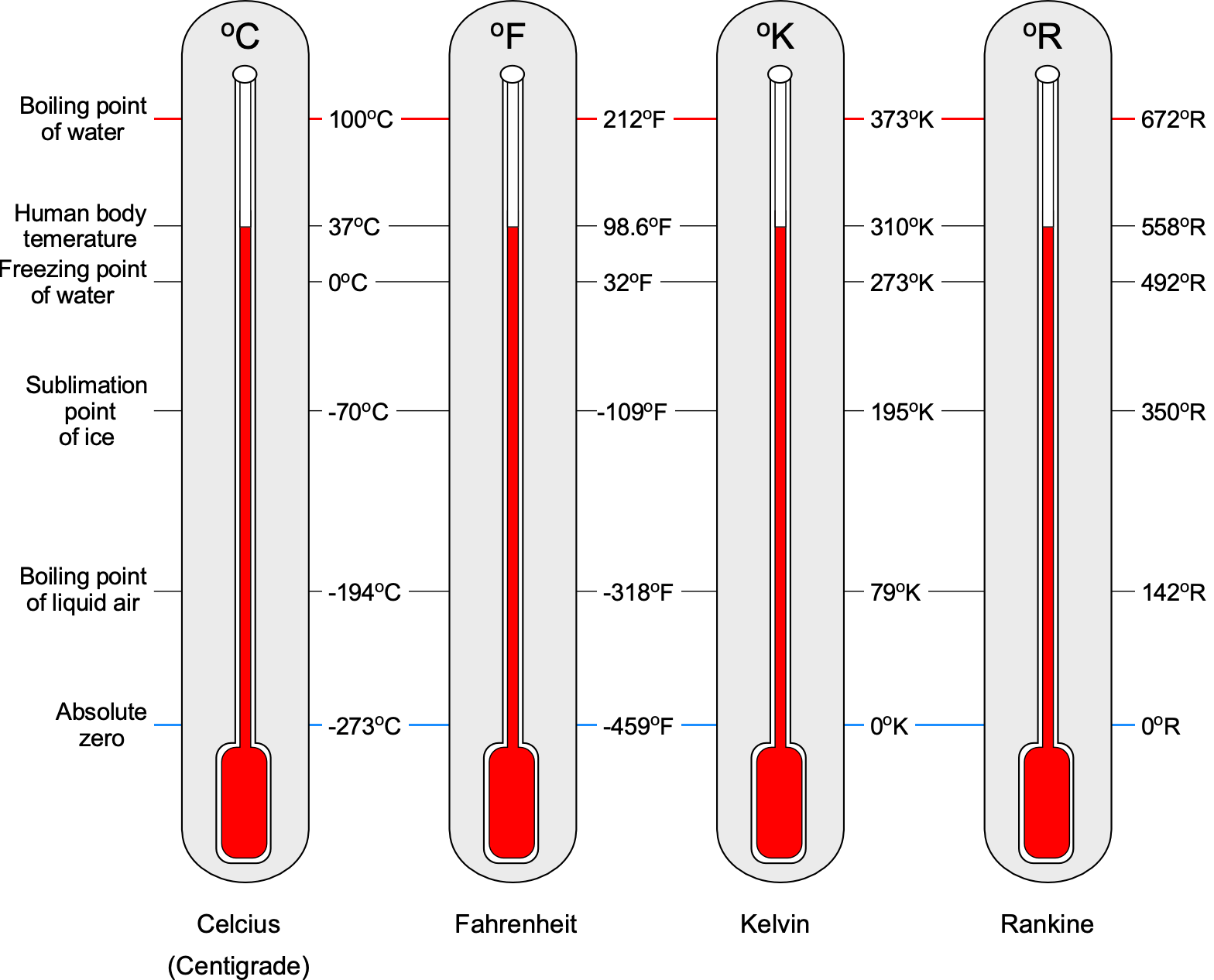
Units of Temperature

The units used for temperature measurement need careful attention by engineers. Temperature is measured in units of Centigrade or Celsius $^{\circ}$ C or Kelvin, K or $^{\circ}$ K, in the SI system, or Fahrenheit $^{\circ}$ F or Rankine, R or $^{\circ}$ R, in the USC system. Kelvin (SI) and Rankine (USC) are the engineering or thermodynamic absolute temperature scales. Converting from one temperature scale to another is straightforward because they are all linearly related, as shown in the figure below, the temperature on one scale being converted to another scale by using

(8) $\begin{equation*} \frac{\mbox{\small Temperature $T$ on any scale} - T_{\rm \mbox{\tiny LFP}}}{T_{\rm \mbox{\tiny UFP}} - T_{\rm \mbox{\tiny LFP}}} = \mbox{\small constant} \end{equation*}$

Therefore,

(9) $\begin{equation*} \frac{T (^{\circ}\mbox{\small C}) - 0}{100} = \frac{T(^{\circ}\mbox{\small F}) - 0}{212 - 32} = \frac{T (^{\circ}\mbox{\small K}) - 273.14}{373.15 - 273.15} = \frac{T (^{\circ}\mbox{\small R}) - 492.67}{672.67 - 492.67} \end{equation*}$

or

(10) $\begin{equation*} \frac{T (^{\circ}\mbox{\small C}) }{100} = \frac{T (^{\circ}\mbox{\small F}) - 0}{180} = \frac{T (^{\circ}\mbox{\small K}) - 273.14}{100} = \frac{T (^{\circ}\mbox{\small R}) - 492.67}{80} \end{equation*}$

Converting temperature values from one scale to another is relatively easy because the scales are all linearly related.

For example, when using Eq. 10, converting to Centigrade or Celsius $^{\circ}$ C from Fahrenheit $^{\circ}$ F gives

(11) $\begin{equation*} T (^{\circ}\mbox{\small C}) = \frac{5}{9} \bigg( T (^{\circ}\mbox{\small F}) - 32 \bigg) \end{equation*}$

Similarly, converting to Fahrenheit $^{\circ}\mbox{\small F}$ from Centigrade or Celsius $^{\circ}\mbox{\small C}$ , gives

(12) $\begin{equation*} T (^{\circ}\mbox{\small F}) = \frac{9}{5} \, T (^{\circ}\mbox{\small C}) + 32 \end{equation*}$

Converting to Kelvin K from Centigrade or Celsius $^{\circ}\mbox{\small C}$ , gives

(13) $\begin{equation*} T (^{\circ}\mbox{\small K}) = T (^{\circ}\mbox{\small C}) + 273.15 \end{equation*}$

Finally, converting to Rankine R from Fahrenheit $^{\circ}\mbox{\small F}$ , gives

(14) $\begin{equation*} T (^{\circ}\mbox{\small R}) = T (^{\circ}\mbox{\small F}) + 459.67 \end{equation*}$

Notice that it is often suggested that the degree symbol $^{\circ}$ not be used when citing temperature units, especially for the Kelvin and Rankine scales. However, many publications can be found with and without the degree symbol. Nevertheless, retaining the degree symbol on the temperature units is entirely acceptable for students and others when working on aerodynamic problems. Finally, it is helpful to remember the standard sea level values of temperature (based on the ISA model), given the symbol $T_0$ , are $15^{\circ}$ C or 59 $^{\circ}$ F, and the absolute zero temperatures are $-273.15^{\circ}\mbox{\small K}$ and $-459.67^{\circ}\mbox{\small R}$ .

Temperature units of Rankine or Kelvin?

In 1848, Professor William Thomson (1824–1907), head of the department of natural philosophy (physics) at the University of Glasgow in Scotland, suggested a thermodynamic temperature scale whereby “infinite cold” (absolute zero) was the reference point. Professor Thomson decided to use the degree Celsius as the temperature unit increment. Professor Thomson became Lord Kelvin in 1892 in recognition of his scientific contributions, so his temperature scale is now known as Kelvin (K or °K). Professor William Rankine (1820–1872) was the first engineering professor at the University of Glasgow and the first to confer degrees in engineering. Not to be outdone by his colleague Professor Thompson, Professor Rankine proposed that his temperature scale be based on the Fahrenheit increment; the Rankine scale has 0 °R (or 0 R) equivalent to 0 °K (or −459.67 °F) as absolute zero. The remainder is history.

Unit Rules and Style Conventions

There are no plural unit symbols! Unit symbols are unaltered in the plural. For example, always use 52.1 cm and never 52.1 cms. Also, you can use 32.4 kg, not 32.4 kgs. A common mistake is using ms as the plural of meter (meters), but the unit symbol for ms is milli-second.
When working with USC units, i.e., in “pounds, feet, and inches,” their symbols are frequently misused. For example, always use 23.1 lb and never 23.1 lbs. The symbol for a foot or feet is ft. Likewise, the symbol for an inch or inches is in. For example, always write 13.6 in or 13.5″ or 1.1 ft or 1.1′. Lengths are often written using a single mark for feet and a double mark for inches. For example, 4 feet 9 inches would be written as 4′ 9″.
Unit symbols are not followed by a period unless at the end of a sentence. For example, always write”…the wing span is 7.5 m long.” and never “…the wing span is 7.5. long.” However, it is fine to write “…the wing span is 7.5 m.”
Always put a space between different units. For example, for a velocity use 250.12 m s^-1 and not 250.12 ms^-1.
Never put a “.” between unit symbols. For example, 230.1 N.m is incorrect and only 230.1 N m is correct.
To avoid ambiguity, using scientific notation for units is always best. For example, use m s^-1, not m/s for velocity units. Likewise, use kg m^-1 s^-1 not kg/m/s.
Units are never italicized. For example, always use 250.1 m s^-1and never 250.1 m s^-1.
Do not mix with unit symbols or names with units. For example, always use kg m^-3 and never kilograms/m³ or kg per m³.
Numerical values should be paired with units. For example, always use 3.4 cm x 5.7 cm and not 3.4 x 5.7 cm. Likewise, use 3.4 cm to 5.7 cm for a range, not 3.4 to 5.7 cm. Likewise, use 20 °C to 30 °C and not 20 to 30 °C.
Do not use combinations of names or abbreviations to denote units. For example, use ft s^-1 and never fps (feet per second). Likewise, always use km hr^-1 and not kph.
Symbols for metric units are written in lower case – except those named after persons. For example, use lowercase m for a meter (meter), but W for watt (Watt). This rule applies even when the prefix symbol is lowercase, as in kW for kilowatt. The symbol L is often used for a liter (litre), which is an exception, although the symbol l is also used.
Generally, a prefix symbol and the unit symbol are combined to form a single symbol. For example, m + L gives mL (millilitre), and M + W gives MW (megawatt) being given the symbol MW.

Working with Units

Engineers, no matter where they are, need to become comfortable using both SI and USC units. When learning engineering problem solving, when presented with a problem in SI units, the problem should be solved entirely in SI units. Likewise, when presented with a problem in USC units, then the problem should be solved entirely in USC units. Refrain from converting back and forth because this is when mistakes usually happen. Roundoff errors with conversion factors can also accumulate, and a final answer may be different by more than 5% when converting back and forth between unit systems. Engineering accuracy is usually considered to be 1%, but that 1% tolerance can be exceeded quickly when numerical roundoff errors are combined with conversion factor roundoff.

Mixed Units

Sometimes, information (values) will be available or presented in mixed units, with some values in SI and others in USC. Converting all the information to either SI or USC is essential, depending on the required outcome. In either case, all information available must be converted to base units before evaluations are conducted, in which case the final desired value or values will also be in base units. If unit conversions are required, official conversion factors can be found by accessing the NIST website from the links below. It is essential that when using unit conversions, the complete accuracy of the conversion factor should be employed. Generally, rounding of numerical values and/or converting to other units should only be done at the end of the calculations.

In the U.S., the engineering field routinely uses a mix of SI and USC units. For instance, NASA uses SI units for all scientific work but USC units for mechanical specifications. The U.S. aerospace industry uses mostly USC units. This duality requires engineers to be especially vigilant.

When NASA lost a $100M spacecraft because of a units mistake!

In September 1999, the NASA Mars Climate Orbiter unexpectedly burned up and crashed into the surface of Mars after almost ten months of space travel. The project cost over $100M. It turned out that engineers had made a massive unit mistake, muddling quantities between the SI and USC systems. NASA’s Jet Propulsion Laboratory (JPL) used the SI system, while Lockheed used the USC system. Because of this blunder, the navigation system flew the spacecraft too close to the atmosphere, where it burned up. Read more about this mistake here as well as some other engineering disasters that have occurred because of the muddling of units. Be sure not to make the same mistakes!

Units in Equations

It is considered bad practice to put units after parameters (symbols) and/or numerical values when they are used in equations and then work them through the problem in parallel like the units were algebraic variables. Take a trivial example of calculating the force, $F$ , required to accelerate a mass, $m$ , of 10.3 kg at an acceleration, $a$ , of 2.4 m/s (or more correctly $a$ = 2.4 m s^-1). All the numerical values are given in base SI units, so the units of the final numerical value will be in Newtons (N). It would be considered good practice to write the solution as

(15) $\begin{equation*} F = m \, a = 10.3 \times 2.4 = 24.72~\mbox{N} \quad \mbox{(This~is~good~practice.)} \end{equation*}$

However, it would be considered bad practice to write the solution as

(16) $\begin{equation*} F = m \, a = 10.3~\left(\rm{kg}\right) \times 2.4~\left(\rm{m \, s}^{-2}\right) = 24.72~\left(\rm{kg \, m \, s}^{-2}\right) \quad \mbox{(This~is~bad~practice.)} \end{equation*}$

even though it should be recognized that the base units of force are kg m s $^{-2}$ , i.e., N $\equiv$ kg m s $^{-2}$ . A more egregious form of Eq. 16 using square brackets around the units is

(17) $\begin{equation*} F = m \, a = 10.3~ \left[\rm{kg} \right] \times 2.4~\left[\rm{m \, s}^{-2}\right] = 24.72~\left[\rm{kg \, m \, s}^{-2}\right] \quad \mbox{(This~is~bad~practice.)} \end{equation*}$

Again, besides using units as parallel algebraic variables, this square bracket format is considered bad practice. Using square brackets means the dimensions or units of a parameter, e.g., $\left[ m \right]$ = kg.

As a corollary to Eq 15, consider the example of solving for the acceleration given the mass and the force, i.e., $m$ = 10.3 kg and $F$ = 24.72 N. It might be concluded after placing units after each variable and carrying them through algebraically that

(18) $\begin{equation*} a = \dfrac{F}{m} = \dfrac{24.72~(\rm{N})}{ 0.3~(\rm{kg})} = 21.5~\mbox{N kg$^{-1}$} \quad \mbox{(This~is~bad~practice.)} \end{equation*}$

which is dimensionally correct, but the numerical result has the wrong units for acceleration. One would “know” (presumably) that the SI units of acceleration are m s $^{-2}$ . Indeed, units of N kg $^{-1}$ are simply (kg m s $^{-2}$ ) kg $^{-1}$ = m s $^{-2}$ .

The bottom line remains, however, that if all numerical data are expressed in base units, then the final answer will be in base units, and there is simply no need to work units through the problem in parallel as algebraic variables. Engineers learn the accepted common base units of all the parameters they work with in SI and USC unit systems. Usus est optimus magister.^[5]

Consider another example where converting all given values into base units is good practice. Suppose the values in the preceding example are given as $m$ = 10,300 g and $a$ = 240 cm s^-1, then first convert to $m$ = 10.3 kg and $a$ = 2.4 m s^-1 and follow the example in Eq. 15. Otherwise, there is a good chance that the units of the final result will be wrong or not what is desired. Not only is it bad practice to write out the solution with units in parentheses after every single parameter, but the use of conversion factors in the units gets confusing, i.e., the form

(19) $\begin{equation*} \hspace*{-10mm} F = m \, a = 10,300~(\rm{g/1,000}) \times 240 ~(\rm{cm/100 \ s}^{-2}) = 24.72~(\rm{kg \, m \, s}^{-2}) = 24.72~(N) \quad \mbox{(This~is~bad~practice.)} \end{equation*}$

Learning what is good practice and what is not takes time. The place to start for students is with their homework, but bad habits die hard.

Check Your Understanding #2 – Working with mixed units

Measurements of the pressure and temperature of the air are reported to be 1,024.5 hPa and 71.3 $^{\circ}$ F, respectively. Calculate the air density in base SI units.

Show solution/hide solution

Because this question involves pressure, temperature, and density, then we will use the equation of state, i.e.,

$p = \varrho \, R \, T$

where $p$ is pressure, $\varrho$ is density, $T$ is absolute temperature, and $R$ is the gas constant for air. Rearranging for the density gives

$\varrho = \frac{p}{R \, T}$

The temperature is 71.3 $^{\circ}$ F = 21.83 $^{\circ}$ C + 273.15 = 294.98 K. The gas constant $R$ for air in SI units is 287.057 J kg $^{-1}$ K $^{-1}$ so the density of the air will be

$\varrho = \frac{p}{R \,T} = \dfrac{\small 102.45 \times 10^3}{\small 287.057 \times 294.98} = \small 1.21~\mbox{kg m${^{-3}}$}$

Remember that we must always use absolute or thermodynamic temperature for calculations. Notice that the temperature is given in USC units of $^{\circ}$ F, but the final result for density must be in SI units. The pressure is given in heca-Pascals (hPa), which is 100 Pa, so 1,024.5 hPa = 102,450 Pa or 102.45 kPa.

Aviation Units

In aviation, the units used during normal operations can be confusing for both engineers and pilots. The International Civil Aviation Organization (ICAO) has recommended that the aviation world move ultimately to SI units, but historical convention remains. In this regard, the different types of units used for distances, airspeed, altitude, and pressure in aviation require some explanation.

Distances

Distances in aviation are measured in terms of nautical miles, which is neither an SI nor USC unit. One nautical mile (nm) is equivalent to one minute of latitude, which is approximately one arc-minute of a great circle of the Earth. It equals 1.852 kilometers (km) or 1.15078 statute miles (sm). Nautical miles(nm) are commonly used to measure horizontal distances in aviation, including for flight distances and navigation purposes. At the same time, the statute mile or kilometer (km) are also employed in some contexts. The statute mile is a unit of length commonly used in the U.S. but not often in aviation. One statute mile (sm) equals 5,280 feet or 1,609.344 meters. The specific unit of distance being used in aviation may also depend on country or regional conventions and possibly other factors. Caution should always be exercised to ensure the use of the appropriate distance units in any given context.

Airspeed

Airspeed is measured in terms of knots (nautical miles per hour). A knot is a unit of speed also used in maritime contexts. One knot (kt) is equal to one nautical mile per hour. Aircraft, wind, and ground speeds are often measured in knots (kts). Pilots use airspeed indicators to measure the aircraft’s speed through the air. Different types of airspeeds include the indicated airspeed (as read directly from the airspeed indicator), the calibrated airspeed (indicated airspeed corrected for instrument and installation errors), the true airspeed (calibrated airspeed corrected for altitude and non-standard temperature), and the ground speed (the actual speed of the aircraft over the ground, considering wind effects).

Pressure

Atmospheric pressure is fundamental for making altitude measurements on an altimeter. An altimeter is a pressure gauge calibrated in units of height (usually in feet), so altitudes are always measured relative to a reference pressure, which can vary. The pilot can set the appropriate pressure reference on the altimeter on the scale. Reference pressures include standard atmospheric pressure, local pressure at sea level, and local pressure relative to ground level.

In aviation, the relevant reference pressure values are usually reported to pilots via a traffic control or broadcast from a weather station in units of inches of mercury (in Hg), hectopascals (hPa), or millibars (mb). Notice that the numerical values of millibars and hectopascals are the same. North America and Japan use inches of mercury for pressure measurement; hectopascals or millibars are used in the remainder of the aviation world. Altimeter manufacturers often provide two setting scales for hPa and inHg, and electronic flight display systems can toggle between units.

Altitude

Altitude plays a crucial role in navigation, air traffic control, and collision avoidance, helping to maintain safe vertical separation distances between aircraft. Altitude is usually measured in feet (ft). Using the units of feet for altitude measurement is in accordance with the ICAO aviation and aeronautical standards. A foot (ft) is a unit of length in the USC system; it is equal to 12 inches (in) or 0.3048 meters (m). Different types of altitudes can be measured, including altitude relative to sea level and altitude relative to the ground. When flying at low altitudes, the altimeter reference is commonly set to show the altitude above sea level, i.e., the QNH setting, which will vary depending on the local atmospheric pressure conditions. Near an airport, the QFE setting may be used (except in the U.S.), where the altimeter will read zero when the aircraft is on the ground. The significance of the reference settings is explained in the figure below.

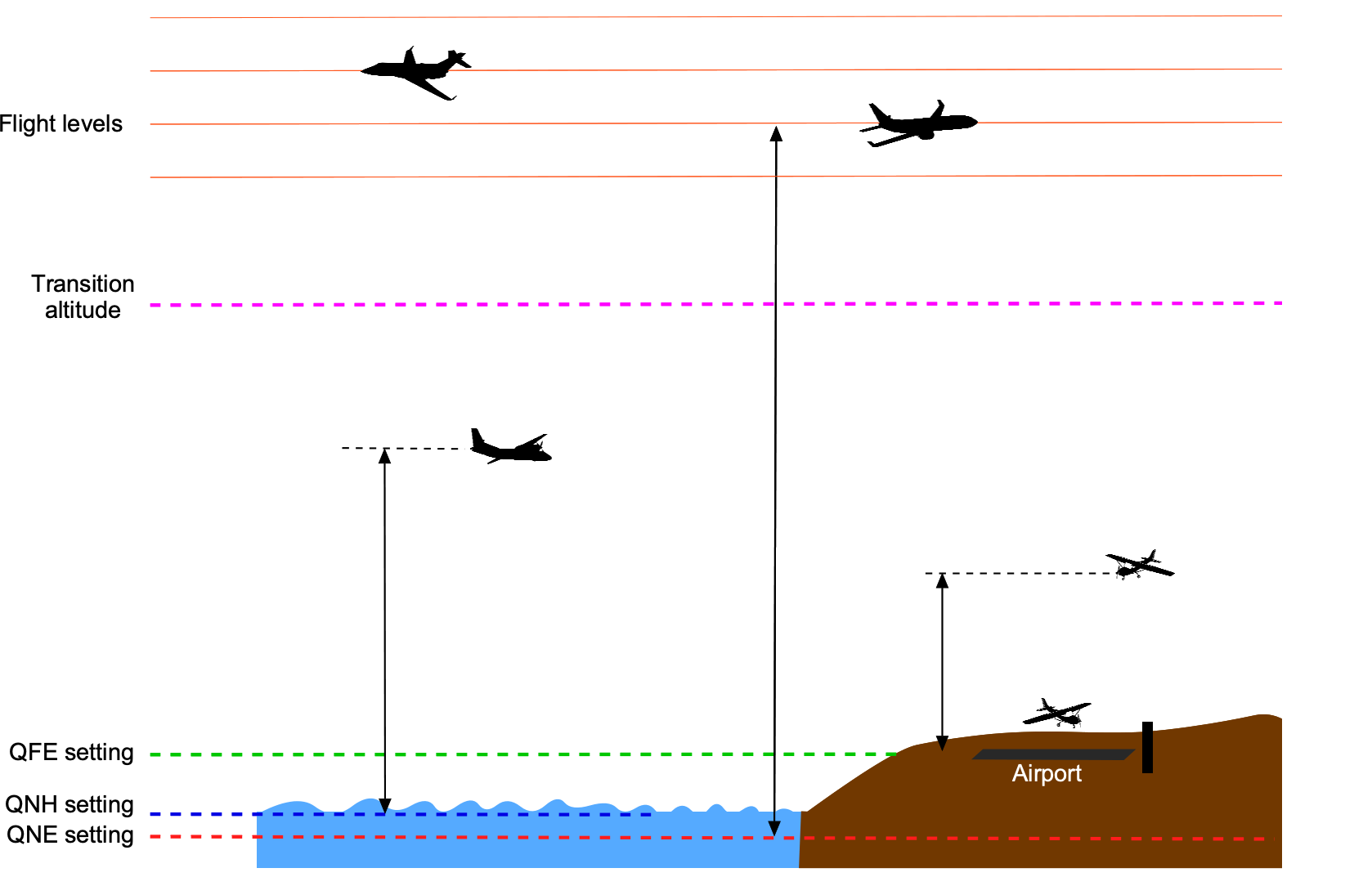
A third type of altitude is called pressure altitude, which is the altitude relative to standard atmospheric pressure, i.e., 29.92 inches of mercury (in Hg) or 1013.25 hectoPascals (hPa). This is sometimes referred to as the QNE setting. Pressure altitude is usually used in flight test work and for standardization of aircraft performance measurements. Pressure altitude is also used to define a flight level (FL) for piloting purposes, but the use of flight levels is limited to higher altitudes above a certain transition altitude. For example, if an aircraft is flying at FL330, it means its altimeter measures a pressure altitude of 33,000 ft. The flight level system helps maintain a consistent altitude reference for aircraft such as jetliners flying at higher altitudes and Mach numbers; it ensures adequate vertical separation and consistency for air traffic control. The transition altitude from using local pressure altimeter settings to using flight levels depends on the airspace and air traffic control system in the country where the aircraft is flying. It is standardized to 18,000 ft in the U.S.

Fuel Quantity

In aviation, fuel quantity is measured primarily in gallons, liters, pounds, or kilograms, depending on regional preferences and standards. Aircraft fuel tanks are labeled with capacities in gallons or liters (litres outside of the U.S.), and pilots must upload a sufficient quantity of fuel that is sufficient for planned flights. It is also critical for pilots to manage the fuel burn and monitor the remaining fuel quantity during flight. Caution should always be exercised to ensure the use of the appropriate fuel measurement units in any given context.

Notice that a U.S. gallon differs from a British (Imperial) gallon. The U.S. gallon is defined as 231 cubic inches or approximately 3.785 liters. The Imperial gallon is defined as 277.42 cubic inches or approximately 4.546 liters. Therefore, one U.S. gallon = 0.832674 Imperial gallons, or one Imperial gallon = 1.20095 U.S. gallons. In addition to volume measurements, fuel weight, often measured in pounds (lb) or kilograms (kg), is crucial for aircraft loading, the center of gravity calculations, takeoff speeds and distance, and numerous other performance calculations.

Unit Conversion Factors

A ratio that converts one unit of measurement into another unit of measurement is called a conversion factor. Engineers often use conversion factors from common measurement units to engineering units or USC units to SI units and vice-versa. Given below is a table of commonly used conversion factors in aerospace engineering:

Common conversion factors used in aerospace engineering.
Quantity	From unit	To unit	Conversion factor
Length	inches (in)	meters (m)	1 in = 0.0254 m
	feet (ft)	meters (m)	1 ft = 0.3048 m
	miles (mi)	kilometers (km)	1 mi = 1.60934 km
	nautical miles (nm)	kilometers (km)	1 nm = 1.852 km
Speed	feet per second (ft/s)	meters per second (m/s)	1 ft/s = 0.3048 m/s
	miles per hour (mph)	kilometers per hour (km/h)	1 mph = 1.60934 km/h
	knots (kt)	kilometers per hour (km/h)	1 kt = 1.852 km/h
Mass	pound-mass (lb)	kilograms (kg)	1 lb_m = 0.453592 kg
	slugs	kilograms (kg)	1 slug = 14.5939 kg
	kilogram	tonne mass (t)	1 t = 1,000 kg
Weight	short (American) ton	ton	1 ton = 2,000 lb
	long (British) ton	long ton	1 long ton = 2,240 lb
	short ton	kilograms (kg)	1 short ton = 907.185 kg
	long ton	kilograms (kg)	1,016.05 kg
Force	pounds (lb)	Newtons (N)	1 lb = 4.44822 N
	kilo Newtons (kN)	pounds (lb)	1 kN = 2,24.809 lb
Pressure	pounds per square inch (psi)	Pascals (Pa)	1 psi = 6,894.76 Pa
	atmospheres (atm)	Pascals (Pa)	1 atm = 101,325 Pa = 101.325 kPa
Temperature	Fahrenheit (°F)	Celsius (°C)	(°F – 32) $\times$ 5/9 = °C
	Celsius (°C)	Fahrenheit (°F)	(°C $\times$ 9/5) + 32 = °F
Energy	foot-pounds (ft-lb)	Joules (J)	1 ft-lb = 1.35582 J
	British Thermal Units (BTU)	Joules (J)	1 BTU = 1055.06 J
Power	horsepower (hp)	Watts (W)	1 hp = 745.7 W
	kilowatts (kW)	horsepower (hp)	1 kW = 1.341 hp
Density	slug per cubic foot (slug/ft³)	kilogram per cubic meter (kg/m³)	1 slug/ft³ = 515.379 kg/m³
Volume	U.S. gallon (gal)	Imperial gallon (Igal)	0.832674
	liter or litre (l or L)	U.S. gallon (gal)	3.78541
Time	hour (hr)	seconds (s)	3,600
	minute (min)	milliseconds (ms)	60,000

One should always double-check the conversion factors and units based on specific needs, as standards may vary in different contexts. For example, pressure may be measured in units of “pounds per square inch” or lb/in $^2$ or psi, but this is not an engineering (base) unit. It usually needs to be converted to “pounds per square foot” or lb/ft $^2$ or psf, i.e., one psi = 1/144 psf where the conversion factor, in this case, is 1/144, the factor 144 being 12 $\times$ 12 where 12 inches equals one foot.

Other pressure measurement units include a “bar” where 1 bar = 100 kPa = 100,000 Pa with the Pa (1 Pascal = 1 Newton per square meter or 1 Pa = 1 N/m $^2$ ) being the base engineering unit of pressure measurement. The bar (given the symbol b) is not an official SI unit and so should not be used in engineering, but is often used in meteorology and weather forecas and for aviation purposes, e.g., reporting atmospheric pressure values in millibars (mb). To obtain pressure units of Pa from measurements of pressure in bars, then 1 Pa = 1/100,000 bar, so the conversion factor, in this case, is 1/100,000 or 10 $^{-5}$ . Recall that a Pascal is a small amount of pressure, so the use of hectoPascals (hPa), which is 100 Pa, kiloPa (kPa), or even MegaPa (MPa), is not uncommon in engineering. Notice that 1 millibar = 1 hectopascal, the hectopascal being the preferred unit in engineering.

Check Your Understanding #3 – Converting units

In each case, convert the numerical values in the units given into equivalent numerical values in base units. State the conversion factor(s) you used.

3.3 L (liters)
1.2 hrs (hours)
15.6 hp (horsepower)
12.8 gals (US gallons)
12.4 kN cm $^{-2}$

Show solution/hide solution

3.3 L (liters) = 3.3/1,000 = 0.0033 m ${^{3}}$ . There are 1,000 liters in a cubic meter.
1.2 hrs (hours) = 3,600 $\times$ 1.2 = 4,320 s. There are 3,600 seconds in an hour.
15.6 hp (horsepower) = 15.6 $\times$ 550 = 8,580 ft-lb s $^{-1}$ . 550 ft-lb s $^{-1}$ is equivalent to one horsepower.
12.8 gals (US gallons) = 12.8 $\times$ 0.13368 = 1.711 ft ${^{3}}$ . One gallon is equal to 0.13368 ft ${^{3}}$ .
12.4 kN cm $^{-2}$ = 12.4 $\times$ 10 ${^3}$ $\times$ 10 $^{4}$ = 12.4 $\times$ 10 ${^{7}}$ Pa = 12.4 $\times$ 10 ${^{7}}$ kg m $^{-1}$ s $^{-2}$ . One kN = 1,000 N, and there are 1,000 square centimeters in a square meter.

Converting units takes some work, but it is essential to do it correctly. The first step is to realize and accept that many quantities we measure daily are not base quantities but need to be converted to base quantities for engineering calculations.

Summary & Closure

In engineering, using units of measurement is not merely a matter of numerical expression but a fundamental aspect that underpins precision, accuracy, and effective communication. Engineers rely on standardized units to communicate results and make the correct decisions. The SI system provides a globally accepted set of units, ensuring uniformity in communication across all engineering disciplines. However, the USC system is still widely used in the U.S., especially within the engineering community, and all engineers will likely have to come to terms with the continued use of USC units for the near future.

Engineers must be vigilant about using units during calculations and conversions to prevent errors and ensure uniformity in calculations, measurements, and technical communications. Confusion with units is a common experience, although it is a normal part of the learning process. Becoming comfortable with units requires much practice and exposure to different measurements and units. Working with unit conversions from real-life applications can build confidence when doing engineering calculations. Remember that units and unit systems (SI and USC) provide crucial context and meaning to measurements, allowing engineers to communicate effectively and make accurate calculations. If in doubt about units or unit conversions, seek clarification from reference sources (such as NIST), course instructors, and the many online resources.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

Discuss the significance of standardized units, focusing on the role of the International System of Units (SI) in ensuring consistency and facilitating global collaboration.
Share experiences and discuss common mistakes related to units that engineering students may have encountered in coursework or projects.
Explore challenges that arise in interdisciplinary projects, where engineers from different backgrounds may use different units or conventions.
Discuss the role of units in ensuring safety standards in engineering and how adherence to specific units contributes to compliance with regulations and codes.
Explore emerging units that might impact the engineering field, e.g., for electric propulsion.
Suggest effective strategies for better teaching and learning of units of measurement in engineering education.
Do some research on the internet on how units of measurement are applied in industry settings, discussing any variations or industry-specific standards. Hint: Consider using units in the U.S. versus Europe, for example.

Other Useful Online Resources

To gain a deeper understanding of measurement units, navigate to the following online resources:

Ever heard of a “ream” or an “octa”? How about a “furlong” or a “fathom” or a “fortnight”? Find out at All About Units!
Metric Trivia Quiz – How much do you know about the metric system (SI)? Try the NIST Metric Trivia Quiz online or use the Alexa skill to test your knowledge and be on your way to thinking metric!
Busting Myths about the Metric System.
Death by Inches: The battle over the metric system in America.

The name "mole" is an 1897 translation of a German unit coined by Wilhelm Ostwald in 1894 from the word molekül (molecule). ↵
The candela is defined as the luminous intensity of a point source that emits monochromatic radiation at a frequency of 540 x 1,012 Hz, and that has a radiant intensity of 1/683 Watt per steradian. The arbitrary (1/683) term was chosen so that the new 2018 SI definition would precisely match the old definition. Although the candela is defined in terms of seconds and Watts (a derived SI unit), the candela is still defined as a base unit in the SI system. ↵
The name "slug" as a unit of mass originates from the concept of mass as inertia, i.e., "sluggish," and has been referred to as the "engineer's mass unit." ↵
Deprecated units are still recognized but are no longer recommended for use. Depreciating a previously used unit is done to maintain clarity, consistency, and precision in scientific communication. ↵
Through repetition and experience, one achieves excellence. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.