Introduction

The turbojet is the name used for a gas turbine engine designed to produce thrust by accelerating air and combustion products through a suitably shaped propelling nozzle. Air enters the front of the engine, is compressed, mixed with fuel, burned in the combustor, and then expanded through the turbine and nozzle. The turbine extracts sufficient power to drive the compressor, while the remaining energy in the hot gas is used to form a high-speed exhaust jet. The change in momentum of the flow through the engine produces the thrust. A cutaway view of a turbojet engine with an axial-flow compressor is shown in Figure 1.

Turbojets were central to the early development of jet aircraft because they provided a compact and practical means of generating the high thrust required for high-speed flight. The first operational jet airplanes of the 1940s, such as the Messerschmitt Me 262 and the Gloster Meteor, used turbojet engines and demonstrated that gas turbine propulsion could overcome many of the speed limitations of piston-engine airplanes. After WWII, turbojets became the dominant propulsion system for early military jets, research aircraft, and the first generation of supersonic airplanes. Their relatively small frontal area, direct flow path, and ability to operate effectively at high altitude made them well suited to streamlined airplane designs for which speed, altitude, and compact installation were important design objectives.

The turbojet engine has since been used on many aircraft types, including supersonic aircraft. Compared with later turbofan engines, turbojets generally have lower propulsive efficiency at lower airspeeds because they produce thrust by accelerating the flow to a high exhaust velocity. This feature makes them less attractive for use on low-speed aircraft. Nevertheless, the turbojet has been, and remains, an important form of aircraft propulsion. Today, turbojets remain relevant for military aviation, cruise missiles, target drones, and some high-speed unmanned aerial vehicles (UAVs). Turbojets have also been employed in cruise missiles and specialized high-speed vehicles where compact size and high thrust are important. In most modern transport aircraft, however, the turbojet has been replaced by the turbofan, which produces the required thrust more efficiently and with less noise by accelerating a larger mass flow through a smaller velocity increase.

Design of a Turbojet

The basic design of a turbojet engine is shown in Figure 2. The engine consists of two principal parts: the cold section and the hot section. The cold section includes the air inlet, the compressor, and the compressor-exit diffuser, which slows the compressor discharge flow and distributes it more uniformly into the combustor. The hot section begins with the combustion chamber, where the compressed air is mixed with fuel and burned, followed by the turbine. The exhaust gas is then expanded through the propelling nozzle, where it is accelerated to a relatively high jet velocity. The resulting thrust is produced by increasing the momentum of the air and combustion products passing through the engine. Although the diffuser hardware is physically attached to the combustor module, it is often regarded as a functional component of the cold section because it precedes fuel addition and combustion.

Operational Principle

The operational principle of a turbojet engine is straightforward, and its thermodynamic operation follows the Brayton cycle. In reference to Figure 2, there are five primary stages.

1. Air intake stage. The intake, located ahead of the compressor, slows the incoming air and raises its static pressure before the flow reaches the compressor. The airflow entering a turbojet compressor must be subsonic, regardless of the aircraft’s flight speed. In supersonic flight, the inlet uses its geometry, ramps, doors, bleed systems, or other flow-control devices to decelerate the incoming flow to suitable subsonic conditions at the compressor face.

2. Compressor stage. The flow is then directed through alternating rows of stationary vanes and rotating compressor blades, where progressively higher pressure is achieved. Older turbojet engines often used fixed stator vanes, whereas many modern engines use variable stator vanes to direct the flow onto the compressor blades at appropriate angles over a range of engine operating conditions. The compressor is driven by the turbine through a shaft that passes forward through the engine core.

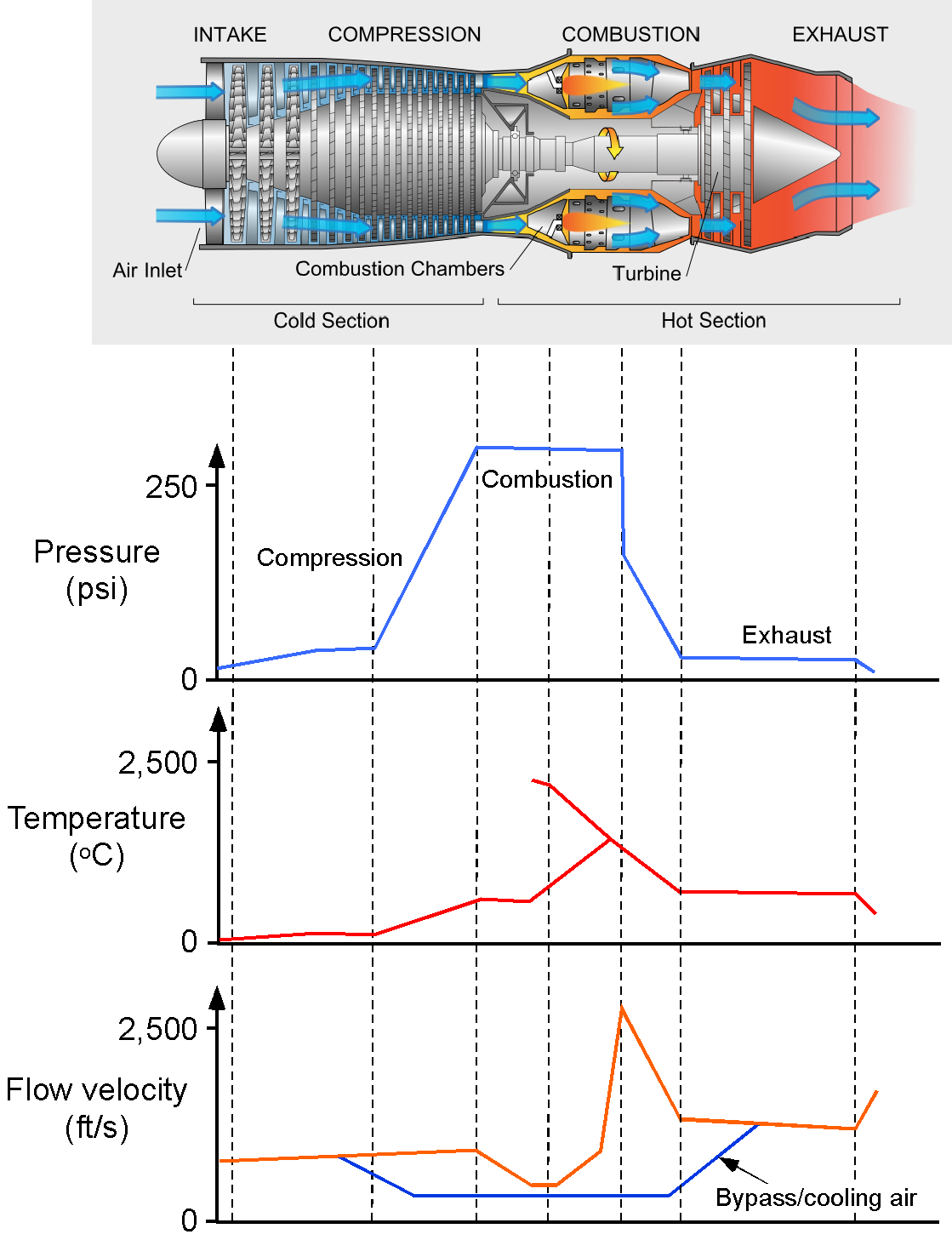
3. Combustion stage. Fuel is injected into the compressed air and burned in the combustor to produce a gas flow at much higher temperature. This process is continuous and occurs at nearly constant pressure, which differs from the intermittent combustion process in a piston engine, where pressure rises rapidly in a confined cylinder volume. In a turbojet, the hot combustion products then pass into the turbine.

4. Turbine stage. The hot combustion gases expand through the turbine, which extracts work from the flow to drive the compressor and engine accessories. In a turbojet, the turbine is designed to extract only the work needed to operate the compressor and accessories, leaving sufficient residual pressure and temperature for the exhaust nozzle to accelerate the flow and produce thrust. Compressor bleed air may also be routed through internal passages to cool turbine vanes and blades, allowing them to operate in a gas stream whose temperature may exceed the allowable metal temperature. Turbine blades and vanes are made from high-temperature alloys and often use sophisticated cooling methods and protective coatings.

5. Exhaust stage through a nozzle. After the turbine, the gases expand through the exhaust nozzle, producing a high-velocity jet that serves as the primary source of thrust. One problem with the high-speed exhaust flow from a turbojet engine is that it creates significant jet noise. Measurements show that jet noise depends strongly on the fully expanded jet velocity, , and is often represented approximately by

(1)  

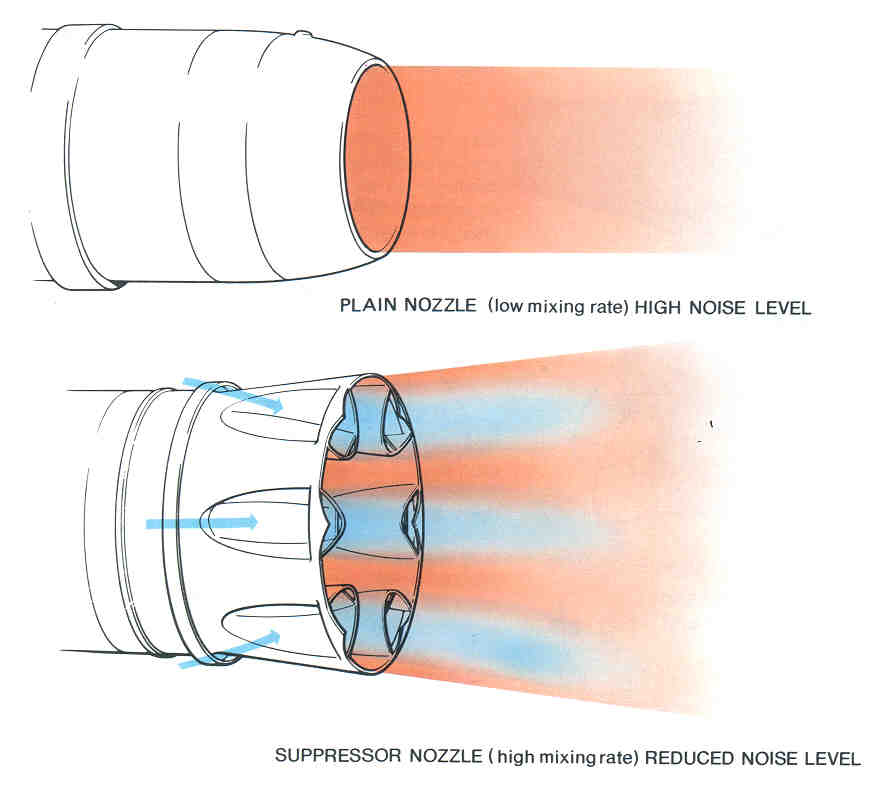
where for subsonic jet conditions is called the eighth-power law, and for supersonic jet conditions is called the third-power law. These are empirical laws based on measurements of jet noise. As shown in Figure 3, some turbojet engines use noise-suppression devices, such as corrugated or lobe-type suppressor nozzles. These devices promote more rapid mixing between the exhaust jet and the surrounding air, reducing the peak jet velocity and making the resulting jet noise less intense to an external observer.

Thrust Production

The thrust produced by a turbojet engine can be examined using conservation principles of fluid dynamics applied to a control volume surrounding the engine, as shown in Figure 4. The basic operating principle is that air enters the inlet, is compressed to a pressure suitable for combustion, mixed with fuel, and burned. Part of the energy in the hot gas is extracted by the turbine to drive the compressor, and the remaining energy is used to accelerate the exhaust through the nozzle. The high-speed exhaust jet increases the momentum of the flow passing through the engine and produces thrust.

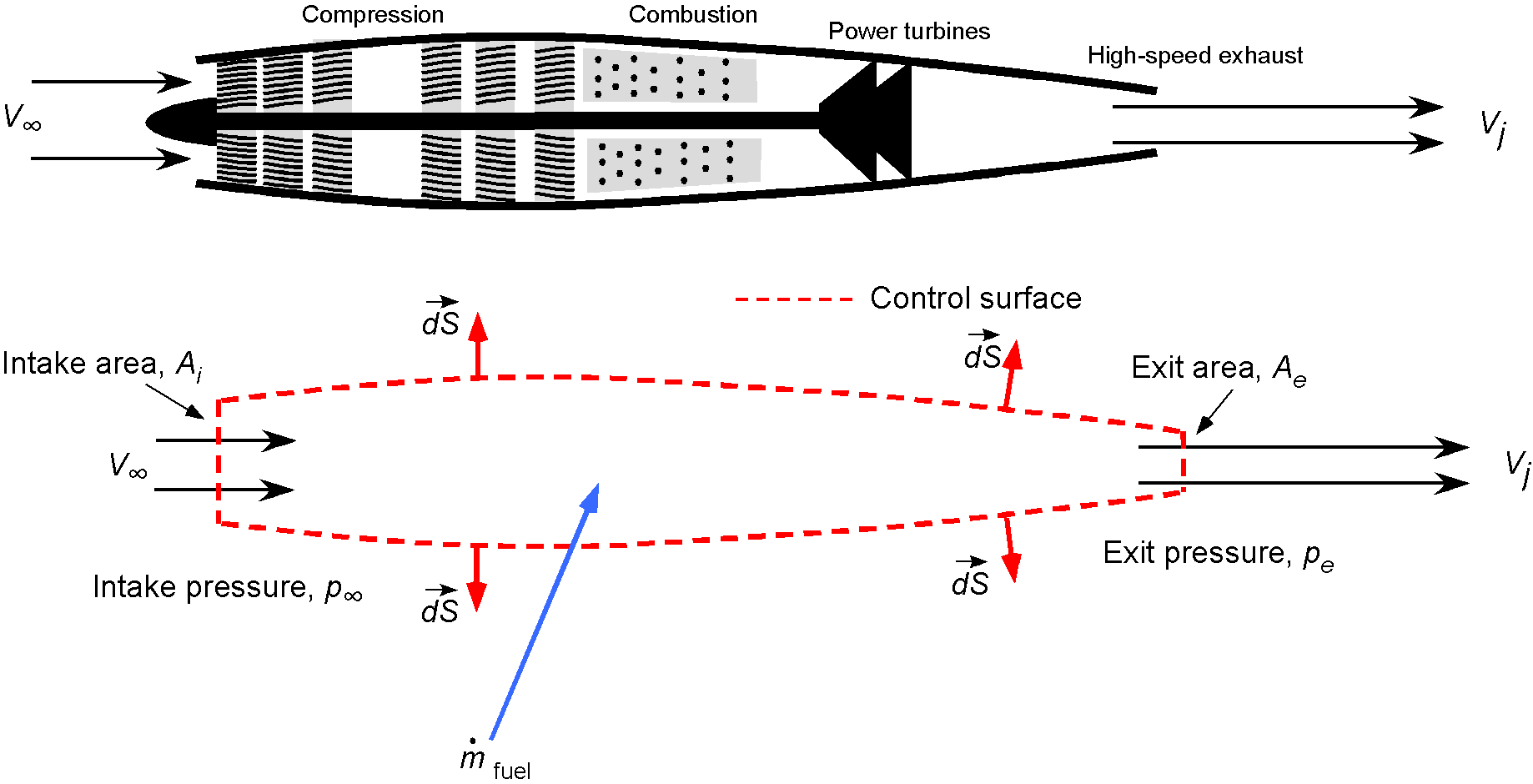
The mass flow rate of air into the engine is

(2)  

where is the inlet capture area. Strictly, is not always the same as the physical area at the engine face. It represents the effective streamtube area of air captured by the inlet under the specified flight condition. The inlet must deliver this flow to the compressor with acceptable pressure recovery, flow uniformity, and low distortion. In subsonic flight, the inlet usually diffuses the flow smoothly before it reaches the compressor. In supersonic flight, the inlet must also decelerate the flow through shock waves and diffusion so that the compressor face still receives subsonic flow.

The fuel mass flow rate is . Applying conservation of momentum to the engine control volume gives the uninstalled thrust in the usual one-dimensional form as

(3)  

where is the nozzle exit area and is the exit or jet velocity, often denoted by . The first term represents the downstream momentum flux of the exhaust, including both the incoming air and the added fuel. The second term is the incoming momentum flux, often called the ram-drag term. The final term is the pressure thrust, which appears when the nozzle exit pressure is not equal to the ambient pressure.

The exhaust nozzle converts the remaining thermal and pressure energy in the gas leaving the turbine into kinetic energy. If the nozzle is ideally expanded, then , and the pressure-thrust term is zero. If , the exhaust is underexpanded and the pressure term adds thrust. If , the exhaust is overexpanded and the pressure term reduces thrust. In many introductory analyses, the nozzle is assumed to be ideally expanded and the fuel mass flow rate is small compared with the air mass flow rate. Under these assumptions, the thrust may be approximated by

(4)  

This approximate equation shows the competing effects of flight speed. As increases, the ram-drag term increases, and the difference may decrease. However, the engine also captures more air mass flow as flight speed increases, and ram compression changes the pressure and temperature conditions entering the compressor. Therefore, the net thrust of a turbojet does not follow from alone; it depends on the combined effects of mass flow, inlet ram pressure, compressor operation, combustor temperature limits, and nozzle expansion.

For a turbojet engine at subsonic Mach numbers, the thrust often remains relatively constant with . At higher flight Mach numbers, thrust may increase with Mach number because of ram effects, but it generally decreases with altitude because the air density and mass flow rate decrease, as shown in Figure 5. A jet engine’s “uninstalled thrust” is typically determined during static tests on a test stand. The engine is calibrated to relate thrust to parameters such as rotational speed, pressure ratio, and exhaust gas temperature. These parameters are also displayed on the pilot’s cockpit instrument panel and, together with information in the form of engine charts in the aircraft flight manual, can be used to estimate the aircraft’s anticipated performance.

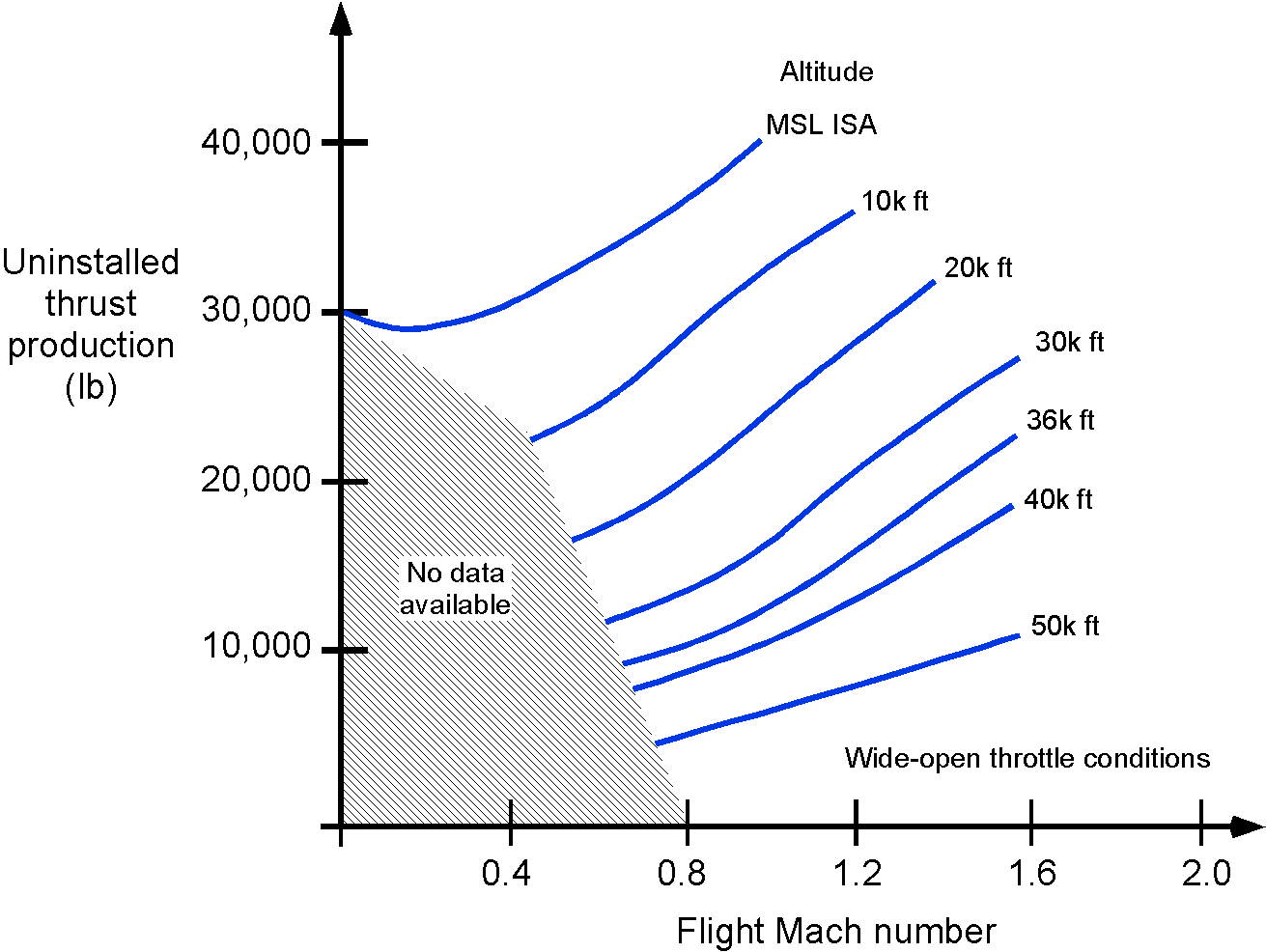
The overall thrust characteristics of a turbojet depend significantly on flight Mach number and operational altitude. In this context, “altitude” often means density altitude, i.e., the altitude in the International Standard Atmosphere (ISA) that corresponds to the local ambient density. Maximum thrust is also influenced by ambient temperature, with thrust decreasing as temperature increases. For this reason, an airplane may require a longer takeoff run on a hot day than on a cooler day.

Engine manufacturers provide a rated thrust value that is guaranteed for use in the airplane’s flight manual. This rated thrust may be “flat-rated,” meaning that the engine control system limits the engine to a specified thrust over a range of ambient conditions until a limiting temperature, speed, or pressure condition is reached. The rated thrust is determined from static engine test data and, where applicable, flight test data.

One approximation for the thrust produced by a turbojet engine is that it increases approximately linearly with flight Mach number over a limited range, i.e.,

(5)  

where is a reference Mach number for which the thrust is known, and is an empirical constant. A simple first-order approximation for the variation of thrust with altitude is

(6)  

where is the thrust produced at mean sea level conditions, is the density at altitude, is the sea-level standard density, and is the density ratio. Air density can be estimated using the ISA equations, which are based on the local ambient pressure and outside air temperature.

Thermodynamics

The Brayton cycle is the fundamental thermodynamic model for gas turbine engines, which power most of modern aviation in the form of turbojets, turbofans, and turboprops. First proposed in the 1870s by George Brayton, the cycle became practical only with the development of axial compressors and turbines in the 20th century. It remains central to propulsion because it illustrates how chemical energy in fuel is converted into either a high-velocity exhaust jet (as in turbojets) or mechanical shaft work (as in turbofans and turboprops), thereby producing thrust.

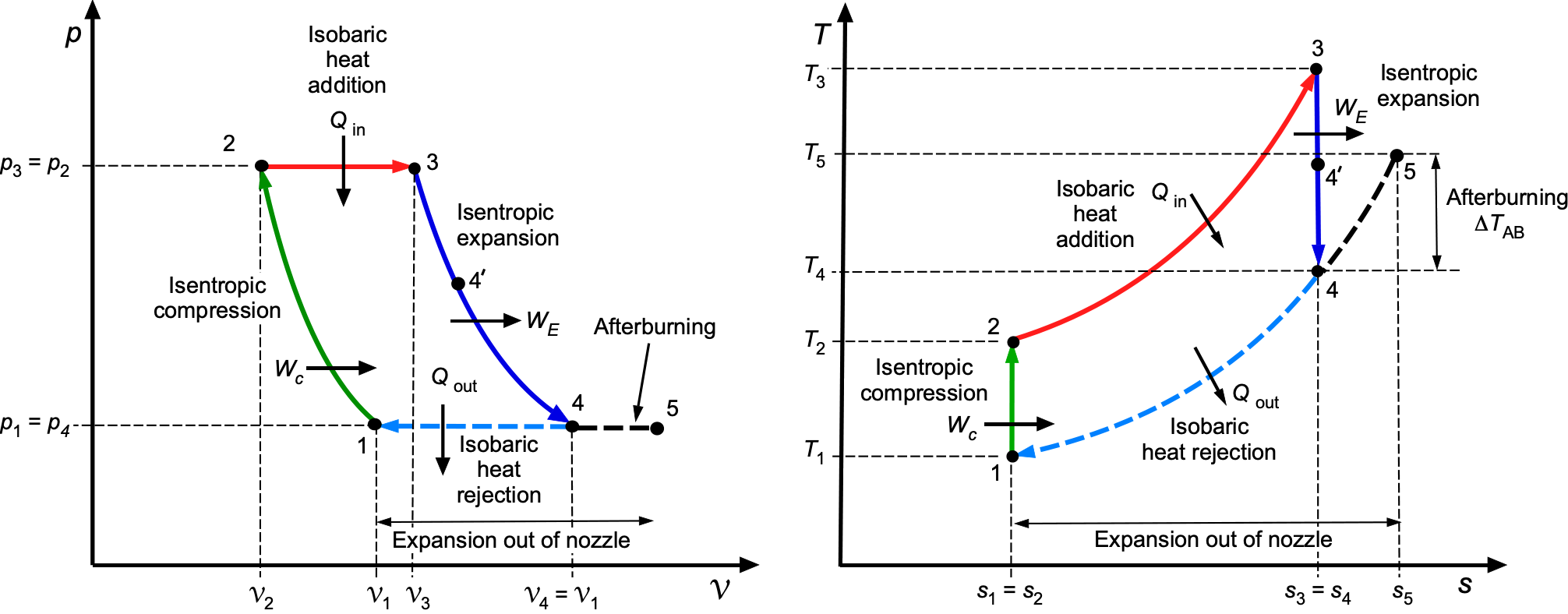
The ideal Brayton cycle consists of four internally reversible processes, as shown in the schematic of Figure  6. The first process (1 to 2) is isentropic compression in the compressor. The second (2 to 3) is constant-pressure heat addition in the combustor. The third (3 to 4) is isentropic expansion through the turbine, producing work. The final process (4 to 1) is constant-pressure heat rejection, representing discharge to the atmosphere.

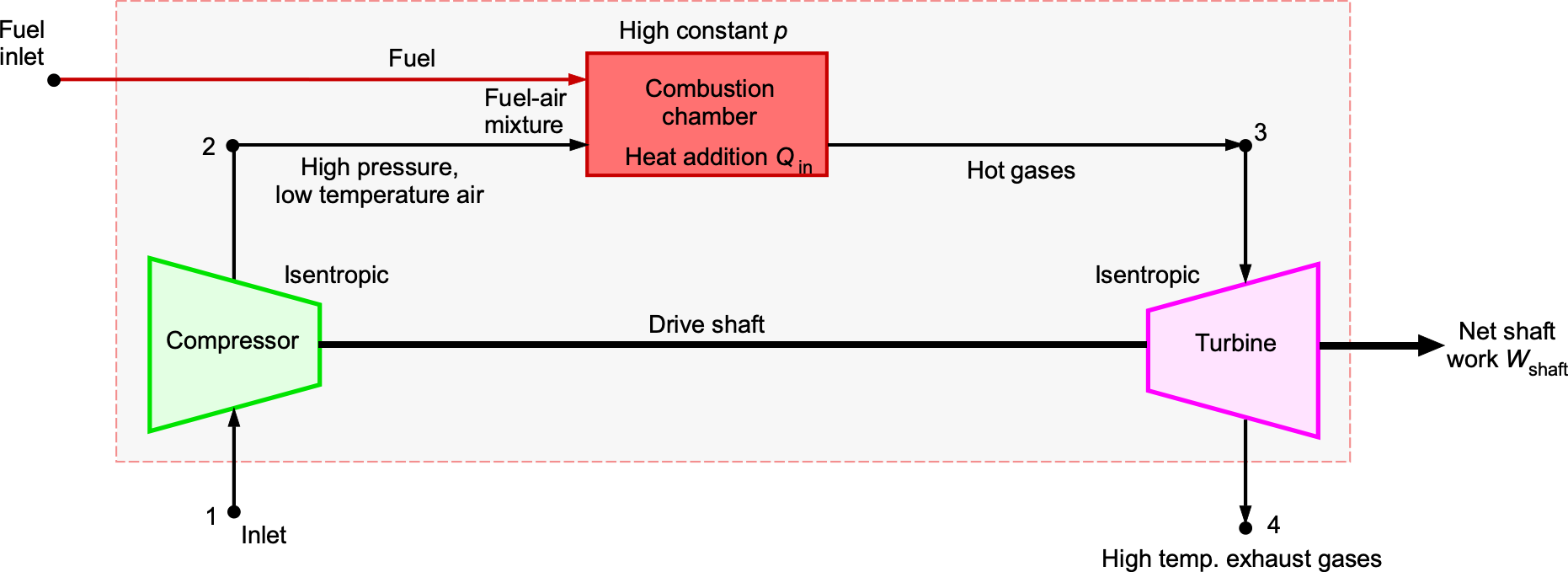
Although a gas turbine operates as an open system, it is often represented as a closed thermodynamic loop so that the cycle can be analyzed consistently using – and – diagrams; see Figure  7. In this representation, the notional process from state 4 to 1 corresponds to heat rejection to the surroundings, conceptually closing the cycle.

The specific heat interactions are

(7)  

and the specific work values are

(8)  

so that . From the isentropic relations, then

(9)  

where is the compressor pressure ratio. Assuming a perfect gas with constant specific heats and isentropic compression and expansion, substitution gives the thermal efficiency as

(10)  

Therefore, the Brayton cycle efficiency improves as the pressure ratio increases. Increasing the turbine inlet temperature increases the specific work output of the cycle but does not directly affect the ideal thermal efficiency.

In a gas turbine cycle, the turbine must supply sufficient work to drive the compressor and to provide useful net work for propulsion via a jet from a suitably shaped nozzle, or as shaft power. The fraction of the turbine work consumed by the compressor is called the back-work ratio (BWR). It is defined as

(11)  

A high back-work ratio (BWR) indicates that a significant fraction of the turbine output is internally used to drive the compressor, leaving less net work available. On the – diagram, this is shown by dividing the turbine expansion into two parts: the segment from state 3 to 4′ supplies exactly the compressor work, while the segment from 4′ to 4 represents the net turbine work output. In modern gas turbines, the BWR is typically 40–60%. Because the compressor consumes a large portion of the turbine work, gas-turbine performance strongly depends on achieving high turbine inlet temperatures. Higher turbine inlet temperatures yield greater expansion work to meet compressor demand while still producing useful net power.

In a turbojet, the turbine normally extracts only enough work to drive the compressor and engine accessories; most of the remaining flow energy is left for expansion through the nozzle, where it produces jet thrust. With the definition

(12)  

the value for a simple turbojet is close to unity, because nearly all turbine work is used internally to drive the compressor. In a turbofan, additional turbine work is extracted to drive the fan, so a compressor-only back-work ratio is not by itself a complete measure of the turbine work split. In turboprop and turboshaft engines, the turbine system extracts still more energy from the gas stream to deliver useful shaft power, leaving much less residual jet energy in the exhaust.

Thrust-Specific Fuel Consumption (TSFC)

The output of a turbojet is thrust, so the specific fuel consumption depends on the amount of thrust produced. Recall that the specific fuel consumption is based on the shaft or brake power for engines that primarily produce shaft power (e.g., a piston engine or a turboshaft engine). The thrust-specific fuel consumption or TSFC is a measure of the fuel consumed per unit thrust produced per unit time, i.e.,

(13)  

Typically, the TSFC is expressed in units of lb lb hr in the USC system or units of kg kN hr in the SI system. In SI usage, the numerator is usually reported as fuel mass rather than fuel weight, while the denominator is expressed in units of thrust. Further caution is warranted, as publications may use different units for TSFC.

The overall propulsive efficiency of a turbojet engine generally improves at higher flight Mach numbers because the aircraft speed becomes a larger fraction of the exhaust jet speed. This is one reason why this engine type is more suitable for higher-speed aircraft. Representative variations of the TSFC of a turbojet engine are shown in Figure 8. Note also that the TSFC of a turbojet engine generally increases slightly as flight Mach number increases.

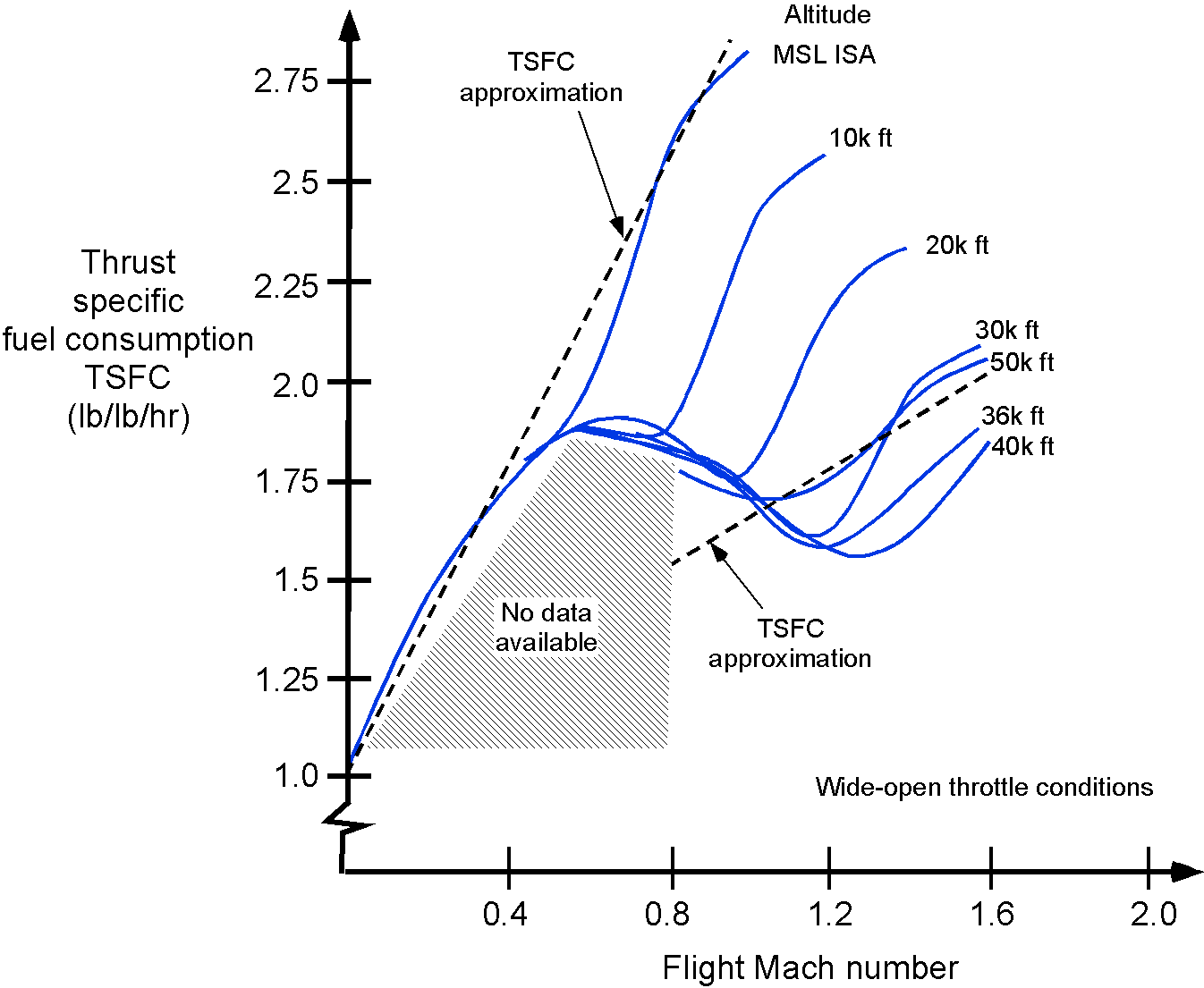
In performance analyses, one linear approximation that can be used for the TSFC in the subsonic regime is

(14)  

which is measured as fuel weight or fuel mass consumed per unit thrust per unit time, depending on the unit system and convention being used. The values of and are engine-specific and also depend on the engine’s throttle setting. However, a turbojet engine typically operates at or near wide-open throttle for most flight operations. Remember that air density is lower at higher flight altitudes, so the mass flow of air into the engine decreases.

Afterburning

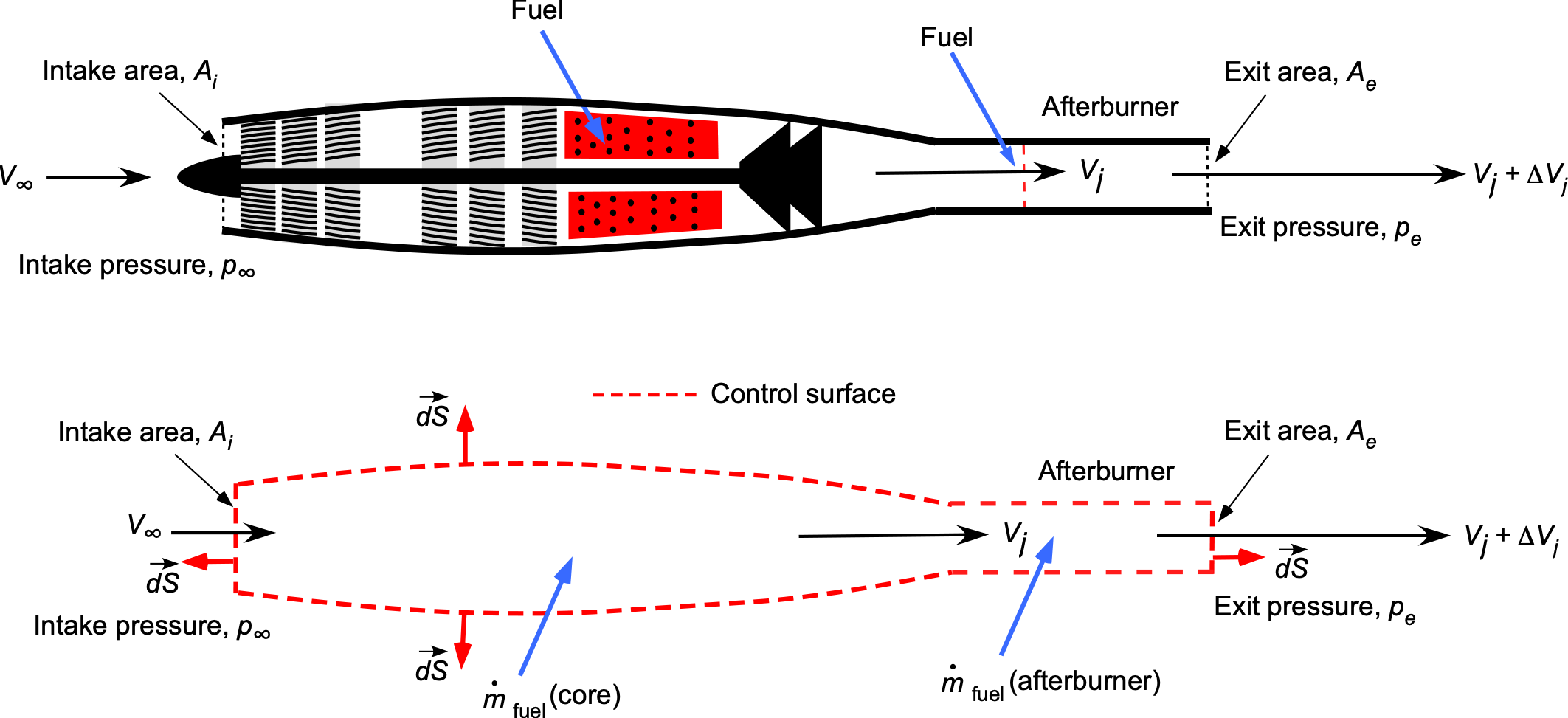
Military aircraft often require a significant increase in engine thrust for a relatively short time, such as during takeoff, climb, acceleration into supersonic flight, or some combat maneuvers. This thrust is achieved using an afterburner, as shown schematically in Figure 9. An afterburner injects additional fuel into the engine exhaust, which then burns in an extended tailpipe. Afterburning is sometimes called reheat.

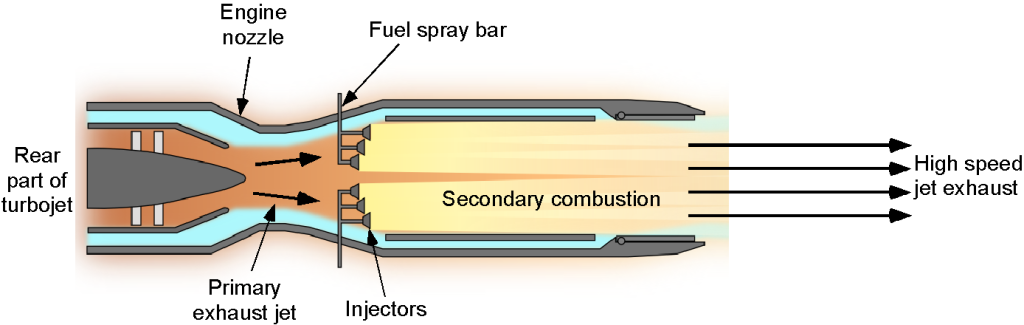
The afterburner tube contains fuel spray bars, flame holders, and an adjustable nozzle. An adjustable exhaust nozzle is required for an afterburning engine; two- or three-position nozzles are typically used. Raw fuel is injected into the engine core exhaust by the fuel spray bars, and the flame holders stabilize the resulting combustion as it develops down the tube and into the tailpipe. The engine’s core exhaust contains sufficient excess oxygen to enable afterburner operation, eliminating the need for additional inlets. The resulting exhaust flame from an afterburner is typically striking because the exhaust plume is supersonic and may exhibit diamond-shaped shock-cell patterns, as shown in the photograph in Figure 10.

In thermodynamic terms, an afterburner can be modeled as a Brayton cycle with an additional isobaric heat-addition process between the turbine exit and the nozzle. The turbine still provides the work to drive the compressor, but the afterburner raises the exhaust stream’s total temperature before it expands in the tailpipe. If is the turbine exit temperature, then afterburning increases the stagnation temperature to , i.e.,

(15)  

where the boost depends on the amount of fuel injected and burned. As shown in Figure 11, the effect on the – diagram is an additional constant-pressure heat-addition process between the turbine exit and the nozzle inlet, during which both temperature and entropy increase. On the corresponding – diagram, an additional heat-addition process is introduced downstream of the turbine; however, the expansion through the nozzle begins from a higher total temperature, resulting in a higher jet velocity and, consequently, greater thrust.

The thrust produced by a turbojet engine with an afterburner can be examined using conservation principles of fluid dynamics applied to a control volume surrounding the engine, as shown in Figure 12. The secondary combustion in the afterburner significantly increases the exhaust velocity from to , which raises the net thrust from to , as described by the momentum thrust relation

(16)  

where denotes the total mass flow rate through the engine. If the fuel mass flow rates are small compared with the air mass flow rate, so that terms involving and can be neglected, the thrust equation simplifies to

(17)  

This shows that the additional thrust produced by the afterburner, ,  is approximately equal to , representing the extra momentum gained from the increase in jet exhaust velocity.

While engine thrust may increase nearly twofold when the afterburner is lit, the engine fuel flow increases by a much larger proportion than the thrust, so the TSFC increases markedly. For example, published values for the Pratt & Whitney F100-PW-220, as used on the F-15 and F-16, are 0.76 lb lb hr (0.76 kg kg hr), without the afterburner and 1.94 lb lb hr (1.94 kg kg hr), with the afterburner. Because of the higher jet velocities out of the tailpipe, engine noise increases dramatically, i.e., according to Eq. 1. Afterburning is usually used by military fighter aircraft for takeoff and initial climb. In this case, the high noise levels produced by an afterburner are particularly noticeable to a ground observer. Concorde used afterburning turbojet engines, but the afterburner was used mainly for takeoff and acceleration through the transonic regime.

Afterburning is also possible with a turbofan engine. Afterburning turbofans are typically found on military aircraft designed to achieve transonic and low-supersonic cruise speeds. When performance requirements span these speed ranges and subsonic flight under various conditions, selecting a low-bypass-ratio turbofan engine is usually the best design compromise to meet them. In all cases, however, matching an engine to an aircraft requires careful consideration of not only the aircraft’s requirements but also weight, cost, and installation issues.

Water Injection

Water injection is a thrust-augmentation technique used on some early turbojet engines, especially for takeoff under hot-day, high-altitude, or short-runway conditions. These conditions reduce the inlet air density, thereby reducing the mass flow rate through the engine. Because the thrust depends strongly on mass flow and jet velocity, the available thrust can decrease substantially just when maximum thrust is needed, such as during takeoff.

Recall that the thrust produced by a turbojet engine may be expressed approximately as

(18)  

where is the mass flow rate through the engine and is the velocity increment given to the flow. If the air mass flow rate decreases because of low ambient density, thrust decreases unless the engine compensates by increasing the jet velocity or processing more mass.

Simply adding more fuel is usually not possible because the engine is limited by the turbine inlet temperature. The turbine blades and vanes can withstand only a finite gas temperature, so the fuel flow must normally be limited to prevent overheating. Water injection changes this constraint. When water is injected into the engine, it evaporates and absorbs heat from the flow. This cooling effect lowers the gas temperature for a given fuel flow, allowing additional fuel to be burned while maintaining the turbine inlet temperature within allowable limits.

The total mass flow through the engine becomes

(19)  

where is the water mass flow rate. However, the increase in thrust is not solely from the added water mass. The larger effect is that evaporative cooling permits an increase in fuel flow, thereby increasing the energy added in the combustor and, consequently, the exhaust momentum. Therefore, water injection is both a mass-flow augmentation method and a temperature-control method that effectively relaxes the turbine temperature constraint.

A simplified energy balance illustrates the effect. If the injected water is heated and vaporized in the gas stream, then it absorbs energy at a rate approximately given by

(20)  

where is the injected water temperature, is the boiling temperature at the local pressure, is the latent heat of vaporization, and is the gas temperature after vaporization. This heat absorption reduces the gas temperature and increases the margin to the turbine temperature limit. The engine fuel control can then admit more fuel, increasing the combustor energy release.

Water may be introduced at different locations in a turbojet engine. Injection at the compressor inlet cools the incoming air, increasing its density and reducing the inlet temperature, thereby raising the corrected mass flow and improving takeoff thrust. Injection at or near the compressor discharge or within the combustor, provided with evaporative cooling of the compressed air, allows higher fuel flow while maintaining the turbine temperature limit. In early turbojets, water-alcohol mixtures were often used, with the water providing cooling and additional mass flow and the alcohol preventing freezing while contributing some heating value. The resulting thrust augmentation depended on the engine design, injection location, and operating conditions, but was typically on the order of 10% to 30%. It was normally a short-duration takeoff rating, with operation limited by the onboard water supply and by engine operating limits.

Water injection also carried significant penalties. The aircraft had to carry the water or water-alcohol mixture, tanks, pumps, plumbing, valves, and controls. The system added weight and maintenance burden. Therefore, although thrust increased, thrust-specific fuel consumption generally worsened during water-injection operation. The injected water could also contribute to corrosion, deposits, compressor erosion, and operational complexity. The mixture required fine atomization to ensure rapid evaporation and to avoid compressor instability, combustion roughness, flameout, or local thermal distortion. In addition, the reduction in flame temperature and the higher fuel flow tended to degrade combustion efficiency, leading to increased soot and unburned hydrocarbons, so that the exhaust during “wet” operation often appeared as a dense gray or black plume (Figure 13), representing a significant increase in visible pollution.

Water injection is not used on modern transport turbofan engines because engine technology has largely eliminated the need for it. Modern high-bypass turbofans produce thrust primarily by accelerating a large mass flow through the fan rather than relying on a small, high-temperature core jet. They also use higher compressor pressure ratios, improved compressor aerodynamics, advanced turbine materials, thermal barrier coatings, and sophisticated turbine cooling. These advances enable high takeoff thrust without the need for a separate water-injection system. Engine control systems can also manage turbine temperature and compressor stability more effectively than earlier mechanical fuel controls.

Why Jet Engines Form Contrails

Look up in the sky! What are those long white streaks trailing behind a high-flying airplane? These visible lines are called contrails, short for condensation trails. They form when the hot, moist exhaust from a jet engine mixes with the frigid air of the upper troposphere. As the mixture cools, it can no longer retain all its water vapor, so the excess condenses and freezes almost instantly, forming a thin line of ice crystals. A good illustration of this process is shown in the photograph in Figure  14.

The amount of water vapor produced by a jet engine is directly proportional to its fuel mass-flow rate, i.e.,

(21)  

where is the water emission index as a ratio of the mass for water vapor to the mass of fuel (in ) and is the fuel flow rate. Because the engine ingests far more air than fuel, it is convenient to define the air-fuel mass ratio as . With this, the exhaust water-vapor mixing ratio, expressed approximately as mass of water vapor per unit mass of air, is

(22)  

This quantity describes the humidity level in the exhaust immediately as it leaves the jet nozzle. After leaving the engine, the exhaust mixes turbulently with the surrounding air. The temperature and humidity of the mixture lie between the exhaust state and the ambient state . If is the fraction of exhaust in the mixture, where is pure exhaust and is pure ambient air, then the mixture temperature and humidity are

(23)  

As the exhaust mixes and cools, which is often very rapid because the ambient air may be colder than , the mixture may reach saturation with respect to liquid water. At that point, water droplets form and then freeze almost immediately into ice crystals. To determine whether initial contrail formation occurs, the actual water-vapor mixing ratio must be compared with the saturation mixing ratio over liquid water at the mixture temperature, denoted . The corresponding saturation ratio is

(24)  

A contrail can form if, at some stage of the exhaust-mixing process,

(25)  

This is the basis of the Schmidt–Appleman formation criterion. Once the droplets freeze, the persistence of the resulting ice-crystal contrail is governed by the ambient saturation condition with respect to ice. If liquid-water saturation is never reached during mixing, a visible contrail does not form even though water vapor is present in the exhaust.

Whether a contrail persists after formation depends on the ambient air’s relative humidity relative to ice. If is the ambient vapor pressure and is the saturation vapor pressure over ice at the ambient temperature, then the relative humidity can be expressed as

(26)  

which is the relative humidity with respect to ice. Ice crystals remain stable or grow when , leading to a persistent contrail that may spread under upper-level winds. When , the ice crystals sublimate, and the contrail dissipates quickly.

In practical terms, the engine type and its characteristics determine how much water enters the exhaust and its initial temperature, but the surrounding atmosphere controls nearly everything else: whether the mixture becomes saturated, whether ice crystals form, and whether the contrail lasts for seconds or for many minutes. This is why two aircraft flying at nearly the same flight level can produce markedly different contrail signatures when they pass through slightly different temperature or humidity layers.

Ramjets & Scramjets

A description of ramjets and scramjets is appropriate in the category of air-breathing jet engines. Both engines use the vehicle’s forward speed to compress the incoming air before combustion, so neither has the compressor, turbine, or other major rotating machinery found in a turbojet. In this sense, the inlet and diffuser serve the role of the compressor in a turbojet. The difference is that a conventional ramjet slows the flow to subsonic speed before combustion, whereas a scramjet, or supersonic-combustion ramjet, maintains supersonic flow through the combustor.

Ramjets

A ramjet is a simple air-breathing jet engine consisting of an inlet or diffuser, a combustor with fuel injection and flame stabilization, and a nozzle, as shown schematically in Figure 15. The simplicity of the ramjet is attractive, but it also means that the engine cannot produce useful static thrust. It must first be accelerated to a sufficiently high flight speed by another propulsion system, such as a rocket booster, turbojet, or carried launch platform.

The operation of a ramjet depends strongly on the inlet conditions. At low speeds, the pressure rise from ram compression is small, so the engine produces little thrust and has poor fuel economy. At supersonic speeds, the inlet slows and compresses the incoming flow before it enters the combustor. In an ideal analysis, this compression may be approximated as isentropic, but real supersonic inlets experience stagnation-pressure losses because of shocks, boundary-layer growth, and possible flow separation. These losses can have a major effect on thrust and fuel consumption.

The combustor of a conventional ramjet usually operates with subsonic flow. Fuel is injected into the compressed air, mixed, and burned while flame holders or other stabilizing devices maintain a stable combustion zone. Slowing the flow to subsonic speed helps stabilize combustion and allows heat addition without the severe losses that would otherwise occur in a supersonic stream. Conventional ramjets may fly at supersonic speeds, but their combustors are normally subsonic-combustion devices.

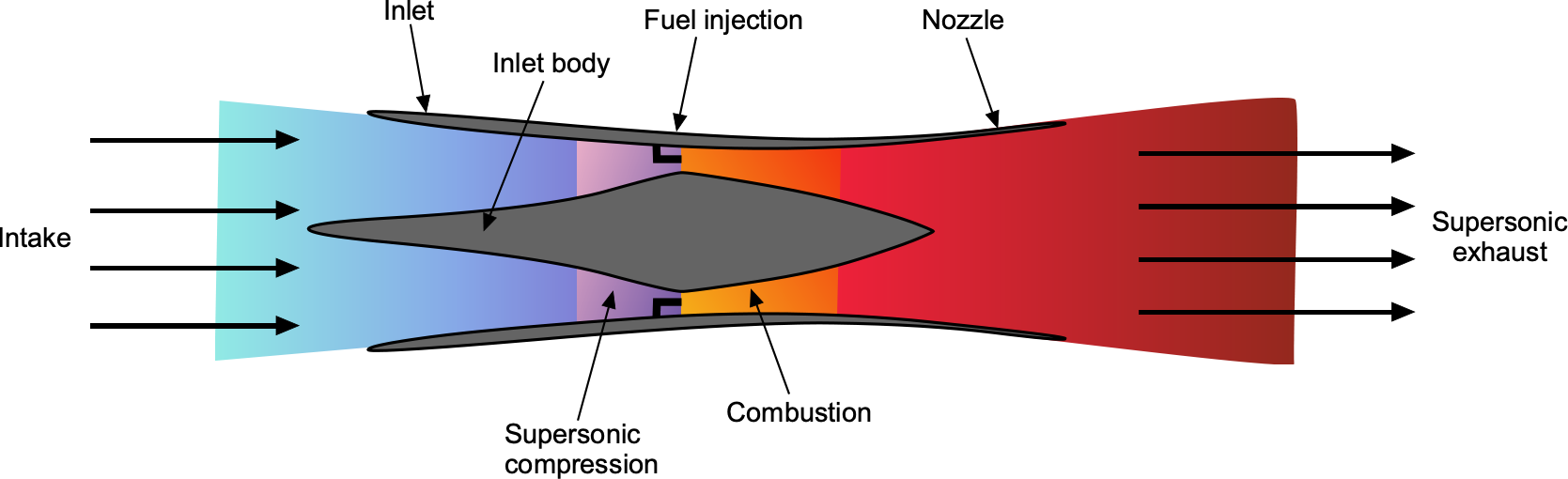
Ramjets, despite their mechanical simplicity, have important limitations. They cannot produce thrust at zero airspeed, are inefficient at low flight Mach numbers, and require another propulsion system for acceleration. As the Mach number increases, ram compression becomes more effective, and the ramjet can become attractive for sustained supersonic flight. However, at still higher Mach numbers, the inlet stagnation temperature becomes very large. This limits the allowable rise in combustor temperature, increases thermal loading, and makes shock losses increasingly severe. These effects define the useful operating envelope of a conventional ramjet and motivate the use of scramjets for still higher Mach numbers.

Ramjets have been used primarily in supersonic missiles and other high-speed vehicles, especially when the mission requires sustained supersonic flight after an initial boost. Related tip-jet systems have also been used in unusual reaction-drive rotor applications. For example, the Fairey Rotodyne gyroplane used tip-mounted jets supplied with compressed air and fuel to drive the rotor during vertical flight. In such applications, the ramjet or pressure-jet concept removes the need to transmit large torque through the rotor shaft, although the fuel consumption and noise penalties can be substantial.

Scramjets

A scramjet is a supersonic-combustion ramjet. Like a ramjet, it uses the vehicle’s forward motion to compress the incoming air, but it does not slow the combustor flow to subsonic speed. Instead, fuel is injected, mixed, and burned while the air remains supersonic, as shown in Figure 16. This approach avoids the very high static temperatures and some of the stagnation-pressure losses associated with slowing very high Mach-number flow to subsonic speed before combustion.

Scramjets are intended for hypersonic flight, where a conventional ramjet becomes increasingly limited by high inlet stagnation temperature, severe shock losses, and thermal loading. However, scramjets are difficult to design because the time available for fuel injection, mixing, ignition, and combustion is extremely short. The inlet, combustor, and nozzle must also be highly integrated with the vehicle shape, so the propulsion system and airframe cannot be treated as independent components. Like ramjets, scramjets do not produce useful static thrust and must be accelerated to high speed by another propulsion system before they can operate effectively.

Ideal Ramjet Performance

A simple ramjet performance estimate can be obtained from a steady, one-dimensional model. The ideal model neglects friction, shock losses, combustor pressure losses, and nozzle losses. It also assumes isentropic flow through the inlet and nozzle and heat addition in the combustor at approximately constant pressure. The freestream velocity is

(27)  

and the stagnation temperature after ideal diffusion is

(28)  

where is the freestream Mach number, is the freestream speed of sound, is the freestream static temperature, is the stagnation temperature after ideal diffusion, and is the ratio of specific heats.

Fuel addition raises the stagnation temperature from to . The hot gas is then expanded through the nozzle. If the nozzle expands the flow ideally to the ambient pressure, then , and the exhaust velocity can be estimated from

(29)  

where is the nozzle-inlet stagnation pressure and is the nozzle-exit static pressure. The corresponding thrust per unit air mass flow rate is approximately

(30)  

when the fuel mass-flow rate and the pressure-thrust term are neglected.

The thrust-specific fuel consumption is

(31)  

where is the fuel-to-air mass ratio. These equations show the main ramjet trend: low specific thrust and high TSFC at low Mach numbers, better performance at supersonic Mach numbers because of stronger ram compression, and degraded performance at very high Mach numbers because of high inlet stagnation temperature, thermal limits, and increasing inlet losses.

The thermodynamic behavior of an ideal ramjet can be represented by the same basic Brayton-cycle processes used for a gas-turbine engine, except that the compression is produced by ram deceleration in the inlet rather than by a mechanical compressor. On a – diagram, the idealized cycle consists of isentropic compression in the diffuser, constant-pressure heat addition in the combustor, and isentropic expansion through the nozzle. This ideal cycle is useful because it illustrates the central idea of ramjet propulsion, i.e., the flight speed itself provides the compression the jet engine needs to operate.

Fuels for Turbojet Engines

Turbojet and other jet engines require fuels that are chemically stable, energy-dense, and capable of reliable performance under extreme operating conditions, including high altitudes and wide temperature variations. Jet fuels are refined to meet these criteria, emphasizing combustion properties, thermal stability, and safety characteristics such as flash point.

The most widely used jet fuels in aviation are categorized into standard types. The two principal grades are Jet A and Jet A-1. Jet A is primarily used in the United States, while Jet A-1 is the international standard. Both fuels are kerosene-based, with Jet A-1 having a slightly lower freezing point of compared to Jet A’s , enhancing its suitability for long-haul international flights at high altitudes. These fuels have a high energy content of approximately 43 MJ/kg and a density of approximately 0.80 kg/L at about .

Jet fuels must have a sufficiently high flash point to minimize fire hazards. Jet A and Jet A-1 have minimum flash points of approximately , ensuring that the fuels do not vaporize excessively at ground temperatures. In addition to flash point, freezing point is critical, as turbine aircraft routinely operate at stratospheric altitudes where ambient air temperatures can fall below .

Another necessary aviation fuel is JP-8, a military-grade kerosene similar to Jet A-1 but with additional additives to enhance thermal stability, reduce icing risk, and improve lubrication. Historically, JP-4, a wide-cut fuel blending gasoline and kerosene fractions, was used extensively in military aviation. Still, it has largely been replaced because of its lower flash point and greater volatility, which increase the risk of fire. Jet B, a wide-cut fuel that contains a higher proportion of lighter hydrocarbons, is used in frigid climates because of its good low-temperature properties. However, its higher volatility and handling risks have limited its adoption in civil aviation.

The combustion of jet fuel in a turbojet engine releases thermal energy that drives the turbine and produces high-velocity exhaust, which generates thrust. The basic energy balance can be expressed by the relationship

(32)  

where is the mass flow rate of the fuel and is the lower heating value of the fuel, typically around 43 MJ/kg for kerosene-based fuels.

Because turbojets operate continuously at high temperatures and pressures, fuel properties such as thermal oxidative stability are also critical. Fuel degradation under heat, known as coking, can lead to deposits in fuel nozzles and afterburners, reducing engine performance and reliability. The proper selection, certification, and management of jet fuels are essential to ensure the safe and efficient operation of turbine-powered aircraft.

Summary & Closure

The turbojet engine is a classic solution for jet propulsion and is best suited for high-subsonic and supersonic flight. Turbojets are now used mainly in military aircraft, missiles, target drones, and some specialized high-speed vehicles. When additional thrust is needed for short periods, a turbojet may be fitted with an afterburner, which adds fuel downstream of the turbine, increasing the nozzle inlet temperature. This approach can produce a large increase in thrust, but only at the cost of much higher fuel consumption and noise. Water injection is another thrust-augmentation method, used mainly on earlier engines to improve takeoff thrust under hot-day or high-density-altitude conditions. Ramjets and scramjets represent still simpler air-breathing engines, using vehicle forward speed rather than rotating compressors to compress the incoming air. However, they cannot produce useful static thrust and are practical only after the vehicle has already been accelerated to high speed.