Introduction^[1]

Rocket engines launch payloads, such as satellites and space probes, into Earth’s orbit. They are also used to propel spacecraft already in orbit. The flow through a rocket nozzle typically involves accelerating hot gases produced by propellant combustion from subsonic to supersonic speeds, converting thermal energy into directed kinetic energy. By imparting a time rate of change of momentum to the gas flow, a force is applied from the rocket engine(s) to the vehicle. Before being expelled from the engine(s), the propellant can be stored in separate fuel and oxidizer tanks, or as a solid mixture of the two. Rocket engines are non-air-breathing; therefore, they require a fuel and an oxidizer, collectively known as a propellant.

Four types of rocket engines can be used for different and relevant applications:

1. Launch Vehicles: The rocket engines used in launch vehicles are designed to deliver high thrust and specific impulse, lifting the vehicle off the ground and into space. They must be powerful enough to overcome Earth’s gravity and give the required kinetic and potential energy for the spacecraft and its payload to reach orbit.
2. Spacecraft: Rocket engines are designed to propel and maneuver vehicles already in space. They are typically smaller and less powerful than the engines used for launch vehicles. Still, they must be highly reliable, efficient, and versatile to enable the spacecraft to travel long distances and perform complex missions.
3. Missiles: Rocket engines used in missiles typically operate on solid propellant and are designed to provide the speed and maneuverability required to deliver warheads or other payloads to their targets. Missiles must be highly precise and reliable, and may be required to operate under various flight conditions and environments.
4. Miscellaneous: There are other applications for rockets, including suborbital flights, scientific experiments, and recreational activities such as model rocketry. These types of rocket engines may have specialized requirements depending on their specific use.

Rocket Propulsion Fundamentals

In a rocket engine, the propellants, i.e., a fuel and an oxidizer, undergo combustion at high pressures and temperatures to produce the necessary thrust. Notice that, unlike an air-breathing engine, the oxidizer must be carried along with the fuel for a rocket engine. A practical way to liberate large amounts of energy rapidly is through combustion, which creates a high-speed gas flow that can be expanded through a nozzle to a high Mach number, producing high thrust. An example of a rocket engine operating at full thrust is the solid-propellant booster shown in Figure 1. Other types of rocket engines can use liquid propellants (fuel and oxidizer) or a hybrid liquid/solid propellant.

A rocket engine must be designed to withstand the combustion pressures and temperatures, while accounting for safety margins. The shape and length of the combustion chamber and exit nozzle are essential design parameters for a rocket engine. The combustion chamber must be sufficiently long to ensure complete propellant combustion before the hot gases enter the nozzle, thereby optimizing combustion efficiency and maximizing thrust. The length of the combustion chamber is typically determined by several factors, including the propellant type, combustion efficiency, and the rocket engine’s overall performance characteristics relative to the mission profile.

Rocket engines operate at extremely high temperatures, usually between 2,500K and 3,500K. Therefore, the combustion chamber and nozzle must be actively cooled to dissipate the heat generated during combustion, thereby preventing overheating and structural failure. With liquid-fueled rocket engines, this process is accomplished by circulating cold fuel around channels or jackets within the walls of the combustion chamber and nozzle. The fuel absorbs the heat by conduction and convects it away, allowing the rocket to operate safely for extended periods. A byproduct is that more efficient combustion is obtained by preheating the fuel before it is combined with the oxidizer. In solid-fuel rocket engines, which typically operate for relatively short durations, the nozzle is made of high-temperature materials that can be ablatively cooled, i.e., the material sheds its surface in layers, carrying the absorbed heat.

Application of Conservation Principles

Newton’s second and third laws are fundamental physical principles that govern the operation of rocket propulsion systems. Consider a typical rocket engine, as shown in Figure 2. The principle of thrust generation in a rocket engine is based on the reaction force associated with accelerating a mass of gases to high velocity through an expansion nozzle. The gases are byproducts of the combustion of the fuel and the oxidizer, which increase their kinetic energy and momentum. Consequently, the gases and products of combustion are accelerated in one direction, and the resultant force on the rocket engine and the vehicle to which it is attached is directed in the opposite direction, per Newton’s third law.

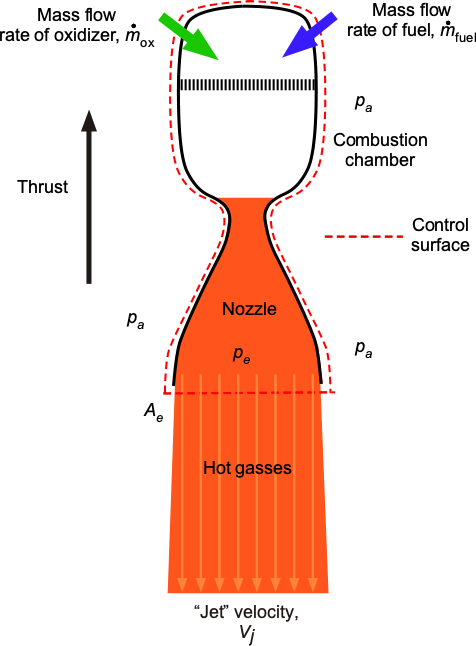
If the flow is assumed to be steady, compressible, and inviscid, then the general form of the momentum equation is

(1)  

The pressure integral on the left-hand side can be written as a sum over the relevant control surface, i.e.,

(2)  

Because the throat area is much smaller than the exit area, the pressure integral at the throat can be neglected relative to the other terms.

The force on the fluid to change its momentum, which by Newton’s 3rd law is in the opposite direction to the thrust, . Therefore, the momentum equation becomes

(3)  

If the flow is assumed to be one-dimensional, which is a reasonable approximation for a rocket nozzle, then the thrust produced by the rocket engine is

(4)  

where is the exit pressure at the nozzle, is the ambient pressure, is the exit area, is the exit or jet velocity, and is the propellant mass flow rate. The first term represents the momentum flux of the exhaust gases, and the second term represents the net pressure force acting on the exit plane. Remember that there is no external air mass flow into a rocket engine, i.e., there is no freestream velocity as with an air-breathing engine.

If , the pressure force term is zero, and the nozzle is said to be ideally or optimally expanded; this condition is a design goal for a rocket engine. For a rocket operating near this condition, the time rate of change of momentum is much larger than any pressure force, i.e., . For performance comparisons, it is often convenient to define an equivalent exhaust velocity such that

(5)  

where

(6)  

The quantity incorporates the pressure term into an equivalent velocity. In general, , but they become equal when .

Nozzle Shape

The nozzle is designed to accelerate the high-pressure, high-temperature gases generated in the combustion chamber to a supersonic exit velocity. As shown in Figure 3, the nozzle typically consists of two sections: convergent and divergent. The resulting shape is often referred to as a nozzle bell. The convergent section narrows the flow area, increasing the gas velocity as it passes through and accelerating it to sonic conditions at the throat.

The convergent section then transitions to the throat, the nozzle’s narrowest part. Beyond the throat, the divergent section widens, allowing the supersonic gases to expand and accelerate to their final velocity, . Ideally, this expansion continues smoothly until the hot gases reach the nozzle exit. Therefore, the nozzle design, including the length and shape of the divergent section, is critical to achieving optimal thrust performance in the rocket engine. The nozzle must be sufficiently long and the exit area sufficiently large so that the exit pressure is close to the ambient pressure outside the nozzle, which maximizes thrust.

The optimum nozzle contour is determined by shaping the wall so that the expanding gases are turned smoothly and leave the nozzle with nearly uniform, parallel velocity. In practice, this process yields the familiar bell-shaped nozzle, as shown in Figure 4, which achieves higher efficiency than a conical nozzle while requiring less length. This reduction in length is important for minimizing structural weight while maintaining high performance.

The nozzle contour can be described approximately in terms of the variation of the radius, , with axial distance from the throat. For a simple conical nozzle, the wall is defined by a constant divergence angle , so that

(7)  

where is the throat radius. While this geometry is straightforward, it causes the exhaust flow to leave the nozzle at a finite angle, resulting in a loss of thrust because the velocity is not fully aligned with the axial direction. In contrast, bell-shaped nozzles use a smoothly varying contour to turn the flow more gradually. In practice, the nozzle is often approximated using curved segments, for example, by a quadratic or parabolic form such as

(8)  

where the coefficients are chosen to satisfy geometric constraints at the throat and exit, including the wall angles and the required exit area.

Exhaust Gas Velocity

As combustion gases enter a nozzle, they initially travel at subsonic velocities. As the nozzle’s cross-sectional area contracts toward the throat, the gas is forced to accelerate until its velocity reaches sonic speed there, where the cross-sectional area is smallest. Downstream of the throat, the cross-sectional area increases again in the diverging section of the nozzle, allowing the gas to expand and accelerate to progressively higher supersonic velocities. This acceleration process converts thermal energy into directed kinetic energy, producing thrust.

Thermodynamic principles can be used to derive an expression for the exhaust velocity. The approach utilizes energy conservation, assuming isentropic, compressible flow. The exhaust velocity is given by

(9)  

where is the exit pressure, is the chamber or combustion pressure, is the ratio of the specific heats of the propellant gas, is the universal gas constant,^[2] and is the relative molecular mass of the propellant. Because the residence time in the chamber is short and the flow is well mixed, the chamber (stagnation) temperature can be treated as approximately uniform, i.e., constant. Equation 9 assumes the expansion through the nozzle is adiabatic and reversible (isentropic) and that the exhaust gases behave as an ideal gas. The nozzle accelerates the gas by converting internal thermal energy into kinetic energy, thereby maximizing the exhaust velocity and producing thrust.

For in-space operations, i.e., in a vacuum where , Eq. 9 may be approximated by

(10)  

where

(11)  

If the combustion temperature is expressed in Kelvin and in kg/kmol, then from Eq. 10 is obtained directly in m/s. For typical rocket exhaust gases with to 1.30, this constant leads to exhaust velocities of order 2–4 km/s.

Typical values of for different types of rocket propellants range from approximately 1,700 to 2,900 m/s for liquid monopropellant engines, 2,900 to 4,500 m/s for liquid bipropellant engines, and 2,100 to 3,200 m/s for solid propellant rocket engines. These values are consistent with experimental data and operational rocket engines. For example, consider combustion gases with a chamber pressure of = 7.0 MPa, an exit pressure of = 0.1 MPa, a combustion temperature of = 3,500 K, = 1.2, and = 22. Substituting these values into the exhaust velocity equation yields an exit velocity of 2,800 m/s, which is consistent with typical solid and bipropellant engine performance.

Nozzle Efficiency

Designing rocket engines for launch vehicles to operate efficiently across a wide range of atmospheric altitudes is a significant engineering challenge that requires careful consideration of multiple factors. These factors include the nozzle’s shape and size, materials, propellant flow rate, fuel and oxidizer combustion characteristics, and the cooling system(s). Designers aim to achieve optimal performance of the rocket engine across the entire altitude range of a rocket’s atmospheric flight, thereby maximizing thrust and efficiency. Rocket engines must also be optimized for efficiency in the vacuum of space.

When the exhaust pressure at the nozzle exit equals the ambient pressure, the expansion is referred to as ideal or optimum expansion, as illustrated in Figure 5. In this ideal state, there is no pressure gradient, and all exhaust gases are directed away from the engine. This situation results in the maximum thrust because nearly all the exhaust gas’s momentum is converted into thrust. This operating condition enables rocket engines to achieve their maximum performance in thrust and efficiency. However, achieving optimal expansion requires careful design and optimization of the bell’s shape.

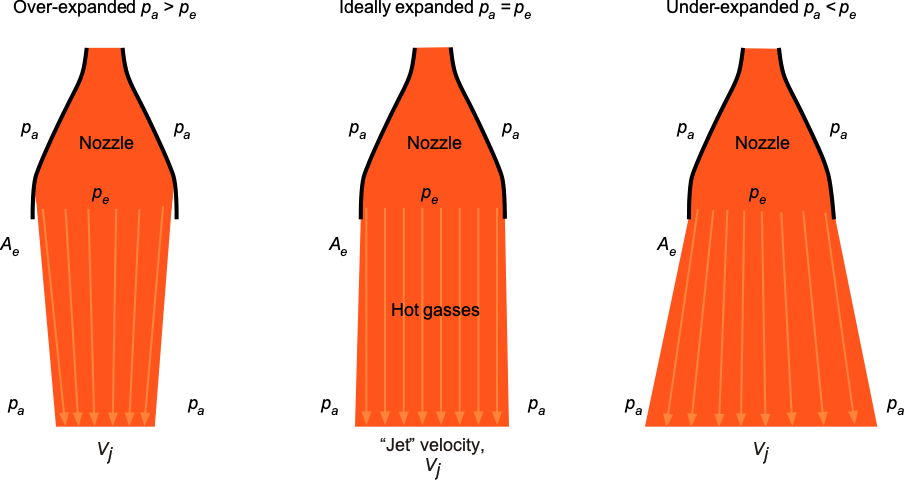
Over-expansion means that the external (atmospheric) pressure, , is higher than the exit pressure, . When an overexpanded flow passes through the nozzle, the higher external pressure at the exit produces a positive (or adverse) pressure gradient that slows the jet, and the jet subsequently converges as it exits the nozzle. The pressure difference may be sufficient to cause flow separation from the nozzle walls. Overexpansion of the gas flow reduces the engine’s thrust and efficiency. The solution, in this case, is to use a shorter bell.

The opposite situation, in which atmospheric pressure is lower than exit pressure, is called underexpanded; in this case, the flow continues to expand outside the nozzle. In this case, the flow continues to expand outward after exiting the nozzle, so this process does not contribute to thrust. The solution for thrust recovery in this case is a larger, longer bell. When designing rocket engines for launch vehicles that must operate in the atmosphere, the nozzle may be designed for slight overexpansion at sea level, recognizing that the exhaust pressure at the nozzle exit will likely be lower than the ambient air pressure. This design approach can better optimize the rocket engine’s performance across a broader range of the launch profile, thereby maximizing overall thrust and efficiency throughout the atmosphere.

Many rocket engines, including the Merlin used in the Falcon 9, feature a nozzle designed to operate efficiently across a wide range of altitudes, from sea level to the stratosphere, where pressure is exceptionally low (see Figure 6). The RS-25 engines, first used in the Space Shuttle program, were optimized for sea-level operation during the launch’s initial phase and then transitioned to vacuum-optimized operation. To this end, the RS-25 engine has a movable nozzle extension to optimize its performance. When rocket engines operate at sea level, the nozzles are typically designed to produce a slightly overexpanded condition, allowing them to become more ideally expanded at higher altitudes.

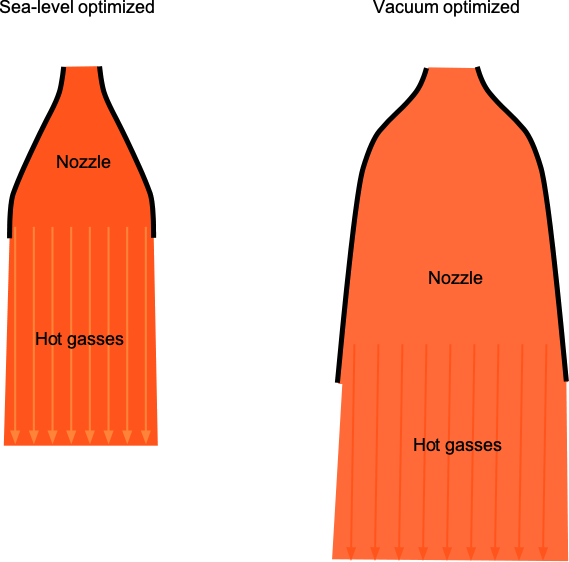
Second- or upper-stage “vacuum-optimized” rocket engines have significantly larger nozzles than those used on sea-level (or atmospheric) optimized engines. The Merlin second-stage engine is a good example. The second stage, the “vacuum-optimized” Merlin, employs the largest practical nozzle to achieve ideal exhaust-gas expansion. The vacuum-optimized Merlin engine features a larger exhaust section and a significantly higher expansion nozzle ratio of 165:1, compared to the sea-level-optimized version, which has a smaller 16:1 expansion nozzle ratio. The larger nozzle enables more ideal, more efficient expansion of the exhaust gases in the vacuum of space, thereby maximizing propulsive thrust and efficiency.

Supersonic Flow Through a Rocket Nozzle

The flow through a rocket nozzle can now be explained in greater detail. In the aerodynamic and thermodynamic analysis of the nozzle, the flow is assumed to pass through three primary regions, as shown in Figure 7: (i) a converging section where subsonic flow is accelerated, (ii) a throat where the flow becomes sonic or choked, and (iii) a diverging or “bell” section where the flow rapidly expands to supersonic velocities. This convergent-divergent nozzle is commonly referred to as a De Laval nozzle after Gustaf de Laval, which was first applied to a rocket by Robert Goddard. Again, the flow is governed by the conservation of mass, momentum, and energy, along with the assumption of isentropic, one-dimensional behavior of an ideal gas.

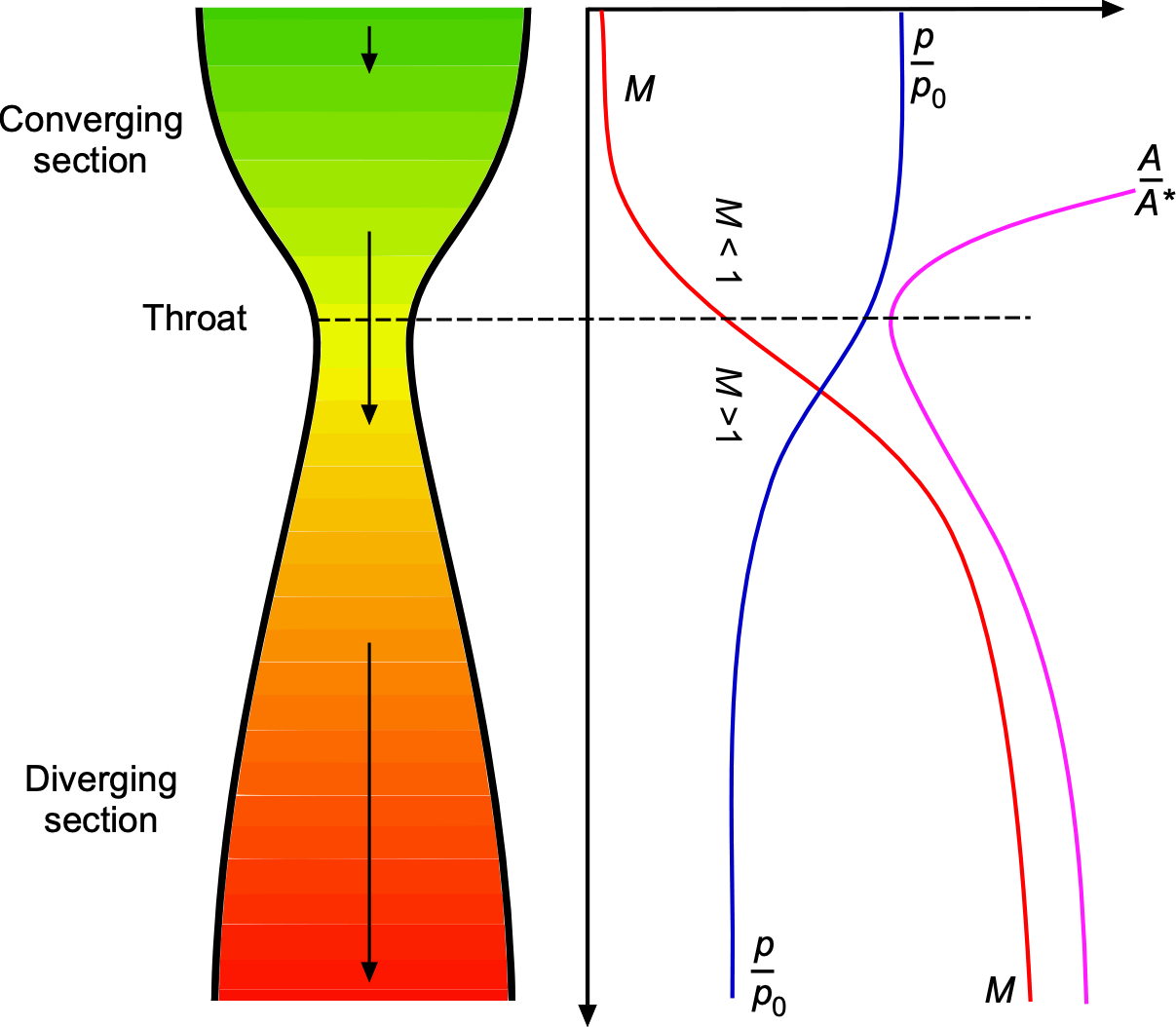
To describe the flow in such a nozzle, several gas-dynamic relations can be used. The area-Mach number relation is given by

(12)  

where is the area at the sonic throat, is the local Mach number, and is the specific heat ratio. This equation determines the Mach number as a function of cross-sectional area and is fundamental to nozzle design.

The thermodynamic quantities also vary with Mach number. The ratio of static to stagnation temperature is given by

(13)  

and the corresponding pressure ratio is

(14)  

The velocity of the flow at any point in the nozzle can be derived from the energy equation. At the exit of the nozzle, where the Mach number is supersonic, the exit velocity is given by

(15)  

where and are the stagnation temperature and pressure in the chamber, respectively, is the exit pressure, and is the gas constant.

When the flow is choked at the throat, i.e., when at , the mass flow rate through the nozzle is fixed and can be expressed as

(16)  

As previously discussed, the total thrust produced by the nozzle consists of two components, i.e., the momentum thrust and the pressure thrust. Therefore, the total thrust is

(17)  

where is the nozzle exit area and is the ambient pressure.

Recall that if the exit pressure equals the ambient pressure, the nozzle is said to be ideally expanded, corresponding to optimum expansion for the given operating condition. If the exit pressure is below the ambient pressure, the flow is overexpanded, which may lead to internal shocks or flow separation. Conversely, if the exit pressure exceeds the ambient pressure, the flow is underexpanded and continues to expand outside the nozzle. Both overexpansion and underexpansion result in a loss of thrust-producing efficiency, as previously explained. These relations form the basis for analyzing the performance of rocket nozzles under both ideal and off-design conditions.

Thermodynamic Process of a Rocket Engine

A rocket engine operates on a fundamentally different thermodynamic principle than an air-breathing engine. In particular, it does not ingest atmospheric air, so it does not follow any of the classical thermodynamic cycles. Instead, it is best described as a steady-flow, open thermodynamic process in which chemical energy is converted directly into kinetic energy of the exhaust. The operation of a rocket engine may be idealized as consisting of two primary processes: (i) energy addition by combustion and (ii) expansion through a nozzle, followed by discharge of the working fluid to the surroundings.

On a – diagram (Figure 8), the rocket process consists of a large temperature increase during combustion, followed by an approximately isentropic expansion through the nozzle. On a – diagram, combustion occurs approximately at constant pressure (nearly isobaric), followed by a rapid expansion to a lower pressure at the nozzle exit. Although the rocket process shares some superficial similarities with the Brayton cycle, it lacks both a compressor and a turbine, and there is no recirculation of the working fluid; energy is converted into kinetic energy rather than shaft work.

Fuel and oxidizer are injected into a combustion chamber, where they react to produce a high-temperature, high-pressure gas. For a steady-flow device, this process occurs almost isobarically, so that constant. The combustion process raises the stagnation enthalpy of the flow to a value , corresponding to the chamber temperature . The high-energy gas then expands through a converging-diverging nozzle, as previously explained. Ideally, this expansion is isentropic, i.e., = constant. In practice, viscous and non-equilibrium effects introduce irreversibilities, so the expansion is not perfectly isentropic and the line on the – diagram is not perfectly vertical. During this process, the stagnation enthalpy is converted into directed kinetic energy of the exhaust stream. Applying the steady-flow energy equation gives

(18)  

where and are the static enthalpy and velocity at the nozzle exit, respectively. The exhaust velocity, given by Eq. 15, depends primarily on the chamber temperature and the pressure ratio across the nozzle. The working fluid is discharged to the surroundings and is not recirculated, so the rocket operates as an open system. The thrust is obtained from the momentum and pressure of the exhaust using Eq. 17.

Types of Rocket Engines

In practice, rocket engines are further classified by how the propellants are pressurized and delivered to the combustion chamber. For example, gas-generator, staged-combustion, and expander processes differ in how they drive turbopumps and manage energy internally. These variations affect overall efficiency and achievable chamber pressure, but they do not change the fundamental thermodynamic process of combustion followed by expansion through a nozzle. Like all propulsion systems, rocket engines convert energy into thrust. The kinetic energy of the expelled propellant (hence the eventual gain in kinetic energy of the vehicle) comes from:

1. Pressurizing the propellant-feed system or storing pressure energy in the tanks.
2. Liberating the chemical potential energy of a fuel and an oxidizer.
3. An electrical or thermal power supply.
4. Some combination of these latter methods.

Rocket engines can be broadly categorized by thrust and thrust-to-weight ratio. Rocket propulsion systems are selected according to mission objectives. There is no single solution that fits all, and multiple rocket propulsion systems can be used for a given space mission. As shown in Figure 9, there are two primary types: liquid-propellant rockets and solid-propellant rockets. The latter type is often used as a secondary booster. Another type, the hybrid rocket engine, is considered later.

High-Thrust Propulsion Systems

High-thrust systems are used to overcome gravity, as in a planetary launch vehicle, or to accelerate a vehicle already in space, as in an orbital ejection maneuver. These systems store energy in the propellant, enabling high-rate conversion that is roughly proportional to the propellant flow rate.

Bipropellant Systems

Bipropellant propulsion systems typically come to mind when considering rocket propulsion; one imagines flames and smoke clouds, as during a NASA Space Shuttle or SpaceX Falcon 9 launch. The propellant is the combustion product of a fuel and an oxidizer. Combustion is generally the fastest way to convert chemical energy into kinetic energy. Bipropellant systems are classified into three main types: gas/liquid propellant systems, solid propellant systems, and hybrid solid-fuel/oxidizer systems.

Gas/Liquid Systems

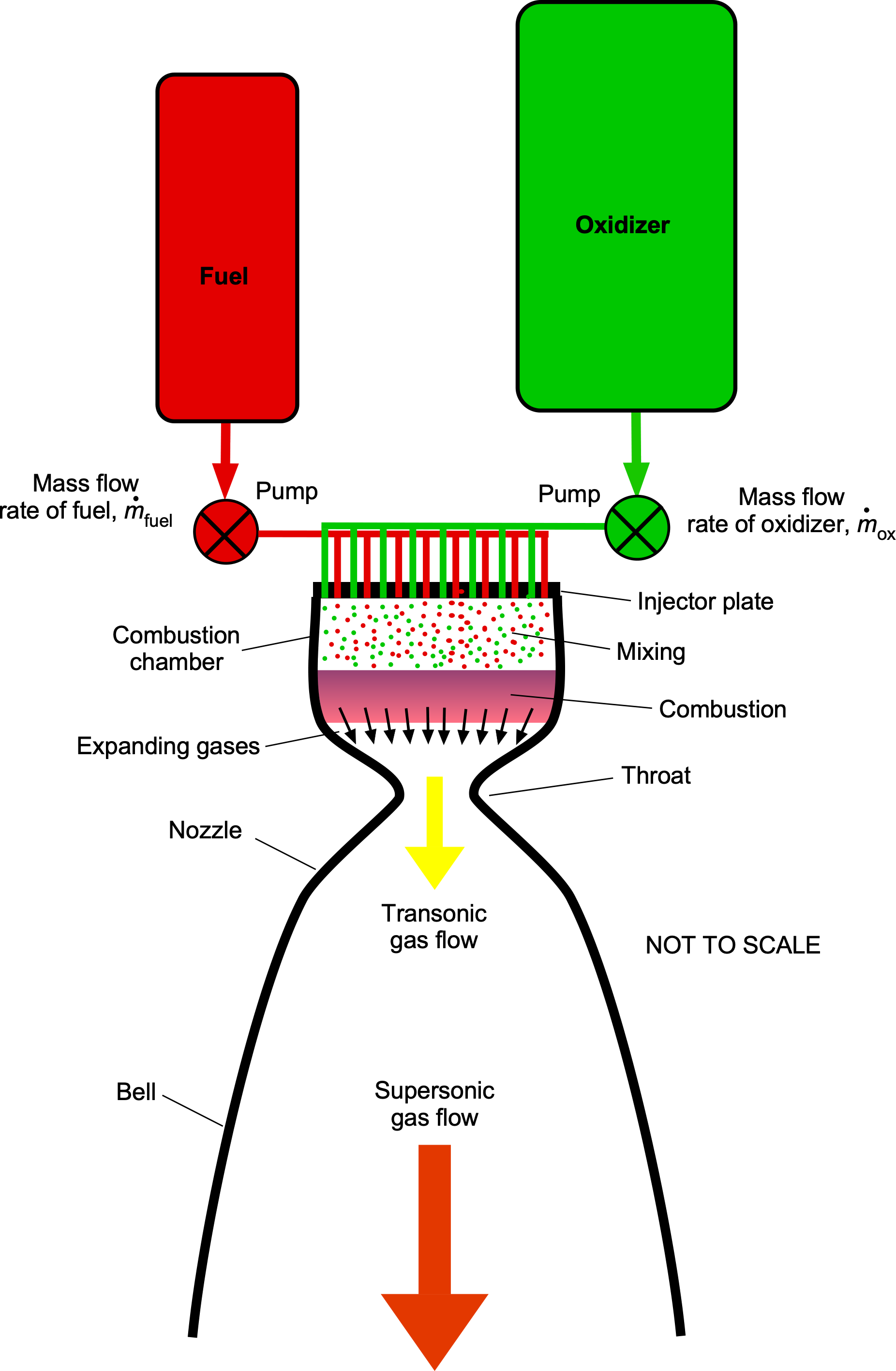
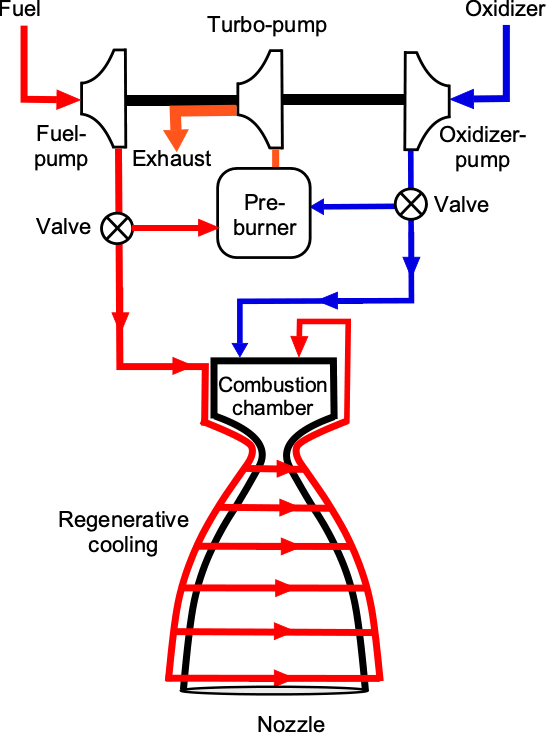
Examples of this type of propulsion system include the Space Shuttle main engine (SSME), which burned liquid hydrogen (LH₂) and liquid oxygen (LOX), and the Merlin engine used on the SpaceX Falcon 9, which burns Rocket Propellant-One or RP-1 (a densified kerosene) and LOX, the combination often being called Kerolox. The process of mixing the fuel and oxidizer in the engine is shown in Figure 10. The enormous volumetric flow rates require turbo-pumps driven by burning a small quantity of fuel and oxidizer tapped off a bypass circuit.

As shown in Figure 11, a Saturn V rocket launched Apollo 11, the first mission to land humans on the moon, and lifted off from Kennedy Space Center in July 1969. The first stage of the Saturn V rocket used five F-1 engines. These engines burned RP-1 fuel with liquid oxygen (LOX) as the oxidizer. The F-1 engine was the most powerful single-nozzle liquid-fueled rocket engine ever flown. The second stage used five J-2 engines, with propellant consisting of liquid hydrogen (LH) and liquid oxygen (LOX). The J-2 engine was designed to provide efficient propulsion at higher altitudes and in space. The third stage of the Saturn V rocket used one J-2 engine, which also powered the trans-lunar injection maneuver, setting the spacecraft on a course toward the Moon.

Liquid methane (CH₄) is gaining popularity for use in commercial rocket engines because of its availability, moderate cost, and good performance. It is also more environmentally benign than RP-1, which produces numerous toxic byproducts. One advantage of a gas/liquid system is that the engine can be throttled by regulating the fuel flow. However, this capability comes at a price, including the complexity and associated weight of pumps, valves, pipes, and cryogenic fuel tanks. Hypergolic propellants are those that combust spontaneously upon contact with one another. These propellants are used for in-space applications rather than for launch vehicles, partly because their performance is much lower than that of hydrocarbon and LOX, or RP-1 and LOX, systems. On the one hand, these chemicals are highly toxic. On the other hand, their advantages include reliability, simplicity (as no ignition system is required), and ignition speed. For example, the Apollo lunar lander used hydrazine (NH) and dinitrogen tetroxide (NO), as did the Space Shuttle reaction control system (RCS).

Solid Fuel Systems

Solid-fuel systems are widely used in both space launch vehicles and military applications because of their simplicity, reliability, and rapid response capability. The Space Shuttle solid rocket boosters (SRBs) are a prominent example of solid-propellant use in orbital launch. Solid propellants are also widely used in military systems, such as air-to-air and surface-to-air missiles, and in intercontinental ballistic missiles (ICBMs), where the ability to store a fully fueled rocket for extended periods and launch on short notice is critical. Solid-fuel systems require minimal pre-launch preparation and, once ignited, deliver high thrust without complex fueling, pressurization, or ignition sequences.

A typical solid-fuel formulation is a composite comprising a finely powdered metallic fuel, a chemical oxidizer, and a polymeric binder. Aluminum (Al) powder is the most common fuel component, chosen for its high energy density and high combustion enthalpy.^[3] Magnesium (Mg) is sometimes used in specialized applications. The most common oxidizer is ammonium perchlorate (AP), although ammonium nitrate (AN) is occasionally used where lower energy performance or lower sensitivity is acceptable. The binder provides structural integrity to the propellant grain and often serves as an additional fuel source during combustion. Typical binders include hydroxyl-terminated polybutadiene (HTPB) and polybutadiene acrylonitrile (PBAN). The Space Shuttle SRBs employed a propellant mixture of powdered aluminum and AP with PBAN as the binder.

The propellant mixture is cast or extruded into a rigid cylindrical structure known as the propellant grain, which is enclosed within a casing. The internal geometry of the grain is designed to control the surface area exposed to combustion and tailor the thrust-time profile. Standard grain configurations include cylindrical, star-shaped, or multi-fin geometries that provide controlled burn-surface evolution as the propellant is consumed. Depending on mission requirements, grain designs can achieve neutral, progressive, or regressive thrust profiles.

Ignition is achieved using an internal igniter, typically a small pyrotechnic charge, which initiates combustion at the center of the grain surface. Upon ignition, combustion gases expand and pressurize the casing. The casing is engineered to withstand the high internal pressures generated during combustion and is typically constructed from steel, aluminum alloys, or composite materials to reduce weight. An internal liner is often applied between the propellant and the casing wall to insulate the casing from high temperatures and prevent direct combustion erosion. Hot combustion gases are accelerated through a nozzle located at the aft end of the rocket. The nozzle of a solid-fuel rocket is typically made of heat-resistant materials, often with ablative liners or graphite inserts.

Solid rockets have critical operational characteristics. Once ignited, they cannot be throttled, shut down, or restarted. Combustion continues until the propellant is exhausted. While this limits mission flexibility compared to liquid-fueled systems, solid-fuel rockets offer significant advantages in simplicity, reliability, storage life, and high initial thrust-to-weight ratios.

Hybrid Systems

Hybrid systems utilize a solid fuel and a gaseous or liquid oxidizer, or, rarely, the reverse, as illustrated in Figure 12. Experimentalists, amateur rocket builders, and small rocket companies favor hybrids because they are relatively inexpensive and straightforward to construct. Unlike solid propellants, they can be throttled and switched on and off.

It is often argued that hybrid systems are safer than solid-propellant or liquid-propellant systems. However, this is only partially correct, as the rocket’s propellant still comprises the same fuel and oxidizer. Nevertheless, solid fuel is more stable because it is not pre-mixed with an oxidizer, allowing it to be stored safely and to have a longer shelf life. Typical oxidizers used in hybrid rockets are gaseous oxygen (O), nitrous oxide (NO), and hydrogen peroxide (HO).

Hybrid rocket engines, however, have not found many applications in commercial space because they have no performance advantage, i.e., they have relatively modest values in terms of thrust-producing efficiency, and designing for optimal performance is tentative and error-prone (i.e., trial and error). A notable exception is SpaceShipOne, which by design uses HTPB and NO.

Experimentalists and amateur rocket builders often use polyvinyl chloride (PVC) or acrylonitrile butadiene styrene (ABS) as a solid fuel because these materials are readily available and inexpensive. Nitrous oxide (NO), also known as “Nitrous,” can be used as an oxidizer with several fuels and is popular in hybrid rockets. Nitrous oxide is readily available at modest cost from automotive stores for use in high-performance race car engines, enabling the engine to burn more fuel and produce more power by providing more oxygen during combustion. NO is also used in medicine as a mild anesthetic, known as “laughing gas.”

Monopropellant Systems

Monopropellants do not burn; they decompose exothermically in the presence of a catalyst. Monopropellant engines generate thrust by propellant flowing through a valve into a catalytic decomposition chamber, where the propellant undergoes a highly energetic decomposition process. The hot gases then accelerate through a nozzle, as shown in Figure 13. These thrusters typically provide thrust levels of up to approximately 3,000 N (674 lb).

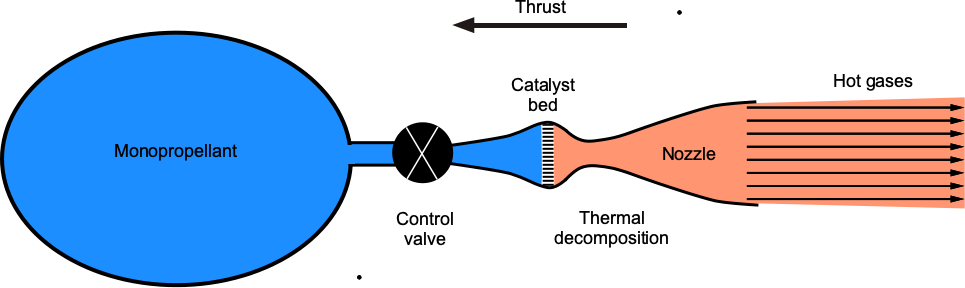
Hydrogen peroxide (H₂O₂) is often used in monopropellant engines because it decomposes into water and diatomic oxygen upon contact with many metal oxides, particularly silver oxide. An H₂O₂ system propelled the Apollo lunar lander trainer. However, hydrazine (N₂H₄₎ has been used more extensively because of its higher performance and ease of reaction initiation. The rocket engine on the New Horizons spacecraft is an N₂H₄ monopropellant system.

Cold Gas Thrusters

Cold gas thrusters are rocket engines that use compressed gas, typically nitrogen or helium, as a propellant. They release the pressurized gas through a nozzle to generate thrust, as shown in Figure 14. Because they do not involve combustion, cold-gas thrusters have a relatively low specific impulse, meaning they deliver less thrust per unit of propellant than other rocket engines. Their simplicity makes them less efficient and powerful than monopropellant or bipropellant engines.

Cold gas thrusters are commonly used for small spacecraft or subsystems that require small, precise movements or adjustments. They are appropriate for CubeSats, nanosats, and small spacecraft attitude control. Any gas can be used as a propellant, but those with lower molecular weights, such as hydrogen (H2), nitrogen (N2), and helium (He), will perform better.

Check Your Understanding #3 – Nitrogen or helium?

You attend an interview with Space Y. During the interview, they ask you whether nitrogen or helium is better for a cold-gas thruster to control the new versions of their StarCom satellites, and why. What is your response?

Show solution/hide solution.

You first explain that helium and nitrogen offer distinct advantages and trade-offs for cold-gas thrusters. You write down and demonstrate that the thrust produced by the thruster will be

   

where is the propellant mass flow rate, and is the exhaust (exit) velocity. Therefore, for a given propellant mass flow rate, the thrust produced will be related to the achievable exhaust velocity, but every AE graduate knows that, so you are not ahead of the game.

However, they begin to get impressed when you go on to say that the best propellants are those with low molecular mass, which give higher values of specific impulse. To compare the potential exhaust velocities of two gases, note that for an ideal-gas expansion at a constant temperature, the exhaust velocity scales approximately as

   

so that

   

If one neglects the (smaller) effect of and compares only molecular mass, then

   

Fortunately, you recall from your chemistry classes that helium () has a relative molecular mass of approximately 4, and nitrogen () has a relative molecular mass of approximately 28. Therefore, you write down that

   

You then explain that this result indicates helium will exhaust at approximately 2.65 times the speed of nitrogen because of its lower relative molecular mass. You add that helium also has a higher value of than nitrogen, so including the factor increases the ratio slightly above 2.65. Therefore, using helium will produce approximately 2.65 times (slightly more) the thrust for a given propellant mass flow rate.

But you are not done! You explain that on the one hand, for the same total propellant mass, , helium will require seven times the volume of nitrogen at the same pressure and temperature. On the other hand, to obtain the same total impulse from the thruster, the required propellant mass scales as , so only about 2.65 times less helium mass is needed than nitrogen to obtain the same total impulse, i.e., to get the same value of , where

   

Consequently, the storage-volume penalty for helium at the same pressure and temperature is reduced to about a factor of 2.65 when comparing equal total impulse.

To clinch the job, you finally explain that helium is more expensive and harder to store because of its small molecules and higher leakage rate, and that it may require more careful tank and regulator design. In contrast, nitrogen is much cheaper, more readily available, and easier to handle. Therefore, nitrogen gas is often chosen for thrusters with moderate performance requirements. Ultimately, you say the choice between the two gases will be mission-specific, balancing performance, storage volume, and cost.

Congratulations!

High-Efficiency Propulsion Systems

In high-efficiency systems, energy is not stored in the propellant; it is generated on board. Therefore, the energy conversion rate is not proportional to the propellant flow rate; instead, it is limited by the power supply system’s capability. For example, solar panels or nuclear power plants can generate electrical or thermal power. Assuming the energy supply rate (power) to the propellant is fixed, a lower propellant flow rate will yield higher efficiency but lower thrust, which is insufficient for use as a launch vehicle. High-efficiency systems are then used for long-duration missions to deep space or to raise satellite orbits.

In each case, this propulsion system need not oppose gravity directly (i.e., “lift” the spacecraft). However, it increases its velocity gradually once the spacecraft is in space. The simplest system heats the propellant gas, which then expands rapidly through a nozzle. A solar thermal system collects and focuses sunlight onto the propellant flow path. A thermal-electric system heats the gas using a resistive element or an electric arc. In other systems, electrical power is used to ionize the propellant gas, producing an electric and/or magnetic field, after which the charged particles are accelerated. Several configurations exist for such systems, including ion, Hall-effect, and magnetoplasmadynamic thrusters.

Electric rocket engines, such as ion thrusters and Hall-effect thrusters, are becoming increasingly attractive for spacecraft applications. These engines produce relatively low thrust but are highly efficient, sustaining thrust for extended periods, making them well-suited for deep-space missions.

Total Impulse & Specific Impulse

Establishing a rocket engine’s thrust and efficiency characteristics requires some quantitative performance measures. The total impulse is defined as the integral of thrust over the engine’s burnout time, i.e., the time during which the engine operates. The efficiency measure used in most rocket performance calculations is specific impulse, defined as thrust divided by propellant flow rate. Generally, the goal is to carry as little propellant as possible. The specific impulse depends on the propellant’s chemical composition and the engine operating conditions, and can be evaluated through a thermodynamic analysis.

Impulse

The impulse is given by

(19)  

If and are constant, as is often a good approximation, then

(20)  

where is the mass of the propellant used. The total impulse, therefore, will be equivalent to the net momentum imparted to a rocket during the engine burn.

Specific Impulse

The specific impulse, , is

(21)  

where is the acceleration under gravity at sea level on Earth, which is used as a reference. Therefore, the higher the value, the more efficiently the rocket engine will produce thrust. It is further apparent using Eq. 5 that

(22)  

where it will be noticed that is measured in units of time (seconds). Therefore, the specific impulse is the total impulse (or change in momentum delivered) per unit weight of the propellant consumed. The value is dimensionally equivalent to the generated thrust divided by the propellant flow rate, expressed as fuel weight per unit of time. So, in some ways, it is equivalent to the inverse of the thrust-specific fuel consumption used by a jet engine.

Notice that if mass (in slugs or kilograms) is used as the unit of propellant, then the specific impulse has units of velocity. If weight (lb or N) is used, which is much more common, the specific impulse is measured in time units, typically seconds. Notice that these two definitions differ by a factor of . The higher the specific impulse, the less propellant is needed to produce a given thrust during a given time. Some propellants and their specific impulse values are shown in the table below. Although H₂/O₂ (LH₂/LOX) has the highest specific impulse, liquid hydrogen requires a much larger (volumetric) fuel tank than RP-1 and is also more expensive and more challenging to transport and store. Liquified methane is increasingly used as a rocket fuel, but it must be stored cryogenically, which introduces the same issues as liquid hydrogen (LH₂₎.

Thermodynamic Considerations

Rockets use combustion or chemical reactions to generate hot gases at very high temperatures. These gases are then expanded through a supersonic nozzle to achieve high exhaust-stream velocities. Rocket engines typically operate at combustion temperatures between 2,500 K and 3,500 K, and even then, only because regenerative cooling protects the combustion chamber and nozzle walls from melting under the extreme thermal loads.

The specific impulse can also be related directly to the thermodynamic properties of the combustion gases. From Eq. 9, the specific impulse is given by

(23)  

where is the absolute combustion temperature, is the molecular weight of the exhaust gas in kilograms per kilomole, is the combustion chamber pressure, and is the exhaust exit pressure.

Equations 10 and 23 show that achieving a high equivalent exhaust velocity and a high specific impulse requires maximizing the combustion temperature and minimizing the molecular weight of the exhaust products. The effect of the specific heat ratio on specific impulse is comparatively less significant than the effects of the combustion temperature and the mean molecular weight of the propellant gases.

To this end, the best-performing chemical propellant combination is liquid hydrogen (LH) and liquid oxygen (LOX). Liquid hydrogen has a relative molecular weight of , and liquid oxygen has ; when combusted together, they produce superheated steam (HO) with a molecular weight of approximately . For cold gas thrusters, inert gases such as helium and nitrogen are commonly used. Helium, with , and nitrogen, with , are both effective choices, although helium is preferred for its low molecular weight despite its lower availability and relatively high cost.

More About Specific Impulse

In SI units, thrust is measured in Newtons (N), and mass flow rate is measured in kilograms per second (kg/s). In USC units, thrust is measured in pounds (lb), a unit of force. Propellant flow rate is sometimes reported in pounds per second (lb/s), but strictly speaking, it should be expressed in slugs per second (slug/s) to maintain dimensional consistency. However, by convention, specific impulse in USC units is defined as thrust divided by the propellant’s weight flow rate, so that retains units of seconds without explicitly converting mass to slugs.

There are two ways to interpret the apparent discrepancy in USC units. Strictly, mass should be expressed in slugs, recognizing that 1 slug mass 32.17 lb of weight. Alternatively, by convention, is viewed as thrust divided by the weight flow rate, meaning the use of pounds per pound-per-second without adjusting for . In either case, specific impulse expressed in seconds provides a convenient normalized measure of exhaust velocity. Recall that the effective exhaust velocity is related to specific impulse by

(24)  

where is the effective exhaust velocity. If the fundamental thrust equation

(25)  

is used, then it follows that

(26)  

Specific impulse, therefore, provides a direct link between the thrust produced and the velocity at which propellant is expelled, scaled by gravitational acceleration to ensure consistent units in both SI and USC systems.

Altitude Dependence on Specific Impulse

A rocket engine’s specific impulse, , varies with altitude because of changing ambient pressure. As a rocket ascends, the surrounding pressure decreases, which alters the thrust produced and hence affects the specific impulse. The thrust produced by a rocket is given by the momentum equation, i.e.,

(27)  

where is the propellant mass flow rate, is the exhaust velocity at the nozzle exit, is the static pressure at the nozzle exit, is the local ambient pressure, and is the nozzle exit area. The second term represents the pressure thrust contribution, which increases as decreases.

Recall that the specific impulse is defined as

(28)  

where is the standard gravitational acceleration. Substituting the expression for thrust gives the altitude-dependent form of the specific impulse, i.e.,

(29)  

As the altitude increases and decreases toward zero, the pressure thrust increases and so does , as shown in Figure 15. Notice the much lower value of for the vacuum optimized engine at sea level, but this quickly changes at higher altitudes.

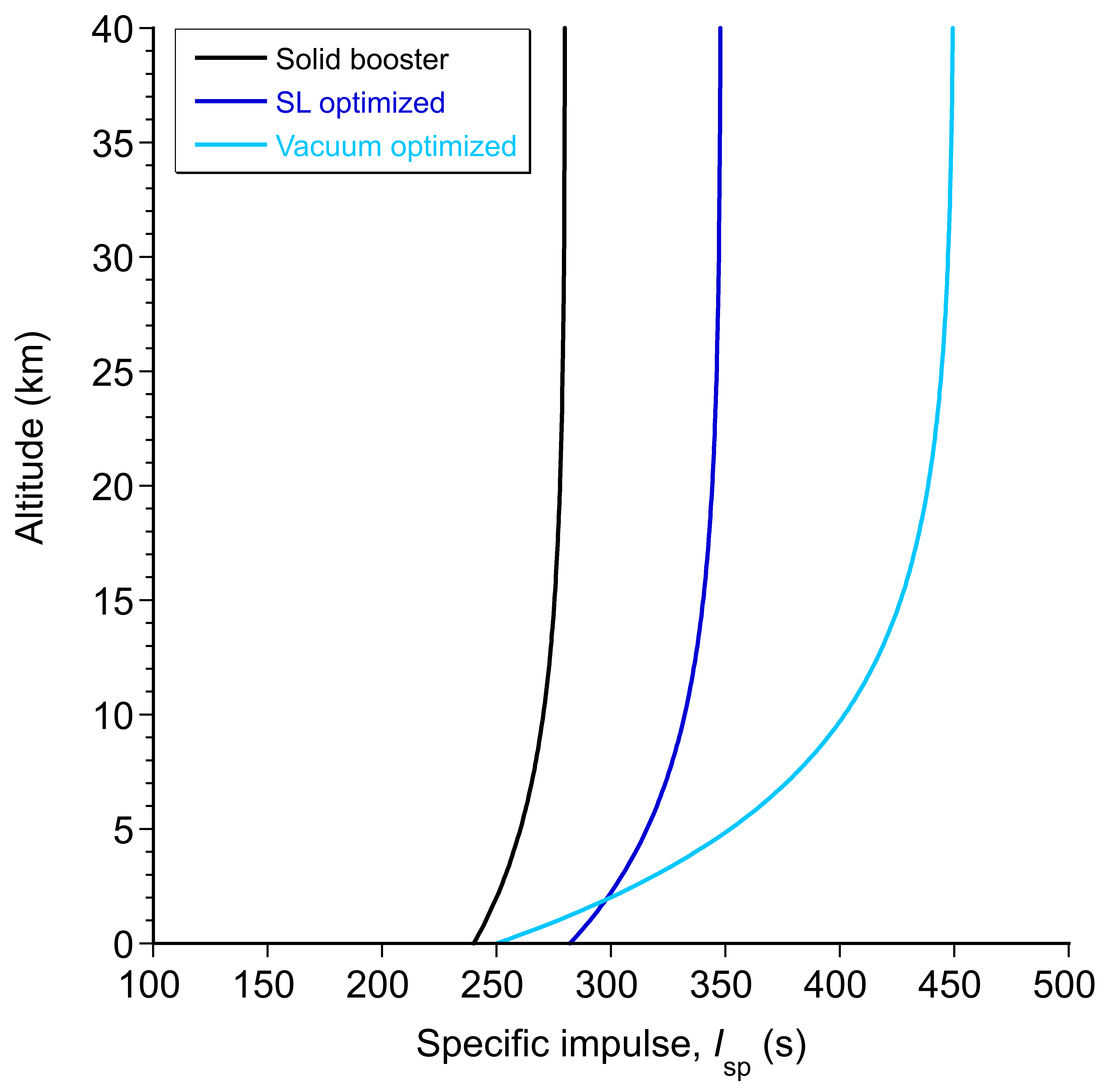
This outcome leads to two commonly cited values for specific impulse: at sea level, and in vacuum. The difference between them can be substantial, especially for engines with large nozzle expansion ratios. For example, a Merlin engine optimized for sea level operation has 282 s at sea level and 348 s in a vacuum. A vacuum-optimized engine such as the RL10 has 250 s at sea level and 450 s in a vacuum.

The increasing trend of with altitude reflects the role of ambient pressure in opposing the exhaust jet. Vacuum-optimized nozzles are typically underexpanded at low altitudes and reach optimal performance only in near-vacuum conditions. This nozzle design tradeoff is a key constraint in staging and mission architecture.

More About Solid-Fuel Rockets

With solid-fuel rockets, the thrust produced is not determined solely by the chemical composition of the propellant. Still, it is also critically influenced by the geometry and evolution of the burning surface, often referred to as the conflagration surface surface. The surface area available for combustion directly controls the rate at which the propellant mass is consumed. The instantaneous mass flow rate of combustion gases, , is proportional to the burning surface area, , and the regression rate, , of the propellant, which can be expressed as

(30)  

where is the density of the solid propellant, is the instantaneous burning surface area, and is the linear burn rate. The thrust generated by the rocket engine is then determined by the exhaust mass flow rate and the effective exhaust velocity according to the standard thrust (momentum) equation, i.e., . Therefore, an increase in burning surface area results in a higher mass flow rate and, therefore, a higher thrust.

In practical solid rocket engine design, the internal geometry of the propellant grain is shaped to control the burning surface area during combustion. The grain geometry determines whether the burning area remains approximately constant, increases, or decreases during the burn, thereby producing thrust profiles described as neutral, progressive, or regressive, respectively. For example, a grain designed for a neutral burn maintains nearly constant thrust over time, whereas a progressive burn profile increases thrust as the surface area grows.

A simple circular bore grain produces a progressive-regressive thrust curve, as shown in Figure 16. The thrust quickly increases and remains relatively constant as the surface area grows, but it eventually decreases as the burning surface area reduces near the end of the burn. An end-burner grain is characterized by a propellant that burns from one axial end face to the other. This configuration produces a steady, long-duration burn. However, end-burners pose thermal management challenges because the burning face remains stationary along the axis, leading to prolonged heating of the structure. Additionally, significant shifts in the center of gravity occur during the burn as mass moves steadily toward the nozzle, potentially complicating the launch vehicle’s stability and thrust vectoring response.

The C-slot grain features a wedge-shaped cutout along the propellant’s axial direction. This design produces a relatively long regressive thrust profile, where the thrust decreases over time as the burning surface area diminishes. However, C-slot grains also experience thermal issues from localized heating and an asymmetric center of gravity. The main advantage of an off-center circular bore is that it produces a progressive-regressive long-duration burn profile, allowing the overall thrust history to be tailored for favorable long-duration performance.

The finocyl grain, typically designed with a five- or six-pointed star-like structure, combines a cylindrical bore with internal fins. This configuration produces a relatively level thrust profile, with a slightly faster burn rate than a pure circular-bore design because of the fins’ increased initial burning surface area. Finocyl grains are often used when a balance between high thrust, efficient burning, and moderate burn duration is required.

Finally, it should be recognized that the burn rate itself is also dependent on the local chamber pressure and the propellant chemistry, typically following an empirical relationship of the form

(31)  

where is a burn rate coefficient that is dependent on the specific propellant formulation, is the local combustion chamber pressure, and is a semi-empirical exponent, usually ranging between 0.2 and 0.5 for most solid propellants. Therefore, the conflagration surface area, the regression rate, and the feedback between burning rate and chamber pressure collectively determine the thrust history of a solid rocket booster. The conclusion from the foregoing is that careful control of grain geometry and propellant characteristics is essential to achieve the desired thrust profile during flight.

Summary & Closure

Gas- or liquid-fuel rocket engines have been employed for many spaceflight applications, including most launch vehicles. Such systems are efficient and have the advantage that the engine can be throttled by regulating fuel flow, for example, to limit dynamic pressure loads on the vehicle during launch. However, this capability comes at a price, including mechanical complexity and associated weight. For some launch vehicles, the thrust from the liquid-fuel engines is augmented by solid rocket boosters, which can provide more than half of the initial thrust at liftoff, as in the Space Shuttle. Solid-fuel engines are also used on missiles and in other in-space applications. The lower performance and non-throttling characteristics of solid propellant engines are acceptable because of their operational simplicity, even though solid rocket boosters are by no means simple propulsion systems.

Since the dawn of human spaceflight in the 1960s, advances have continued to be made through improved propellants and rocket engine designs. Today, most space missions use a combination of engines and fuels selected to optimize thrust at each mission stage, including launch and in space. Rocket engines produce extremely high thrusts and operate near their safe limits, albeit for relatively short times. However, the reliability of rocket engines remains a concern, especially when they are recovered and reused to reduce launch costs. In addition, the environmental compatibility of rocket fuels has become a growing concern in recent years, and the shift toward alternative propellants, such as methane, will continue.