53 Flight Range & Endurance

Introduction

There are flight profiles and missions in which an airplane must either fly as far as possible (to maximize range) or remain airborne for as long as possible (to maximize endurance). In both cases, the critical factor is fuel availability, namely, the amount of fuel the aircraft can carry relative to its consumption rate. However, the usable fuel load is often limited by tank volume or by the maximum allowable fuel weight. In most airplanes, a trade-off exists between payload capacity (including passengers and cargo) and fuel capacity, as both contribute directly to the airplane’s total takeoff weight.

For example, long-haul commercial flights require a significant nonstop range. Transporting passengers and cargo across the Atlantic Ocean demands a flight range exceeding 3,700 nautical miles (6,850 km). In such cases, range takes priority over endurance. As of February 2025, the longest nonstop commercial flight is Singapore Airlines’ service from Singapore to New York. This route covers approximately 8,300 nautical miles (15,350 km), is scheduled to take 18 hours and 50 minutes, and is operated by an Airbus A350-900ULR with a capacity of 161 passengers. The actual flight range over the ground is also affected by wind, with headwinds reducing range and tailwinds extending it. Maximizing range while flying at high airspeed is essential for minimizing total flight time and requires careful route planning.

Conversely, some flight missions, particularly military operations, prioritize endurance. For example, a surveillance or reconnaissance mission may require an airplane to loiter over a specific area for an extended period. In some scenarios, military aircraft must optimize both range and endurance at different phases of the same mission. A maritime search-and-rescue operation exemplifies this requirement. A good flight range at the highest practical airspeed is needed to reach the search area, while good endurance is crucial for conducting a prolonged search. One example of an aircraft designed for endurance is the P-3K2 Orion, which can remain airborne for more than 15 hours. To conserve fuel, it can shut down two of its four engines during extended patrol operations.

Learning Objectives

  • Recognize the role of specific fuel consumption in fuel burn, flight endurance, and range.
  • Identify the optimal flight conditions for maximizing range or endurance.
  • Apply the appropriate Breguet equations to estimate endurance and range for both propeller and jet aircraft.
  • Calculate total fuel burn and interpret payload-range diagrams to assess aircraft performance.
  • Understand the effects of airplane aerodynamics and propulsion systems on an airplane’s range and flight speeds.

Fuel Flow & Specific Fuel Consumption (SFC)

Flight range and endurance depend on the amount of fuel that can be carried and the fuel flow rate, which, in turn, depend on the thrust or power produced by the engine(s) and on their other characteristics (e.g., thermodynamic and mechanical). The fuel flow or fuel burn rate is the volume (or, more typically, the mass or weight) of fuel burned by the engine(s) per unit of time. Remember that one metric used to measure an engine’s efficiency is its specific fuel consumption.

BSFC

For engines that deliver power to a shaft, such as those driving a propeller, the SFC is expressed as power-specific fuel consumption, or “brake” power-specific fuel consumption (BSFC). The BSFC is defined as the weight of fuel burned per unit power produced per unit time of operation, i.e.,

(1)   \begin{equation*} \mbox{BSFC} = \frac{\text{\small Weight~of~fuel~burned}}{ (\text{\small Unit power})\text{(\small Unit time~=~hour)}} \equiv \frac{\text{\small Weight of fuel burned per hour }}{\text{\small Unit power}} = \dfrac{\overbigdot{m}_f}{P} = c_b \end{equation*}

When delivering a given power output, an engine with a lower BSFC is more efficient because it consumes less fuel per unit of time.

In USC, then c_b has units of lb bhp^{-1} hr^{-1}, where “bhp” means “brake horsepower,” so this is the power in hp that can be delivered at the engine’s shaft.[1] In SI units, BSFC is often measured in kg kW^{-1} hr^{-1}; remember that in aviation, weight is usually calculated in units of kg although it is strictly a unit of mass; one can convert to Newtons (if needed) by multiplying by acceleration under gravity, g, where g = 9.81 m/s2 = 32.17 ft/s2.

TSFC

In jet engines, SFC is defined as thrust-specific fuel consumption (TSFC). The TSFC is defined as

(2)   \begin{equation*} \mbox{TSFC} = \frac{\text{\small Weight of fuel burned}}{ \text{(\small Unit thrust)(\small Unit time~=~hour)}} \equiv \frac{\text{\small Weight of fuel burned per hour }}{\text{\small Unit thrust}} = \dfrac{\overbigdot{m}_f}{T} = c_t \end{equation*}

The value of c_t also measures engine efficiency in converting fuel energy into useful thrust; the lower the TSFC, the more efficient the engine. For example, in USC units, the TSFC has units of lb lb^{-1} hr^{-1}; in SI units, the TSFC would be measured in units of kg kg^{-1} hr^{-1} or just hr^{-1}.

Notice that the reciprocal of the TSFC is measured in units of time, which is called the specific impulse I_{\rm sp}. Values of I_{\rm sp} are often given in units of seconds, so the higher the number of seconds, the more efficient the engine is in producing thrust. However, the TSFC is typically used for jet engines, while I_{\rm sp} is used for rocket motors.

Note on fuel weight and TSFC units.

Although TSFC can be interpreted to have units of “per hour” (hr^{-1}) or “per second” (s^{-1}), it is generally always quoted in units of lb lb^{-1} hr^{-1} or kg kg^{-1} hr^{-1}. Using the kilogram as a unit of weight is an anomaly in the SI system that can cause considerable confusion if not carefully addressed. Nevertheless, in aviation practice, fuel weight is almost always expressed in terms of pounds (lb) or kilograms (kg). Fuel density conversions are critical: Jet-A is about 0.8 kg/L, so 1 t \approx 1,250 L. For larger quantities, especially in airline operations, the metric tonne (1,000 kg) is commonly used. In the United States, however, fuel weights are typically expressed in pounds, and when the term “ton” is used, it usually refers to the short ton (2,000 pounds). This mixture of units across regions and systems is mainly historical, reflecting national conventions in aircraft certification and airline operations. Consequently, when working with performance data or fuel planning, it is essential to confirm the reference unit system to avoid numerical inconsistencies.

Variations in SFC

A complication in dealing with internal combustion engines (reciprocating or jet) is that BSFC or TSFC values are generally not constant and depend on the engine throttle setting. For jet engines, TSFC also depends on altitude and flight Mach number, as shown in Figure 1 for a modern turbofan (note that the TSFC scale exaggerates the differences). At any given flight condition, both thrust and specific fuel consumption (SFC) vary together with the throttle setting. When plotted on a thrust-versus-SFC graph, the data form a curve known as a thrust hook.

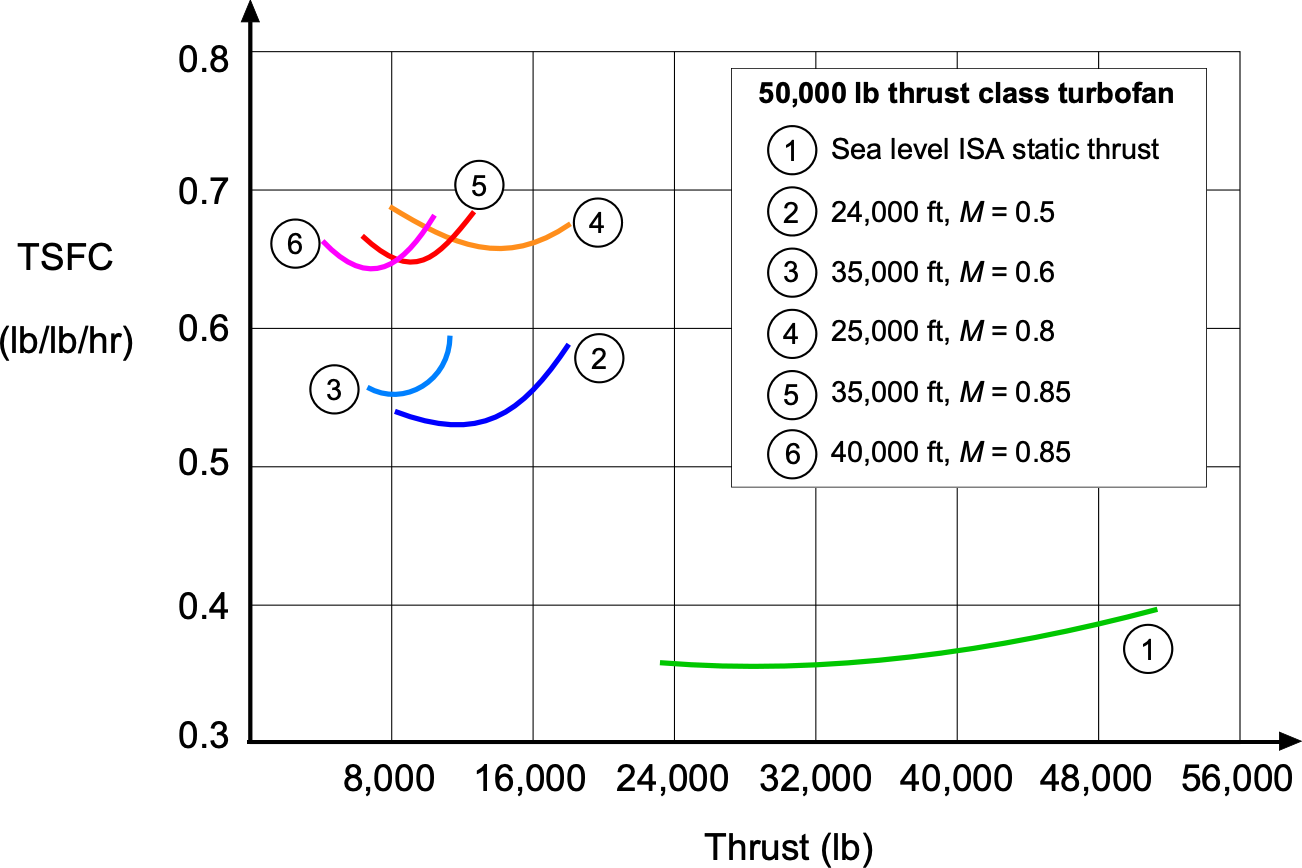
At any given flight condition, both thrust and thrust-specific fuel consumption (TSFC) vary together with the throttle setting.

More detailed performance calculations require careful modeling of the specific engine’s performance characteristics, necessitating the use of engine charts or engine decks.[2] An engine deck is a data set that describes the engine’s performance across its full operating range.

Aircraft designers use engine decks to model propulsion performance and fuel consumption throughout the flight envelope. Such detailed information about engine performance is typically available only to aircraft manufacturers planning to use the engine on their aircraft.

Piston engine performance (at least for normally aspirated engines) does not depend substantially on airspeed, but it does depend on density altitude, i.e., the altitude corresponding to the ambient pressure and temperature as defined by the ISA. All variants of these engines are typically designed to achieve their best (lowest) BSFC at wide-open throttle and at or near their rated power, appropriate for the airplane they are selected to propel. At lower throttle settings, the BSFC tends to increase slightly, indicating that the engine becomes less efficient and consumes more fuel per unit of power. For a normally aspirated piston engine, BSFC typically decreases (improves) at altitudes up to approximately 10,000 feet (~3,000 meters), then increases again at higher altitudes. With a supercharged engine, however, the BSFC stays relatively constant at all operational altitudes.

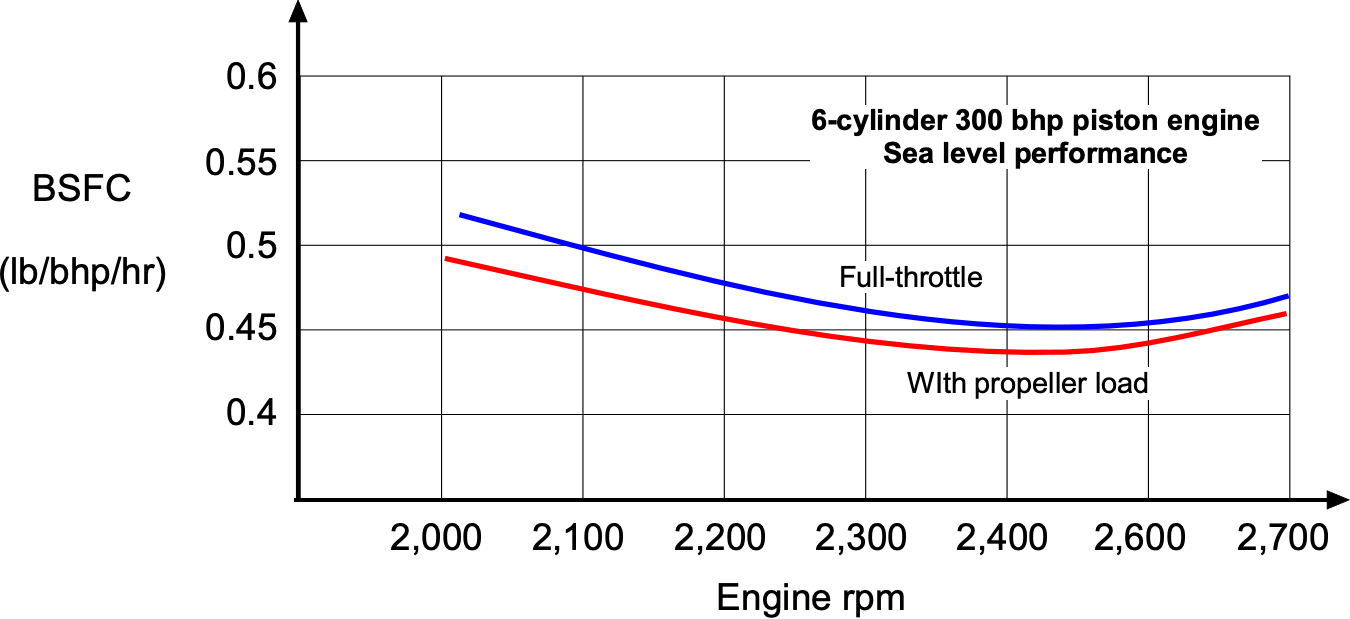
Airplane piston engines are designed to achieve their best BSFC at wide-open throttle and at or near their rated power.

Because the BSFC or TSFC curves for aircraft engines are often relatively flat (constant) over the range of almost wide-open throttle settings used in flight, it is a reasonable assumption for an aircraft engine to assume that the BSFC or TSFC is constant. This latter assumption facilitates estimation of net fuel burn during flight across different airspeeds, weights, and operating altitudes, at least in the first iteration, when detailed engine performance characteristics may not be available. However, BSFC or TSFC characteristics must be known (or estimated) to properly determine actual fuel burn.

Therefore, if the BSFC or the TSFC is known, then the corresponding fuel flow rate curves can be determined (estimated) because they are proportional to the power required for a propeller-driven airplane and the thrust for a jet-driven airplane. A generic fuel flow example is shown in Figure 3. Notice that there is an airspeed on the fuel flow curve at which the minimum fuel flow is required for flight (point A) and also an airspeed at which the ratio of airspeed to fuel flow is a maximum (point B), both of which are significant in terms of flight operations.

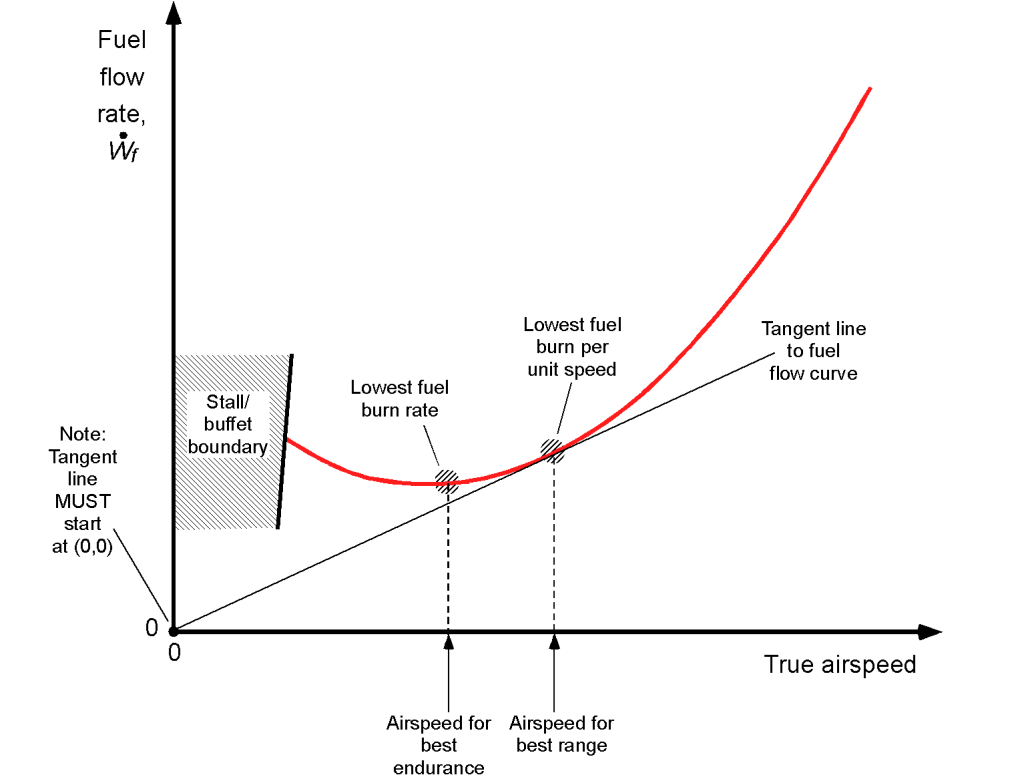
An airplane’s generic fuel-flow curve will mirror the shape of a jet aircraft’s thrust curve and a propeller aircraft’s power-required curve.

For a given quantity of fuel carried on the airplane, the airspeed to fly for minimum fuel flow (point A) corresponds to the flight condition that gives the longest flight time, i.e., the maximum flight endurance. The tangent of the straight line from the origin to the fuel-flow curve (point B) corresponds to the condition for which the ratio of airspeed to fuel flow is a maximum. Because distance in still air is airspeed multiplied by time, point B corresponds to the furthest still-air distance covered for a given quantity of fuel, i.e., the airspeed to fly to achieve the best range.

Fuel Flow Curves – Propeller Airplanes

The power required, P_{\rm req}, for a propeller-driven airplane is assumed to be the brake power required (i.e., the brake power at the shaft, P_{\rm bp}), which will also reflect the effects of the propeller efficiency, i.e.,

(3)   \begin{equation*} { P_{\rm req} = P_{\rm bp} = \frac{T V_{\infty}}{\eta_p} = \frac{D V_{\infty}}{\eta_p} = \frac{1}{\eta_p} \left( \frac{1}{2} \varrho_0 \, \sigma \, V_{\infty}^3 \, S \left( C_{D_{0}} + k {C_L}^2 \right) \right) } \end{equation*}

A constant-speed propeller will have a propulsive efficiency, \eta_p, that will be reasonably constant over the normal range of flight speeds. This assumption is reasonable for analyzing turboprop and high-performance piston-engine aircraft. The propulsive efficiency of a fixed-pitch propeller is not constant; it can vary significantly with airspeed. Therefore, the aircraft performance analysis requires consideration of the propeller charts to determine \eta_p at actual flight conditions. Notice that in most cases, the density of the air has been referenced to ISA conditions, where \varrho_{\infty} = \varrho_0 \, \sigma, and the value of \sigma comes from the ISA equations.

If it is assumed that the engine BSFC is constant (this is a reasonable but not a general assumption), then the fuel flow (in appropriate units of time) will be

(4)   \begin{equation*} \frac{dW_f}{dt} = \overbigdot{W}_{\!f} = ({\rm BSFC}) P_{\rm bp} = c_b \, P_{\rm bp} \end{equation*}

where the BSFC is now denoted by c_b. The fuel flow is, therefore,

(5)   \begin{equation*} \overbigdot{W}_{\!f} = \left( \frac{1}{2} \varrho_0 \, \sigma \, V_{\infty}^3 \, c_b \, S \right) \frac{1}{\eta_p} C_{D_{0}} + \left( \frac{k \, c_b }{\eta_p} \right) \frac{2 W^2}{\varrho_0 \, \sigma \, S \, V_{\infty} } \end{equation*}

which is of the form

(6)   \begin{equation*} \overbigdot{W}_{\!f} = A V_{\infty}^3 + \frac{B}{V_{\infty}} \end{equation*}

for a constant weight and/or altitude, where

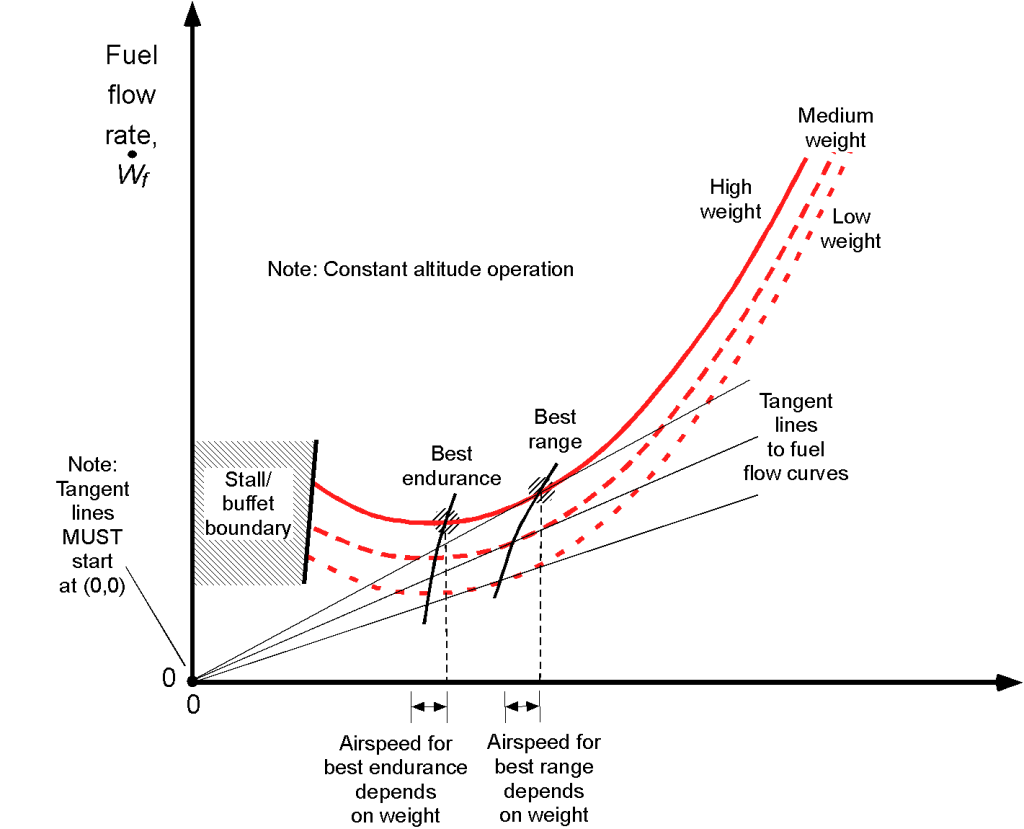
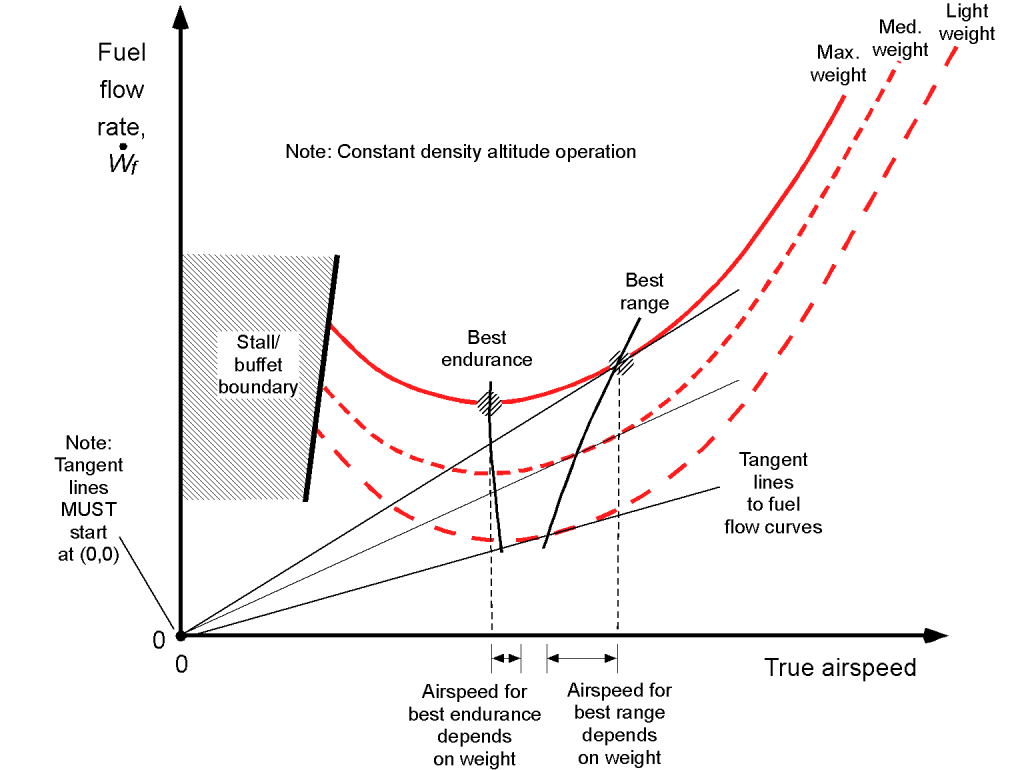
(7)   \begin{equation*} A = \frac{\varrho_0 \,\sigma \, S}{2 \, \eta_p}\,c_b\,C_{D_{0}} \qquad \text{and} \qquad B = \frac{2\,W^2}{\varrho_0 \,\sigma \, S}\,\frac{k\,c_b}{\eta_p} \end{equation*}

Remember the general “U” shaped characteristic of the power required for a propeller-driven airplane flight curve; these power curves are a function of airspeed and depend on the weight of the airplane and the equivalent density altitude at which it is flying. Therefore, the fuel flow curves will mimic the shapes of the power curves. For example, the effects of the airplane’s in-flight weight on its fuel flow characteristics are shown in Figure 4. Note that a higher flight weight increases the required power and, in turn, the corresponding fuel consumption. Additionally, the points for best endurance (lowest fuel flow) and best range (lowest fuel flow per unit speed or distance) are indicated; however, these speeds are not constant and depend on the flight weight.

Representative fuel flow curves for a propeller-driven airplane as a function of airspeed and in-flight weight.

The speed to fly for the lowest fuel burn (hence maximum flight endurance) can be determined by finding when \overbigdot{W}_{\!f} is a minimum. Differentiating the fuel flow result given by Eq. 6 with respect to {V_{\infty}} gives

(8)   \begin{equation*} \frac{d \overbigdot{W}_{\!f}}{d V_{\infty}} = 3 A V_{\infty}^2 - \frac{B}{V_{\infty}^2} \end{equation*}

which is zero for a minimum, i.e.,

(9)   \begin{equation*} 3 A V_{\infty}^2 - \frac{B}{V_{\infty}^2} = 0 \end{equation*}

and so the speed to fly for the best endurance will be

(10)   \begin{equation*} V_{\infty} = V_{\rm be}= \left( \frac{B}{3A} \right)^{1/4} = \left(\frac{2W}{\varrho_0 \,\sigma \, S}\right)^{1/2}\!\left(\frac{k}{3\,C_{D_{0}}}\right)^{1/4} \end{equation*}

confirming that V_{\rm be} will depend on both weight and altitude. The corresponding lift coefficient is

(11)   \begin{equation*} C_{L,{\rm be}} = \sqrt{\frac{3\,C_{D_{0}}}{k}} \end{equation*}

The best range is obtained when the ratio \overbigdot{W}_{\!f}/V_{\infty} is a minimum. In this case

(12)   \begin{equation*} \frac{\overbigdot{W}_{\!f}}{V_{\infty}} = A V_{\infty}^2 + \frac{B}{V_{\infty}^2} \end{equation*}

so that

(13)   \begin{equation*} { \frac{d(\overbigdot{W}_{\!f}/V_{\infty})}{dV_{\infty}} = 2 A V_{\infty} - \frac{2B}{V_{\infty}^3} } \end{equation*}

which is zero for a minimum, i.e.,

(14)   \begin{equation*} 2 A V_{\infty} - \frac{2B}{V_{\infty}^3} = 0 \end{equation*}

and so

(15)   \begin{equation*} V_{\infty} = V_{\rm br} = \left( \frac{B}{A} \right)^{1/4} = \left(\frac{2W}{\varrho_0 \,\sigma \, S}\right)^{1/2}\!\left(\frac{k}{C_{D_{0}}}\right)^{1/4} \end{equation*}

also confirming that V_{\rm br} will depend on both weight and altitude, and where the corresponding lift coefficient is given by

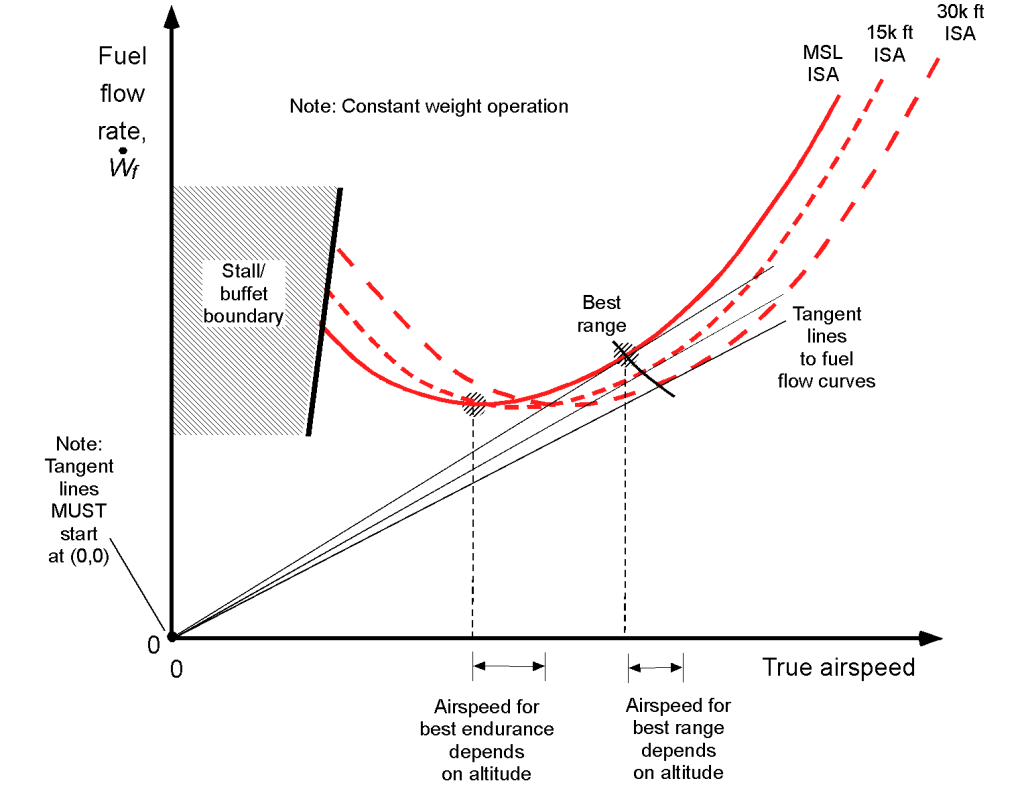
(16)   \begin{equation*} C_{L,{\rm br}} = \sqrt{\frac{C_{D_{0}}}{k}} \end{equation*}

The effects of altitude on the fuel flow characteristics are shown in Figure 5. Notice that at lower airspeeds, the effects of altitude increase the required power, resulting in higher fuel flow. This outcome is because it can be deduced that at low airspeeds, the power required is dominated by the induced component (see Eq. 6). Again, the points for best endurance (lowest fuel flow) and best range (lowest fuel flow per unit speed or distance) are indicated; these speeds are not constant and depend on the weight and can be calculated using Eqs. 10 and 15, respectively.

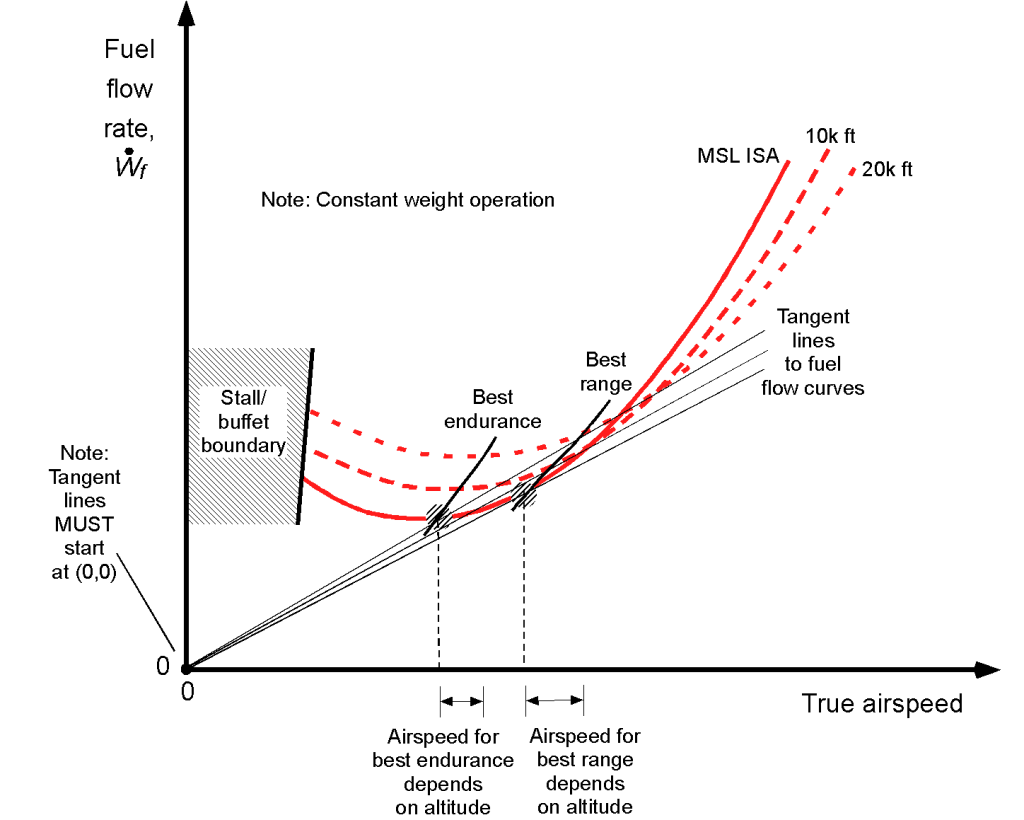
Representative fuel flow curves for a propeller-driven airplane as a function of airspeed and operational altitude.

Fuel Flow Curves – Jet Airplanes

As for propeller-driven airplanes, the fuel flow for a jet aircraft will be a function of airspeed, in-flight weight, and operating altitude. While the shapes of the fuel flow curves are different because they depend on thrust, they retain the qualitative U-shapes described by the thrust-required equation, i.e.,

(17)   \begin{equation*} T = \frac{1}{2} \varrho_0 \, \sigma V_{\infty}^2 \, S \, C_D = \frac{1}{2} \varrho_0 \, \sigma V_{\infty}^2 S \left( C_{D_{0}} + k {C_L}^2 \right) \end{equation*}

If it is assumed that the TSFC is constant (again, this is a reasonable assumption), then the fuel flow (in appropriate units of time) will be

(18)   \begin{equation*} \frac{dW_f}{dt} = \overbigdot{W}_{\!f} = ({\rm TSFC}) T_{\rm req} = c_t \, T_{\rm req} \end{equation*}

where the TSFC is now denoted by c_t. The fuel flow is, therefore,

(19)   \begin{equation*} \overbigdot{W}_{\!f} = \frac{1}{2} \varrho_0 \, \sigma V_{\infty}^2 \, S \, c_t \, C_{D_{0}} + \frac{2 k \, c_t \, W^2}{\varrho_0 \, \sigma \, S \, V_{\infty}^2} \end{equation*}

which, in this case, is of the form

(20)   \begin{equation*} \overbigdot{W}_{\!f} = A V_{\infty}^2 + \frac{B}{V_{\infty}^2} \end{equation*}

for a constant weight and/or altitude, where

(21)   \begin{equation*} A = \frac{1}{2}\,\varrho_0 \,\sigma \, S \, c_t \, C_{D_{0}} \qquad \text{and} \qquad B = \frac{2\,k \, c_t \, W^{2}}{\varrho_0 \,\sigma \, S} \end{equation*}

The effects of the jet airplane’s in-flight weight on the fuel flow characteristics are shown in Figure 6. Notice again that a higher flight weight increases the power and fuel required. The points for best endurance (lowest fuel flow) and best range (lowest fuel flow per unit speed or distance) are indicated; these speeds depend on the airplane’s weight.

Representative fuel flow curves for a jet airplane as a function of airspeed and in-flight weight.

The speed to fly for the lowest fuel burn (hence maximum flight endurance) can be determined by finding when \overbigdot{W}_{\!f} is a minimum. Differentiating the fuel flow result given by Eq. 20 with respect to {V_{\infty}} gives

(22)   \begin{equation*} \frac{d\overbigdot{W}_{\!f}}{d V_{\infty}} = 2A V_{\infty} - \frac{2B}{V_{\infty}^3} \end{equation*}

which is zero for a minimum, i.e.,

(23)   \begin{equation*} { 2 A V_{\infty} - \frac{2 B}{V_{\infty}^3} = 0 } \end{equation*}

and so the speed to fly for the best endurance for a jet aircraft will be

(24)   \begin{equation*} V_{\infty} = V_{\rm be} = \left( \frac{B}{A} \right)^{1/4} = \left(\frac{2W}{\varrho_0 \,\sigma \, S}\right)^{1/2}\!\left(\frac{k}{C_{D_{0}}}\right)^{1/4} \end{equation*}

confirming that V_{\rm be} will depend on both the weight of the airplane and its operating altitude. The corresponding lift coefficient is

(25)   \begin{equation*} C_{L,{\rm be}}=\sqrt{\frac{C_{D_{0}}}{k}} \end{equation*}

As previously discussed, the best range is obtained when the ratio \overbigdot{W}_{\!f}/V_{\infty} is a minimum. In this case, for a jet, then

(26)   \begin{equation*} \frac{\overbigdot{W}_{\!f}}{V_{\infty}} = A V_{\infty} + \frac{B}{V_{\infty}^3} \end{equation*}

so that

(27)   \begin{equation*} \frac{d(\overbigdot{W}_{\!f}/V_{\infty})}{dV_{\infty}} = A - \frac{3B}{V_{\infty}^4} \end{equation*}

which is zero for a minimum, i.e.,

(28)   \begin{equation*} A - \frac{3B}{V_{\infty}^4} = 0 \end{equation*}

and so

(29)   \begin{equation*} V_{\infty} = V_{\rm br} = \left( \frac{3B}{A} \right)^{1/4} = 3^{1/4}\!\left(\frac{2W}{\varrho_0 \,\sigma \, S}\right)^{1/2}\!\left(\frac{k}{C_{D_{0}}}\right)^{1/4} \end{equation*}

Additionally, it is confirmed that V_{\rm br} will depend on both weight and altitude for a jet. The corresponding lift coefficient is

(30)   \begin{equation*} C_{L,{\rm br}}=\sqrt{\frac{C_{D_{0}}}{3 \, k}} \end{equation*}

The effects of altitude on the fuel flow characteristics are shown in Figure 7. Notice that at lower airspeeds, the effects of altitude increase the required power, resulting in higher fuel flow. Again, the points for best endurance (lowest fuel flow) and best range (lowest fuel flow per unit speed or distance) are indicated; these speeds are not constant and depend on the weight and can be calculated using Eqs. 24 and 29, respectively.

Representative fuel flow curves for a jet airplane as a function of airspeed and altitude.

Total Fuel Burn

Determining the aircraft’s total fuel burn over the intended flight or mission requires knowing the fuel flow as a function of aircraft weight, operating altitude, and true airspeed (or Mach number). While the fuel flow curves have previously been delineated for the separate effects of weight and altitude, the aircraft’s weight, altitude, and airspeed can vary continuously during flight. Additionally, the climb and descent phases of the flight must be considered. Therefore, the net fuel burn is calculated by summing the fuel burned for each flight segment. An estimated fuel burn will be used for flight planning to ensure sufficient fuel (plus reserve) is loaded onto the aircraft.

A representative fuel flow rate-time plot is shown in Figure 8 for a typical civil flight, including takeoff, climb, cruise to the destination, and landing. By integration over time, the total fuel burned can be determined in units of weight, i.e., for the interval between {t = t_1} and {t = t_2}, then the weight of fuel burned is

(31)   \begin{equation*} { W_f = \int_{t_1}^{t_2} \overbigdot{W_f} \, dt } \end{equation*}

which is just the area under the fuel flow curve between t_1 and t_2. The total fuel burn, therefore, is the total area under the fuel flow curve from takeoff to landing.

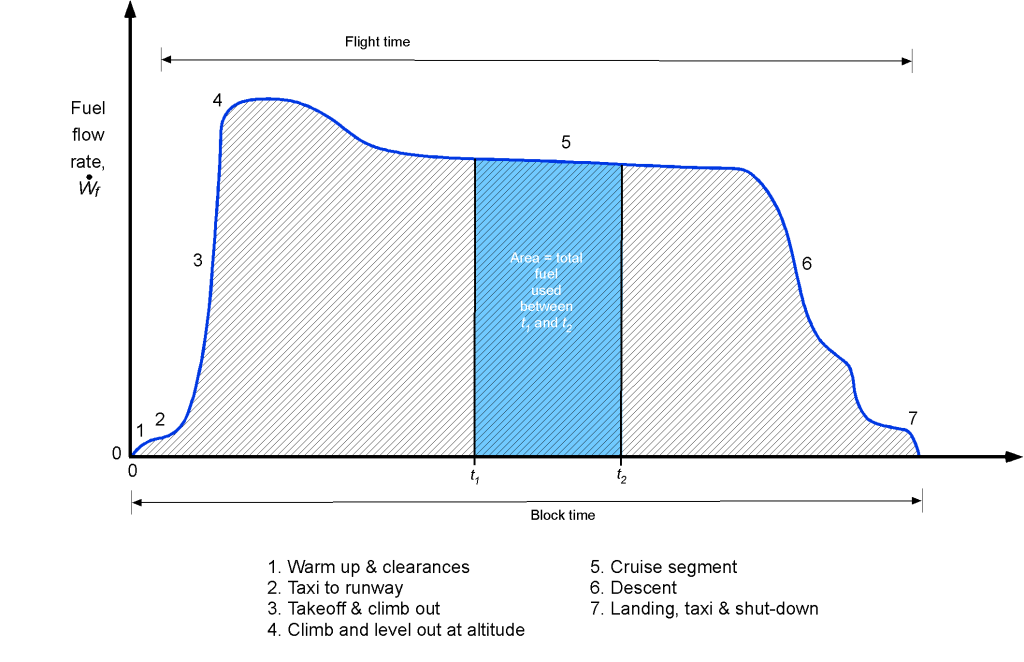
A representative fuel burn profile (fuel flow rate versus time) for a commercial airliner. The area under the fuel flow rate curve between two time points equals the total fuel burned during that interval.

As a special case, if \overbigdot{W}_{\!f} is assumed to be constant (which is reasonable over relatively short flight times in the cruise segment of flight), then the weight of fuel burned, {W_f}, would be

(32)   \begin{equation*} W_f \approx \overbigdot{W}_{\!f} \left( t_2 - t_1 \right) \end{equation*}

In general, however, the total fuel burn for each flight segment must be obtained by integration.

If the initial weight of the airplane at t_0 is {W_0} and the fuel available is {W_f}, then when all of this fuel is burned, the new weight of the airplane at {t_1} will be {W_0 - W_f = W_1}. Using a propeller-driven airplane as an example, the change in weight of the airplane with time will be

(33)   \begin{equation*} \frac{dW}{dt} = -\, c_b \, P_{\rm bp} \end{equation*}

so rearranging and integrating gives

(34)   \begin{equation*} { \int_{t_1}^{t_2} dt = - \int_{W_0}^{W_1} \frac{ \, dW}{c_b \, P_{\rm bp}} = \int_{W_1}^{W_0} \frac{ \, dW}{c_b \, P_{\rm bp}} } \end{equation*}

The minus sign indicates that the airplane’s weight W decreases with time; this is rectified by reversing the limits of integration. Therefore, the flight time corresponding to the fuel burned will be

(35)   \begin{equation*} t_2 - t_1 = \Delta t = \int_{W_1}^{W_0} \frac{ \, dW}{c_b \, P_{\rm bp}} \end{equation*}

If {W_f} is further assumed to be the total fuel available, then \Delta t, in this case, becomes the endurance E, i.e.,

(36)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{ \, dW}{c_b \, P_{\rm bp}} \end{equation*}

which would use all the available fuel. Again, as a special case, if P_{\rm bp} and c_b are assumed to be constant, then the flight endurance for a given fuel weight would be

(37)   \begin{equation*} E \approx \frac{W_f}{c_b \, P_{\rm bp} } \end{equation*}

Regarding range, the focus is on the distance an airplane can cover over the ground for a given amount of fuel. Multiplying both sides of Eq. 33 by {V_{\infty}} gives

(38)   \begin{equation*} V_{\infty} \frac{\, dW}{dt} = -\,V_{\infty} \, c_b \, P_{\rm bp} \end{equation*}

and then rearranging gives

(39)   \begin{equation*} V_{\infty} \, dt = -\,\frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} \end{equation*}

The distance covered in a given time, or the range R, is then

(40)   \begin{equation*} R = \int_{t_0}^{t_1} V_{\infty} \, dt \end{equation*}

which gives

(41)   \begin{equation*} { R = \int_{t_0}^{t_1} V_{\infty} \, dt = -\int_{W_0}^{W_1} \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} = \int_{W_1}^{W_0} \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} } \end{equation*}

so that

(42)   \begin{equation*} R = \int_{W_0-W_f}^{W_0} \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} \end{equation*}

where W_1 = W_0 - W_f. The physical meaning of this integral is also related to the area under the fuel flow curve. Again, as a special case, if P_{\rm bp} and c_b are assumed to be constant, then the flight range for a given fuel weight would be

(43)   \begin{equation*} R = \frac{V_{\infty} \, W_f}{c_b \, P_{\rm bp} } \end{equation*}

Reserve fuel: Why is it needed?

The need for reserve fuel must always be considered when estimating flight range. For example, the flight crew may arrive at their final destination to find air traffic control delays or adverse weather preventing them from landing. The aircraft may also need to enter a holding pattern or divert to an alternative airport. For this reason, reserve fuel is always required. The FAA regulations prescribe minimum fuel requirements that depend on the operating rules and flight conditions. For an airplane operating under visual flight rules (VFR), sufficient fuel must be carried to reach the intended landing point and then continue for at least 30 minutes during the day or 45 minutes at night. For an airplane operating under instrument flight rules (IFR), sufficient fuel must generally be carried to reach the intended destination, proceed to an alternate airport when required, and then fly for an additional 45 minutes at normal cruising speed.

Breguet Equations

The preceding principles are formally embodied in the Breguet equations for airplane endurance and range, first developed by Louis Charles Breguet. These are among the most famous equations in aeronautical engineering. Understanding how they are derived is crucial, as is recognizing what information they can reveal about an airplane’s flight performance.

Breguet Endurance Equation – Propeller Airplanes

For flight endurance, it has been previously stated that the endurance is given by

(44)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{dW}{c_b \, P_{\rm bp}} \end{equation*}

Assuming lift equals weight (L = W) and P = D \, V_{\infty}, then in level flight the endurance is

(45)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{ \eta_p \, dW}{c_b \, D \, V_{\infty}} = \int_{W_0 - W_f}^{W_0} \frac{ \eta_p \, L}{c_b \, D \, V_{\infty}} \frac{\, dW}{W} \end{equation*}

The lift required (which must equal the weight) is

(46)   \begin{equation*} W = L = \frac{1}{2} \varrho_0 \, \sigma \, V_{\infty}^2 \, S \, C_L \end{equation*}

so solving for the airspeed {V_{\infty}} gives

(47)   \begin{equation*} V_{\infty} = \sqrt{ \frac{2 W}{\varrho_0 \, \sigma \, S \, C_L}} \end{equation*}

Also, for the drag on the aircraft, then

(48)   \begin{equation*} D = \frac{1}{2} \varrho_0 \, \sigma V_{\infty}^2 \, S \, C_D \end{equation*}

Substituting the previous results means that the endurance equation now becomes

(49)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{ \eta_p}{c_b } \left(\frac{C_L^{\, 3/2}}{C_D}\right) \sqrt{ \frac{\varrho_{\infty} \, S}{2} } \frac{dW}{W^{3/2}} \end{equation*}

Notice that the ratio C_L^{\, 3/2}/C_D appears in this latter equation, not the lift-to-drag ratio C_L/C_D. While the numerical values are similar, the airspeeds at which the maximum values occur are distinctly different, as shown in Figure 9.

The best endurance and best range airspeeds of a propeller-driven airplane occur at different aerodynamic conditions.

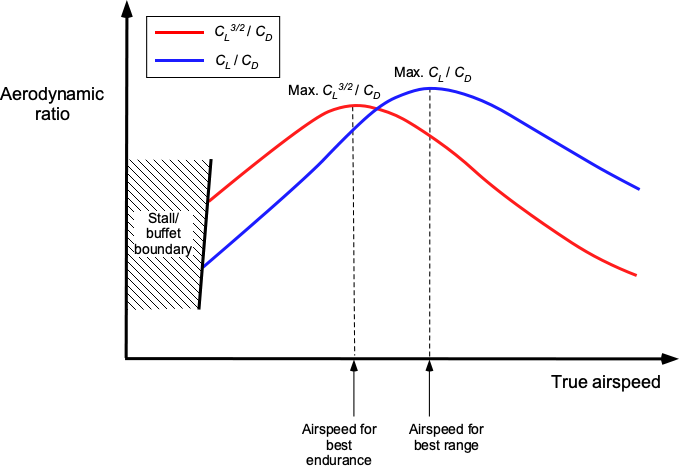
Proceeding further by assuming that the value of C_L^{\, 3/2}/C_D is constant over the flight time, which might be reasonable for shorter flight times where the weight of the airplane does not change by much, as well as assuming that \eta_p, c_b and \varrho_{\infty} = \varrho_0 \, \sigma are constant (i.e., the airplane is flying at a constant altitude), then after integration of Eq. 49 the endurance will be

(50)   \begin{equation*} { E = \frac{ \eta_p}{c_b} \left(\frac{C_L^{\, 3/2}}{C_D}\right) \sqrt{2 \varrho_0 \, \sigma \, S} \left( \frac{1}{\sqrt{W_0 - W_f}} - \frac{1}{\sqrt{W_0} } \right) } \end{equation*}

which is known as the Breguet endurance equation for a propeller-driven airplane.

The latter equation estimates the flight endurance for a given total fuel weight. If no assumptions were made before the analytic integration, determining the required fuel and endurance would typically require numerical integration.

Therefore, from the Breguet endurance equation, it becomes clear that to maximize flight endurance, the airplane must be flown in such a way that:

  1. The propeller is operated at (or near) its best propulsive efficiency; this is typical of a constant-speed (variable-pitch) propeller.
  2. The engine is operated at (or near) the power setting that yields its best BSFC, although this may not be possible at lower power settings, which are likely altitude-dependent.
  3. The airplane carries the largest quantity of fuel. However, fuel quantity may be constrained by factors other than tankage volume, such as the need to carry a specific payload, which must be balanced against the fuel load.
  4. The airplane flies at (or close to) the best aerodynamic ratio of C_L^{\, 3/2}/C_D.

Breguet Range Equation – Propeller Airplanes

Now, consider the flight range of the propeller-driven airplane. As was previously established, the range is given by

(51)   \begin{equation*} R = \int_{W_0-W_f}^{W_0} \frac{V_{\infty} \, dW}{c_b \, P_{\rm bp}} \end{equation*}

After the substitution of the relationships used previously for endurance, then

(52)   \begin{equation*} R = \int_{W_0-W_f}^{W_0} \frac{V_{\infty} \, \eta_p \, dW}{c_b \, D \, V_{\infty}} = \int_{W_0-W_f}^{W_0} \frac{\eta_p \, dW}{c_b \, D} \end{equation*}

Again, for steady level flight, L = W, so

(53)   \begin{equation*} R = \int_{W_0-W_f}^{W_0} \frac{\eta_p}{c_b} \left( \frac{L}{D}\right) \frac{\, dW}{W} = \int_{W_0-W_f}^{W_0} \frac{\eta_p}{c_b} \left(\frac{C_L}{C_D}\right) \frac{\, dW}{W} \end{equation*}

where in this case the lift-to-drag ratio C_L/C_D is involved.

As performed before with the endurance integral, if C_L/C_D, \eta_p and c_b are assumed to be constant then the range is

(54)   \begin{equation*} { R = \frac{\eta_p}{c_b} \left( \frac{C_L}{C_D} \right) \int_{W_0-W_f}^{W_0} \frac{dW}{W} } \end{equation*}

which, after integration, leads to

(55)   \begin{equation*} R = \frac{\eta_p}{c_b} \left( \frac{C_L}{C_D}\right) \ln \left( \frac{W_0}{W_0-W_f}\right) \end{equation*}

which is usually known as the Breguet range equation. Again, if the actual values of C_L/C_D, \eta_p, and c_b corresponding to a given flight condition were to be used, then the integral would be evaluated numerically.

Statute Miles or Nautical Miles?

Nautical miles are used to measure distances in the aeronautical and aviation world. A nautical mile is 1/60th of a degree or one minute of latitude and is 6,076 ft or 1,852 m long. Speed is typically measured in nautical miles per hour (nmi/h) or knots (kts), and airplane airspeed indicators are calibrated in knots. The familiar land mile is a statute mile, measuring 5,280 ft and based on the Roman unit of length, the 1,000 paces. The statute mile was standardized as exactly 1,609.344 meters by an international agreement in 1959. A nautical mile is abbreviated to “M” or “NM,” but more commonly, “nm” is used in many publications. The statute mile was previously abbreviated to “m” but is now written as “mi'” to avoid confusion with the SI unit meter (or metre).

Therefore, based on the preceding, it is clear that to maximize the flight range, the airplane must be flown in such a way that:

  1. The propeller is operated at (or near) its best propulsive efficiency, as previously discussed.
  2. The engine is operated at (or near) the power setting to achieve its optimal BSFC, subject to the caveats previously discussed.
  3. The airplane carries the largest quantity of fuel in the tanks, subject to operating weight limits.
  4. The airplane flies at or near the best lift-to-drag ratio C_L/C_D.

In summary, when thinking about the design of a propeller-driven airplane, achieving the best flight endurance and/or range is about four things:

  1. Carrying as much fuel as possible.
  2. Achieving a high aerodynamic efficiency from the airframe, i.e., designing the airplane to minimize drag as much as possible.
  3. Striving for high engine efficiency, i.e., obtaining the lowest possible value of BSFC from the engines.
  4. Obtaining high propulsive efficiency, i.e., designing the propeller in this case for optimal overall aerodynamic efficiency, will inevitably require a variable-pitch (i.e., constant-speed) propeller.

Check Your Understanding #1 – Finding the range of a propeller-driven airplane

A small propeller-driven aircraft is flying at an estimated in-flight weight of 2,100 lb and an airspeed of 120 knots at 2,000 ft, where the air density is 0.00216 slugs/ft{^3}. The aircraft has only 8 gallons of usable fuel (excluding reserves), and the pilot must fly 120 nautical miles to the home airport. Is there enough fuel to do this? Assume no winds. The engineering characteristics of the aircraft are wing span, b = 36 ft, wing area, S = 174 ft{^{2}}, non-lifting drag coefficient, {C_{D_{0}}} = 0.02, propeller efficiency, \eta_p = 0.85, Oswald’s efficiency factor, {e} = 0.81, and BSFC, c_b = 0.45 lb bhp^{-1} hr^{-1}.

Show solution/hide solution.

There are only 8 gallons of AVGAS fuel, and AVGAS weighs 6.0 lb per gallon, so {W_f} = 48 lb of fuel. Because the usable fuel weight is small relative to the total aircraft weight, the weight change during the flight can be neglected, and the aerodynamic performance can be evaluated at the initial in-flight weight of 2,100 lb. An airspeed of 120 kts is equivalent to 120 \times 1.688 = 202.54 ft/s = {V_{\infty}}. The initial operating lift coefficient of the wing, C_L, is

    \[ C_L = \frac{2W}{\varrho \, V^2 S} = \frac{2 \times 2,100}{0.00216 \times 202.54^2 \times 174.0} = 0.272 \]

To find the induced drag coefficient, the aspect ratio of the wing, AR, is needed, i.e.,

    \[ AR = \frac{b^2}{S} = \frac{(36.0)^2}{174.0} = 7.45 \]

The induced drag coefficient {C_{D_{i}}} will be

    \[ C_{D_{i}} = \frac{{C_L}^2}{\pi \, AR \, e} = \frac{0.272^2}{\pi \times 7.45 \times 0.81} = 0.0039 \]

Therefore, the total drag coefficient, C_D, is

    \[ C_D = C_{D_0} + C_{D_i} = C_{D_0} + \frac{{C_L}^2}{\pi \, AR \, e} = 0.02 + 0.0039 = 0.0239 \]

and the lift-to-drag ratio of the aircraft at the given conditions of flight is

    \[ \frac{L}{D} = \frac{C_L}{C_D} = \frac{0.272}{0.0239} = 11.38 \]

The Breguet range equation for a propeller-driven airplane is

    \[ R = \frac{\eta_p}{c_b} \left( \frac{C_L}{C_D}\right) \ln \left( \frac{W_0}{W_0-W_f}\right) \]

IMPORTANT: Notice that the value of the brake-specific fuel consumption, or BSFC, in this problem is given in units of lb bhp^{-1} hr^{-1}, which must be converted to base units before using it in the Breguet equation. One brake horsepower (bhp) is equivalent to 550 ft-lb s^{-1}, and there are 3,600 seconds in an hour, i.e., by dividing the given value by 550 x 3,600.

Therefore, inserting the known values gives the potential approximate range of the aircraft as

    \[ R = \frac{0.85 \times 550 \times 3,600}{0.45} \left( 11.38 \right) \ln \left( \frac{2,100}{2,100 -48}\right) = 1.03 \times 10^6~\mbox{ft} \]

which is approximately 170 nautical miles. In conclusion, the aircraft has sufficient fuel to reach the home airport with a margin, allowing the pilot to relax and enjoy the remainder of the flight.

Breguet Endurance Equation – Jet Airplanes

In evaluating jet aircraft performance, the engine’s required thrust is the primary factor affecting fuel consumption. However, the estimation of endurance and range follows a path similar to that previously used for the propeller-driven airplane.

For a jet engine, the thrust-specific fuel consumption (TSFC) is defined as

(56)   \begin{equation*} \mbox{TSFC} = \frac{\text{Weight of fuel burned}}{ \text{(Unit thrust produced)(time~=~hour)}} = \frac{\text{lb of fuel}}{ \text{(lb of thrust)(hr)}} = c_t \end{equation*}

in units of lb lb^{-1} hr^{-1}. Therefore, the fuel flow rate is

(57)   \begin{equation*} \frac{dW_f}{dt} = \overbigdot{W}_{\!f} = T_R \, c_t \end{equation*}

where T_R is the required thrust from the engine. Therefore, to determine the fuel flow rate, the engine thrust required must be calculated; in level flight, this equals the airplane’s drag.

As fuel is burned, the weight of the airplane changes proportionally, so the change in weight of the airplane is

(58)   \begin{equation*} \frac{dW}{dt} = -\, T_R \, c_t \end{equation*}

The airplane’s weight is W_0 at time t = t_0 and W_1 at time t = t_1, where W_1 is the initial weight minus the fuel burned, i.e., W_1 = W_0 - W_f. Therefore,

(59)   \begin{equation*} \int_{t_0}^{t_1} dt = \Delta t = -\int_{W_0}^{W_1} \frac{dW}{c_t \, T_R} = \int_{W_1}^{W_0} \frac{dW}{c_t \, T_R} = \int_{W_0 - W_f}^{W_0} \frac{dW}{c_t \, T_R} \end{equation*}

which gives the time of flight, \Delta t, to burn the fuel weight, {W_f}. Now, if {W_f} is the total fuel available then \Delta t is equal to the endurance E so

(60)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{dW}{c_t \, T_R} \end{equation*}

For level flight then T_R = D and L = W and after substitution then

(61)   \begin{equation*} E = \int_{W_0 - W_f}^{W_0} \frac{1}{c_t} \left( \frac{L}{D} \right) \frac{dW}{W} = \int_{W_0 - W_f}^{W_0} \frac{1}{c_t} \left( \frac{C_L}{C_D} \right) \frac{dW}{W} \end{equation*}

It will be noted immediately that this is a different result from the propeller-driven airplane because, in this case, the endurance depends on C_L/C_D and not C_L^{\, 3/2}/C_D for the propeller airplane.

By assuming that c_t and C_L/C_D are constant, the foregoing endurance equation integrates out to be

(62)   \begin{equation*} E = \frac{1}{c_t} \left( \frac{C_L}{C_D} \right) \ln \left(\frac{W_0}{W_0 - W_f} \right) \end{equation*}

which is referred to as the Breguet endurance equation for a jet airplane.
Therefore, to maximize the flight endurance of a jet airplane, it must be flown in such a way that:

  1. The engine(s) is/are operated at (or near) the power setting to achieve their best TSFC. For most jet engines, this condition inevitably occurs at higher altitudes, which is by design.
  2. The airplane carries the largest quantity of fuel, although this may be limited by weight rather than available tankage.
  3. The airplane flies at or near the best lift-to-drag ratio C_L/C_D.

Breguet Range Equation – Jet Airplanes

As before, the differential equation to account for the change in the weight of the airplane as fuel is burned is

(63)   \begin{equation*} \frac{dW}{dt} = -\,T_R \, c_t \end{equation*}

or by rearrangement

(64)   \begin{equation*} dt = -\,\frac{dW}{T_R \, c_t} \end{equation*}

The distance flown is the product of airspeed and time, so multiplying both sides of the preceding equation by {V_{\infty}} gives

(65)   \begin{equation*} V_{\infty} \, dt = ds = -\,\frac{V_{\infty} \, dW}{T_R \, c_t} \end{equation*}

where ds is the incremental distance traveled. The airplane’s weight is W_0 at time t = t_0 and W_1 at time t = t_1, where W_1 is the initial weight minus the fuel burned, i.e., W_1 = W_0 - W_f. Integrating Eq. 65 gives

(66)   \begin{equation*} { s = \int_{t_0}^{t_1} V_{\infty} \, dt = -\int_{W_0}^{W_1} \frac{V_{\infty} \, dW}{T_R \, c_t} = \int_{W_1}^{W_0} \frac{V_{\infty} \, dW}{T_R \, c_t} } \end{equation*}

For level flight, then T_R = D and L = W, and after the substitution, the distance traveled on a given weight of fuel {W_f} is

(67)   \begin{equation*} s = \int_{W_1}^{W_0} \frac{V_{\infty}}{c_t} \left( \frac{L}{D} \right) \frac{dW}{W} = \int_{W_1}^{W_0} \frac{V_{\infty}}{c_t} \left(\frac{C_L}{C_D} \right) \frac{dW}{W} \end{equation*}

which would be the maximum range R if the value of {W_f} was all the useful fuel. Also

(68)   \begin{equation*} V_{\infty} = \sqrt{ \frac{2 W}{\varrho_0 \, \sigma S C_L}} \end{equation*}

so that after substitution, the range of the airplane becomes

(69)   \begin{equation*} R = \int_{W_1}^{W_0} \frac{1}{c_t} \sqrt{\frac{2}{\varrho_0 \, \sigma \, S}} \left(\frac{C_L^{1/2}}{C_D} \right) \frac{dW}{W^{1/2}} \end{equation*}

which again yields a different result to the propeller-driven airplane, as it depends on the aerodynamic ratio {C_L^{1/2}/C_D} rather than {C_L/C_D}, as shown in Figure 10. The airspeed for the best value of {C_L^{1/2}/C_D}, and so the best range, is generally significantly higher than that for best endurance.

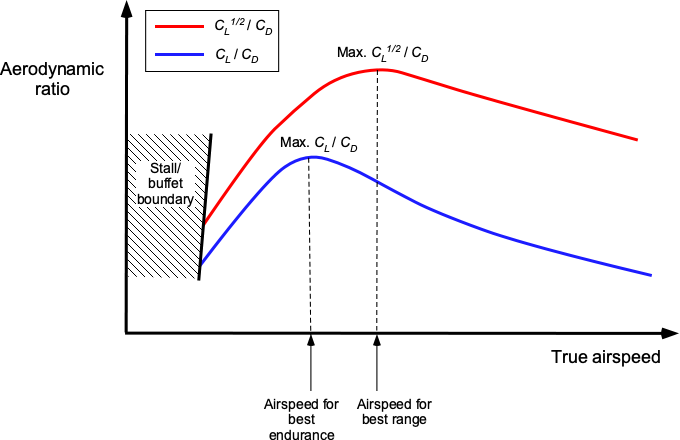
A jet airplane’s best endurance and range airspeeds also occur at distinctly different aerodynamic conditions.

By assuming that c_t, C_L, and C_D are constant, the foregoing endurance equation integrates out to be

(70)   \begin{equation*} R = \frac{1}{c_t} \sqrt{\frac{2}{\varrho_0 \, \sigma \, S}} \left(\frac{C_L^{1/2}}{C_D} \right) \int_{W_1}^{W_0} \frac{dW}{W^{1/2}} = \frac{2}{c_t} \sqrt{ \frac{2}{\varrho_0 \, \sigma \, S}} \left(\frac{C_L^{1/2}}{C_D} \right) \left( W_0^{1/2} - W_1^{1/2} \right) \end{equation*}

which is referred to as the Breguet range equation for a jet airplane.

Therefore, to maximize the flight range of a jet airplane, it must be flown in such a way that:

  1. The engine operates at (or near) the thrust (throttle) setting to achieve its best TSFC.
  2. The airplane carries the largest quantity of fuel.
  3. The airplane flies at or near the best value of the aerodynamic ratio {C_L^{1/2}/C_D}.

Check Your Understanding #2 – Finding the range of a jet aircraft

A small, single-engine, jet-powered aircraft has an initial in-flight weight, W, of 5,000 lb and carries 1,000 lb of usable fuel. The aircraft is at an altitude of 25,000 ft ISA. Its drag polar can be expressed as C_D = 0.018 + 0.095 \, C_L^ {\,2}. It has a wing area of 180 ft2. The TSFC of the engine is c_t = 1.0 lb/lb/hr. What is the best range of the aircraft in these conditions, and at what airspeed should the pilot fly to reach this range?

Show solution/hide solution.

For a jet aircraft, the conditions for maximum range are achieved when the aerodynamic ratio {C_L^{1/2}/C_D} is maximized. If the drag polar is

    \[ C_D = C_{D_{0}} + k \, C_L^ {\,2} = 0.018 + 0.095 \, C_L^ {\,2} \]

then

    \[ \frac{C_D}{C_L^{1/2}} = \frac{ C_{D_{0}} + k \, C_L^ {\,2}}{C_L^{1/2}} = \frac{C_{D_{0}}}{C_L^{1/2}} + k C_L^{\, 3/2} \]

To find a maximum (or minimum), the preceding expression is differentiated with respect to C_L and then set to zero, i.e.,

    \[ \frac{ d (C_D/C_L^{1/2})}{d C_L} = -\frac{1}{2}\frac{C_{D_{0}}}{C_L^{3/2}} + \frac{3}{2} k C_L^{1/2} = 0 \]

Therefore, the needed lift coefficient for this best range condition is

    \[ C_L = \sqrt{ \frac{C_{D_{0}}}{3k} } = \sqrt{ \frac{0.018}{3 \times 0.095} } = 0.251 = C_{L_{\rm br}} \]

The corresponding drag coefficient will be

    \[ C_D = 0.018 + 0.095 \, C_L^ {\,2} = 0.018 + 0.095 \times 0.251^2 = 0.024 \]

Therefore,

    \[ \left( \frac{ C_L^{1/2}}{ C_D} \right)_{\rm br} = \frac{ 0.251^{1/2}}{0.024} = 20.875 \]

The Breguet range equation for a jet aircraft is

    \[ R = \frac{2}{c_t} \sqrt{ \frac{2}{\varrho_0 \, \sigma S}} \left(\frac{C_L^{1/2}}{C_D} \right)_{\rm br} \left( W_0^{1/2} - W_1^{1/2} \right) \]

The initial weight is W_0 = 5,000 lb, and the final weight, W_1, is the initial weight less the fuel weight burned, so W_1 = 4,000 lb. At an altitude of 25,000 ft ISA conditions, \varrho_{\infty} = \varrho_0 \, \sigma = 0.001066 slug/ft3. It is essential to be cautious: c_t is expressed in units per hour; thus, a factor of 3,600 is required to convert to units per second. Inserting all the values gives

    \[ R = \frac{2\times 3,600}{1.0} \sqrt{ \frac{2}{0.001066 \times 180.0}} \left( 20.875\right) \left( 5,000^{1/2} - 4,000^{1/2} \right) \]

which gives R = 3,622,400 ft = 596 nautical miles. The airspeed for the best range is obtained using

    \[ V_{\rm br} = \sqrt{ \frac{2 W}{\varrho_{\infty} \, S \, C_{L_{\rm br}}}} = \sqrt{ \frac{2 \times 5,000}{0.001066 \times 180.0 \times 0.251 }} = 455.7~\mbox{ft/s} \]

which is a true airspeed of 270 knots.

Best Airspeed for Maximum Range in a Wind

A common misconception concerns how wind affects an airplane’s optimal range. The key is to distinguish between the airplane’s speed through the air and its speed over the ground. The airplane’s aerodynamic characteristics are unaffected by a steady wind, but the wind changes the ground speed and, hence, the distance traveled over the ground for a given quantity of fuel.

As previously discussed, still-air range depends on the ratio of true airspeed to fuel flow. For a jet airplane with approximately constant TSFC, the fuel flow is proportional to the required thrust or drag, so maximum still-air range is obtained by maximizing

(71)   \begin{equation*} \frac{V_{\infty}}{D} \end{equation*}

or, equivalently, for steady level flight with a parabolic drag polar, by maximizing

(72)   \begin{equation*} \frac{C_L^{1/2}}{C_D} \end{equation*}

For a propeller-driven airplane with approximately constant BSFC and propeller efficiency, maximum still-air range is obtained by maximizing L/D. Therefore, the best-range airspeed depends on both the aerodynamic drag polar and the type of propulsion system.

In the presence of a direct wind component, the ground speed is

(73)   \begin{equation*} V_{\rm gs} = V_{\infty} + V_w \end{equation*}

where V_w is positive for a tailwind and negative for a headwind. For winds from other directions, only the component along the flight path over the ground is relevant, as shown in Figure 11.

The wind component along the flight path affects the aircraft’s ground-range performance.

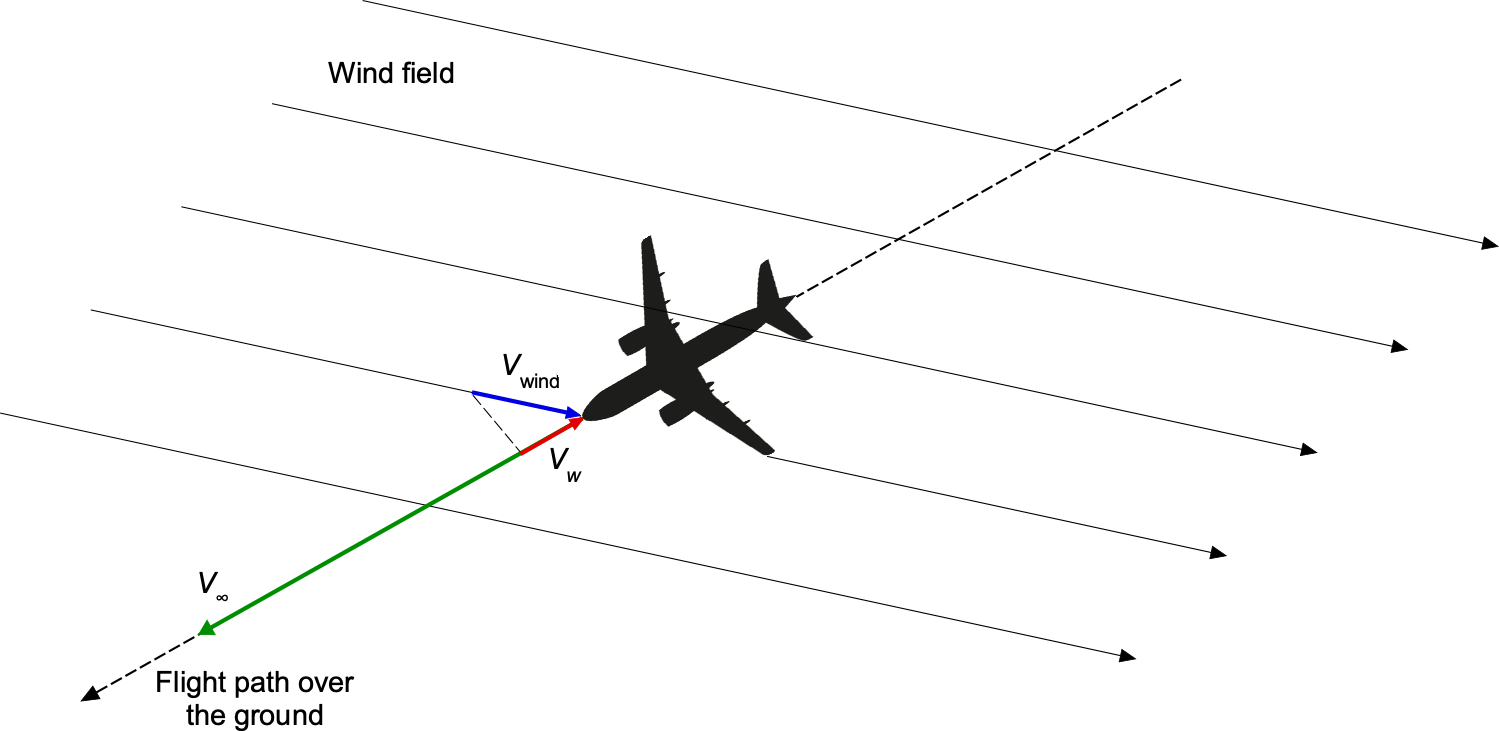
For a jet airplane with constant TSFC, the fuel flow rate is

(74)   \begin{equation*} \overbigdot{W}_{\!f} = c_t \, D \end{equation*}

Therefore, the fuel burned per unit distance over the ground is proportional to

(75)   \begin{equation*} \frac{\overbigdot{W}_{\!f}}{V_{\rm gs}} = \frac{c_t \, D}{V_{\infty}+V_w} \end{equation*}

The best-range true airspeed in wind is obtained by minimizing this quantity, i.e.,

(76)   \begin{equation*} \frac{d}{dV_{\infty}} \left( \frac{c_t \, D}{V_{\infty}+V_w} \right) = 0 \end{equation*}

For a jet airplane with a parabolic drag polar, the drag can be written as

(77)   \begin{equation*} D = A V_{\infty}^{2} + \frac{B}{V_{\infty}^{2}} \end{equation*}

where A and B depend on the airplane weight, altitude, wing area, and aerodynamic characteristics. Substitution into the optimum condition gives

(78)   \begin{equation*} A V_{\infty}^{5} + 2 A V_w V_{\infty}^{4} - 3 B V_{\infty} - 2 B V_w = 0 \end{equation*}

This equation is typically solved numerically to determine the optimal true airspeed.

The result can also be written in nondimensional form. The still-air best-range speed for the jet airplane is

(79)   \begin{equation*} V_{\rm br} = \left(\frac{3B}{A}\right)^{1/4} \end{equation*}

Defining

(80)   \begin{equation*} x = \frac{V_{\rm br,o}}{V_{\rm br}} \qquad \text{and} \qquad \lambda = \frac{V_w}{V_{\rm br}} \end{equation*}

the optimum-speed condition becomes

(81)   \begin{equation*} 3x^5 + 6\lambda x^4 - 3x - 2\lambda = 0 \end{equation*}

where V_{\rm br,o} is the best-range true airspeed in wind.

For a headwind, V_w 0, and the optimum true airspeed is lower. The magnitude of the correction depends on the airplane’s drag polar and on the ratio of wind speed to the still-air best-range speed.

Check Your Understanding #3 – Wind effects on the airspeed for the maximum range of a propeller-driven airplane

How does wind affect the optimal airspeed for maximum range in a propeller-driven airplane, and how can the best-range airspeed be determined in the presence of wind?

Show solution/hide solution.

For a propeller-driven airplane with constant brake-specific fuel consumption and propeller efficiency, the fuel flow is proportional to the required shaft power, i.e.,

(82)   \begin{equation*} \overbigdot{W}_{\!f} = c_b \, P_{\rm req} \end{equation*}

where c_b is the brake-specific fuel consumption. In still air, the distance traveled per unit of fuel is proportional to

(83)   \begin{equation*} \frac{V_{\infty}}{P_{\rm req}} \end{equation*}

so the best-range condition is obtained by minimizing

(84)   \begin{equation*} \frac{P_{\rm req}}{V_{\infty}} = D \end{equation*}

This condition corresponds to minimum drag or maximum L/D.

In the presence of a direct wind component, the ground speed is

(85)   \begin{equation*} V_{\rm gs} = V_{\infty} + V_w \end{equation*}

where V_w is positive for a tailwind and negative for a headwind. The fuel burned per unit distance over the ground is proportional to

(86)   \begin{equation*} \frac{\overbigdot{W}_{\!f}}{V_{\rm gs}} = \frac{c_b \, P_{\rm req}}{V_{\infty}+V_w} \end{equation*}

The best-range true airspeed in wind is obtained by minimizing this quantity, i.e.,

(87)   \begin{equation*} \frac{d}{dV_{\infty}} \left( \frac{P_{\rm req}}{V_{\infty}+V_w} \right) = 0 \end{equation*}

For a propeller-driven airplane with a parabolic drag polar, the required shaft power can be written as

(88)   \begin{equation*} P_{\rm req} = A V_{\infty}^{3} + \frac{B}{V_{\infty}} \end{equation*}

where A and B depend on the airplane weight, altitude, aerodynamic characteristics, and propeller efficiency. Substitution into the optimum condition gives

(89)   \begin{equation*} 2 A V_{\infty}^{5} + 3 A V_w V_{\infty}^{4} - 2 B V_{\infty} - B V_w = 0 \end{equation*}

This equation is typically solved numerically to determine the optimal true airspeed.

The still-air best-range speed is

(90)   \begin{equation*} V_{\rm br} = \left(\frac{B}{A}\right)^{1/4} \end{equation*}

Defining

(91)   \begin{equation*} x = \frac{V_{\rm br,o}}{V_{\rm br}} \qquad \text{and} \qquad \lambda = \frac{V_w}{V_{\rm br}} \end{equation*}

the optimum-speed condition becomes

(92)   \begin{equation*} 2x^5 + 3\lambda x^4 - 2x - \lambda = 0 \end{equation*}

where V_{\rm br,o} is the best-range true airspeed in wind.

For a headwind, V_w 0, and the optimum true airspeed is lower. The corrected speed must be obtained from the airplane’s power-required curve or by solving the preceding equation.

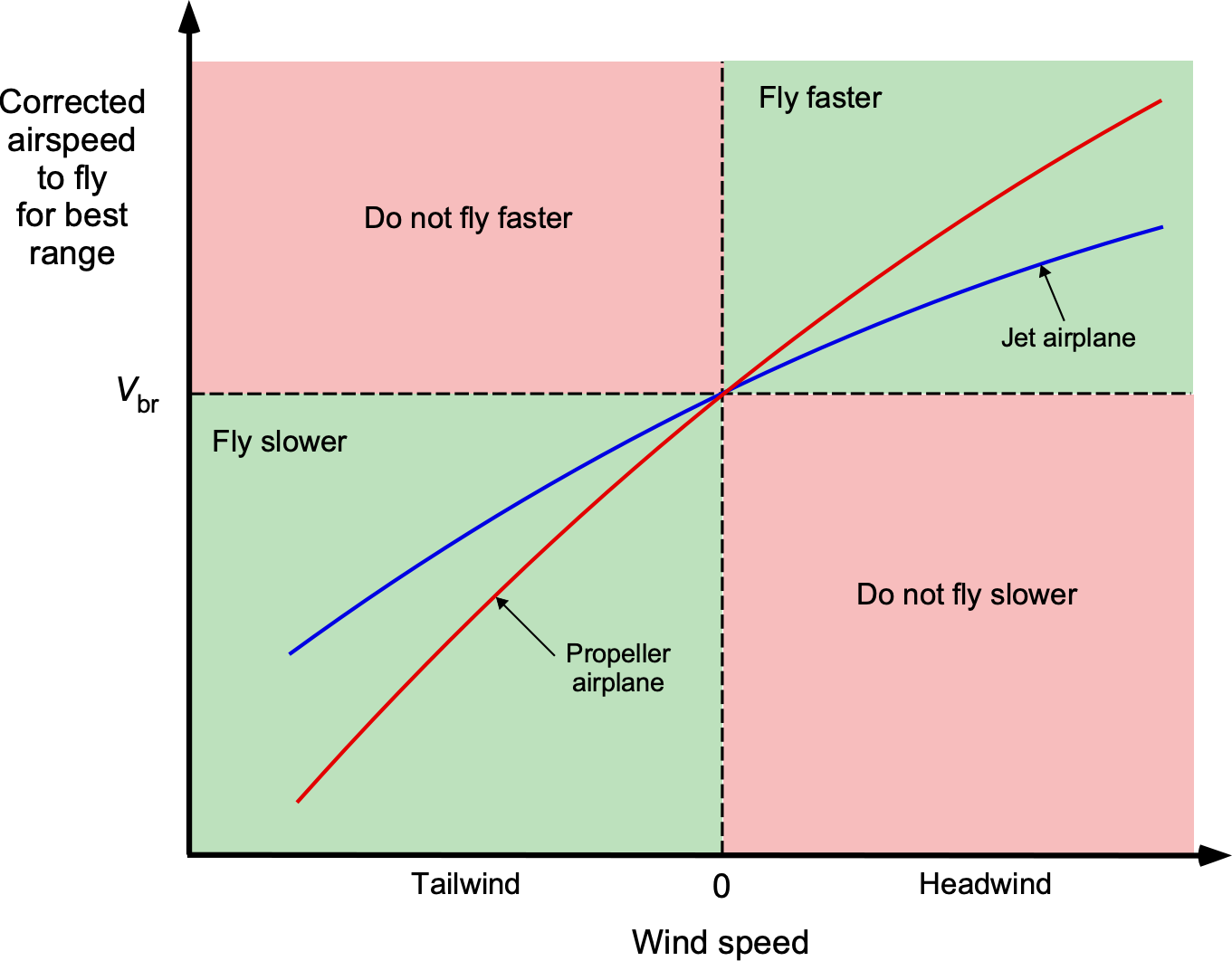
Payload-Range & Endurance Charts

The range an airplane can fly on a given quantity of fuel depends on its weight, aerodynamic efficiency, propulsion system efficiency, and operating altitude. The airplane’s total weight is the sum of its empty weight and useful load, where the useful load includes both payload and fuel. Payload consists of the passengers, cargo, weapons, or other specific mission equipment carried by the airplane, whereas fuel is consumed during flight and is not considered part of the payload.

For most aircraft, the maximum takeoff weight limits the combined payload and fuel that can be carried. Beyond a particular range, additional fuel can be loaded only by reducing the payload. i.e., according to the payload-range chart for that aircraft. For aircraft carrying external stores, such as fighter aircraft, the trade is more complicated because external fuel tanks and weapons also add parasite drag, structural weight, and installation penalties that can further reduce range and performance.

Airliners

Figure 12 illustrates a typical payload-range diagram for a commercial airliner. Airliners are mostly point designs because they spend most of their flight time cruising at a constant airspeed (Mach number) and high altitudes. The typical shape of the payload-range diagram is such that the aircraft can carry a maximum payload only within a specified range, i.e., the gray area bounded by the horizontal line between points A and B. 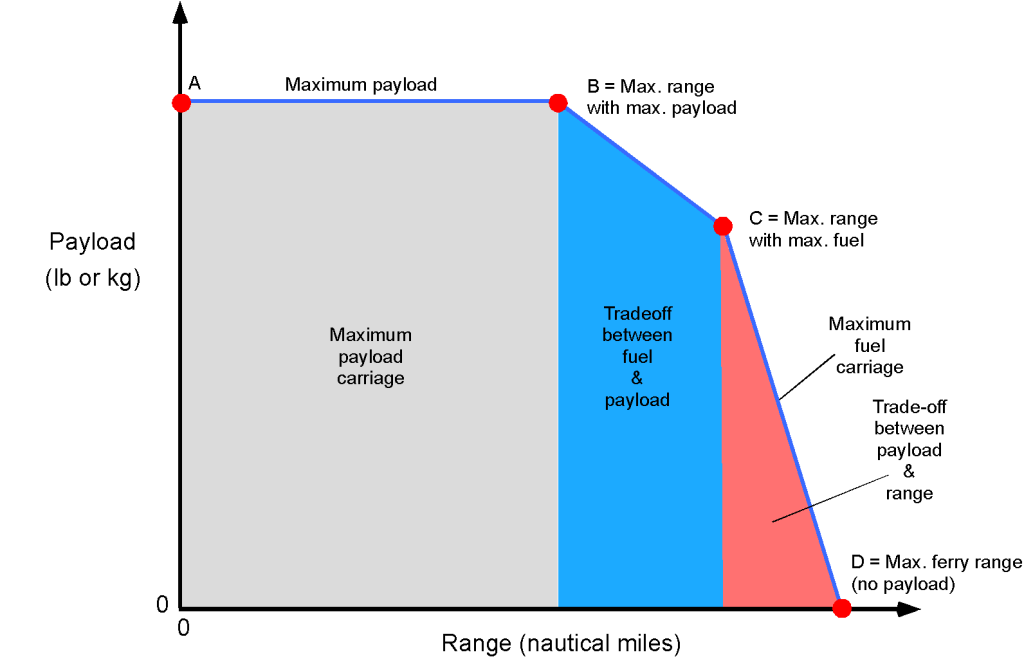When an aircraft operates at maximum payload, the fuel tanks are generally not filled to their full capacity; otherwise, they will become a constraint on achievable range.

A representative payload-range chart for a commercial airliner. The flight will be flown at a nominally constant cruise altitude and Mach number.

It can be seen from Figure 12 that longer flight ranges can be flown by reducing payload (i.e., limiting the number of passengers and cargo) in exchange for fuel, i.e., the blue area with the boundary marked between points B and C. Point C would be the maximum range with maximum fuel, i.e., the maximum fuel weight allowed for takeoff. However, for an airline operating in this region, it might not be economically viable, as it would require a significant payload reduction to achieve only a modest increase in range; in such cases, using another aircraft type or model might be preferable.

Along the boundary from C to D, the payload must be significantly reduced to achieve the required range; again, this might not be an economically viable operating condition. Point D would, for example, correspond to a ferry flight or to a situation in which a technical issue precludes carrying passengers, in which the aircraft is flown over an extended distance with maximum fuel but without any payload.

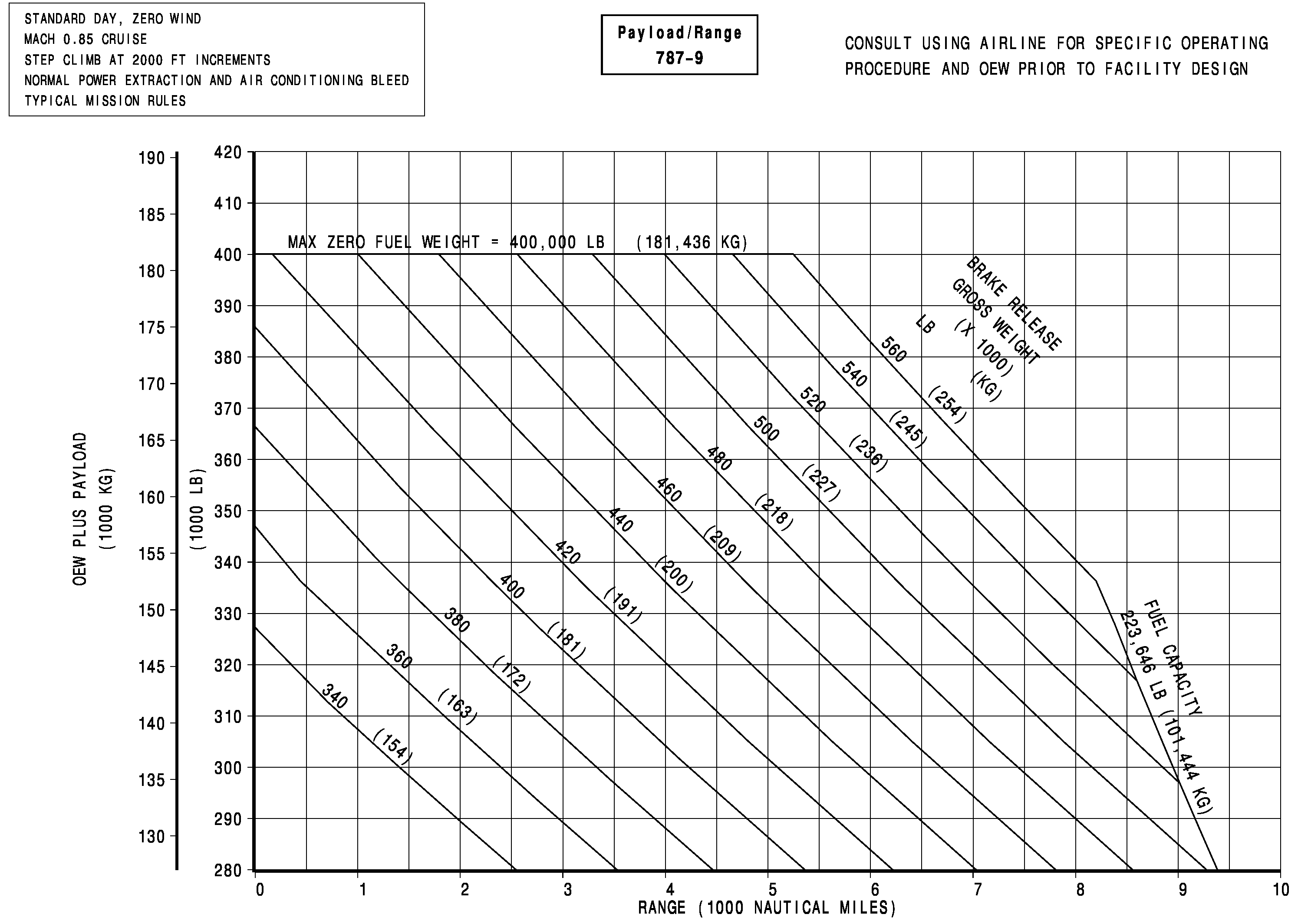
As an example, the payload-range chart for the Boeing B-787 Dreamliner is shown in Figure 13. Notice that with a maximum payload of passengers and cargo, the aircraft has a range of over 5,000 nautical miles at a cruise Mach number of 0.85. To achieve greater ranges, the payload must be traded off against fuel capacity. With maximum fuel but a substantially reduced payload, the aircraft can achieve a range of over 8,000 nautical miles. However, as noted previously, this will depend on the airline and how it is economically operated. Nevertheless, some airlines may opt for ultra-long-range flights with reduced passenger loads, thereby introducing higher ticket prices, for example, by operating the entire aircraft in an all-business-class configuration.

 

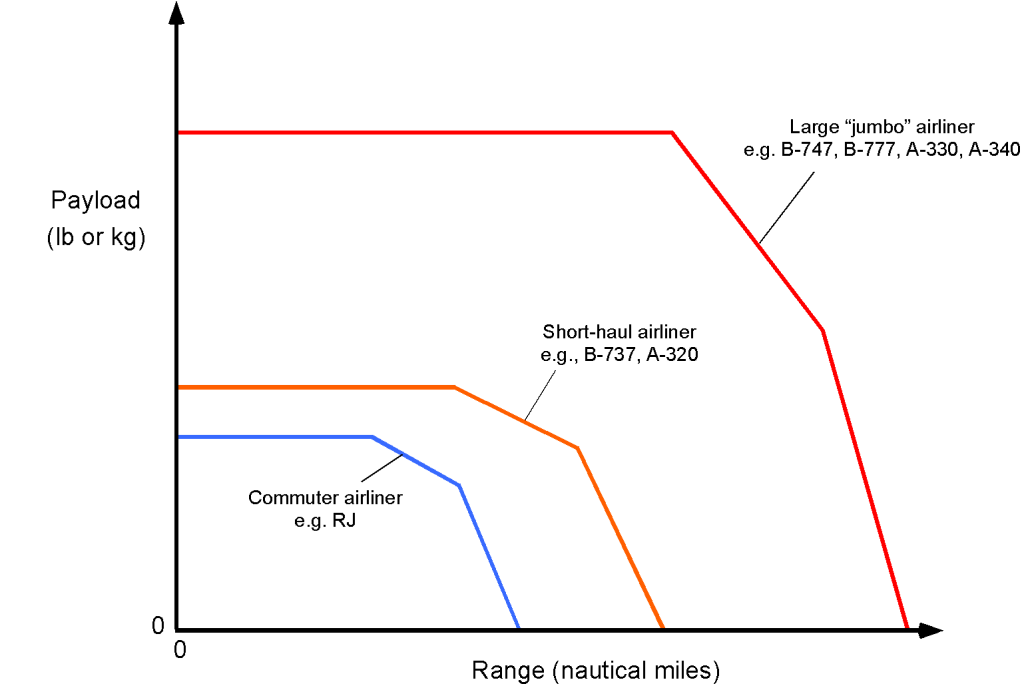
Payload-range chart for a Boeing B-787 Dreamliner. The payload-range trade-off becomes necessary for flight ranges exceeding 5,000 nautical miles.

The payload-range chart will vary by aircraft make and model. The payload and range of commercial airliners are carefully tailored to meet specific route requirements, thereby maximizing profitability. Different models of the same airliner will have different range and payload capabilities, e.g., the B-737 and A320 series. More generally, however, there is not a “one-size-fits-all” solution. Airliners are designed for either commuter flights of less than 500 nautical miles, short-haul flights of between 1,000 and 2,000 miles, or long-haul flights for transcontinental and transoceanic distances of 4,000 to 5,000 miles, as shown in the payload-range chart in Figure 14. For example, it would not make sense to operate a B-787 on short-haul segments when carrying only 100 passengers, and an RJ, with its more limited range, would require too many stops to serve direct transcontinental flights.

Representative payload-range charts for commuter airliners, short-haul airliners like the B-737, and long-haul “jumbo” airliners like the A-350.

Accessing payload-range and other performance characteristics

For access to airliner payload-range diagrams and other performance data, manufacturers provide “Airplane Characteristics for Airport Planning” documents. These include payload-range trade-offs, runway performance, airplane dimensions, and weight limitations. You can find these resources on the websites of Boeing and Airbus, as well as on the operator portals of Embraer and Bombardier. These documents are essential for engineers, airport planners, and operators analyzing aircraft performance and airport compatibility.

Military Aircraft

The payload-range trade-off for a military aircraft is more complicated than for an airliner because fuel tanks, weapons, and other stores may be carried externally (though not always). These stores add weight and drag and occupy mounting stations that could otherwise carry fuel or weapons. The takeoff weight can be written as

(93)   \begin{equation*} W_0 = W_{\rm empty} + W_{\rm crew} + W_{\rm internal\,fuel} + W_{\rm external\,fuel} + W_{\rm tanks} + W_{\rm weapons} \end{equation*}

subject to W_0 \leq W_{\rm TO,max}. If the airplane is already at its maximum takeoff weight, adding external fuel requires reducing the number of weapons or other stores.

External fuel tanks increase the available fuel but also increase the zero-lift drag coefficient of the aircraft, i.e.,

(94)   \begin{equation*} C_D = C_{D_0} + \Delta C_{D,\rm tanks} + \Delta C_{D,\rm weapons} + k C_L^2 \end{equation*}

The additional fuel increases the weight ratio in the Breguet range equation, while the added drag reduces the lift-to-drag ratio. For a representative flight segment, the range is

(95)   \begin{equation*} R = \frac{V_{\infty}}{c_t} \left(\frac{L}{D}\right) \ln\left(\frac{W_i}{W_f}\right) \end{equation*}

An external tank provides a net range benefit only when the increase in the weight-ratio term exceeds the reduction caused by the lower value of L/D. Because the weight-ratio term varies logarithmically, each additional tank generally provides a smaller incremental increase in range.

For a fighter aircraft, combat radius is usually more important than maximum one-way range. Combat radius is the maximum distance from the operating base at which the airplane can complete its mission, return, and retain the required fuel reserve, as previously shown in Figure 2. The fuel load must account for several mission segments, i.e.,

(96)   \begin{equation*} W_{\rm fuel} = W_{\rm climb} + W_{\rm outbound} + W_{\rm combat} + W_{\rm return} + W_{\rm reserve} \end{equation*}

Because the aircraft’s weight, drag, altitude, airspeed, and engine setting may differ across these segments, combat radius will not simply be half the ferry range.

External tanks are often used during the outbound cruise and released before combat. If the tanks are dropped, the range calculation must be divided into separate segments because the airplane becomes lighter and experiences less drag. Ideally, the external fuel is consumed first so that an empty tank can be dropped without wasting fuel. Retaining an empty tank incurs unnecessary weight and drag penalties, while releasing a partially full tank sacrifices fuel.

The configuration with the greatest ferry range may not provide the greatest military capability. Carrying maximum external fuel may require fewer weapons and may reduce climb, acceleration, and maneuvering performance. Conversely, a large weapons load increases weight and drag and reduces combat radius. The practical objective is to select the combination of fuel and weapons that allows the airplane to reach the required mission radius, complete the mission, return safely, and retain the prescribed fuel reserve. Careful mission planning requires knowledge of the aircraft’s performance characteristics.

Check Your Understanding #4 – External fuel tanks and fighter range

A fighter aircraft can be flown in either of the following configurations: Configuration A carries internal fuel and a full weapons load. Its initial cruise weight is 28,000 lb, its final weight after burning the usable cruise fuel is 21,000 lb, and its aerodynamic efficiency at the best-range condition is \left(C_L^{1/2}/C_D\right)_A = 20.0. Configuration B carries two external fuel tanks. The additional fuel increases the initial cruise weight to 31,500 lb, while the empty tanks and pylons increase the final weight to 21,800 lb. The drag of the tanks reduces the aerodynamic efficiency to \left(C_L^{1/2}/C_D\right)_B = 16.5.
Assume that both configurations fly at the same altitude and have the same wing area and TSFC. Using the Breguet range equation for a jet airplane, determine which configuration has the greater cruise range and the percentage increase or decrease relative to Configuration A. What additional factors must be considered before concluding that Configuration B provides the better combat configuration?

Show solution/hide solution.

For a jet airplane flying at the same altitude with the same wing area and TSFC, the range is proportional to

    \[ R \propto \left(\frac{C_L^{1/2}}{C_D}\right) \left(W_i^{1/2}-W_f^{1/2}\right) \]

For Configuration A, then

    \[ R_A \propto 20.0 \left( 28,000^{1/2}-21,000^{1/2} \right) = 448.4 \]

For Configuration B, then

    \[ R_B \propto 16.5 \left( 31,500^{1/2}-21,800^{1/2} \right) = 495.2 \]

Therefore,

    \[ \frac{R_B}{R_A} = \frac{495.2}{448.4} = 1.104 \]

so the external-tank configuration increases the estimated cruise range by approximately

    \[ \left(1.104-1\right)\times 100 = 10.4% \]

The additional fuel provides a net range benefit despite the reduction in aerodynamic efficiency. However, the increase in range is much smaller than the percentage increase in fuel consumption because the external tanks add both weight and drag.

Configuration B is not necessarily the better combat configuration. The external tanks may occupy weapon stations, require a reduction in weapons load to meet the maximum takeoff weight limit, and reduce acceleration, climb rate, maneuverability, and the allowable load factor. The actual combat radius must also include climb, outbound cruise, combat maneuvering, return flight, and reserve fuel.

General Aviation Aircraft

Of course, there are many other types of aircraft besides airliners, including general aviation (GA) airplanes, drones, and helicopters, for which payload, range, and endurance are also important. Therefore, pilots need to know, for example, the fuel required for a given range or the flight conditions that maximize range for flight planning. These aircraft types have relatively low payloads relative to their gross weight, so the payload-range trade-off is less severe than for an airliner. However, the aircraft’s range is still affected by altitude and engine power settings.

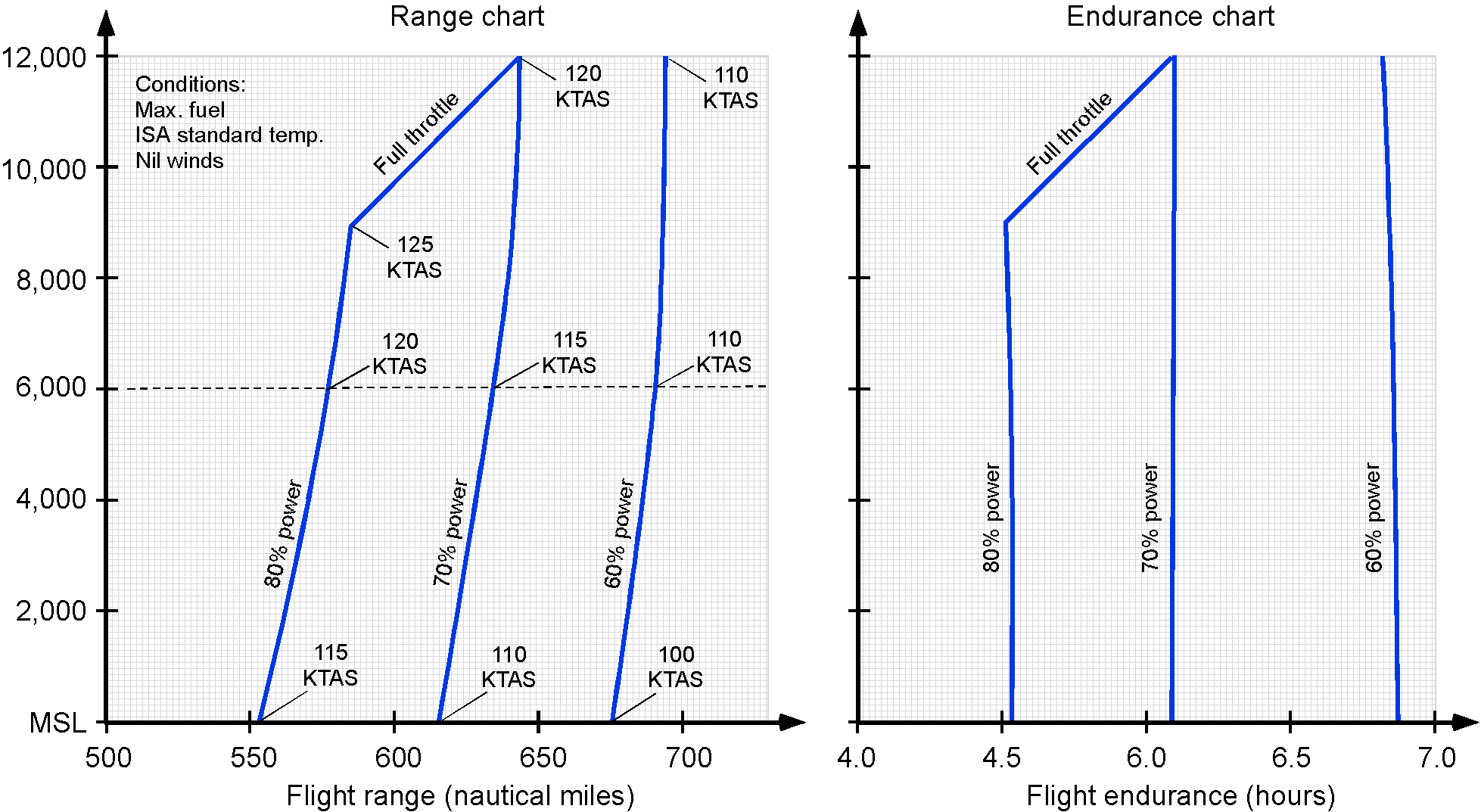
Figure 15 shows a propeller-driven GA aircraft’s range and endurance performance charts. For an airliner, flight endurance is not a particularly significant operating condition. However, a GA aircraft or drone (with a piston or jet engine) could be used for reconnaissance, surveillance, or other applications where flight endurance is a primary mission requirement. In this regard, range and endurance charts are available for flight planning.

Representative range and endurance charts for a general aviation aircraft.

Electric Airplanes

For an electrically powered airplane or drone, both endurance and range are directly determined by the battery’s energy capacity and the power required during flight. Unlike a fossil-fuel-burning aircraft, the mass of the energy source remains constant during discharge, yielding straightforward linear relationships.

However, the total energy available for propulsion will not be the battery’s full rated capacity; it will be the usable fraction remaining after accounting for the allowable depth of discharge (DOD) and any required energy reserve, e.g., for landing and contingencies. If the nominal stored energy is E_{\mathrm{bat}}, the usable energy is

(97)   \begin{equation*} E_{\mathrm{use}} = \eta_{\text{\scriptsize DOD}} \,(1-\alpha)\,E_{\mathrm{bat}} \end{equation*}

where \eta_{\text{\scriptsize DOD}} is the depth-of-discharge fraction (typically 0.8–0.9) and \alpha is the reserve fraction that must remain at the end of flight for safety or regulatory reasons.

The endurance, or total flight time, is then

(98)   \begin{equation*} t_E = \frac{\eta_{\mathrm{sys}}\,E_{\mathrm{use}}}{P_{\mathrm{req}}} = \frac{\eta_{\mathrm{sys}}\,\eta_{\text{\scriptsize DOD}}\,(1-\alpha)\,E_{\mathrm{bat}}}{P_{\mathrm{req}}} \end{equation*}

where P_{\mathrm{req}} is the shaft power required to sustain the desired flight condition and \eta_{\mathrm{sys}} is the electrical-system efficiency, including the battery, controller, and motor, but excluding the propeller.

For a steady cruise of a fixed-wing drone, the required power can be written as

(99)   \begin{equation*} P_{\mathrm{req}} = \frac{D\,V_\infty}{\eta_p} \end{equation*}

where D is the aerodynamic drag, {V_\infty} is the flight speed, and \eta_p is the propeller efficiency.

The flight range R is the horizontal distance traveled during that time, i.e.,

(100)   \begin{equation*} R = V_\infty \,t_E = V_\infty\,\frac{\eta_{\mathrm{sys}}\,\eta_{\text{\scriptsize DOD}}\,(1-\alpha)\,E_{\mathrm{bat}}}{P_{\mathrm{req}}} \end{equation*}

Substituting for P_{\mathrm{req}} for the airplane gives

(101)   \begin{equation*} R = \frac{\eta_{\mathrm{sys}}\, \eta_p\,\eta_{\text{\scriptsize DOD}}\,(1-\alpha)\,E_{\mathrm{bat}}}{D} \end{equation*}

Because the drag can be written as D = W/(L/D), this previous result becomes

(102)   \begin{equation*} R = \eta_{\mathrm{sys}} \, \eta_p\,(L/D)\,\eta_{\text{\scriptsize DOD}}\,(1-\alpha)\,\frac{E_{\mathrm{bat}}}{W} \end{equation*}

This expression shows that range increases linearly with the stored energy per unit weight and with the aerodynamic efficiency L/D, but is limited by the depth of discharge and any required reserve fraction. Typical values are \eta_{\text{\scriptsize DOD}} = 0.8–0.9 and \alpha = 0.1–0.2, so the usable energy may be 65–80% of the nominal battery capacity.

Figure 16 shows the calculated endurance and range of an electric drone as functions of available battery energy. The nominal stored energy is E_{\mathrm{bat}} = 1,000 Wh, of which only a fraction is usable after accounting for the depth of discharge \eta_{\text{\scriptsize DoD}} = 0.85 and a reserve fraction \alpha = 0.15. The resulting usable energy is E_{\mathrm{use}} = 722 Wh. With a system efficiency \eta_{\mathrm{sys}} = 0.85, required cruise power P_{\mathrm{req}} = 500 W, and flight speed V_\infty = 20 m/s, the maximum flight time is about 1.2 hours, and the corresponding range is approximately 87 km. The shaded region beyond E_{\mathrm{use}} indicates the energy that cannot be used because of battery discharge and reserve limitations.

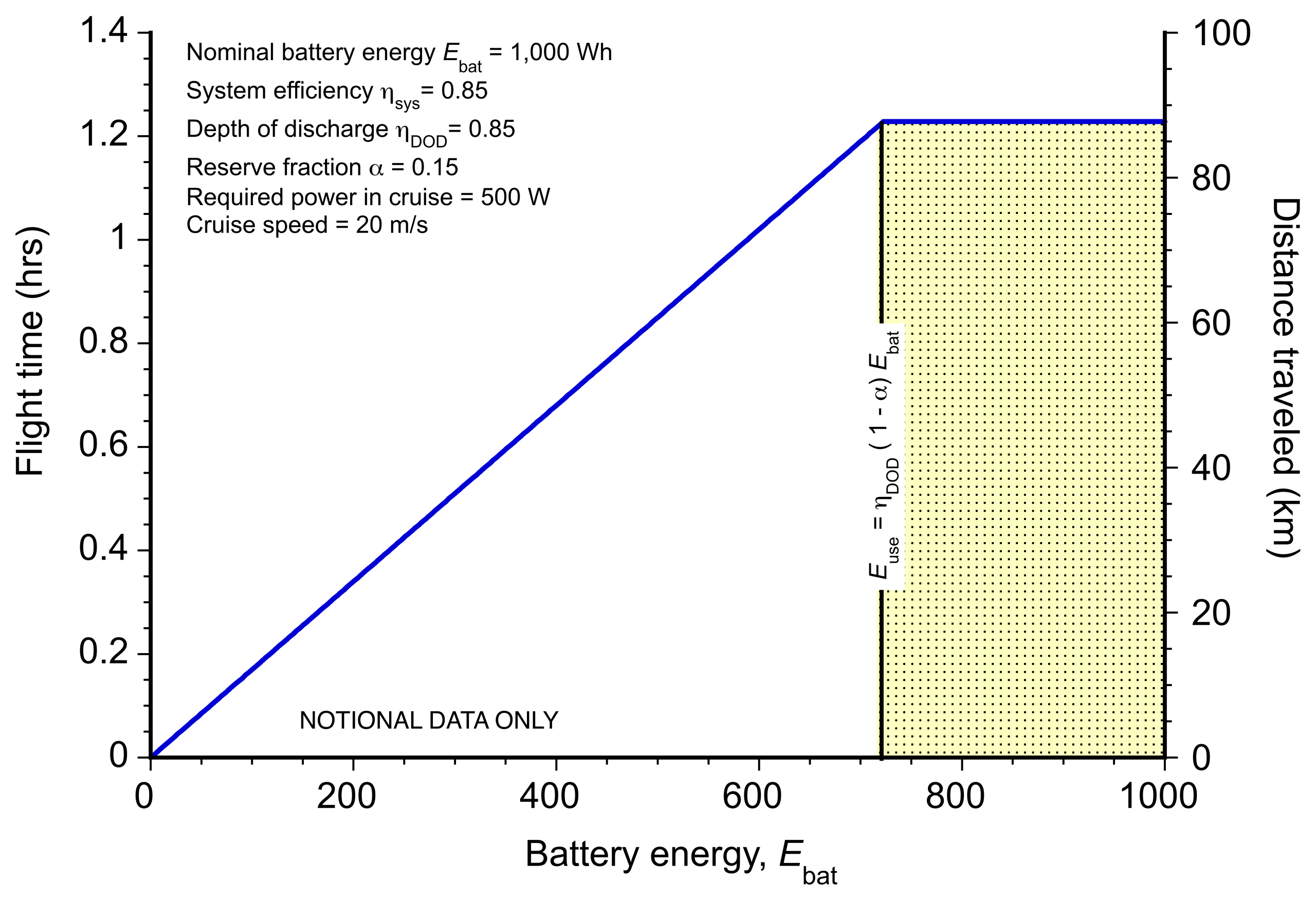
Endurance and range of an electric drone as functions of stored battery energy. Both increase linearly with usable energy.

The battery energy density, which is typically 200–300 Wh/kg for lithium-ion systems, therefore sets an upper bound on flight time and range. The overall efficiency \eta_{\mathrm{sys}}\eta_p usually lies between 0.7 and 0.9. Hovering multirotor drones require significantly higher power because hover power scales approximately with W^{3/2}, which shortens their flight time relative to fixed-wing aircraft. Environmental factors, including air density, temperature, and discharge rate, will also impact the achievable flight endurance.

Summary & Closure

Estimating flight range (distance) and flight endurance (time) is fundamental to the design process for all aircraft types. In many (most) cases, such as for a commercial airliner, the aircraft’s primary mission is to fly as far as possible on the least fuel and at the lowest cost. In this regard, aerodynamic efficiency (a good lift-to-drag ratio) and engine efficiency (low specific fuel consumption) are critical. The maximum flight endurance is irrelevant for an airliner. However, the flight conditions for maximum range are typically at a slightly lower airspeed than the top cruise speed. In practice, an aircraft typically flies at an airspeed slightly above the maximum-range speed to minimize transit time. Military missions often include reconnaissance, which means aircraft are flown to maximize total time in the air, i.e., at airspeeds that provide the best flight endurance. However, maximizing range and endurance depends on engine and aerodynamic efficiency.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • Think of some actual airplane flight profiles or missions where maximum flight range would be essential and where maximum flight endurance would be necessary.
  • For a reconnaissance or search mission in a P3 Orion, should the airplane be flown at the airspeed that provides the best range or the airspeed that offers the best endurance? Explain carefully.
  • For what type(s) of flight profile or mission would an airplane not be flown at its best range or endurance airspeeds?
  • What kind of flight profile (mission) is typically flown by a blimp?
  • Explain why the airspeeds to fly for the best endurance or range depend on the airplane’s weight and altitude. Use any equations and/or graphs you think are needed to make the points of your arguments.
  • Does the flight range and the speed to fly for the best range depend on the winds? Explain.
  • Does flight endurance depend on the winds? Explain.
  • When designing a new variant of a jet aircraft, it is desirable to increase airspeed to optimize range. What steps are necessary to achieve this? Assume operations at the same flight altitude.

Other Useful Online Resources

To dive deeper into fuel burn, flight range, endurance, payload-range charts, etc., check out some of these online resources:

  1. The power is measured on a brake dynamometer, which is a mechanical device that provides resistance to the engine shaft. ↵
  2. Historically, the term engine deck referred quite literally to a deck of punch cards containing the engine performance data supplied by the engine manufacturer to the airframe company. Although those days are long past, the name has persisted. Today, an engine deck is typically delivered as a digital data package or an executable program, enabling the aircraft manufacturer to model the engine’s performance across various flight conditions and throttle settings. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2026 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n37

Share This Book