"

42 Altitude Definitions & Measurement

Introduction

As with airspeed, an aircraft’s altitude is critical to piloting and engineering. Pilots are concerned with an aircraft’s altitude relative to sea level or above ground, particularly during takeoff and landing and when avoiding terrain. Naturally, the altitude reference (datum) used is essential, as all airplanes must fly at altitudes measured relative to the same standard reference, which is necessary for air traffic control and collision avoidance. Pilots must also anticipate their aircraft’s performance, which primarily depends on altitude and ambient air temperature.

Engineers, however, are more interested in measuring air density at a given flight altitude. In this case, altitude can be determined from air density, which is computed from pressure and temperature using the equation of state. Additionally, an altimeter is a pressure-measuring instrument that enables the determination of local air pressure from altitude. The outside air temperature can also be measured during flight using a thermometer. Therefore, the proper basis of altitude measurement and how such measurements are used in engineering practice to find air density must be understood.

Learning Objectives

  • Understand how an altimeter works and how to read one.
  • Appreciate the principles associated with altitude measurement.
  • Know the differences between pressure altitude and density altitude.
  • Be able to calculate density altitude from values of temperature and pressure altitude.

What is an Altimeter?

Like the airspeed indicator (ASI), an altimeter is a pressure-measuring (pneumatic) instrument. An altimeter responds to ambient static pressure, so it must be connected to the aircraft’s static pressure reference source, i.e., the static port. However, unlike an airspeed indicator with two ports, one for total (or ram) pressure and the other for static pressure, an altimeter has only one port for static pressure. The mechanical design of an altimeter is shown in the schematic below. Although it appears relatively simple, it is a delicate and precise instrument that requires careful, repeated calibration for use in aviation practice.

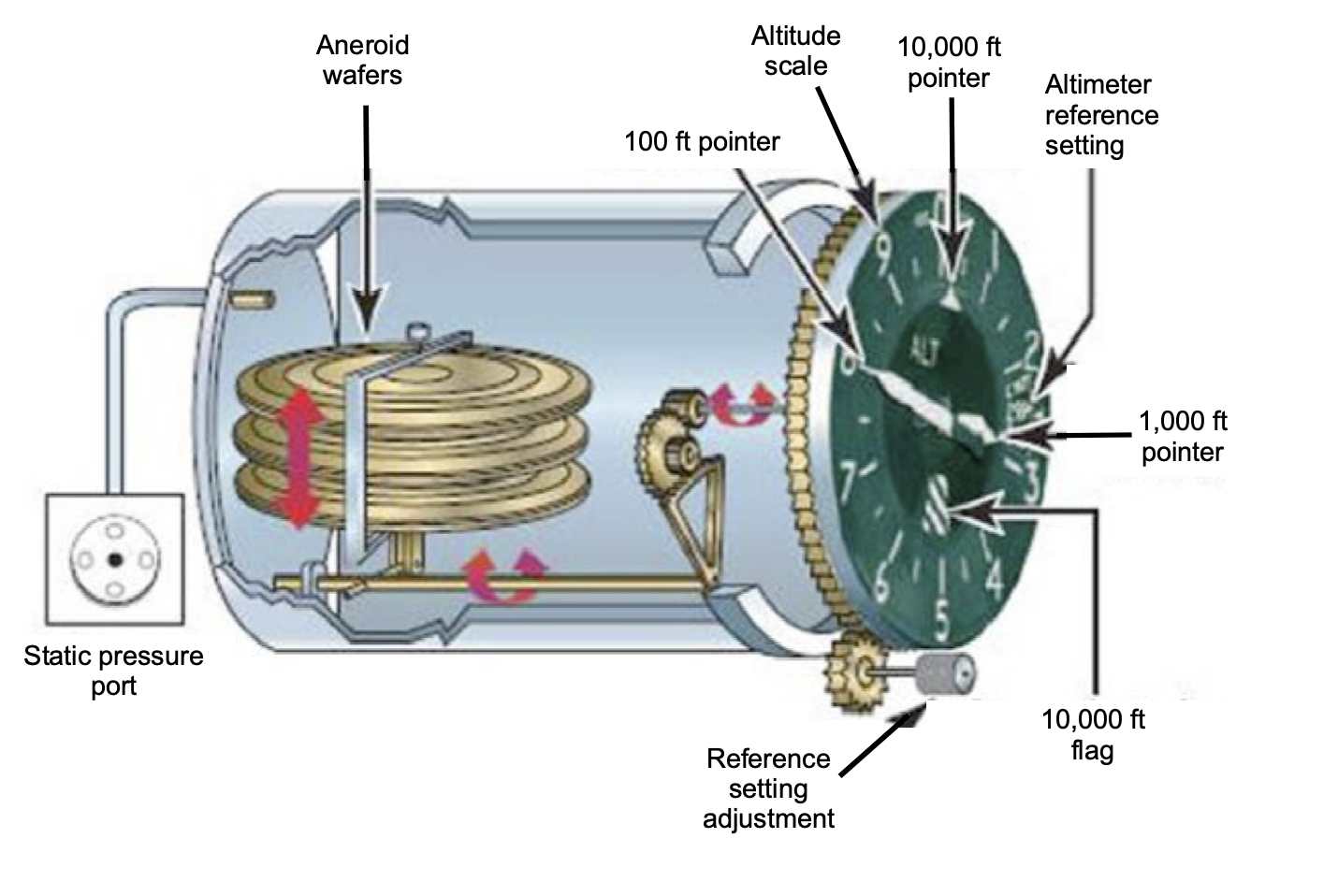
The inner workings of an altimeter. The altimeter’s face features a circular scale, similar to a clock, with three pointers that measure altitude to approximately ±10 feet.

Inside the altimeter, the expansion and contraction of an evacuated aneroid wafer stack are detected by a system of levers and gears and then displayed by the rotational movement of the pointer (needles) on a face with a scale, much like that of a clock. An altimeter display has three needles or hands: one for 100s of feet, another for 1,000s of feet, and a third for 10,000s of feet. Notice from the figure above that the altimeter also has a setting window called the Kollsman window. On the bottom-left side of the altimeter is a knurled adjustment knob for adjusting the reference pressure displayed in the Kollsman window. The altimeter will therefore read differently depending on the reference pressure value set in this window.

Reading an Altimeter

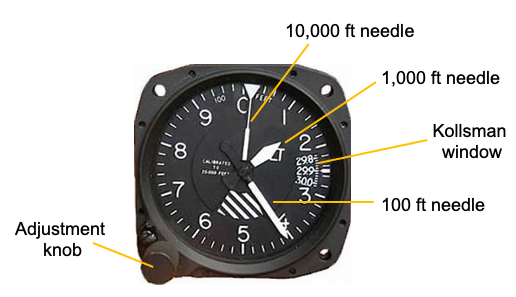
Reading an altimeter is relatively easy, but it does require some practice. In reference to the image below, the 10,000-foot pointer is the longest and narrowest needle on the altimeter; it rotates by one unit for every 10,000-foot change in altitude. The shortest and widest needle measures increments of 1,000 feet, so a full rotation of the needle is an altitude increment of 10,000 feet. The medium-length hand reads 100s of feet, so a full rotation corresponds to an altitude increment of 1,000 feet. In this regard, the numbers on the dial each represent 100-foot increments, and the tick marks between them represent 20-foot increments.

For example, in the case shown below, the 100-foot pointer is just past the number 4 (410 feet), the 10,000-foot pointer has just moved from 0, and the 1,000-foot pointer is between the 1 and the 2, so it is 1,000 feet plus. Therefore, in this case, the altimeter, as shown, reads 1,410 feet relative to the pressure datum value set in the Kollsman window.

In this case, the altimeter’s face displays a reading of 1,410 ft.

All aviation altimeters are formally calibrated to account for pressure variations in the International Standard Atmosphere (ISA). Typically, the mechanical design of an altimeter allows calibration within a certain tolerance, typically {\pm}20 feet for a general aviation (GA) aircraft, which is sufficient for piloting. However, for engineering use, a more precise and formal calibration will be necessary to account for mechanical errors, as with the ASI. This calibration is obtained by measuring the altimeter in a vacuum tank against known pressure values or against a previously calibrated reference altimeter. Again, the results of the mechanical correction are usually presented as a chart or a table of values, along with those for the airspeed indicator.

Test Your Understanding of How to Read an Altimeter

Examine the faces of the three altimeters, A, B, and C, shown below. What is the altitude reading in each case?

Answers: A: 10,500 feet. B: 14,500 feet. C: 9,500 feet

Review of ISA Pressure & Density Variations

Before proceeding with the formal definitions of pressure altitude and density altitude, it is helpful to summarize the previously derived equations of the International Standard Atmosphere (ISA).

ISA Temperature Variations

The temperature T in the international standard atmosphere is given by

(1)   \begin{equation*} T = T_0 - B \, h = 59.0 -\left( \frac{3.57}{1,000} \right) h \quad \hbox{in units of $^{\circ}$F} \end{equation*}

or

(2)   \begin{equation*} T = 59.0 - 0.00357 \, h \quad \hbox{in units of $^{\circ}$F} \end{equation*}

In this case, {h} is expressed in feet (ft), and B is called the standard atmospheric lapse rate. This temperature lapse equation is valid only up to the troposphere’s limit, approximately 36,000 ft. The value of B is 3.57^{\circ}F per 1,000 ft of altitude or 0.00357^{\circ}F per ft = 0.00357^{\circ}R per ft.

In SI units, the ISA temperature lapse equation can be written as

(3)   \begin{equation*} T = T_0 - B \, h = 15.0 - \left( \frac{6.5}{1,000} \right) h\quad \hbox{in units of $^{\circ}$C} \end{equation*}

or

(4)   \begin{equation*} T = 15 - 0.0065 \, h\quad \hbox{in units of $^{\circ}$C} \end{equation*}

where {h} is expressed in meters (m), and the ISA lapse rate, in this case, is 6.5^{\circ}C per 1,000 m. This lapse rate is also equivalent to 1.981^{\circ}C per 1,000 ft, giving

(5)   \begin{equation*} T = 15 - 0.001981 \, h \quad \hbox{in units of $^{\circ}$C} \end{equation*}

with {h} being measured in feet (ft). Measuring altitude in feet for aeronautical and aviation purposes is standard practice. Often, the ratio of the ISA temperature at a given altitude to the MSL temperature is used, which is given the symbol \theta, i.e.,

(6)   \begin{equation*} \theta = \frac{T}{T_0} \end{equation*}

ISA Pressure Variations

The resulting local pressure in the ISA, p, at any altitude {h} relative to the value at MSL, p_0, is

(7)   \begin{equation*} \frac{p}{p_0} = \delta = \left( 1 - \frac{B}{T_0} \, h \right)^{g/RB} = \left( 1 - 6.883\times 10^{-6} \, h \right)^{5.256} \end{equation*}

where {h} in this latter equation is measured in feet (ft). Notice that in USC units, then

(8)   \begin{equation*} \frac{B}{T_0} = \frac{3.57/1,000}{59.0+ 459.67} = 6.883\times 10^{-6} \end{equation*}

The gas constant for air, R, in USC units is 1716.49 ft lb slug^{-1}R^{-1} and in SI units it is 287.057 J kg^{-1} K^{-1}. Therefore, the value of g/RB, which is a non-dimensional grouping, is

(9)   \begin{equation*} \frac{g}{R B} = \frac{32.17}{1716.49 \times 0.00357} = \frac{9.81}{287.057 \times 0.0065} = 5.256 \end{equation*}

so its numerical value does not depend on the unit system. If {h} were to be measured in meters (m), then

(10)   \begin{equation*} \frac{p}{p_0} = \delta = \left( 1 - \frac{B}{T_0} \, h \right)^{5.256}= \left( 1 - 2.256\times 10^{-5} \, h \right)^{5.256} \end{equation*}

where, in this case, using SI units gives

(11)   \begin{equation*} \frac{B}{T_0} = \frac{6.5/1,000}{15.0+ 273.15} = 2.256\times 10^{-5} \end{equation*}

Remember that under standard MSL conditions, the value of p_0 is 2116.4 lb/ft{^{2}} or 101.325 kN/m^{^2}.

ISA Density Variations

In accordance with the assumptions made with the ISA model, the pressure and density can be related using the equation of state, i.e.,

(12)   \begin{equation*} \frac{\varrho}{\varrho_0} = \frac{p}{p_0} \left( \frac{T_0}{T} \right) \end{equation*}

Therefore, if the local temperature corresponds to the standard local temperature in the ISA, i.e., T_0 - B \, h, then

(13)   \begin{equation*} \frac{\varrho}{\varrho_0} = \frac{p}{p_0} \left( \frac{T_0}{T_0 - B \, h} \right) \end{equation*}

and so the local density in the ISA relative to MSL is

(14)   \begin{equation*} \frac{\varrho}{\varrho_0} = \sigma = \bigg( 1 - \frac{B}{T_0} \, h \bigg)^{\left(\displaystyle{\frac{g}{R B} - 1 }\right)} = \left( 1 - 6.883\times 10^{-6} \, h \right)^{4.256} \end{equation*}

where {h} is measured in feet (ft). If {h} is measured in meters (m), then

(15)   \begin{equation*} \frac{\varrho}{\varrho_0} = \sigma = \left( 1 - \frac{B}{T_0} \, h \right)^{4.256} = \left( 1 - 2.256\times 10^{-5} \, h \right)^{4.256} \end{equation*}

Remember that under standard MSL conditions, the value of \varrho_0 is 0.002378 slugs/ft{^{2}} or 1.225 kg/m^{^3}.

Pressure Altitude

As previously described, an altimeter is a calibrated pressure gauge, and its calibration is based on the ISA. Therefore, it is appropriate to use the altimeter to measure the air pressure at which the aircraft is flying, as indicated by the pressure altitude. By definition, the pressure altitude, h_p, is the altitude in the ISA corresponding to the prevailing ambient local static pressure. The advantage of using pressure altitude as a reference is that its value depends solely on the local ambient pressure.

Using the relationship for pressure in the ISA given by Eq. 10, the value of the pressure altitude, h_p, as measured in feet (ft), is given by

(16)   \begin{equation*} h_p = \frac{T_0}{B} \left( 1 - \left( \frac{p}{p_0} \right)^{0.1903} \right) = \frac{518.67}{0.00357} \left( 1 - \left( \frac{p}{p_0} \right)^{0.1903} \right) \end{equation*}

where T_0 = 59.0 + 459.67 = 518.67^{\circ}R in USC, so

(17)   \begin{equation*} h_p = 145286.0 \left( 1 - \left( \frac{p}{p_0} \right)^{0.1903} \right) \end{equation*}

The measurement pressure altitude from the altimeter will also be subject to static position (SPE) errors and mechanical errors (instrument error correction, or IEC), which must be obtained through calibration. The SPE error is obtained in a manner similar to that of the airspeed indicator (ASI): the true static pressure is measured well behind the aircraft during flight testing using a trailing-cone apparatus, as shown in the figure below. The SPE altitude error, \Delta h_{p_{\rm SPE}}, as it affects the true pressure altitude value, must be mapped out over the entire operating envelope of the airplane.

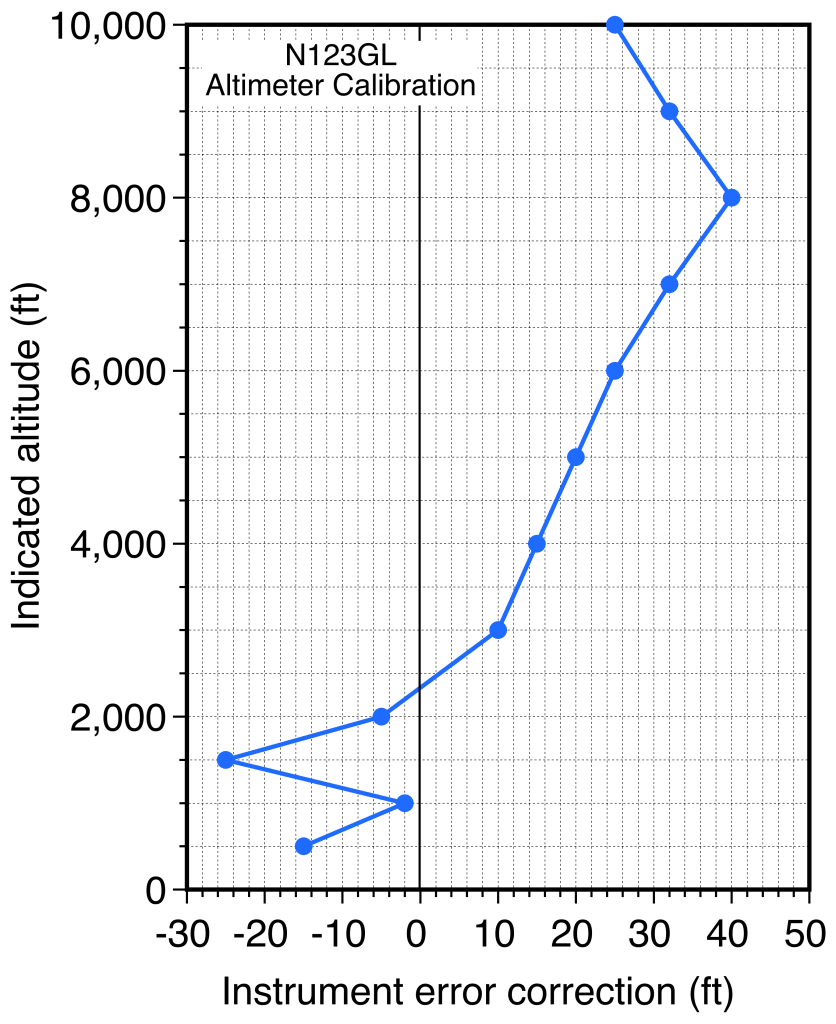
A SPE error correction chart for an altimeter, which may read high or low depending on airspeed and altitude.

Likewise, with the IEC, the altimeter must be calibrated against a reference altimeter in an evacuated chamber to obtain \Delta h_{p_{\rm IEC}}, as shown in the example below. The data is usually presented in tabular form, although a curve fit may be used. The errors are generally minor but are non-negligible for engineering purposes.

A mechanical instrument error calibration (IEC) chart for an altimeter, which may read high or low.

The corrected pressure altitude is then

(18)   \begin{equation*} h_p = h_{p_{\rm \, IND}} - \Delta h_{p_{\rm \, SPE}} - \Delta h_{p_{\rm \, IEC}} \end{equation*}

where {h_{p_{\rm \, IND}}} is the indicated pressure altitude on the altimeter. Such errors are usually small enough to be ignored for piloting purposes, but they must be accounted for in engineering calculations, including those related to aircraft and engine performance measurements.

Density Altitude

While pressure altitude can be measured directly on a suitably calibrated altimeter, ultimately, the air density in which the aircraft is flying affects its performance and its engines. Therefore, determining air density is required for engineering analysis and performance work.

By definition, the density altitude, h_{\varrho}, is the altitude in the ISA that corresponds to the prevailing ambient density. The value of the density altitude (again, measured in units of feet) can be obtained by rearranging Eq. 14 to get

(19)   \begin{equation*} h_{\varrho} = \frac{T_0}{B} \left( 1 - \left( \frac{\varrho}{\varrho_0}\right)^{0.235}\right) = \frac{518.67}{0.00357} \left( 1 - \left( \frac{\varrho}{\varrho_0}\right)^{0.235} \right) \end{equation*}

Therefore,

(20)   \begin{equation*} h_{\varrho} = 145286.0 \left( 1 - \left( \frac{\varrho}{\varrho_0}\right)^{0.235}\right) \end{equation*}

where h_{\varrho} is in units of feet.

Relating Density Altitude & Pressure Altitude

As previously explained, pressure altitude can be read directly using an altimeter calibrated according to the ISA using Eq. 17. However, the altimeter’s reference pressure must be set to the standard MSL value. This is done by setting the reading Kollsman window to the MSL ISA value of 29.92 in Hg (inches of mercury) or 1013.2 millibars (depending on the specific altimeter), which are equivalent to the ISA MSL or p_0 values of 2116.4 lb/ft{^{2}} or 101.325 kPa, respectively, in engineering units. The value of h_p can then be directly read off the altimeter, assuming it is properly calibrated and that mechanical and static position errors are corrected.

Unlike pressure altitude, density altitude must be calculated from pressure altitude measurements corrected for non-standard ambient temperature conditions relative to the ISA temperature standard. In this regard, “nonstandard” refers to a local temperature that deviates (i.e., is higher or lower) from the ISA standard temperature value at a given pressure altitude. For example, density decreases with increasing temperature, whereas density altitude is higher than pressure altitude.

Density Altitude Calculation

Recall that pressure and density are related using the equation of state, so the density ratio in the ISA can be written as

(21)   \begin{equation*} \frac{\varrho}{\varrho_0} = \frac{p}{p_0} \left( \frac{T_0}{T_{\rm {\tiny ISA}}} \right) \end{equation*}

where T_{\rm {\tiny ISA}} is the local standard temperature according to the ISA, as given by

(22)   \begin{equation*} T_{\rm {\tiny ISA}} = T_0 - B \, h_p \end{equation*}

where h_p is the pressure altitude. If the pressure altitude and the outside air temperature, T_{\rm {\tiny OAT}}, are both available (e.g., measured), then by using Eqs. 17 and 20 and some algebra, then the corresponding density altitude can be determined from

(23)   \begin{equation*} h_{\varrho} = \frac{T_0}{B} - \frac{T_{\rm {\tiny OAT}}}{B} \left( \frac{T_0 - B \, h_p}{T_{\rm {\tiny OAT}}} \right)^{\displaystyle{\frac{1}{1 - RB/g}}} \end{equation*}

Because g/RB = 5.256 then

(24)   \begin{equation*} h_{\varrho} = \frac{T_0}{B} - \frac{T_{\rm {\tiny OAT}}}{B} \left( \frac{T_0 - B \, h_p}{T_{\rm {\tiny OAT}}} \right)^{1.235} \end{equation*}

This means that Eq. 24 can be used to find the density altitude for any given pressure altitude and outside air temperature values. It can also be seen that if the local temperature equals the standard ISA temperature at the pressure altitude, i.e., T_{\rm {\tiny OAT}} = T_0 - B \, h_p = T_{\rm {\tiny ISA}}, then h_{\varrho} = h_p. Remember that all temperature values in these equations are absolute temperatures.

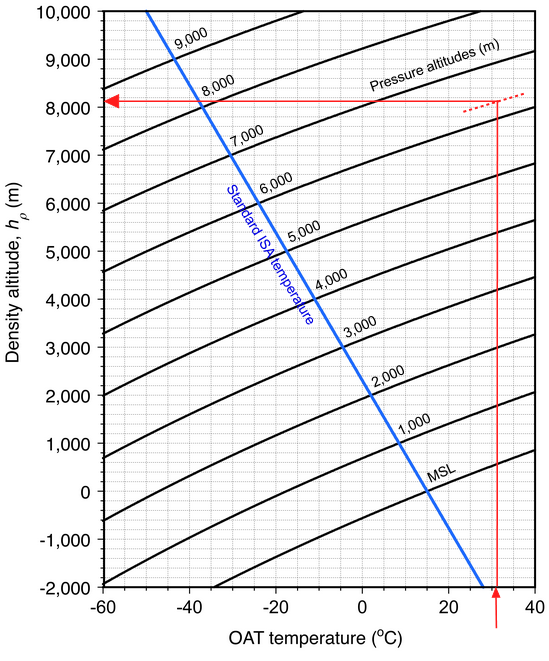
Armed with these equations, it is now possible to examine variations in density altitude with temperature for different pressure altitudes, as shown in the chart below in SI units. In this regard, it should be remembered that the value of B in SI units B is 6.5^{\circ}C per 1,000 m or 1.981^{\circ}C per 1,000 ft. The diagonal lines represent constant-pressure altitudes. The blue line is the standard ISA temperature variation, giving h_{\varrho} = h_p. Taking as an example T_{\rm {\tiny OAT}} = 32^{\circ}C and h_p = 6,300 m, then by following the red lines on the chart, the chart gives an estimated value of h_{\varrho} of 8,200 m.

A pressure/density altitude chart in SI units. Density altitude can be estimated from measurements of pressure altitude and outside air temperature.

The same type of presentation, showing the variation in density altitude with temperature changes at different pressure altitudes, is shown in the chart below in USC units. In this case, B is 3.57^{\circ}F per 1,000 ft of altitude or 0.00357^{\circ}F per ft = 0.00357^{\circ}R per ft. Again, taking T_{\rm OAT} = 85^{\circ}F and h_p = 17,500 ft, following the red lines on the chart yields an estimated h_{\varrho} of 23,000 ft.

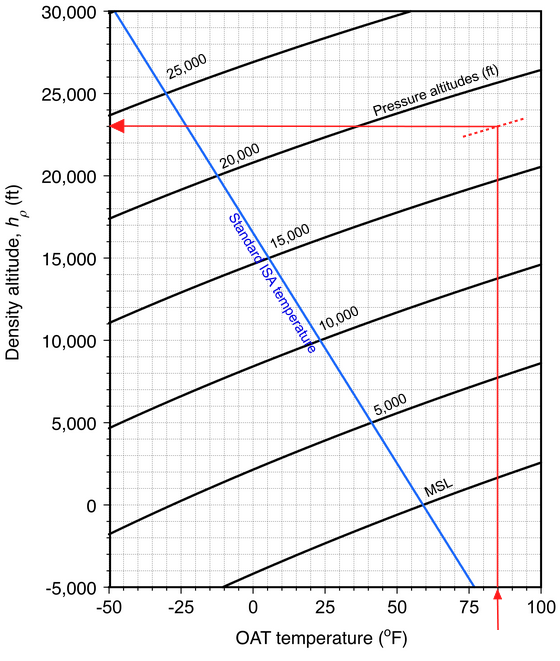
A pressure/density altitude chart in USC units. Density altitude can be estimated from measurements of pressure altitude and outside air temperature.

Notice that interpolation is inevitably required when using these charts, but the eye and brain are excellent interpolators. Nevertheless, while the charts provide a reasonable visual representation of the differences between pressure altitude and density altitude for variations in non-standard temperature, they should not be used as a substitute for the ISA equations for engineering purposes.

Density Ratio Calculation

Another useful metric that can be calculated from the pressure altitude and outside air temperature is the density ratio, \sigma, which is often required for the analysis of aircraft and engine performance. The value of \sigma can be obtained from

(25)   \begin{equation*} \sigma = \frac{\varrho}{\varrho_0} = \frac{T_0}{(T_{\rm {\tiny OAT}} +273.16)} \left( 1 - \frac{B \, h_p}{T_0} \right)^{5.252} = \frac{288.16}{(T_{\rm {\tiny OAT}} +273.16)} \left( 1 - \frac{0.001981~h_p}{288.16} \right)^{5.252} \end{equation*}

where the local pressure altitude, h_p, is in feet and the local T_{\rm {\tiny OAT}} is in units of ^{\circ}C or using

(26)   \begin{equation*} \sigma = \frac{\varrho}{\varrho_0} = \frac{518.4}{(T_{\rm {\tiny OAT}} +4 59.4)} \left( 1 - \frac{0.001981 \, h_p}{288.16} \right)^{5.252} \end{equation*}

where h_p is in feet and T_{\rm {\tiny OAT}} is in units of ^{\circ}F. It is also useful to remember that the equation of state can be written as \delta = \sigma \, \theta, which is helpful when converting between density, pressure, and temperature in the ISA.

Check Your Understanding #1 – Calculating the density altitude

Use the ISA equations to calculate the corresponding density altitude, given a measured outside air temperature of 32^{\circ}C and a pressure altitude of 6,300 m.

Show solution/hide solution.

The relevant ISA equation is

    \[ h_{\varrho} = \frac{T_0}{B} - \frac{T_{\rm {\tiny OAT}}}{B} \left( \frac{T_0 - B \, h_p}{T_{\rm {\tiny OAT}}} \right)^{1.235} \]

where in this case T_{\rm {\tiny OAT}}  = 32^{\circ}C and h_p = 6,300 m. Inserting the other SI values gives

    \[ h_{\varrho} = \frac{288.15}{0.0065} - \frac{T_{\rm {\tiny OAT}}}{0.0065} \left( \frac{288.15 - 0.0065 \times 6,300}{32.0 + 273.15} \right)^{1.235} = 8,136~\mbox{m} \]

This result indicates that although the altimeter reads 6,300 m, the aircraft operates as if it were at 8,136 m because of a higher-than-standard air temperature. Note also that this calculated density altitude value agrees with the previously shown chart example.

Measuring Outside Air Temperature

In aviation terminology, the outside air temperature (OAT) refers to the air surrounding an aircraft during its flight. However, its value is assumed to be unaffected by the aircraft’s passage through it; it is therefore often referred to as a static temperature. For engineering purposes, the outside air temperature (OAT) must be measured to determine air density. A simple OAT gauge can be used below a Mach number of 0.3 (the incompressible flow regime), as shown in the photograph, to provide a relatively accurate measurement of the static air temperature. In this application, the probe is shielded from airflow, thereby minimizing temperature errors caused by direct sunlight-induced heating. The probe typically protrudes through the aircraft’s windshield or the side of the fuselage near the cockpit, exposing it to atmospheric air. The instrument head is mounted inside the windshield in a suitable location where the pilot can easily read it.

To read the outside air temperature (OAT), a temperature probe can be mounted through a window or the fuselage skin.

At higher airspeeds, the compressibility of the flow makes accurate air temperature measurements somewhat more challenging. In this case, the total air temperature (TAT) is defined as the static air temperature plus the temperature rise from the airflow. TAT probes are designed to accurately measure this temperature value and transmit signals for cockpit indications, such as airspeed and Mach number, for use in various engine and aircraft systems, as illustrated in the figure below.

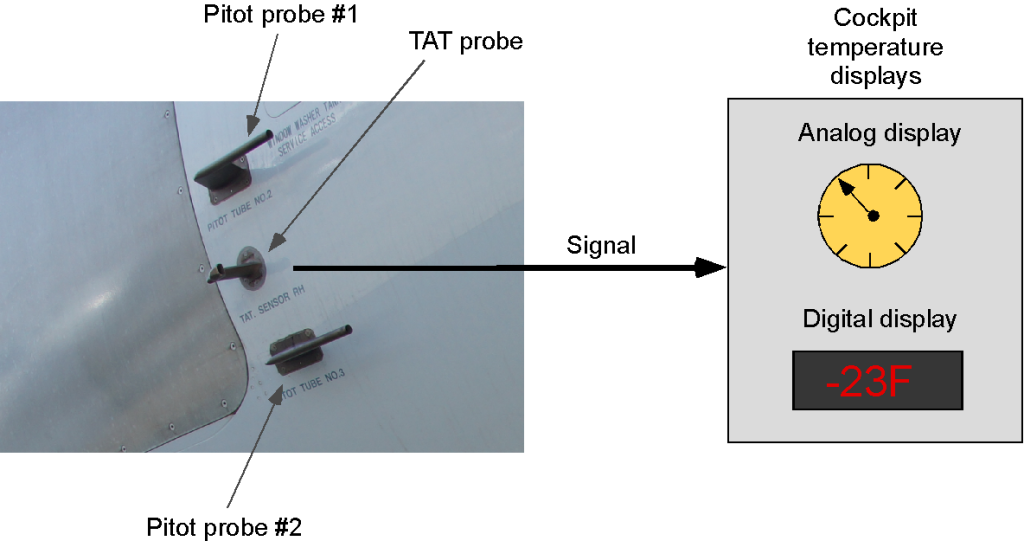
Outside air temperature (OAT) or total temperature (TAT) probes are needed to measure the local ambient air temperature, which can be displayed on various cockpit instruments.

The possibility of ice formation complicates the design of a TAT probe, as it does with total-pressure or Pitot probes. Therefore, the TAT probe must be heated. In this regard, the ambient airflow must be carefully directed through the probe to measure the actual outside air temperature without any influence from the heater. Several manufacturers specialize in TAT probes for aircraft applications.

Practical Use of Density Altitude

The ISA equations are widely used to standardize aircraft performance and evaluate flight-test data. In many cases, a rapid estimate of the density altitude can be helpful for piloting. For example, the information in an aircraft’s operating manual may be expressed as a function of density altitude. As previously discussed, pressure altitude can be measured directly on the altimeter. In contrast, density altitude is determined by calculating the pressure altitude and the local outside air temperature at that altitude.

Linearization of the ISA Equations

It will be seen from the graphs of density altitude changes versus temperature for a given pressure altitude that the relationship is almost linear, which suggests an approximation to Eq. 24 is likely to be useful for rapid estimates of density altitude, i.e., for piloting purposes when a quick estimate is required, such as for advanced flight planning. Such linearizations, however, would never be used in flight-test work.

To linearize Eq. 24, it can be expanded as a Taylor series about the ISA standard temperature value at a given pressure altitude and retaining only the first derivative of the series to give

(27)   \begin{equation*} h_{\varrho} \approx h_p + \frac{R}{g - R B} \left( T_{\rm {\tiny OAT}} - T_{\rm {\tiny ISA}} \right) \end{equation*}

where T_{\rm {\tiny ISA}} is the ISA standard temperature at the given h_p, i.e.,

(28)   \begin{equation*} T_{\rm {\tiny ISA}} = T_0 - B \, h_p \end{equation*}

in appropriate units. Notice that

(29)   \begin{equation*} \frac{R}{g - R B} = \frac{287.057}{9.81 - 287.057 \times 0.0065} = 36.135~\mbox{m/$^{\circ}$C} \end{equation*}

Therefore,

(30)   \begin{equation*} h_{\varrho} \approx h_p + 36.13 \left( T_{\rm {\tiny OAT}} - T_{\rm {\tiny ISA}} \right) \end{equation*}

when h_{\varrho} and h_p are in units of meters and T_{\rm {\tiny OAT}} and T_{\rm {\tiny ISA}} are in units of ^{\circ}C. Remember that T_{\rm {\tiny ISA}} in this equation is the ISA standard temperature at the given value of h_p. Alternatively, in mixed units, then

(31)   \begin{equation*} h_{\varrho} \approx h_p + 118.55 \left( T_{\rm {\tiny OAT}} - T_{\rm {\tiny ISA}} \right) \end{equation*}

where h_{\varrho} and h_p are in units of feet and T_{\rm {\tiny OAT}} and T_{\rm {\tiny ISA}} are in ^{\circ}C. Finally, in entirely USC units, then

(32)   \begin{equation*} \frac{R}{g - R B} =\frac{1716.49}{32.17 - 1716.49 \times 0.00357} = 65.91~\mbox{ft/$^{\circ}$F} \end{equation*}

so the density altitude will be

(33)   \begin{equation*} h_{\varrho} \approx h_p + 65.91 \left( T_{\rm {\tiny OAT}} - T_{\rm {\tiny ISA}} \right) \end{equation*}

where h_{\varrho} and h_p are in feet and T_{\rm {\tiny OAT}} and T_{\rm {\tiny ISA}} are in ^{\circ}F.

Therefore, the linearization of the ISA equations shows that density altitude exceeds pressure altitude by approximately 120 ft per oC or 65 ft per oF when the temperature exceeds the standard ISA temperature at a given pressure altitude. However, these results are approximate but reasonably accurate for moderate variations of non-standard ISA temperature at a given pressure altitude. However, for engineering work, the approximations should never be used in place of the ISA equations, i.e., Eqs. 17, 20 and 24.

Check Your Understanding #2 – Calculating the approximate density altitude

Given a measured outside air temperature of 32^{\circ}C and a pressure altitude of 6,300 m, calculate the corresponding density altitude using the approximate conversion rules.

Show solution/hide solution.

The relevant ISA equation in Example #1 gives h_{\varrho} = 8,136 m. The approximation for density altitude from Eq. 31 is

    \[ h_{\varrho} \approx h_p + 36.13 \left( T_{\rm {\tiny OAT}} - T_{\rm {\tiny ISA}} \right) \]

The standard ISA temperature at 8,136 m is

    \[ T_{\rm {\tiny ISA}} = T_0 - B \, h_p = 15 - 0.0065 \times 6,300 = -15.95~\mbox{$^{\circ}$C} \]

Therefore, inserting the numerical values gives

    \[ h_{\varrho} \approx 6,300 + 36.13 \left( 32.0 - (-15.95) \right) = 6,300 + 1,732 = 8,032~\mbox{m} \]

Therefore, this density altitude underpredicts the value obtained from the complete ISA equation by only about 100 m.

Reference Pressures for Piloting

To compensate for variations in atmospheric pressure, the pilot must continuously adjust the Kollsman window setting. In the U.S., the altimeter reference pressure is typically set to the local mean sea level (MSL) pressure, ensuring that all aircraft in the vicinity fly relative to the local MSL reference. In this case, when the aircraft is on the ground, the altimeter should read the approximate field elevation, which also serves as a check to ensure the altimeter is functioning correctly. The local value of MSL pressure at any given time is available from air traffic control, weather stations, and other sources.

In other countries, altimeter settings called QFE and QNH are used. The QFE is the reference pressure set in the Kollsman window of the altimeter to indicate its height above the reference elevation being used, which is usually the elevation of an airfield. In this case, the altimeter will read zero when the aircraft is on the ground. The QNH is the reference pressure used to indicate the altimeter’s height above sea level and is the default in the U.S.

Above 18,000 ft, pilots are required to set the altimeter to the standard MSL reference pressure of 29.92 inches of Hg, in which case the altitude reading is referred to as a flight level (FL). Therefore, flight level 230 (FL230) is equivalent to a pressure altitude of 23,000 ft. All aircraft must be flown at higher altitudes relative to the same pressure datum. Over the Atlantic Ocean, for example, horizontal separation distances between aircraft may be only a few miles, and vertical separation altitudes may be as little as 1,000 feet; therefore, all aircraft must fly at an altitude referenced to the same pressure datum.

Check Your Understanding #3 – A question for pilots & engineers

Suppose the reported local altimeter setting at your local Florida airport before an approaching hurricane is 29.32 inches of Hg, which is the pressure at sea level for that airport at the time of day. The airport is located 88 feet above mean sea level (MSL) and features a 2,000-foot-long runway. Moving your Cessna 172 airplane and family to Alabama would be best to avoid the hurricane. The reported local temperature at their airport is 34oC, with light showers. What is the estimated density altitude for takeoff, and should you be concerned about it?

Show solution/hide solution.

The difference between the reported altimeter setting and the standard ISA reference is

    \[ 29.32 - 29.92 = -0.6~\mbox{inches of Hg} \]

The negative value indicates that the local pressure is lower than the standard pressure; therefore, even the density altitude at the ISA standard temperature will be higher. Converting to units of feet gives the equivalent pressure altitude for an altimeter setting of 29.32 as

    \[ h_p = 924.664 \times 0.6 = 555~\mbox{ft} \]

where the value of 924.664 is the conversion factor from inches of Hg to feet. The standard ISA temperature at 555 ft is

    \[ T_{\rm {\tiny ISA}} = T_0 - B \, h_p = 15.0 - 0.0065 \times 555.0 = 11.4~\mbox{$^{\circ}$C} \]

Using the approximation in Eq. 31 to obtain density altitude from pressure altitude gives

    \[ h_{\varrho} \approx h_p + 118.55 \left( T_{\rm {\tiny OAT}} - T_{\rm {\tiny ISA}} \right) \]

with heights being measured in feet and temperatures in oC. Inserting the values gives

    \[ h_{\varrho} \approx 555.0 + 118.55 \left( 34.0 - 11.4 \right) = 555.0 + 2,679.2 = 3,234~\mbox{ft} \]

While the airport is only 88 feet above MSL, the atmospheric conditions are such that the airplane will perform as if flying at an altitude of 3,200 feet. With a full passenger load, a short and wet runway, and a relatively modest powered Cessna 172, you should worry about getting off the runway in these conditions and clearing the trees.

Altimetry in the Stratosphere

As will now be apparent, a pressure altimeter is a fundamental instrument in aviation for determining an aircraft’s altitude by measuring ambient static pressure. The relationship between pressure and altitude is derived from the ISA model, which defines how pressure, temperature, and density vary with altitude under standard atmospheric conditions. This model includes a linear lapse rate in the troposphere and an isothermal layer in the lower stratosphere.

Mechanical altimeters designed for use at high altitudes, including the stratosphere, contain two aneroid capsules that expand and contract in response to ambient pressure. This motion is transmitted through a system of levers, gears, and cams to rotate a needle on the altimeter dial. Because the relationship between pressure and altitude in the ISA is nonlinear and piecewise-defined, the internal gearing must be specifically designed to match the entire ISA pressure-altitude curve, including:

  1. The troposphere, where temperature decreases linearly with height, i.e.,

        \[\]

    (34)   \begin{equation*} T(h) = T_0 + B \, h, \quad \text{for } h \leq 11{,}000~\text{m} \end{equation*}

    where the constant B is the standard temperature lapse rate in the troposphere in the ISA model, as defined by B = -6.5 \times 10^{-3} K/m = -6.5 K/km = -6.5^{\circ}C/km. It represents the linear rate at which temperature decreases with altitude in the troposphere up to 11,000 meters, and where T_0 = 15^{\circ}C = 288.15 K is the standard sea-level temperature. This yields the pressure-altitude relationship

    (35)   \begin{equation*} p(h) = p_0 \left( \frac{T(h)}{T_0} \right)^{- \dfrac{g}{B \, R}} \end{equation*}

    where R = 287.05 J kg^{-1} K^{-1} is the specific gas constant for air.

  2. The stratosphere is modeled as isothermal, so that

        \[\]

    (36)   \begin{equation*} T(h) = \text{constant} = T_{11} = 216.65~\text{K}, \quad \text{for } h > 11{,}000~\text{m} \end{equation*}

    The corresponding pressure in this isothermal region decays exponentially with altitude, so that

    (37)   \begin{equation*} p(h) = p_{11} \exp\left( -\frac{g_0 (h - 11,000)}{R T_{11}} \right) \end{equation*}

    where T_{11} = 216.65 K is the standard temperature at 11,000 m, p_{11} = 22,632 Pa  is the corresponding pressure.

These ISA-defined pressure-altitude relationships are used to calibrate the altimeter’s interior mechanism. The gearing and dial spacing are designed to match the ISA profile precisely, including the change in behavior at the tropopause (approximately 11 km in altitude). Although the altimeter is purely mechanical, it still reads correctly across both atmospheric layers.

If a mechanical altimeter continued to assume a linear lapse rate above 11 km, rather than switching to the isothermal model, it would severely underestimate altitude in the stratosphere. For example, at an altitude of 20,000 m, the pressure is approximately p(20,000) = 5,474 Pa (ISA). If the lapse-rate model were wrongly extrapolated beyond 11 km, this pressure would correspond to only about { h\approx} 15,000 m, which is an error of nearly 5,000 m.

Fortunately, such an error does not occur in properly calibrated altimeters. High-altitude aircraft, including supersonic aircraft, rely on accurate altimetry for maintaining vertical separation. Their altimeters, whether mechanical or digital, are designed to follow the complete ISA model. Therefore, when flying at FL600 (60,000 ft), the altimeter will display the correct pressure altitude, consistent with both Air Traffic Control and the aircraft’s certified flight envelope. This approach ensures consistent and accurate altitude indication across the full range of atmospheric flight, including into the stratosphere.

Electronic Flight Displays (EFD)

Advances in electronics and software engineering have significantly transformed the instrumentation used for modern aircraft with the introduction of Electronic Flight Displays (EFDs) and Electronic Flight Information Systems (EFIS), which are often referred to as “glass cockpits.” Glass cockpits replace traditional analog gauges and instruments with digital displays, providing pilots with a more intuitive and information-rich interface, an example being shown in the figure below.

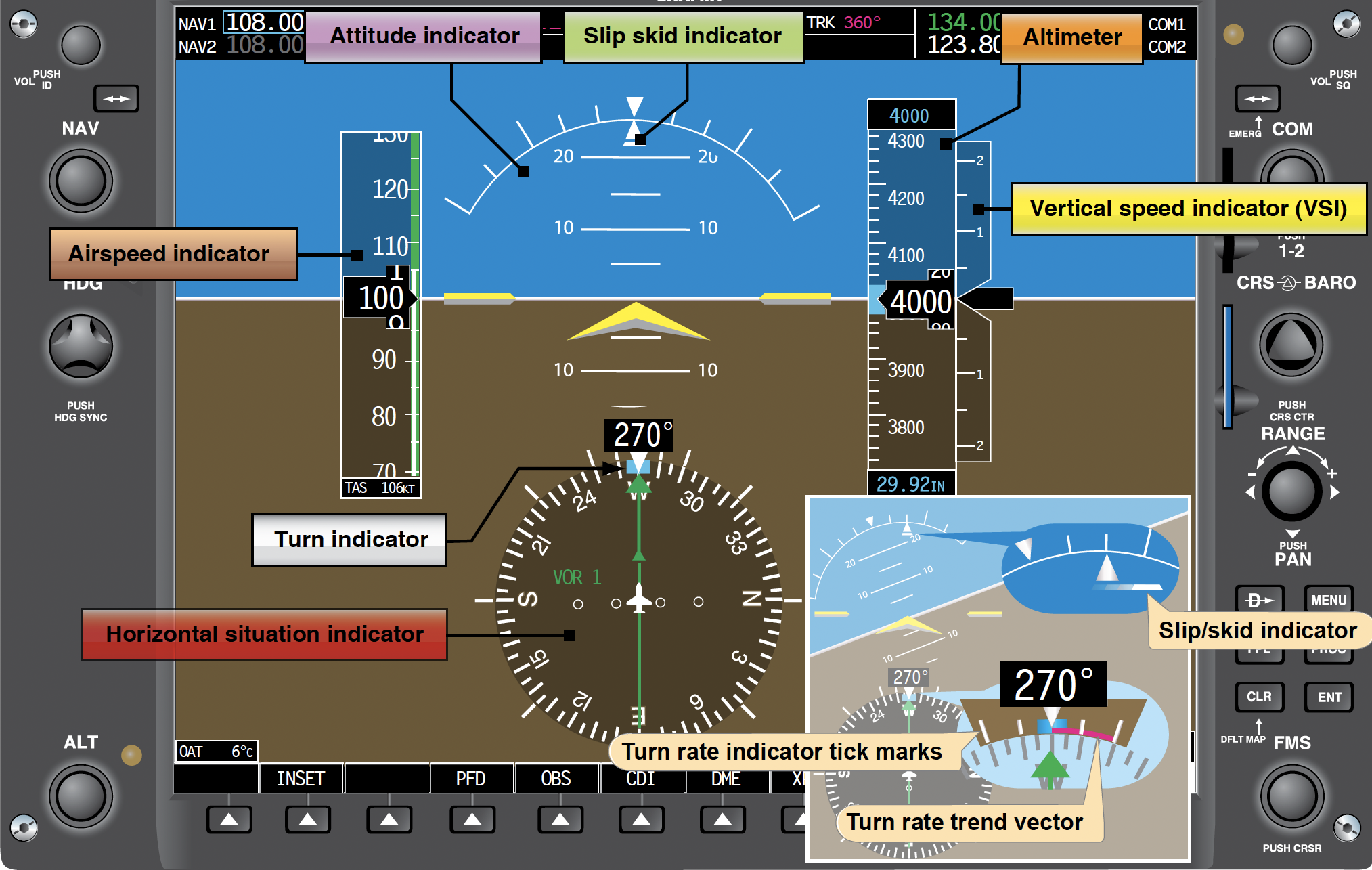
An example of an EFIS primary flight display that has largely replaced the traditional mechanical altimeter, airspeed indicator, and other analog instruments on modern aircraft.

EFDs use the same types of instrument inputs as traditional analog gauges; however, their processing systems differ fundamentally. An Air Data Computer (ADC) first receives the Pitot and static pressure inputs. The ADC computes the difference between total and static pressures and uses equations to generate the information required to display airspeed on the PFD. Outside air temperatures are also monitored and introduced into various components within the software, and they are displayed on the PFD screen. These are the essential elements of an EFIS:

  1. Pitot-Static Inputs: EFDs still receive pitot-static inputs, in which the pitot tube measures total pressure, and the static ports measure static pressure. As with a traditional mechanical instrument, static pressure enables altitude calculation, whereas dynamic pressure provides the information needed to calculate airspeed.
  2. Analog-to-Digital Converter (ADC): The pitot-static inputs are converted into digital signals by an Analog-to-Digital Converter (ADC). The ADC converts the analog signals from the pitot-static system into a digital format for processing by the EFD’s software and electronic system.
  3. Air Data Computer (ADC): The ADC, a component of the EFD system, receives digitized pitot-static inputs. It computes the difference between total and static pressure to determine the airspeed. All necessary corrections for SPE can be included in the software. The ADC then generates the information required to display airspeed on the Primary Flight Display (PFD).
  4. Outside Air Temperature (OAT) Monitoring: EFDs also measure OAT. This temperature data is essential for various components within the aircraft systems, such as engine performance calculations and fuel management. The OAT and TAT are displayed on the PFD screen, providing pilots with real-time temperature information.

Summary & Closure

A measurement of an aircraft’s altitude during flight is fundamental to both its piloting and engineering. However, as with airspeed, the exact altitude type must be carefully specified. Density altitude affects aircraft and powerplant performance; it is a measure of the air density at the altitude at which the aircraft is flying. Density altitude, however, cannot be measured directly and must be calculated from pressure altitude and air temperature. The higher the temperature above the standard temperature at a given altitude, the higher the density altitude, i.e., the lower the value of air density. The local air density will always affect both aircraft and powerplant performance.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • An airplane is flying at a pressure altitude of 10,000 ft where the outside air temperature is -10oF. What is the corresponding density altitude?
  • An ERAU aircraft is preparing to take off from Daytona Beach (identifier KDAB) in the summer, where the outside air temperature is 95oF. What is the approximate density altitude, and why must the pilot know this?
  • If a pilot wants to estimate the approximate value of density altitude before takeoff, explain how that should be done using the cockpit instruments.
  • When an aircraft flies from warmer air into an area with colder air, how will the reading on the altimeter change, and why?
  • A pilot notices that the altimeter in the cockpit reads -200 ft when set to 29.92 inches of Hg. Under what circumstances could this occur?
  • What are the limitations of altimeters and factors that can affect their accuracy?
  • How do pilots use altimeters to navigate and comply with air traffic control instructions?
  • Can you describe the effects of altitude on aircraft performance?
  • How are altimeters calibrated and tested for accuracy?
  • What are the safety considerations when relying on altimeters during flight?

Other Useful Online Resources

Many internet resources discuss altimetry and the practical use of altimeters in aviation. Here are just a few worth investigating:

  • Read here what the FAA officially has to say about altimeters.
  • A good description from a pilot’s perspective on the importance of determining altitude.
  • This video provides more detailed information on the distinction between pressure altitude and density altitude.
  • Video explaining the inner workings of an altimeter.
  • A downloadable FAA document explaining the concept of density altitude.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2026 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n30

Share This Book