"

28 Bluff Body Flows

Introduction

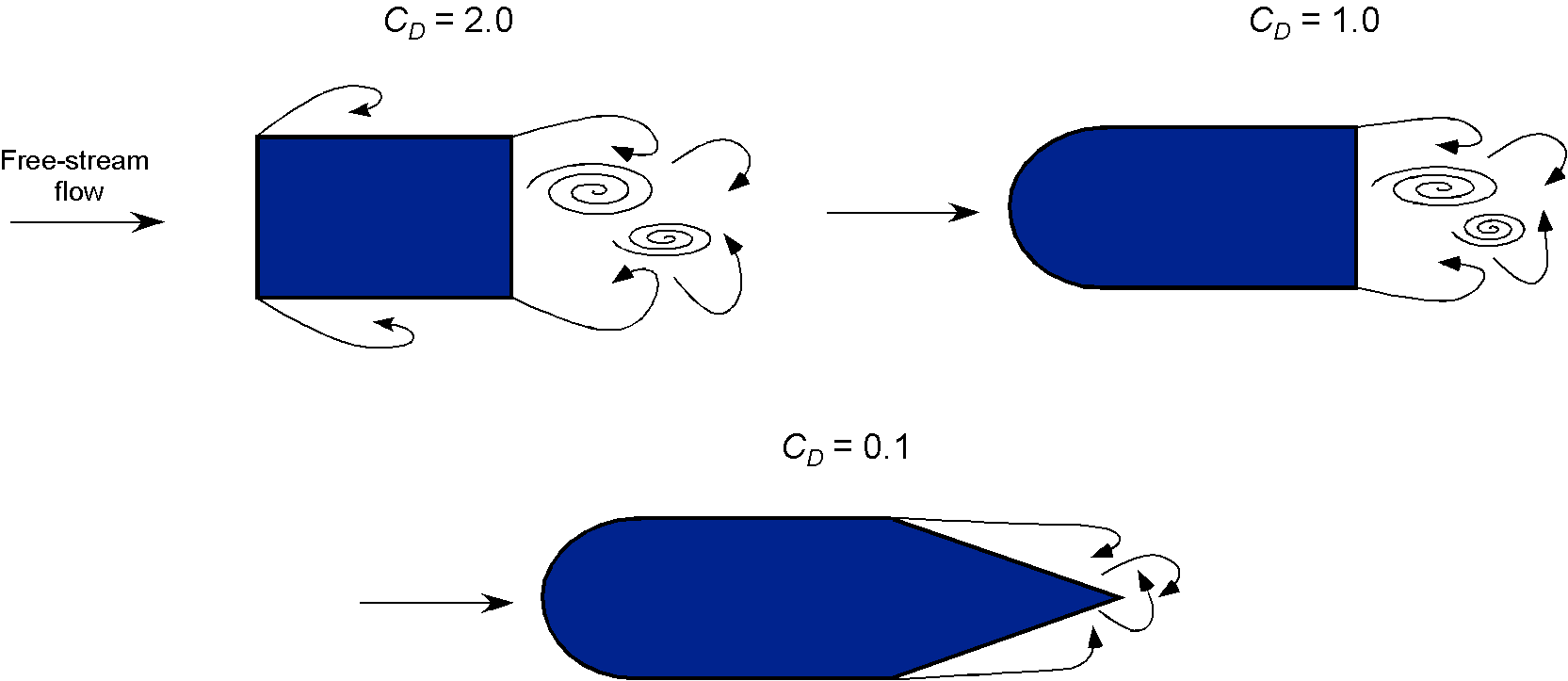
Aerospace engineers are more often than not interested in the aerodynamics of smooth, slender, streamlined shapes that gradually taper to a sharp point at their trailing edges, e.g., airfoils and wings. However, non-streamlined or unstreamlined shapes with blunt front and/or rear faces, called bluff bodies (sometimes referred to as blunt bodies), are also encountered in many engineering applications. While the drag force on a body shape comprises two primary contributors, skin-friction drag and pressure drag, the total drag on bluff bodies is typically dominated by pressure drag. This outcome results from the effects of the large low-pressure zone formed in the body’s wake, as illustrated in Figure 1.

The differences in the flows between a streamlined body and a bluff body. The bluff body induces flow separation and a large, broad wake, characterized by low pressure and high drag.

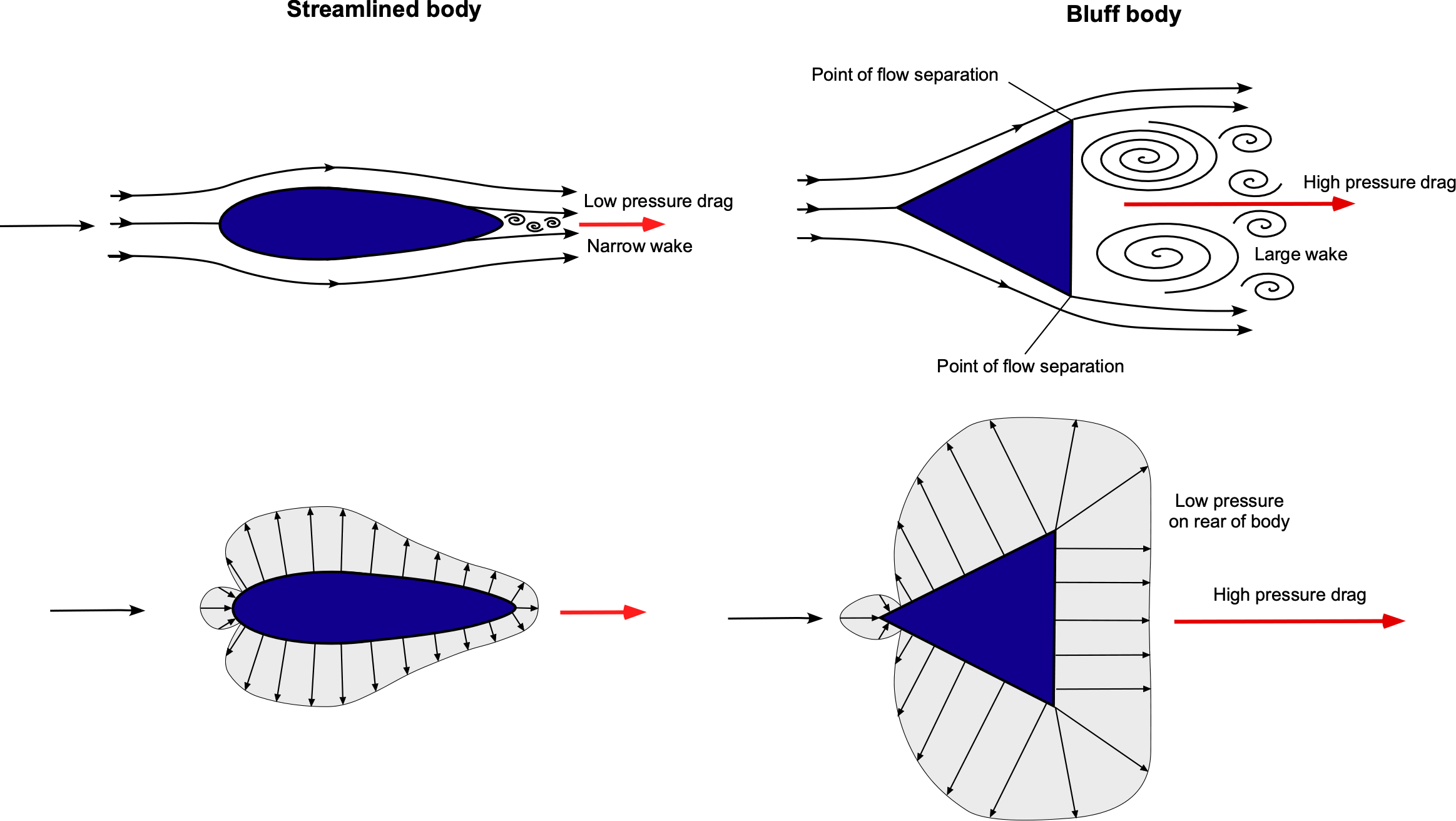
Understanding bluff-body aerodynamics is essential because of its wide-ranging applications across various engineering fields. Studying how non-streamlined objects interact with airflows helps design more efficient structures and vehicles. For instance, understanding unsteady wind loads on bluff bodies, such as buildings and bridges, is essential for ensuring aeroelastic stability and preventing failures. Optimizing vehicle shapes reduces drag, improves fuel efficiency, and leads to better performance. The aerodynamics of bluff bodies also play a role in many sports, including golf, tennis, and baseball. For example, the dimples on a golf ball create turbulent flow, reducing drag and allowing the ball to travel farther. In tennis, the spin imparted on the ball affects its trajectory and speed. Similarly, in baseball and cricket, the stitching on the ball and the manner in which it is thrown, including spin, produce aerodynamic effects that vary with the players’ skill.

Learning Objectives

  • Distinguish the fundamental differences between the flows of streamlined versus bluff bodies.
  • Understand the use of reference areas in defining bluff body drag coefficients and the concept of equivalent drag area.
  • Appreciate why the drag of bluff bodies with smooth surfaces, such as circular cylinders and spheres, shows sensitivities to Reynolds number variations.
  • Become familiar with the Magnus effect on spinning cylinders and spheres.
  • Know about the process of streamlining of aircraft and terrestrial vehicles.
  • Be able to calculate the drag from a parachute and other bluff bodies.

Drag Coefficients

For bluff bodies, the interest is usually in the drag on that body, mainly because experiments have found that drag is the dominant force. This observation, however, does not imply that bluff bodies cannot produce lift because many do. Nevertheless, initially examining only the drag characteristics of such bodies is convenient. Furthermore, bluff bodies may produce pitching moments, which are sometimes necessary for specific engineering applications, such as determining torsional loads.

Recall that the two-dimensional drag coefficient is

(1)   \begin{equation*} C_d = \frac{D'}{\frac{1}{2} \varrho_{\infty} \, V_{\infty}^2 \, l} \end{equation*}

where {D'} is the drag per unit span, and {l} is a characteristic length, e.g., for a circular cylinder, l = d, where {d} is its diameter.

In most cases, the drag coefficients for two-dimensional bluff bodies are presented in terms of the body length, b, so the drag coefficient is defined as

(2)   \begin{equation*} C_D = \frac{D}{\frac{1}{2} \varrho_{\infty} \, V_{\infty}^2 \, l \, b} \end{equation*}

where the product l\,b is equivalent to an area. In general, for a three-dimensional object, the drag coefficient is defined as

(3)   \begin{equation*} C_D = \frac{D}{\frac{1}{2} \varrho_{\infty} \, V_{\infty}^2 \, A_{\rm ref}} \end{equation*}

where A_{\rm ref} is defined as the reference area, usually the projected frontal area. Using a sphere of diameter {d} as an example, its projected area is {A_{\rm ref} = \pi d^2/4}. Likewise, a cube with side length {l} will have a reference area of A_{\rm ref} = l^2

However, caution must be exercised when defining drag coefficients for three-dimensional bodies, as the drag coefficient always depends on the definition of the body’s reference area, which may not be unique. For example, on the one hand, for specific bodies of revolution, the volumetric drag coefficient is used by convention, in which the reference area is the square of the cube root of the volume. On the other hand, in hydrodynamics, the analysis of submerged streamlined bodies uses the wetted surface area as the reference area. Therefore, to consistently use and compare drag coefficients, it is imperative to adopt the convention used in the particular field of application.

To avoid ambiguity in the definitions of drag coefficients for different body shapes, drag coefficients per se are not always used. Instead, the equivalent drag area is used, often denoted by {\scriptstyle{f}} or A_{\mathrm{eq}}. The equivalent drag area is defined as

(4)   \begin{equation*} f \equiv A_{\mathrm{eq}} = \frac{D}{\frac{1}{2} \varrho_{\infty} \, V_{\infty}^2} \end{equation*}

where {\scriptstyle{f}} or A_{\mathrm{eq}} would be measured in units of area.

The advantage of using equivalent drag areas is that they eliminate ambiguity in defining a reference area. This approach is often used to estimate the drag of complex shapes composed of many simpler shapes, such as an entire airplane. In such a case, the equivalent drag area of the complex shape is obtained by a drag synthesis of the equivalent drag areas of N simple shapes, i.e.,

(5)   \begin{equation*} f = f_1 + f_2 + f_3 + ..... + f_N \end{equation*}

However, it would be incorrect to write

(6)   \begin{equation*} { C_D = C_{D_{1}} + C_{D_{2}} + C_{D_{3}} + .... + C_{D_{N}} } \end{equation*}

because the reference areas on which each value of C_D is based could be different, and generally will be. To take into account component interference, i.e., to make some allowance for flow interference effects between the different components, then

(7)   \begin{equation*} f = K \left( f_1 + f_2 + f_3 + ..... + f_N \right) \end{equation*}

where K > 1 and often K = 1.2 will be used for aircraft drag synthesis without any other information, i.e., a 20% drag penalty from component interference effects.

Drag Coefficients of Simple Shapes

There are many bluff body shapes for which the drag (or drag coefficient) must be known for engineering purposes. However, in practice, far fewer such shapes are encountered, most of which have been well-studied, and the drag coefficients have been measured in wind tunnels. Furthermore, flows around bluff bodies are often unsteady and can produce various types of vortex shedding, as shown in the animation in Figure 2. Therefore, the measurement or computation of drag is usually made over a relatively long period, known as an ensemble time average.

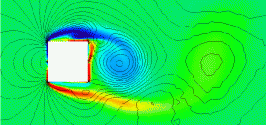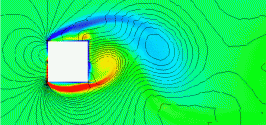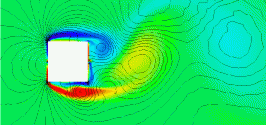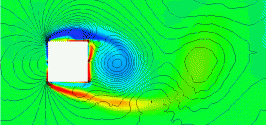
CFD simulation of the unsteady flow and periodic vortex shedding produced by a bluff body shape.

Drag coefficients for standard two- and three-dimensional bluff-body shapes are widely published and serve as a valuable resource for engineers. These shapes can be further categorized into two primary subclasses of bluff bodies: 1. Those with sharp, angular shapes tend to have fixed points of flow separation and drag coefficients that are insensitive to the Reynolds number. 2. Those with smooth contours exhibit variable flow separation points and may be sensitive to Reynolds number. These effects are summarized in the schematic of Figure 3.

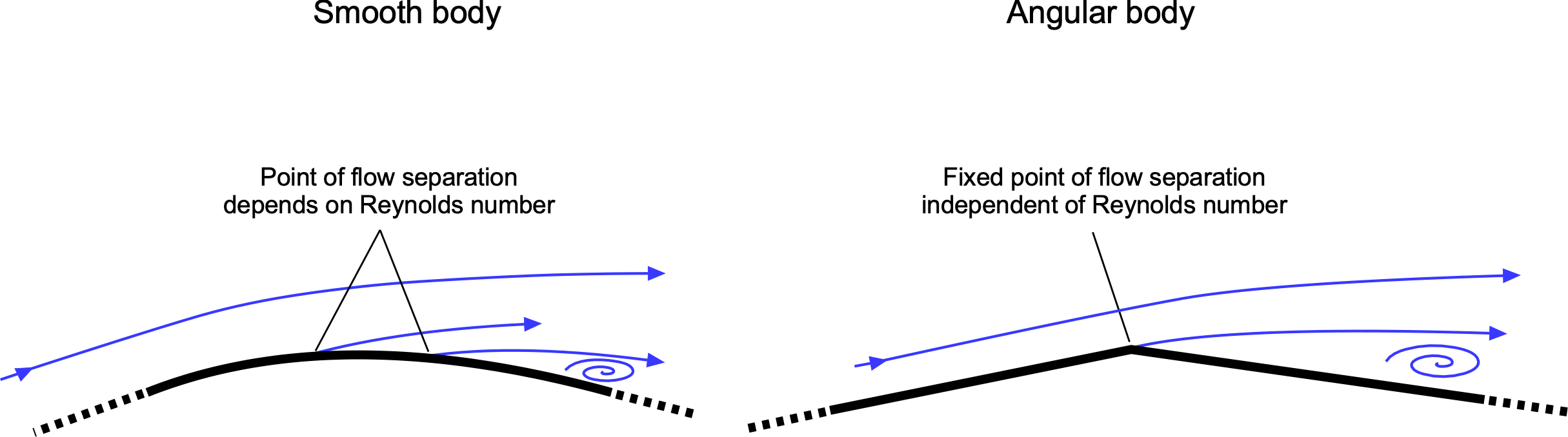
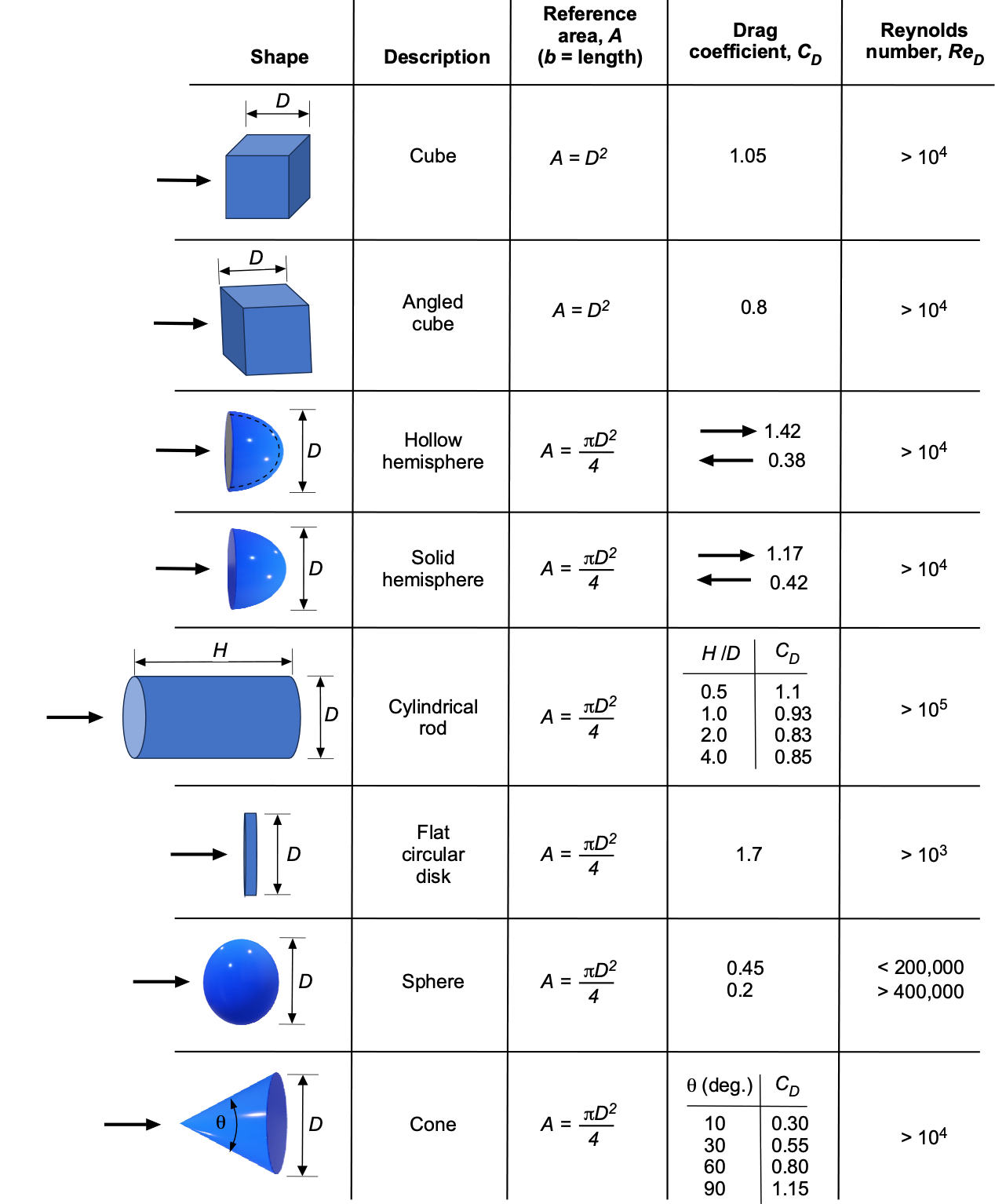
The aerodynamics of smooth bluff bodies depend on the Reynolds number, but angular bodies with sharp corners tend to have fixed flow separation points.

Of course, there is always the possibility that some bluff body shapes combine smooth contours and sharp edges. In this case, determining the drag coefficient and the effects of the Reynolds number may require specialized wind-tunnel measurements. Values for some common bluff-body shapes are shown in the tables in Figures 4 and 5.

 

Measured drag coefficients of some simple two-dimensional bluff bodies.

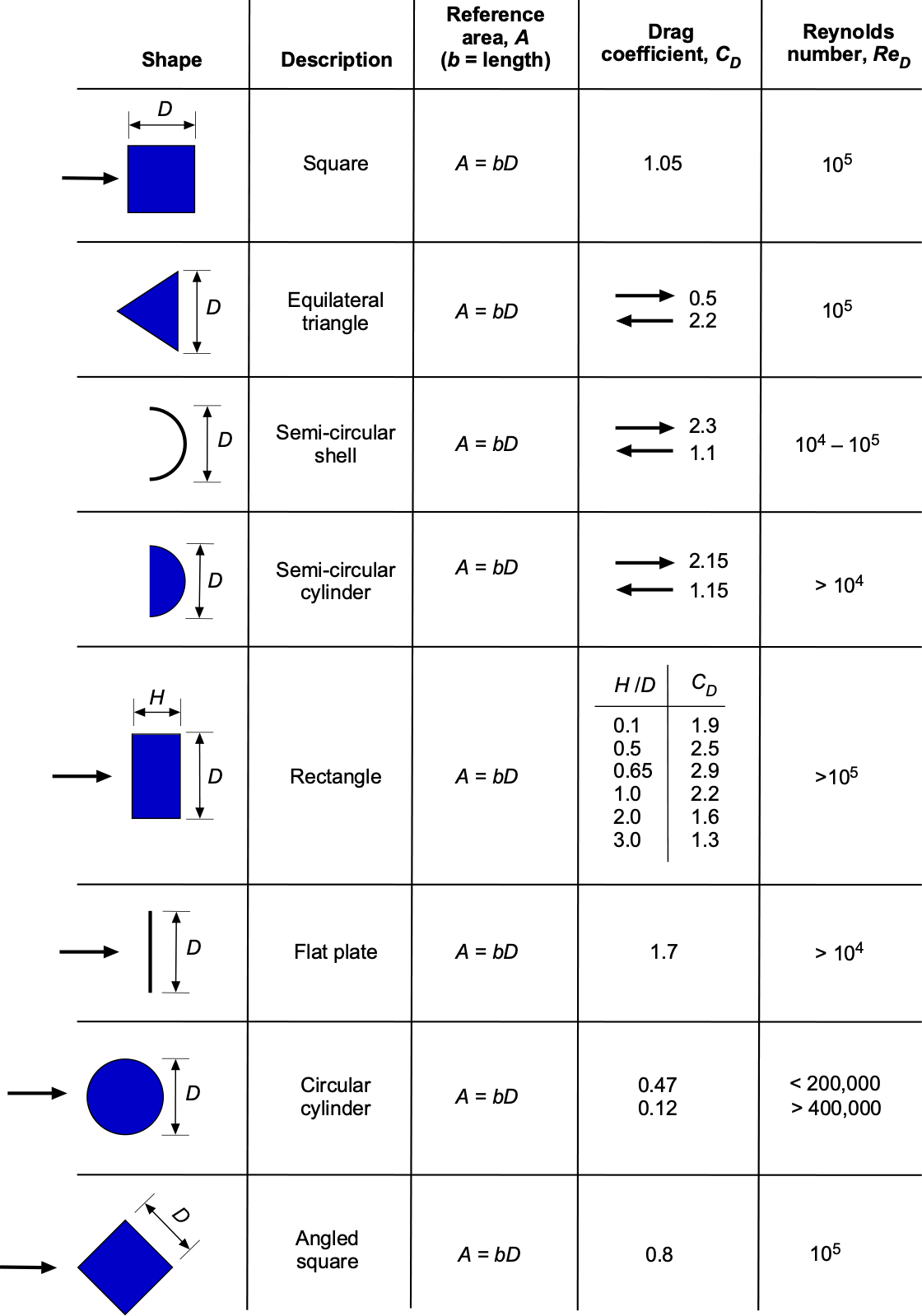
For example, a sphere or a cylinder is smooth, whereas a cube is angular. The flows about smooth bluff bodies or those with rounded corners generally exhibit some sensitivity to the Reynolds number, and their drag coefficients vary as a consequence, as shown in the tables. In contrast, angular shapes exhibit little to no variation with changes in the Reynolds number, at least after reaching a minimum threshold.

 

Measured drag coefficients of some simple three-dimensional bluff bodies.

Check Your Understanding #1 – Calculating the drag on a bluff body

What will be the drag on a solid hemisphere with a frontal area of 0.26 m2 and a flow speed of 100 m/s? Hint: The drag will depend on which side of the hemisphere points into the wind.

Show solution/hide solution.

The drag force on the hemisphere is given by

    \[ D = \frac{1}{2} \varrho V ^2 \, C_D \, A_{\rm ref} \]

where A_{\rm ref} = 0.26 m2 and V = 100 m/s, and if MSL ISA conditions are assumed then \varrho = 1.225 kg/m3. Looking up the value of a solid hemisphere’s drag coefficient in the table in Figure 5, it can be seen that the C_D value depends on whether the smooth side or the flat side faces the relative wind. In the former case, C_D = 0.42, and in the latter case, C_D = 1.17. Inserting the values for the smooth side facing the flow gives

    \[ D = \frac{1}{2} \varrho V ^2 \, C_D \, A_{\rm ref} = 0.5 \times 1.225 \times 100.0^2 \times 0.42 \times 0.26 = 668.9 \mbox{ N} \]

And for the flat side facing, the flow gives

    \[ D = \frac{1}{2} \varrho V ^2 \, C_D \, A_{\rm ref} = 0.5 \times 1.225 \times 100.0^2 \times 1.17 \times 0.26 = 1,863.2 \mbox{ N} \]

Flow Patterns Around a Circular Cylinder

A classic example of a well-studied two-dimensional bluff body flow is that of a circular cylinder, for which the flow readily separates near its maximum thickness or just downstream; representative examples are shown in Figure 6. A wake is produced downstream of the cylinder, which usually contains turbulence and various sizes of vortical eddies. As might be expected for a smooth body, the flow about the cylinder and the resulting wake structure and drag are sensitive to variations in Reynolds number, which in this case is defined based on the diameter of the cylinder, {d}.

Various flow states can be produced around a circular cylinder, depending primarily on the Reynolds number.

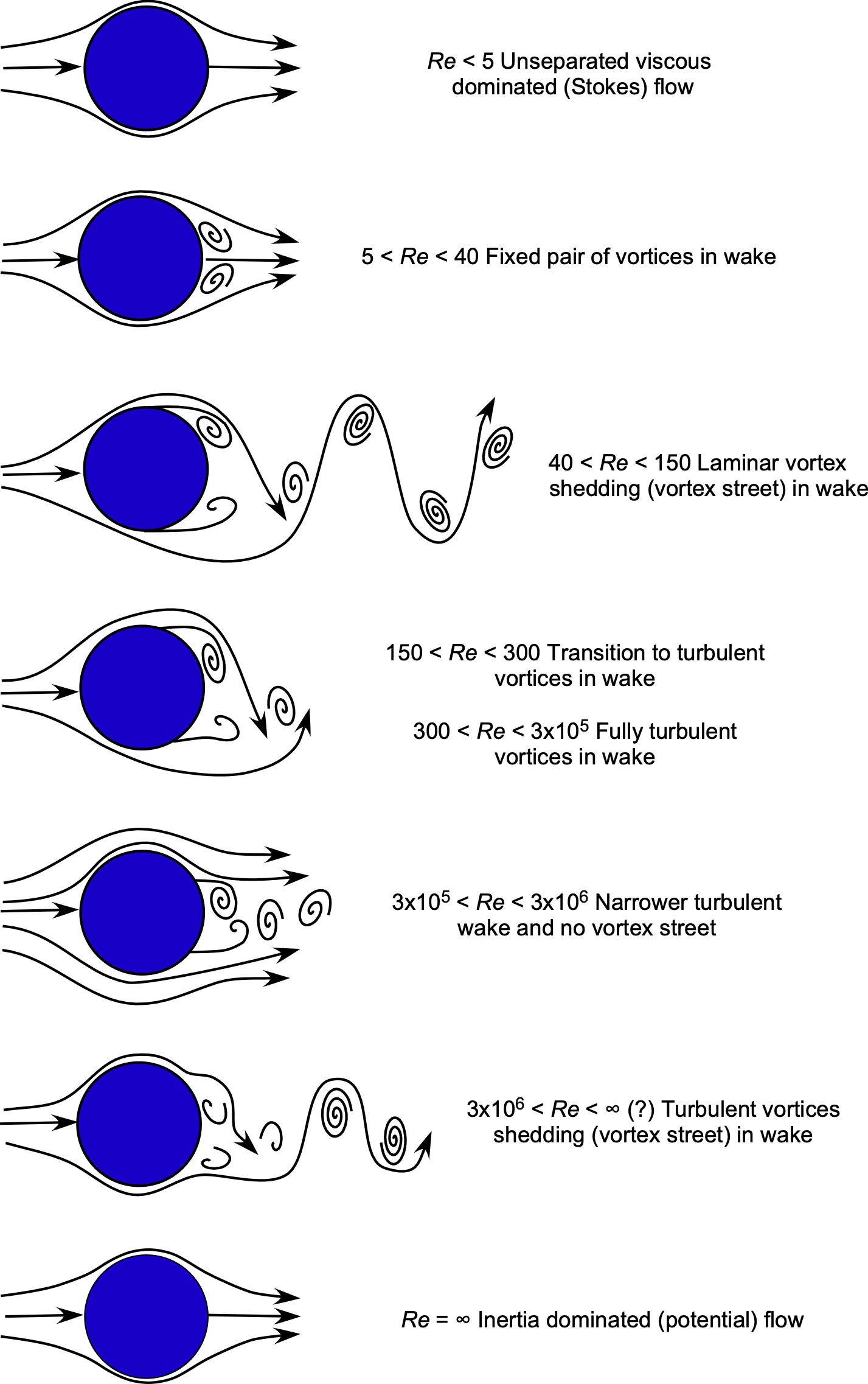
At very low Reynolds numbers, near unity, known as “creeping flow” or “Stokes flow,” the behavior is significantly influenced by viscosity rather than inertia. At slightly higher Reynolds numbers but for Re < 5, a stable pair of symmetric vortices is formed in the wake of the cylinder; the flow is mainly steady, but a high drag coefficient is produced.

As the Reynolds number is further increased, the drag coefficient decreases to a point. The wake vortices move farther downstream of the body via alternate vortex shedding, producing two rows of counter-rotating vortices known as a von Kármán vortex street. This is an unsteady flow, creating an unsteady drag on the cylinder. However, no time-averaged unsteady lift is produced because of the strong asymmetry in the flow with respect to the flow direction. Interestingly, this latter type of periodically alternating flow also creates a periodic pressure field that manifests as a sound, known as an Aeolian tone (after Aeolus, the Greek god of the wind). This effect is the source of the buzzing or “singing” sound sometimes heard when the wind blows over high-tension power wires.

As the Reynolds number increases, the periodic flow around the cylinder at lower Reynolds numbers becomes highly aperiodic, yet it still exhibits alternating vortex shedding. Here, the wake flow is more turbulent. However, the turbulent boundary layer separates farther downstream along the surface, producing a narrower wake. Because the downstream wake is narrower, the low-pressure region on the downstream side is smaller, thereby reducing drag.

As the Reynolds number increases, inertia effects dominate viscous effects. Consequently, the flow becomes attached everywhere, with a much smaller wake downstream of the cylinder; i.e., it approaches an inviscid flow. Because the flow is symmetric upstream and downstream, the cylinder experiences no lift or drag. This outcome is known as d’Alembert’s Paradox, after the mathematician Jean le Rond d’Alembert, who first addressed the problem by concluding that his theory of flow did not align with experiments on cylinders in a wind tunnel. The reason was that d’Alembert did not consider the action of viscosity in his solution, i.e., he considered only an inviscid flow. However, as shown in the images above, this flow type does not occur naturally because real fluids are always viscous to some degree, and the Reynolds number is finite.

Drag of Circular Cylinders & Spheres

The corresponding drag coefficient on a circular cylinder as a function of the Reynolds number is shown in Figure 7. Note that the results are for a smooth cylinder; surface roughness will alter the quantitative relationships. The drag coefficient for a sphere is also shown for reference. The drag reduces quickly with increasing Reynolds number Re (note the logarithmic scales) until Re reaches approximately 10^3, after which the drag remains nominally constant. This outcome arises because the point of flow separation (laminar boundary-layer separation) is delayed to a greater downstream distance, eventually separating near the points of maximum thickness.

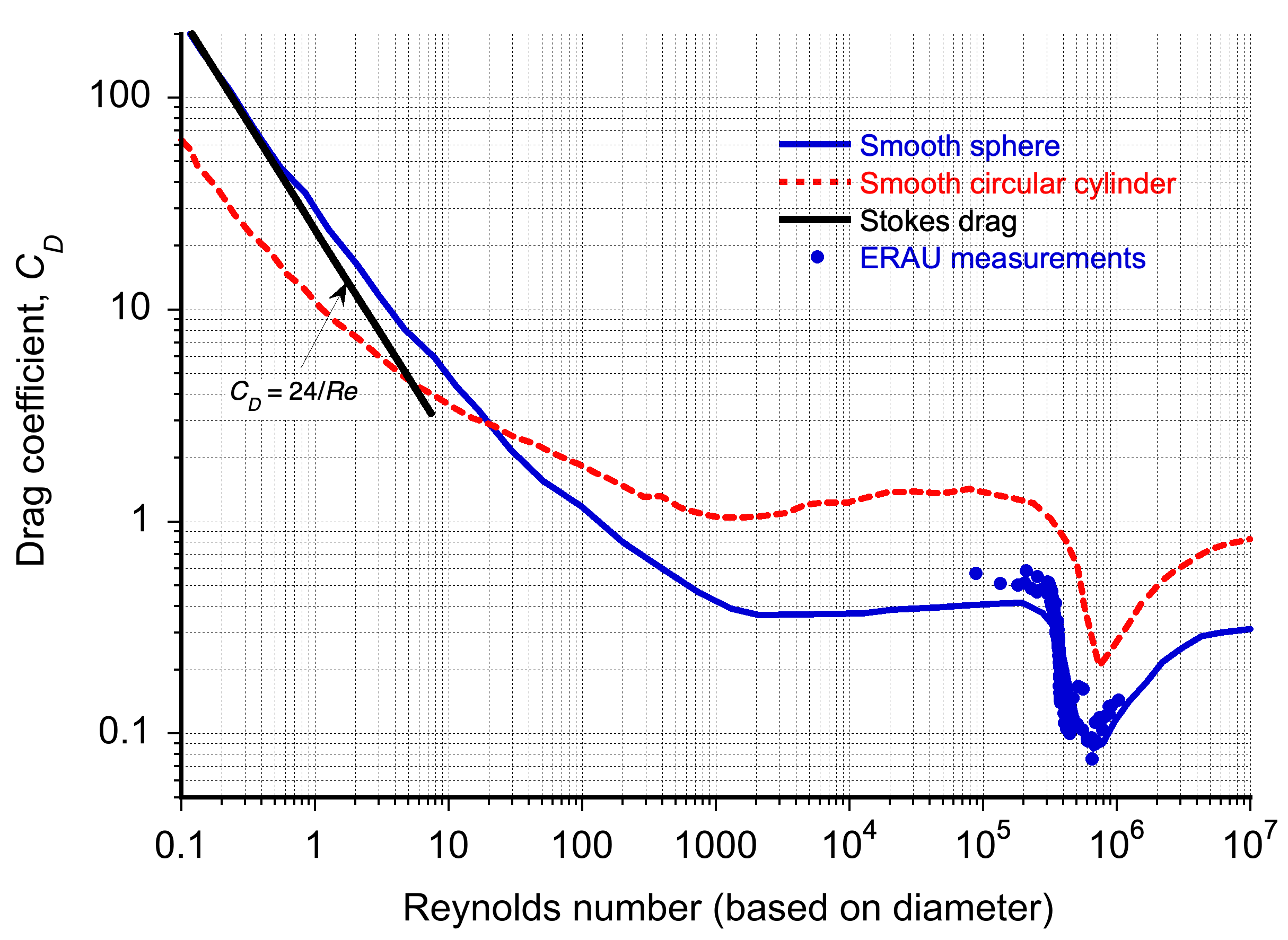
The drag coefficient of a circular cylinder and a sphere as a function of Reynolds number based on diameter. Notice the logarithmic scales.

With further increases in Re, it will be apparent that there is a critical value of Re where the drag suddenly decreases by almost an order of magnitude. This condition, called the critical Reynolds number, is often termed the drag crisis (after Hoerner) and corresponds to the reattachment of the previously separated laminar boundary layer to a turbulent boundary layer, which then separates downstream on the rear of the cylinder. The critical Reynolds number for a cylinder is about Re = 2 \times 10^5. The narrower wake subsequently reduces pressure drag and overall drag. However, note that with further increases in Re, drag increases again from the higher surface shear stresses (i.e., skin friction) produced by the turbulent boundary layer as the flow speed and Reynolds number increase.

The drag coefficient of smooth and rough spheres as a function of Reynolds number. The results for a circular disk are also shown as a reference.

The aerodynamic behavior of a sphere is qualitatively similar to that of a circular cylinder, as shown in Figure 8. Again, there is a sudden drop in drag as the Reynolds number reaches a critical value because of the transition from laminar flow separation to turbulent separation. However, in this case, the surface roughness effects are of some interest, which can cause the drag reduction on the sphere to occur at a lower value of the critical Reynolds number.

Check Your Understanding #2 – Drag coefficient of a circular cylinder

Consider nominally two-dimensional flow past a long circular cylinder of diameter D = 0.4~\mathrm{m}. The freestream velocity is V_{\infty} = 50~\mathrm{m/s}. The properties of air at standard conditions are \varrho_{\infty} = 1.225~\mathrm{kg/m^3} and \mu_{\infty} = 1.7894 \times 10^{-5}~\mathrm{kg\,m^{-1}\,s^{-1}}.

  1. Determine the Reynolds number for this flow.
  2. Identify the flow regime around the cylinder.
  3. Estimate the sectional drag coefficient, C_d, for the cylinder.
Show solution/hide solution.
  1. The Reynolds number is

    (8)   \begin{equation*} Re_D = \frac{\varrho_{\infty} \, V_{\infty} \, D}{\mu_{\infty}} \end{equation*}

    Substituting values gives

    (9)   \begin{equation*} Re_D = \frac{1.225 \times 50.0 \times 0.4}{1.7894 \times 10^{-5}} = 1.37 \times 10^6 \end{equation*}

  2. This Reynolds number lies well above the critical value (Re_D \approx 2 \times 10^5) associated with boundary-layer transition on a circular cylinder. In this regime, the boundary layer becomes turbulent before separation, delaying separation and significantly reducing pressure drag. The flow is therefore in the supercritical regime.
  3. From standard drag curves for a smooth circular cylinder, the drag coefficient in the supercritical regime is typically in the range C_d \approx 0.2 to 0.3, noting that the exact value will depend on surface roughness and freestream turbulence.

Surface Roughness Effects on Cylinders & Spheres

Surface roughness modifies the flow around cylinders and spheres, primarily affecting their drag by promoting earlier transition of the boundary layer to turbulence. When the transition occurs before laminar boundary layer separation, the turbulent boundary layer can resist the adverse pressure gradients better, flow separation is delayed, the downstream wake narrows, base pressure rises, and the total drag coefficient C_D drops sharply. This behavior first occurs at (or near) a critical Reynolds number or transition Reynolds number, Re_{\text{crit}}. The underlying flow physics is essentially the same for both circular cylinders and spheres.

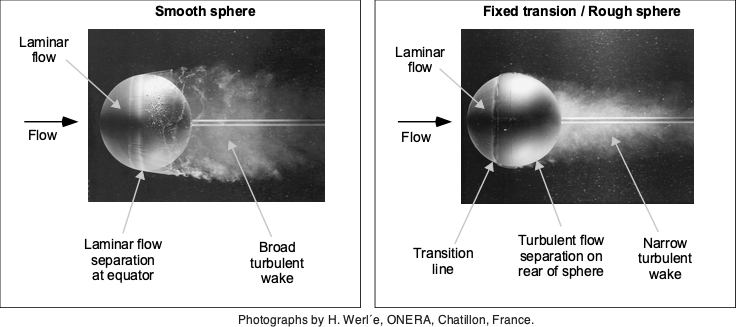
This behavior is illustrated in Figure 9, using flow visualization of a sphere, where the roughness causes a noticeable reduction in the width and extent of the downstream wake. It explains the reduction in drag: the roughness increases the effective Reynolds number. The surface roughness causes the laminar boundary layer on the upstream side of the sphere to transition immediately into a turbulent boundary layer, which can remain attached to the sphere’s surface much longer than a laminar boundary layer. The consequence of this behavior is a narrower low-pressure wake, leading to lower drag on the sphere. In effect, adding roughness produces the same outcome that would naturally occur at higher Reynolds numbers, i.e., a turbulent boundary layer and delayed separation. This is why roughness is often described as increasing the effective Reynolds number, as it shifts the flow state into the post-critical regime at a lower actual Reynolds number.

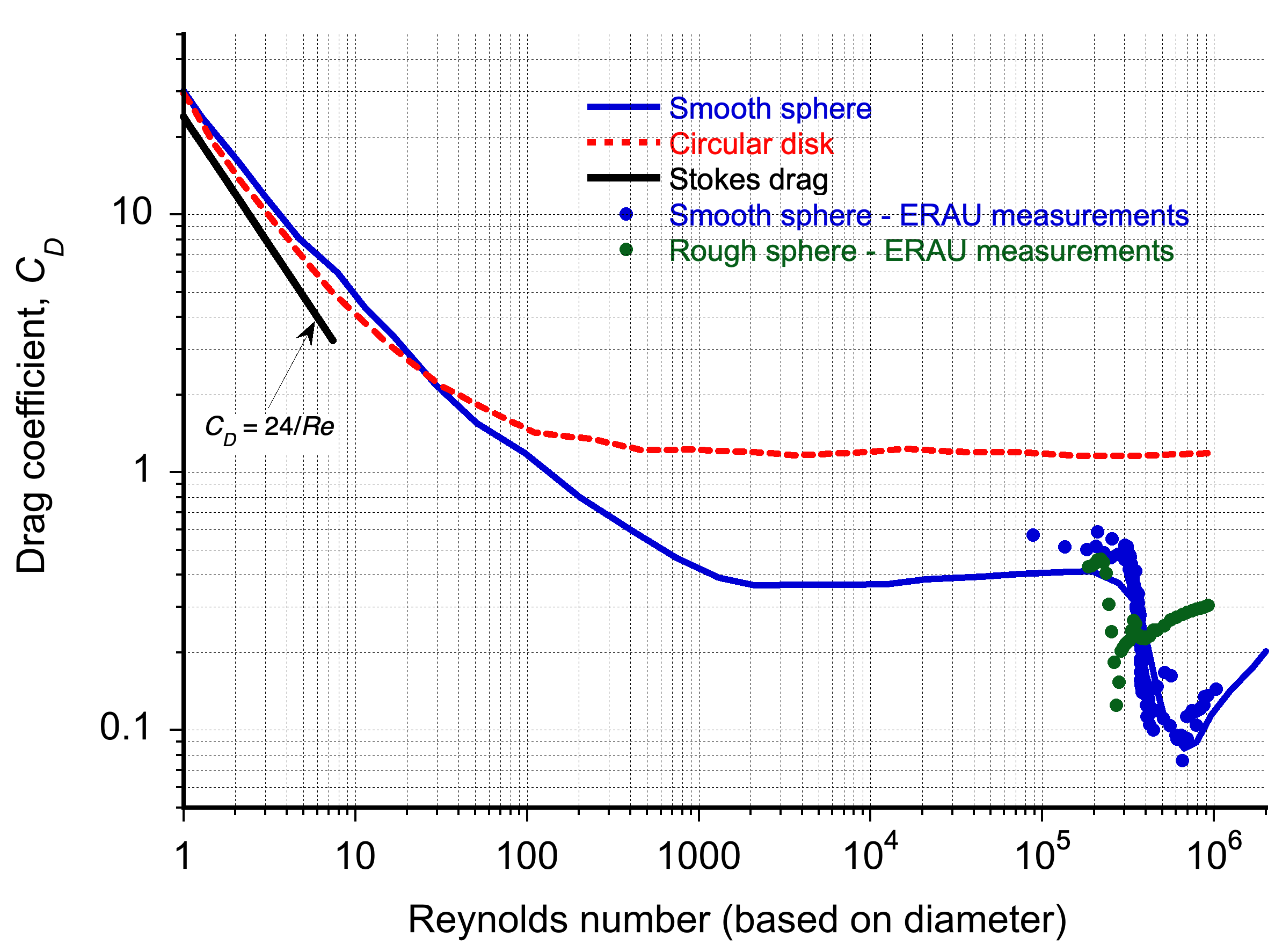
Flow visualization about a sphere with a smooth surface (left) at a Reynolds number of about Re = 3 \times 10^5, and the same sphere at the same Reynolds number with surface roughness (right).

The drag coefficient measurements in Figure 10 indicate that increasing roughness reduces the effective critical Reynolds number. Hence, the “crisis” in the flow state occurs earlier and increases drag below that threshold. The influence of roughness on the external flow over cylinders and spheres can be conventionally described using the nondimensional parameter \dfrac{\epsilon}{D}, where \epsilon is a characteristic surface roughness height and D is the cylinder or sphere diameter; this ratio provides a convenient way to compare the effects of roughness across different body sizes. In practical terms, smooth surfaces (\epsilon/D \lesssim 10^{-4}) cause the drag crisis to occur later, near Re \sim 3\times10^{5}. Moderate roughness (i.e., \epsilon/D \sim 10^{-3}–10^{-2}) promotes earlier boundary layer transition and can lower the critical Reynolds number down to Re \sim 5\times10^{4}. For large amounts of roughness (i.e., \epsilon/D \gtrsim 10^{-2}), the point of flow separation may move upstream instead, increasing C_D throughout the Reynolds number range.

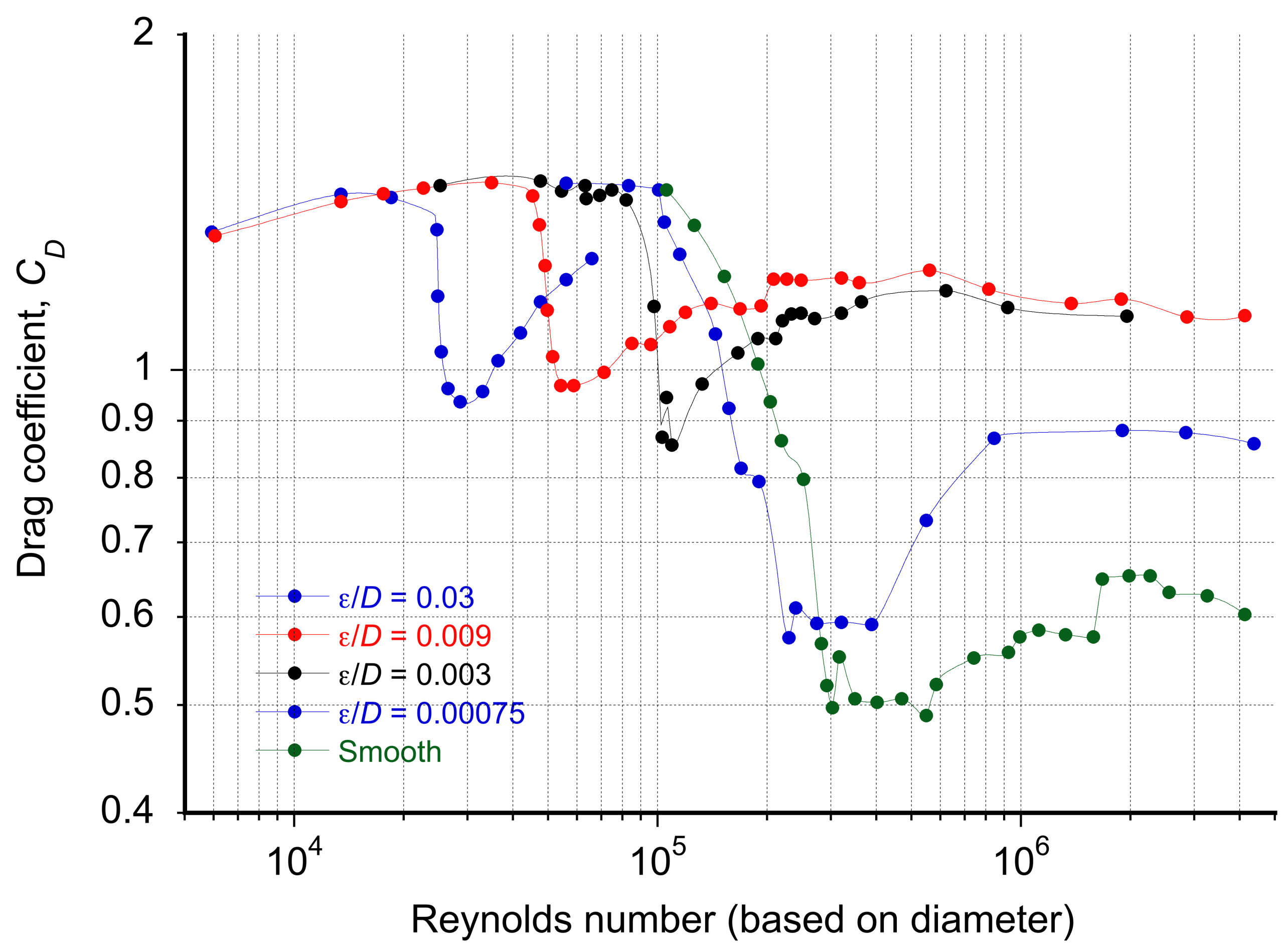
The drag coefficient of a circular cylinder as a function of Reynolds number and surface roughness. Re_{\text{crit}} decreases with increasing roughness.

The underlying flow physics is essentially the same for spheres. Once the Reynolds number exceeds the critical value, the boundary layer transitions to turbulence, delaying the onset of separation, narrowing the downstream wake, and thereby reducing drag. The details of the transition process and wake structure differ between cylinders and spheres, but the overall sequence of the changes in the flow regimes is analogous. A smooth sphere has a subcritical C_D \approx 0.45 with laminar separation, then a sharp decrease to C_D \approx 0.2–0.3 near Re \approx 2–4\times10^5, followed by a mild increase in the post-critical regime. Surface roughness (e.g., as in a golf ball with dimples) promotes an earlier transition. It shifts the crisis conditions to lower values of Re_D (often \sim5\times10^4), enabling substantial drag reduction at flight speeds/length scales where the flow about a smooth sphere remains subcritical. This overall behavior is summarized in the table below.[1]

Representative drag coefficients for smooth versus. rough/tripped cylinders and spheres. Exact values depend on {\epsilon/D}.
Body Regime (Re) Smooth C_D Rough/Tripped C_D Notes
Cylinder 1×104 ≈ 1.2 ≈ 1.3 Roughness increases drag well below crisis
Cylinder 5×104 ≈ 1.2 0.6–1.0 Crisis may begin if {\epsilon/D} ∼ 10−2
Cylinder 2–4×105 0.25–0.35 0.25–0.35 Drag minimum region (earlier for rough)
Sphere 5×104 ≈ 0.45 0.25–0.35 Dimples/roughness can trigger early crisis
Sphere 2–4×105 0.20–0.30 0.20–0.30 Critical / post-critical zone

Why Do Golf Balls Have Dimples?

Ever wonder why a golf ball has dimples? Did you know that in the earliest days of golf, in the windy, cold links of Scotland, kilted golfers[2] made a remarkable discovery? They found that older, worn, and rougher balls traveled farther than new ones. This discovery was not merely an observation; it significantly affected the game’s outcomes. Golfers[3]using these rough balls gained a golfer a considerable competitive edge, requiring many fewer strokes from the tee to the hole.

Scottish golfers eventually discovered that old, worn-out balls traveled much further than new, smooth balls.

Unsurprisingly, the unique behavior of these rough spheres caught the attention of scientists, who began studying their aerodynamics in wind tunnels, as previously shown in Figure 10. These experiments revealed that rough spheres could have less aerodynamic drag than their smooth counterparts because the flow separated from the ball differently depending on their roughness, as shown in Figure 12. The Reynolds number for a golf ball’s flight is approximately 8 x 104 to 2.1 x 105. This discovery also led to the realization that standardizing golf balls was necessary to ensure a fair playing field for all golfers. 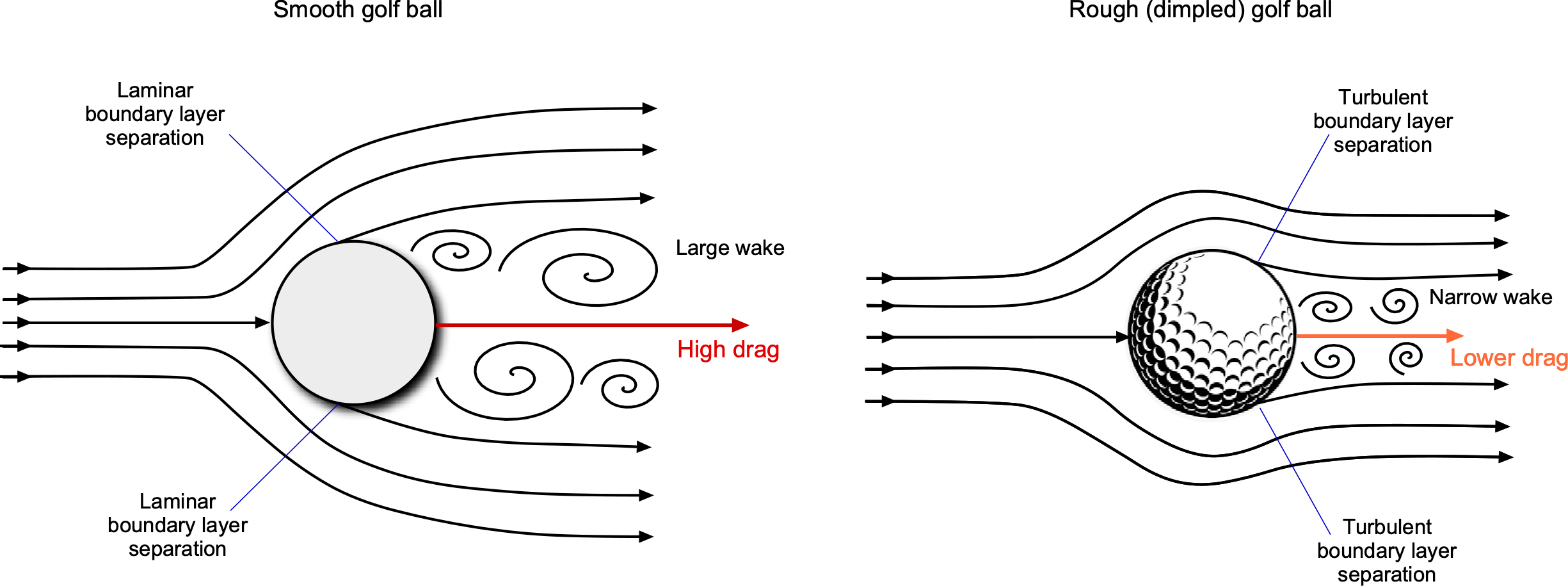This outcome is important because roughness reduces the ball’s aerodynamic drag in a way that depends on how hard it is struck. A smooth ball would favor only golfers who could drive it fast enough to approach the drag crisis, whereas the roughness causes the drag reduction to occur over a lower range of Reynolds numbers. Therefore, the dimples make the game fairer by reducing the aerodynamic disadvantage suffered by players with lower swing speeds.

The reduction in drag of the dimpled ball at the Reynolds number of its flight causes it to travel about twice as far as a smooth ball of the same diameter.

A modern golf ball is a machine-dimpled sphere, and the dimples provide a high level of surface roughness to deliberately alter its aerodynamics. The dimples, a standardized form of roughness, cause the boundary layer on the upstream side of the ball to transition from laminar to turbulent flow, delaying flow separation and thereby reducing drag. At the Reynolds numbers corresponding to the ball’s flight, which is about Re = 3 \times 10^5, the flow on a smooth ball would usually be laminar, and the flow would easily separate near the equator and cause higher pressure drag, as shown in Figure 12.

However, a turbulent boundary layer, created using surface roughness, will remain attached to the ball’s surface much longer than a laminar boundary layer before it separates. This behavior results in a narrower low-pressure wake and lower pressure drag. Interestingly, creating turbulence reduces drag, i.e., the dimples serve as a form of flow control. However, do not expect dimples to work on streamlined bodies, such as those of wings. The objective here is to keep the flow as smooth (laminar) as possible for as long as possible, thereby reducing skin-friction drag, which is the dominant drag source on streamlined shapes at low angles of attack. Adding dimples can only increase drag on a streamlined body.

The consequence of reduced drag is that a golfer can hit the ball farther. This distance can be estimated using the principles of dynamics and aerodynamics. One useful approximation for the range of the ball is

(10)   \begin{equation*} R \approx \frac{2 \, m}{\varrho \, A \, C_D}\, \ln\left(1+\frac{\varrho \, A \, C_D\,V_0^2\sin(2\theta)}{2 \,m \, g}\right) \end{equation*}

where V_0 is the initial velocity of the ball as it leaves the club, \theta is the initial hit trajectory angle of the ball, A is the projected frontal area of the ball, m is the mass of the ball, \varrho is the air density, and C_D is the Reynolds number dependent drag coefficient based on ball diameter. This expression is only an approximation because it neglects the effects of backspin, which produces lift and can significantly increase range, and assumes that C_D remains approximately constant during flight. Also, because of drag, the launch angle for maximum range is generally less than 45^\circ. Nevertheless, this result shows that reducing the drag coefficient increases the range, all other factors being equal.

Check Your Understanding #3 – Reynolds number of a golf ball

What is a golf ball’s flight Reynolds number? What is the ball’s drag coefficient under the conditions of flight? Why is this important regarding the flight distance of a golf ball? To answer this question, the issues to address are: What is the diameter of a golf ball? How fast does a golf ball travel?

Show solution/hide solution.

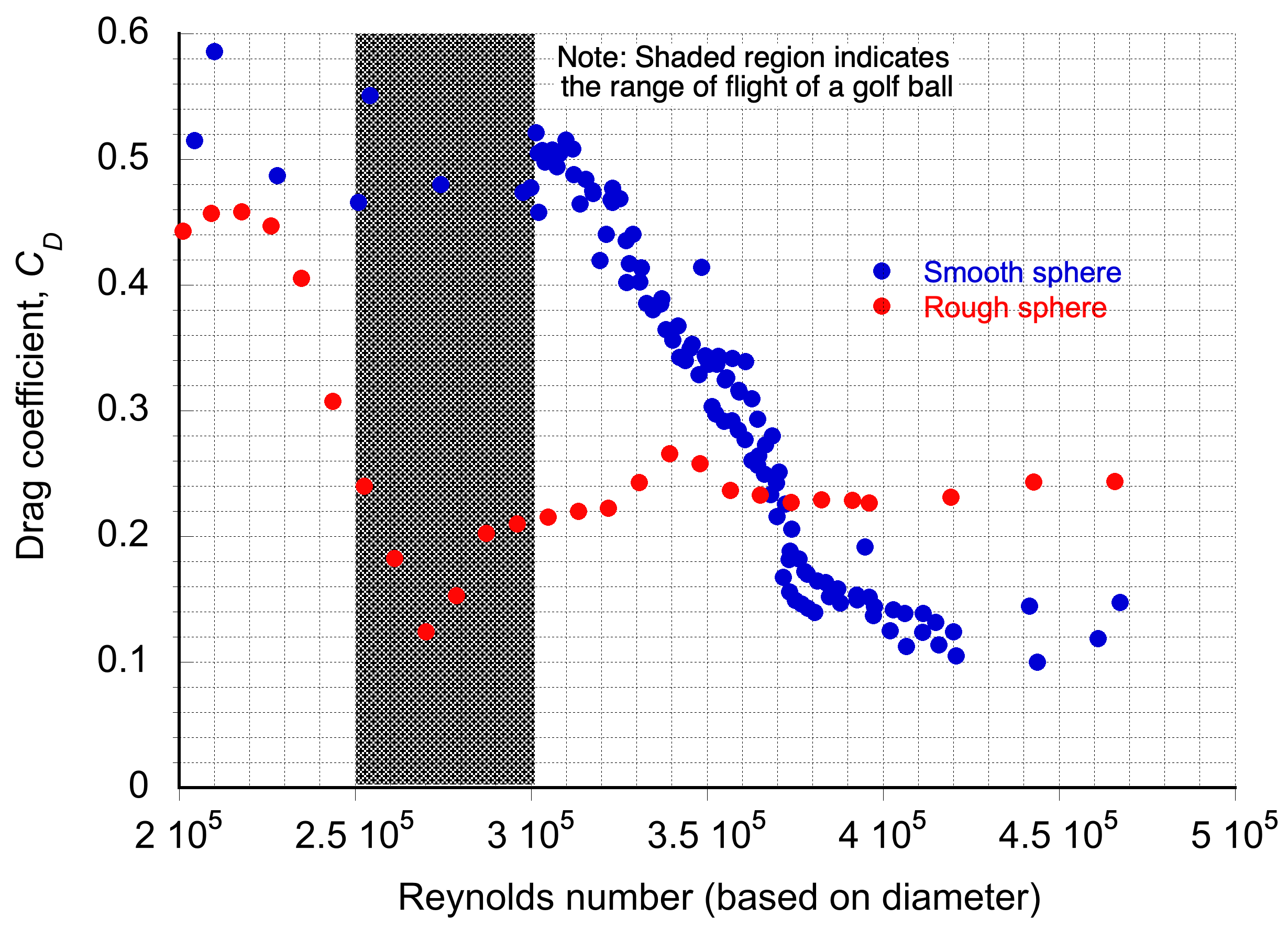
A little research will reveal that, according to golf rules, a golf ball’s diameter must be at least 1.68 inches (42.67 mm). Additionally, an amateur golfer typically hits a ball at an average speed of 125 mph (201.2 kph) with a driver club. However, those speeds can vary significantly with a golfer’s skill level, ranging from about 60 mph (96.6 kph) to 160 mph (257.5 kph). Therefore, the Reynolds number of a golf ball can only be established within certain bounds.

The Reynolds number of the golf ball based on its diameter is

    \[ Re_D = \frac{\varrho \, V D}{\mu} \]

where \varrho and \mu can be assumed to take MSL ISA values, i.e., in SI units, then \varrho = 1.225 kg/m3 and \mu = 1.7894 x 10-5 kg m-1 s-1. Inserting the values using 257.5 kph or 71.53 m/s gives

    \[ Re_D = \frac{1.225 \times 71.53 \times 0.04267}{1.7894 \times 10^{-5}} = 2.09 \times 10^5 \]

and for 201.2 kph or 55.88 m/s gives

    \[ Re_D = \frac{1.225 \times 55.88 \times 0.04267}{1.7894 \times 10^{-5}} = 1.63 \times 10^5 \]

and for 96.6 kph or 26.82 m/s gives

    \[ Re_D = \frac{1.225 \times 26.82 \times 0.04267}{1.7894 \times 10^{-5}} = 7.8 \times 10^4 \]

Therefore, the Reynolds number for a golf ball’s flight is approximately 8 x 104 to 2.1 x 105.

Examining the C_D versus Reynolds number for this range, as shown in the graph below, it can be seen that, based on measurements, the drag coefficient of a rough ball in this range will be less than half of a smooth ball, i.e., the dimples promote earlier transition of the boundary layer and delay separation. This outcome is supported by experience and empirical data from golf.
This outcome is important because the dimples reduce the ball’s aerodynamic performance, depending on how hard it is struck. A smooth ball would favor only golfers who could drive it fast enough to approach the drag crisis, whereas the roughness causes the drag reduction to occur over a lower range of Reynolds numbers. Therefore, the dimples make the game fairer by reducing the aerodynamic disadvantage suffered by players with lower swing speeds.

This reduction in drag is very important regarding the flight distance of a golf ball. One approximate expression for the range is

(11)   \begin{equation*} R \approx \frac{2 \, m}{\varrho \, A \, C_D}\, \ln\left(1+\frac{\varrho \, A \, C_D\,V_0^2\sin(2\theta)}{2 \,m \, g}\right) \end{equation*}

where V_0 is the initial velocity of the ball, \theta is the initial hit trajectory angle of the ball, A is the projected frontal area of the ball, m is the mass of the ball, \varrho is the air density, and C_D is the Reynolds number dependent drag coefficient based on ball diameter. Therefore, a reduction in C_D produced by the dimples will increase the range, all other factors being equal.

Using a representative amateur launch speed of 135 mph (60.39 m/s), a launch angle of about 15^\circ, a golf ball mass of m = 0.0459 kg, a diameter of 0.04267 m (so that A = 1.43 \times 10^{-3} m2), and a representative value of C_D \approx 0.5, the approximate range from the preceding expression is R \approx 150 m, or about 165 yards.

Aerodynamics of Spinning Cylinders & Spheres

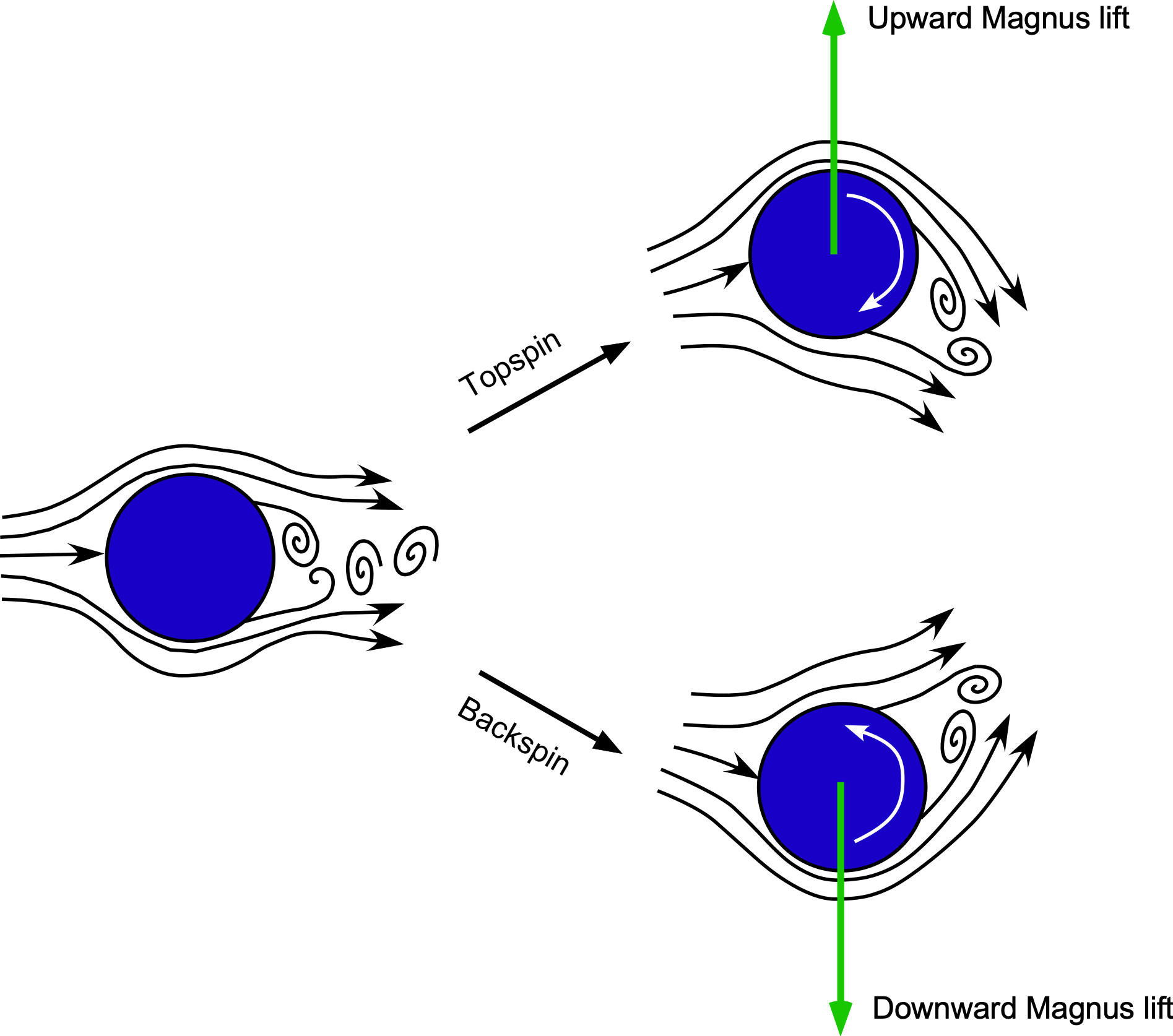
Another effect experienced by golf balls and other balls used in various games and sports is a lift force produced by their spinning motion, such as backspin or topspin. The ball’s spin spoils the flow’s horizontal symmetry, creating differential pressure and producing a lift force. This phenomenon is known as the Magnus effect, named after Heinrich Magnus, the German scientist who first studied it in the 19th century, as illustrated in Figure 13. In some cases, Magnus observed a tendency of a cannonball to curve or veer significantly away from their expected flight path. He concluded that this behavior was a result of the residual spinning motion of the cannonball as it left the barrel. Isaac Newton also observed this same behavior while watching people play tennis.

The spin of a ball (sphere), in this case, a topspin or a backspin, will cause a type of lift called a Magnus lift.

The dependence of the Magnus lift coefficient, C_L, on the translational and rotational speeds of a smooth cylinder of diameter D has been investigated and measured in wind tunnels, a summary of some results being reproduced in Figure 14, where {V_\infty} is its translational or freestream velocity and \Omega is the rotational angular velocity. The results can be generalized in terms of a non-dimensional spin rate, i.e.

(12)   \begin{equation*} S = \frac{\Omega \, D}{2\, V_\infty} = \frac{\Omega \, R}{V_\infty} \end{equation*}

where R = D/2. Notice the additional dependency on the Reynolds number, as given by

(13)   \begin{equation*} Re_D = \frac{\varrho_\infty \, V_\infty D}{\mu_\infty} \end{equation*}

Indeed, the results are highly dependent on the Reynolds number, which is highly nonlinear. These effects are related to a “moving wall” effect that alters the boundary-layer characteristics over the top and bottom halves of the cylinder, resulting in premature laminar separation on the upper half and delayed separation on the lower half. This latter behavior is also characteristic of spheres and is central to the physics of all ball games. Below the critical Reynolds number, there is a “reverse Magnus effect,” which is again tied to boundary-layer behavior.

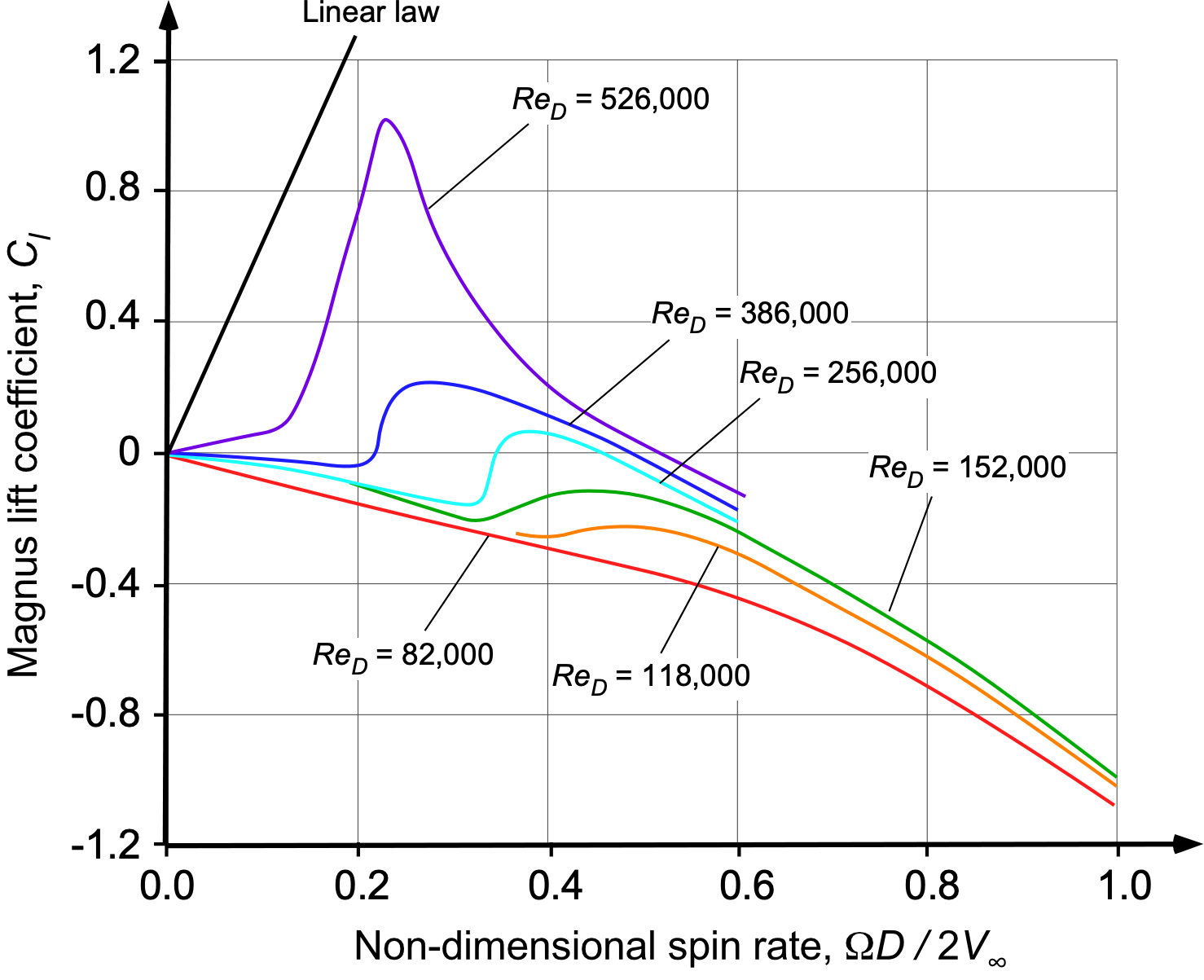
Results showing the Magnus lift coefficient, C_l, on the translational and rotational speeds of a smooth cylinder.

For attached flow at lower spin ratios, the circulation, which is given the symbol \Gamma,[4] about a rotating cylinder may be approximated as \Gamma = 2\pi \, R^2 \, \Omega, and so the lift per unit span is obtained from the Kutta-Joukowski theorem as

(14)   \begin{equation*} L' = \varrho_\infty \, V_\infty \, \Gamma = 2\pi \varrho_\infty \, V_\infty \, R^2 \,\Omega \end{equation*}

The corresponding “linear law” of lift coefficient, normalized by the dynamic pressure and diameter D = 2R, is

(15)   \begin{equation*} C_l = \frac{L'}{\frac{1}{2}\varrho_\infty \, V_\infty^2 (2D)} = 2\pi \left( \frac{\Omega \, R}{V_\infty} \right) = 2\pi \, S \end{equation*}

At lower Reynolds numbers, boundary layer transition and separation alter the circulation so that the linear Magnus lift law, i.e.,

(16)   \begin{equation*} C_l \simeq 2\pi S \end{equation*}

no longer holds. The behavior is similar on both spinning cylinders and spheres (balls). Wind tunnel measurements[5] shows that the lift initially follows this linear trend at small spin ratios S, but begins to saturate at higher S because the circulation cannot increase indefinitely. An empirical representation that accounts for this limitation is

(17)   \begin{equation*} C_l (S,Re) = F_\Gamma(Re_D)\left( \frac{2\pi \, S}{1 + \beta(Re_D) \, S} \right) \end{equation*}

where the factor F_\Gamma(Re_D) represents amplification or suppression of circulation depending on whether the boundary layer is laminar or turbulent, and \beta(Re_D) is an empirical constant that controls the onset of lift saturation. In the limit of small spin ratios, this model recovers the linear Magnus law, scaled by F_\Gamma(Re_D), i.e.,

(18)   \begin{equation*} C_l \simeq 2\pi \, F_\Gamma(Re_D)\, S \end{equation*}

while for large spin ratios the lift approaches a finite asymptotic maximum, consistent with observations, i.e.

(19)   \begin{equation*} C_{l,\max}(Re_D) \simeq \frac{2\pi}{\beta(Re_D)}\,F_\Gamma(Re_D) \end{equation*}

Surface roughness is known to promote earlier transition to turbulence and stronger circulation.[6] This effect can be included through the definition of an effective Reynolds number, i.e.,

(20)   \begin{equation*} Re_{\rm eq} = Re_D\left(1 + \chi\,\frac{\epsilon}{D}\right) \end{equation*}

where \epsilon is the characteristic roughness height and {\chi} is an empirical constant. In this way, both F_\Gamma and \beta become functions of Re_{\rm eq} rather than the nominal Re.

For the case of a spinning sphere of radius R, measurements show that the Magnus lift still scales with the spin ratio S, but with a smaller proportionality constant than the 2\pi value found for cylinders. A common empirical form is

(21)   \begin{equation*} C_{L,\text{sph}}(S,Re_D) = F_{\Gamma,\text{sph}}(Re_D)\,\frac{\alpha\, S}{1 + \beta_{\text{sph}}(Re_D) \, S} \end{equation*}

where \alpha is an empirical constant, typically less than 2\pi. At small spin ratios, this reduces to

(22)   \begin{equation*} C_{L,\text{sph}} \simeq \alpha\,F_{\Gamma,\text{sph}}(Re_D)\,S \end{equation*}

while the lift again saturates at higher S, approaching

(23)   \begin{equation*} C_{L,\max,\text{sph}}(Re_D) \simeq \frac{\alpha}{\beta_{\text{sph}}(Re_D)}\,F_{\Gamma,\text{sph}}(Re_D) \end{equation*}

Therefore, the explanation for the curving behavior of a ball lies in aerodynamics. In the case of a topspin, the surface motion accelerates the flow over the upper surface, producing a higher velocity and lower pressure there. This results in a net downward force (negative lift), so a topspin will cause a ball to dip more quickly toward the ground. Conversely, a backspin slows the flow over the upper surface, producing a higher pressure above and a net upward force (positive lift). A backspin will therefore cause a ball to stay aloft longer and travel farther. Sidespin produces an analogous lateral force, giving rise to the curved trajectories seen in a baseball “curveball” or a soccer “banana kick.”

Backspin, topspin, and sidespin are used in various ball games, enhancing players’ skills and the unpredictability of the game, ultimately adding to the fun. The effects of Reynolds number and surface roughness mean that the curving characteristics depend on the size and surface finish of the ball. For example, this is evident in a smooth ping-pong ball compared with the seams on a baseball or soccer ball. However, one can only spin the ball so fast before the lift saturates, beyond which further increases in spin rate produce no additional effects.

Complex Three-Dimensional Bluff Bodies

The flows produced by more general three-dimensional bluff body shapes are considerably more complex. Other types of flow phenomena are shown in Figure 15, which depicts the behavior of the so-called “airwake” over a ship’s surface. Scarf or horseshoe vortices tend to form and wrap around the base (or foot) of bluff bodies that protrude from a surface (wall), in this case, the funnel. These vortices are, again, another source of drag. In addition, complex flow separation and reattachment regions on the body often make the a priori estimation of drag on such bodies very difficult.

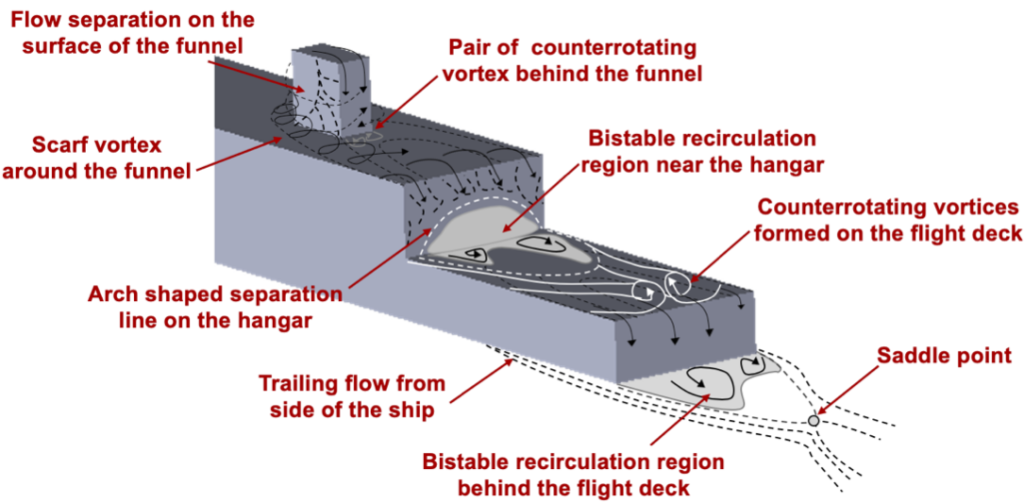
The flow around a complex bluff body, especially one that protrudes from a surface, is highly complex and three-dimensional. In this case, the flow concerns the rear of a ship with a flight deck for helicopter operations.

Vortex-Induced Vibration

One concern with three-dimensional bluff-body flows is that the aerodynamic forces generated by vortex shedding can be sufficiently strong to excite the structure itself. One of the most important effects in this regard is vortex-induced vibration (VIV), where the unsteady aerodynamic excitation produced by vortex shedding causes the structure to vibrate or even flutter. VIV problems can arise in many engineering applications, not just in aerospace systems, wherever periodic vortex shedding occurs. Long, slender cantilevered structures such as wires, chimneys, and suspension bridges are particularly susceptible.

The Strouhal number is commonly used to characterize vortex shedding. It relates the shedding frequency to the flow velocity and a characteristic dimension of the body (the diameter d for a cylinder). The Strouhal number St is defined as

(24)   \begin{equation*} St = \frac{f_{\rm st} \, d}{V_{\infty}} \end{equation*}

where f_{\rm st} is the vortex shedding frequency and {V_{\infty}} is the freestream velocity. For a circular cylinder, the Strouhal number is approximately St \approx 0.2 over a wide range of Reynolds numbers.

The lock-in phenomenon occurs when the vortex-shedding frequency approaches a system or structure’s natural vibration frequency, leading to severe oscillation or even flutter. Although the onset of flutter will usually always reach a limit cycle in some form, the associated high cyclic stresses produced on a metallic structure can quickly cause fatigue failure.

Wakes Shed from Bridges

In civil engineering, vortex shedding from suspension bridges, which are bluff bodies in cross-section, is a significant cause of concern and can lead to bridge failures. When the Tacoma Narrows Bridge over Puget Sound in Washington state collapsed in 1940 because of a torsional flutter caused by stiff winds, it was captured on film. The lessons learned have become a textbook example of vortex-induced vibration. However, this bridge is one of many affected by VIV and flutter.

Figure 16 shows the essence of the problem. The bluff “H”- shaped cross-section of the bridge causes vortex shedding, resulting in periodic, unsteady aerodynamic forces. This behavior causes the bridge deck to twist under wind loading. Depending on the bridge’s characteristics, such as weight and dynamic frequencies, the deformations can be substantial and may quickly exceed 20 degrees.

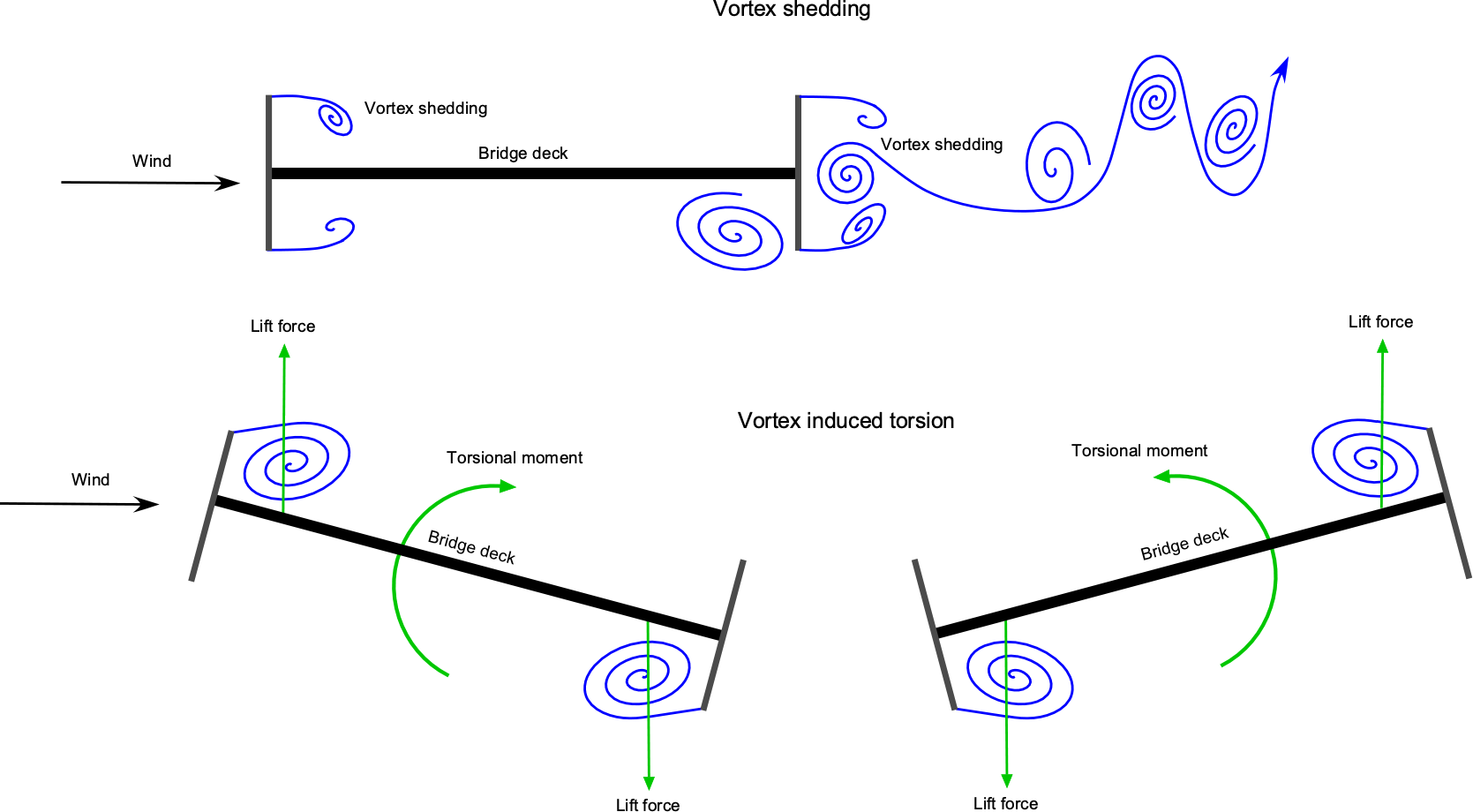
In cross-section, a bridge deck can cause vortex shedding and oscillatory aerodynamic forces.

Twisting of the bridge deck increases flow separation, thereby forming stronger vortices and higher aerodynamic loads, which further twist the deck. While the deck structure resists lifting and twisting because of its inherent torsional stiffness, this behavior can lead to a “lock-in” event and the development of “torsional flutter.” In some cases, it may be possible to modify the bridge’s cross-sectional shape to reduce vortex shedding and increase wind speed, thereby mitigating torsional flutter.

Streamlining

Streamlining a bluff or otherwise unstreamlined body shape is an effective technique for reducing drag. For example, the basic idea is shown in Figure 17. Adding a tail and/or nose fairing can significantly delay flow separation, reducing drag. A consideration, however, is that the fairing adds extra weight to the aircraft.

Streamlining a body can reduce drag, although it is not always a viable design option.

While streamlining may not be a viable engineering option in some cases because of practical or cost constraints, it is always worthwhile to reduce an aircraft’s overall drag and improve its performance, even at the expense of a slight increase in structural weight. For example, carefully blending a wing to the fuselage using a fairing can eliminate the horseshoe vortex and reduce interference drag from the resulting streamlining, as shown in the photograph in Figure 18 for a general aviation airplane, with an almost negligible increase in airframe weight. For a commercial aircraft, the wing root fairing is designed to reduce interference drag and is part of the transonic drag reduction process, utilizing Whitcomb’s area rule. The area rule states that the cross-sectional area should vary smoothly and continuously, rather than abruptly, to minimize drag on an airplane; that is, the second derivative of the area change should be continuous.

A wing root fairing can help reduce interference drag between the wing and the fuselage, thereby decreasing the total aircraft drag.

An airplane with a fixed landing gear can benefit from adding fairings and spats around the landing gear and wheels. Of course, retracting the wheels entirely is the only way almost to eliminate the drag. However, the extra weight and higher cost of a mechanical system for retractable landing gear are not usually viable for smaller aircraft, such as those in the general aviation class.

Other aircraft that can benefit from streamlining include helicopters, which have relatively unstreamlined airframes for their utility. Using fairings at strategic locations on a helicopter’s airframe can reduce drag by 10% to 30%, allowing it to fly faster and/or achieve better range or endurance.

Streamlining of Terrestrial Vehicles

The aerodynamic drag of terrestrial vehicles, such as automobiles, trucks, and trains, increases significantly at higher driving speeds. For a given drag coefficient, C_D, the drag, D, on the vehicle will increase with the square of its speed V, i.e.,

(25)   \begin{equation*} D = \frac{1}{2} \varrho V ^2 \, C_D \, A_{\rm ref} \end{equation*}

So the power required to propel the vehicle P_{\rm req} will increase with the cube of its driving speed over the ground, i.e.,

(26)   \begin{equation*} P_{\rm req} = D V = \frac{1}{2} \varrho \, V ^3 \, C_D \, A_{\rm ref} \end{equation*}

Therefore, it is also apparent that the required fuel or energy increases with the cube of the speed. Rolling resistance, or friction, also affects the net resistance on the vehicle and the fuel or energy needed for propulsion; however, aerodynamic effects dominate at higher speeds.

As with flight vehicles, terrestrial vehicles can reduce energy consumption by lowering drag, i.e., by streamlining to minimize C_D. Aerospace engineers possess the training and expertise to understand the steps required to achieve profitable drag reductions. Much of the testing of terrestrial vehicles is conducted in wind tunnels, although CFD solutions can also be beneficial.

Automobiles & Cars

The automotive industry has become proficient at streamlining vehicle designs to reduce fuel consumption and internal noise, a process that typically requires extensive wind tunnel testing. Turbulence about the vehicle, such as from rear-view mirrors, can be a significant source of internal noise. The photograph in Figure 19 below shows an example of flow visualization about an automobile. The judicious use of smoke filaments and appropriate lighting can provide insight into flow patterns, indicating where flow is attached or separated, thereby informing decisions about where streamlining may be needed.

Example of smoke flow visualization about an automobile in a wind tunnel.

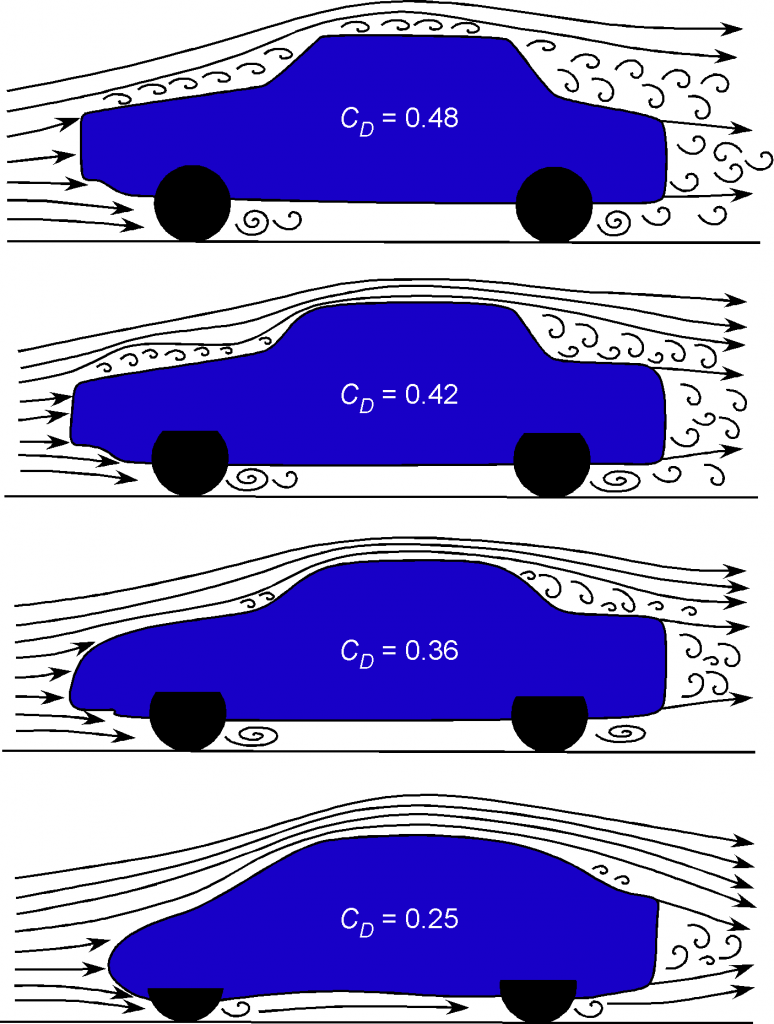
As shown in Figure 20, the careful streamlining of automobile shapes can reduce drag. The result is a significant decrease in fuel consumption and a notable reduction in internal noise, as a result of corresponding reductions in turbulence. However, streamlining can only be taken so far, beyond which compromises in the vehicle’s utility may become problematic. Exposed wheels are a significant source of drag, so there has been a trend toward more careful streamlining of the wheel well and the vehicle’s underside.

Streamlining an automobile by rounding off sharp corners can cut drag by half and commensurately improve fuel consumption.

Trucks (Lorries) & Buses

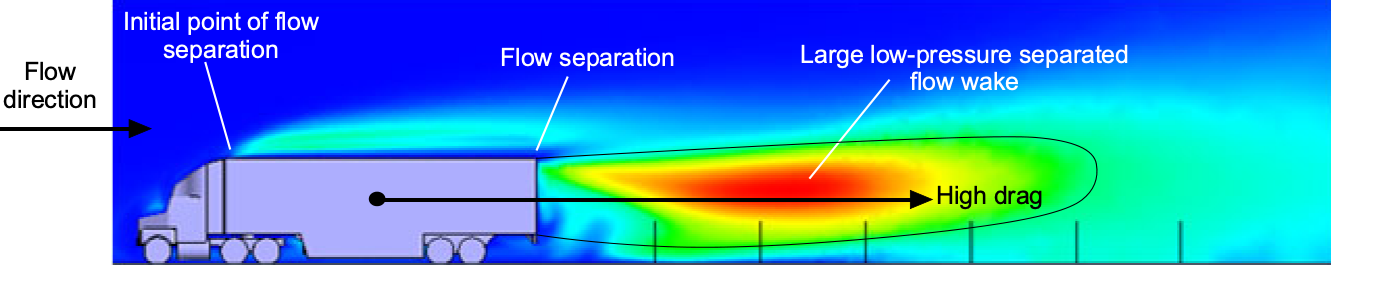
As shown in Figure 21, trucks (lorries) and buses are aerodynamically inefficient because of their “boxy” shapes, which result in high base pressure drag. For most trucks, their average fuel consumption is 50% to 200% higher than that of automobiles. For example, an 18-wheeler truck used to transport most goods to supermarkets and similar establishments might achieve 5 to 8 miles per gallon (2.1 to 3.4 km per liter). Still, these values can vary significantly depending on engine size, driving speed, and load (weight). The large, rectangular, box-like shapes often seen being towed by tractor-trailers are poor aerodynamic shapes, characterized by high drag. These boxes are typically referred to as CONEX or Intermodal Shipping Containers or ISO boxes (ISO 6346).

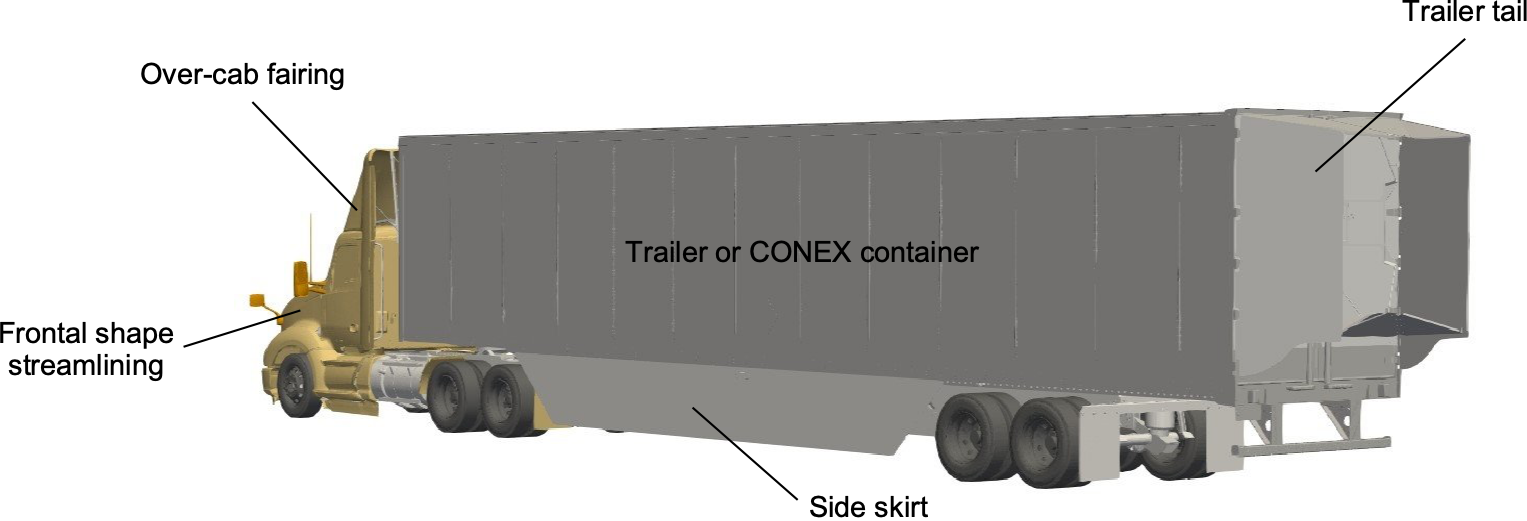
Tractor-trailers are bluff bodies and suffer from high drag and poor fuel economy.

Engineers have four significant areas of interest in obtaining meaningful aerodynamic drag reduction on trucks and lorries. These are:

  1. The frontal shape of the tractor part, which is somewhat unstreamlined, is partly because of utility requirements (engine access) and cooling needs.
  2. The gap between the tractor’s end and the trailer’s leading edge (or the front of the CONEX container) can cause flow separation and turbulence.
  3. The shapes of the sides and underbody of the trailer, which shed turbulence and create drag.
  4. The very back of the trailer is a significant source of pressure drag.

Continuous improvements to the aerodynamics of trucks have reduced their drag, resulting in increased fuel efficiency. Minimizing the gap between the trailer and the tractor is essential, so fairings on the top of the tractor are often used, as shown in Figure 22. In addition, rubber skirts can be installed beneath the trailer and along its sides to redirect high-speed airflow away from the trailer’s underside, thereby reducing drag from the wheels, which also act as bluff bodies.

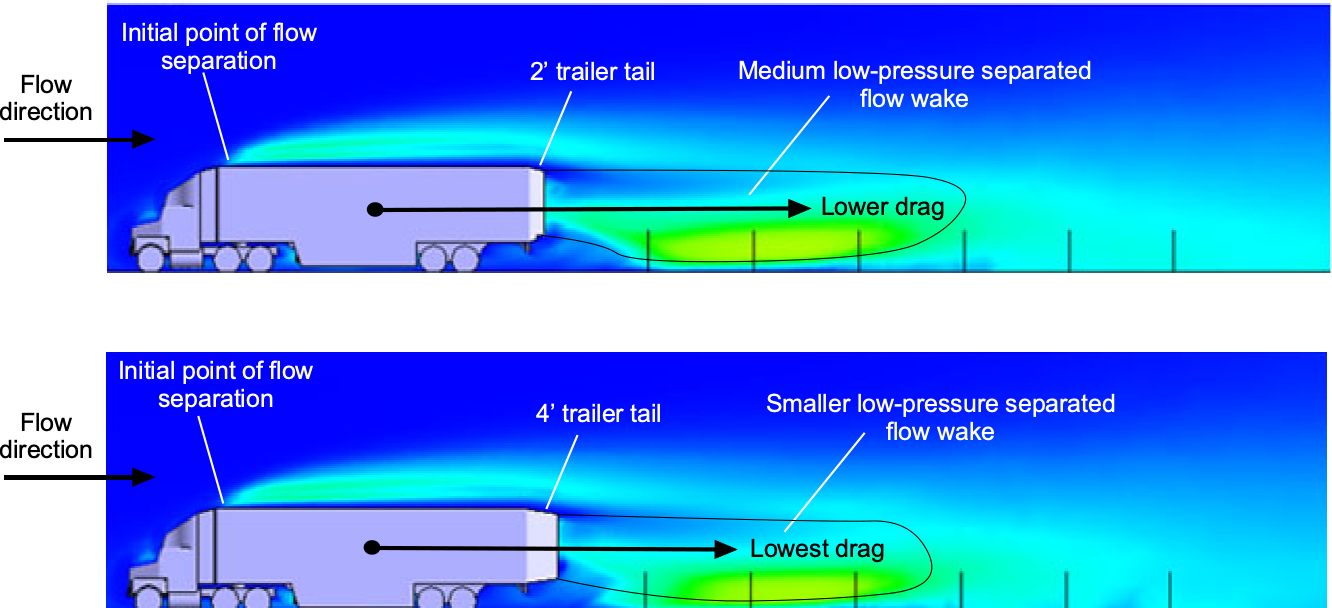
Reductions in drag can be achieved by minimizing the gap between the tractor and trailer, modifying the trailer’s sides and underbody, and adding a fairing at the rear.

Trailer tails are increasingly used on trucks, which are pop-out afterbody fairings, as also shown in Figure 22. Although relatively crude in shape, they help reduce drag from flow separation and turbulence at the trailer’s rear end. Figure 23 shows that even a short trailer tail reduces base-pressure drag. The corresponding reduction in fuel consumption makes their use worthwhile when considering the overall fuel costs of the truck fleet. Indeed, a slight decrease in drag can significantly reduce fuel costs when the number of vehicles and the total miles traveled are considered cumulatively.

Trailer tails (in this case, the effects of a 2-ft. long trailer tail versus a 4-ft. long tail) can significantly reduce a truck’s drag and, thus, improve its fuel efficiency.

Streamlining the aerodynamics of buses and coaches is also essential in improving fuel efficiency. Manufacturers have begun introducing increasingly more streamlined shapes with minimized frontal areas and curved or tapered roofs. Spoilers, underbody skirts, and wheel covers further improve airflow management, while the careful design of doors, mirrors, and other external components helps reduce turbulence. While employing wind tunnel testing and computational fluid dynamics simulations during the design phase of a bus or coach is a significant investment in time and cost, the resulting improved aerodynamic performance can yield substantial fuel savings and a lower environmental impact.

Trains

Traveling by train has long been a vital mode of transportation. High-speed railway networks continue to grow, particularly in Europe, China, and Japan. As with all vehicles, the aerodynamic drag of a train increases with the square of its speed, so the power and energy required to propel it increase significantly at higher speeds. Related issues for trains include supplying the necessary traction from the wheels to the rails and the significant pressure changes (felt by passengers) when trains pass each other at high speeds or travel through tunnels.

Because the length-to-width ratio of a train is much larger than that of any other ground vehicle, the aerodynamic characteristics of trains tend to be more complex than those of cars, trucks, or airplanes. Nevertheless, significant drag reductions can be achieved through streamlining, as shown in the photograph below. The basic principles are similar to those for airplanes, including a streamlined nose and rounded corners along the entire length of the train. Again, much of the work on the most effective drag-reduction measures for high-speed trains using various forms of streamlining is conducted in wind tunnels.

A high-speed train with a highly streamlined nose and rounded corners on the carriages can significantly reduce drag.

Creating Drag – Parachutes

A parachute slows an object’s motion through the air by creating drag. This situation exemplifies how creating high drag can yield positive outcomes. Parachutes come in many shapes and sizes, but the classic design of a parachute canopy is a hemispherical shell, as shown in Figure 25.

Parachutes are used for various purposes, the classic canopy being hemispherical.

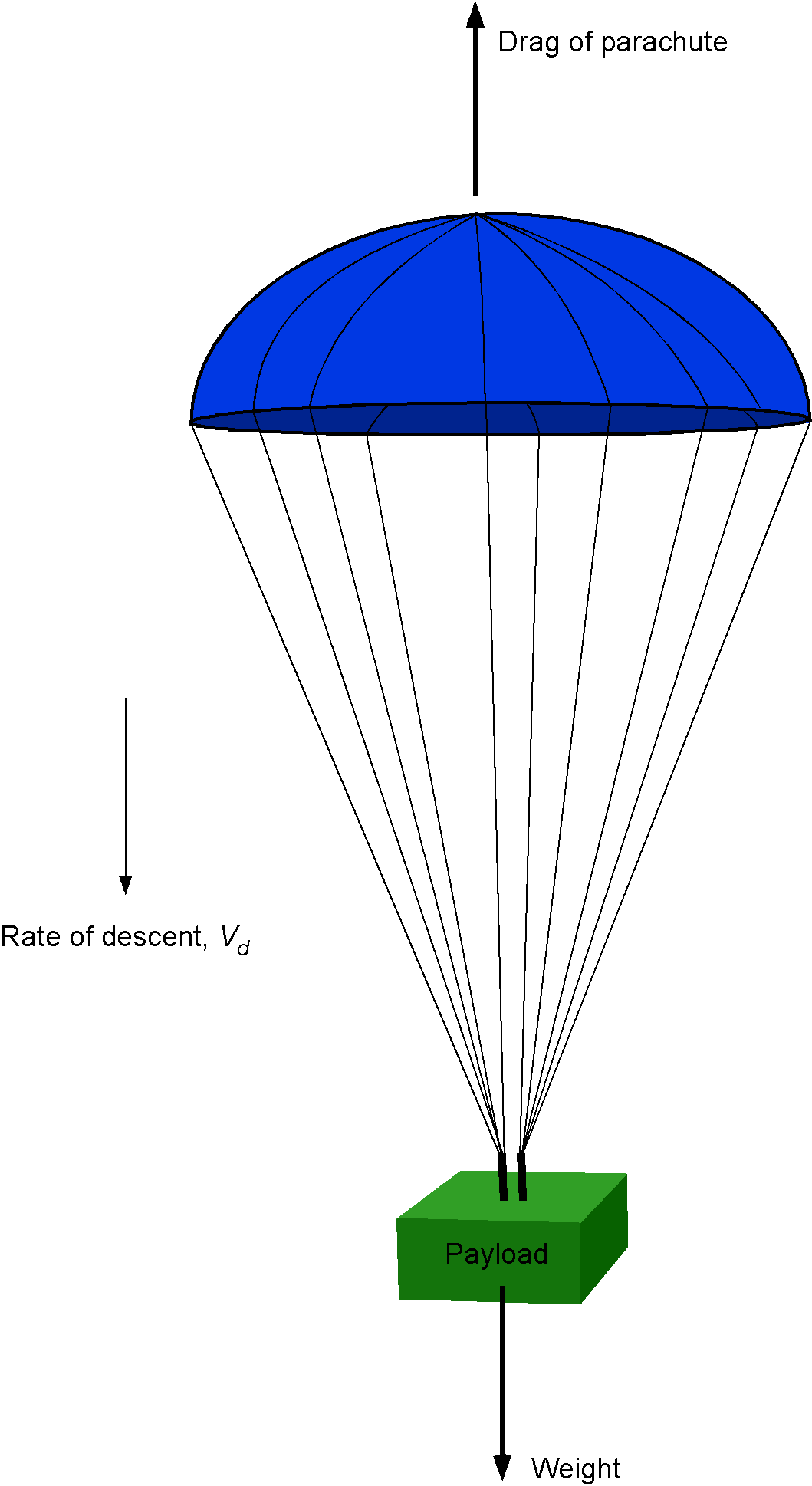
The drag coefficient of a hemispherical shell based on the projected frontal area is about 1.42. Notice that for an open hemispherical shell of diameter {d}, its projected frontal area (i.e., the reference area on which the drag coefficient is based) is just the area of a circle of this diameter. The drag coefficient for most parachutes is close to 1.42, depending on their construction.

If the weight suspended from the parachute is W_p, and if the weight of the parachute itself is neglected, then steady force equilibrium gives

(27)   \begin{equation*} W_p - D = 0 \end{equation*}

where D is the drag of the parachute. The drag is given by

(28)   \begin{equation*} D = \frac{1}{2} \varrho \, A \, C_D \, V_d^2 \end{equation*}

where A is the projected frontal area of the parachute, \varrho is the density of the air, and C_D = 1.42 for an open hemispherical shell. The projected frontal area is A = \pi d^2/4, where {d} is the diameter. Solving for V_d (the rate of descent) gives

(29)   \begin{equation*} V_d = \sqrt{\frac{2 W_p}{\varrho \, A \, C_D}} \end{equation*}

Notice that the rate of descent increases for a higher weight and/or for a smaller area parachute.

For an average person, parachutes are designed to provide a decent speed of 10–20 mph (16–32 kph). Of course, a more detailed analysis of this problem would account for the weight of the parachute and the backpack, though it would likely only increase the actual rate of descent by a small amount. Holes or vents can be introduced into the canopy to improve the parachute’s stability and provide it with some forward motion, which aids the parachutist in controlling the descent; the vents also slightly alter the drag coefficient.

Bluff Bodies at Supersonic Speeds

The behavior of bluff bodies at high speeds is also of interest to aerospace engineers, particularly for spacecraft re-entering Earth’s atmosphere. The drag of supersonic projectiles has been studied in wind tunnels. The results show that their drag is comprised not only of a high value of pressure drag from flow separation on the aft part of the body but also wave drag from the formation of shock waves, as illustrated in Figure 26 for a sphere (ball) flying at supersonic speeds. Notice the strong compression bow shock that stands off from the leading edge of the sphere, as well as the turbulence in the wake behind the sphere.

Schlieren flow visualization image of a sphere flying at a supersonic Mach number of 1.53.

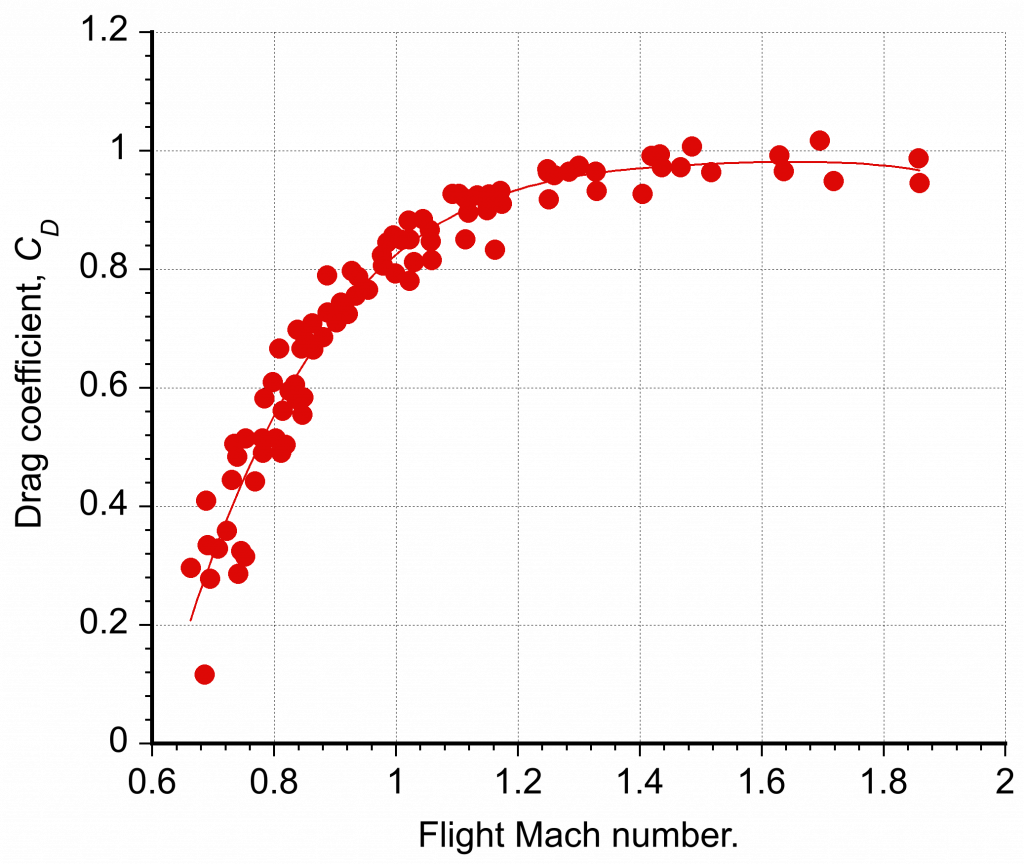
The effects of Reynolds number on the drag of a sphere have been previously discussed, but what about the effects of Mach number? The most accurate high Reynolds number data for spheres flying at Mach numbers between 0.6 and 2.0 date back to the 19th century, when Francis Bashforth conducted drag measurements on supersonically spherical projectiles between 1870 and 1880, as shown in Figure 27. Interestingly, the drag coefficient plateaus at higher Mach numbers.

Francis Bashforth measured the drag coefficient of supersonic spheres, showing that the drag coefficient was independent of the Mach number.

H. Julian “Harvey” Allen, an aeronautical engineer at NASA, designed a spacecraft that would return to re-enter the Earth’s atmosphere. His approach recognized that bluff or “blunt” bodies moving at very high supersonic and hypersonic Mach numbers generate strong shock waves, known as a bow shock, that form ahead of the body, as shown in the image in Figure 28. Note that the bow shock is positioned away from the body surface, a distance referred to as the standoff distance. Because temperature changes in flows across strong shock waves are significant, shock waves that stand off from the surface allow much more heat to be dissipated into the air rather than into the body itself.

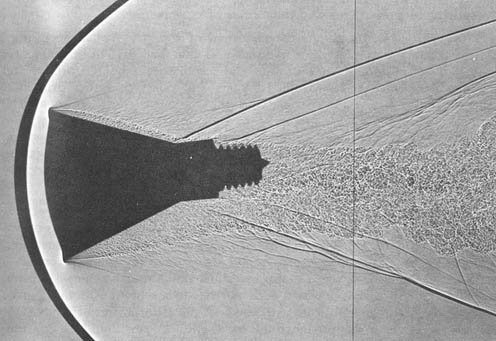
A bluff body at a high supersonic Mach number represents a space capsule during re-entry into the atmosphere.

The heat transfer is related to the radius of curvature of the leading edge of the body, {R_{\rm le}}, by the relationship

(30)   \begin{equation*} \mbox{\small Heat transfer} \, \propto \, \dfrac{1}{\sqrt{R_{\rm le}}} \end{equation*}

Clearly, the larger (blunter) the shape, the lower the heat transfer. Also, note the significant flow separation and turbulence in the body’s wake in this image. The bluff-body shape also generates significant pressure drag, helping slow the spacecraft as it re-enters the atmosphere until it is sufficiently decelerated for a parachute to be deployed, illustrating how drag can be beneficial.

Towed Banners

A towed banner provides a useful counterexample to the classical definition of a bluff body. Banners towed behind general aviation airplanes (Figure 29) are used for aerial advertising and consist of a flexible fabric suspended on a towline that deforms and billows in the airstream, producing a large effective drag area dominated by pressure drag and an unsteady wake. A bluff body, by contrast, has a fixed geometry that enforces large-scale flow separation and a well-defined wake. A banner does not impose separation in this deterministic way; the coupled interaction between aerodynamic loading and fabric deformation governs its instantaneous shape. Consequently, there are no fixed separation points or uniquely defined wake structures, and the flow remains inherently unsteady with continuously evolving regions of separation and vortex shedding.

Banners towed behind general aviation airplanes are used for advertising.

The key point is that the banner undergoes continuous, unsteady motion, including billowing, fluttering, and oscillation, producing a broad downstream wake and a drag comparable to that of a bluff body. The drag behavior of a banner is best expressed in terms of drag coefficient, C_D, defined by

(31)   \begin{equation*} C_D = \frac{D}{\tfrac{1}{2}\,\varrho_{\infty} \, V_{\infty}^2 \, A} \end{equation*}

where D is the measured drag of the banner of physical area A.

The drag coefficient measurements in Figure 30 for four banners in a wind tunnel show that, for a given banner, the drag coefficient is approximately constant over a wide range of wind speeds. This behavior confirms that the time-averaged drag scales approximately with the dynamic pressure, even though the banner’s instantaneous motion may be highly unsteady. Notice that C_D depends strongly on the aspect ratio of the banner, A\!R. For a banner of length L and width W, the planform area is A = L \, W and the aspect ratio is

(32)   \begin{equation*} A\!R = \frac{L}{W} \end{equation*}

For banners of the same fabric area, lower-aspect-ratio shapes produce a larger drag coefficient than longer, more slender banners.

Drag coefficient of fabric banners as a function of wind speed for different aspect ratios.

Banners are known to produce a turbulent downstream wake because of their unsteady deformations, so the aspect-ratio dependence may be interpreted using a wake-scaling argument. The majority of the drag is associated with the wake, so that

(33)   \begin{equation*} D \sim \varrho_{\infty} \, V_{\infty}^2 \, A_{\mathrm{wake}} \end{equation*}

where A_{\mathrm{wake}} is an effective cross-sectional area of the disturbed flow. If the characteristic lateral extent of the wake is denoted by \delta, then A_{\mathrm{wake}} \sim L\,\delta. As a simple scaling model, suppose that the transverse excursion of the banner scales with its width but decreases with increasing aspect ratio, for example, as

(34)   \begin{equation*} \delta \sim \frac{W}{\sqrt{A\!R}} \end{equation*}

Therefore,

(35)   \begin{equation*} A_{\mathrm{wake}} \sim \frac{L \, W}{\sqrt{A\!R}} = \frac{A}{\sqrt{A\!R}} \end{equation*}

It follows that

(36)   \begin{equation*} C_D = \frac{A_{\mathrm{eq}}}{A} \sim \frac{A_{\mathrm{wake}}}{A} \sim A\!R^{-1/2} \end{equation*}

which is consistent with the measured trend in Figure 30, that the equivalent drag area decreases with increasing aspect ratio.

A physical interpretation of this drag behavior is that lower-aspect-ratio banners undergo greater transverse excursions and produce broader wakes (see Figure 31). In contrast, higher-aspect-ratio banners or streamers tend to align more closely with the flow, undergo smaller deformations, and generate narrower downstream wakes, resulting in lower drag. The oscillatory motion itself is generally multimodal in both the lateral and longitudinal directions, and the production of any appreciable pressure difference between the sides of the banner may cause it to curl up along its longitudinal edges. At lower wind speeds, large-amplitude, low-frequency motions tend to dominate, whereas at higher wind speeds the motion shifts toward smaller-amplitude, higher-frequency oscillations. Transitions between these modes can produce noticeable changes in drag, as verified by the wind tunnel tests. The contribution of viscous shear stresses (skin-friction drag) is also present, but it is not the dominant source of drag on a towed banner.

Testing suggests that long, slender banners tend to produce less drag than short, wide banners.

Another interpretation of banner drag can be obtained from an energy perspective. As the freestream flows past the banner, energy is continuously transferred from the mean flow into the turbulent wake and into the unsteady deformation of the flexible fabric, so that

(37)   \begin{equation*} D\,V_{\infty} \sim \overbigdot{E}_{\mathrm{wake}} + \overbigdot{E}_{\mathrm{osc}} \end{equation*}

where \overbigdot{E}_{\mathrm{wake}} is the rate of kinetic energy dissipation in the wake and \overbigdot{E}_{\mathrm{osc}} is the rate of energy absorbed by the oscillatory motion of the banner, the balance depending in part on the fabric properties. For a towed system, this energy must be supplied by the towing aircraft, so the additional power required is

(38)   \begin{equation*} \Delta P_{\mathrm{tow}} = D \, V_{\infty} \end{equation*}

which shows that the drag arises from a continual drain of energy from the flow into wake losses and structural motion; consequently, banner towing demands a significant increase in power for sustained flight.

Check Your Understanding #5 – How draggy is a banner compared to a parachute?

Figure 30 shows wind tunnel measurements of the drag coefficient, C_D, for flexible fabric banners of different aspect ratios, AR, for a reference area of 0.075 m2. The goal is to consider a banner with A\!R=10 and compare its drag with that of a hemispherical parachute. For the hemispherical canopy, the drag coefficient is approximately C_{D,\mathrm{hem}} = 1.42, based on its projected frontal area.

  1. Show that the equivalent drag area of the hemispherical parachute is A_{\mathrm{eq,hem}} = 0.71 A_f.
  2. From the plotted data in Figure 30, estimate C_D for the AR=10 banner and explain its signifiance.
  3. Compare the drag of the banner with that of the hemispherical parachute for the same fabric area.
  4. Consider a banner 2 m high and 20 m long. Estimate its equivalent drag area, and show that for this case, its drag is approximately the same as that of a hemispherical parachute whose diameter is about equal to the banner height.
Show solution/hide solution.

1. For a hemispherical parachute canopy of radius R, the fabric area is A_f = 2\pi R^2 and the projected frontal area is

    \[ A_p = \pi R^2 = \frac{A_f}{2} \]

Therefore, because the drag coefficient based on projected frontal area is C_{D,\mathrm{hem}} = 1.42, the equivalent drag area of the hemispherical parachute is

    \[ A_{\mathrm{eq,hem}} = C_{D,\mathrm{hem}} \, A_p = 1.42\left(\frac{A_f}{2}\right) = 0.71 \, A_f \]

2. From Fig. 30, for AR=10, the drag coefficient of the banner is C_D \approx 0.13. For the test banner, the fabric area is A_f = 0.075\ \mathrm{m}^2, so

    \[ A_{\mathrm{eq,ban}} = C_D \, A_f \approx 0.13 \times 0.075 \approx 0.01\ \mathrm{m}^2 \]

and its significance is that this drag coefficient directly gives the equivalent drag area when multiplied by the fabric area.

3. For the same fabric area, then

    \[ A_{\mathrm{eq,ban}} \approx 0.13 \, A_f \qquad \text{and} \qquad A_{\mathrm{eq,hem}} = 0.71 \, A_f \]

Therefore,

    \[ \frac{A_{\mathrm{eq,ban}}}{A_{\mathrm{eq,hem}}} = \frac{0.13}{0.71} \approx 0.18 \]

so the A\!R=10 banner produces only about 18% of the drag of a hemispherical parachute made from the same amount of fabric. Note that this comparison cannot be performed using the drag coefficient because the reference areas differ.

4. Scaling to a banner 2 m high and 20 m long, then A_f = 40\ \mathrm{m}^2 and A\!R = 10. Its equivalent drag area is A_{\mathrm{eq,ban}} \approx 0.13 \times 40 = 5.2\ \mathrm{m}^2. For a hemispherical parachute of diameter d, then

    \[ A_{\mathrm{eq,hem}} = 1.42 \frac{\pi \, d^2}{4} \]

Equating this to the banner drag area gives

    \[ 1.42 \frac{\pi \, d^2}{4} = 5.2 \]

so d \approx 2.1\ \mathrm{m}. Therefore, in this case, the drag of the 2 m by 20 m banner is approximately equivalent to that of a hemispherical parachute whose diameter is about equal to the banner height. As a final step, one can show that this equivalence is not a general result but depends on the banner’s aspect ratio.

Summary & Closure

While aerospace engineers are more often concerned with minimizing drag through streamlining, in other cases, creating drag can also be beneficial. The study of bluff-body shapes, with their almost infinite possibilities, is not merely theoretical; it also has practical applications. Many standard shapes have been studied in wind tunnels, and their drag characteristics are well known and published as functions of the Reynolds number and, in some cases, the Mach number. Examples include projectiles and re-entry vehicles, which are crucial in aerospace engineering.

The flow features and drag characteristics of angular bluff body shapes are primarily independent of variations in Reynolds number, whereas smooth bluff bodies show more sensitivity to Reynolds number. Most smooth bluff bodies (e.g., circular cylinders and spheres) exhibit a critical Reynolds number, below and above which the flow state changes significantly and the resulting drag behavior differs. Drag reduction for terrestrial vehicles remains a substantial challenge for reducing fuel consumption. While conventional streamlining practices are highly effective, they are approaching diminishing returns. However, the future may see more innovative concepts, such as active flow-control devices, to further reduce drag.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • Make a list of the parts of an airplane that are potentially bluff-body-producing drag elements. Besides removing them, what steps could be taken to reduce the drag of these elements?
  • A rectangular sensor package is desired to be mounted on the external fuselage of a high-speed aircraft. What are the potential engineering concerns?
  • If dimples can reduce drag on golf balls, then why are dimples not used on the surfaces of airplanes or automobiles?
  • For the nose cone of a rocket, is it best to use a sharply pointed nose or a blunt, rounded nose, and why?

Other Useful Online Resources

For more information on bluff bodies, check out some of these online resources:

  1. Data ranges adapted from Achenbach (1971), Schlichting & Gersten (Boundary-Layer Theory), Hoerner (Fluid-Dynamic Drag), and modern golf-ball aerodynamics studies (e.g., Aoki et al., 2015). NASA Glenn research primers and review articles on the drag crisis provide additional reference curves for spheres. ↵
  2. They were probably not wearing kilts but trews (trousers), although it still makes a good story. ↵
  3. In Scots, the term is gowfers ↵
  4. It is equivalent to the spin of the fluid. ↵
  5. See J. Achenbach, “Experiments on the flow past spheres at very high Reynolds numbers,” Journal of Fluid Mechanics, Vol. 54, 1972, pp. 565–575, as well as R. G. Watts and R. Ferrer, “The lateral force on a spinning sphere: Aerodynamics of a curveball,” American Journal of Physics, Vol. 55, No. 1, 1987, pp. 40–44. ↵
  6. P. W. Bearman and J. K. Harvey, “Golf ball aerodynamics,” Aeronautical Quarterly, Vol. 27, 1976, pp. 112–122 as well as R. D. Mehta, “Aerodynamics of Sports Balls,” Annual Review of Fluid Mechanics, Vol. 17, 1985, pp. 151–189. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2026 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n25

Share This Book