Essential Formulae
Note: All symbols have their usual meanings as used in the text. These essential formulas may be made available for use on quizzes and exams with the permission of the instructor.
- Structural stress/strain relationships:
- Equation of state:
- Hydrostatic pressure in a stagnant fluid:
- Hydrostatic pressure in scalar form:
- Hydrostatic equation:
- Unique solutions to the hydrostatic equation:
-
- For a constant-density fluid:
-
- Pressure change with a linear thermal gradient with temperature lapse
between two heights
and
:
- Pressure change with a linear thermal gradient with temperature lapse
-
- Pressure change with an isothermal temperature
between two heights
and
:
- Pressure change with an isothermal temperature
- Specific gravity SG of a liquid =
- Specific weight
of a liquid =
- Temperature conversions:
-
- Convert temperature
to Kelvin K from Centigrade or Celsius
:
- Convert temperature
-
- Convert temperature
to Rankine R from Fahrenheit
:
- Convert temperature
- Speed of sound:
- Mach number:
- Reynolds number based on length
:
- Kinematic viscosity =
- Shear stress in a Newtonian fluid:
- Equations of a streamline:
- Continuity equation for a fluid:
- Continuity equation in 1-D form:
- Momentum equation for a fluid:
- Momentum equation in 1-D form:
- The energy equation for a fluid:
- The energy equation for the single-stream system:
- Bernoulli equation:
- The hydraulic diameter of a pipe:
- Pressure drop
for a pipe flow along a uniform diameter pipe of length
:
- Head loss for a pipe flow:
- Pumping power for a pipe flow:
- Area of a wing:
- The aspect ratio of a wing:
- Mean aerodynamic chord (MAC) of a wing:
- Free stream dynamic pressure:
- Aerodynamic coefficients for an airfoil section:
-
- Lift coefficient,
- Lift coefficient,
-
- Drag coefficient,
- Drag coefficient,
-
- Moment coefficient at some point
,
- Moment coefficient at some point
- Aerodynamic coefficients for a finite wing:
-
- Lift coefficient,
- Lift coefficient,
-
- Drag coefficient,
- Drag coefficient,
-
- Moment coefficient about some point
,
- Moment coefficient about some point
- Induced drag coefficient of a finite wing:
- The drag coefficient for an airplane:
- General equations of motion of an airplane:
- Breguet endurance and range equations for a propeller aircraft:
- Breguet endurance and range equations for a jet aircraft:
- Thrust produced by a turbojet:
- Thrust specific fuel consumption (TSFC):
- Brake power specific fuel consumption (BSFC):
- Propulsive efficiency for a jet-producing device:
- The equivalent exit velocity of a rocket in terms of specific impulse:
- Thrust equation for rocket:
- Rocket equation (with gravity loss term):
- Mean equivalent exhaust velocity (for multiple boosters):
- Conversion factors:
- 1 knot = 1.68781 ft/s
- 1 knot = 0.51444 m/s
- 1 mph = 0.44704 m/s
- 1 mph = 1.46667 ft/s
- 1 ft = 0.3048 m
- 1 statute mile = 5,280 ft
- 1 nautical mile = 6,076 ft
- 1 hp = 550 ft-lb s
- Table of ISA Properties at MSL:
| Property | Symbol | SI units | USC units |
| Pressure | 1.01325 |
2116.4 lb ft |
|
| Density | 1.225 kg m |
0.002378 slugs ft |
|
| Temperature | 15.0 |
59.0 |
|
| Dynamic viscosity | 1.789 |
3.737 |
|
| Speed of sound | 340.3 m s |
1116.47 ft s |
|
| Gas constant | 287.057 J kg |
1716.49 ft-lb slug |
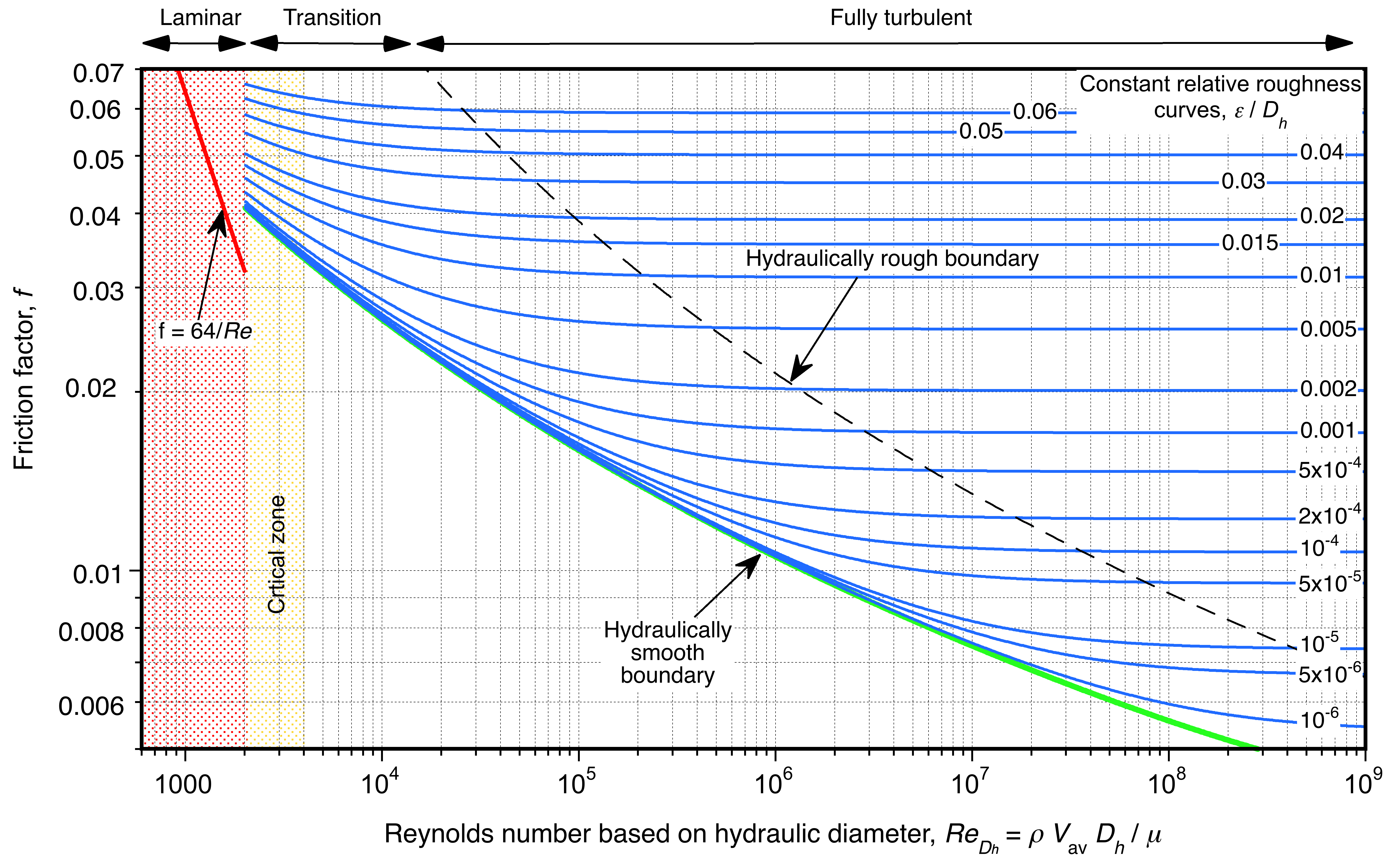
- Moody chart for the estimation of the Darcy-Weisbach friction factor: