Introduction

Wind tunnel testing remains a cornerstone of aerodynamic research for all types of flight vehicles. Wind tunnels vary in size and configuration, with test-section speeds ranging from subsonic to hypersonic. Their design and operation rely heavily on internal-flow principles to ensure a clean, uniform, and steady flow environment within the test section. This controlled flow enables the systematic measurement of aerodynamic forces, surface pressures, and velocity fields on scaled wings, complete airplane models (Figure 1), propellers, and other components. Accurate wind tunnel measurements are indispensable for validating design decisions and ensuring that predictive methods yield not only the correct results but also for the correct physical reasons.

Although a few basic wind tunnels had been built in the 19th century, the origins of modern wind tunnels and testing techniques can be traced to the Wright brothers’ 1901 wind tunnel. From this beginning, wind tunnel technology advanced rapidly in the early 20th century, including those designed by Gustave Eiffel and Ludwig Prandtl. Several national research institutions soon constructed increasingly capable facilities, such as those at the Royal Aircraft Establishment (RAE) in Britain, at AVA Göttingen, DFL Berlin-Adlershof, and LFA Völkenrode in Germany, and at the NACA in the United States. These wind tunnel facilities enabled pioneering research on compressibility effects in high-speed aerodynamics and on wings, as well as large-scale aircraft testing. By mid-century, wind tunnels had become indispensable to both research and industry, with specialized facilities supporting the study of supersonic and hypersonic missiles, reentry vehicles, and propulsion systems. For the following decades, advances in instrumentation expanded the range of measurable quantities, and optical diagnostics began to reveal the fine-scale structure of turbulence and flow separation.

In the 1980s, as computational fluid dynamics (CFD) advanced rapidly, some critics predicted the demise of the wind tunnel and even suggested that physical facilities might eventually be closed. With hindsight, the opposite has proven true. Rather than replacing wind tunnels, CFD has complemented them, and the two approaches, computation and measurement, have evolved into a strongly synergistic framework for aerodynamic development. Wind tunnels remain indispensable for validation and calibration, particularly in complex flow regimes where predictive capability remains limited, including high-Reynolds-number separated flows, transition, and unsteady flows. Today, the field has come full circle, with modern research and development programs relying on a balanced combination of CFD and wind-tunnel data to ensure reliable aerodynamic predictions.

Over time, the applications of wind tunnels have broadened well beyond traditional aeronautics. Today, wind tunnels are used extensively in automotive and racecar design, wind-turbine development, ship airwake and naval-aviation studies, sports engineering, and civil-engineering projects involving bridges, towers, and tall buildings. They are also employed in testing unoccupied aerial systems, parachutes and airdrop systems, and spacecraft entry configurations. Their ability to produce controlled, repeatable flow fields makes them uniquely suited for both fundamental research and applied development across many engineering disciplines. Consequently, wind tunnels have become essential multidisciplinary research tools rather than solely aerospace facilities. For example, Figure 2 shows a 5-m-diameter wind turbine being tested in the large 80-by-120-ft wind tunnel at NASA Ames Research Center.

Wind tunnels, therefore, remain an essential tool in the aerospace engineer’s repertoire, providing a controlled environment in which aerodynamic forces, flow behavior, and performance characteristics can be examined under well-defined and repeatable simulated flight conditions. A clear understanding of their design features, capabilities, limitations, operational characteristics, and measurement methods is fundamental for anyone engaged in experimental aerodynamics, where the reliability of results depends as much on facility knowledge and test technique as on the measurements themselves.

History

Before the advent of wind tunnels, free-flight and whirling arm devices were used to study aerodynamics. Free-flight tests, such as those conducted by George Cayley, provided limited quantitative information beyond whether the concept flew well or not. Whirling arms rotated a test article through the air at the end of a long, cantilevered arm. Pioneered in the early 19th century by Francis Wenham, Horatio Phillips, and Hiram Maxim, these whirling rigs enabled them to measure lift on various bodies and surfaces, revealing insights into the effects of angle of attack. In Maxim’s design, which is shown in Figure 3,^[1] his wings and airplane designs were mounted on a set of “grocer’s scales” (i.e., a balance), and iron or lead weights were used until a pointer showed that the lift was precisely balanced. However, these devices were severely limited by three-dimensional, unsteady flow and wake interference, often yielding inaccurate, if not misleading, measurements.

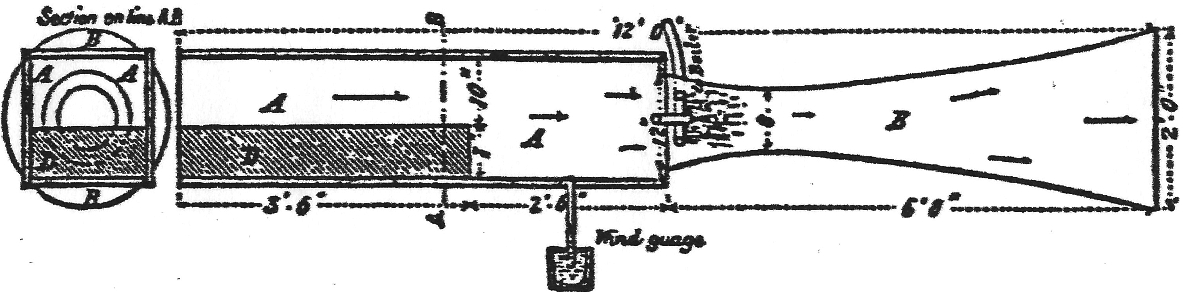
The origins of wind tunnel testing date back to the mid-19th century, when the limitations of free-flight experiments and whirling-arm tests became increasingly apparent. Around 1871, under the auspices of the Aeronautical Society of Great Britain, the construction of what is now regarded as the first wind tunnel was led by Francis Wenham at Penn’s engineering works in England. This device consisted of a 10-foot-long (3.05-meter) rectangular duct with an 18-inch-square (0.46-meter-by-0.46-meter) cross-section. John Penn used one of his steam engines to drive a fan, thereby generating the necessary airflow. Wenham used the tunnel to measure the lift and drag of various surfaces inclined to the flow, thereby demonstrating for the first time the aerodynamic benefits of longer, slender wings with high aspect ratios. Although the flow in this primitive wind tunnel was poorly characterized, it provided quantitative data on aerodynamic forces and, for the first time, shifted the study of flight toward a more scientific approach.

In the 1880s, Horatio Phillips constructed a wind tunnel with higher-quality airflow, as shown in Figure 4. The test section was 6 feet (1.8 meters) long, with a square cross-section measuring approximately 17 inches (43 centimeters) on each side. He placed a restrictor in the section, which increased the flow speed to 60 ft/s (18.3 m/s). The models were installed on a balance, which allowed measurements of lift and drag. Phillips studied cambered airfoils, though his results were reportedly of questionable quality. Nevertheless, he demonstrated the growing need for testing under controlled-flow conditions if aerodynamic behavior were ever to be understood.

During the same period, William Kernot and Nikolay Zhukovsky constructed small wind tunnels for aerodynamic testing. Zhukovsky’s 1891 tunnel enabled the investigation of airfoil shapes, particularly the leading- and trailing-edge geometry, which in turn led to the development of the circulation theory of lift.^[2] This theory was to prove to be the foundation for many advances in the understanding of the aerodynamics of airfoils and wings.

In 1894, Hiram Maxim constructed a small wind tunnel with a square cross-section measuring 1.7 feet (0.52 meters) and a “contraction chamber” measuring 2 feet (0.61 meters) across, as illustrated in Figure 5. The airflow was generated by a pair of counter-rotating propellers powered by a 100 hp (75 kW) engine. To reduce turbulence, the flow passed through a series of flow-conditioning elements, including screens and guide vanes. The tunnel reportedly produced a relatively smooth flow at speeds up to 50 ft/s (22 m/s). The test models were mounted on a “mobile frame” equipped with mechanical scales, using counterweights and levers, to measure lift and drag forces. Maxim’s reportedly higher quality experiments conclusively demonstrated the aerodynamic efficiency of higher-aspect-ratio wings and cambered airfoils.

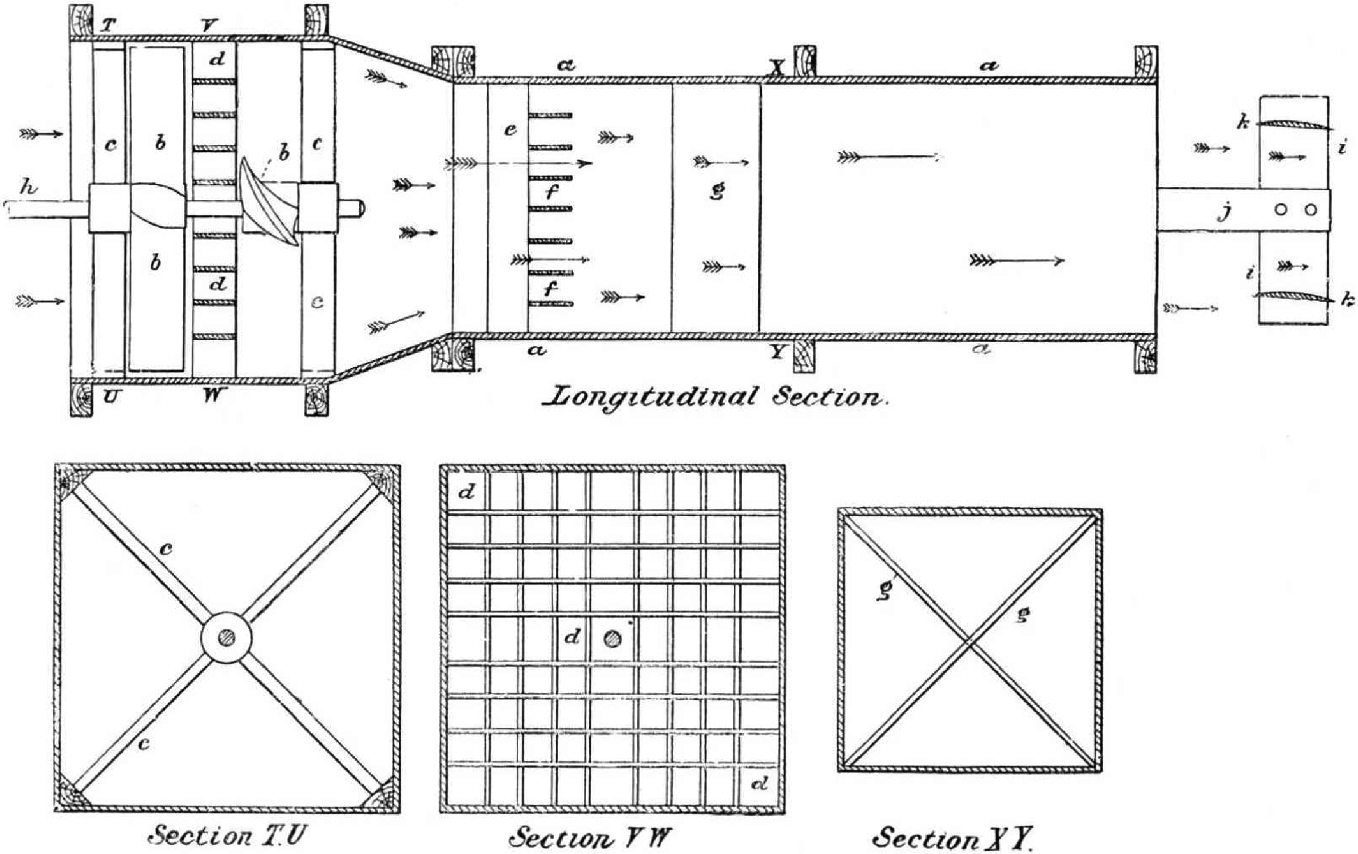
In 1901, dissatisfied with the poor performance of their gliders and the apparent inaccuracy of existing aerodynamic data, the Wright brothers set out to obtain more accurate measurements.^[3] They first mounted small test wings on their bicycles to measure lift and drag while riding, but this approach proved unsatisfactory. They then built a wind tunnel in their bicycle shop, about 6 feet (1.8 m) long, with a 16-inch-square (0.41 m × 0.41 m) test section, as shown in Figure 6. Using a balance of their own design, they conducted repeatable measurements of lift and drag on numerous wings and airfoil shapes.

Their systematic experiments confirmed the importance of aspect ratio, which directly led to the successful design of the 1902 glider and was a key factor in the Wright Flyer’s success in 1903. Equally important, their work introduced core testing principles, such as geometric scaling, balances, and non-dimensional coefficients, and validated them through flight testing. Most would argue that their work marked a decisive turning point, transforming the wind tunnel from a qualitative experimental apparatus into a quantitative tool for aerodynamic analysis and engineering development.

Another significant development in wind tunnel design occurred in 1909, when Gustave Eiffel constructed a compact wind tunnel near the Eiffel Tower in Paris. Motivated by a desire to understand the wind loads on large civil engineering structures, Eiffel developed an open-circuit, free-jet design with a carefully shaped converging nozzle and flow-straightening screens, as illustrated in Figure 7. Eiffel’s instrumentation combined a force balance with distributed pressure taps. He was also the first to systematically test complete aircraft models, introducing what he termed the “polar diagram,” a plot of lift and drag coefficients as functions of angle of attack that remains a standard form of aerodynamic analysis to this day.

Eiffel’s 1912 tunnel had a larger-diameter test section and could achieve higher flow speeds; his work further standardized aerodynamic testing procedures. By the 1920s, wind tunnel technology was rapidly maturing, and Eiffel’s wind tunnel design principles were widely adopted. Variants of what is now referred to as the “Eiffel tunnel,” an open-circuit, single-return layout with a contraction upstream of the test section, were constructed worldwide to meet the expanding demands of aviation research and development.

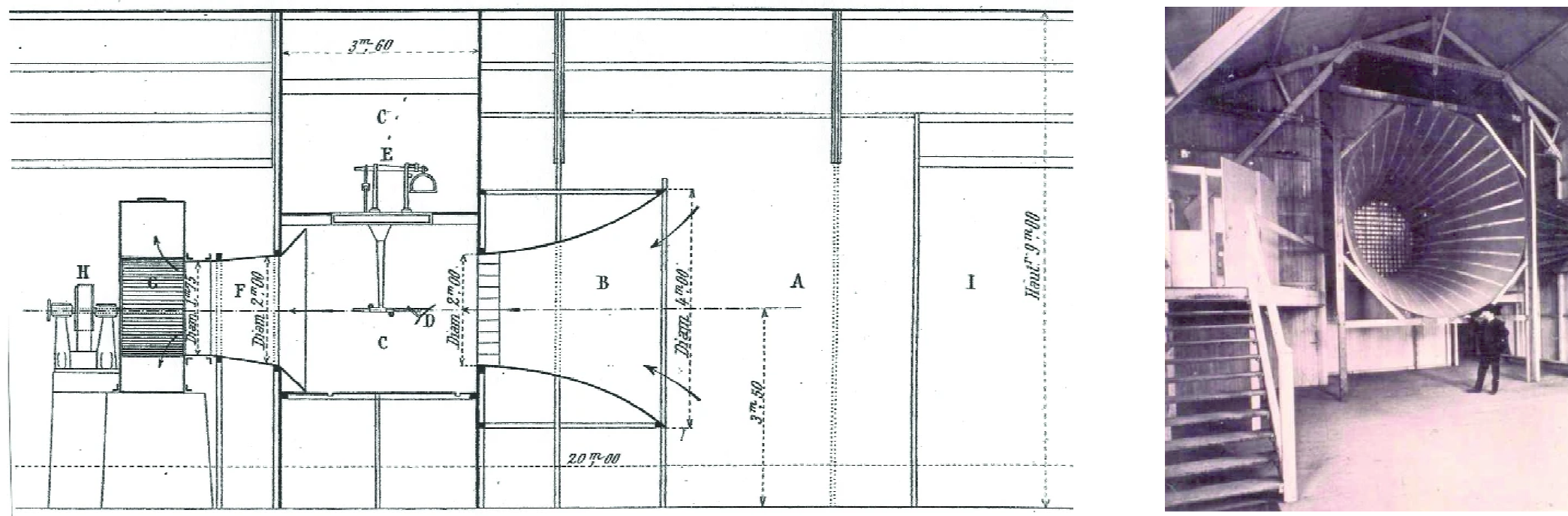
In 1909, Ludwig Prandtl introduced a fundamentally new wind tunnel configuration: the closed-return (closed-circuit) wind tunnel. Prandtl’s design, which became known as the “Göttingen-type” of wind tunnel, directed the flow in a closed-loop configuration, offering better energy efficiency and flow quality than the Eiffel tunnels. The corners featured turning airfoils or “vanes,” and a honeycomb screen was employed to straighten the flow at the inlet to the test section, thereby achieving greater flow uniformity and lower turbulence. Prandtl’s facility, shown in Figure 8, enabled more accurate measurements on airfoils, wings, and propellers. He and his students made significant advances in aerodynamics and laid the groundwork for subsequent developments in wind-tunnel testing methods.

National laboratories and major universities soon followed suit, building their own Eiffel- and Göttingen-type wind tunnels. These wind tunnels became standard tools for use in aircraft design, providing a means to test new configurations, refine airfoil sections and wing shapes, and investigate stability and control problems with a level of repeatability not possible through flight testing. By the end of the 1920s, most major aviation nations worldwide had established at least one significant wind tunnel facility. These early tunnels varied in size, flow speed, and design. Still, collectively they marked the transition from improvised testing and time-consuming flight testing to systematic aerodynamic measurements made under well-controlled conditions. They established foundational methods, including scale modeling, force-balance measurements, pressure measurements, and flow-visualization techniques, which led to explosive growth in the aerodynamic understanding of wings and airplanes.

By the early 1930s, the Royal Aircraft Establishment (RAE) operated several large closed-return tunnels capable of high-quality integrated force and distributed-pressure measurements on airfoils and complete aircraft configurations. The 24-foot (7.3-meter) tunnel and the 11.5-foot (3.5-meter) tunnel were particularly significant in advancing British aircraft design during the pre-war and WWII years. One of the most ambitious facilities was the RAE High-Speed Tunnel, designed to achieve flow speeds of up to 880 ft/s (268 m/s, 600 mph, 965 kph) and to operate at pressures ranging from one-fifth to four times atmospheric pressure. This wind tunnel, shown in Figure 9, played a central role in the development of high-speed aircraft. During the 1950s, it was modified to accommodate transonic flow testing, enabling experiments to be conducted over the Mach 0.9-1.15 range.

The NACA Variable Density Tunnel (VDT), completed in 1923 at Langley Field, used pressurized air at up to 20 atmospheres to achieve full-scale Reynolds numbers with subscale models. This innovation allowed unprecedented fidelity in low-speed aerodynamic testing. Notably, the VDT produced aerodynamic data^[4] for many airfoil shapes. These data were used in the design of several airplanes of the time, including the Douglas DC-3, the Boeing B-17 Flying Fortress, and the Lockheed P-38 Lightning. Additionally, the VDT was used to test low-drag “laminar flow” airfoils employed in the wing design of the P-51 Mustang.

In the pre-war and WWII eras, Germany established a network of advanced wind tunnel facilities that advanced aeronautical research on boundary-layer theory, compressibility effects, and swept-wing aerodynamics. The use of missiles and guided bombs during WWII sparked an interest in slender, supersonic configurations. These required more specialized wind tunnels to explore higher supersonic flight regimes and to investigate frictional kinetic heating and shock-wave drag. The research facilities at the Peenemünde Army Research Center included blowdown tunnels and expansion nozzles capable of reaching supersonic and hypersonic speeds up to Mach 7, enabling aerodynamic investigations of high-speed flight vehicles, as shown in Figure 10. After WWII, many of these German wind tunnels, which were well in advance of those elsewhere, were transferred to the U.K. and U.S. under Operation Paperclip, contributing to the development of high-speed wind tunnel testing facilities, including at the Arnold Engineering Development Complex (AEDC) and the Naval Ordinance Laboratory (NOL).

By 1931, NACA had constructed the 30-by-60-foot Full-Scale Tunnel, the largest low-speed wind tunnel ever built until the 40-by-80-foot wind tunnel at NACA Ames was completed in 1949. It enabled full-scale aircraft tests, significantly improving the understanding of aerodynamic drag, stability, and control. Other NACA wind tunnels, such as the 7-by-10-Foot High-Speed Tunnel at Ames Research Center and the 16-Foot Transonic Tunnel at Langley, became central to much of the research. The 40-by-80-foot wind tunnel quickly became one of the most advanced in the world, capable of testing large test articles at low speeds, including full-scale airplanes, autogiros, and helicopters (Figure 11). A key feature was the nominally oval test section, which improved flow uniformity while minimizing wall interference.

The emergence of faster aircraft in the 1930s and 1940s brought new aerodynamic challenges. As speeds approached supersonic (Mach 1), compressibility effects, such as shock waves, associated flow separation, and flight control issues, became prominent. These phenomena could not be studied in existing wind tunnels, prompting the development of supersonic wind tunnel testing capabilities. The importance of these tunnels was underscored by the Bell X-1’s 1947 achievement of exceeding the Mach 1 “sound barrier,” a photograph of the test being shown in Figure 12, which required an understanding of shock-wave development on the wings, gained through high-speed wind-tunnel testing.

In the postwar decades, attention also shifted to military airplanes capable of supersonic and, potentially, hypersonic flight, as well as to aeronautics and high-speed commercial airplanes. New research frontiers included thermal heating and shock-layer interactions. Hypersonic tunnels, typically operating at Mach 5-15, were being built. These facilities posed numerous design challenges, including relatively short runtimes. The facilities included the AEDC von Kármán Gas Dynamics Facility (Figure 13), the Hypersonic Free Flight Tunnel at NASA Ames, and the shock-expansion tubes at NASA Langley Research Center and the California Institute of Technology (CalTech).

In the 21st century, wind tunnel facilities have adapted to new aerospace challenges, including electric propulsion, urban air mobility (UAM), drones, various new types of launch vehicles and spaceflight systems, and hypersonic vehicles. Modern wind tunnels increasingly support joint studies in which wind-tunnel measurements are combined with CFD simulations to validate and improve predictive capabilities. Cryogenic tunnels, adaptive wall designs, and automated test frameworks now extend the capabilities of even legacy infrastructure. NASA continues to modernize key assets, including the National Transonic Facility (NTF) and the Unitary Plan Wind Tunnel (UPWT). A recent example of facility rejuvenation is the return to operation of the 11-Foot Transonic Wind Tunnel in 2022 (see Figure 14), which is one of three test sections within the UPWT complex, following extensive upgrades. This initiative reflects the trend of repurposing and modernizing legacy infrastructure rather than building entirely new wind tunnels.

The 80-by-120-foot wind tunnel at NASA Ames Research Center, part of the National Full-Scale Aerodynamics Complex (NFAC), was completed in 1982 as an expansion of the existing 40-by-80-foot (12.2-by-24.4-meter) tunnel. This addition was a key component of a comprehensive modernization project initiated in 1972 to enhance the facility’s capacity to test larger aircraft and advanced aerospace systems. The updates included installing a new fan drive system and constructing the upstream 80-by-120-foot (24.4-by-36.6-meter) test section, as shown in Figure 15. With its combined test sections, the NFAC became the world’s largest wind tunnel facility, capable of testing full-scale airplanes and rotorcraft, and supporting critical aerospace research.

Apart from academic wind tunnels, new construction in the U.S. over the last decade has primarily focused on smaller-scale, high-speed tunnels for classified programs, particularly in hypersonics, for which few public details are available. One standout example of a modern academic wind tunnel is the Embry‑Riddle Aeronautical University’s Micaplex Low-Speed Wind Tunnel, completed in 2018 (Figure 16). This closed-return, low-turbulence subsonic tunnel features a 4-by-6-by-12 ft (1.22-by-1.83-by-3.66 m) test section, with flow speeds of up to 250 mph (400 km/h), a six-component external force balance, and extensive optical access for PIV. The facility is used in research, undergraduate aerodynamics laboratories, and senior capstone projects. Another example is the recently rebuilt Wright Brothers Wind Tunnel at MIT, completed in 2021. The updated closed-circuit facility now features modern test instrumentation, increased test-section speeds, and enhanced flow quality.

In Europe, ONERA’s S1MA tunnel (Figure 17)remains one of the world’s most capable transonic facilities. DLR also operates advanced subsonic and hypersonic wind tunnels across multiple sites in Germany. In Asia, China’s JF-12 hypersonic shock tunnel is the world’s largest, and India’s DRDO and ISRO have expanded their test infrastructure for military and space applications. Australia’s University of Queensland maintains leadership in hypersonic aerothermodynamics with its X2 and X3 shock tunnels, while Japan’s JAXA and JAMSS support high-speed aerodynamic research using several specialized wind tunnel facilities.

Today, wind tunnels span the full flight regime of aerospace flight vehicles. Subsonic tunnels support general aviation, rotorcraft, road vehicles, and many other applications, including ship airwake studies, as shown in Figure 18

Wind Tunnel Requirements

All wind tunnels have both general and specific requirements. In general, flow uniformity and long-term steadiness with low turbulence in the test section are critical to ensuring reliable test conditions. These requirements necessitate careful design of tunnel components to minimize turbulence intensity and flow angularity. Mach and Reynolds number scalings must also be addressed to ensure that the flow behavior observed in the tunnel closely represents full-scale conditions.

More specific goals often involve adjusting model size, flow speeds, working fluid properties (in specialized facilities), or instrumentation requirements. In high-speed tunnels, precise control of pressure and temperature is essential for reproducing in-flight conditions. Large closed-return tunnels often incorporate cooling systems to dissipate excess heat generated by viscous losses as the flow circulates around the loop.

Summary of wind tunnel requirements and typical design targets.

Requirement	Description	Typical Target
Flow quality	The flow in the test section should remain uniform across the cross-section, steady over time, with very low turbulence and angularity.	Turbulence intensity < 0.1% (low-speed); angularity < 0.2°; velocity uniform to within 1–2% of mean; steadiness 0.1% over 10 s.
Scaling	Conditions must approximate full scale through Mach and/or Reynolds similarity, sometimes requiring pressurization, cryogenics, or larger models.	Blockage ratio (frontal area of model to test section area) 0.05; confinement ratio (span of model to test section with or height) 0.7.
Thermal control	Closed-return tunnels need cooling to remove heat; high-speed tunnels must regulate pressure and temperature precisely.	Temperature variation across test section < 1 °C; stable pressure and temperature during runs.
Acoustics & vibration	Noise and vibrations from the fan and drive system must not interfere with sensitive balances or instruments.	Balance platform vibration < 1 m; minimal acoustic spill into test section.
Instrumentation	Balances, pressure sensors, and optical diagnostics such as PIV/DIC must be integrated with good optical access and proper laser measures.	Pressure resolution < 0.01% FS; synchronized data acquisition; clear reference frames and polarity conventions.
Repeatability	Key test points should be repeated to confirm stability of the data and tunnel conditions.	Force and moment repeatability < 0.1% of full scale (typical in low-speed tunnels).

Acoustic and vibration isolation is also critical, particularly in high-speed or high-precision measurement applications. Mechanical noise and structural vibrations from the fan and drive motor can interfere with sensitive balances, potentially requiring seismically isolated slabs. Supersonic or hypersonic tunnels are often constructed at remote facilities because of the high noise levels they generate.

Instrumentation and data acquisition systems in modern tunnels include sensitive pressure transducers, strain-gauge balances, and advanced optical diagnostics. In particular, optical systems, such as Particle Image Velocimetry (PIV), must be integrated into the test section with sufficient optical access, and strict safety measures must be implemented when using high-power lasers.

Types of Wind Tunnels

There are many types of wind tunnels, though most fall into a single category, such as open- or closed-return. Even then, there is no “one size fits all” wind tunnel, and its specific design is directly related to the required operating speed, the size of the test articles, and instrumentation requirements, among other factors. Wind tunnels are generally classified by three primary criteria: speed regime, circuit configuration, and test section size, each reflecting specific design requirements and testing objectives. This systematic classification enables engineers to match the wind tunnel type to the type and size of the test article, as well as the aerodynamic phenomena being studied. For example, a model of a supersonic airplane would need to be tested in a wind tunnel capable of producing the appropriate range of supersonic flow in the test section and equipped with the proper instrumentation for measurements.

Subsonic Designs

Subsonic wind tunnels operate at Mach numbers below 0.3 and are primarily used to test general aviation aircraft, drones, automobiles, and civil engineering structures such as bridges and buildings. In this low-speed regime, compressibility effects are negligible. The primary design focus of subsonic tunnels is to achieve low turbulence intensity and a uniform velocity profile within the test section. Maintaining a steady, well-conditioned airflow over extended testing times is crucial for obtaining accurate aerodynamic measurements. These tunnels typically operate as continuous-flow facilities, using large fans driven by powerful electric motors to sustain the airflow. While the energy requirements are often modest compared to transonic or supersonic wind tunnels, continuous operation still entails significant overall power consumption. Nevertheless, the steady-state conditions achievable enable precise, repeatable measurements of aerodynamic forces, moments, and surface pressures.

Open-Circuit Designs

Open-circuit (Eiffel-type) wind tunnels draw in ambient air and exhaust it back into the environment, as illustrated in Figure 19. They are mechanically simple and inexpensive to construct and operate, typically consisting of a contraction section, a test section, and a diffuser leading to the fan outlet. Their main drawback is sensitivity to external conditions; drafts, temperature gradients, or recirculated room air can perturb the inlet flow and increase turbulence in the test section. Consequently, these tunnels are not well-suited to precision aerodynamic measurements, and careful flow characterization is required before they are used for quantitative testing.

Nevertheless, open-circuit tunnels, as shown in the photograph in Figure 20 below, remain widely used for instructional work and small experimental studies. Their low cost, simplicity, and accessibility make them ideal for student laboratories, where they provide hands-on learning experiences in measuring aerodynamic forces, pressures, and flow patterns on different types of wings and other models.

Closed-Circuit Designs

Closed-circuit (Göttingen-type) wind tunnels recirculate the working air in a continuous, closed-loop configuration, as illustrated in Figure 21. In this arrangement, the flow exiting the test section is guided through a system of turning vanes and diffusers. Then, energy is added by the drive fan before the flow completes the loop and re-enters the test section. Because the air’s properties remain within the circuit, external influences are significantly reduced. This approach not only improved flow quality but also enabled precise control of key flow parameters, including velocity and temperature.

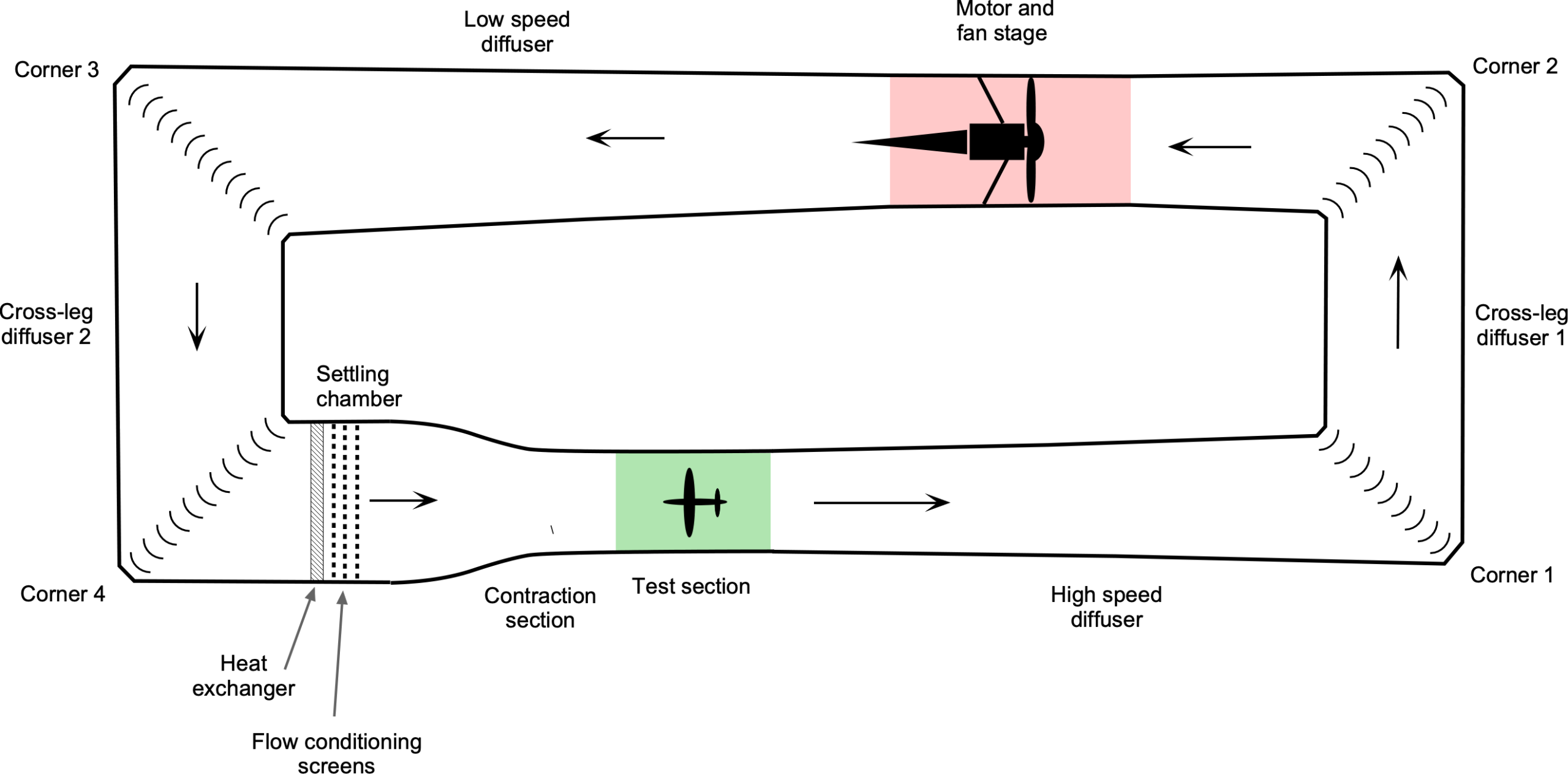
The recirculating nature of the design also improves energy efficiency, as the fan maintains the flow against system losses, unlike in open-circuit tunnels. Furthermore, noise levels are typically lower than in open-circuit designs, making the environment more suitable for sensitive instrumentation. For these reasons, closed-circuit wind tunnels are preferred in research and testing applications where high repeatability and measurement accuracy are essential.

Semi-Open Circuit Designs

Semi-open-circuit wind tunnels incorporate features of both open- and closed-circuit designs; see Figure 22. In this configuration, a portion of the airflow is recirculated through the circuit, while the remainder is exchanged with the surrounding atmosphere. This hybrid approach reduces sensitivity to external environmental variations compared to a purely open-circuit Eiffel design, while avoiding the higher construction complexity and the cost associated with a fully closed-circuit tunnel.

Semi-open tunnels have improved energy efficiency relative to open circuits while maintaining easier access for test article changes and instrumentation. They are often selected for specialized applications, such as aeroacoustic testing, where the test section’s outer surfaces are lined with sound-absorbing materials to suppress reflections and enable accurate noise measurement, as shown in the photograph below. This feature makes them particularly suitable for evaluating propeller and helicopter rotor noise, fan-blade tonal characteristics, and other unsteady aerodynamic phenomena in which acoustic fidelity is essential.

Transonic Wind Tunnels

Transonic wind tunnels operate at Mach numbers of approximately 0.8 to 1.2, where compressibility effects become important and aerodynamic behavior changes rapidly with speed. In this regime, portions of the flow around a test article can accelerate locally to supersonic speeds, then abruptly decelerate through shock waves. These shocks can interact with the boundary layer, causing flow separation, buffeting, and other nonlinear phenomena that strongly influence the lift and drag on the test article.

To address these challenges, transonic tunnels are typically equipped with slotted or perforated test-section walls that allow a controlled amount of flow to pass through; an example of a test section with slotted walls is shown in Figure 23. This feature reduces the strength of shock-wave reflections from the tunnel walls, thereby minimizing wall-interference effects and providing more representative free-flight conditions. Advanced wind tunnel configurations may also incorporate adaptive wall technology to reduce blockage further and streamline curvature effects.

Because transonic flow is inherently complex, typically involving a combination of subsonic, sonic, and supersonic regions over the test article, such facilities are indispensable for understanding the aerodynamic intricacies that underpin the design of commercial transport aircraft, business jets, and certain military aircraft. They provide critical data for optimizing wing sweep, airfoil design, and control-surface effectiveness in the speed range where shock-induced drag increases, and for assessing how changes in flight stability characteristics can significantly impact the overall performance of the flight vehicle.

Supersonic Wind Tunnels

Beyond Mach 1.2, where the flow about a body or aircraft is entirely supersonic, dedicated supersonic wind tunnels are required to reproduce the aerodynamic and thermodynamic conditions of high-speed flight. These facilities typically operate at speeds up to Mach 4-5 and are designed to generate steady, uniform supersonic flows suitable for controlled aerodynamic testing.

Most supersonic tunnels are of the blowdown type, which operate by releasing compressed air from high-pressure storage tanks into the circuit. The air is stored in a large reservoir at high pressure and then discharged through a precisely contoured de Laval nozzle, as shown in Figure 24. The convergent section of the nozzle accelerates the flow to Mach 1 at the throat, after which the divergent section further expands it to the required supersonic Mach number in the test section. The nozzle contour is carefully designed to produce a uniform Mach number and suppress residual shock structure. Depending on the reservoir capacity and flow rate, test durations can range from a few seconds to several minutes. During these runs, the flow remains quasi-steady, enabling accurate measurements of aerodynamic forces, pressures, and temperatures.

Upstream of the nozzle is a settling chamber or plenum, fitted with honeycomb straighteners and multiple fine screens to remove swirl and turbulence. These features ensure that the flow entering the nozzle has a uniform total pressure and temperature. Because the static temperature in a supersonic expansion drops sharply, often below 100 K at Mach 4, the air must often be preheated before each run to prevent condensation, icing, or unrealistically low Reynolds numbers. Electrical heaters are commonly used to raise the stagnation temperature to approximately 700–900 K for Mach-4 operation.

The overall tunnel layout consists of a high-pressure reservoir, a flow-conditioning settling chamber, a convergent-divergent nozzle, a test section, and a downstream diffuser that discharges to either the atmosphere or a vacuum, depending on the facility type. Downstream of the test section, a supersonic diffuser decelerates the flow through a series of weak oblique shocks before returning it to subsonic speed. The diffuser then exhausts either directly to the atmosphere or, in short-duration facilities, to a low-pressure reservoir to maintain the desired pressure ratio across the nozzle. Proper diffuser design is essential to prevent flow unstart and ensure stable operation.

The test section is usually rectangular and fitted with optically flat windows for schlieren or shadowgraph visualization of shock structures and expansion regions. The walls may be slightly diverging to compensate for boundary-layer growth, and pressure taps along the walls provide data for calibration of the Mach number. Models are mounted on slender sting supports or struts designed to minimize interference.

In supersonic testing, the primary focus is on understanding how high-speed flow phenomena such as shock waves, expansion fans, and shock–boundary–layer interactions affect drag, lift, stability, and control. These effects are central to the design of slender bodies, supersonic wings, and air intakes for propulsion systems. Flow visualization techniques, including schlieren and shadowgraph imaging, are widely used to observe the sharp density gradients associated with Mach waves, shock waves, and expansion regions.

Supersonic wind tunnels are essential for the development of high-speed aircraft, missiles, and propulsion systems. They provide the controlled conditions needed to study phenomena that cannot be replicated at lower Mach numbers, such as transonic-to-supersonic shock transitions, high-speed control-surface effectiveness, and inlet performance for supersonic engines. Above Mach 5, aerodynamic heating and real-gas effects become increasingly dominant, requiring even more specialized hypersonic wind-tunnel facilities to replicate these extreme flow conditions.

Hypersonic Wind Tunnels

Hypersonic wind tunnels, operating at Mach numbers greater than 5, are designed to reproduce the extreme aerothermal conditions encountered during atmospheric reentry and spaceflight. At these speeds, the air experiences high-temperature gas effects such as vibrational excitation, molecular dissociation, ionization, and intense boundary-layer heating. These effects must be accurately simulated to obtain meaningful aerodynamic and thermodynamic data. Hypersonic tunnels are used to investigate the combined aerodynamic and thermal environments experienced by high-speed vehicles, particularly for evaluating thermal-protection systems.

Hypersonic facilities exist in several configurations, including continuous-flow, blowdown, and impulse types such as shock tunnels and expansion tunnels, one example being shown in Figure 25 below. Each configuration can generate the very high total pressures and enthalpies required for representative flight testing, but they differ in their operating principles, durations, and fidelity. Continuous-flow facilities can achieve relatively long test times but typically operate at a reduced total enthalpy because of power limitations. In contrast, impulse facilities can reproduce accurate flight-level stagnation enthalpy for only brief periods, typically milliseconds, by releasing stored energy from a high-pressure driver section.

Shock and expansion tunnels are impulse facilities explicitly designed for hypersonic and reentry research. In a shock tunnel, a diaphragm rupture generates a strong shock wave that compresses and heats the test gas before it expands through the nozzle into the test section (Figure 26). An expansion tunnel adds a stage that further accelerates the flow, achieving even higher Mach numbers and total enthalpies representative of orbital reentry. Although the useful test duration is still limited to milliseconds or, at best, a few seconds, these facilities can accurately reproduce the temperature, pressure, and chemical state of gases at reentry speeds. This capability makes them indispensable for studying high-temperature gas dynamics, validating computational fluid dynamics models, and assessing the performance of thermal-protection materials under extreme aerothermal loading.

Comparison of Supersonic and Hypersonic Wind Tunnels

Supersonic and hypersonic facilities share the same fundamental purpose, which is to produce steady, well-characterized high-speed flow for aerodynamic testing. Still, they differ markedly in the physical effects that must be modeled and in the facility design required to reproduce them. The table below summarizes their principal distinctions.

Components of a Low-Speed Wind Tunnel

As previously discussed, there are many different types and sizes of wind tunnels. Still, it is helpful to examine in detail a relatively common low-speed, closed-return (Göttingen-type) wind tunnel. Most educational and research laboratories are equipped with one or more subsonic wind tunnels, which are essential for learning the principles and practices of aerodynamic testing. These facilities provide steady, uniform flows at moderate speeds, enabling engineers and students to study lift, drag, stability, and flow visualization under controlled, repeatable conditions.

A schematic of such a low-speed wind tunnel is shown in Figure 27 below. This particular wind tunnel has a 4 ft by 6 ft (1.22 m by 1.83 m) rectangular test section, 12 ft (3.66 m) long, with flow speeds of up to 420 ft/s (128 m/s). Additionally, the test section features approximately 65% of its surface area made of optical-grade glass, enabling flow measurements using optical diagnostic methods such as PIV.

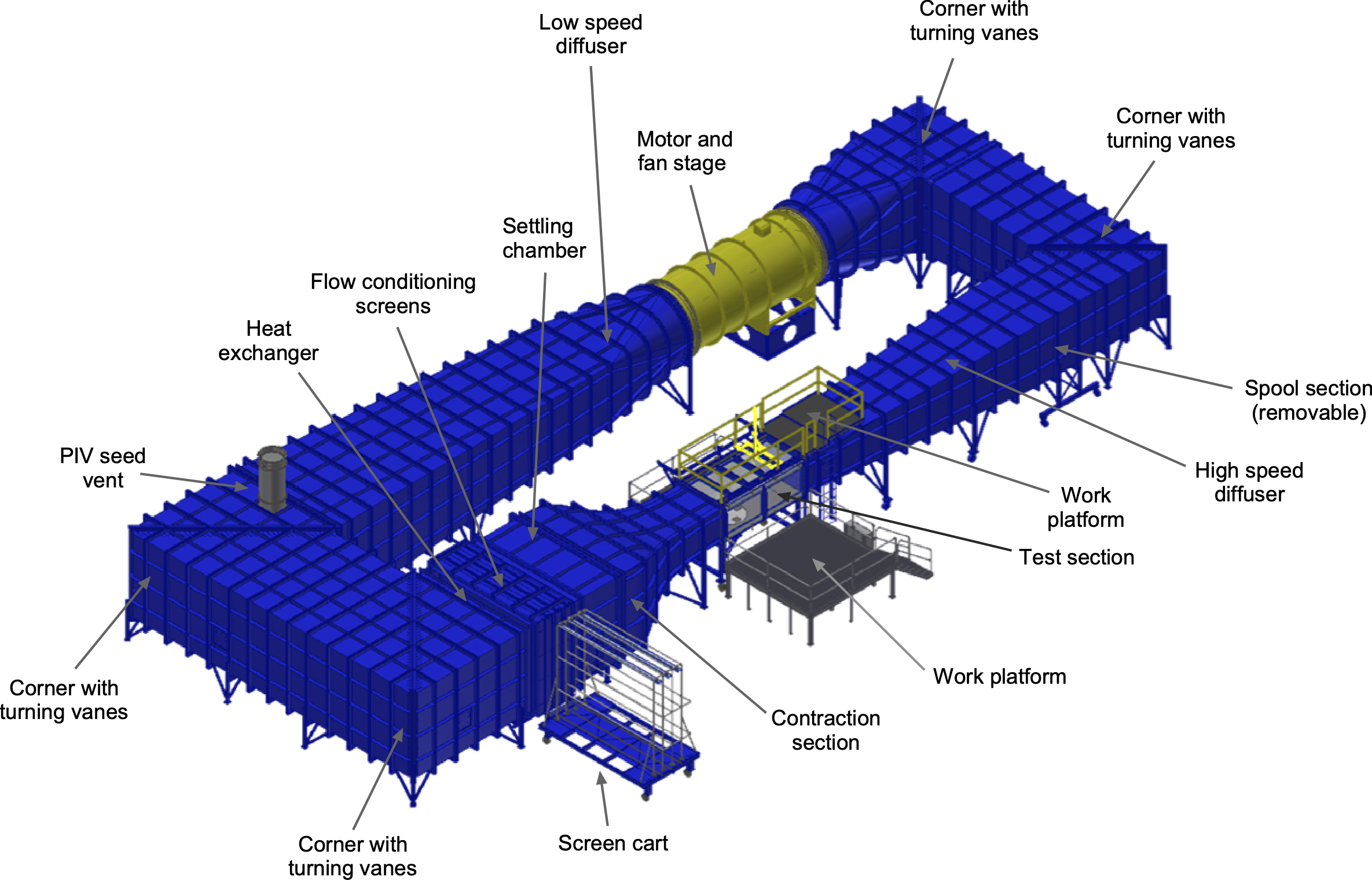
The primary components of the wind tunnel include the test section, high-speed diffuser, turning corners and cross-leg diffusers, motor and fan stage, low-speed diffuser, settling chamber, flow-conditioning section, and contraction section. Many wind tunnels are constructed of steel in shipyards, which have the necessary facilities and skilled workers to build such large, heavy structures. Indeed, many wind tunnels look like ships turned inside out, with the frames and stringers on the outside and the smooth (flow) side on the inside.

Test Section

The test section is the most essential component of all wind tunnels, where the model or object under study is placed. This is the part in the tunnel circuit where the flow speed is highest; all other sections have lower velocities to minimize frictional pressure losses. Test sections may be modular and mounted on wheels or castors, as shown in Figure 28, which allows different test sections to be moved in and out of the wind tunnel loop. Large doors provide easy access to the test section for installing, adjusting models, and setting up instrumentation. Today, high-quality glass walls are typically used in the test section to permit optical measurements. At the same time, provisions for instrumentation, such as pressure taps, load cells, and high-speed cameras, can also be included. Work platforms or gantries on the sides and top of the test section may be used for access, positioning instrumentation, and designated areas for engineers to work.

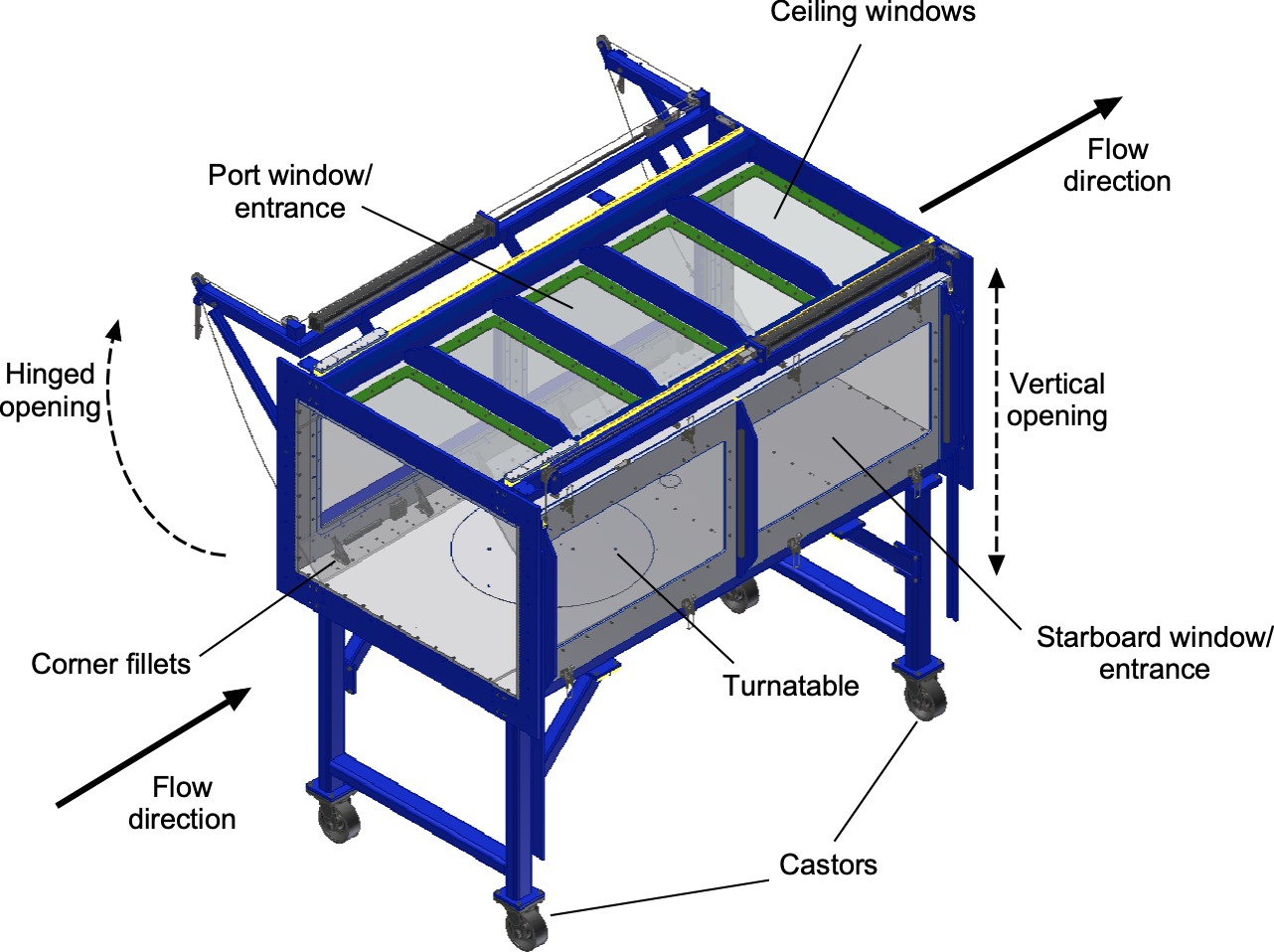
The shape of the test section is designed to minimize boundary layer effects and ensure a uniform, low-distortion flow. Corner fillets are incorporated to suppress flow separation in the corners and are tapered to zero along their length toward the downstream end. As the flow progresses downstream, viscous effects cause boundary layers to develop and grow along all four walls of the rectangular test section. This growth reduces the effective flow area, thereby accelerating the core flow velocity. To maintain uniform velocity and avoid adverse pressure gradients, the cross-sectional area of the test section is gradually increased to compensate for the boundary-layer displacement thickness. If left uncorrected, these pressure gradients can introduce horizontal buoyancy effects and distort force measurements, particularly the drag.

High-Speed Diffuser

After leaving the test section, the airflow enters the high-speed diffuser (Figure 29), where its velocity is gradually reduced to minimize pressure losses. This diffuser is typically long and features a shallow expansion angle, enabling smooth deceleration without flow separation. To maintain attached flow, the half-angle of expansion is usually kept below about 3, and the overall area ratio is moderate, often in the range of 1.2–1.3. A well-designed high-speed diffuser can achieve pressure recovery coefficients of 0.85–0.90, corresponding to losses of only 10–15%.

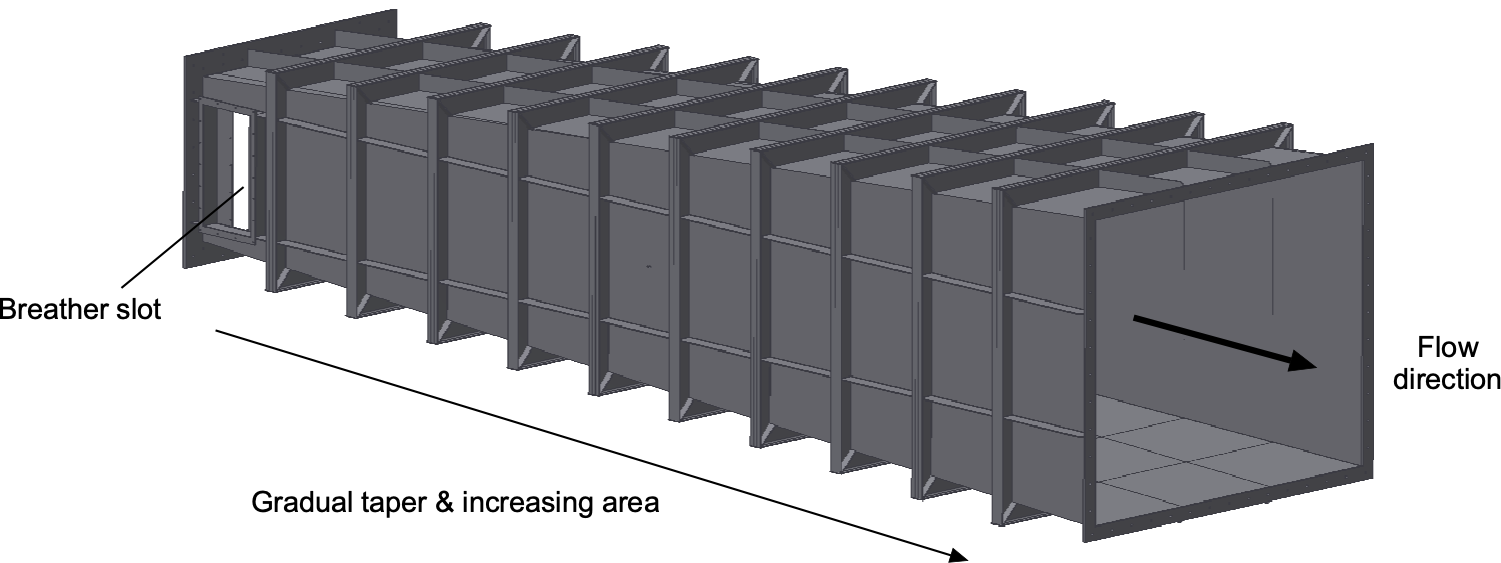
Many high-speed diffusers are fitted with breather slots at their entrance. These slots enable a controlled exchange of air between the test section and the surrounding atmosphere, thereby equalizing static pressure differences that can accumulate in a closed-return tunnel. The result is a steadier and more uniform flow in the test section. However, as air passes across the openings, the slots can generate considerable noise. To mitigate this effect, they are often fitted with external mufflers or baffles that direct the noise away from the test section. While this approach reduces the acoustic environment at the test section, it also lowers the turbulence levels, as pressure fluctuations and acoustic disturbances can act as sources of turbulence in the core flow.

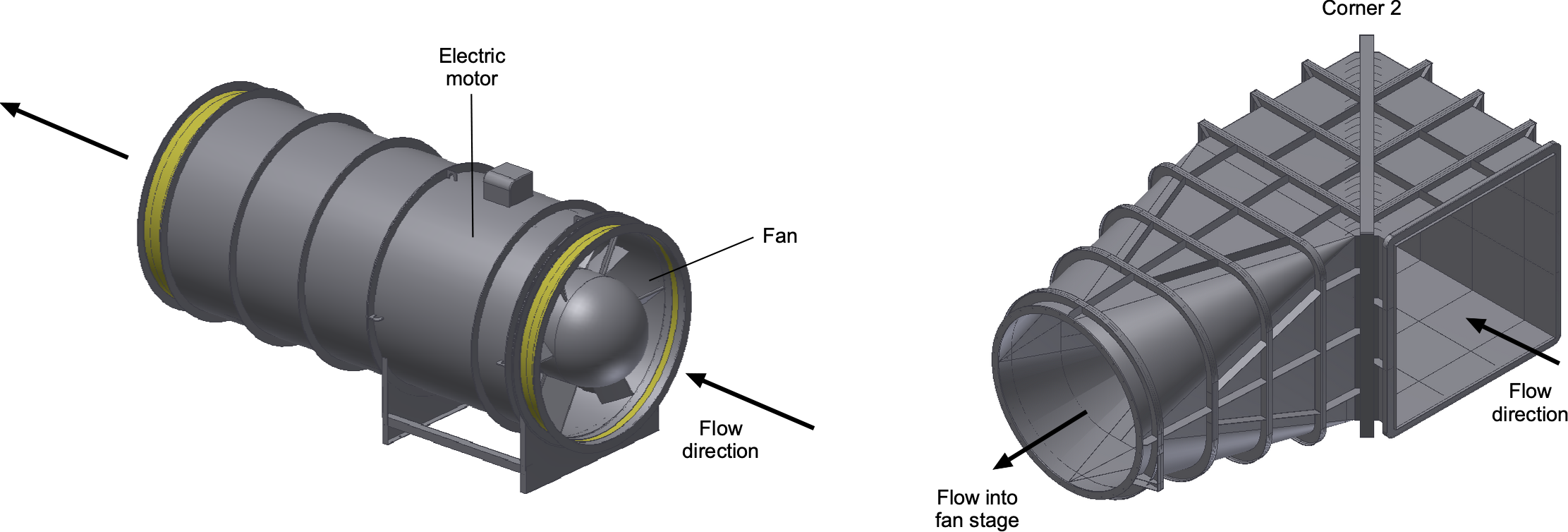
Cross-Leg Diffusers

The purpose of the first cross-leg diffuser (Figure 30), spanning from corner 1 to corner 2, is to redirect, further expand, and decelerate the flow as it approaches the fan. Each corner employs a cascade of circular-arc airfoil guide vanes with sufficient area or solidity to prevent flow separation and the formation of secondary vortices in the flow. These vane cascades allow the flow to turn efficiently, suppressing swirl and turbulence buildup, and help keep total-pressure losses to only a few percent per corner.

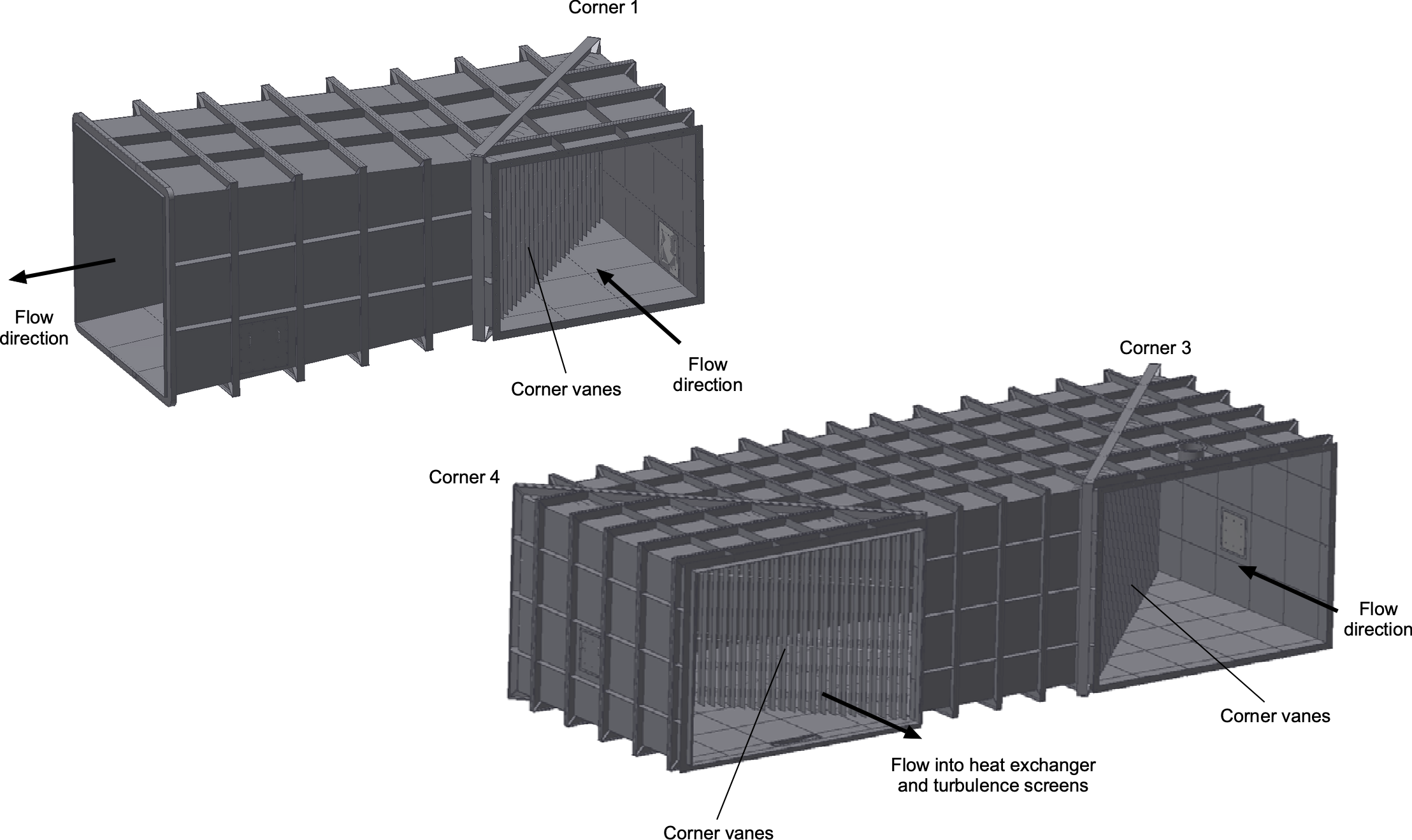
To minimize the total length, this diffuser section should be kept as short as practical, but the divergence angle must not be so large that the boundary layer separates from the walls. In practice, a half-angle of about 2–3 ensures a very low risk of separation in long diffusers, whereas values of 7–10 can be tolerated if the diffuser is short and the flow is well guided by turning vanes or corner fillets.

The second cross-leg diffuser extends from corner 3 to corner 4 and is generally larger in both cross-section and overall length. Because it accommodates more area growth and flow realignment, the acceptable divergence angles are governed by the same trade-offs. Longer, shallower diffusers provide more uniform flow and higher pressure recovery, while shorter, steeper diffusers reduce tunnel length but increase pressure loss and the risk of non-uniformity. Corner 4 forms the final turn before the flow enters the flow-conditioning section, where achieving a uniform velocity profile and low turbulence intensity is crucial for maintaining downstream flow quality.

Corner Vanes

Airflow recirculation in a closed-circuit wind tunnel requires efficient flow turning at each corner of the return circuit. Simply curving the tunnel walls along a circular arc is insufficient because the strong curvature leads to boundary-layer thickening, flow separation, and significant energy losses. To maintain a uniform velocity distribution and prevent the buildup of swirl or turbulence, each corner is fitted with a cascade of turning vanes that guides the flow smoothly around the bend. The vanes may be curved plates (most common) or airfoil sections.

The performance of these vanes is characterized by their solidity, which quantifies the ratio of vane chord to spacing in the cascade and is defined as

(1)  

where is the vane (airfoil) chord and is the center-to-center pitch measured normal to the local flow, as shown in Figure 31 below.

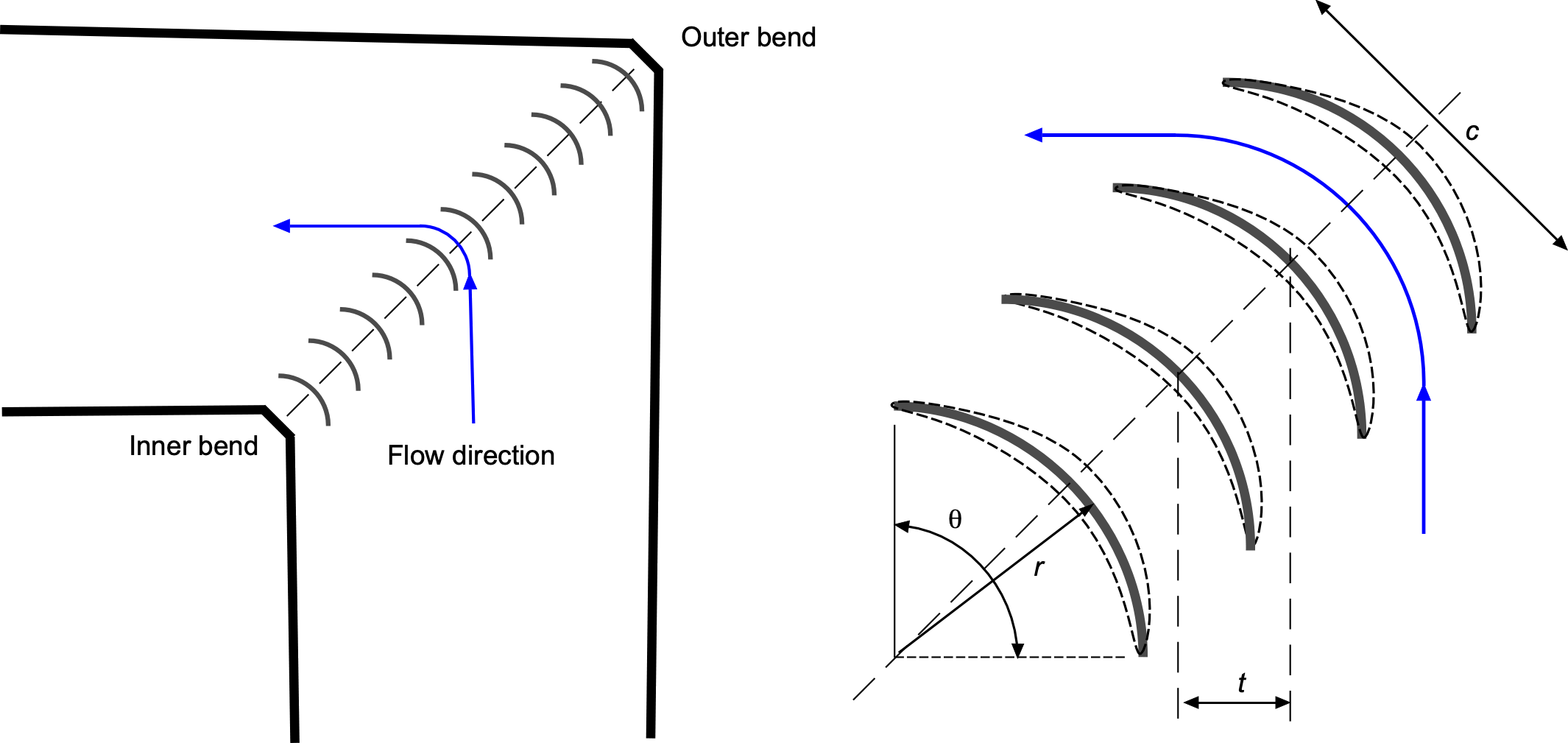
For a curved corner cascade turning through an angle (typically ) with turning vanes, the local pitch at radius is

(2)  

giving an approximate local solidity of

(3)  

Higher solidity values increase turning capability and reduce the likelihood of flow separation, but also raise blockage and pressure losses. Too low a solidity can lead to under-turning and the formation of vortices and turbulence. Using airfoil sections instead of simple curved plates typically reduces pressure losses by about 10–15%. Still, the extra cost of their manufacture usually does not make it worthwhile. In practice, each tunnel corner employs a cascade of circular-arc guide vanes with solidity values typically in the range of 1.0–1.5.

Motor and Fan section

The drive section houses the electric motor and fan that generate and sustain the airflow through the wind tunnel; see Figure 32. By the time the air enters the fan, its velocity has been reduced to roughly one-tenth of the test-section speed through the action of the upstream diffusers. The fan functions as a pump, imparting energy to the flow by raising its total pressure just enough to overcome the distributed losses incurred around the tunnel circuit.

Earlier generations of wind tunnels relied on fan drives such as multi-speed motors, gearboxes, or hydraulic couplings, which could only deliver discrete speed increments. These approaches often produced coarser control of test-section velocity and higher mechanical losses. Modern wind-tunnel fans are driven by precisely controlled variable-speed motors, usually employing variable-frequency drive (VFD) systems.

The use of VFDs enables continuous adjustment of motor speed, resulting in steady, repeatable test-section velocities across the tunnel’s entire operating range. VFD-controlled motors provide smooth fan acceleration and deceleration, precise set-point control, and improved energy efficiency. This technology also reduces mechanical stresses on the drive system and allows automated test sequences in which the flow speed is ramped according to a programmed profile.

Design practice often sets the fan diameter at two to three times the test section width, ensuring sufficient mass flow handling without excessive tip speeds. In many facilities, the fan blades themselves may also have adjustable pitch, allowing the operating point to be matched to the required flow condition. Variable pitch not only improves efficiency over a wide speed range but also helps suppress instabilities, such as stall and surge, in the fan stage. To reduce compressibility and noise, fan tip speeds are generally kept below Mach 0.7, thereby limiting rotational speed for a given diameter. The motor power requirement scales with the dynamic pressure in the test section and the tunnel cross-sectional area, so even modest increases in flow velocity lead to significant increases in installed drive power. In well-designed drive sections, the overall efficiency of power transfer from the motor, converted to test-section flow energy, can exceed 80%, making this component central to tunnel performance.

Low-Speed Diffuser

After the fan stage, the airflow enters the low-speed diffuser (Figure 33), where its velocity is reduced further to recover static pressure and minimize pressure losses. Like the high-speed diffuser, this component is relatively long and has a shallow expansion angle, enabling smooth deceleration without boundary-layer separation. Typical half-angles are limited to approximately 2–3, and overall area ratios of 1.3–1.5 are commonly achieved to ensure good pressure recovery.

Flow Conditioning & Settling Chamber

After corner 4, the flow connects to the settling or stilling chamber, which is located at the entrance to the test section. Its primary purpose is to precondition the air and reduce turbulence levels before it reaches the contraction. This goal is achieved using flow straighteners, such as plates or honeycomb structures. Turbulence is then reduced using fine-mesh screens. These elements begin to remove the turbulent and angular components of the airflow, ensuring a more uniform velocity profile as it enters the contraction section. In closed-circuit wind tunnels, a heat exchanger in these regions is used to regulate the temperature of the recirculating air. The air in a closed-loop wind tunnel can become very hot from frictional losses that generate heat.

Turbulence intensity can be reduced using “turbulence screens,” a staple of wind tunnel operations. These screens, also known as “anti-turbulence screens,” are made of fine wire mesh with various gauges and grid spacings, as shown in Figure 34. Positioned before the contraction to the test section, they break up the larger turbulent eddies into progressively smaller ones that decay rapidly over short downstream distances. 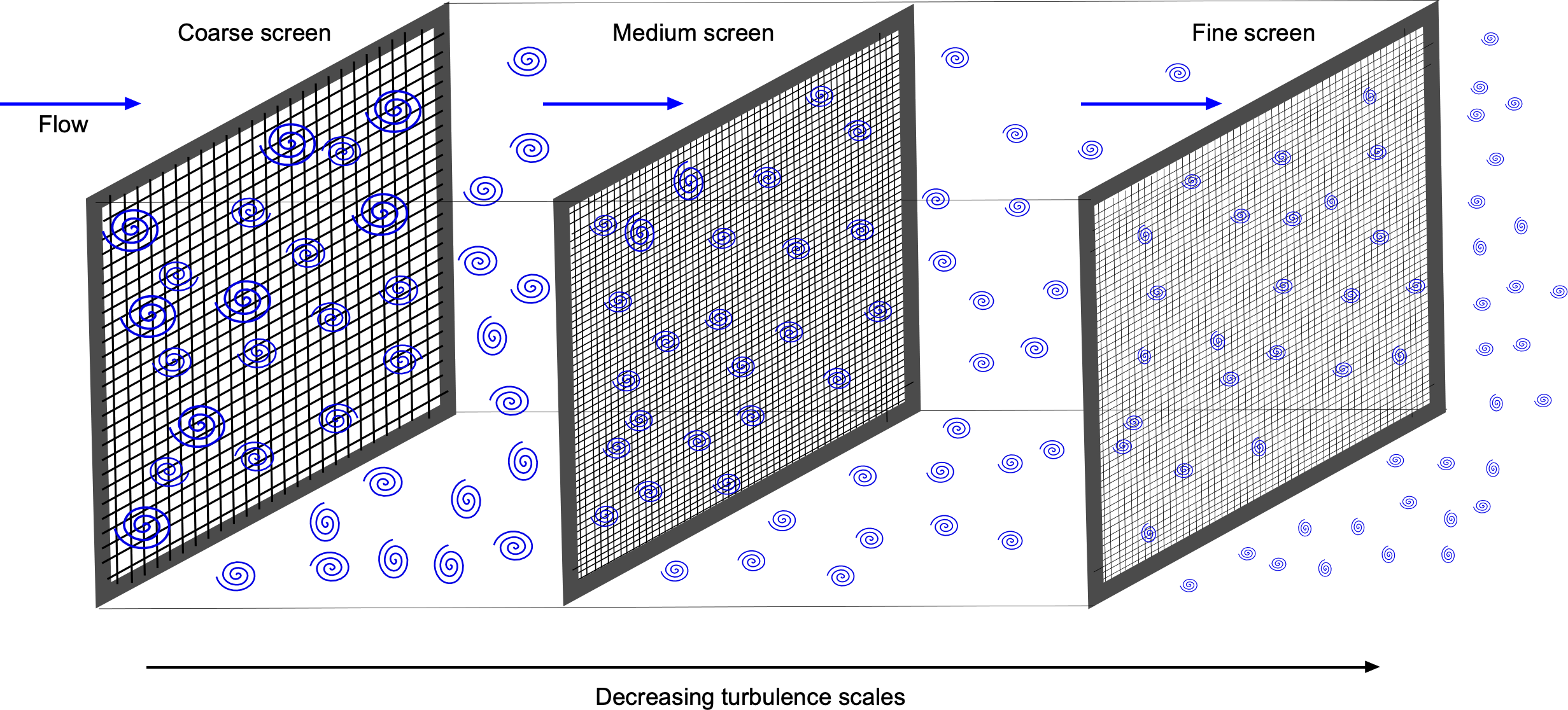A “settling chamber” downstream of the last turbulence screen, which is usually just a short length of the constant-area, further reduces the turbulence, allowing the flow to reach an equilibrium state with more homogeneous turbulence levels. This process ensures smoother, less turbulent flow in the test section, a prerequisite for high-quality flow measurements.

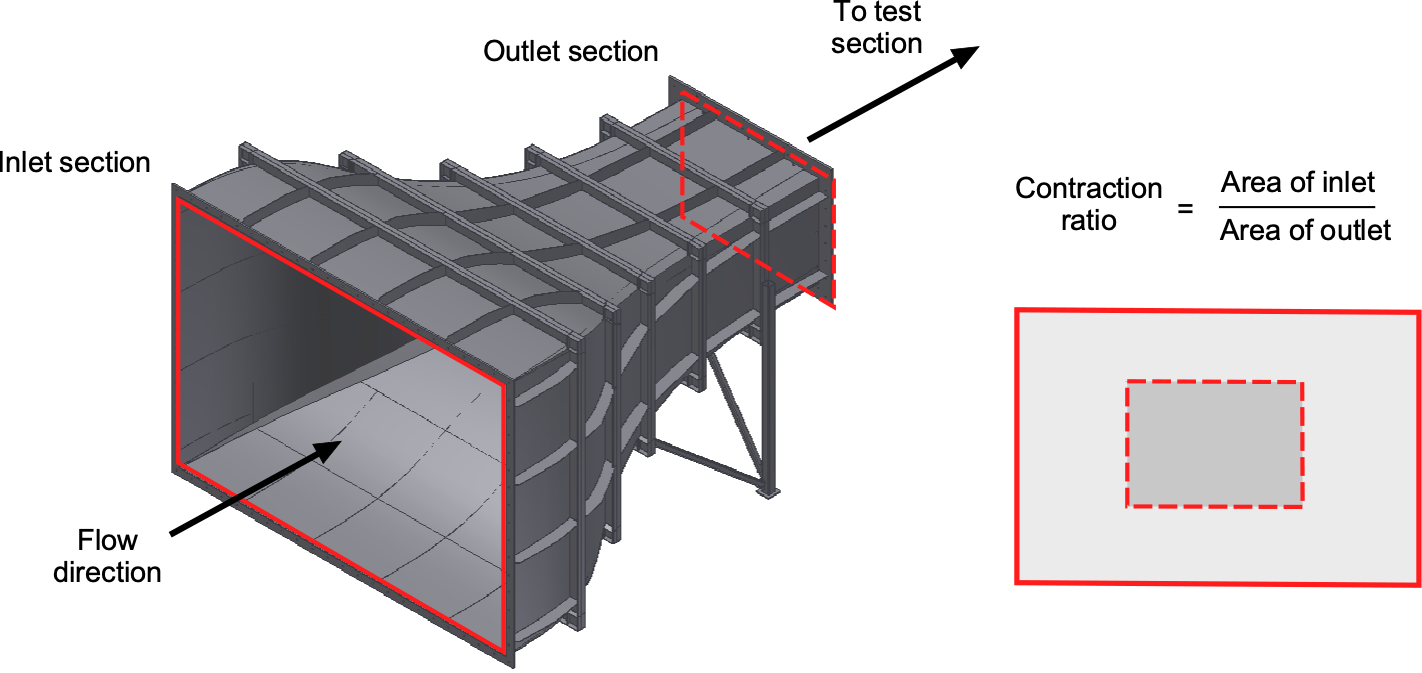
Contraction Section

The contraction section accelerates the airflow and directs it into the test section; see Figure 35. The shape of the contraction is typically parabolic or exponential, allowing for smooth, continuous acceleration. The ratio of the inlet area to the outlet area, known as the contraction ratio, is carefully selected based on the desired flow characteristics, and is typically about 7:1. While the purpose of the contraction is to speed up the flow before it reaches the test section, it also acts to squeeze out and “relaminarize” small turbulence eddies and further reduce turbulence levels of the flow in the test section; the flow entering the test section becomes almost laminar, although not entirely so. Turbulence levels of less than 0.1% of the freestream velocity are considered good enough to represent the flow in the higher atmosphere.

Flow Quality

The design of a modern wind tunnel is complex because it is typically customized to meet specific testing requirements, including the test articles and the types of measurements to be made. One of the challenges in wind tunnel design is achieving uniform flow properties in the test section, i.e., uniform velocities in both magnitude and direction, with minimal flow angularity (typically less than 0.1 degree is a goal) throughout its entire length. This process requires close attention to the internal flow quality throughout the wind tunnel circuit, including the flow characteristics produced by the fan. Special attention must also be paid to the contraction before the test section.

Today, CFD methods are used to aid in the design of wind tunnels and to predict boundary-layer thickness and turbulence levels. The shape of the contraction can then be contoured iteratively to ensure optimal flow uniformity at the entrance to the test section and along its entire length, as shown in Figure 36. Appropriately shaped and tapered corner fillets, extending from the contraction and along the test section length, are also part of the design solution to account for boundary layer displacement effects.

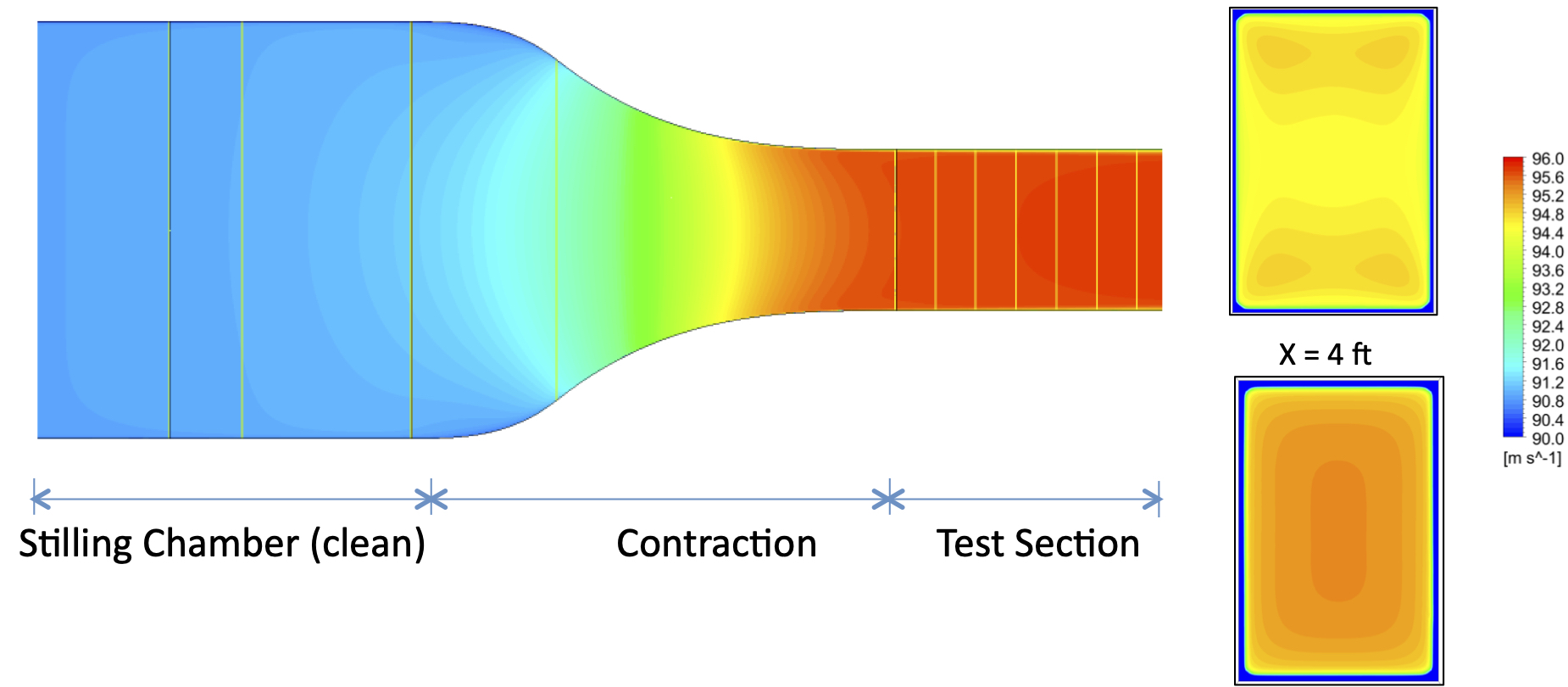
Flow quality is one of the most critical indicators of a wind tunnel’s performance, as it sets the baseline for the accuracy and repeatability of all aerodynamic measurements. Even if balances, sensors, and reduction methods are flawless, poor flow quality will undermine the fidelity of the results. For this reason, flow quality is treated as a defining characteristic of every facility. Four primary metrics are used to assess flow quality, namely uniformity, steadiness, turbulence intensity, and flow angularity.

Uniformity

Uniformity requires the freestream velocity to remain nearly constant across the test section. In high-quality tunnels, the velocity typically varies by no more than one to two percent of the mean value across the test-section’s cross-sectional area, ensuring that lift, drag, and moment data are not biased by spanwise or chordwise velocity gradients.

Steadiness

The second metric is steadiness, defined as the absence of low-frequency, time-varying disturbances in the mean flow. Variations in mean velocity are generally kept within over periods of ten seconds or longer. Such steadiness is vital for capturing subtle aerodynamic effects and for ensuring repeatability across different test runs.

Turbulence Intensity

The third metric is turbulence intensity, defined as the ratio of the root-mean-square velocity fluctuations to the mean freestream speed,

(4)  

where represents the velocity fluctuation and is the mean freestream velocity. High-quality low-speed tunnels maintain turbulence intensities below 0.1%, allowing fine aerodynamic increments to be resolved. This value is comparable to the level of atmospheric turbulence in the lower stratosphere.

Flow Angularity

The fourth metric is angularity, a measure of the deviation of the local flow direction from the nominal tunnel axis. Angularity is usually required to remain below in both pitch and yaw to avoid corrupting force and moment data by effectively altering the model’s angle of attack. Careful design of diffusers, corners, and flow-conditioning screens is needed to minimize this effect.

A variety of diagnostic methods can be used to characterize and verify flow quality. Basic smoke visualization can reveal gross flow non-uniformities, while hot-wire anemometry (HWA) provides quantitative measurements of turbulence intensity. Traverses with Pitot probes, typically 5- or 7-hole, are used to assess velocity uniformity and angularity. Advanced optical methods, such as Particle Image Velocimetry (PIV), may offer more detailed, full-field diagnostics.

Ultimately, the ability of a tunnel to maintain high flow quality directly determines the reliability of the aerodynamic data it produces. Facilities with excellent steadiness, high uniformity, very low turbulence intensity, and minimal angularity enable the precise and repeatable determination of aerodynamic coefficients, such as lift, drag, and pitching moments, as well as surface pressures. This makes flow quality the foundation upon which all wind tunnel testing depends.

Test Section Shapes & Sizes

The flow quality in the test section is strongly influenced by its size and shape. Test sections are designed to provide a uniform, well-characterized flow environment, enabling aerodynamic measurements with minimal distortion. The intended application dictates the geometry, operating speed regime, and scale of the test models.

Cross-Section

The most common cross-sectional shapes are rectangular, circular, octagonal, and (less commonly) elliptical, as shown in Figure 37. Rectangular test sections are widely used in low-speed and transonic tunnels, where slotted or perforated walls can be incorporated to alleviate wall interference. Their flat walls also simplify optical access, model mounting, and the installation of interchangeable wall panels, making them exceptionally versatile. However, care is needed to manage secondary flows in the corners, which can influence boundary-layer growth and test results.

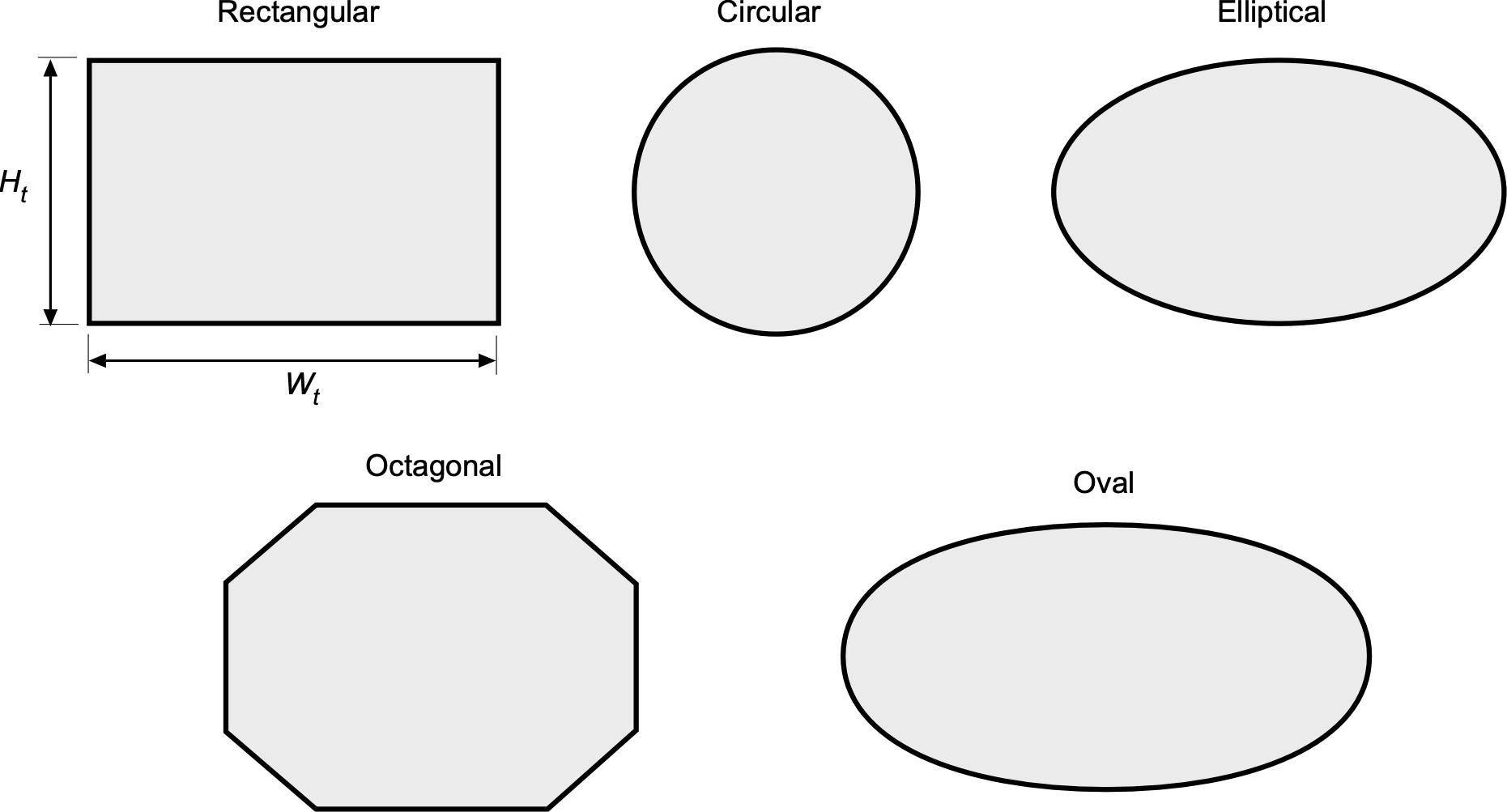
Circular cross-sections are commonly used in pressurized supersonic and hypersonic tunnels because their geometry efficiently resists hoop stresses and simplifies the fabrication of thick-walled pressure vessels. The circular cross-section also facilitates the design of axisymmetric contoured nozzles and diffusers, allowing smooth flow expansion and minimizing corner-induced secondary flows. However, many continuous-flow and research tunnels adopt square or rectangular test sections to accommodate models, optical access, and instrumentation. Therefore, the choice between circular and rectangular sections reflects a trade-off between structural efficiency, flow uniformity, and experimental accessibility.

Octagonal test sections are common in low-speed tunnels. They offer a compromise between circular and rectangular designs, providing flat panels that are easier to fabricate and that facilitate the installation of windows, instrumentation ports, or interchangeable wall inserts. They also tend to reduce wall interference effects when testing finite wings, compared with rectangular sections. An example of a wind tunnel with an octagonal test section is shown in the photograph of Figure 38.

Elliptical test sections offer aerodynamic advantages by reducing corner-induced secondary flows and promoting more uniform boundary-layer growth. However, their higher construction cost, structural inefficiency compared to circular designs, and incompatibility with slotted or perforated wall inserts used for interference relief have limited their adoption in practice. A summary of the relative advantages of several common wind-tunnel cross-sections is given in the table below.

Special-purpose facilities may use modified cross-sections to serve specific needs. Aeroacoustic tunnels, for instance, may line their walls with acoustic treatments to absorb reflected noise. In contrast, optical test tunnels employ high-quality glass panels with anti-reflective coatings for precise imaging. Some facilities also use interchangeable wall inserts (e.g., solid, slotted, or two-dimensional) so that the test section can be tailored to different test programs while preserving flow quality. The photograph in Figure 39 below shows a two-dimensional insert placed between two false walls inside a low-speed wind tunnel. The objective is to simulate flow over an airfoil section without using a high-aspect-ratio wing or one that spans the entire horizontal or vertical dimension of the wind tunnel.

Finally, it should be noted that the model’s physical scale strongly influences the selection of test-section dimensions, the target Reynolds number, and the allowable blockage ratio. To minimize wall interference, blockage is typically maintained below 5–10%. Low-speed research tunnels, therefore, often have larger test sections to accommodate bigger models and achieve higher Reynolds numbers. In comparison, supersonic and hypersonic tunnels generally use smaller test sections to keep power requirements and total pressure demands within practical limits.

Section Length

The length of the test section must be sufficient to ensure a uniform core between the nozzle exit and the collector or first diffuser, while limiting wall-boundary-layer growth. If the section is too short, the measurements overlap the end regions, where residual nozzle nonuniformity and pressure gradients are most pronounced. If it is too long, wall boundary layers thicken, and the effective area contracts, introducing an axial pressure gradient that can bias force and pressure measurements. Most closed-return facilities utilize a nearly constant-area test section or a very slight controlled divergence to offset boundary-layer displacement and maintain approximately uniform static pressure along the length.

Avoiding wake ingestion into the high-speed diffuser is critical; this phenomenon is known as wake truncation. Diffusers require a relatively uniform, low-shear inflow to achieve stable pressure recovery. When a model generates a long-separated wake, common with bluff bodies, highly loaded wings, or high-angle-of-attack stalled-flow conditions, the wake can couple with the diffuser’s adverse pressure gradient, degrade pressure recovery, and feed back into the freestream velocity in the test section as a notable unsteadiness.

Facilities that test such bluff bodies or models that produce extended wakes are often built with extended-length test sections, typically on the order of twice the largest cross-sectional dimension, and they position the model so that much of the wake intensity decays upstream of the collector. As a practical rule of thumb, when sizing and testing bluff-bodies, it is recommended to avoid issues by allowing the wake to freely develop in the test section for a distance of roughly twice the model length before the collector or diffuser entrance. It is generally not possible to apply force and pressure corrections to account for wake truncation.

Freestream Speed Measurement

Accurate determination of freestream airspeed in the test section of a wind tunnel is fundamental to establishing consistent test conditions, normalizing aerodynamic forces, and calculating non-dimensional coefficients. To this end, flow speeds are determined from static and dynamic pressure measurements upstream of the test section, using the Bernoulli equation. Probes are typically not placed in the test section because they would disrupt the clean, uniform flow intended for measurement. All low-speed wind tunnels are a large Venturi, in which airflow is accelerated through the contraction section into the test section and then decelerated by the diffuser section. Supersonic wind tunnels use De Laval nozzles to accelerate the flow and achieve the desired Mach number in the test section.

Static Pressure Drop Method

Consider the configuration shown in Figure 40 below, in which the flow speed in the test section is determined by the static pressure drop across the settling chamber and the entrance to the test section. The airflow enters the mouth of area at a flow velocity with pressure . The cross-section then contracts to a smaller area, , at the test section, where the velocity has increased to = ; the velocity in the test section must increase if continuity is satisfied. The test section is vented to ambient pressure, so .

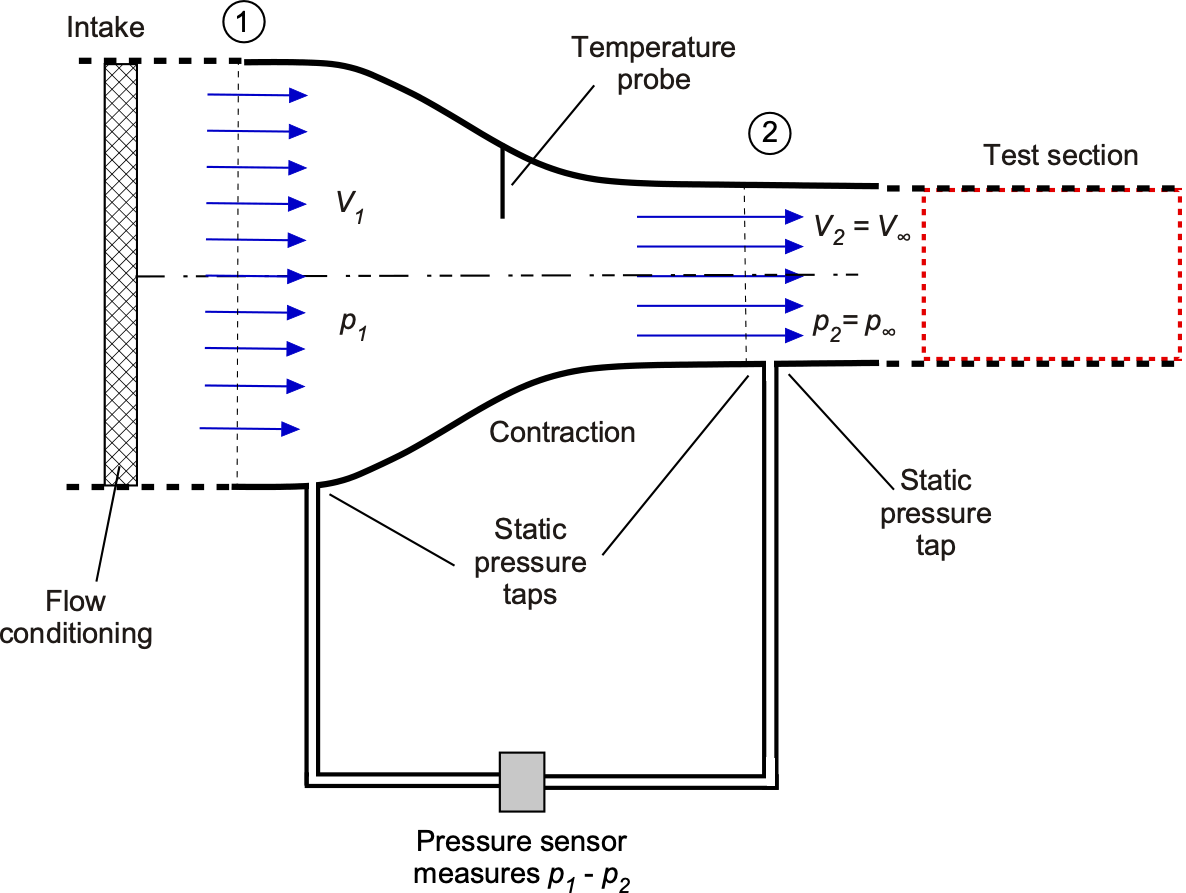
From the continuity equation, the flow velocity in the test section is

(5)  

The area ratio is fixed for a given wind tunnel. The pressures are then related using the Bernoulli equation, i.e.,

(6)  

so that the flow velocity in the test section is

(7)  

where is the density of the air in the test section. Air density is obtained from the ideal gas law, i.e.,

(8)  

where is the static pressure, the absolute temperature, and the specific gas constant. In unsteady facilities such as blowdown tunnels, these parameters must be measured continuously and synchronized with force and moment data to ensure proper normalization throughout the run.

Typically, static pressures are obtained by averaging the pneumatic readings from four taps placed around each section. This approach corrects for small static-pressure errors. However, the method is also calibrated to ensure the accuracy of the test-section flow velocity measurement. In the calibration, a reference Pitot probe is placed in the test section, and the pressure drop is measured for a range of flow speeds; any discrepancy leads to a calibration factor, , that can be used to determine the flow speed more accurately, i.e., using

(9)  

In practice, the calibration factor for a low-speed wind tunnel is usually very close to unity. If it is not, there are unexplained losses that require investigation.

Pitot Probe Method

Another method for measuring the flow velocity in the test section is to use a Pitot probe in the settling chamber, as illustrated in Figure 41. The Pitot probe measures the total pressure, , in the upstream section or any other convenient upstream section. This approach tends to yield a more accurate measure of dynamic pressure because it involves the difference between a higher and a lower pressure, rather than between two lower pressures of similar magnitude. The Pitot probe is sufficiently upstream in a slower-moving flow that its downstream effects are negligible.

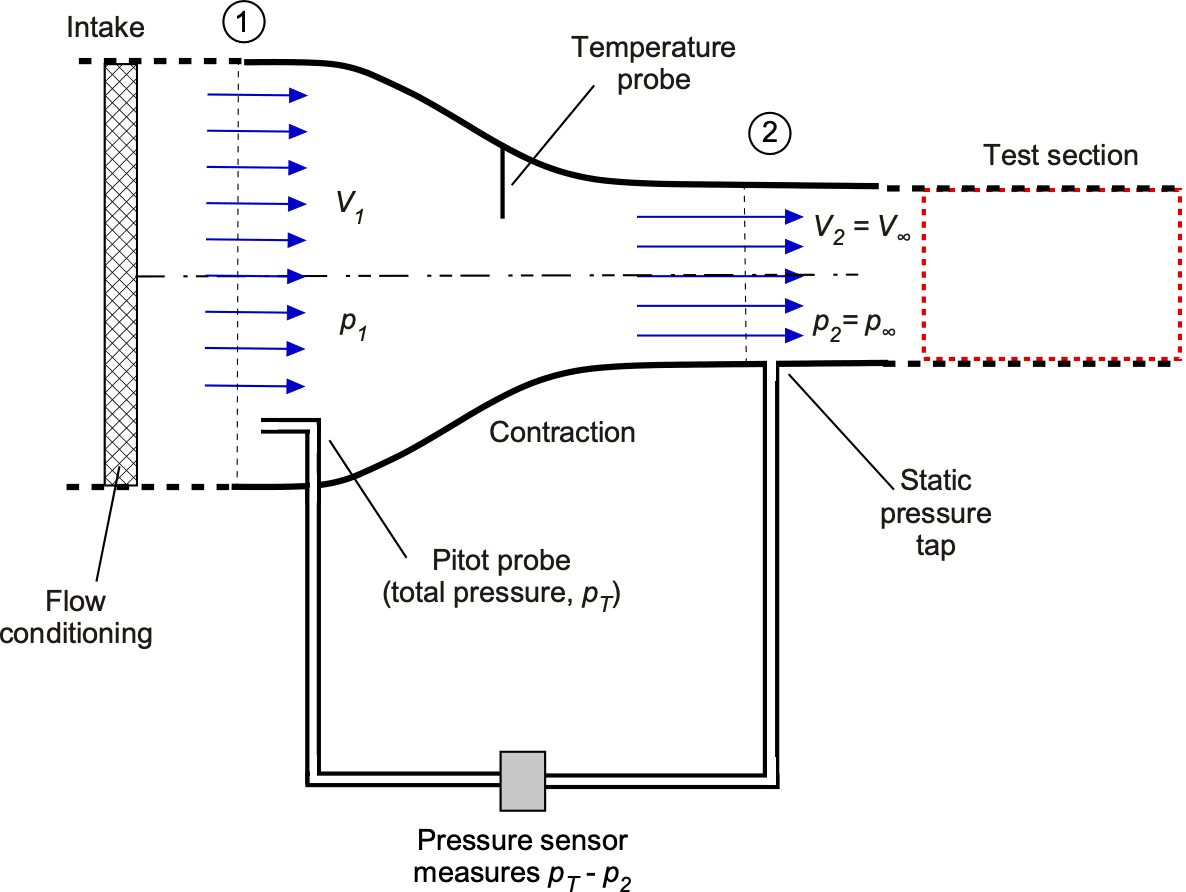
From the Bernoulli equation, then

(10)  

so that

(11)  

Again, the value of density, , can be obtained from static pressure and temperature measurements in conjunction with the equation of state. Again, the calibration would be verified by placing a Pitot probe in the test section to obtain a calibration factor, , i.e.,

(12)  

where, again, will be very close to unity.

Compressible Flow Corrections

At higher Mach numbers (typically ), compressibility effects must be considered. For an isentropic flow of a perfect gas, the Mach number is given by

(13)  

And the airspeed is then

(14)  

where is the ratio of specific heats (1.4 for air), is the specific gas constant for air.

One of the most reliable methods for determining the flow speed and Mach number in a supersonic wind tunnel is the use of a Pitot probe, which measures the stagnation pressure. Combined with a measurement of the static pressure, typically taken from the wall of the test section, the Mach number can be determined using isentropic relations. The stagnation pressure and static pressure are related to the Mach number through the isentropic flow relation

(15)  

where is the ratio of specific heats for the gas, e.g., for air. Solving this equation numerically for yields the local Mach number in the test section. Once the Mach number is known, the flow speed can be obtained from

(16)  

where is the local speed of sound, is the specific gas constant, and is the static temperature of the flow.

If the stagnation temperature is known, then the static temperature can be inferred using the isentropic relation, i.e.,

(17)  

Together, these measurements enable the complete characterization of the flow’s thermodynamic and velocity states.

Pressure Losses

One key challenge in wind tunnel design is determining the required fan or motor power to generate a desired test-section velocity or dynamic pressure. This requirement depends on an accurate estimation of pressure losses throughout the tunnel circuit. Because wind tunnels contain ducts with varying cross-sectional areas and shapes, as well as transition pieces, the flow through them experiences friction and other losses, particularly at higher Reynolds numbers. Additional pressure losses arise from the turning vanes placed at the corners of the circuit. Typically, these are cascades of thin, airfoil-shaped plates that help redirect the flow but can introduce substantial frictional resistance. Careful estimation of these cumulative losses is essential to ensure the tunnel meets its performance targets.

In the conventional approach to wind tunnel design, the frictional losses can be estimated for the fan and initial sizing of the motor by breaking the tunnel circuit into its primary parts: 1. Cylindrical sections (even if just transition pieces), 2. Corners, 3. Expanding sections, i.e., diffusers, 4. Contracting sections (i.e., nozzles ), 5. Turbulence screens, 6. Heat exchangers, 7. Other miscellaneous parts. In each of these sections (and there may be more than one of each), energy is lost in the form of a static pressure drop , which can be expressed as a dimensionless local loss coefficient given by

(18)  

where is the local dynamic pressure of the flow. For corners, bends, and turning vanes, the loss coefficient is typically based on empirical data, as previously discussed. This loss is referenced to the test section values (subscript 0) using

(19)  

Although Poiseuille’s law applies to fully developed laminar flow and is not directly applicable to the high-Reynolds-number, turbulent flows in wind tunnels, a similar scaling relationship can still be used to approximate geometric effects. Specifically, for ducts of varying cross-sections, pressure loss coefficients can be scaled based on the fourth power of the hydraulic diameter

(20)  

where is the local hydraulic diameter of the tunnel section, and is the hydraulic diameter of the test section. The hydraulic diameter is defined as

(21)  

where is the cross-sectional area and is the wetted perimeter of the section.

The next step is to express the energy loss per unit time, , in terms of the test section conditions, i.e.,

(22)  

which simplifies to

(23)  

The so-called energy ratio, , can then be defined as

(24)  

so that

(25)  

This formulation shows that minimizing , which includes corner losses through , improves the tunnel’s efficiency and reduces the fan’s power requirement.

The energy ratio, , characterizes the efficiency of a wind-tunnel circuit and is inversely proportional to the total pressure losses in the flow path. For a well-designed closed-return tunnel, typically lies between 4 and 7. Lower losses imply higher efficiency and reduced fan and motor power. The dominant losses generally occur in diffuser sections and corner-turning vanes, so their aerodynamic design is critical.

Evaluation of requires determining the loss coefficients, , for each component of the circuit using standard relations for turbulent flow in ducts, fittings, screens, and vanes. Losses associated with the fan and motor are normally excluded so that reflects the efficiency of the tunnel circuit itself. The required pumping power to achieve a specified test-section velocity follows directly from the summed pressure losses around the loop. Because some losses cannot be accurately predicted before construction, practical designs incorporate power margins to ensure that the specified flow conditions are met. Minimizing circuit losses is therefore essential, as it directly reduces the required fan size and installed motor power.

Model Scaling & Similarity Parameters

In wind tunnel testing, models are typically smaller than the full-scale vehicle to reduce cost and facility requirements. However, to obtain meaningful results, the model must replicate the relevant flow physics of the full-scale object. This goal is accomplished by preserving the key non-dimensional parameters governing the system’s fluid dynamics.

A model is said to be geometrically similar if it preserves a constant ratio between corresponding lengths and angles. This ensures that the shape matches the full-scale object in all three dimensions. But geometric similarity alone does not guarantee aerodynamic similarity. Dynamic similarity requires that the ratios of the forces acting on a body in a flow are preserved. In practice, this means that certain non-dimensional parameters, most notably the Reynolds and Mach numbers, must be matched between the model and the full-scale case.

Reynolds number

The Reynolds number () is the ratio of inertial to viscous forces. It governs boundary layer behavior, transition, and separation. For large-scale models or pressurized tunnels, it can be matched directly. Otherwise, corrections may be applied. Matching the Reynolds number exactly is often impractical, especially for low-speed flows in small tunnels. Instead, high-Reynolds tunnels (e.g., pressurized or cryogenic) are used, or corrections are applied based on empirical or computational fluid dynamics (CFD) data. The location of the laminar-turbulent transition, separation behavior, and drag prediction are sensitive to Reynolds number.

Mach Number

The Mach number () is the ratio of flow velocity to the speed of sound. It is important in compressible flows for shock formation and wave drag. In compressible flows, particularly in transonic and supersonic regimes, the concept of Mach number similarity is crucial. Unlike the Reynolds number, the Mach number is usually easier to match. Tunnels designed for compressible flows often prioritize precise control of Mach and pressure to isolate compressibility effects.

The Reynolds-Mach Number Conflict

In practice, it is rarely possible to match both Reynolds number and Mach number simultaneously in a wind tunnel. To see why, consider that

(26)  

Suppose a model is scaled down (reducing ). In that case, the Reynolds number decreases unless the viscosity is lowered (e.g., through cryogenic testing) or the density is increased (e.g., by using pressurized air or a heavy gas). But increasing velocity to compensate will also raise the Mach number, possibly beyond the regime of interest. Conversely, maintaining the correct Mach number fixes the flow velocity, which may result in a Reynolds number that is far too low.

This trade-off explains why high-speed wind tunnels typically match Mach number but operate at lower Reynolds numbers, applying corrections or boundary-layer trips to simulate transition. In high-Reynolds tunnels (pressurized or cryogenic), conditions are set to reach flight Reynolds numbers, even if Mach similarity cannot be maintained. In subsonic low-speed tunnels, it is common to match the Reynolds number approximately (to represent boundary-layer physics) while allowing the Mach number to differ. In supersonic tunnels, Mach similarity is prioritized to represent shock-wave behavior, whereas Reynolds corrections are applied either analytically or empirically.

Froude Number

The Froude number () is a dimensionless parameter that is relevant when gravity plays a significant role in the flow field, particularly in free-surface or stratified-flow simulations. While not typically a governing similarity parameter in conventional wind tunnel testing, it becomes essential in water flow facilities used to simulate ship hydrodynamics, amphibious vehicle performance, or wave-structure interaction problems. In such contexts, proper Froude scaling ensures dynamic similarity between the model and the full-scale scenario by matching the ratio of inertial to gravitational forces.

Wall Interference

Wall interference effects are a critical concern in wind tunnel testing, particularly in narrow test sections or when testing large models. Because the model occupies space within the flow, it displaces air and alters the pressure and velocity fields around it. This artificial distortion differs from the conditions encountered during free flight and must be accounted for to ensure accurate aerodynamic measurements.^[5]

To reduce wall interference, some wind tunnels may employ slotted or perforated walls to allow lateral pressure relief, better simulating unbounded flow. In advanced facilities, adaptive-wall systems can adjust their contour in real time. Various correction methods are also used during data reduction, many of which have been developed empirically for each wind tunnel through calibration.

Blockage & Boundary Interference

Several primary mechanisms contribute to boundary, or wall, interference in wind tunnel testing. These arise because the solid tunnel walls constrain the flow differently than in free flight. The tunnel boundaries alter streamline curvature, restrict lateral and vertical expansion, and reflect pressure disturbances, all of which produce measurable deviations in aerodynamic forces and surface pressures on the model.

The principal manifestations of wall interference are: (1) solid blockage, associated with the displacement of streamtubes around the finite thickness of the model; and (2) wake blockage, caused by the momentum deficit carried in the viscous wake of the body. In both cases, the underlying mechanism is the enforced curvature of streamlines by the tunnel walls, which alters the pressure field and feeds back on the loads measured on the model. Collectively, these boundary-induced effects are grouped under the term “wall interference,” and they must be accounted for so that wind tunnel measurements can be reduced reliably to free-air conditions.

Solid Blockage

Solid blockage is associated with the physical volume of the model, which displaces flow and reduces the available cross-sectional area of the test section. The consequence is that the streamlines can no longer develop as in free air, as shown in Figure 42. A common measure of solid blockage is the blockage ratio, which is

(27)  

where is the model’s projected frontal area and is the test-section area. When exceeds about 0.05 (5%), some solid-blockage effects can be expected.

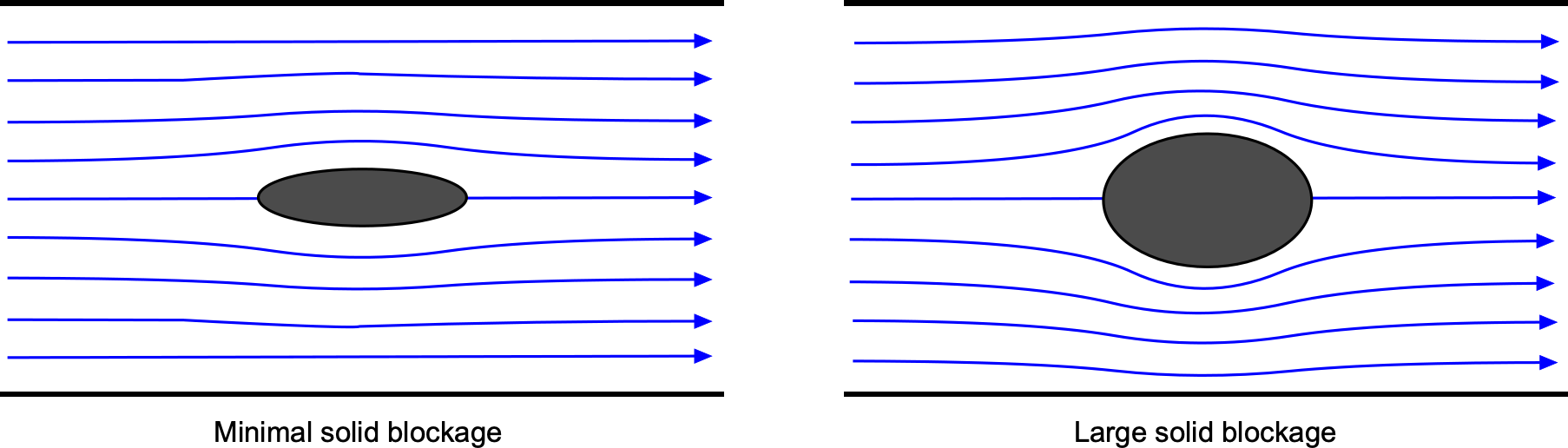
There is no closed-form theoretical prediction of the effects; therefore, semi-empirical correlations are employed. These are often expressed as an effective freestream velocity increment of the form

(28)  

where is an empirical factor of order unity that depends on model shape and tunnel geometry. The corrected dynamic pressure is then

(29)  

which is used to rescale aerodynamic coefficients back to their equivalent free-air values. For example, the lift coefficient may be corrected by writing

(30)  

so that the measured coefficient decreases proportionally to the blockage ratio and an empirical calibration factor. Similar forms are often applied to other force and moment coefficients.

The practical remedies for solid blockage include either applying corrections using facility-specific calibration factors or reducing the blockage ratio by testing a smaller model. Using a smaller model, however, may introduce issues associated with the Reynolds number. Practical guidelines for most wind tunnels recommend keeping blockage ratios below approximately 5%. For example, in a 3.0 m test section, a model with = 0.15 m gives = 0.05, which is acceptable.

Wake Blockage

Wake blockage occurs because the model’s viscous wake cannot expand naturally within the confined test section, as shown in Figure 43. The deficit must be balanced by a streamwise pressure rise across the control volume that encloses the model and its immediate wake. Again, the consequence is that the streamlines outside the wake cannot develop as they would in free air, and the tunnel walls constrain this natural wake development.

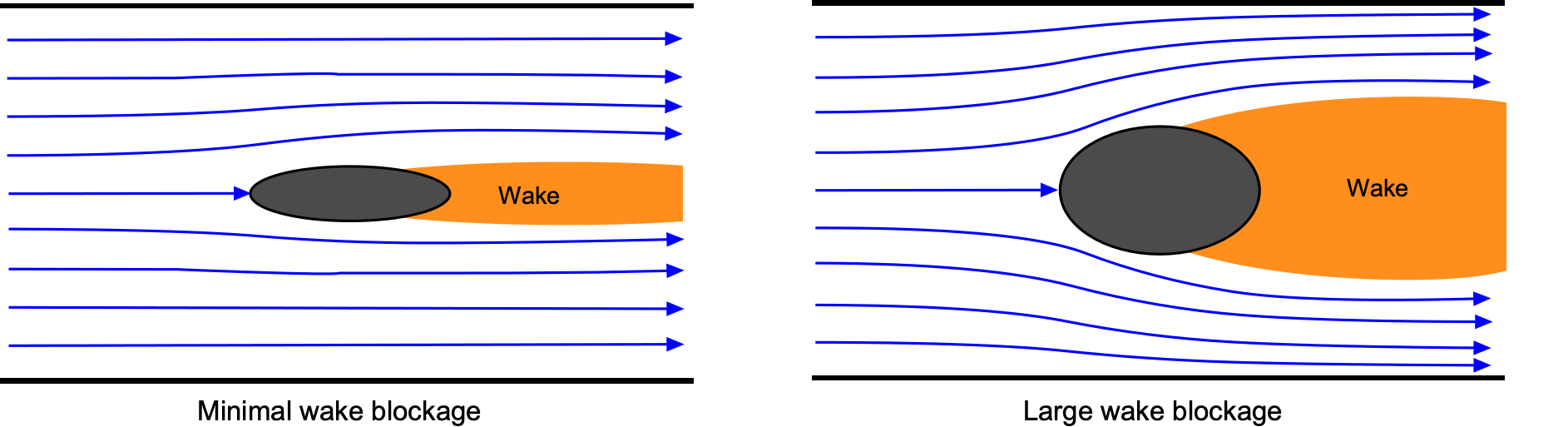
Consider steady, incompressible flow of density in a test section of area with nominal freestream speed . Let the model have reference area and drag coefficient defined with respect to , so that

(31)  

where is the blockage ratio. The integral form of the momentum equation can now be applied to a short control volume that spans the test section and encloses the model and its wake. If wall friction inside the control volume is small and the section area is nearly uniform so that the change in bulk kinetic-energy flux is small compared to the pressure forces, the streamwise momentum balance gives

(32)  

and

(33)  

Referencing pressures to the freestream dynamic pressure , the associated order-of-magnitude bias in pressure coefficient is

(34)  

In practice, the pressure field distortion is not perfectly uniform. Facilities often embed the semi-empirical factor to account for details such as wall boundary layers, nonuniform wake profiles, mild streamwise area changes, and modest compressibility, i.e., , so that

(35)  

Here denotes the pressure coefficient corrected for the nearly uniform offset induced by wake blockage. When is unknown, an iterative approach can be used. This is done by first estimating from the uncorrected data, then applying Eq. 35 to compute , and then repeating until convergence.

It is essential to distinguish wake blockage from solid blockage, and their effects have different corrections. Recall that solid blockage originates from inviscid acceleration and streamtube contraction around finite-thickness or bluff bodies, even in the absence of viscous drag. Wake blockage, by contrast, is tied directly to the momentum deficit produced by viscous separation and bluff-body drag. The two effects are additive in the limit of small , and comprehensive tunnel corrections typically include both, together with model-support interference and, at higher Mach numbers, mild compressibility corrections. For most streamlined models at low values of , the leading bias to from wake blockage scales with as in Eq. 34. Therefore, while solid blockage can exist without much wake effect, wake blockage cannot occur without some degree of solid blockage.

Boundary (Wall) Interference

Boundary interference occurs when the flow induced by the model interacts with the solid walls of the test section, producing streamline curvature and local acceleration absent in free flight. For a finite wing or a model such as an airplane, a useful nondimensional measure is the generalized confinement ratio given by

(36)  

where is the wing span, the test-section width, the model’s height, and the test-section height. Typically, to avoid wall interference effects.

Classical wall-interference theory models the presence of walls using the image method, which originates in Glauert’s lifting-line theory. The mirror systems in the lateral and vertical directions induce a modified value of the upwash at the wing, as shown in the schematic of Figure 44. Using this as a basis, NACA developed methods and formulas that express the tunnel-free-air difference as a correction proportional to the model’s lift and to a geometry factor built from the confinement.^[6]

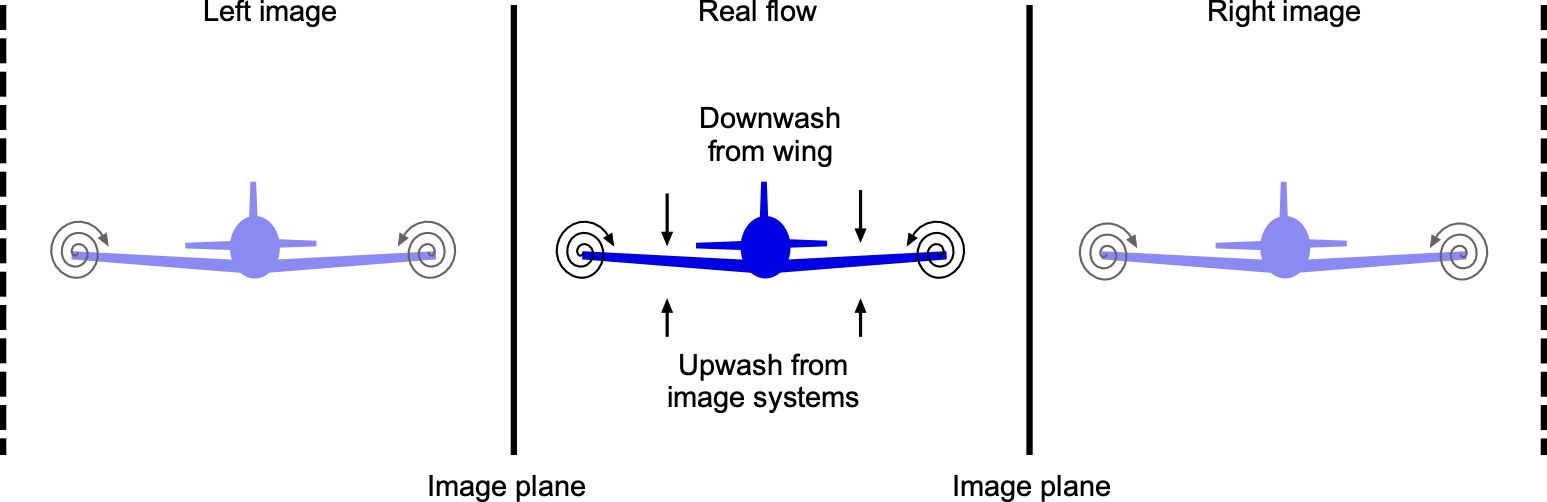
To a first order, for a model with a wing centered in the section and for small , then

(37)  

where and , with Glauert’s compressibility factor . This form represents the limiting case of the more general solutions and directly shows how wall-induced upwash increases with confinement.

The induced upwash increases the model’s effective angle of attack in the tunnel; thus, at a fixed geometric angle, the measured lift is greater than in free air. Using the free-air slope , then

(38)  

Equivalently, the apparent lift curve slope in the tunnel will be

(39)  

Therefore, the results can be interpreted as an apparent increase in the lift-curve slope, or, in lifting-line terms, as if the wing had a higher effective aspect ratio. A one-to-one mapping to an “effective aspect ratio” is not unique, but the interpretation highlights that wall interference alters the apparent aerodynamic efficiency.

Because the corrections scale with and by , the assumption of free-air conditions deteriorates rapidly once the model gets big relative to the test section, as shown in Figure 45. Experience has established that, for typical low-speed tunnels and finite wings, keeping holds the interference within a few-percent envelope so that normal linear corrections are reliable.

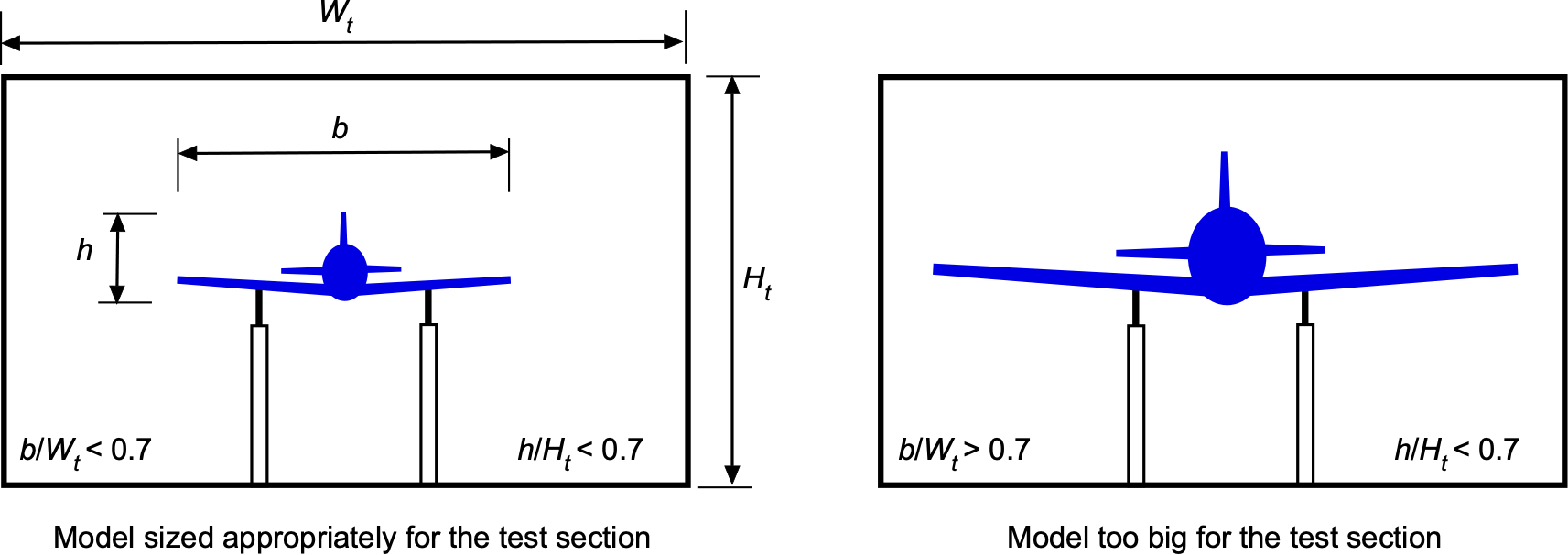
For example, if a wing has a span = 1.0 m in a = 1.5 m test section, then = 0.67, and so this is acceptable. Increasing these values further will produce noticeable wall-interference effects, necessitating corrections. As approaches or exceeds 0.8, the required corrections become large and increasingly nonlinear, and the basic first-order relations lose accuracy. In such regimes, the recommended remedy is to reduce confinement (e.g., by using a smaller model or a larger section) rather than relying on higher-order solid-wall corrections.

It should be noted that this confinement-ratio criterion applies primarily to lifting wings and surfaces. For bodies of revolution or non-lifting shapes, the more relevant measure is the blockage ratio based on frontal area, which is typically kept below about 5% of the test-section cross-sectional area to ensure acceptable free-air conditions.

Horizontal Buoyancy

Wall interference also encompasses the effects of longitudinal and vertical gradients in fluid density, pressure, or temperature in the test section, which generate buoyancy forces. The and buoyancy forces on an elemental volume from pressure gradients is

(40)  

Such gradients can arise from boundary-layer growth along the walls of the test section, as illustrated in Figure 46. For an axisymmetric body of length and frontal area , the horizontal buoyancy drag increment becomes

(41)  

In most tunnels, the longitudinal pressure gradient is designed to be negligible or slightly negative, so is positive and acts as a positive drag tare, which can be corrected for.

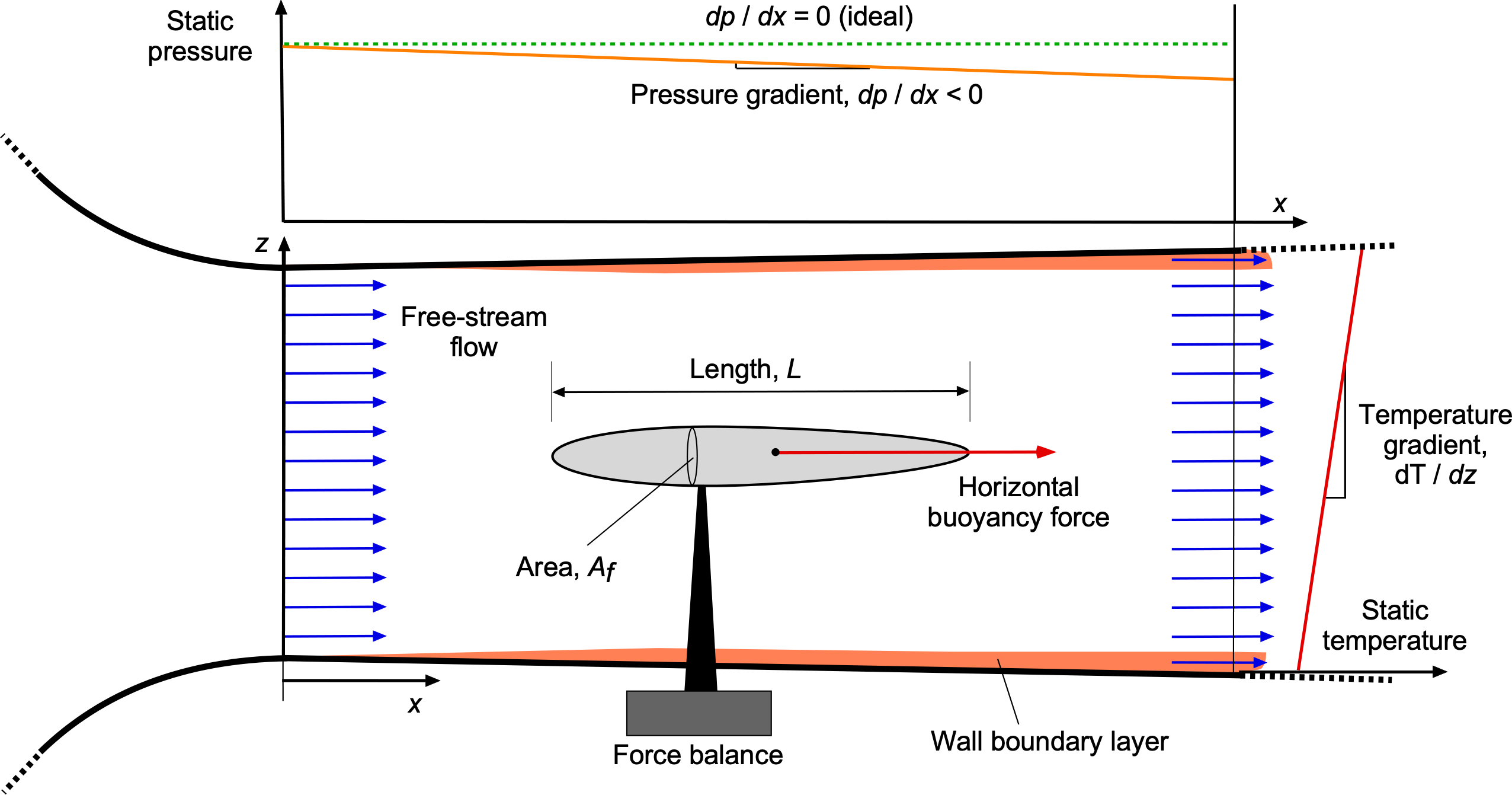
Vertical pressure gradients in wind tunnels are usually negligible. However, temperature and density gradients can also contribute to this phenomenon. For example, solar heating of the tunnel shell may introduce a vertical temperature gradient . Using the equation of state together with the hydrostatic relation, then

(42)  

and the resulting horizontal buoyancy drag tare is

(43)  

Although generally small in most wind tunnels, such taring effects can be significant in precise drag measurements.

Boundary Layer Growth

A source of wall interference related to horizontal buoyancy effects is the growth of boundary layers on the test-section walls, as shown in Figure 47. As the flow develops downstream, viscous effects reduce the effective cross-sectional area, thereby increasing the core-stream velocity. To correct for this, the displacement thickness is introduced, i.e.,

(44)  

where is the boundary layer thickness, is the local velocity, and the freestream velocity.

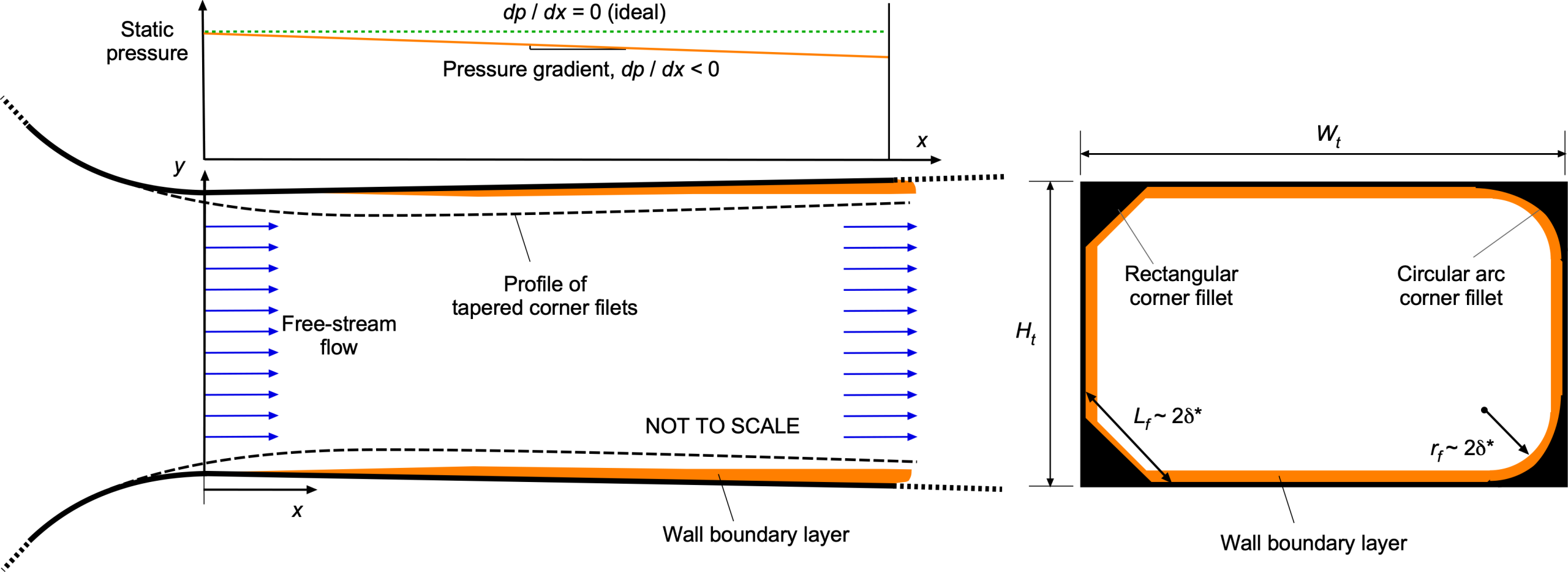
For a rectangular test section of width and height , the effective area is

(45)  

To maintain constant mass flux, the tunnel geometry must expand at a rate that offsets the displacement-blocked area, i.e.,

(46)  

Neglecting second-order terms gives

(47)  

Empirical estimates for turbulent layers include

(48)  

or, using the one-seventh power law, then

(49)  

A practical criterion for sizing the test-section corner fillets is to relate them to the boundary-layer displacement surface. The underlying principle is that the core flow behaves as if it were bounded by a virtual wall displaced inward from the physical wall by the local displacement thickness, . At the downstream end of the test section, this offset may be expressed as .

For a circular arc fillet, the virtual flow boundary corresponds to a circle of radius . To ensure that this virtual boundary is not smaller than that defined by the two intersecting straight walls, the following condition must be satisfied

(50)  

from which it follows that

(51)  

For a straight chamfer, providing clearance for the virtual boundary at the corner point leads to the requirement

(52)  

Adherence to these geometric constraints promotes improved flow uniformity within the test section and minimizes the development of longitudinal pressure gradients.

Powered Models

When testing powered aircraft such as VTOL configurations, helicopter rotors, propellers, and similar installations, wall interference effects can be substantial. At low freestream velocities, the rotor/propulsor wakes and entrained secondary flows tend to recirculate within the closed test section, so “free-air” measurements are effectively impossible. At higher tunnel speeds, the wakes are convected downstream, and the flow condition generally improves. However, residual pressure gradients and swirl can still bias the data if the blockage and induced velocities are significant. Powered models also add energy to the flow, reducing the pressure jump that the fan must generate. Therefore, tracking the freestream speed is essential, and sufficient time is required between test points with a powered model for the flow speed to stabilize.

Tests of scaled helicopter rotors are commonly performed in wind tunnels, as illustrated in Figure 48. However, because the tunnel walls confine the air, the flow through the rotor can differ significantly from that obtained in free air. The rotor imparts momentum to the surrounding air within a limited volume, accelerating the streamtube and wake through the test section, which may also impinge upon the tunnel floor. Consequently, the rotor experiences a modified induced-velocity environment, which generally leads to overestimation of both thrust and power relative to free-air operation. These confinement effects can be corrected analytically by applying suitable blockage and “ground-effect” factors to the measured data, thereby enabling reliable extrapolation to free-air conditions. In contrast, hover testing of rotors is typically conducted on an outdoor test stand or tower, where no corrections are necessary.

The essence of wind-tunnel corrections applied to rotor models stretches back to the work of Harry Heyson at NACA.^[7] A first-order correction for wall or blockage effects for the rotor can be expressed directly in terms of the measured quantities as

(53)  

where is the ratio of rotor-disk area to test-section area, and is an empirical constant that depends on the tunnel geometry. Typical values are for closed rectangular test sections and for open-jet tunnels. Here and denote the measured thrust and power recorded by the balance, torque, or power instrumentation, i.e., before the application of any wall corrections.

A further correction is required to account for rotor wake distortion, a form of wake blockage. At low forward speeds, the rotor wake is skewed relative to the freestream, as shown in Figure 49. The effective distance between the rotor and the floor is then based on the normal separation to the wake centerline, i.e., , where the wake-skew angle is given approximately by

(54)  

in terms of the advance ratio and the inflow ratio , where is the hover tip speed of the rotor, which is used as a reference. The term represents the mean induced velocity through the rotor disk; it is related to the total flow velocity normal to the disk, which is the sum of the freestream component normal to the disk and the induced velocity. The airspeed component normal to the disk is , where is the rotor disk-tilt angle. For steady flow, the induced velocity can be obtained from the momentum (actuator-disk) relationship, i.e.,

(55)  

where . In hover (), so that the induced velocity is

(56)  

while in forward flight, a useful approximation to the induced velocity is

(57)  

Therefore, the induced velocity governs the wake skew angle and the inflow angle at the disk.

A classic correction for the ratio of the induced velocity in ground effect to that in free air is based on the method of images and can be approximated by

(58)  

which is valid for . When the rotor is far from the floor (), the ratio approaches unity, and the ground effect disappears. Substituting into the ground-effect expression gives

(59)  

which accounts for the reduced influence of the floor as the wake becomes increasingly inclined at higher forward speeds. As the flow speed increases, the wake impinges on the tunnel floor farther downstream, and the ground-effect contribution diminishes so that at moderate advance ratios.

Therefore, the final corrections for free-air equivalents of thrust and power are

(60)  

For typical small rotors in moderate-sized tunnels, wall corrections increase the measured thrust and power by only a few percent, while the ground-effect term becomes negligible as the forward speed increases.

In forward flight, the variation of the effective wake interference factor diminishes, as shown in Figure 50. As the freestream flow increases, the wake skews back, shifting the impingement point on the tunnel floor aft. Consequently, the ground-effect factor tends toward unity as either the height ratio or the wake skew angle increases. For values of , then corrections to the thrust and power are viable. However, a better approach is to try to avoid them altogether. For example, suppose the corrected values give . In that case, certain test conditions may need to be avoided, or the applied corrections to free-air conditions may be unreliable.

If a fuselage or support body lies beneath the rotor, its projected frontal area can be included in the blockage ratio using

(61)  

where is the body’s frontal area, and is a blockage coefficient accounting for body shape and local slipstream acceleration. It is sufficient to use for bodies in closed sections, and for streamlined bodies or bodies in open-jet tunnels. Then can be used in place of everywhere the wall term appears in the corrections, i.e.,

(62)  

and so

(63)  

Another way to monitor wall interference is to install static-pressure taps along the sidewalls of the test section. Comparing the measured wall pressures with the expected uniform static level provides a direct indicator of interference: a flat distribution suggests acceptable “free-air equivalent” conditions, whereas persistent departures from ambient, axial gradients, or cross-sectional asymmetries indicate conditions in which such equivalence cannot be achieved. In these cases, mitigation may include operating at higher test speeds, repositioning the model to increase distance from the collector, using slotted or perforated walls, adding downstream bleed, or otherwise adjusting the facility setup to isolate the floor and walls from the wake.

Instrumentation & Measurement Techniques

Modern wind tunnel testing relies on a wide range of instrumentation systems to measure aerodynamic forces, surface pressures, flow velocities, and structural deformations on models. The choice of instrumentation depends strongly on the test objectives, the required level of accuracy and spatial/temporal resolution, and the flow regime under investigation.

Force and moment balances provide integrated aerodynamic loads, while pressure transducers and pressure-sensitive paints resolve surface pressure distributions. Velocity fields are measured using techniques such as hot-wire anemometry (HWA), Laser Doppler Velocimetry (LDV), and Particle Image Velocimetry (PIV), each suited to different spatial and temporal scales. Structural deformations are monitored using strain gauges, photogrammetry, or optical marker tracking, such as Digital Image Correlation (DIC), thereby enabling the measurement of aeroelastic effects alongside aerodynamic measurements.

Balance Measurements

The force balance is a fundamental instrument in wind tunnel testing because it provides direct measurement of the total aerodynamic forces and moments acting on a model. Modern balances use strain-gauge-based transducers that are carefully calibrated to resolve the six aerodynamic components: lift, drag, and side force, together with the corresponding pitching, rolling, and yawing moments. Accurate force measurement is essential because all aerodynamic coefficients ultimately derive from these balance outputs.

Balances may be either internal or external. Internal balances are mounted within the model, typically within the fuselage, and are connected to the tunnel support via a cantilevered sting. Their principal advantage is that no external support hardware is exposed to the flow, minimizing aerodynamic interference and preserving the model’s intended aerodynamic characteristics. External balances, an example shown in Figure 51, support the model from outside the test section. They are mechanically robust and can accommodate higher loads, but the associated struts and linkages introduce support interference that must be quantified and removed during data reduction.

Most balances are integrated with model-positioning systems that allow the model attitude to be adjusted remotely and repeatably. Pitch is typically imposed through controlled motion of a pitch strut, while yaw is introduced through a turntable beneath the test section. Some sting arrangements also permit roll. Automated positioning systems enable preprogrammed test sequences, improving repeatability and increasing data-acquisition efficiency.

Wind tunnel balances employ high-quality, temperature-compensated load cells (and sometimes pressure-compensated load cells) to maintain calibration stability over extended test runs. They are designed to be sufficiently stiff to avoid resonant vibration while retaining the compliance needed to resolve small force increments. In low-turbulence tunnels, where aerodynamic force changes may be small, modern balances can achieve accuracies of a fraction of a percent of the full-scale load, enabling reliable determination of aerodynamic coefficients.

Calibration Process

Before measurements can be made, force balances must be carefully calibrated. Calibration involves zeroing the balance under static load conditions and applying known forces and moments through lever arms and frictionless pulleys to establish the calibration matrix. The balance relationship can be expressed in matrix form as

(64)  

where is the vector of physical forces and moments, is the vector of measured bridge outputs, and is the calibration matrix. For a six-component balance, this expands to

(65)  

Here, the diagonal terms represent the primary (linear) sensitivity of each force or moment component to its intended load. The off-diagonal terms () represent the cross-couplings or cross-sensitivities, where a load in one axis induces a measurable response in another channel. The matrix is typically diagonally dominant, with cross-couplings at least two orders of magnitude smaller in well-designed balances.

The calibration process is conducted by applying known loads (see Figure 52), while a data acquisition system records the balance outputs . The relationship can be written as

(66)  

where maps the applied forces to measured voltages. The desired matrix used in testing is then obtained from the numerical inverse, i.e.,

(67)  

which is a trivial computation. Least-squares methods are typically used to ensure that both the main-diagonal sensitivities and the off-diagonal cross-coupling terms are faithfully represented in the calibration matrix.

Mounting Configurations

Wind tunnel models can be mounted in several ways, depending on the model’s size, the type of balance used, and the aerodynamic objectives of the test. Common arrangements include single- and two-strut systems as well as sting mounts, each typically incorporating some form of tail strut, as shown in Figure 53. In strut systems, the tail strut connects to the model positioning system so its vertical motion changes the model’s angle of attack. Strut systems are mechanically robust and can support relatively large or heavy models; however, the exposed struts introduce interference drag and may perturb the local flow field around the model, which must be accounted for during the data reduction.

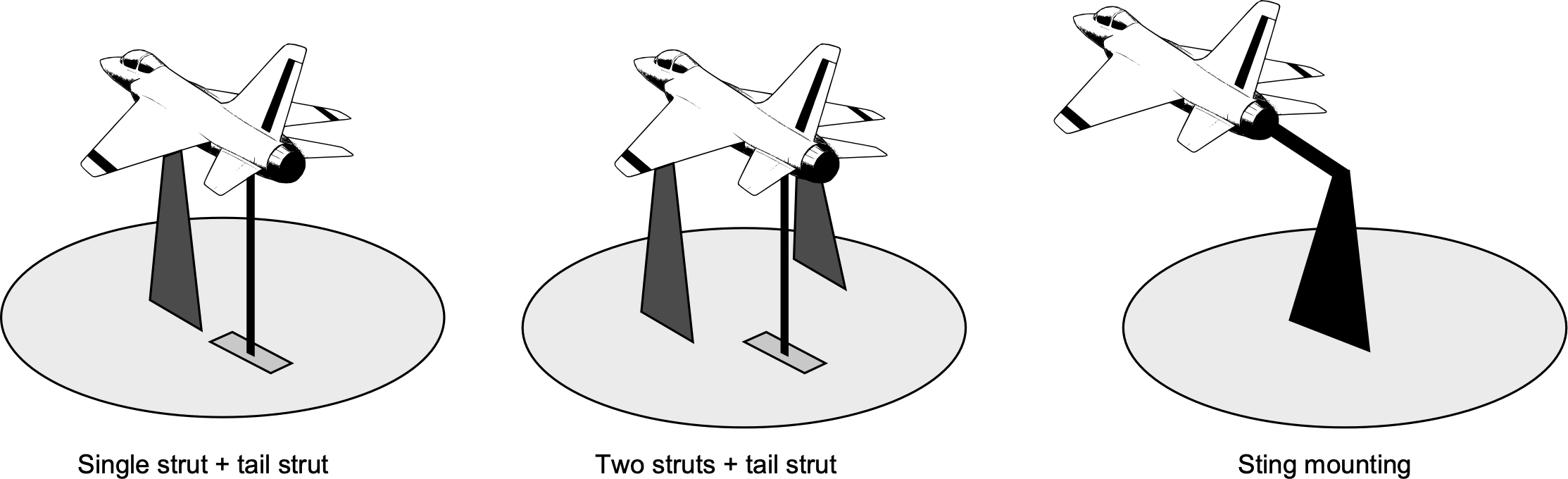
Another widely used arrangement is the sting support, in which the model is carried on a cantilevered beam projecting from a vertical support. Because the sting extends behind the model, it minimizes flow interference on the wings and fuselage forebody, providing cleaner aerodynamic data. Stings are often used with internal balances mounted inside the fuselage. The disadvantages are that the sting must be very stiff to resist bending and vibration, thereby limiting its use to models of moderate weight. Strut mounts are favored for stability and control studies or when larger forces must be carried, whereas sting mounts are preferred when minimizing support interference is critical. Sting mounts can also be integrated with a model positioning system.

Figure 54 shows a wing mounted horizontally on two vertical supports, which are connected to an external balance. A tail strut, connected to the model-positioning system, is used to set the angle of attack. These support systems introduce aerodynamic tares that appear in the balance loads. The primary supports are covered with streamlined fairings to reduce direct aerodynamic drag, but some exposed hardware remains, and the effects on the measurements must be quantified. The fairings are generally not extended to the model because doing so can introduce additional flow interference and restrict the model’s motion within the positioning system. Although support tares are usually small, they must be determined through a standard tare procedure and subtracted from the balance measurements to obtain forces and moments representative of the model alone. Most of these tares appear in the drag measurements.

Models can also be mounted vertically on the turntable, as shown in Figure 55, where the angle of attack of the wing is obtained from yaw movements. To reduce the influence of the tunnel floor boundary layer, the wing is mounted on an offset plug with a splitter plate. This arrangement also mirrors the other half of the wing panel, using the method of images in potential-flow analysis. A small clearance gap is required to allow free movement, but it can be sealed with a thin application of hydraulic grease to prevent leakage and flow disturbances that would otherwise disrupt the boundary layer.

Tares

There are two types of tares: gravity (or weight) tares and aerodynamic tares. Accounting for the gravity tare is relatively straightforward. After the model is mounted, the balance can be re-zeroed. However, as the model moves within the positioning system, the gravity loads change; therefore, a zero reading must be taken at each position (e.g., pitch and/or yaw angle). The gravity tares are then saved and can be automatically subtracted in the data acquisition system from the wind-on loads on the model at each position.

However, accounting for aerodynamic tares is more involved. There are two types of aerodynamic tares: (1) a direct tare, such as the drag on a support post or tail strut, and (2) an interference tare where the supports modify the flow about the model and the model modifies the flow about the support. Both effects are included in wind-on measurements using an external balance and can affect all forces and moments. The most significant effect is usually on drag, but for models tested at high angles of attack, all components may be affected.

The procedure for determining aerodynamic tares involves three steps, as illustrated in Figure 56 below. The first step is testing the model in a normal upright position on the support post(s), so that

(68)  

where is representative of one of the force (or moment) values. The value of is what is needed, namely the aerodynamic effects produced on the model alone without the effects of the supports. The aerodynamic tare of the lower (L) supports adds to this value, so the balance measures the total force .

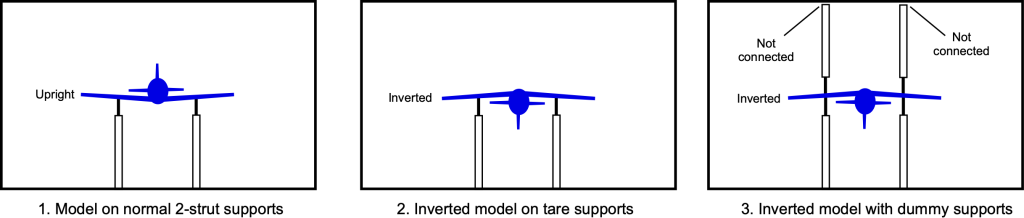
In the second step, the model is inverted on the support post(s), and the tests are repeated. Mountings must therefore be installed on both the upper and lower surfaces of the model. Only in exceptional cases where the aerodynamic tares are already known from a prior calibration, or where reliable symmetry assumptions can be made, can this step be omitted. The second set of measurements is

(69)  

where is the balance value obtained from the model in the inverted position, and is the aerodynamic tare from the supports now acting on the upper (U) side of the model.

In the third step, the model is tested in the inverted position with a dummy “image” support post, wind fairing, and pitch-rod system installed. The dummy “image” post is connected to the model but not to the ceiling plate, which mimics the additional aerodynamic effects of the lower (L) supports on the model when it is in the normal upright position. In this case,

(70)  

Subtracting from gives

(71)  

Therefore, the effects of the lower supports are

(72)  

Returning to the upright measurement in Eq. 68, the aerodynamic force on the model alone is obtained from

(73)  

One can be forgiven for concluding here that two wrongs are being used to make a right.

The aerodynamic tares also depend on wind speed, so unlike gravity tares, a different aerodynamic tare file is required for each wind speed. These tare data are typically applied during post-processing to obtain corrected data that represent only the model aerodynamics, without the aerodynamic effects of the supports. Although many assumptions underlie this method, including the validity of superposition, it has been found to perform well for wings and other models at low angles of attack, as evidenced by comparisons with measurements obtained using sting balances.

Balance Measurement of Unsteady Aerodynamics

Unsteady aerodynamic loads may be required in some wind-tunnel investigations, including dynamic stability and control studies, forced-oscillation testing to determine aerodynamic damping derivatives, and validation of unsteady aerodynamic models. Fighter airplanes, for example, exhibit different aerodynamic responses because of maneuvers made at high rates and high angles of attack. In such tests, the model is driven through a prescribed motion at a finite rate, typically in pitch and/or yaw, and the resulting time-varying forces and moments are measured with the balance; see Figure 57. This balance can be internal or external, although the two differ somewhat in their mechanical behavior, as previously mentioned.

The objective is to isolate the aerodynamic loads associated with imposed motion from all non-aerodynamic contributions introduced by the balance and model support system. When a model is moved at a finite rate in a wind tunnel, the balance measures not only the aerodynamic loads but also the inertial and gravitational loads associated with the imposed motion, as well as any transient mechanical response of the balance and support structure. If the motion rates and frequencies are kept sufficiently low and well separated from structural or balance resonances, the balance and support system behaves essentially as a quasi-static transducer, and the dynamic distortion of the measurements may be assumed to be small.

Low Rates of Change

As a practical guideline, to ensure a quasi-steady aerodynamic behavior^[8]the reduced frequency should generally be less than about 0.05, where is the oscillation frequency, is a characteristic length scale for the model (such as chord), and is the tunnel flow speed. For non-oscillatory motions, the corresponding non-dimensional pitch rate should typically be less than about 0.01, where is the maximum pitch rate. In this case, the measured loads may be written with the assumption of linear superposition without any aerodynamic transfer function as

(74)  

where represents the aerodynamic forces,^[9]  represents the rigid-body inertial and gravity contributions, and represents the transient response of the balance and support system.

For a model of mass with inertia tensor , translational acceleration , and angular acceleration about the pitch axis, the non-aerodynamic rigid-body loads referred to the balance reference center will be

(75)  

for the forces. For the corresponding moments, then

(76)  

where is the gravity vector resolved in the body axes and is the vector from the balance reference center to the center of gravity. These terms can be calculated directly from the prescribed motion and are useful for estimating the magnitude of motion-induced loads; however, they are not typically used for direct correction.

In practice, the approach to making unsteady airload measurements is to first perform identical motion schedules on the model with the wind off. The resulting measurements provide a complete time-varying gravity and motion-induced tare, i.e., all non-aerodynamic contributions to the balance output, including inertial loads and the transient response of the balance and support system. Therefore, the tare force can be expressed as

(77)  

This is now a time-dependent tare and would typically be repeated several times to obtain an average. The corresponding wind-on measurements may be written as

(78)  

The unsteady aerodynamic loads by themselves are then obtained by subtraction of the motion tare using

(79)  

For sufficiently low motion rates and/or frequencies, the transient response term is usually small and repeatable,^[10] so subtraction of the wind-off tare effectively removes all non-aerodynamic contributions. Under these conditions, the balance behaves as a quasi-static transducer with an effective transfer function close to unity over the range of interest, and no further dynamic correction is normally required.

High Rates of Change

At higher rates of change, the same motion-induced tares described previously will remain present, but the balance can no longer be treated as a quasi-static measurement device. The balance and mounting system will exhibit a transient dynamic response, so the measured loads can no longer be assumed equal to the instantaneous applied loads. Instead, the balance behaves as a linear dynamic system that filters the combined aerodynamic and motion-induced loads. The problem then becomes one of dynamic calibration and inversion rather than simple, time-dependent tare subtraction.

The measured loads may be written using the Duhamel convolution integral, i.e.,

(80)  

where is a dummy time variable of integration, is the impulse-response matrix of the balance and mounting system, and is the total applied load on the model, i.e., the sum of aerodynamic and motion-induced (inertial and gravity) loads. In the time domain, represents the dynamic characteristics of the balance and its mounting system. In principle, may be obtained experimentally using an impulse (or “bonk”) test performed with the wind off, in which a short-duration applied load approximates a delta function and the measured response yields the impulse response directly. Experienced wind-tunnel engineers often use a suitably sized wooden baton to strike an appropriate part of the balance in a controlled, repeatable manner. The corresponding transfer function is then obtained from the Fourier transform of using standard signal-processing tools.

In the frequency domain, the equivalent relationship becomes

(81)  

where is the transfer function of the balance and support system. As the excitation rates and/or frequencies increase, will depart from unity, depending on the balance design, producing amplitude distortion and phase lag in the measured loads. Therefore, the total applied load (aerodynamic plus inertial and gravity contributions) is obtained by inversion, i.e.,

(82)  

with determined from a wind-off dynamic calibration of the balance and mounting system over the frequency range of interest. In practice, a dynamic shaker is generally required to characterize the response in a controlled manner over the required frequency range.

For a prescribed sinusoidal motion at excitation frequency , the amplitude and phase of each measured channel are extracted synchronously using its complex Fourier coefficient, i.e.,

(83)  

with the integral averaged over multiple cycles to improve the signal-to-noise ratio. After dynamic correction, i.e.,

(84)  

gives the total applied load, i.e., the aerodynamic plus the motion-induced loads.

To isolate the aerodynamic contribution, the identical motion program is repeated with the wind off. After applying the same dynamic correction to both data sets, the wind-off loads are subtracted from the wind-on loads so that

(85)  

This procedure extends the same motion-tare methodology used in the quasi-static regime to cases in which the balance’s dynamic response must be removed via transfer-function inversion.

Such dynamic calibrations of force balances are not straightforward and are constrained by the motion system’s bandwidth and fidelity, as well as by load constraints on the balance itself. Additionally, considerable effort is required not only to make the measurements but also to process the data, which must be performed at each model position. Care must be taken to avoid overstressing or damaging the balance during any form of transient or dynamic excitation, so reliable identification of is generally confined to modest load amplitudes and to a restricted frequency range that is well below any dominant structural and actuator dynamics or load limits. In some cases, the balance load limits may be reached before the balance’s dynamic response can be fully quantified. Fatigue limits on the balance may also constrain the ability to perform unsteady measurements.

Pressure Measurements

Steady and unsteady aerodynamic loads on models can be determined using surface pressure measurements. These pressures are traditionally measured using arrays of small pressure taps drilled into the model surface and connected to hypodermic tubes. The taps are typically arranged along chordwise and spanwise lines, as shown in Figure 58, enabling reconstruction of pressure distributions over the wing, tail, or fuselage. The taps must be as small as possible to avoid interfering with the boundary layer and may be staggered so that no one tap is immediately behind another.

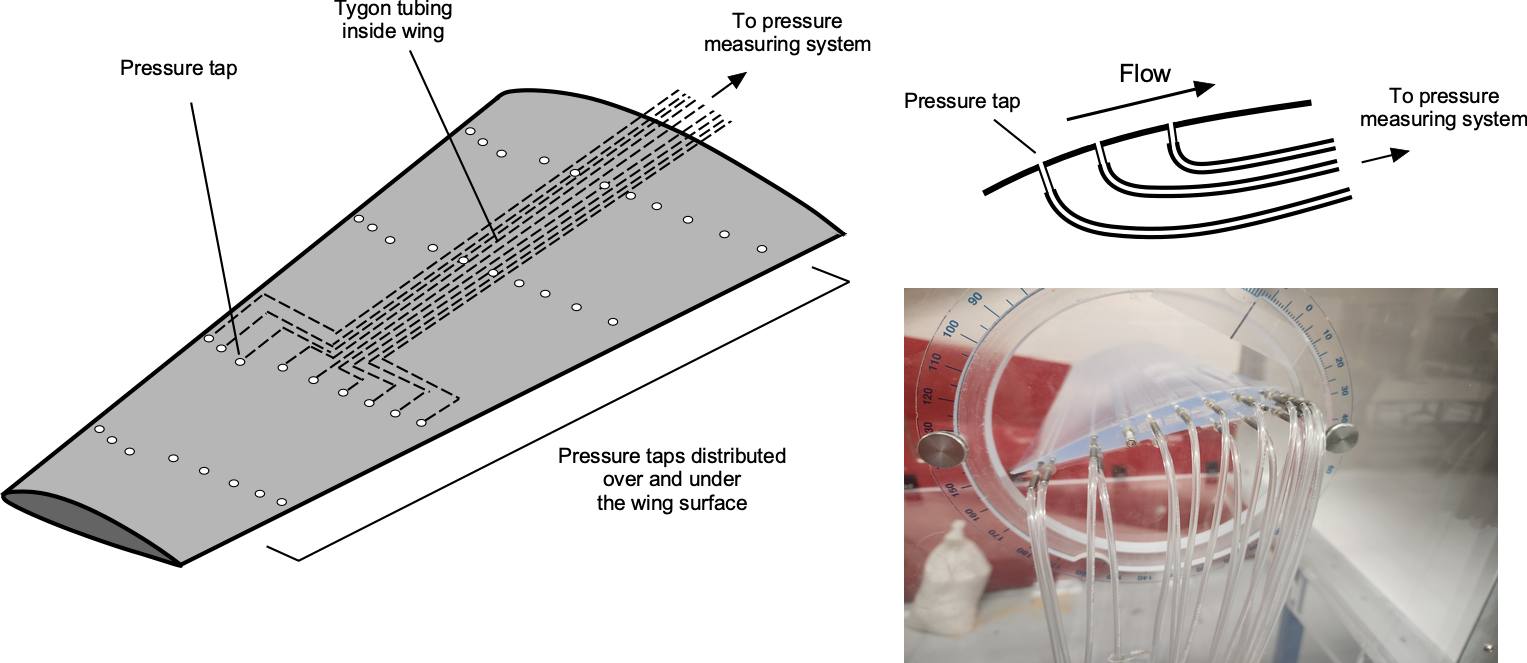
Each tap is then connected via fine Tygon tubing to an electronic pressure transducer or pressure scanner (see Figure 59), which converts the pressure into a digital signal for acquisition and processing. Modern electronic scanning systems can handle tens or hundreds of pressure taps simultaneously, enabling rapid, automated mapping of pressure fields. The modules include signal conditioning and analog-to-digital conversion, so they must be connected to a computer via an Ethernet cable.

For unsteady or high-speed flows, conventional tubing systems may introduce phase lag and damping. In such cases, fast-response transducers are mounted close to the surface to minimize pneumatic delay, thereby enabling accurate measurement of rapid pressure fluctuations, such as those in buffet, vortex shedding, or aeroacoustic studies. In this case, each transducer is connected to a suitable signal-conditioning system before being digitized and stored in a computer. Each pressure transducer must be individually calibrated, typically conducted in situ by applying a known pressure to each pressure port; see Figure 60.

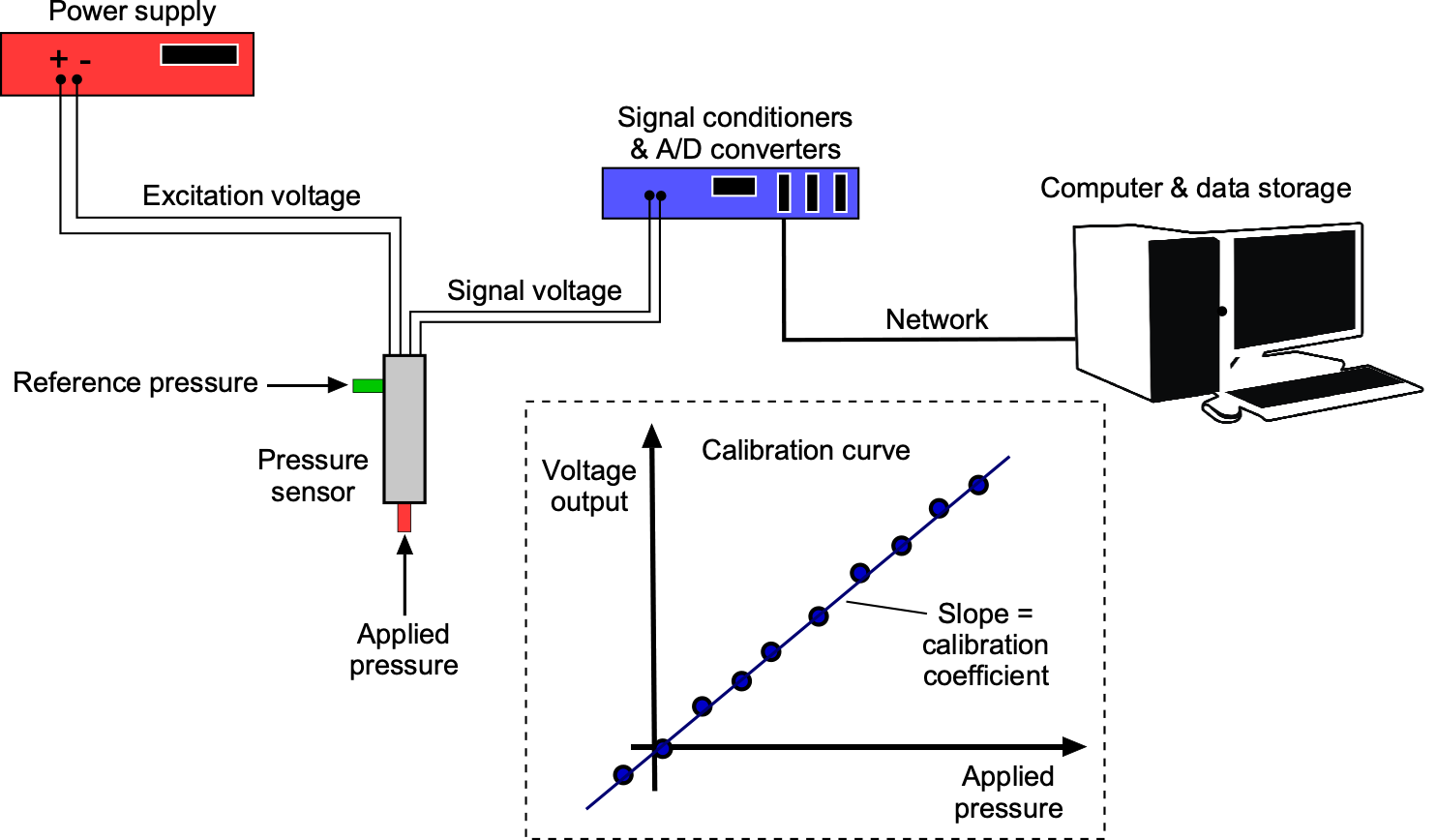
In recent decades, pressure-sensitive paint (PSP) techniques have become increasingly valuable. PSP is applied as a thin, luminescent coating onto the model’s surface. When illuminated, its emission intensity varies with the partial pressure concentration of oxygen, which is directly related to the surface pressure. The pink paint shines (Figure 61) when exposed to blue light, glowing brighter or dimmer depending on the air pressure in the area. This method provides full-field pressure maps with high spatial resolution, allowing detailed visualization of flow structures that would be difficult to measure with discrete taps alone. However, PSP requires careful calibration, is sensitive to temperature, and typically demands low-turbulence optical environments for best accuracy.

Flow Visualization

Flow visualization techniques are widely used in wind tunnels, in conjunction with quantitative measurements, to provide deeper insight into aerodynamic behavior. These methods are among the most immediately satisfying measurement approaches because they reveal features such as boundary-layer separation, vortex formation, shock structures, and streamline patterns. These features may not be apparent from force or pressure data alone, thereby enhancing both experimental interpretation and the communication of results, such as in reports and papers.

Smoke & Dye Injection

Smoke and dye injection methods introduce visible tracers into the flow to highlight streamline paths, vortex shedding, or regions of recirculation. Smoke filaments or dye streaks make unsteady structures directly observable, though seeding can sometimes disturb delicate low-speed flows. Figure 62 shows a scale model of an F/A-18 aircraft inside the NASA Dryden Flow Visualization Facility. Colored dyes are pumped through tubes equipped with needle valves, then released at strategic points on the surface. The dyes then flow back along the airframe and over the wings, highlighting their aerodynamic characteristics.

Surface Oil-Flow Visualization

Oil-flow visualization involves applying a thin film of low-viscosity oil, often mixed with a pigment or dye, to the model’s surface. Using high-quality mineral oil with titanium dioxide powder or white emulsion paint is a common approach. As the flow shears the film, the oil is redistributed or blown off, leaving white streak patterns that reveal regions of attachment, separation, and reattachment. Painting the surface black gives maximum contrast. An example is shown in Figure 63, depicting the complex regions of flow separation on the superstructure of a generic Navy ship.

These surface patterns offer excellent insight into local shear stresses and also help researchers gain a deeper understanding of integrated aerodynamic behaviors, such as lift and drag. A fluorescent type of oil can also be used; when illuminated with ultraviolet light, it produces high-contrast patterns that enhance the visibility of subtle flow features (Figure 64). However, oil-flow methods require careful lighting and high-resolution imaging to see the details effectively. The use of filters on the camera lens for visible light further improves the contrast.

Tufts

Tufts are small strands of yarn or ribbon that are attached to the surface of the wind tunnel model, as shown in Figure 65, providing a reliable and straightforward indication of local flow direction, attachment, or separation. They are inexpensive and easy to interpret, but they provide less detail than oil-flow methods and must be applied sparingly to avoid disturbing the boundary layer. Nevertheless, they are quick and easy to apply. They can be quite helpful for identifying regions of flow separation and cross-checking other measurements, such as wings near the onset of stall, as shown in the photograph below.

A refinement of this method uses fluorescent minitufts, which are short polyester monofilament fibers impregnated with a UV-sensitive dye and affixed to the surface, as shown in Figure 66. Under flow, the minitufts align with the local direction. When illuminated by a UV flash, they fluoresce, appearing brighter and more visible, which significantly improves the clarity of flow visualization in photographs and videos.

Schlieren & Shadowgraph

Schlieren and shadowgraph techniques exploit variations in refractive index caused by density gradients in the flow, thereby making compressibility effects such as shock waves, expansion fans, and shear layers visible. Such methods are widely used in high-speed wind tunnels but can also be applied at lower speeds, depending on the flow. For example, the high-speed wakes behind jet engines and the tip vortices of propeller and helicopter rotors are often visualized using such density-gradient methods.

The connection between optical measurements and aerodynamic flow fields is provided by the Gladstone-Dale relation, i.e.,

(86)  

where is the refractive index of the gas, is the local flow density, and is the Gladstone-Dale constant. This constant depends weakly on the gas composition and the wavelength of the light used. For air at standard conditions in the visible spectrum, m/kg. Although is typically of order , it is directly proportional to , making even small density variations optically detectable.

To describe the geometry, let denote the line-of-sight (LOS) direction of the optical system, the horizontal axis in the image plane, and the vertical axis in the image plane. Small variations in refractive index bend light rays passing through the flow. For weak gradients and small deflections, geometric optics gives

(87)  

where is the ambient refractive index and is the line-of-sight coordinate. Using the Gladstone-Dale relation, these become

(88)  

These deflection angles provide the physical link between variations in flow density and the observed camera images.

In schlieren systems, these angular deflections are converted into brightness variations by a knife-edge or filter at the focal point, so even weak shocks or thermal plumes become visible. The system utilizes a point light source and one or two spherical or parabolic mirrors, which must be optically aligned with care. A single-mirror system is illustrated in Figure 67.

The quality of the alignment determines sensitivity. Even a slight misplacement of the knife edge or source can blur the image or reduce contrast. The measured light intensity is proportional to the LOS integral of the first derivative of density, i.e.,

(89)  

where is the direction perpendicular to the knife edge. By rotating the knife edge, one can choose whether to emphasize vertical or horizontal density gradients. Schlieren, therefore, highlights smooth but extended density gradients, such as those found in boundary layers, shear layers, wakes, and shock structures, with an example shown in Figure 68. With pulsed light sources or high-speed cameras, schlieren can also capture the unsteady motion of shock waves, vortex shedding, and other unsteady phenomena.

Shadowgraph systems rely on the same physical ray deflections but record the curvature of the rays instead of their angles. In practice, light passes through the test section and onto a retroreflective screen, which is designed to reflect the rays back toward their source. Retro-reflector material is available in large, self-adhesive plastic sheets, enabling its application to almost any surface. Refraction effects in the flow deflect the rays so that they no longer perfectly retrace their paths, and these deviations are imaged on the camera after passing through a beamsplitter plate. The measured intensity is proportional to the LOS integral of the second derivative of density,

(90)  

which makes shadowgraphy especially sensitive to sharp, localized gradients, such as shocks, expansion fans, and shock-boundary-layer interactions. Because the signal depends on the curvature of the density field, shadowgraph images emphasize discontinuities but may lose detail in regions of more gradual density variation.

Nevertheless, shadowgraph systems are easier and less expensive to set up than schlieren systems, require fewer optical elements (no mirrors), and provide a much wider field of view (they are not limited to the diameter of a minor) while still revealing most of the same compressible-flow phenomena. For this reason, they are widely used in supersonic and hypersonic testing, particularly where simplicity and robustness are needed.

Velocity Field Measurements

A variety of techniques are used to measure velocity fields and visualize flow structures in wind tunnel testing. Pitot-static probes provide local estimates of mean flow speed by comparing total and static pressures and remain a standard method for rapid surveys of velocity distributions. Hot-wire and hot-film anemometry enable the resolution of fine-scale velocity fluctuations and turbulence intensity, with a very high frequency response. However, they require careful calibration and are intrusive in the flow.

5- and 7-Hole Probes

Multi-hole probes are used to measure local flow direction and velocity components by resolving the pressure distribution around a small sensing head. They are especially valuable in three-dimensional flows where a conventional Pitot-static tube cannot measure the velocity vector.

A 5-hole probe consists of a central tube surrounded by four peripheral pressure ports, arranged typically in a cruciform pattern. The central port measures a stagnation-like pressure, whereas the peripheral ports sense pressure differences that vary with the yaw and pitch angles. By calibrating the probe in a known flow field, the measured pressure coefficients can be related to the local magnitude of the flow velocity and its angular orientation. 5-hole probes can therefore resolve the three velocity components () at a point.

A 7-hole probe extends this principle by adding two additional ports, usually arranged in a hexagonal pattern around the central port, as shown in Figure 69. The additional ports enhance sensitivity and angular range, thereby improving accuracy for flows with large incidence angles or strong cross-flow components. However, they cannot resolve separated regions where turbulent energy is dissipated into heat rather than appearing as recoverable pressure.

The general principle is to relate the pressure distribution on the probe head to the local flow direction and velocity magnitude. During calibration, the probe is placed in a uniform reference flow and systematically yawed and pitched through a range of angles. At each orientation, the pressures from the central and peripheral ports are recorded. Using these data, calibration functions are constructed that relate measured pressure differences to flow angles.

A common definition is to form non-dimensional pressure coefficients relative to the central port, i.e.,

(91)  

where is the pressure at peripheral port , is the central port pressure, and is the reference dynamic pressure. Suitable combinations of these coefficients, such as

(92)  

are then correlated to the local pitch angle and yaw angle of the flow. The total velocity magnitude can be obtained from the calibrated relation between the central port pressure (or a weighted average of all ports) and the reference freestream pressure. In practice, these calibration functions are stored as multi-dimensional lookup tables or polynomial fits. When the probe is used in an unknown flow, the measured pressure set is converted into velocity components (u, v, w) by interpolating within the calibration map.

Although intrusive, the probes are manufactured from very fine hypodermic stainless-steel tubing with diameters often less than a millimeter. This allows the probe head to be extremely small, minimizing flow disturbance and permitting measurements in regions with significant velocity gradients. However, pressure probes have limited frequency response because the port-tubing-transducer system acts as a low-pass filter. While they can track slow variations in flow angle or magnitude, they cannot capture the effects produced in unsteady flows. Consequently, they are best suited for steady or quasi-steady flows.

Additionally, pressure probes (multi-hole or otherwise) cannot fully resolve regions that are either completely separated or highly turbulent. In such flows, the assumptions of Bernoulli’s equation break down because total pressure is no longer conserved along a streamline. A portion of the mechanical energy is extracted into turbulent losses, which do not appear as recoverable pressure at the probe ports. Because a Pitot probe relies on interpreting measured pressure distributions to infer the direction and magnitude of velocity, it loses validity when flow separates.

This limitation can be expressed directly from the mechanical energy equation. For steady, incompressible flow along a streamline without losses, Bernoulli’s equation is

(93)  

Here, any change in velocity is reflected as a corresponding change in pressure, allowing the probe to infer the velocity vector from measured pressure differences. When separation or strong turbulence is present, however, an additional loss term must be included, i.e., in this case

(94)  

where represents the irreversible conversion of mechanical energy into turbulence and heat. In terms of stagnation pressure, then

(95)  

showing that the total pressure sensed by the probe is reduced. Because the calibration of 5- and 7-hole probes assumes negligible loss, the pressure distribution no longer maps uniquely to a velocity vector.

Multi-hole probes are robust and relatively easy to use. However, they require careful calibration, have a limited frequency response compared to optical or hot-wire methods, and can still perturb sensitive flows. Their use in unsteady or separated flows (e.g., wakes) should be avoided. Despite their limitations, they remain widely used in wind tunnel applications to map three-dimensional flow fields with reasonable accuracy.

Hot-Wire Anemometry (HWA)

A minimally intrusive measurement technique widely used in experimental aerodynamics is Hot-Wire Anemometry (HWA), which can be used for resolving velocity fluctuations, particularly in turbulent flows. The method relies on the principle that the convective heat loss from a thin, electrically heated wire is directly related to the local flow velocity.

A very fine wire (often platinum or tungsten, with a diameter of a few microns) is electrically heated to a temperature above ambient air temperature. They are available in single-, two-component, and three-component forms. An example of a three-component wire is shown in Figure 70, where the wires are supported between two prongs. As airflow passes over the wire, it cools it by forced convection. To maintain a constant temperature (CTA = Constant-Temperature Anemometer) or to measure the changing resistance (CVA = Constant-Voltage Anemometer), the electrical circuit must supply power in proportion to the local flow velocity.

The response depends on the heat-transfer relationship from the wire, which can be written as King’s law to empirically relate the mean square of the wire voltage to the velocity magnitude, i.e.,

(96)  

where is the measured voltage across the wire, is the local velocity, and , , and are calibration constants determined experimentally, usually by calibrating in a small jet flow.

Because of the wire’s minimal thermal inertia, hot-wire anemometers can resolve velocity fluctuations at very high frequencies (tens of kHz or higher), making them extremely useful for turbulence research. However, the technique is limited to gases, requires careful in situ calibration, and the fragile wires can break easily in high-turbulence, dusty, or particle-laden flows.

Laser Doppler Velocimetry (LDV)

Laser Doppler Velocimetry (LDV) is a non-intrusive technique that measures local flow velocities by detecting the Doppler frequency shift of laser light scattered by small seeding particles that follow the flow. Two coherent laser beams are made to intersect at a small ellipsoidal volume, forming an interference fringe pattern. As they pass through this volume, the scattered light is modulated at a frequency proportional to the component of the velocity along the bisector of the beams, and this modulation can be detected using a suitable optical element and a photomultiplier tube.

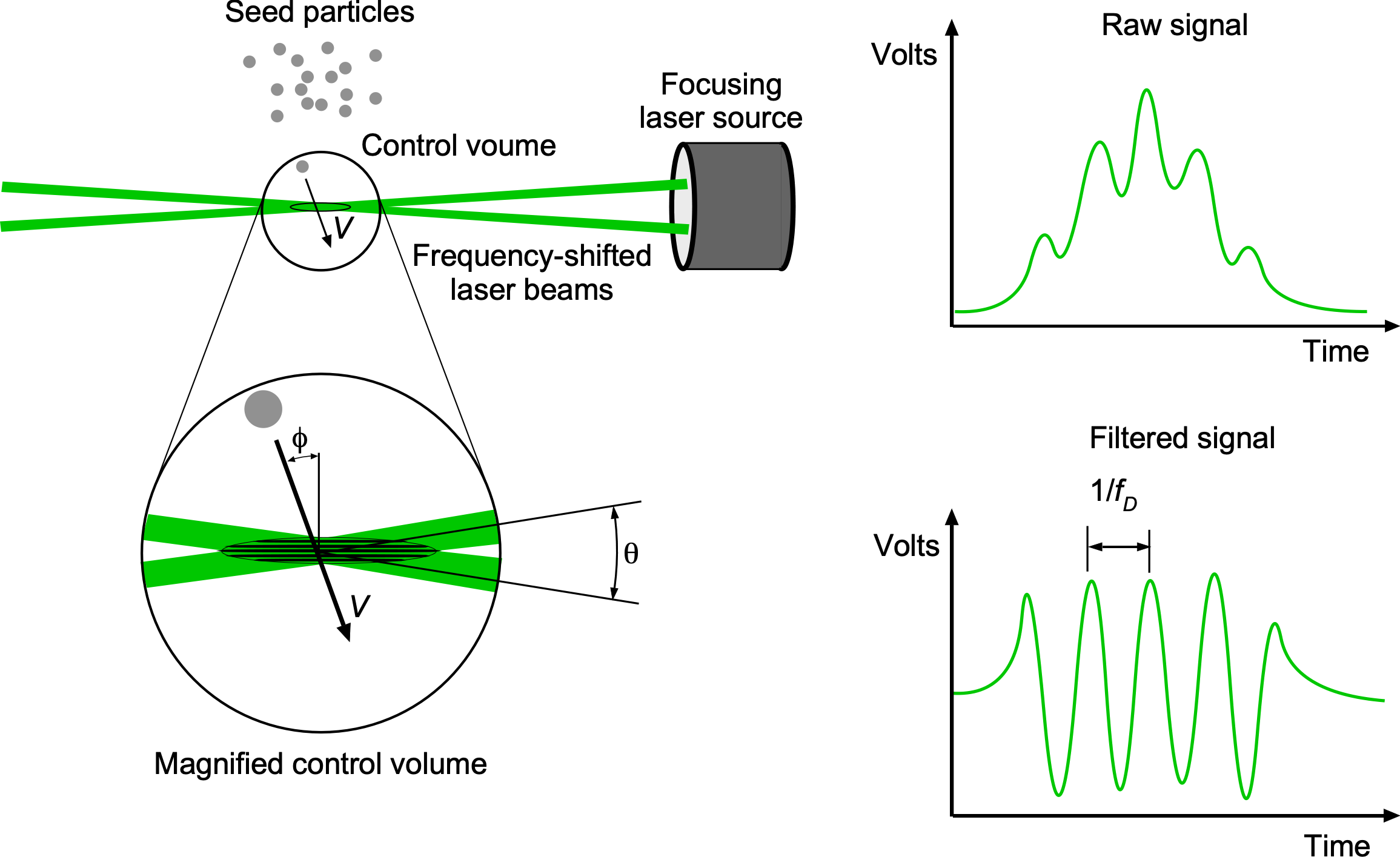
The fringe spacing is given by

(97)  

where is the wavelength of the laser beams and is the intersection angle between the beams. The measured Doppler frequency is

(98)  

where is the particle velocity and is the angle between the particle trajectory and the fringe pattern. Therefore, the velocity component along the measurement axis can be determined from

(99)  

By measuring this frequency with a photodetector, the instantaneous velocity at that point can be determined with very high spatial and temporal resolution, which is still significantly higher than currently possible with PIV.

Multi-component LDV systems are obtained by adding beam pairs created by splitting the primary wavelength (typically green) into blue, indigo, and violet components and by frequency-shifting one of the pairs. This approach allows the discrimination of direction and enables simultaneous measurement of two or three orthogonal velocity components. LDV is particularly valuable in turbulent-flow research, where accurate pointwise velocity measurements are needed without disturbing the flow field. Measurement volumes of the order of 80 m are possible, which is thinner than the thickness of a human hair.

Particle Image Velocimetry (PIV)

Particle Image Velocimetry (PIV) has largely replaced LDV and extends this optical measurement capability to entire flow fields, capturing two-dimensional or volumetric velocity maps. In PIV, small tracer particles are illuminated by a thin laser sheet and tracked between successive camera exposures, allowing velocity vectors to be reconstructed across the illuminated region. Time-resolved PIV systems can resolve unsteady flow phenomena such as vortex shedding, separation, and wake interactions. The flow is seeded with tracer particles and illuminated by a pulsed laser sheet. With PIV, two successive images separated by a small time (microseconds) are recorded by a high-resolution camera, as shown in the schematic below. The displacement of particle groups between the exposures is obtained using cross-correlation techniques, yielding velocity vectors over the illuminated region. With appropriate optics, this approach provides planar or even volumetric maps of the velocity field with excellent spatial coverage.

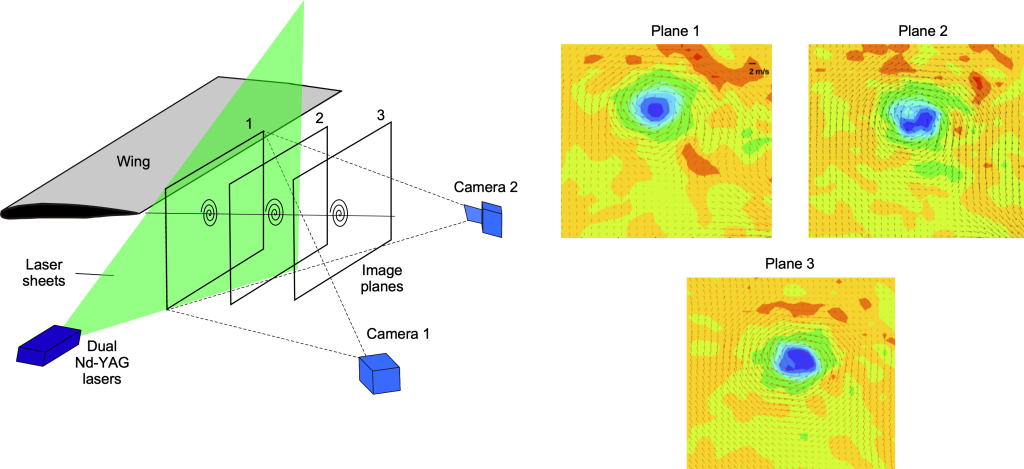
The basic relation for obtaining the velocity field from measured particle displacements is

(100)  

where is the measured particle-image displacement vector and is the known time delay between exposures, which is typically very small, of the order of 10 s. More formally, the cross-correlation function in an – plane is

(101)  

with and denoting the recorded particle images. The peak of the correlation function corresponds to the most probable particle displacement, from which the velocity field is determined after further numerical processing.

In practical wind-tunnel applications, PIV systems typically employ pulsed Nd:YAG or Nd:YLF lasers to generate the illuminating light sheet and high-resolution cameras synchronized with the laser pulses. The flow is seeded with small tracer particles, often oil droplets or smoke, that follow the local flow motion with minimal lag. Careful optical alignment and calibration are required to ensure that the illuminated plane and imaging system produce accurate displacement measurements. Modern systems can acquire thousands of image pairs per second, enabling detailed visualization and quantitative measurement of complex flow phenomena around aerodynamic bodies.

Model Deformation & Aeroelastic Measurements

For flexible or lightweight models, it is essential to quantify deformation under aerodynamic loading. Several optical and embedded-sensor techniques are available for this purpose. Stereo photogrammetry and laser scanning methods track surface displacements in real time and reconstruct changes in model shape throughout the test.

More recently, Digital Image Correlation (DIC) has become widely used for structural measurements in wind tunnels. DIC employs one or more high-resolution cameras to record a random speckle pattern applied to the model surface, as shown in the photograph below. By analyzing pairs of images with cross-correlation algorithms, full-field surface displacements and local strains can be resolved with high spatial accuracy. This non-intrusive technique enables the measurement of both static and dynamic deformations without altering the model’s structure. Conceptually, DIC is similar to particle image velocimetry (PIV). At the same time, PIV tracks seeded particles in the flow to determine velocity fields, DIC tracks speckle features on the model surface to determine deformation and strain fields.

From the measured displacement fields, strain components can be determined directly. For a three-dimensional displacement field, , the normal strain components are

(102)  

and the shear strains are

(103)  

Here, , , and represent the measured displacement components in the , , and directions, respectively.

It is essential to note that two-dimensional DIC recovers only the in-plane displacements and corresponding strain components, making it particularly suitable for thin, flat specimens viewed normal to the surface. In contrast, three-dimensional DIC employs at least two synchronized cameras to reconstruct the out-of-plane displacement , thereby enabling full recovery of the strain tensor and accurate measurements of complex structural deformation in wind tunnel models.

Complementing optical methods, strain gauges bonded to critical structural locations provide direct measurements of local strain. Modern facilities also employ fiber-optic sensors, such as fiber Bragg gratings, which can be embedded in the model to record distributed strain histories. These embedded techniques are particularly valuable for real-time aeroelastic analysis and for the development of active control systems, where rapid response to structural feedback is required.

Flutter Testing

Flutter testing in a wind tunnel is an important branch of experimental aeroelasticity, but it is also inherently risky because a failure can damage both the model and the facility. Flutter is a dynamic instability that arises from the interaction of aerodynamic, elastic, and inertial forces. When these forces act in phase, the motion can become self-excited, and oscillations may increase in amplitude until structural failure occurs. The purpose of flutter testing is to determine the flutter boundary, defined as the airspeed or dynamic pressure at which the total system damping becomes zero. Tests may also be used to assess active control systems for flutter suppression or to evaluate how changes in stiffness, mass, or aerodynamic configuration affect the aeroelastic stability.

Flutter experiments are typically conducted in transonic or high-speed subsonic wind tunnels where the flow conditions and dynamic pressures are representative of flight, as illustrated in the photograph below. The introduction of thin, highly swept wings during the 1950s raised many new concerns about aeroelastic stability and methods to prevent flutter. Flutter considerations can strongly influence the location of engines, fuel tanks, and other concentrated masses within the airframe. They also play a significant role in determining the required distribution of structural stiffness throughout the wing and fuselage to ensure adequate dynamic margins and to prevent destructive oscillations during flight. NASA Langley’s Transonic Dynamics Tunnel and ONERA’s S2Ch facility are examples of specialized facilities for this type of work. Low-speed tunnels are sometimes used for small-scale models or to investigate control-surface buzz, while supersonic tunnels are employed for missiles and slender wings.

The aeroelastic model must reproduce the essential mass, stiffness, and damping characteristics of the full-scale structure. Ideally, the model satisfies a velocity-scaling relationship that enforces dynamic similarity between aerodynamic and elastic forces. Starting from the Cauchy number, i.e.,

(104)  

where is the flow velocity, is the elastic modulus of the structure, and is the air density, dynamic similarity requires , i.e.,

(105)  

where the subscripts and denote the model and full scale, respectively. Solving for the velocity ratio gives

(106)  

This same result can be expressed in terms of the dynamic pressure , i.e.,

(107)  

The matching of (or equivalently ) is necessary but insufficient for flutter similarity. The structural dynamics must also scale so that the relevant natural frequencies and mode shapes match, i.e., the bending and torsion modes are the same. For a geometrically similar model with a characteristic length , a representative natural frequency scales as

(108)  

where is the material density of the structure. Preserving the reduced frequency , which is a characteristic length scale, such as wing chord, then introduces the additional constraint that

(109)  

Together with , this ensures that the fluid-structure time scales are matched and that the same coupled modes are engaged at flutter.

Because exact similarity in , , , and geometry is rarely attainable, models are tuned with added masses and tailored flexures so that the principal modes have the correct frequencies and shapes while satisfying, as closely as practical, the (or ) condition. In practice, wind tunnel models are often much more flexible than their full-scale counterparts, and the target is to match the modal content and reduced frequencies of the modes that participate in flutter.

During flutter testing, the wind speed is gradually increased while the model’s motion is recorded. Flutter may be excited by small shakers or by the flow itself. Measurements of displacement, acceleration, and unsteady pressure are used to determine the natural frequencies and modal damping. When the total damping becomes zero, the system reaches the flutter boundary , where is the damping ratio and is the critical dynamic pressure. Beyond this point, the oscillations may remain bounded as a limit-cycle oscillation or diverge rapidly depending on the aerodynamic nonlinearity.

Flutter testing in the wind tunnel is performed cautiously because an instability can develop suddenly. Airspeed is increased in small increments near the predicted boundary, and emergency shutdown systems protect the model and tunnel. Nets are often installed downstream of the test section to catch parts that may have detached from the model. Data must be recorded at high sampling rates to capture the onset and growth of oscillations. When the flutter boundary is exceeded, the motion may either diverge to failure or stabilize at a finite amplitude known as a limit-cycle oscillation. Failure of the model is not a good outcome, but it happens, often within a fraction of a second. Such self-sustained motions arise from nonlinear aerodynamic or structural effects and are most common in lightly damped systems. Data from wind tunnel tests are essential for validating models of this nonlinear behavior, especially for configurations with control surfaces, external stores, or other features that alter stiffness and flow separation.

Data Reduction

Raw measurements from wind tunnel tests are rarely usable in their initial form. A systematic process of data reduction and correction is essential to produce results that reflect the model’s aerodynamic behavior under idealized, free-flight conditions. This process accounts for local flow conditions, non-dimensionalization, and known tunnel effects such as wall and support interference. Through calibration, correction, normalization, and uncertainty analysis, raw measurements are transformed into high-fidelity aerodynamic data that can be compared with theory, CFD simulations, or flight tests, and scaled to full-flight conditions. The data-reduction process can take considerable time and must be accounted for when estimating the overall duration of a wind tunnel test campaign.

Non-Dimensionalization of Data

The first step is to non-dimensionalize the measured data, such as pressures, velocities, forces, and moments. Aerodynamic coefficients are normalized by the freestream dynamic pressure, as is standard. The dynamic pressure is

(110)  

where is the freestream density and the freestream velocity. For example, the lift and moment coefficients are

(111)  

where is the lift, is the pitching moment, the reference area, and the reference chord. Similar expressions define the other force and moment coefficients. Moments reported about one reference point may be transferred to another using the principles of statics, so it is essential to state the reference geometry and sign conventions.

In addition to forces and moments, pressures and velocities themselves are routinely expressed in nondimensional form to facilitate comparison between different flow conditions and configurations. Local pressures are commonly represented by the pressure coefficient, i.e.,

(112)  

which indicates the relative pressure level compared to the freestream dynamic pressure and allows pressure distributions measured on models of different sizes or at different speeds to be compared directly. Likewise, local velocities are often nondimensionalized by the freestream velocity, , thereby providing a direct measure of flow acceleration or deceleration relative to the incoming stream. In compressible flows, velocities may also be expressed in terms of Mach number, , where is the local speed of sound. These nondimensional representations allow flow features such as stagnation regions, separation, and shock waves to be identified and compared across different operating conditions without reference to specific dimensional values.

Corrections for Interference

Correcting wind-tunnel interference effects in the measured data is another essential step. Even after nondimensionalizing pressures, velocities, forces, and moments, the presence of tunnel walls and support hardware alters the flow field around the model and can bias the measured aerodynamic coefficients. Empirical correction charts or numerical models are often required to recover equivalent free-flight conditions. Most wind tunnel facilities have standard correction procedures developed over years of testing experience, and these should be followed carefully. In particular, stings, struts, and mounting brackets disturb the flow and introduce spurious forces and moments. Their contribution is quantified by tare measurements with the support hardware alone, which are then subtracted from the full-model data.

Tunnel-effect corrections typically include solid and wake blockage corrections, which account for the increase in local velocity caused by the displacement of streamlines around the model and its wake within the confined test section. Wall-interference corrections are then applied to account for changes in streamline curvature and pressure distribution induced by the tunnel walls, which can affect the measured lift, drag, and pitching-moment coefficients. Additional corrections may be required for buoyancy effects (if relevant to the force component being inferred from a balance operating in air), as well as for support-system interference from stings or struts.

Further adjustments are often needed to account for differences between wind-tunnel test conditions and the intended flight conditions. Reynolds-number corrections may be applied when viscous effects at model scale differ from those at full scale, particularly for drag and boundary-layer behavior. Compressibility corrections may be required when Mach number effects influence pressure distributions and aerodynamic coefficients, even at moderately subsonic speeds. Temperature and humidity corrections may also be applied where air-property variations affect density, viscosity, or speed of sound. In propulsion or powered-model testing, corrections may be needed for inlet distortion, jet interference, or thrust stand calibration. Balance calibration corrections and data-reduction corrections, including alignment and zero-offset adjustments, are also routinely applied to ensure measurement fidelity.

Corrections to the angle of attack are particularly important because wall interference and tunnel flow angularity can shift the effective flow direction seen by the model. The effective angle of attack may be written as

(113)  

where the correction terms are determined from facility flow-angularity surveys, calibration measurements, or in situ pressure-rake data. Application of these corrections ensures that the final aerodynamic coefficients more accurately represent free-air conditions and can be compared meaningfully with flight-test data, theoretical predictions, and computational results.

Uncertainty Analysis

Ultimately, a comprehensive uncertainty analysis is necessary. for all of the measured data. This is an important step that is often overlooked, but essential if the data are to be published. Each measured or derived quantity carries uncertainty, and these uncertainties propagate into the aerodynamic parameters and coefficients. For example, a function , the combined standard uncertainty is given by

(114)  

for uncorrelated inputs, with covariance terms added if correlations exist. In reporting, it is common to present the expanded uncertainty, i.e.,

(115)  

where is the coverage factor, typically = 2 for a 95% confidence level. This provides a transparent confidence interval around the reported aerodynamic coefficients and other data.

Uncertainties should distinguish Type A (statistical) and Type B (systematic) components and, when selecting the coverage factor , use an effective degrees of freedom (e.g., Welch-Satterthwaite) to reflect finite sample sizes and correlated inputs (notably all those entering into the values of ).

Test Planning & Execution

Let’s do a wind tunnel test! Wind tunnel testing is a time-consuming and resource-intensive activity that demands meticulous planning to yield meaningful, repeatable, and efficient results. From defining the test goals to preparing a matrix of conditions and executing the test runs, every phase must be carefully orchestrated. Wind tunnel testing is most productive when objectives, hardware, and operations are harmonized in advance. With detailed planning, rigorous execution, and careful quality control, each run will contribute reliable data to the overall campaign and maximize the value of the experimental effort.

Defining Test Objectives

The first step in a successful wind tunnel campaign is to define the test objectives clearly. These may range from measuring aerodynamic force and moment coefficients to doing PIV measurements to validate CFD predictions, examining the effectiveness of control surfaces, or studying complex phenomena such as flow separation, shock formation, or aeroacoustics. The clarity and specificity of the objectives inform the design of the test article, the choice of instrumentation, and the methods of data analysis. A carefully prepared pre-proposal is required, which can then be refined into a full proposal after input from the wind tunnel staff.

Model Design & Preparation

Model design is a balance between geometric accuracy, structural integrity, and test utility. The chosen scale and aspect ratio influence the Reynolds number and susceptibility to wall effects. A smooth surface finish ensures predictable boundary-layer development, while the internal arrangement must accommodate pressure taps, wiring, and mounting hardware. Modular construction enables rapid configuration changes, such as swapping control surfaces or simulating various flight conditions. Precision in manufacturing and documentation is critical to ensure consistency across test campaigns.

Equally important is structural design. Wind tunnel models are subjected to aerodynamic loads, inertial forces from mounting systems, and, at times, dynamic oscillations. For a drone, merely being able to fly does not guarantee it will survive a wind tunnel test without structural modifications. Stress analysis must therefore be conducted to verify that the model can withstand the maximum expected wind-tunnel loads. All wind tunnels have factor-of-safety rules. The factor of safety (FOS) is defined as

(116)  

where is the failure stress of the material and is the maximum applied stress during testing. Conservative factors of safety are typically chosen, typically ranging from 2 to 4, depending on material properties, structural complexity, and load-prediction uncertainty. Lower or higher values of FOS may be used depending on the projected risk to the wind tunnel facility.

Before any model is allowed into the test section, it must undergo thorough bench testing. Bench testing involves applying known static (and perhaps dynamic) loads to verify the structural strength, stiffness, and integrity of instrumentation under controlled conditions. This step ensures that the model will not fail catastrophically inside the tunnel, where damage to the facility and risk to instrumentation would be severe. Bench testing also allows the identification of weak points, the calibration of any strain gauges on the model, and the validation of the mounting arrangements.

Lightweight models intended for testing must strike a careful balance between stiffness and mass to avoid excessive deformation, while flexible models designed for aeroelastic studies require controlled compliance. In either case, the combined application of stress analysis, conservative safety margins, and bench testing ensures that models deliver reliable results without risking structural failure during wind tunnel operation. Flight safety strain gauges may be required and monitored during tests to ensure that loads remain below critical levels.

Instrumentation & Facility Setup

The instrumentation suite and facility configuration must always be tailored to the specific objectives of any given wind tunnel test. Careful planning and verification of the instrumentation and facility configuration, therefore, underpin the accuracy, repeatability, and ultimate usefulness of wind tunnel data. This process begins with the installation and careful calibration of balances, pressure sensors, and flow meters or probes to ensure reliable measurements. The model itself must be precisely aligned with the tunnel axis and coordinate system, as even small misalignments can introduce systematic errors in the measured forces and moments.

Freestream conditions, including velocity, temperature, and turbulence intensity, must be verified and documented before testing to establish a reliable reference state. Data acquisition systems are configured to sample at rates sufficient to measure the relevant flow phenomena, with filtering applied to suppress noise while preserving the signal content. Synchronization between model instrumentation and tunnel operating conditions is crucial, especially during tests that require measuring unsteady components.

Reference frames and sign conventions must be standardized across the test campaign. Without this discipline, even well-executed measurements can be misinterpreted. In addition, a system health check is typically performed before tunnel operation, during which the data acquisition system is operated without flow to confirm sensor zeroing, baseline stability, and the absence of electrical noise. A typical example is the reversal of angle sweeps, which can lead to systematic errors that propagate throughout the dataset if not detected during pre-test checks.

Test Matrix & Run Schedule

A detailed test matrix provides the framework for the entire experimental campaign by specifying the conditions under which the model will be evaluated. This includes the range of angles of attack, sideslip angles, and control surface deflections to be investigated, as well as the freestream Mach and Reynolds numbers to be simulated. Configuration changes, such as flap settings, external stores, or alternative geometries, must also be incorporated.

Efficient use of tunnel time requires careful scheduling beyond the primary data points. Startup and shutdown periods must be accounted for, along with tare runs to quantify the effects of support and instrumentation. Contingency plans should be in place to address unexpected model issues or equipment malfunctions, thereby preventing the waste of valuable tunnel time.

Redundancy is also an essential feature of a well-designed test matrix. Repeating selected test points at intervals throughout the campaign allows the experimenter to check data repeatability and identify any drift in instrumentation, flow conditions, or model alignment. The test matrix balances completeness and efficiency, ensuring the wind tunnel campaign produces a reliable, representative dataset while making the most of the limited facility time.

Tests that utilize optical flow diagnostics, such as particle image velocimetry (PIV), require substantial setup and calibration, including laser-sheet alignment, camera and lens calibration and mapping, timing synchronization, seeding uniformity checks, and safety procedures. This preparation often spans several days and must be explicitly accounted for in the facility schedule and resource plan, not only in the allocated run time, to avoid compressing objectives or compromising data quality.

Data Acquisition & Quality Control

During each run, data quality must be continuously monitored in real time. Force and pressure signals are examined for convergence and consistency, while anomalies such as drift, excessive noise, or sudden step changes may indicate malfunctions or setup issues. Flow visualization methods, such as smoke, tufts, or Schlieren, can reveal unexpected behavior, including boundary-layer separation, shock motion, or structural vibration that may not be immediately evident in the balance data.

Repeat runs at identical conditions are routinely performed to assess repeatability and to separate genuine aerodynamic trends from measurement artifacts. Rapid, preliminary (“quick-look”) processing during the test enables early detection of anomalies and allows the plan to be adjusted while tunnel time remains. Entire wind-tunnel campaigns have been ruined when anomalous behavior was only recognized after the tests were completed.

Summary & Closure

Despite continuing advances in computational aerodynamics, wind-tunnel testing remains indispensable for establishing aerodynamic performance and validating design assumptions. Scale-model testing inevitably involves compromises because Reynolds and Mach numbers, as well as structural similarity, cannot usually be matched simultaneously. Nevertheless, with careful experimental practice and informed interpretation, reliable aerodynamic trends and performance data can still be obtained. Measurements of forces, moments, and surface pressures remain the primary outputs of most tests. At the same time, modern optical diagnostics such as particle image velocimetry now provide detailed visualization of vortical flows, wakes, and separated regions that were previously inferred only indirectly.

Wind tunnels offer controlled, repeatable access to the physical flow field and provide measurements against which all predictive methods must ultimately be judged. Their design and operation reflect more than a century of accumulated experience in producing uniform, low-turbulence flow suitable for quantitative work. Credible results require careful attention to similarity requirements, wall and support interference, calibration procedures, and the systematic estimation of measurement uncertainty. Without such discipline, even extensive testing can yield misleading conclusions.

Successful wind-tunnel investigations depend as much on experimental methodology as on the facility’s capabilities. Clear test objectives, well-designed models, properly selected and calibrated instrumentation, and consistent data-reduction procedures are essential elements of any meaningful program. When these fundamentals are observed, wind-tunnel measurements provide the most reliable aerodynamic information available and remain the standard reference for assessing theoretical predictions and computational results.

Future aerodynamic development will continue to rely on a complementary use of computation and experiment. High-fidelity CFD can explore complex flow phenomena and extended operating envelopes, but wind-tunnel measurements remain necessary to establish physical accuracy and to anchor predictive methods in reality. Continued improvements in diagnostics, adaptive test-section technology, and automated data acquisition will enhance the efficiency and capability of experimental testing, ensuring that wind tunnels remain central to aerospace research, development, and certification.