20 Continuity Equation

Introduction

Having laid down the fundamental forms of the flow models used in aerodynamic analyses, the governing equations can now be formulated to describe fluid dynamic or aerodynamic flows. The approach uses the three physical conservation principles: mass, momentum, and energy. In this first case, the applicable physical principle is that mass can neither be created nor destroyed. The resulting governing equation is the continuity equation. It is a general governing equation valid for three-dimensional, unsteady flows and applies to all types of flows, e.g., compressible or incompressible, viscous or inviscid, steady or unsteady.

Learning Objectives

  • Know how to derive the most general form of the continuity equation in its control volume or integral form.
  • Learn how to solve simple flow problems using the continuity equation.
  • See how the continuity equation can be derived from the Reynolds Transport Equation.

Continuity Equation – Integral Form

As previously discussed, the flow model is a control volume that may either be fixed in space with the fluid moving through it (the most common application), which is called an Eulerian description of the flow, or the volume can move with the fluid such that the identical fluid particles are inside it, which is called a Lagrangian model. In either case, the physical conservation principles must be applied to the fluid inside the control volume and any fluid crossing its boundaries.

Flow Model

Consider a fixed finite control volume \mathcal{V} bounded by a surface of area S, which is in an Eulerian frame of reference, as shown in the figure below. The symbol S defines the area of the closed surface that bounds the control volume containing a fluid of volume {\cal{V}}. The control volume is abbreviated to “C.V.” and the control surface to “C.S.” All properties are allowed to vary with spatial location (i.e., with respect to x, y, and z) and in time t so that

(1)   \begin{eqnarray*} \varrho & = & \varrho ( x, y, z, t ) \\[6pt] \vec{V} & = & \vec{V} (x, y, z, t) \end{eqnarray*}

A finite control volume, fixed in space, with the fluid flowing in and out across a control surface.

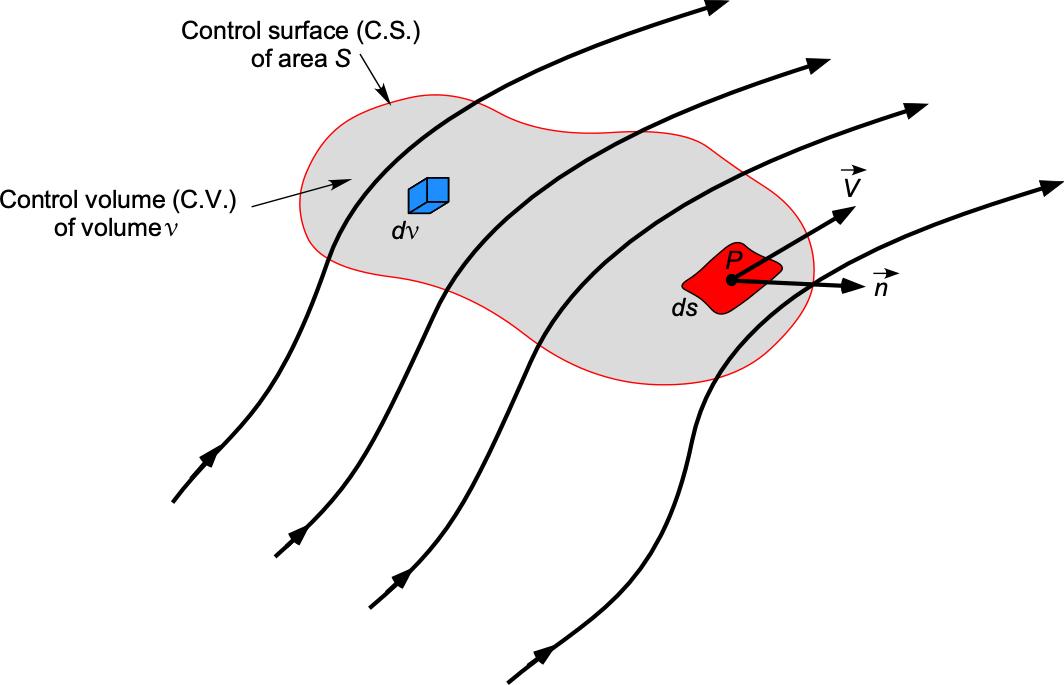
At any point on the C.S., the velocity is \vec{V}, which is given in terms of the Cartesian components as

(2)   \begin{equation*} \vec{V} = u \, \vec{i} + v \, \vec{j} + w \, \vec{k} \end{equation*}

At the same point, the unit normal vector area is d\vec{S}. Also, let d{\cal{V}} be an elemental fluid volume inside the totality of the C.V.

Conservation of Mass

The fundamental principle of the conservation of mass requires that the net mass flow out of the C.V. over surface S is equal to the time rate of decrease of mass inside {\cal {V}}. Now, that physical statement must be translated into mathematics.

Following the concept of mass flow and mass flux discussed previously, the elemental mass flow across area dS is \varrho \, \vec{V} \bigcdot d\vec{S}. Remember that by convention, d\vec{S} always points out of the C.V., so the value of \vec{V}\bigcdot d\vec{S} will be positive. Therefore, the total mass flow rate (i.e., the integral of the mass flow rate over the entire surface area) is

(3)   \begin{equation*} \text{Total mass flow rate over the C.S.} = \oiint_{\rm C.S.} \varrho \, \vec{V} \bigcdot d\vec{S} = \oiint_S \varrho \, \vec{V} \bigcdot d\vec{S} \end{equation*}

which can be physically interpreted as a net outflow leaving the C.V. Notice that the double integral here means the summation over the surface S, i.e., an area integral.

The small fluid mass contained within the elemental volume inside the C.V. is \varrho \, d{\cal {V}}. Hence, the total mass inside the C.V. is

(4)   \begin{equation*} \text{The total mass inside the C.V.} = \oiiint_{\rm C.V.} \varrho \, d {\cal{V}} = \oiiint_{\cal{V}} \varrho \, d {\cal{V}} \end{equation*}

where the triple integral means a volume integral. So, the time rate of decrease of mass inside the C.V. is

(5)   \begin{equation*} \text{Time rate of decrease of mass inside the C.V.} = -\frac{\partial}{\partial t}\oiiint_{\rm C.V.} \varrho \, d {\cal{V}} = -\frac{\partial}{\partial t}\oiiint_{\cal{V}} \varrho \, d {\cal{V}} \end{equation*}

noting that the minus sign represents a decrease of mass, i.e., what is leaving the C.V.

Because the principle of conservation of mass requires that the net mass flow out of the C.V. be zero, then Eq. 3 must equal Eq. 5, i.e.,

(6)   \begin{equation*} \oiint_S \varrho \, \vec{V} \bigcdot d\vec{S} = -\frac{\partial}{\partial t}\oiiint_{\cal{V}} \varrho \, d {\cal{V}} \end{equation*}

or

(7)   \begin{equation*} \boxed{\underbrace{\frac{\partial}{\partial t}\oiiint_{\cal{V}} \varrho \, d {\cal{V}}}_{\begin{tabular}{c} \scriptsize Time rate of \\[-3pt] \scriptsize change of mass \\[-3pt] \scriptsize inside C.V. \end{tabular}} + \underbrace{ \oiint_S \varrho \, \vec{V} \bigcdot d\vec{S}}_{\begin{tabular}{c} \scriptsize Net mass \\[-3pt] \scriptsize flow rate \\[-3pt] \scriptsize out of C.V. \end{tabular}} = 0}^{~*} \end{equation*}

This latter equation in Eq. 7 is called the continuity equation for a fluid flow, in this case, in the integral or control volume form. It is a “star” equation because it is the most general form of the governing equation, i.e., it is valid for three-dimensional, unsteady flows. It applies to all types of flows, e.g., compressible or incompressible, viscous or inviscid. In addition, it can be used to relate aerodynamic phenomena over a finite region of the flow, e.g., the properties of the flow as it comes into and leaves the specified control volume. The unknowns in the equation include the flow velocities and the flow density.

Simplifications of the Continuity Equation

Various reductions or simplifications of the continuity equation can be used to solve practical problems, and these forms also allow commensurate simplifications in the overall mathematics. For example, for a steady flow, nothing changes with respect to time, i.e., \partial/\partial t \equiv 0. This simplification means that the continuity equation reduces to

(8)   \begin{equation*} \oiint_S \varrho \, \vec{V} \bigcdot d\vec{S} = 0 \end{equation*}

In other words, the mass flow that comes into the control volume per unit of time then leaves the control volume simultaneously, i.e., no mass accumulates inside the control volume. If this assumption can be justified, eliminating time dependencies in aerodynamic problems is a significant and worthwhile simplification in most forms of practical analysis.

In the case of a steady flow, the mass flow into the control volume equals the mass flow out of the control volume.

Proceeding further by assuming that the flow is a steady (\partial/\partial t \equiv 0) single stream system and one-dimensional, e.g., a uniformly axisymmetric flow, then the reduced form of the continuity equation is

(9)   \begin{equation*} \oiint_S \varrho \left( \vec{V} \bigcdot d\vec{S} \right) = \sum_{S} \varrho \left( \vec{V} \bigcdot \vec{A} \right) = 0 \end{equation*}

where \vec{A} is the unit vector area, which is positive when it points out of the C.V., as shown in the figure below. A much easier way to express this one-dimensional result for the continuity equation is in scalar form such that

(10)   \begin{equation*} \sum_{S} \varrho \, A \, V = \overbigdot{m} = \mbox{constant} \end{equation*}

which is a statement that the summation of the mass flow rates through the C.V. is constant for a steady flow.

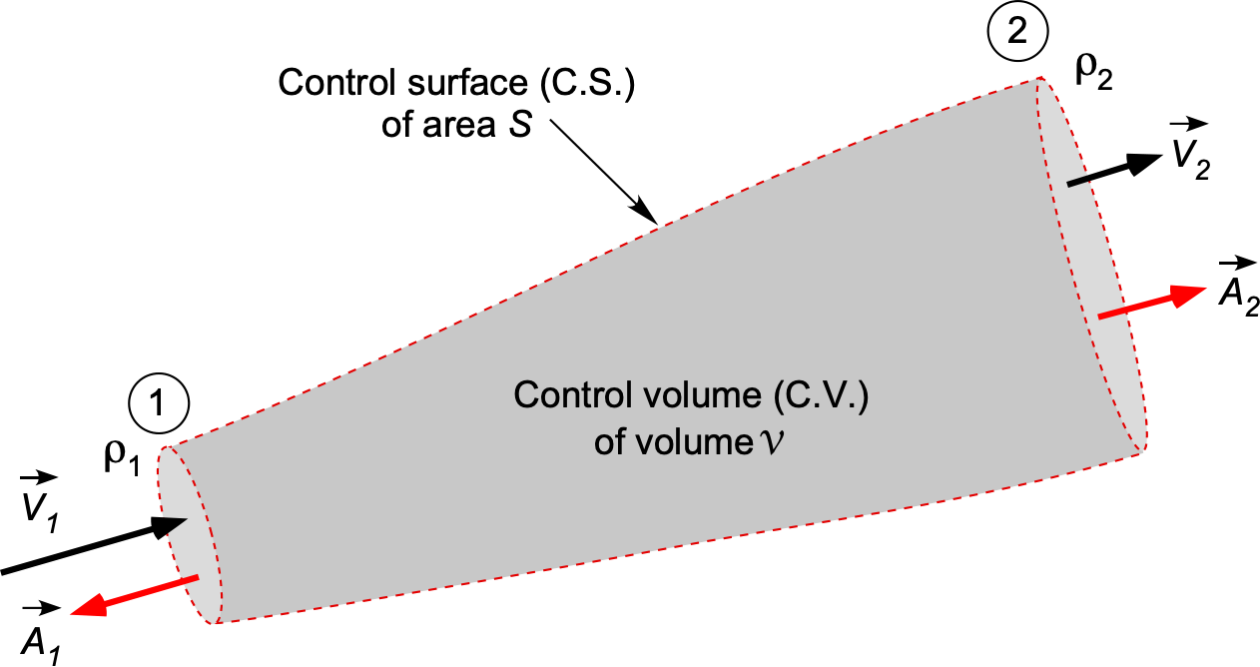
Single stream system to illustrate the principle of conservation of mass for a fluid.

For the situation of a single stream inlet and outlet, then

(11)   \begin{equation*} \sum \varrho \, A \, V = - \varrho_1 \left( \vec{V}_1 \bigcdot \vec{A}_1 \right) + \varrho_2 \left( \vec{V}_2 \bigcdot \vec{A}_2 \right) = 0 \end{equation*}

noting the sign on the first term because \vec{V}_1 is in the opposite direction to \vec{A}_1. This result can also be written in scalar form in terms of magnitudes as

(12)   \begin{equation*} -\varrho_1 \, V_1 \, A_1 + \varrho_2 \, V_2 \, A_2 = 0 \end{equation*}

or

(13)   \begin{equation*} \varrho_1 \, V_1 \, A_1 = \varrho_2 \, V_2 \, A_2 = \overbigdot{m} = \mbox{constant}. \end{equation*}

which is just a statement that \overbigdot{m}_1 = \overbigdot{m}_2, i.e., mass flow is conserved.

If the flow is incompressible, i.e., \varrho = constant, then the continuity equation becomes

(14)   \begin{equation*} \oiint_S \vec{V} \bigcdot d\vec{S} = \sum_{S}\vec{V} \bigcdot \vec{A} = 0 \end{equation*}

which leads to a further simplification because of the elimination of \varrho as an unknown. Therefore, only the flow velocities need to be related, i.e.,

(15)   \begin{equation*} Q = \sum_{S} \vec{V} \bigcdot \vec{A} = \mbox{constant} \end{equation*}

where Q is the volume flow rate. In this case, then

(16)   \begin{equation*} - \varrho_1 \, V_1 \, A_1 + \varrho_2 \, V_2 \, A_2 = 0 \end{equation*}

or

(17)   \begin{equation*} V_1 \, A_1 = V_2 \, A_2 = Q \end{equation*}

which means that Q_1 = Q_2 = Q, i.e., volume flow is conserved.

Finally, consider a reduction to a steady (but compressible), uniform, one-dimensional flow in the x direction. In this case, \vec{V} = u \vec{i} and so

(18)   \begin{equation*} \oint_S \varrho \, \left( u \vec{i} \bigcdot d\vec{S} \right) = \sum_{S} \varrho \, u \, A = \sum_{S} \varrho \, u \, l (1) = 0 \end{equation*}

or

(19)   \begin{equation*} \varrho_1 \, u_1 \, l_1 = \varrho_2 \, u_2 \, l_2 \end{equation*}

Notice that the areas A_1 and A_2 become areas per unit length, i.e., l_1 and l_2, respectively.

Flow Through a Converging/Diverging Duct

Consider the steady, uniform flow through a converging/diverging duct with a circular cross-section with inlet area A_1 and outlet area A_2, as shown in the figure below. This is a classic problem when learning fluid dynamics. The two sectional areas are known, such as by measurement. If the flow is assumed to be steady and uniformly axisymmetric (i.e., one-dimensional), then determine the relevant form of the continuity equation to relate the flow conditions at the outlet to those at the inlet.

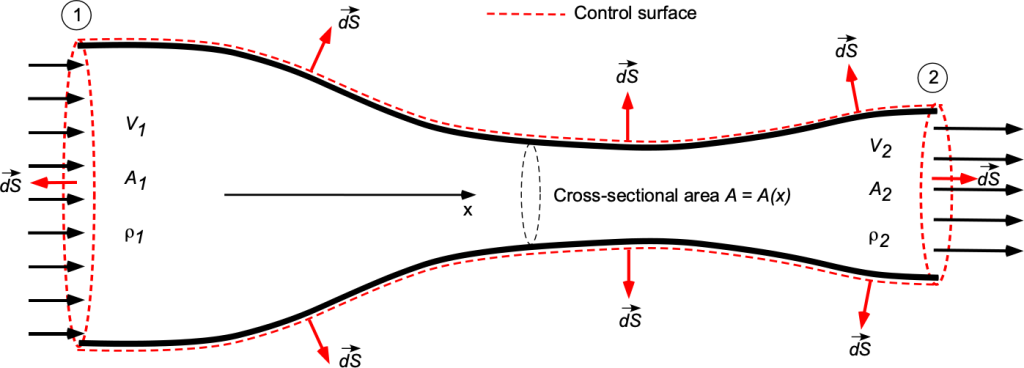
Flow model of a converging/diverging duct with a circular cross-section.

The first step in the solution is to define a coordinate system and the control surface/volume over which to apply the principle of conservation of mass. In this case, the decision on the C.S. and C.V. is relatively easy as the duct itself bounds the flow. There can be no mass flow over the walls of the duct, which naturally applies no matter the duct’s shape.

The flow is steady, so \partial/\partial t \equiv 0, and no further justification is needed in this case. However, nothing is mentioned about whether the flow is compressible or incompressible. Because air is a gas, it must be assumed that the flow is compressible and that density must be retained as a variable. Furthermore, suppose the flow is uniformly axisymmetric. In that case, the flow velocity changes only in one direction, i.e., in the x direction based on the adopted coordinate system, another significant simplification toward the solution of this problem.

In light of the preceding assumptions, therefore, in this case, then

(20)   \begin{equation*} \oiint_{S} \varrho \, \vec{V} \bigcdot d\vec{S} = \iint_{1} \varrho \, \vec{V} \bigcdot d\vec{S} + \iint_{2} \varrho \, \vec{V} \bigcdot d\vec{S} + \iint_{\rm walls} \vec{V} \bigcdot d\vec{S} = 0 \end{equation*}

where the latter term is zero because there is no mass flow over the walls, i.e.,

(21)   \begin{equation*} \iint_{\rm walls} \varrho \, \vec{V} \bigcdot d\vec{S} = 0 \end{equation*}

The mass flow coming into the C.V. through the left-hand side (face 1) is

(22)   \begin{equation*} \iint_{1} \varrho \, \vec{V} \bigcdot d\vec{S} = -\left( \varrho \, \vec{V} \bigcdot \vec{A} \right)_1 = -\varrho_1 A_1 V_1 \end{equation*}

the one-dimensional assumption being used and the minus sign on the first term indicating that the flow is in the opposite direction to d\vec{S}. Similarly, the flow coming out of the right-hand side (face 2) is then

(23)   \begin{equation*} \iint_{2} \varrho \, \vec{V} \bigcdot d\vec{S} = \left( \varrho \, \vec{V} \bigcdot \vec{A} \right)_2 = \varrho_2 A_2 V_2 \end{equation*}

which is positive in this case because the flow is now in the direction of d\vec{S}. Therefore, because the flow is steady, the principle of conservation of mass states that the net mass flow is zero, so what mass flow comes into the C.V. per unit time must equal the net mass flow out of the C.V. per unit time, i.e.,

(24)   \begin{equation*} -\varrho_1 A_1 V_1 + \varrho_2 A_2 V_2 = 0 \end{equation*}

or simply that

(25)   \begin{equation*} \varrho_1 A_1 V_1 = \varrho_2 A_2 V_2 = \overbigdot{m} = \mbox{constant} \end{equation*}

Rearranging the latter equation gives the outlet conditions

(26)   \begin{equation*} \varrho_2 V_2 = \left( \frac{A_1}{A_2} \right) \varrho_1 V_1 \end{equation*}

i.e., the mass fluxes are related by the area ratio A_1/A_2. If the flow was further assumed to be incompressible, then \varrho = constant, and so

(27)   \begin{equation*} V_2 = \left( \frac{A_1}{A_2} \right) V_1 \end{equation*}

Finally, this latter result must be examined to see if it reconciles expectations and makes sense. Engineers get into the habit of asking such questions in practical problem solving, i.e., based on the final equation(s), does (do) the result(s) make physical sense?

For example, if the outlet area were to be smaller than the inlet area (i.e., A_2 < A_1), then the expectation is that the flow velocity will increase as it flows into and out of the C.V, which it does according to the equations because A_1/A_2 > 1. Notice that while this particular problem may appear easy, and indeed it is in this case, it provides an excellent example of how the conservation laws, in the integral form, can be applied to a fluid dynamics or aerodynamics problem.

Check Your Understanding #1 – Calculating flow velocities in a converging duct

Consider the steady flow of a particular gas through a horizontal, converging pipe with an inlet diameter d_1 of 0.22 m and an outlet diameter d_2 of 0.16 m. The density of the gas is known to change from \varrho_1 = 0.91 kg/m{^3} at the inlet to \varrho_2 = 0.83 kg/m{^3} at the outlet. If the inlet flow velocity of the gas V_1 is 5.1 m/s, what is its exit velocity V_2? Assume one-dimensional flow.

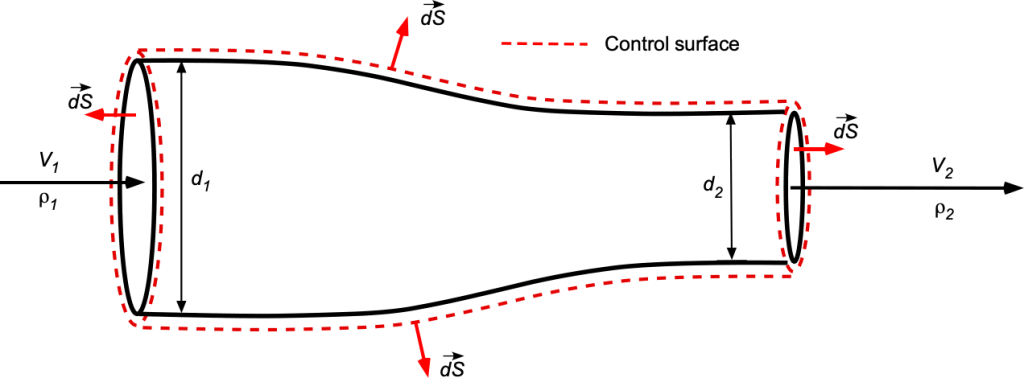
Show solution/hide solution.

The general form of the continuity equation is

    \[ \frac{\partial}{\partial t}\oiiint_{{\cal{V}}} \varrho \, d{\cal{V}} + \oiint_S \varrho \, \vec{V} \bigcdot d\vec{S} = 0 \]

In this case, for steady, one-dimensional flow, then

(28)   \begin{equation*} -\varrho_1 \, A_1 \, V_1 + \varrho_2 \, A_2 \, V_2 = 0 \end{equation*}

or

    \[ \overbigdot{m} = \mbox{constant} = \varrho_1 V_1 A_1 = \varrho_2 V_2 A_2 \]

where the density must be retained as a variable. In terms of diameters, then

    \[ \varrho_1 V_1 d_1^2 = \varrho_2 V_2 d_2^2 \]

And solving for V_2 gives

    \[ V_2 = \frac{\varrho_1 V_1 d_1^2}{\varrho_2 d_2^2} \]

Substituting the numerical values gives

    \[ V_2 = \frac{0.91 \times 5.1 \times 0.22^2}{0.83 \times 0.16^2} = 10.57~\mbox{m s$^{-1}$} \]

Flow Through a Branched Pipe

Consider the flow of fluid through a branch circuit of a pipe, as shown below. The objective, again, is to use the principles of the conservation of mass to determine a relationship between the flow properties and the inlet and outlet conditions. The inlet and outlet areas of the pipe are assumed to be known. Remember that the first step in the analysis is to think about a sketch of the C.V. and the C.S., and annotate it appropriately. It will be assumed that the fluid is incompressible, i.e., \varrho = constant, steady, and one-dimensional; the one-dimensional assumption is that the flow velocities are constant over every cross-section.

Flow model of branched Y-shaped pipe with a circular cross-section.

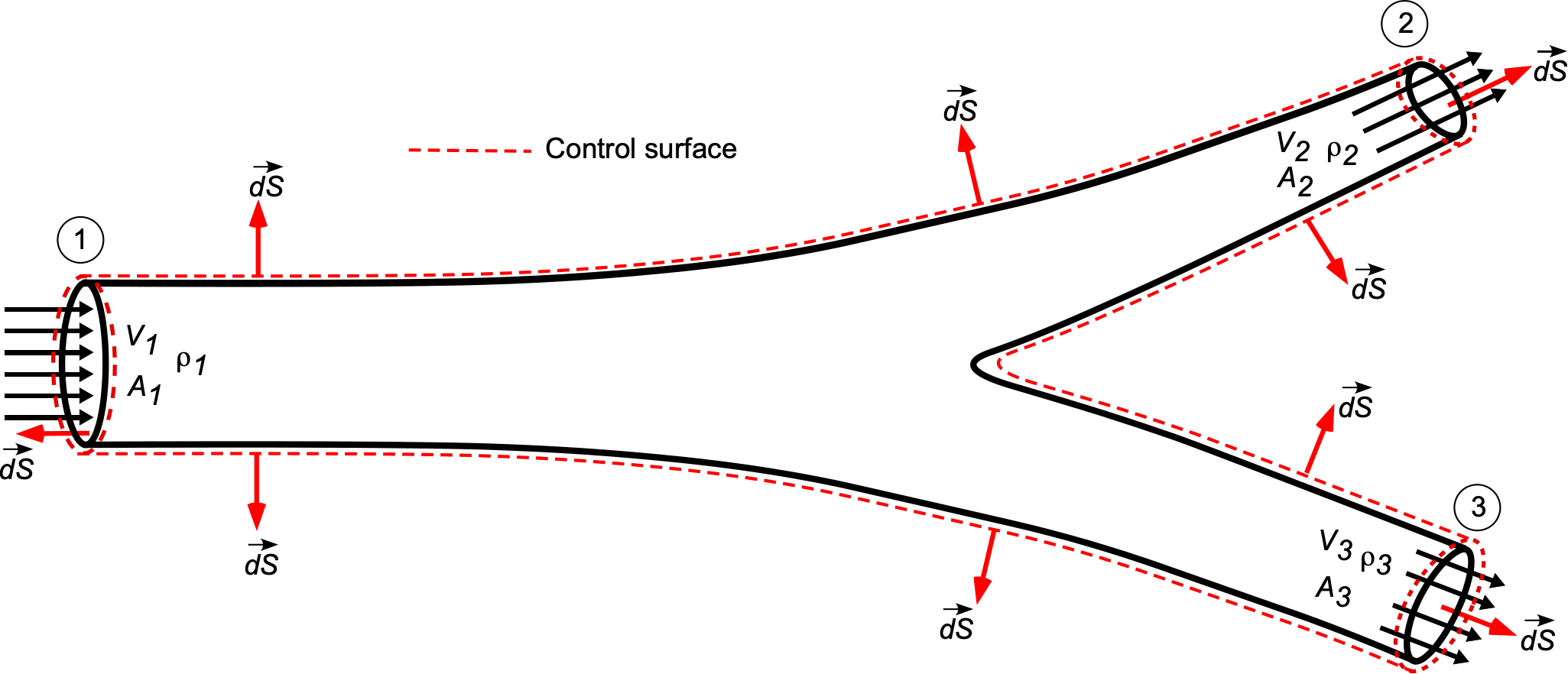
The governing equation for continuity of flow, in this case, becomes

(29)   \begin{equation*} \oiint_{S} \varrho \, \vec{V} \bigcdot d\vec{S} = \oiint_{1} \varrho \, \vec{V} \bigcdot d\vec{S} + \oiint_{2} \varrho \, \vec{V} \bigcdot d\vec{S} + \oiint_{3} \varrho\vec{V} \bigcdot d\vec{S} + \oiint_{\rm walls} \varrho \, \vec{V} \bigcdot d\vec{S} = 0 \end{equation*}

where the mass flow over the solid walls would be zero, i.e.,

(30)   \begin{equation*} \oiint_{\rm walls} \varrho \, \vec{V} \bigcdot d\vec{S} = 0 \end{equation*}

If the flow velocities are constant over their respective areas (the one-dimensional assumption), then

(31)   \begin{equation*} -\varrho A_1 V_1 + \varrho A_2 V_2 + \varrho A_3 V_3 = 0 \end{equation*}

And if the density is constant (which it is for a liquid), then

(32)   \begin{equation*} -A_1 V_1 + A_2 V_2 + A_3 V_3 = 0 \end{equation*}

noting the negative sign on the first term and its significance. Another way of looking at this latter result for the branch flow is to write it as

(33)   \begin{equation*} A_1 V_1 = Q = A_2 V_2 + A_3 V_3 \end{equation*}

where Q is the volume flow rate. Of course, if there was no third exit, then the problem could be reduced to the one previously considered, and

(34)   \begin{equation*} A_1 V_1 = A_2 V_2 = Q = \mbox{constant} \end{equation*}

In general, considering the flow out of the junction as positive and the flow into the junction as negative, then for steady flow at any junction, the algebraic sum of all the mass flows must be zero, i.e.,

(35)   \begin{equation*} \sum_{i = 1}^{N} \varrho_i \, A_i \, V_i = 0 \end{equation*}

For an incompressible flow, i.e., a liquid, then volume is also conserved, i.e.,

(36)   \begin{equation*} \sum_{i = 1}^{N} A_i \, V_i = 0 \end{equation*}

Check Your Understanding #2 – Converging flows into a junction

Two pipes of diameters d_1 and d_2 converge to form a single pipe of diameter d. If a liquid flows with a velocity of V_1 and V_2 in the two pipes, respectively, what will be the flow velocity V_3 in the third pipe? Assume steady, one-dimensional, incompressible flow with no losses.

Show solution/hide solution

In this case, two pipes merge to produce one pipe. Conserving mass and using average flow properties, then

    \[ \overbigdot{m} = \mbox{constant} = \varrho_1 V_1 A_1 + \varrho_2 V_2 A_2 = \varrho_3 V_3 A_3 \]

If the fluid is a liquid then the assumption that \varrho = \varrho_1 = \varrho_2 = \varrho_3 = constant is justified so

    \[ Q = \mbox{constant} = V_1 A_1 + V_2 A_2 = V_3 A_3 \]

Therefore, the flow velocity in the third pipe is

    \[ V_3 = \frac{V_1 A_1 + V_2 A_2}{A_3} = \frac{V_1 (\pi \, d_1^2/4) + V_2 (\pi \, d_2^2/4)}{ (\pi \, d^2/4)} = \frac{V_1 \, d_1^2 + V_2 \, d_2^2}{d^2} \]

Flow Through Parallel Pipes

Consider the flow of fluid that splits through a branch circuit with parallel circular pipes, as shown in the figure below, and then joins together again. The flow enters at 1 and leaves at 4. The two branches, 2 and 3, could have different cross-sectional areas. Again, it will be assumed that the fluid is incompressible, i.e., \varrho = constant, steady, and one-dimensional; recall that the one-dimensional assumption is that the flow velocities are constant over every cross-section.

Flow model of branched Y-shaped duct with a circular cross-section.

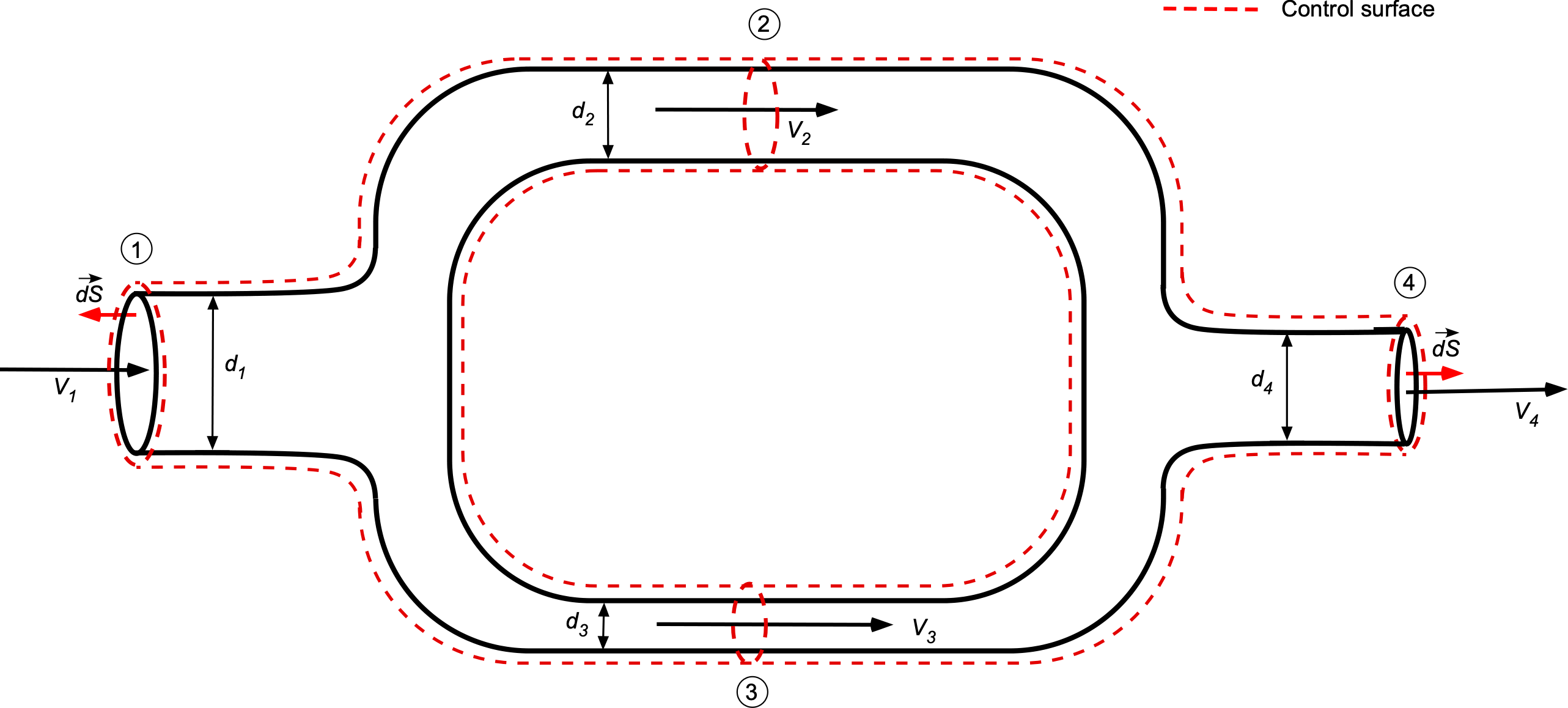
The governing continuity equation is

(37)   \begin{equation*} \oiint_{S} \varrho \, \vec{V} \bigcdot d\vec{S} = \oiint_{1} \varrho \, \vec{V} \bigcdot d\vec{S} + \oiint_{4} \varrho \, \vec{V} \bigcdot d\vec{S} = 0 \end{equation*}

Notice also that for the two branches that

(38)   \begin{equation*} \oiint_{1} \varrho \, \vec{V} \bigcdot d\vec{S} = \oiint_{2} \varrho \, \vec{V} \bigcdot d\vec{S} + \oiint_{3} \varrho \, \vec{V} \bigcdot d\vec{S} = \oiint_{4} \varrho \, \vec{V} \bigcdot d\vec{S} \end{equation*}

If the flow velocities are constant over their respective areas (i.e., the one-dimensional assumption), then

(39)   \begin{equation*} -\varrho A_1 V_1 + \varrho A_4 V_4 = 0 \end{equation*}

If the density is constant, then

(40)   \begin{equation*} -A_1 V_1 + A_4 V_4 = 0 \end{equation*}

or

(41)   \begin{equation*} A_1 V_1 = A_4 V_4 = Q \end{equation*}

where Q is the volume flow rate. Notice that for the branches, then

(42)   \begin{equation*} Q = A_1 V_1 = A_2 V_2 + A_3 V_3 = A_4 V_4 \end{equation*}

Check Your Understanding #3 – Flows through parallel pipes

Water flows through a main pipe, which splits into two parallel pipes and then rejoins into a single pipe downstream. The main pipe has a diameter of 10 cm, one parallel pipe has a diameter of 6 cm, and the other has a diameter of 4 cm. If the velocity of the water in the main pipe before the split is 2.0 m/s, find the velocities in each parallel pipe. Assume steady, one-dimensional, incompressible flow with no losses.

Show solution/hide solution

For the main pipe, the area is

    \[ A_1 = \pi \left(\frac{d_1}{2}\right)^2 = \pi \left(\frac{10}{2}\right)^2 = 25\pi \, \mbox{cm}^2 \]

For the first parallel pipe (6 cm diameter), the area is

    \[ A_2 = \pi \left(\frac{d_2}{2}\right)^2 = \pi \left(\frac{6}{2}\right)^2 = 9\pi \, \text{cm}^2 \]

and for the second parallel pipe (4 cm diameter)

    \[ A_3 = \left(\frac{d_3}{2}\right)^2 = \pi \left(\frac{4}{2}\right)^2 = 4\pi \, \text{cm}^2 \]

The continuity equation for incompressible flow states that the flow rate in the main pipe must equal the combined flow rate in the parallel pipes, i.e.,

    \[ Q = A_1 V_1 = A_2 V_2 + A_3 V_3 \]

Substituting the numerical values gives

    \[ 25\pi \times 2 = 9\pi \times V_2 + 4\pi \times V_3 \]

leading to

    \[ 50 = 9V_2 + 4V_3 \]

It will be apparent that V_2 and V_3 can only be solved uniquely with additional information or assumptions. One reasonable assumption is to assume that the flow is split proportionally based on the cross-sectional areas, which means the velocity in each pipe is inversely proportional to its sectional area, i.e.,

    \[ \frac{V_2}{V_3} = \frac{A_3}{A_2} = \frac{4}{9} \]

Proceeding with this assumption gives

    \[ V_2 = \frac{4}{9} V_3 \]

Substituting this into the continuity equation gives

    \[ 50 = 9 \left(\frac{4}{9} V_3\right) + 4V_3 = 4V_3 + 4V_3 = 8V_3 \]

Therefore,

    \[ V_3 = \frac{50}{8} = 6.25~\mbox{m/s} \quad \mbox{ and} \mbox V_2 = \frac{4}{9} \times 6.25 = 2.78~\mbox{m/s} \]

Continuity Equation – Differential Form

To derive the continuity equation in its differential form, consider a small fluid element in the flow field defined in a Cartesian coordinate system with length dimensions dx, dy, and dz, as shown in the figure below. The volume of this fluid element is d{\cal{V}} = dx \, dy \, dz, and so the mass of the fluid element is

(43)   \begin{equation*} dm = \varrho \, dV = \varrho \, dx \, dy \, dz \end{equation*}

where \varrho is the density of the fluid at point B in three-dimensional space and time t, i.e., \varrho = \varrho(x, y, z, t).

Differential fluid element approach used to derive the continuity equation.

The net mass flow rate through the differential element is the sum of the mass rates through each pair of opposite faces of the element. Consider first the mass flow in the x direction through the left face of the element of area dy \, dz, i.e.,

(44)   \begin{equation*} \text{Mass flow rate into } d{\cal{V}} \text{ in the } x \text{ direction} = (\varrho \, u ) dy \, dz = \varrho \, u \, dy \, dz \end{equation*}

where u is the velocity component of the flow in the x direction. Likewise, for the right face of the element of area dy \, dz, then

(45)   \begin{equation*} \text{Mass flow rate out of } d{\cal{V}} \text{ in the } x \text{ direction} = \varrho \, u \, dy \, dz + \left(\dfrac{\partial (\varrho u)}{\partial x} \right) dx \, dy \, dz \end{equation*}

Therefore, the total mass flow rate through the element in the x direction is

(46)   \begin{equation*} \left( \varrho \, u \, dy \, dz + \left(\dfrac{\partial (\varrho u)}{\partial x} \right) dx \, dy \, dz \right) - \varrho u \, dy \, dz = \dfrac{\partial (\varrho u)}{\partial x} \, dx \, dy \, dz \end{equation*}

Similarly, for the y and z directions, then

(47)   \begin{equation*} \text{Mass flow rate out of } d{\cal{V}} \text{ in the } y \text{ direction} = \frac{\partial (\varrho v)}{\partial y} \, dx \, dy \, dz \end{equation*}

and

(48)   \begin{equation*} \text{Mass flow rate out of } d{\cal{V}} \text{ in the } z \text{ direction} = \frac{\partial (\varrho w)}{\partial z} \, dx \, dy \, dz \end{equation*}

where v and w are the velocity components in the y and z directions, respectively. Therefore, the total net mass flow rate out of the differential element is the sum of the net fluxes in all three directions, i.e.,

(49)   \begin{equation*} \text{Net mass flow rate out of } d{\cal{V}} = \left( \frac{\partial (\varrho u)}{\partial x} + \frac{\partial (\varrho v)}{\partial y} + \frac{\partial (\varrho w)}{\partial z} \right) dx \, dy \, dz \end{equation*}

Now consider the time rate of change of mass inside the differential element (fixed volume), which will be

(50)   \begin{equation*} \frac{\partial (\varrho \, d{\cal{V}})}{\partial t} = \frac{\partial \varrho}{\partial t} \, d{\cal{V}} = \frac{\partial \varrho}{\partial t} \, dx \, dy \, dz \end{equation*}

If mass is conserved (and the volume element is fixed in space and time), then the net mass flow rate out of the fluid element is equal to the time rate of decrease of mass inside the fluid element, i.e.,

(51)   \begin{equation*} \left( \frac{\partial (\varrho u)}{\partial x} + \frac{\partial (\varrho v)}{\partial y} + \frac{\partial (\varrho w)}{\partial z} \right) dx \, dy \, dz = -\frac{\partial \varrho}{\partial t} \, dx \, dy \, dz \end{equation*}

and rearranging and simplifying gives

(52)   \begin{equation*} \frac{\partial \varrho}{\partial t} + \underbrace{ \frac{\partial (\varrho u)}{\partial x} + \frac{\partial (\varrho v)}{\partial y} + \frac{\partial (\varrho w)}{\partial z}}_{ {\nabla \bigcdot (\varrho \vec{V})} } = 0 \end{equation*}

Therefore, the differential form of the continuity equation (using vector notation) becomes

(53)   \begin{equation*} \frac{\partial \varrho}{\partial t} + \nabla \bigcdot (\varrho \vec{V}) = 0 \end{equation*}

where \vec{V} = (u, v, w). This is a mathematical statement in the differential form that mass is neither created nor destroyed.

Proceeding by noticing that expanding \nabla \bigcdot (\varrho \vec{V}) using the product rule gives

(54)   \begin{equation*} \nabla \bigcdot (\varrho \vec{V}) = \varrho (\nabla \bigcdot \vec{V}) + \vec{V} \bigcdot \nabla \varrho \end{equation*}

so the continuity equation now becomes

(55)   \begin{equation*} \frac{\partial \varrho}{\partial t} + \varrho (\nabla \bigcdot \vec{V}) + \vec{V} \bigcdot \nabla \varrho = 0 \end{equation*}

The left-hand side contains the terms that make up the substantial derivative of \varrho, i.e.,

(56)   \begin{equation*} \frac{D\varrho}{Dt} = \frac{\partial \varrho}{\partial t} + \vec{V} \bigcdot \nabla \varrho \end{equation*}

so the final form of the continuity equation becomes

(57)   \begin{equation*} \frac{D\varrho}{Dt} + \varrho (\nabla \bigcdot \vec{V}) = 0 \end{equation*}

As in the case of the integral form in Eq. 7, the result in Eq. 57 applies to all types of flows, e.g., compressible or incompressible, viscous or inviscid.

Simplifications to the general form of the continuity equation include steady flow, i.e., \dfrac{\partial}{\partial t} = 0, and incompressible flow, i.e., \varrho = constant. If the flow is steady and incompressible, the continuity equation becomes

    \[ \nabla \bigcdot \vec{V} = 0 \]

or in terms of the scalar components when \vec{V} = (u, v, w), then

    \[ \nabla \bigcdot \vec{V} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0 \]

Therefore, this latter equation states that to satisfy the conservation of mass, the divergence of the local velocity field must be identically zero. If it is not, then the flow would be non-physical. Notice that this condition must be satisfied regardless of whether the flow is steady or unsteady.

Check Your Understanding #4 – Physically possible flow?

Consider a steady, incompressible flow of an inviscid fluid in a two-dimensional space described by the velocity field

    \[ \vec{V} = (u, v) = (y, -x) \]

Does this flow exist (physically)?
Derive the equations of the streamlines for this velocity field.
Sketch the streamlines and show their direction.

Show solution/hide solution

The differential form of the continuity equation is

    \[ \nabla \bigcdot \vec{V} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \]

For u = y and v = -x:

    \[ \frac{\partial u}{\partial x} = 0 \quad \mbox{and} \quad \frac{\partial v}{\partial y} = 0 \]

Therefore, the continuity equation is satisfied, i.e.,

    \[ \nabla \bigcdot \vec{V} = 0 + 0 = 0 \]

so this IS a physically possible flow.

The equation of the streamline in 2D is

    \[ \frac{dy}{dx} = \frac{v}{u} = \frac{-x}{y} \]

Separating variables and integrating both sides gives

    \[ \int y \, dy + \int x \, dx = C \]

The solution is

    \[ y^2 + x^2 = C \quad (C = R^2 ?) \]

These are clockwise-rotating circular streamlines centered at the origin, which is called a forced vortex.

Continuity Equation from the RTE

Recall that the Reynolds Transport Equation (RTE) can be expressed as

(58)   \begin{equation*} \underbrace{\frac{D}{Dt} \oiiint_{\mathrm{sys}} \beta \, \varrho \, d\mathcal{V}}_{\begin{tabular}{c} \scriptsize Time rate of \\[-3pt] \scriptsize change of $B$ \\[-3pt] \scriptsize inside the system.\end{tabular}} = \underbrace{\frac{\partial}{\partial t} \oiiint_{\mathcal{V}} \beta \, \varrho \, d\mathcal{V}}_{\begin{tabular}{c} \scriptsize Time rate \\[-3pt] \scriptsize of change of $B$ inside\\[-3pt] \scriptsize the control volume.\end{tabular}} + \underbrace{\oiint_{S} \beta \, \varrho ( \vec{V}_{\mathrm{rel}} \bigcdot d\vec{S}) }_{\begin{tabular}{c} \scriptsize Rate at which $B$ is \\[-3pt] \scriptsize leaving through the \\[-3pt] \scriptsize control surface.\end{tabular} } \end{equation*}

Integral Form

In the case of mass, then \beta = 1, and for a fixed C.V., the mass of the system and the C.V. are the same, so

(59)   \begin{equation*} \frac{D}{Dt} \oiiint_{\mathrm{sys}} \beta \, \varrho \, d\mathcal{V} = 0 \end{equation*}

Therefore, the RTE becomes

(60)   \begin{equation*} 0 = \frac{\partial }{\partial t} \oiiint_{{\cal{V}}} (1) \varrho \, d {\cal{V}} + \oiint_{S} (1) \varrho ( \vec{V} \bigcdot d\vec{S} ) \end{equation*}

or

(61)   \begin{equation*} \frac{\partial }{\partial t} \oiiint_{{\cal{V}}} \varrho \, d {\cal{V}} + \oiint_{S} \varrho \vec{V} \bigcdot d\vec{S} = 0 \end{equation*}

which will be recognized as the continuity equation in its integral form, i.e., Eq. 7.

Differential form

The differential form of the continuity equation can also be derived from the RTE. Recall that using the divergence theorem, the RTE for a fixed control volume becomes

    \[ \oiiint_{{\cal{V}}} \bigg[ \frac{\partial (\beta \, \varrho)}{\partial t} + \beta \, \varrho \,\left( \nabla \bigcdot \vec{V} \right) \bigg] d{\cal{V}} = 0 \]

The control volume is arbitrary, so the integrand must also be zero, and the differential form of the RTE becomes

    \[ \frac{\partial (\beta \, \varrho)}{\partial t} + \beta \, \varrho \,\left( \nabla \bigcdot \vec{V} \right) = 0 \]

where in this case, \beta = 1 and the mass of the system and the C.V. are the same. Therefore,

    \[ \frac{\partial \varrho}{\partial t} + \varrho \,\left( \nabla \bigcdot \vec{V} \right) = 0 \]

which will be recognized as Eq. 57 given previously and will apply at every point in the flow.

Check Your Understanding #5 — Discerning a Velocity Field

Consider an incompressible, two-dimensional, steady flow field where the velocity components are given by u(x, y) = -2Ax and v(x, y) = Ay where A is a constant. 1. Show that the given velocity field satisfies the incompressible continuity equation. 2. Explain the physical significance of the given velocity components and what type of flow they represent.

The incompressible continuity equation in two dimensions is

    \[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 \]

Computing the partial derivatives gives

    \[ \frac{\partial u}{\partial x} = \frac{\partial (-2Ax)}{\partial x} = -2A \]

and

    \[ \frac{\partial v}{\partial y} = \frac{\partial (Ay)}{\partial y} = A \]

so that

    \[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = -2A + A = -A \]

Because A \neq 0, the given velocity field does not satisfy the incompressible continuity equation. This outcome suggests an error or assumption violation in the problem setup. To ensure incompressibility, we can proceed to correct the velocity field to satisfy the continuity equation. Suppose the corrected velocity components are u(x, y) = -Ay and v(x, y) = Ax, then

    \[ \frac{\partial u}{\partial x} = \frac{\partial (-Ay)}{\partial x} = 0 \]

and

    \[ \frac{\partial v}{\partial y} = \frac{\partial (Ax)}{\partial y} = 0 \]

so that

    \[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 + 0 = 0 \]

which now satisfies the incompressible continuity equation. Notice that the corrected velocity components represent a rotational flow where u(x, y) = -Ay implies a velocity in the xdirection that varies linearly with y, and v(x, y) = Ax implies a velocity in the y direction that varies linearly with ith x. This type of flow is often seen in vortex or rotational motion, where the fluid exhibits circular or spiral patterns around a central point.

Summary & Closure

Applying the principle of the conservation of mass to fluids results in a governing “star” equation called the continuity equation. This equation applies to all fluids, viscous or inviscid, compressible or incompressible, steady or unsteady. In application, the continuity equation can be simplified from its most general form by making various assumptions as they may apply to the problem of interest. However, it should be remembered that all assumptions must be justified, which in some cases may be challenging to establish a priori, so caution should be used. The most common simplification is to write the continuity equation in one-dimensional form, i.e., in terms of fluid properties that change in only one direction. While the continuity equation can help solve certain simple classes of fluid flow problems, the solution of most real problems will generally need to invoke conservation principles of momentum and energy to elicit the required information.

5-Question Self-Assessment Quickquiz

For Further Thought or Discussion

  • Think about a situation where the size of the control volume changes with time. What form of the continuity equation would be needed in this case?
  • Think of some fluid flow problems where a Lagrangian flow model might be preferable to solve the problem.
  • How might the continuity equation be applied to analyze blood flow in arteries and veins in the human circulatory system?
  • Explain how the continuity equation could be used to design and analyze water distribution systems, such as municipal water supply networks.
  • How does the continuity equation relate to streamlines in fluid flow? Provide an example to illustrate this relationship.

Additional Online Resources

  • A good video on some basics of the continuity equation.
  • Another video on the use of the continuity equation in fluid mechanics.
  • A simple application of the conservation of mass for a fire hose.

License

Icon for the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License

Introduction to Aerospace Flight Vehicles Copyright © 2022–2025 by J. Gordon Leishman is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, except where otherwise noted.

Digital Object Identifier (DOI)

https://doi.org/https://doi.org/10.15394/eaglepub.2022.1066.n16