58 Aircraft Stability & Control
Introduction[1]
The term stability, in reference to an airplane, refers to its tendency to remain in or return to a prescribed or trimmed flight condition after being subjected to a disturbance. An aircraft is considered stable when it maintains the flight condition intended by the pilot, even in the presence of external influences such as gusts or control inputs. Trim or trimmed flight describes an equilibrium state in which all forces and moments acting on the vehicle are balanced. If the aircraft diverges from this condition when disturbed, it is considered unstable. Most aircraft are designed to be inherently stable, ensuring that they can be operated safely by an average pilot with only modest control effort. The term workload describes how easy or difficult the aircraft is to fly, while control refers to the pilot’s (or autopilot’s) ability to command changes in flight attitude or trajectory. An aircraft’s natural stability and its controllability are closely interconnected.
The stability and control of a flight vehicle are inherently complex, not only because of the mathematics involved but also because of the interaction between aerodynamic forces, inertial properties, and control inputs. These factors together determine how an aircraft responds to disturbances and pilot commands. The fundamental principles, however, can be introduced physically without heavy reliance on mathematics. While advanced practice in this field requires specialist knowledge, particularly in dynamic analysis, control system design, and flight testing, all aerospace engineers need to understand the fundamentals and their importance in the design process. Stability and control considerations influence nearly every aspect of design, from overall configuration and mass distribution to control surface layout and handling qualities, making them integral to the field of aeronautical engineering.
Learning Objectives
- Appreciate the fundamentals of an aircraft’s stability and control, and why stability is essential for flight.
- Understand how to develop the equations of motion of an airplane and cast them into linearized form.
- Be able to understand and explain the meaning of stability derivatives.
- Know the differences between an aircraft’s static and dynamic stability.
- Become familiar with flight dynamic terms, such as short-period and long-period responses, phugoid, Dutch roll, and spiral divergence.
- Be aware of the primary design features that contribute to an airplane’s static and dynamic stability characteristics.
- Know how to assess aircraft stability and control characteristics.
- Understand what is meant by aircraft handling qualities assessments.
Historical Background
The subject of aircraft stability and control has been central to the development of practical flight since the beginning of aviation. Early pioneers struggled not only to generate sufficient lift and thrust on the airplane but also to maintain its equilibrium and steer it predictably. Stability and control, therefore, emerged as the “third major problem of aeronautics” after lift and propulsion.[2] The foundations were laid by Sir George Cayley, who in 1799 sketched the modern airplane configuration, separating the functions of lift, propulsion, and stability. His glider experiments demonstrated the importance of tail surfaces for stability, foreshadowing solutions adopted nearly a century later.
By the late nineteenth century, most flying machines remained inherently unstable. Otto Lilienthal’s gliders provided valuable data on lift and drag, but they had marginal stability, and weight-shifting was a limited means of control.[3] Samuel Langley’s Aerodrome of 1903 had a capable propulsion system, but the machine lacked stability, and its repeated crashes underscored the challenges in solving that.[4] The breakthrough came with the Wright brothers in 1903. More than any of the other pioneers, they recognized that positive three-axis control was essential for sustained powered flight. Their Flyer employed a forward canard, wing-warping, and a rudder to provide control.[5] It was “barely stable,” requiring constant pilot correction, but later Wright designs adopted tailplanes as the benefits of static stability became clearer.[6]

The first rigorous theories followed soon after. Frederick Lanchester introduced aerodynamic methods, including an analysis of flight stability,[7] while Ludwig Prandtl and the Göttingen school analyzed tailplane contributions and dynamic stability.[8] By WWI, the principles of longitudinal stability and the stabilizing role of the tailplane were generally understood, though often applied more by experience than by calculation. Between the wars, the complexity of faster, heavier monoplanes demanded quantitative predictions of dynamic stability. The phugoid oscillation, Dutch roll, and spiral divergence were formally described during this period.[9] By WWII, the design of control surfaces and trim devices had become standardized, later codified by Perkins & Hage.[10]
The jet age introduced new challenges. Transonic compressibility effects led to phenomena such as Mach tuck and a propensity for Dutch roll with swept-wing aircraft,[11] Sustained supersonic flight saw changes in the pitch stability characteristics, which prompted the development of formal handling-qualities standards, codified in MIL-F-8785 and subsequent specifications.[12] By the late twentieth century, digital electronics and redundant actuators enabled fly-by-wire (FBW) control. Military aircraft were designed with relaxed static stability to reduce drag and enhance maneuverability,[13] while stability-augmentation systems and autopilots became integral to flight control architectures. Soon, modern airliners also incorporated FBW technology, and today, pilot-in-the-loop handling qualities, artificial stability, and advanced flight-control laws are fundamental to airplane design.
Roadmap of Aircraft Stability & Control
The complexity of the field of aircraft stability and control is such that a roadmap, as illustrated below, can help explain how the subject evolves from fundamental principles to modern control systems. It begins with the forces and moments of flight, leading to the equations of motion that describe how the aircraft responds to disturbances and control inputs. From these arise the definitions of stability in the longitudinal, lateral, and directional axes, followed by the concepts of trim and equilibrium as the basis for steady flight.
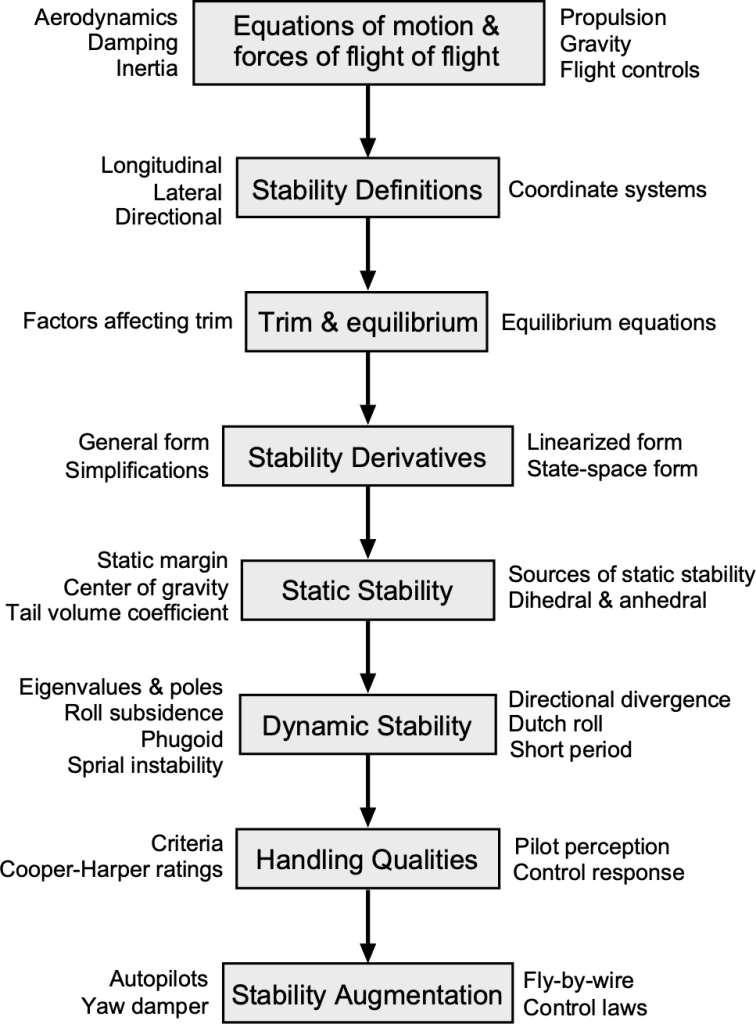
The analysis then turns to stability derivatives, which quantify how aerodynamic forces and moments vary with changes in angle, rate, and control deflection. These lead naturally to static and dynamic stability, defining both the airplane’s tendency to return to equilibrium and the characteristic modes of its motion. The final stages encompass handling qualities and stability augmentation, linking aerodynamic behavior to pilot perception and modern control systems such as autopilots and fly-by-wire.
Forces & Moments of Flight
Following the seminal instructional work of Arthur Babister, flight dynamics concerns an aircraft’s flight characteristics and motion through the air. Stability in flight dynamics refers to an aircraft’s ability to maintain or return to a particular flight condition after being disturbed by external forces. Static stability refers to an aircraft’s initial tendency to return to its original attitude. Positive static stability indicates that the aircraft returns to its original flight condition, while neutral static stability means it remains in the new condition. Negative static stability means it moves further away from its original condition and attitude.
Dynamic stability refers to an aircraft’s behavior over time following a disturbance, often resulting in an oscillatory response. For example, a disturbance in pitch may cause the dynamic response to consist of a series of slightly nose-high and nose-down pitching motions. Positive dynamic stability means that the oscillations will decrease in amplitude and return to their original condition. Neutral dynamic stability means that the oscillations will remain constant in amplitude and frequency. Negative dynamic stability refers to the phenomenon where oscillations increase in amplitude over time.
Aerodynamic Effects
Aerodynamic forces and moments depend on the aircraft’s angular orientation relative to the flow, as well as its linear velocities. These are often referred to as static forces and moments because they depend on the aircraft’s instantaneous position in three-dimensional space. In particular, an aircraft’s lift and drag forces depend on its linear velocities through the air. Aerodynamic effects are also influenced by the aircraft’s angle of attack, flight velocities, air density, and wing and empennage geometry. For high rates of change, unsteady aerodynamic effects may be significant because instantaneous velocities are insufficient to fully describe the aerodynamics. Therefore, to calculate the aerodynamics, what happened to the aircraft’s motion at a prior time, i.e., a hereditary effect, may be necessary to know.
Aerodynamic Damping Effects
Aerodynamic damping forces and moments arise from the aircraft’s angular velocities, also known as rotary forces and moments. Damping typically reduces the transient or oscillatory motion and is usually a desirable flight dynamic characteristic that contributes favorably to the aircraft’s stability. An aircraft’s wing, horizontal tail surfaces, and vertical tail surfaces primarily contribute to damping. For higher rates of change, apparent mass aerodynamic effects (also called added mass) may also be significant. Negative aerodynamic damping may occur in unusual flight conditions, such as high angles of attack and stalled flow.
Inertia Effects.
These effects arise from the aircraft’s mass distribution in response to linear and angular accelerations. These forces and moments are of two types: linear inertial and angular inertial effects. Linear inertial effects produce forces that arise from the aircraft’s mass in response to linear accelerations. Angular effects occur from the aircraft’s mass distribution and angular accelerations, which are governed by its moments of inertia. Higher moments of inertia are undesirable because they generally make the aircraft less agile and more sluggish, and sometimes more challenging to fly. In most cases, the balance between aerodynamic and inertial forces significantly influences the aircraft’s handling qualities.
Effects of Flight Controls
The application of flight controls can significantly affect the aircraft’s aerodynamics, which is obviously by design. Examples of flight controls are the ailerons, elevator, and rudder. These flight controls can affect the aircraft’s motion and stability in roll, pitch, and yaw. Furthermore, the flaps and slats (if any) and spoilers (if any) can affect the aircraft’s flight characteristics, particularly at low airspeeds, such as during takeoff and landing. The size and aerodynamic effectiveness of the flight control surfaces must be designed as an integral part of the aircraft’s stability and control assessments.
Gravitational Effects
Gravity manifests as weight (a force) and the distribution of weight, i.e., the position of the center of gravity, usually denoted by CG, c.g., c of g, or cg, with the symbols often used interchangeably; c.g. is used here. The center of gravity (c.g.) is the point at which the aircraft’s weight can be considered to act, and it has a significant effect on the aircraft’s stability and control. If the center of gravity (c.g.) is too far behind the acceptable range, the aircraft may become more challenging to fly or even unstable in pitch. At the same time, if the c.g. is too far forward, the aircraft may become excessively stable, challenging to maneuver, and/or difficult to control. The fuel load, along with passengers and cargo, must be distributed within the design limits of the specific aircraft to maintain trim and stability throughout the flight, while accounting for the weight of fuel burned. Commercial airliners, for example, burn off a considerable fraction of their fuel during flight, typically as much as 30% of their takeoff weight.
Propulsive Effects
These are the effects of the engine(s) that propel the aircraft forward. The propulsive thrust affects the aircraft’s speed, acceleration, and overall performance. The magnitude of the thrust depends on several factors, including the type and design of the engine, the power setting, and the aircraft’s speed. For example, changes in propulsive thrust can produce pitching moments or yawing moments on the aircraft. In a multi-engine aircraft, losing one engine may cause yaw, pitch, and/or roll, significantly affecting its flight and overall stability. Aircraft with large propellers may also have gyroscopic and slipstream effects that may influence their stability and control characteristics. Of recent significance are issues with the Boeing 737 MAX, which features larger, more powerful engines mounted further forward on the wing, exacerbating thrust/pitch coupling.
Other Factors
Other factors influencing aircraft flight dynamics include atmospheric conditions, flight altitude (i.e., density altitude), flight airspeed (i.e., true airspeed and dynamic pressure), and the corresponding Mach number. These factors can affect the aircraft’s aerodynamic characteristics and its propulsion system(s). So, they will directly or indirectly impact the aircraft’s performance, flight dynamics, and overall handling characteristics. Other factors include meeting stability and control requirements, which are not limited to regulations. However, aircraft must also meet rigorous stability and control standards set by aviation authorities such as the FAA (Federal Aviation Administration) and EASA (European Union Aviation Safety Agency).
Stability Definitions
An airplane is just one type of aircraft, but its analysis forms an essential basis for understanding the dynamics and control characteristics of all flight vehicles. The issue of concern is with its stability and control characteristics about all three flight axes, as shown in the figure below, namely:
- Longitudinal stability and control concern the airplane’s response in the pitch or angle-of-attack degree of freedom.
- Lateral stability and control relate to the lateral axis or rolling degree of freedom.
- Directional stability and control relate to the yawing axis or directional (weathercock) degree of freedom.
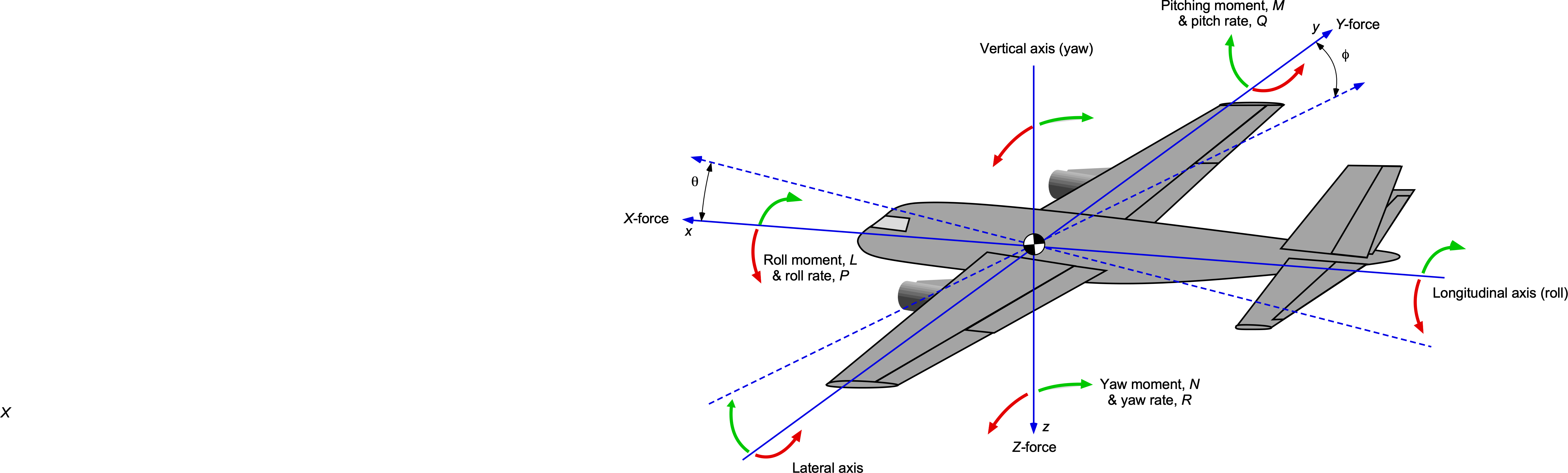
While the flight responses and control inputs of any airplane tend to be coupled about the three axes to some degree, it is found in practice that its pitch or angle of attack motion is mainly decoupled from the roll and yaw responses. However, an airplane’s lateral (roll) and directional (yaw) stability characteristics tend to be significantly more coupled; usually, one cannot be considered separately from the other for a stability and control analysis.
Coordinate Systems
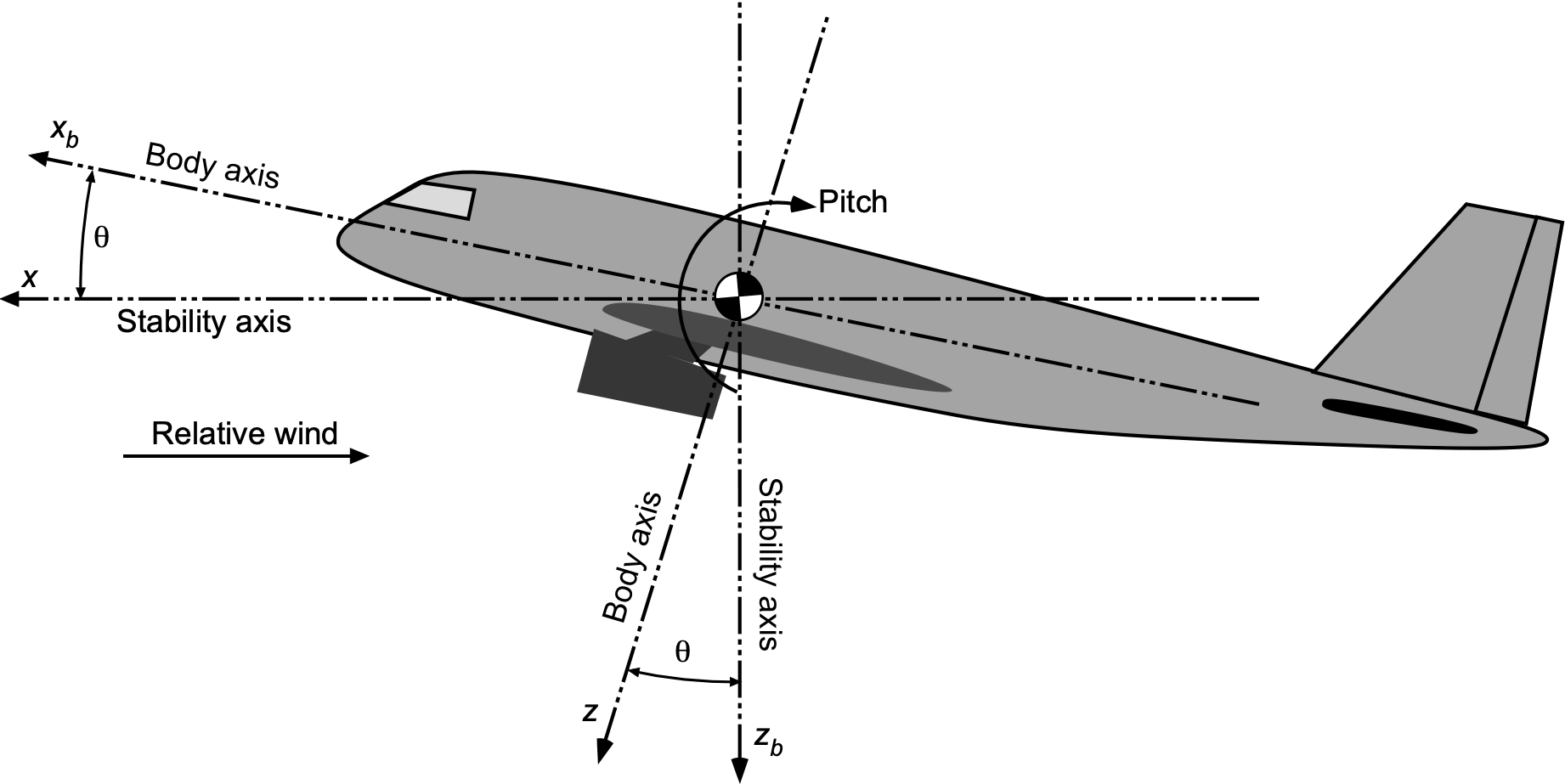
The airplane’s body axis is typically defined as a right-handed Cartesian coordinate system centered at the airplane’s center of gravity (c.g.). The direction is defined as positive along the airplane’s longitudinal axis, with positive values indicating forward motion in the direction of flight. The
direction is positive along the starboard wing, and
is positive downward. The locations of the axes in the vertical (pitching) plane are shown in the figure below.
The stability coordinate system, also known as the stability axis system, is essential in flight dynamics for analyzing an aircraft’s stability and control characteristics. This system is designed to align with the relative airflow and is distinct from the body-axis system, which is fixed relative to the aircraft. In the stability axis system, also called the wind axes, the -axis points forward along the aircraft’s velocity vector, the
-axis points to the right, and the
-axis points downward. This orientation is more natural and simplifies the analysis of aerodynamic forces and moments because they are directly aligned with the airflow.
If required, the transformation from the body axis system to the stability axis system involves rotations by the angle of attack and sideslip angle. This realignment makes it easier to understand how aerodynamic forces such as lift, drag, and side force act on the aircraft and how it responds to them. The stability coordinate system is particularly useful for deriving the equations of motion that describe the aircraft’s response to control inputs and external disturbances. By resolving aerodynamic forces and moments in this system, engineers can more effectively analyze and ensure the aircraft’s stability and control during flight.
Attention! Potential for symbol conflict
It is essential to note the potential for symbol conflict between flight dynamic terms and aerodynamic forces and moments, which must be carefully distinguished and properly reconciled in any analysis to prevent undesirable mathematical outcomes. Flight dynamic moments, typically denoted as ,
, and
, representing roll, pitch, and yaw moments, respectively, can sometimes conflict with aerodynamic forces and moments which are often represented by the same symbols but with different meanings, e.g.,
for lift,
for aerodynamic pitching moment, and
for normal force. A clear, consistent notation system should be adopted to mitigate this potential for confusion. By defining these symbols and consistently applying them throughout the analysis, misunderstandings and errors can be avoided.
Trimmed Flight
For an airplane to be in static equilibrium or trim at a particular flight condition, the net sum of all the forces and moments acting on the airplane must be zero, i.e., the position and attitude of the aircraft will be in perfect balance about all three flight axes, namely pitch, roll, and yaw. The two tables below summarize the forces and moments, with one table for the forces and the other for the moments.
| Axis | Force | Linear Velocity | Description |
|---|---|---|---|
| Fore/aft | |||
| Sideward | |||
| Heave or plunge |
| Axis | Moment | Moment Coefficient | Angular Displacement | Angular Velocity | Non-dimensional angular rate | Description |
|---|---|---|---|---|---|---|
| Roll | ||||||
| Pitch | ||||||
| Yaw/sideslip |
In flight mechanics, there are two common conventions for the body-axis velocity components. In the first, which is used mainly in linearized stability and control analysis, the uppercase symbols denote the steady trim values and the lowercase symbols
, with
forward,
lateral (to starboard), and
downward, denote perturbations about the trimmed flight condition, so that
(1)
In the second convention, the components are written as ; the airspeed is then
(2)
Consider the equilibrium of an airplane in straight and level unaccelerated flight at a constant airspeed and altitude, as shown in the figure below. In trim, the lift on the airplane equals its weight, and for most purposes, the weight can be considered to act at the airplane’s c.g. The thrust (from the propulsion system) equals the aerodynamic drag at that in-flight weight, airspeed, and altitude. Therefore, as previously defined, no net forces or moments can act on the airplane about the c.g. when in the trim condition.
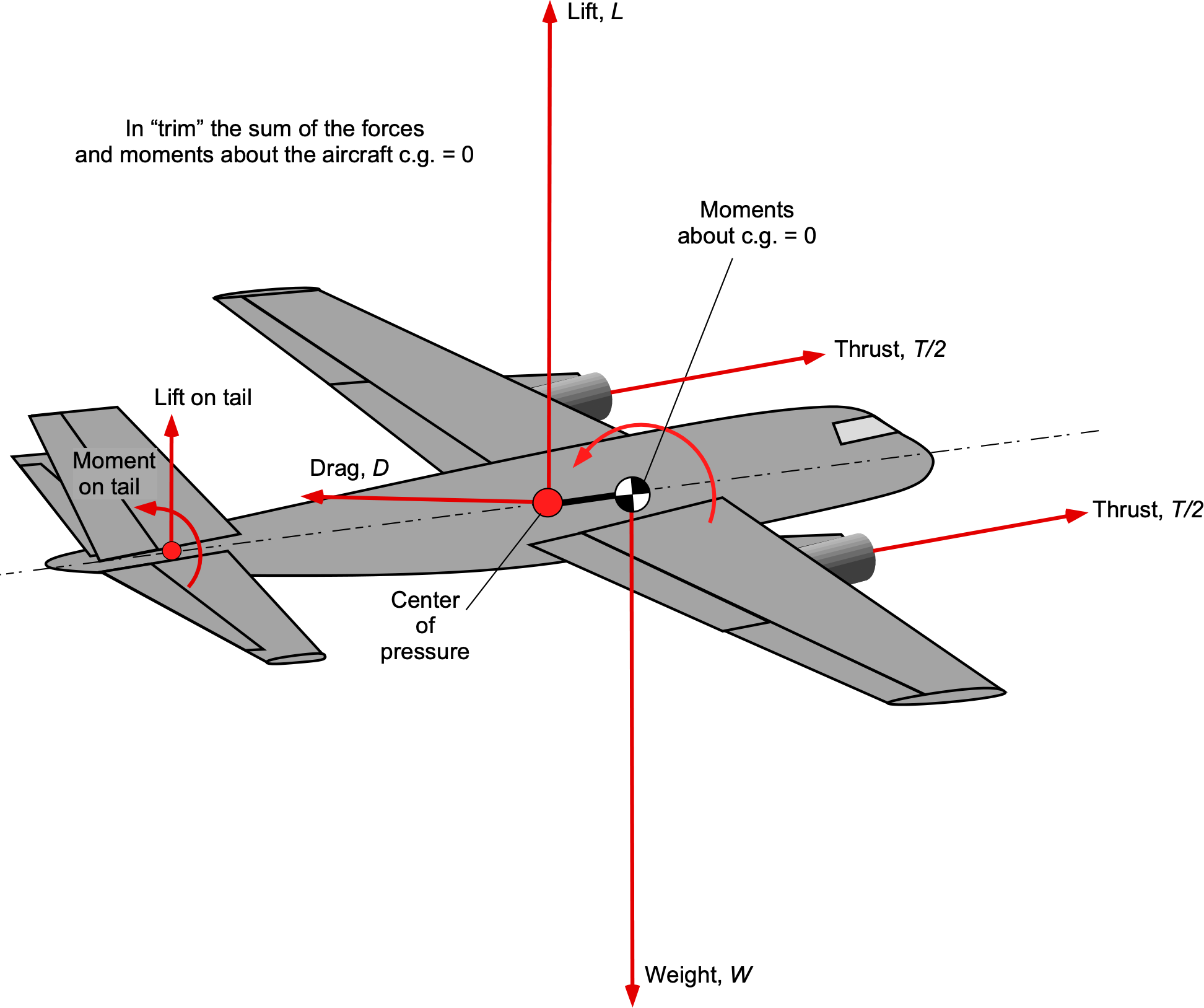
The aerodynamic forces on the airplane can be considered to act at an effective location on each lifting component, such as the main wings and the horizontal and vertical tails. Of more significance is the lifting contributions, in aggregate, which can be assumed to act at a single point. The center of pressure is a convenient point, usually denoted by CP or cp or c.p. (depending on author or source), because this location has no net aerodynamic moment. The c.g. is generally located in front of the c.p. (for stability), and the horizontal tail and flight controls are needed to create the necessary aerodynamic forces (and hence moments) to reach a balanced pitch or trimmed flight condition.
The main wing produces most of the lift on the airplane, but the tail may make some small increments. Hence, the center of pressure of the entire airplane is usually very close to the center of pressure of the wing by itself, which, for the lift coefficients typical of flight, is near the 1/4-chord point. The horizontal tail acts like a smaller version of the main wing and can produce either positive or negative changes in lift through the use of elevator control. Because of the typically long distance (arm) from the horizontal tail to the c.g. location (but not always), only relatively small changes in the lift on the tail are required to produce significant longitudinal pitching moments.
Trim Equilibrium Equations
For an airplane to be in static equilibrium (or in trim) at a particular flight condition, the net sum of all the forces and moments acting on the airplane must be zero. This implies that the airplane’s position and attitude will be perfectly balanced about the pitch, roll, and yaw axes. In trim, the conditions for force equilibrium are
(3)
where represents the sum of all forces. Because there are no net forces, there will be no resultant accelerations on the airplane, which can be expressed as
(4)
where ,
, and
are the components of the velocity in the body-fixed frame along the
,
, and
axes, respectively.
For rotational equilibrium, there are no net moments about the flight axes. Therefore,
(5)
In trim, the angular velocities about the flight axes are zero, i.e.,
(6)
where ,
, and
are the roll, pitch, and yaw rates, respectively. For level, symmetric, coordinated flight with no yaw or sideslip, the trim conditions are
(7)
Therefore, the airspeed component in the -direction is
, where
is the true airspeed. Furthermore, if the wings are level, then the roll angle is zero, i.e.,
= 0.
Factors Affecting Trim
The trim state of an airplane, which ensures balanced steady-state flight, is influenced by multiple factors, including the aircraft’s weight and center of gravity (c.g.) position, aerodynamic forces, control surface deflections, and thrust. Changes in configuration, such as flap settings and landing gear position, also affect trim, as do atmospheric conditions, such as air density. Additionally, fuel load distribution and external stores on military aircraft affect the c.g. and trim. These factors collectively determine the precise adjustments needed to maintain the desired flight attitude and stability.
Flight Controls
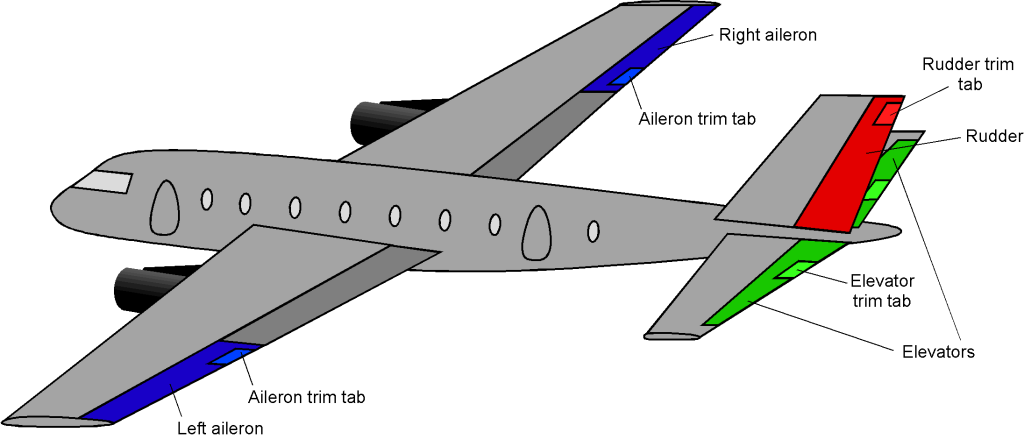
Pilot inputs and autopilot systems play a crucial role in adjusting control surfaces and engine power to maintain the desired trim state, as illustrated in the figure below. These adjustments involve precise movements of the elevator, ailerons, rudder, and thrust levels to counteract deviations caused by changes in weight distribution, aerodynamic forces, and atmospheric conditions. Proper management of these factors ensures that the aircraft remains stable, balanced, and efficient throughout the flight, compensating for shifts in the c.g. and alterations in configuration such as flap settings and landing gear position (up/down). Small “trim tabs” are often used on the primary control surfaces to eliminate any residual load on the pilot’s controls, allowing the airplane to be flown “hands off.”
Center of Gravity Location
Consider what would happen if the center of gravity (c.g.) moved forward. In this case, a more significant nose-down gravitational moment would act on the airplane, which would need to be compensated for by increasing downforce (negative lift) on the tail. Therefore, the pilot would need to deflect the elevator up by moving the control column aft, which reduces the aerodynamic upward force on the tail and helps reestablish the airplane’s trim. Small changes in aerodynamic forces and moments from the control surfaces can be achieved using trim tabs, as shown in the figure above. These tabs can be actuated separately to trim the airplane and eliminate any residual forces from the pilot’s controls.
Propulsion Effects
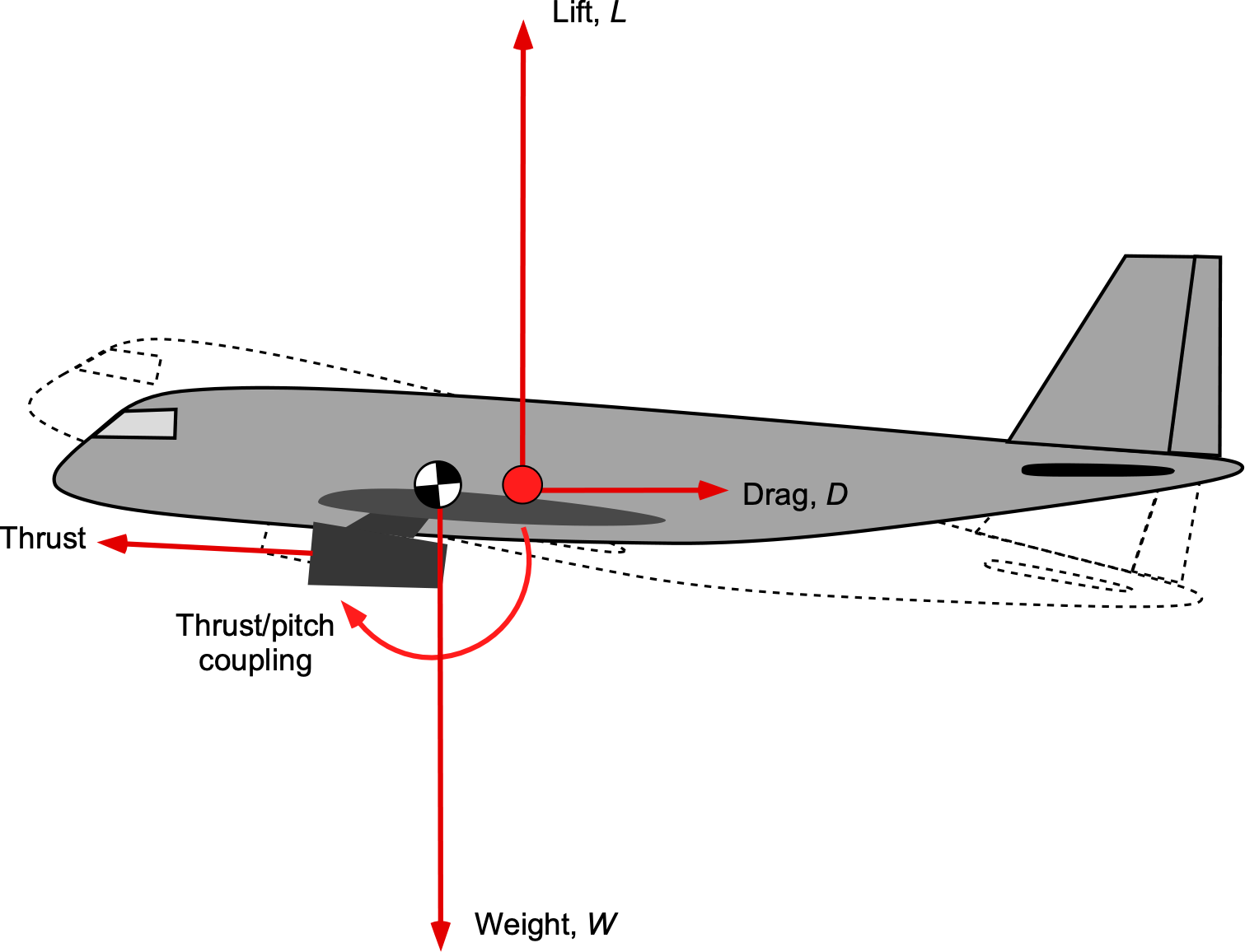
The propulsion system can also affect the airplane’s stability and control characteristics. Propulsion will create a thrust vector, which may have a line of action that is vertically or horizontally offset from the location of the c.g. Thrust can also produce a pitching moment, i.e., a form of thrust/pitch coupling, which tends to increase the pitch attitude nose-high; this latter effect is illustrated in the figure below. Airplanes with underslung engines that produce thrust vectors centered below the c.g. are prone to this type of coupling, which can also be interpreted in combination with the airspeed coupling effect. In this regard, changes in thrust setting will affect airspeed. Increasing thrust generally increases airspeed and causes nose-up pitch, while reducing thrust decreases airspeed and can cause the nose to drop.
Center of Pressure Changes
Both the c.g. and the airplane’s center of pressure (or center of lift) may, and generally will, change during flight. As fuel is burned off and the airplane’s weight changes, the c.g. may move forward or aft, depending on the type of airplane and how it is loaded with its payload. Therefore, the airplane’s stability characteristics can (and often will) change slowly during flight, and further trimming by the pilot or flight control system may be required. To reduce trim drag on a commercial airliner, fuel is pumped from one tank to another to manage the longitudinal and lateral center of gravity (c.g.) position during flight, rather than accepting the increased drag from the application of trim tabs. As shown in the photograph below, all-flying horizontal tails may also be used on airliners to trim out the pitching moments. The markings “UP” and “DOWN” indicate the angles required for “nose-up” and “nose-down” trim, respectively.

The center of pressure may also change with airspeed, especially at higher Mach numbers in high-speed flight. Approaching transonic and into supersonic flight, the center of pressure typically migrates aft on the wing from near the 1/4-chord to closer to the 1/2-chord. The resulting effect is a pronounced nose-down pitching moment. This effect is called Mach tuck, and it can be a stability and control issue for a supersonic airplane as it transitions from subsonic to supersonic flight. Of course, these effects can often be trimmed out using the elevator (or a trimmable tail surface). Still, there will be a limit to this type of control capability depending on the combination of the c.g. and/or c.p. movements during flight. On some larger airplanes, it is necessary to pump fuel longitudinally from one tank to another to keep the c.g. between the required limits during supersonic flight, such as was done on the Concorde using trim tanks.
Stability Derivatives
The stability characteristics of an aircraft in response to disturbances from trimmed flight can be explained using stability derivatives, i.e., the change in a specific force or moment with respect to particular types of disturbances. To this end, it can be assumed that the forces and moments on the aircraft are functions of the instantaneous values of the disturbance velocities (translational and angular), as well as their time rates of change. Unsteady or hereditary effects (i.e., what happened in previous times) can be ignored, which is often referred to as a quasi-steady assumption.
General Representations
Therefore, the quasi-steady forces on the aircraft can be expressed in general terms as
(8)
and for the corresponding moments, then
(9)
The function, , in each case, represents the relationship between the aircraft’s instantaneous motions (or disturbances) and the resulting forces (
,
, and
) and the corresponding moments (
,
, and
) on the aircraft. With 12 dependencies in each case and potentially non-linear, interdependent (coupling) effects, it becomes clear why the mathematical description of an aircraft’s flight dynamics can be complicated.
Furthermore, if the effects of the flight control deflections, , are added, where the subscript
refers to the ailerons,
refers to the elevator, and
refers to the rudder, then there will be 18 dependencies in each case, i.e.,
(10)
More contributions could also be added to the list, such as those for the effects of flaps and engine thrust, so the problem quickly becomes formidable and even intractable from any reasonable practical perspectivò0.
Linearization Process
The method used in flight dynamics is to linearize the preceding relationships with a Taylor series expansion about the trim state and then retain only the first-order derivatives. Therefore, the perturbations to the forces and moments, i.e., , are now desired. The equilibrium is defined as
, representing the balanced forces and moments on the airplane in the trimmed flight condition. For example, for the
force, then
(11)
If the higher-order derivatives are now neglected, which is a reasonable assumption because they can be expected to be small in value, then
(12)
The first-order partial derivatives in the preceding equation are called the stability derivatives. They can be used to determine the aircraft’s response to disturbances or perturbations about the trim state. However, it is essential to remember that all of the stability derivative terms will be a function of the specific trim state of the aircraft during flight, as denoted by the subscript , so they are not necessarily constants.
The full set of force perturbations can now be expressed as
(13)
and the corresponding full set of moment perturbations will be
(14)
Each term involving a control deflection is often referred to as the control derivative. In total, it is apparent that there are 18 derivatives for each equation and, therefore, a total of 108 derivatives, which is unmanageable in any practical context.
Simplifications
Fortunately, the preceding equations can be simplified under reasonable assumptions. For a symmetric flight condition in the –
plane, the asymmetric forces and moments, i.e.,
,
,
, will be zero. Therefore, the derivatives of the asymmetric quantities and their derivatives with respect to
,
,
,
,
,
,
,
, will be zero. The reciprocal effect applies, so the derivatives of the symmetric forces and moments, i.e.,
,
, and
, with respect to the asymmetric variables and their derivatives,
,
,
,
,
,
,
,
,
,
, are also zero. The control rate derivatives are considered small enough to be negligible. It has also been found through aircraft flight testing that all derivatives with respect to accelerations are insignificant, allowing for further simplifications. These simplifications now yield a significantly shorter subset of the original equations.
Based on the linearization about the trim conditions and using the preceding simplifications, the perturbation forces now become
(15)
(16)
(17)
The corresponding perturbation moments are
(18)
(19)
(20)
The stability derivatives, i.e., the terms, which can be seen as gradients or slopes in the preceding equations, represent the aircraft’s linearized response to small perturbations around an equilibrium trim state. The numerical values of the various derivatives can be estimated using simulations and wind tunnel tests, and then verified through flight testing. As previously mentioned, a complication is that the values of the derivatives will change with the trim state and are likely to depend on factors such as altitude (i.e., density altitude), airspeed, Mach number, angle of attack, the aircraft’s configuration, and other variables.
Linearized Equations
An aircraft’s linearized equations of motion are valuable because they simplify complex nonlinear dynamics into manageable forms. This approach is essential for analyzing stability, designing control systems, and predicting aircraft responses to inputs and disturbances. These equations facilitate the design of control systems using linear techniques, provide insights into dynamic behavior, and are crucial for initial design testing and real-time flight simulations.
The linearized force and moment perturbations may be substituted into the aircraft’s linearized equations of motion about the trim condition, i.e., the net force in each direction equals the aircraft’s mass times its acceleration. For simplicity, only the three symmetric terms, i.e., for flight in the –
plane, are retained, as shown in the figure below.

In reference to the figure, then the perturbation forces in the direction are
(21)
For the perturbation forces in the direction, then
(22)
Finally, for the perturbation in the pitching moment, then
(23)
where .
Stability Derivatives in State-Space Form
The state-space form of the equations of motion is helpful because it condenses the complicated, coupled differential equations into a compact matrix representation that can be analyzed using linear algebra. The eigenvalues of the system matrix directly reveal the aircraft’s stability and oscillatory modes. In contrast, the input and output matrices explicitly show the effects of control deflections and their relationships to the measured variables. In this way, the state-space equations provide both physical insight into how aerodynamic derivatives influence stability and a practical framework for modern control analysis, design, and simulation.
Starting from the quasi-steady assumption, the aerodynamic forces and moments can be regarded as general functions of the instantaneous body-axis velocities, angular rates, and control deflections. Linearization about a steady trim condition leads to the first-order small-disturbance equations given by
(24)
where ,
and
, together with the kinematics
,
, and
, as well as
and
for brevity. With the usual symmetry and decoupling simplifications, the longitudinal and lateral-directional motions separate. For the longitudinal motion, take
and
. Retaining the dominant derivatives, i.e.,
, and dividing
and
by
and
by
, gives
(25)
where the and gravity entries arise from linearizing the kinematics and weight components in the body axes. For the lateral-directional motion, take
and
. Retaining the dominant derivatives in this case, i.e.,
, gives
(26)
where the term multiplying
in the
equation is a Coriolis term
, and the last two rows follow from the kinematics about the trimmed pitch angle
. The matrices
are, therefore, expressed directly in terms of the linearized (dimensional) stability derivatives. Output equations of the form
are appended as needed to represent measured variables such as airspeed, angle of attack, pitch/roll/yaw angles, or accelerometer outputs. The yaw derivatives in the third row of
and
arise directly from the dimensional aerodynamic yawing moment derivatives
, etc.; the fifth row is a kinematic relationship.
Longitudinal Static Stability
It is initially convenient to describe the principles concerning an airplane’s longitudinal or pitching response, mainly because the responses in pitch are clean and uncoupled from the responses in roll and yaw. Consider the situation in which the balance of forces and moments in the trim state is disturbed, such as by a vertical gust due to atmospheric turbulence. However, it should be remembered that gusts can come from virtually any direction, affecting the airplane’s response about any axis. Still, vertical or -velocity gusts typically have the most significant effect on the aircraft’s responses.
Starting from the longitudinal moment equation in Eq. 56 together with the kinematic relation , the static (quasi-steady) case is obtained by setting
and
. For stick-fixed response, the elevator is held fixed, so
. The reduced static moment balance is therefore
(27)
At the instant a vertical gust is encountered, the initial kinematics are and
, and the small-angle relation between angle of attack and velocity perturbations is
(28)
so that, for the initial gust input with frozen and no instantaneous streamwise response (
), then
(29)
Therefore, the restoring requirement for a vertical gust is
(30)
and this is consistent with the angle-of-attack form because
(31)
which gives the equivalence
(32)
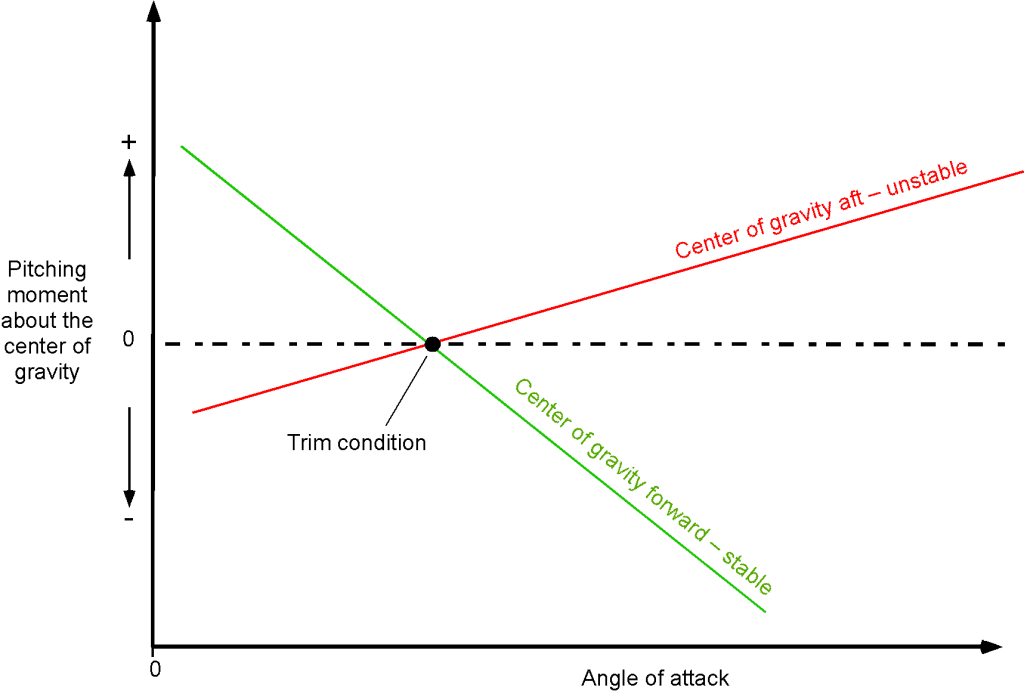
A vertically upward gust, , will cause an increase in the wing’s angle of attack, increasing its lift, and the airplane’s inherent reaction is that its nose will pitch up slightly. The consequence of this effect is that the airplane is no longer in stable equilibrium and will deviate from its trimmed flight condition, as shown in the figure below. If the subsequent forces and moments generated on the airplane from the gust disturbance tend to return it to its trimmed condition, the airplane’s response would be referred to as being statically stable, as shown in scenario (b). Mathematically, when expressed in terms of a stability derivative, then
(33)
which must be negative to produce a restoring moment.
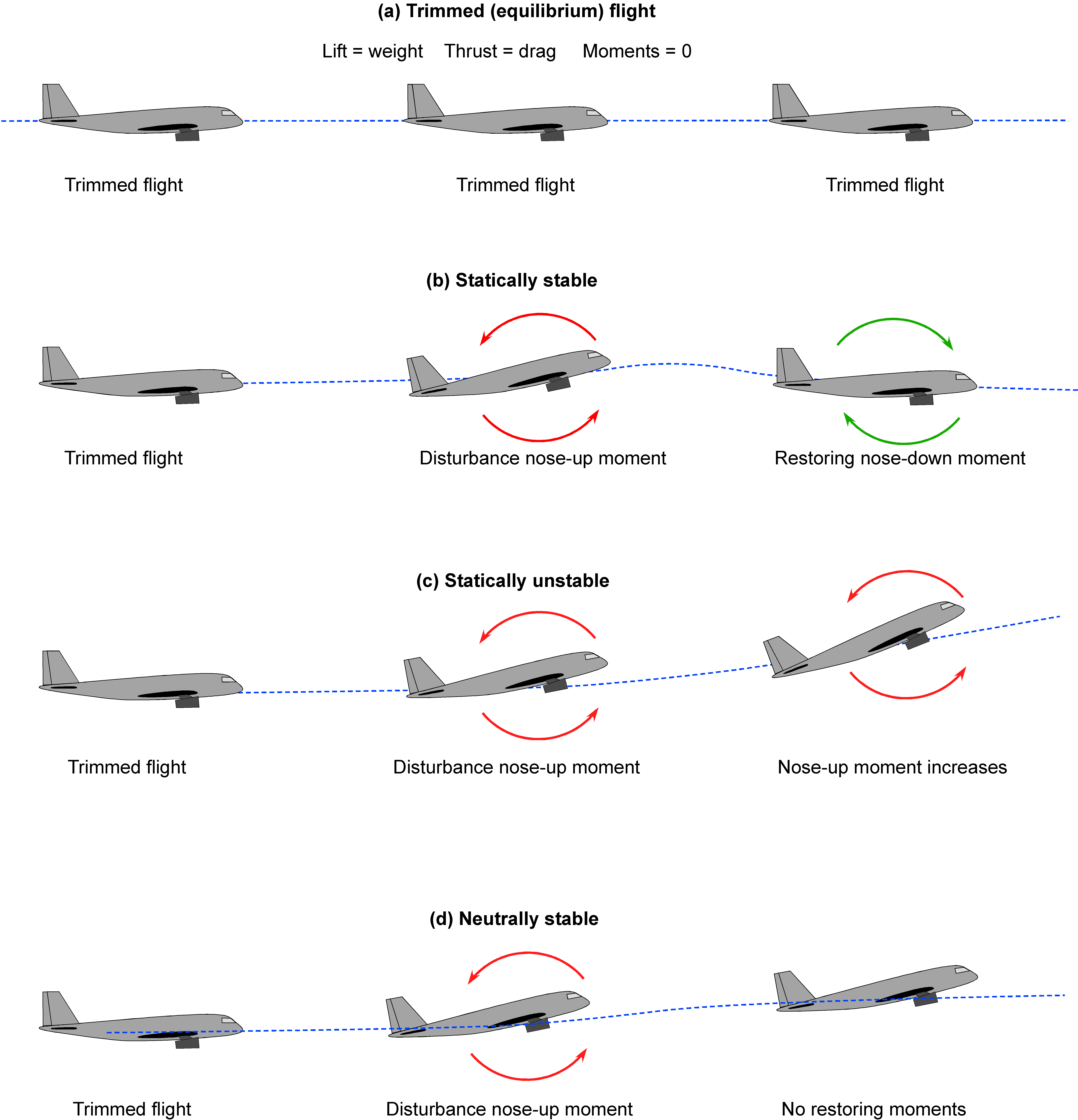
However, if the forces and moments introduced by the gust or other disturbance tend to cause the nose to pitch up further, then the airplane would be considered statically unstable, which is scenario (c). In this case, then
(34)
If the airplane is genuinely statically unstable, its subsequent motion may cause a divergence of the flight path and, most likely, a departure from controlled flight. When the airplane remains indefinitely disturbed, as shown in scenario (d), then it is considered to have neutral static stability, i.e.,
(35)
but this is not a common characteristic of an airplane.
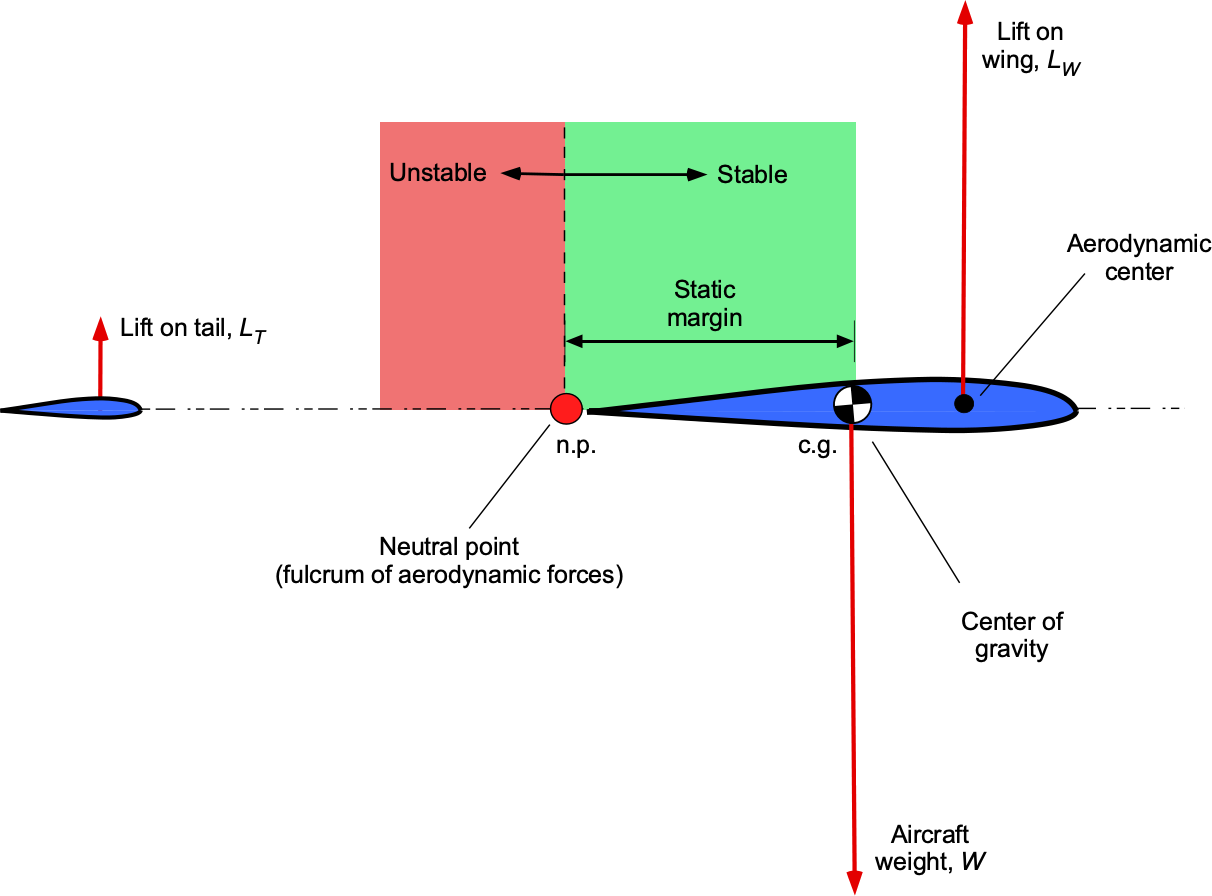
Static Margin
The conditions ensuring sufficient longitudinal static stability can now be formally established, leading to the parameter known as the static margin, which quantifies the static stability in pitch. The static margin is a distance measured in length units, although it is often expressed as a fraction or percentage of the mean wing chord.
Assuming the trim condition where , for vertical equilibrium, then
(36)
where is the weight of the aircraft,
is the wing lift, and
is the tail lift. The wing lift is conventionally expressed as
(37)
where is the wing (reference) area,
is the angle of attack, and
is the zero-lift angle. Here,
denotes the aerodynamic lift-curve slope of the wing (at the appropriate combination of Mach number and Reynolds number), which will either be assumed or determined from wind tunnel measurements.
The lift force from the tailplane also depends on its angle of attack (which will differ from that of the main wing). It is also affected by the upstream wing’s downwash, which lowers its effective angle of attack by . Depending on flight conditions, the lift force acting on the tail may be upward or downward. Therefore, in trim
(38)
where is the horizontal tail area,
is the elevator deflection angle, and
is the lift-curve slope of the tail with respect to elevator deflection. Assuming the lift-curve slope of the tail to changes in
and
(but not
) is the same as that of the main wing, then
(39)
In reference to the figure shown below, taking moments (positive nose-up) about the c.g. gives
(40)
where is the location of the c.g. relative to the aerodynamic center on the wing, and
is the moment arm for the horizontal tail. In trim,
. Differentiating Eq. 40 with respect to
gives
(41)
Considering the total lift as acting at a distance behind the c.g., then
(42)
Differentiating this equation with respect to gives
(43)
For pitch stability, must be negative for a positive change in
. Therefore, both
and
being positive implies
must be negative, indicating the c.g. must be ahead of the c.p.
Assuming equal lift-curve slopes for the wing and tail, then
(44)
Equating Eqs. 41 and 43, then the equation
(45)
defines the static margin .
Assuming the flight controls (elevator in this case) are fixed and do not contribute to the aerodynamics (), termed the “stick-fixed” response, in non-dimensional terms, then
(46)
The mean chord is the mean aerodynamic chord (MAC) of the main wing, i.e.,
(47)
where is the semi-span, and
is the wing area. The parameter
(48)
is called the non-dimensional tail volume coefficient for the horizontal tail (HT), typically ranging from 0.50 to 0.7 for conventional airplanes. For the vertical tail (VT), this coefficient, denoted by , is usually smaller, in the range from 0.2 to 0.4.
From Eq. 46, the location of the c.g. on the edge of static stability in pitch can be calculated, known as the neutral point , i.e.,
(49)
The neutral point serves as the pivot point of aerodynamic forces. Therefore, the static margin, defined as the distance between the neutral point (np or n.p.) and the c.g., is non-dimensionally expressed (based on preceding definitions and assumptions) as
(50)
If the c.g. is ahead of the n.p., the aircraft is statically stable; if behind, it is unstable. For static stability, a negative static margin is required. However, the value is often quoted such that positive static stability corresponds to a positive static margin, i.e.,
(51)
Check Your Understanding #1 – Estimating the static margin
Consider an airplane with a conventional tail. The airplane is trimmed for straight, level, and unaccelerated flight. The main wing has a lift curve slope of 0.08 per degree. The tail has a lift curve slope of 0.06 per degree and an estimated downwash of 0.1 degrees per degree. The horizontal tail volume coefficient is 0.8. The center of gravity is at 0.36 aft of the datum. Estimate the static margin relative to the position of the center of gravity. Will the aircraft be statically stable?
Show solution/hide solution.
The static margin relative to the position of the center of gravity (c.g.) as a fraction of the mean chord can be expressed by
However, in this case, with different lift curve slopes for the wing and the tail, the static margin must be written more generally as
The values of all the terms in the second term on the right-hand side of the equation are known. However, they must be converted to angular units (radians). For the downwash, then
For the wing, then
For the horizontal tail, then
Therefore,
Entering the numerical values gives
This result confirms that the aircraft has a positive static margin and is statically stable. Note that the tail volume coefficient influences the static margin; therefore, if this value becomes too small, the static margin can be reduced to unacceptable levels, typically resulting in adverse stability characteristics.
Sources of Longitudinal Static Stability
Notice from Eq. 46 that the horizontal tail significantly contributes to the static margin, with a more significant tail volume coefficient increasing the static margin. Indeed, a larger tail area will contribute more to the static stability, as well as a longer distance between the center of pressure on the tail and the wing.
The typical steady (static) pitching moment contributions about the c.g. for a conventional airplane as a function of the angle of attack are shown in the figure below. In this regard, a conventional airplane has a single wing and tail combination. There is a net-zero pitching moment at the trim angle of attack, . The sign convention is that positive moments are nose-up moments, i.e.,
, which tend to increase the wing’s angle of attack and destabilize the airplane. Notice that different pitching moment contributions (both in magnitude and sign) are caused by the various components of the airplane, e.g., the wing, the fuselage, and the tail, which all produce different aerodynamic effects. Therefore, these components produce other moments about the c.g.
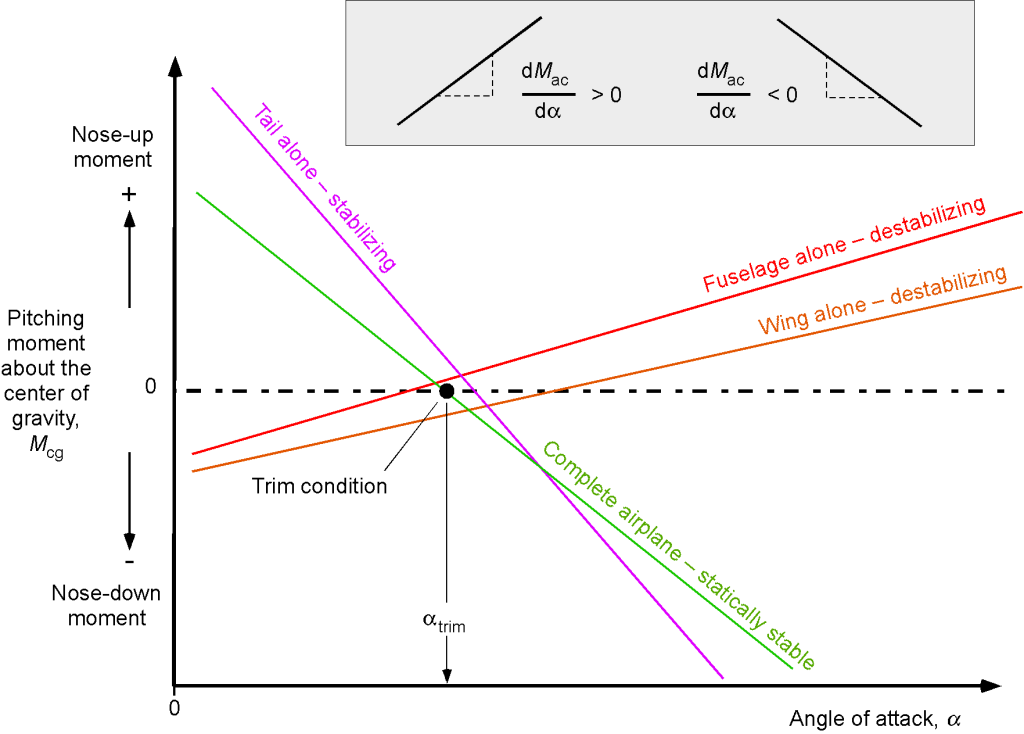
The wing lift component by itself is destabilizing in that it produces a nose-up moment about the c.g., i.e., the slope of the moment curve, , is positive for the wing by itself. Likewise, the fuselage has a destabilizing effect. However, it can be seen that the horizontal tail produces a decisive nose-down moment about the c.g., with a negative slope of the moment curve, providing a significant stabilizing effect, hence the name “horizontal stabilizer” for the horizontal tail.
The combined effect of all the components on the entire airplane is a negative slope, making the airplane statically stable. Generally, a larger horizontal tail will produce a more statically stable airplane, but the physical position of the tail on the fuselage relative to the c.g. (and other things) also plays an important role. In practice, the area of the tail surfaces must be sufficient to provide the airplane with adequate pitch and directional stability. Still, too much stability will also make the airplane less maneuverable and often “tail-heavy” because of the larger surfaces.
Therefore, one goal in airplane design is to provide the tail surfaces with sufficient area to achieve the necessary stability characteristics, without being so large as to adversely affect weight or the location of the center of gravity. It is common for tail surfaces to be undersized during the typical design process, which will become apparent after flight testing. Adding dorsal fins is often a solution that can be implemented with minimal changes to design, weight, and cost.
Check Your Understanding #2 – Horizontal and vertical tail sizing for static stability
In the preliminary design of a specific turboprop aircraft, it is necessary to estimate the size (area) of the horizontal and vertical tails to provide the airplane with sufficient longitudinal and yaw (directional) static stability. Using historical values of the tail volume coefficients for this class of aircraft, = 0.80 and
= 0.2, estimate the areas of both the horizontal and vertical tails if
where the length of the fuselage,
, is 46 ft. Assume that
at the tail surfaces. The reference wing area,
, is 300 ft2 with a mean chord,
, of 5.2 ft.
Show solution/hide solution.
The horizontal tail volume coefficient can be expressed by
Therefore, the horizontal tail area needed for sufficient pitch stability will be
Similarly, the vertical tail volume coefficient is given by
Therefore, the vertical tail area needed for sufficient directional (yaw) stability will be
Dynamic Stability
While static stability ensures that restoring moments exist and that an airplane will tend to return to its trimmed state after a disturbance, it does not explain how the motion unfolds over time. For example, if an airplane is statically stable in pitch, the restoring forces and moments will cause the nose to pitch down after an initial upgust. The same principle applies to yaw and roll disturbances, provided the aircraft has positive static stability. However, this desirable static response does not necessarily mean the airplane will immediately reestablish its trimmed flight condition. Two airplanes may both satisfy the static pitch criterion , yet one may return smoothly to equilibrium while the other may oscillate or take a long time to settle. These differences fall under the study of dynamic stability, which concerns the time-dependent response of an airplane to a disturbance and answers questions such as: Will the motion decay or grow? Will it be monotonic or oscillatory? Will any oscillations be well damped or only lightly damped?
To this end, several possibilities could happen:
1. The airplane may continue to pitch nose-down and overshoot the initial trimmed state. Then the nose comes back up and returns toward trim, but overshoots again. This process may continue in a series of nose-up and nose-down pitching motions, i.e., an oscillating or oscillatory response. Suppose these oscillatory motions eventually damp out over time and cause the airplane to return to the initial trim. This decaying oscillatory motion indicates that the airplane is dynamically stable.
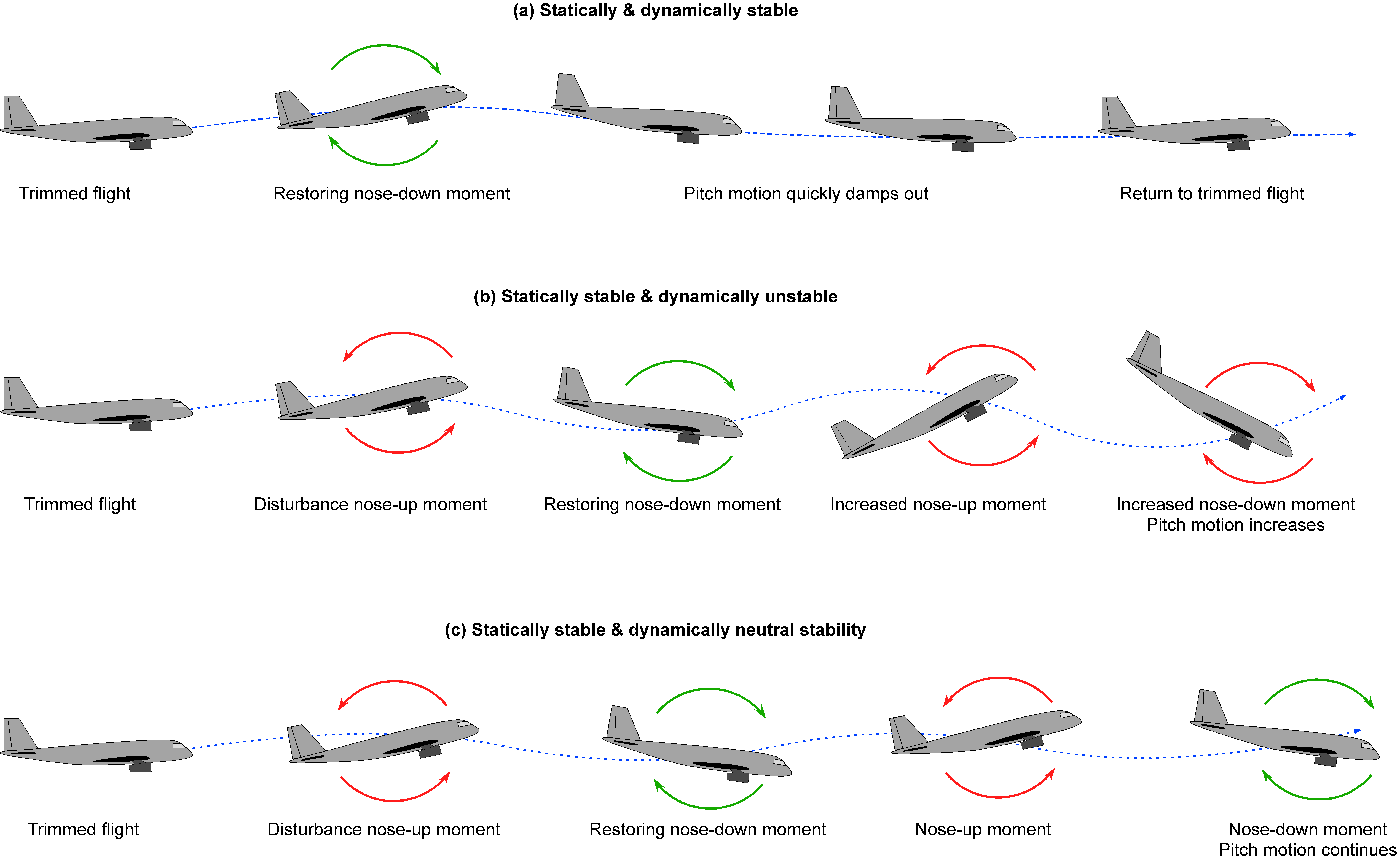
2. The airplane does not overshoot the trimmed state and settles out quickly to reestablish its trim, a process known as subsidence. In this case, the airplane is dynamically stable, and the damping is said to be critically damped or to have a deadbeat response. Some airplanes exhibit this characteristic, but most do not because they would need larger-than-desirable horizontal tail surfaces, which, from a structural design perspective, become a weight issue.
3. The airplane may continue with a continuous nose-up and down pitching motion, with the subsequent oscillations in pitch remaining at an almost constant amplitude. In this case, the airplane’s resulting “roller-coaster” dynamic response exhibits neutral dynamic stability. While the pilot can dampen long-period responses by applying compensatory flight control inputs, it is still undesirable for an airplane.
4. In a worst-case scenario, the airplane may respond with nose-up and nose-down pitching oscillations with increasing amplitude. This type of response would be called a dynamically unstable response. As with weak or neutral damping, an unstable aircraft does not necessarily mean it is unsafe if the unstable tendency has a long period (10s of seconds) and can be controlled by the pilot.
Notice that an airplane must be statically stable to be dynamically stable; i.e., static stability is a prerequisite for dynamic stability. Therefore, a statically unstable airplane will also be dynamically unstable. A statically and dynamically stable airplane is generally easier to fly and control. However, an airplane may be statically stable and dynamically unstable yet still perfectly flyable, especially if the dynamic response is slow enough for the pilot to control it with appropriate “damping” flight control inputs. Short-period responses are very difficult for the pilot to control. However, such an aircraft generally has inferior flying qualities and can impose a high workload on the pilot. The dynamic response may also depend on the aircraft’s weight, the c.g. location, and airspeed.
Eigenvalues & Poles
The mathematics describing the dynamic responses of an airplane are obtained from the linearized equations of motion, written in state-space form, whose eigenvalues (or poles) define the airplane’s natural modes of motion. Each eigenvalue contains two pieces of information: 1. The real part gives the rate of growth or decay. A negative real part indicates a stable mode that decays over time, while a positive real part indicates an unstable mode. 2. The imaginary part gives the oscillation frequency. A purely real eigenvalue corresponds to a non-oscillatory mode, while a complex conjugate pair corresponds to an oscillatory mode.
When the equations of motion of an aircraft are written in linearized form, they can be expressed as a system of first-order differential equations, i.e.,
(52)
where is the vector of state variables,
is the input vector, and
and
are constant matrices that depend on the aircraft geometry and flight condition. This is called state-space form. The homogeneous solution (with
= 0 ) has the form
(53)
where are the eigenvalues of the matrix
,
are the corresponding eigenvectors, and
are constants determined by the initial conditions. The eigenvalues are obtained by solving the characteristic polynomial of
,
(54)
which is a polynomial of order in
. For example, in a two-state system, the result is a quadratic, i.e.,
(55)
whose roots give . The comparison with the canonical second-order form,
, allows the natural
frequency and damping ratio
of that mode to be identified directly from the coefficients. The eigenvalues
are fundamental because they govern how the system responds in time:
- If
, the response decays with time and the mode is stable.
- If
, the response grows with time and the mode is unstable.
- If
, the response persists without growth or decay (neutral stability).
- If
, the response oscillates with frequency
.
The figure below shows a pole plot of classical modes of airplane motion. The horizontal axis shows the real parts of the eigenvalues, which determine stability: poles to the left of the imaginary axis are stable, while those to the right are unstable. The vertical axis gives the imaginary part, which corresponds to the oscillation frequency. Each dynamic mode is directly identified with a particular location of poles (eigenvalues) in the complex plane, and both the real and imaginary parts are needed to understand the nature of the motion.
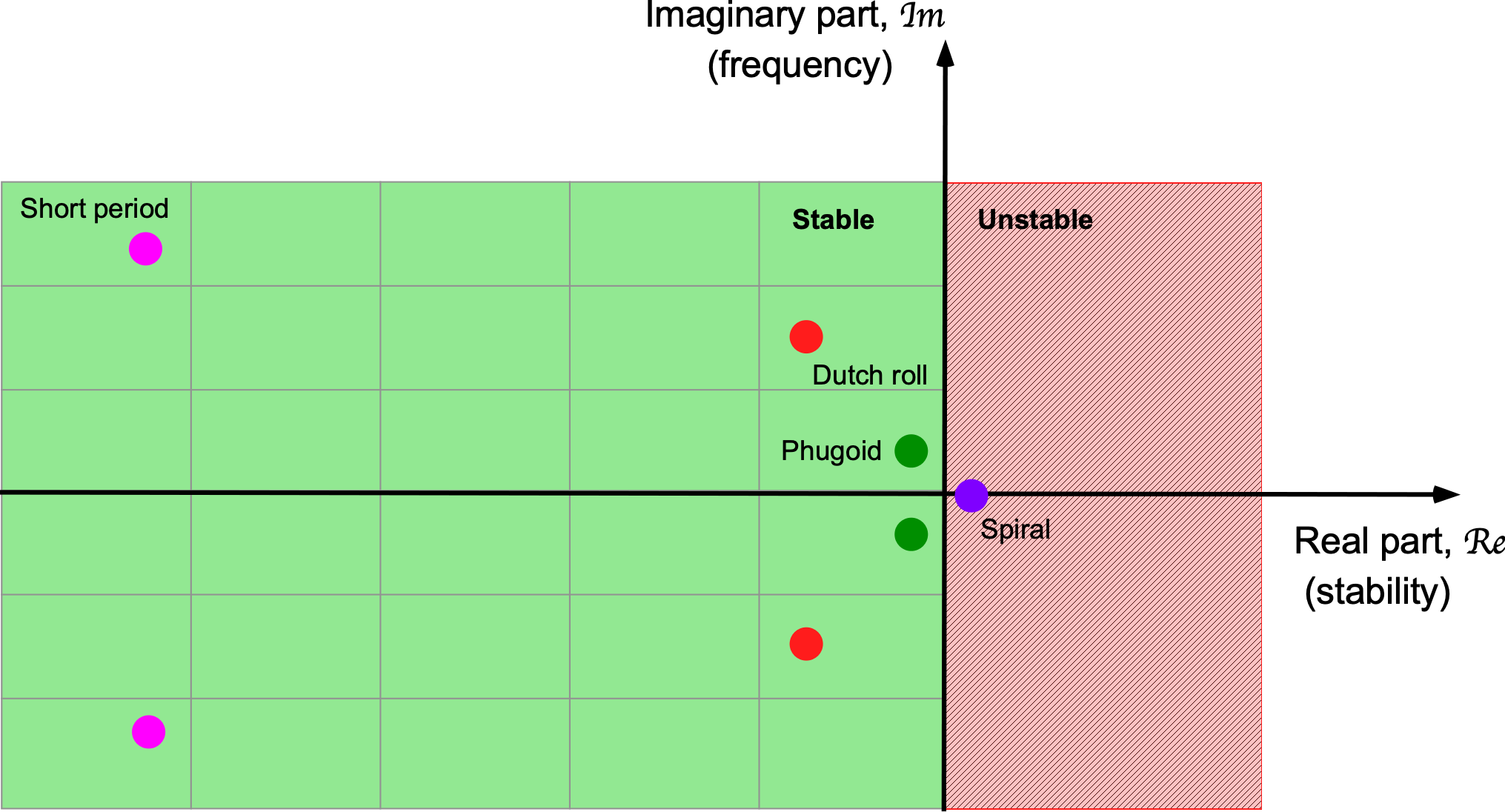
For aircraft motion, the eigenvalues of the longitudinal or lateral-directional equations of motion correspond to the classic modes of motion: 1. Longitudinal, e.g., short-period and phugoid. 2. Lateral-directional, e.g., roll subsidence, Dutch roll, and spiral. Each mode has its own pair of eigenvalues (poles), and by examining their real and imaginary parts, the frequency, damping, and stability of the mode can be determined. In this way, dynamic stability extends the ideas of static stability into the time domain.
Longitudinal (Pitch) Stability
Dynamic pitch stability refers to the behavior of an aircraft’s pitch angle (the angle between its longitudinal axis and the horizon) over time after it has been disturbed from its equilibrium state. In general, two forms of longitudinal dynamic and oscillatory responses are observed in airplanes: the long-period and short-period dynamic responses, as illustrated in the figure below for pitch motion. On the one hand, the short-period response is typically highly damped and lasts less than a second. On the other hand, the long-period or phugoid mode of oscillation is a slower, weakly damped oscillation of the aircraft’s flight path that lasts for many seconds or even minutes.
The starting point for longitudinal dynamics is the linearized pitching moment equation about the trim condition, i.e.,
(56)
together with the kinematic relation , where
is the perturbation in forward speed,
is the perturbation in vertical speed,
is the pitch rate, and
is the elevator deflection. Here, the quantities
denote the dimensional stability derivatives evaluated at the trim state. To close the system, the corresponding force equations in the
– and
-directions may be included, along with the small-angle link between vertical velocity, angle of attack, and attitude, i.e.,
(57)
These equations form the basis for the two characteristic longitudinal modes of motion. The short-period mode arises when the fast dynamics of and
dominate, while
and
vary slowly. Conversely, the phugoid mode arises when the slow exchange between
and
dominates and
remains nearly constant. By making the appropriate approximations, each mode can be reduced to a two-state system, whose eigenvalues define its frequency and damping.
Long-Period Response
The long-period response, also known as the phugoid, is one of the most interesting aspects of an aircraft’s flight dynamic behavior. As shown in the figure below, it is typically a weakly damped oscillatory motion in which the airplane exchanges kinetic and potential energy at nearly constant angle of attack. The term “phugoid” was initially coined by Frederick Lanchester for the dynamic pitch response of an aircraft; the word has a literal translation from Greek meaning “fleeing” rather than the word Lanchester wanted, which was “flying,” so it is a misnomer. The short-period oscillatory response mode is of a higher frequency. It is a highly damped oscillatory response that often appears in an airplane’s dynamic response after encountering gusty air or applying quick elevator inputs, such as during landing. However, the short-period response is usually unnoticed by the pilot and does not require control. All three flight axes will typically exhibit short-period dynamic responses, which will be damped out in all cases.
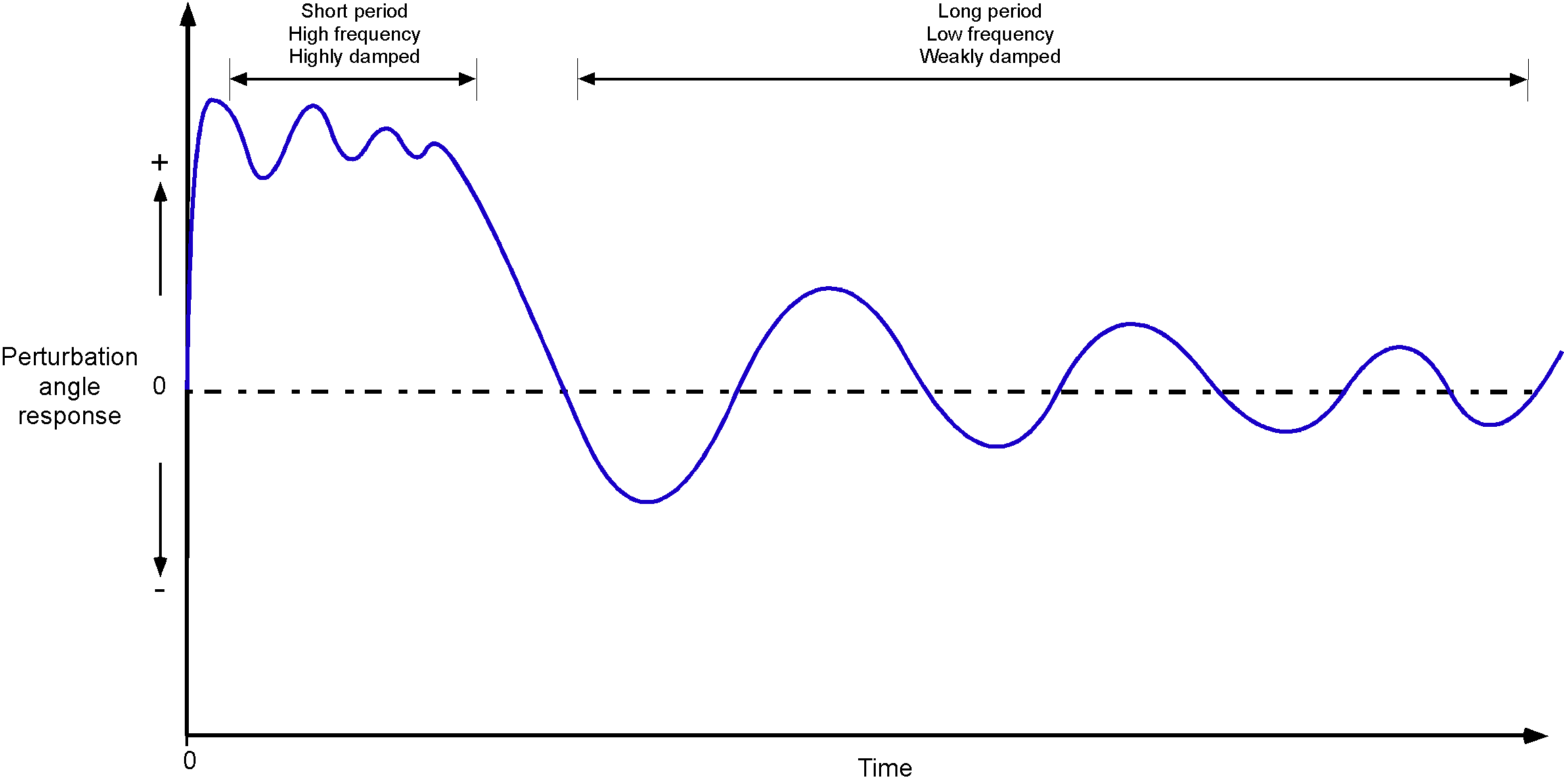
Lanchester Solution
Lanchester modeled the phugoid response using small-perturbation assumptions, i.e., the angle of attack remains nearly constant, lift is approximately equal to weight, and thrust variations are negligible over the motion. Let be the forward-speed perturbation and
the flight-path angle perturbation about the trimmed flight condition at speed
. The force balance along the flight path is
(58)
where is the mass of the airplane and
is the drag perturbation. Notice that
is used to prevent symbol conflict with moment derivatives. With
nearly constant, drag varies mainly with dynamic pressure, so linearizing about
gives
, where
is the trim drag. Substituting this into the force equation gives
(59)
In the phugoid approximation, the pitch attitude is the sum of the trim attitude and the flight-path angle, i.e.
(60)
because the angle of attack changes very little during the motion. The kinematic relation between and
then follows from the constant angle of attack assumption, i.e.,
(61)
Differentiating this and substituting for gives
(62)
which is the standard second-order form for the phugoid. Comparing with the canonical form of a second-order spring-mass-damper system, , the natural frequency and damping ratio of the phugoid are
(63)
These scalings show that decreases with increasing airspeed, while the damping ratio is proportional to the drag-to-lift ratio at trim. For small perturbations, a common historical approximation attributed to Lanchester is simply the above pair, i.e.,
(64)
which highlights why the phugoid is often very lightly damped for aerodynamically efficient aircraft with large ratios, such as sailplanes.
For underdamped motion , the pitch attitude and speed perturbation can be written as
(65)
where is the damped frequency,
is the damping ratio,
and
are constants determined by the initial conditions, and
is the trim airspeed. Because
is proportional to the time derivative of
, it is approximately
out of phase with
for a lightly damped phugoid, illustrating the slow exchange between kinetic and potential energy at nearly constant angle of attack.
State-Space Form
Lanchester’s original description of the phugoid used the small-perturbation assumptions of constant angle of attack, lift equal to weight, and negligible thrust variations. From these assumptions, the force balance along the flight path and the kinematic link between forward speed and pitch/flight-path angle lead to the familiar second-order equation (Eq.62) in which the restoring effects are governed primarily by forward airspeed and flight-path perturbations rather than by rapid changes in and
. It is often convenient, however, to recast the same relations in matrix form. Choosing the state vector as the forward-speed perturbation
and the flight-path angle
, the linearized phugoid equations become
(66)
where the entries of the state matrix are exactly those that appear in Lanchester’s derivation. The characteristic equation of
leads to the same natural frequency and damping ratio as above, i.e.,
(67)
Therefore, the matrix form and the historical scalar derivation are entirely consistent: the former emphasizes system structure and eigenvalue interpretation, while the latter illustrates the underlying physical balance of forces and energy.
Measuring the Long-Period Response
The long-period response is one of the most interesting aspects of an aircraft’s flight dynamics, typically characterized by a weakly damped oscillatory motion. It can be measured in flight, and many engineering schools have access to an airplane that can be used to demonstrate the long-period “phugoid” response. Students then get to see the long-period mode as a real, measurable aircraft behavior, feel its characteristics in flight, and learn how to quantify it from data, transforming equations into something they can measure, calculate, and interpret with confidence.
Representative in-flight measurements from flights in a Cessna are shown in the figure below. However, such results could also arise from a flight dynamics simulation using solutions to the equations of motion. These types of responses are obtained by disturbing the aircraft from its trimmed condition by the sudden application of the elevator (i.e., pulling back quickly, holding for a few seconds, and then releasing) and then measuring the displacements using suitable instrumentation, such as angle-of-attack sensors and accelerometers. If sufficiently large, the resulting pitch excursions can often resemble a roller-coaster ride!
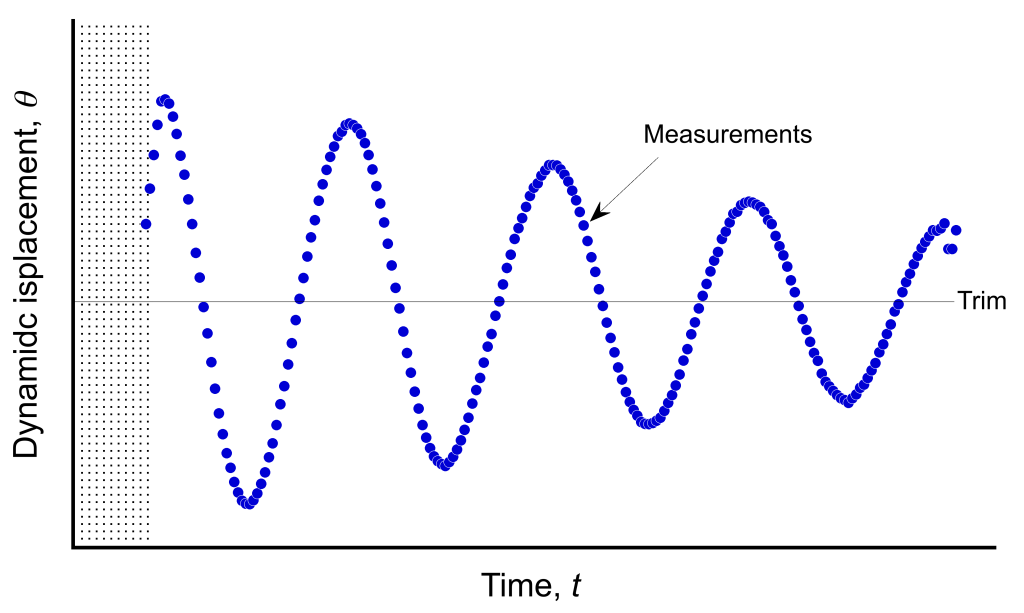
Characteristic Response
For disturbances about a mean or trim pitch attitude, the dynamic motion can be expressed in another form of Eq. 65 as
(68)
where is the pitch displacement,
is the trim angle,
is the undamped natural frequency of the motion, and
is the damped natural frequency. The constants
and
are determined by the initial conditions at the moment of disturbance. The relationship between the damped and undamped frequencies is
(69)
where is the damping ratio. Because
for a stable oscillation, the damped frequency is always less than the undamped frequency. In practice, the principal quantity of interest from flight-test measurements of the phugoid is the damping ratio, which can be determined from the oscillatory time history using the logarithmic decrement method.
The logarithmic decrement represents the rate at which the amplitude of the phugoid displacement decreases. It can be defined as the ratio of any two successive amplitudes in the time history of the motion. These amplitudes could represent peaks or valleys in the motion, enabling the development of different methods to estimate damping. In the ideal cases, measurements of the complete time history of the aircraft’s dynamic motion will be available. In other cases, only the times of the peaks and valleys in the dynamic response may be available for analysis. If any of these results are available, the damping of the dynamic motion can be estimated.
Method of Analysis
Let and
be the times corresponding to a successive peak and valley (or a successive valley and peak) in the dynamic response. These displacements are measured about the trim angle and are one-half cycle apart, so
, where
is the period of the oscillation.
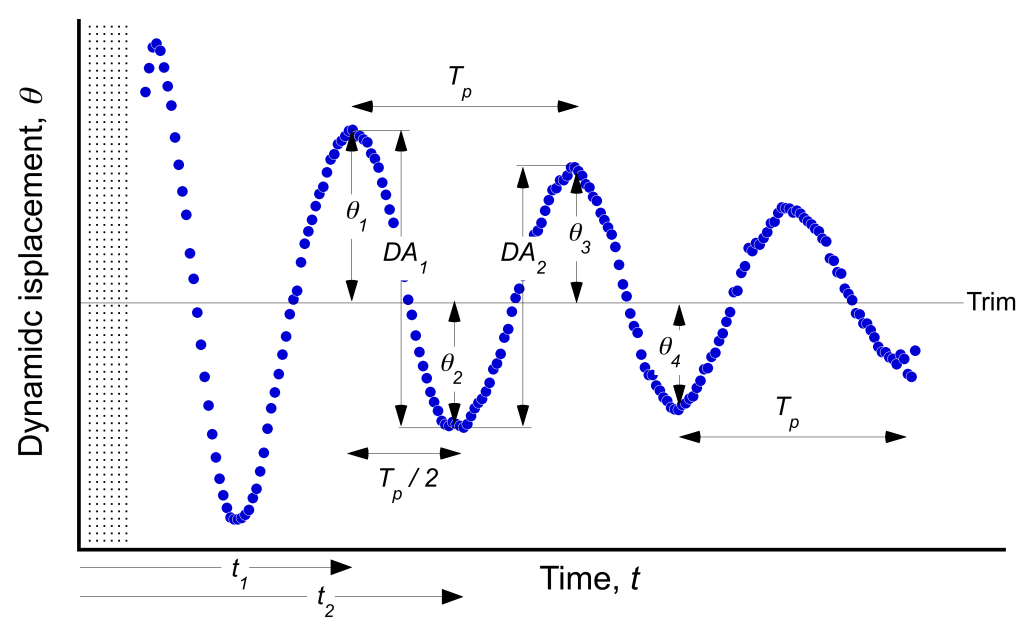
For a lightly damped oscillation, the pitch displacement is
(70)
where . At
and
, the displacements are
(71)
If the two peaks are exactly one period apart, then
(72)
so that
(73)
The ratio of the peaks is then
(74)
To improve accuracy, an average can be taken over many such peak ratios. This is called the Transient Peak Ratio (TPR) method, i.e.,
(75)
The logarithmic decrement is then
(76)
Using gives
(77)
and rearranging gives the damping ratio as
(78)
An alternative is the peak-to-valley method. Let ,
, and so on, with peaks and valleys half a cycle apart. For example,
(79)
Similarly,
(80)
The ratio of successive values is then
(81)
The corresponding TPR is
(82)
and the logarithmic decrement is
(83)
The damping ratio follows from
(84)
The average period over cycles can be found from
(85)
the average damped frequency from
(86)
and the undamped natural frequency from
(87)
In a flight-test exercise, these methods enable the direct measurement of phugoid characteristics from flight data and their comparison with theoretical predictions. By deliberately exciting the long-period mode in an aircraft and recording the resulting pitch-attitude and airspeed time histories, one can determine the oscillation period, the damped and undamped natural frequencies, and the damping ratio using the TPR or peak-to-valley methods. The results can then be compared to a theoretical model of the airplane or used in another context to verify its dynamic response characteristics.
Short-Period Response
The short-period mode is the high-frequency complement to the phugoid. It is usually well damped and dominated by rapid changes in angle of attack and pitch rate, with minimal changes in flight path or forward speed. Because of its rapid dynamics, it is often superimposed on slower pitch motions. To a pilot, the short-period mode often feels like a brief but rapid pitching motion of the airplane. Because the motion is quick and usually well-damped, it is not always consciously recognized during normal flight. Still, it defines the immediate feel of the airplane to a pitch input. This is in contrast to the phugoid, which is slower, larger in amplitude, and much more easily perceived.
Starting from the pitching-moment equation in Eq. 56 and eliminating the slow variables and
, a reduced longitudinal model for the short-period response may be written in terms of
and
as
(88)
together with the kinematic relation . Here
is the angle of attack and
is the pitch rate. The state matrix for
is
(89)
The characteristic polynomial of is
(90)
so that
(91)
For small short-period motions, changes nearly in proportion to
, so the same second-order form applies to
. The pitch-attitude time history is
(92)
where is the trim attitude,
is the damped frequency, and
and
depend on initial conditions. In flight test, the short-period mode is often identified by applying a brief elevator pulse and fitting
and
from the resulting
or
records, which can then be compared with predictions from the aerodynamic derivatives.
In some circumstances, the pilot may inadvertently excite the short-period responses, such as during landing or in severe turbulence, when making quick, deliberate movements of the control stick to adjust the aircraft’s flight attitude. In particular, a landing requires significantly increased attention from the pilot on the controls. In some cases, the pilot’s control inputs may become entirely out of phase with the aircraft’s short-period response, resulting in what is known as a pilot-induced oscillation (PIO).
A PIO is just one type of Airplane-Pilot Coupling (APC) effect. A PIO is often a hazardous flight condition because the pilot’s inputs may cause the short-period response to become quickly divergent, resulting in a mishap or a crash. Most pilots initially tend to induce APC effects when flying sailplanes or jet fighters with relatively sensitive flight controls. The solution to developing a PIO is for the pilot to relax their grip on the flight controls, which removes the pilot’s out-of-phase inputs from the control loop and allows the airplane’s natural response to damp out.
Summary of Longitudinal Pitch Dynamics
The short‐period and long‐period (phugoid) modes represent the two primary oscillatory responses in the airplane’s longitudinal dynamics. Although both are governed by the same underlying equations of motion, their frequency content, damping, and pilot perception differ substantially. The short‐period mode is characterized by rapid, heavily damped pitch‐attitude changes. In contrast, the phugoid involves slow, lightly damped exchanges between potential and kinetic energy at nearly constant angle of attack. The table below compares the principal characteristics of these two modes, providing an easy reference for recognizing and interpreting them.
| Characteristic | Short‐Period Mode | Long‐Period (Phugoid) Mode |
|---|---|---|
| Typical frequency | High (1–3 Hz) | Low (0.05–0.2 Hz) |
| Typical damping ratio | 0.3–0.8 (well damped) | 0.02–0.1 (lightly damped) |
| Dominant motion | Angle of attack and pitch rate | Flight path angle and speed |
| Effect on airspeed | Minimal | Significant |
| Pilot perception | Often unnoticed | Easily perceived |
| Control requirement | None under normal operations | May require small corrections |
| Primary energy exchange | Between aerodynamic and inertial pitching moments | Between kinetic and potential energy |
Check Your Understanding #3 – Short-period pitch dynamics
An airplane is in straight and level flight at an airspeed of = 60 m/s (assume
). Its weight is
= 5,000 N, giving
509.7 kg. The pitching moment of inertia is
4,500 kg m
. The following stability derivatives are known:
= -4,000 N/rad,
= 0,
= -30,000 N/rad,
= -1.20
10
N m/rad,
= -2.50
10
N m s/rad, and
= -9.00
10
N m/rad.
- Form the short-period state matrix
for the states
.
- Find the eigenvalues of
.
- Determine the natural frequency
, damping ratio
, damped frequency
, peak time
, settling time
(2%), and overshoot
.
- For a step elevator input
= -5
, describe the qualitative nature of the short-period response.
Show solution/hide solution.
When including the elevator control, , he short-period dynamics can be written in the standard form as
and
Substituting the given values of ,
, and the stability derivatives gives
with the input matrix
From the state matrix, the characteristic polynomial is
Expanding out gives
with
Therefore,
and the eigenvalues (short-period poles) are
This confirms an oscillatory (complex conjugate) and stable (negative real part) mode. The natural frequency is the magnitude of the eigenvalues, i.e.,
The damping ratio is the fraction of the real part to , i.e.,
From these, the damped frequency is
and the associated time-domain metrics are
The overshoot for a unit step is
For a step elevator input = -5
= -0.087 rad, the system exhibits a moderately damped oscillation in
and
. The pitch rate peaks at about
s with roughly a 13% overshoot, and the oscillation decays to within 2% of its final value in about 1.4 s. Because this is the short-period mode, the response is “stiff,” so the angle of attack and pitch rate change rapidly, while forward speed and flight path angle remain nearly unchanged. This is the pitch behavior that pilots recognize as the airplane’s short-period response.
Center of Gravity Effects & Limits
As previously discussed, the c.g. location of an airplane is critical because it has a powerful effect on its stability and control characteristics, e.g., if the c.g. moves with respect to the neutral point or if the neutral point moves (because of compressibility effects) with respect to the c.g. If the c.g. location moves progressively aft (toward the tail), such as when fuel is burned off, then the moment curve slope becomes less negative and eventually becomes zero at the neutral point; in this case, the airplane will have neutral static stability.
If the c.g. is moved further back, the airplane will become unstable. This behavior can become a problem on some airplanes if the c.g. moves too far rearward, such as when a load is discharged in flight, e.g., weapons, cargo, or parachutists. Likewise, for whatever reason, suppose the c.g. moves toward the nose. In that case, the moments must be trimmed out using elevator control inputs or a horizontal tail with trim capability. Eventually, suppose the c.g. location moves too far forward so that the upward elevator displacements on the tail surfaces will not generate enough aerodynamic force to compensate. In this case, the airplane cannot be trimmed and becomes unflyable, nosing down toward the ground and building airspeed, often with a catastrophic outcome.
It is clear, therefore, that design engineers must carefully establish the c.g. limits (fore and aft) on all airplanes to ensure that they fall within an acceptable range for safe flight and that any c.g. movements during the flight will not compromise their stability and control characteristics. An example of a c.g. chart for an airplane is shown below. Based on the estimated takeoff weight and the calculated c.g. location, the values must lie within the aircraft’s defined and certified envelope to be safe to fly. The area marked in red is outside of the acceptable flight envelope.
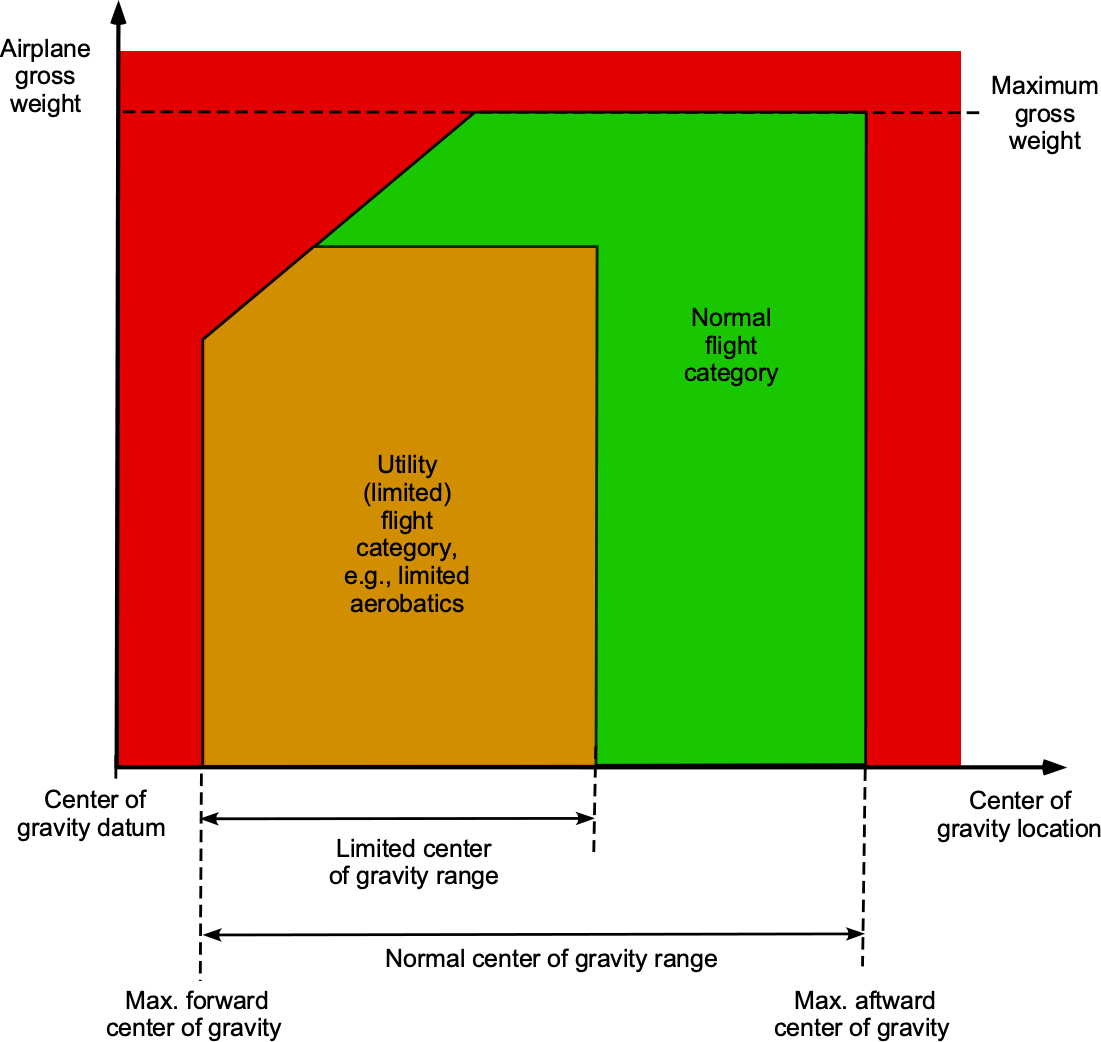
In practice, the pilot must ensure that the airplane is loaded correctly before the flight, with all passengers and cargo, and that the c.g. location is within the certified limits before takeoff. Indeed, airplanes have crashed because they were not loaded correctly, the cargo shifted during flight, or fuel and weight were burned off, causing the c.g. to move out of the allowable envelope. The airplane either became unstable, or the control forces became too high for the pilot to manage.
Lateral (Roll) Stability
Lateral stability and control refer to displacements about the longitudinal or roll axes. For example, an airplane has lateral static stability if, after a disturbance is applied, it rolls and acquires a bank angle, but simultaneously generates new aerodynamic forces and moments that tend to reduce the bank angle and return the airplane to its initially trimmed flight condition. All airplanes have at least some inherent lateral stability, although because roll and yaw responses are coupled, the resulting dynamic response characteristics tend to be more complicated.
Roll Subsidence
Roll subsidence is the simplest lateral-directional motion of the airplane. It is an aperiodic, non-oscillatory mode that describes how any initial roll rate, , decays over time due to aerodynamic damping in the roll motion. If the pilot commands a roll with the ailerons and then releases the control, the wings gradually return to level flight as the roll rate damps out.
Mathematically, the linearized rolling-moment equation about trim is
(93)
where is the roll moment of inertia,
is the rolling-moment derivative with respect to roll rate, and
is the rolling-moment derivative with respect to aileron deflection
. With the ailerons fixed
, the homogeneous equation reduces to
(94)
Because is negative for a stable airplane, the solution is
(95)
which shows an exponential decay of roll rate with time. The time constant of the decay is
(96)
so that stronger roll damping (more negative ) gives faster decay, while a large moment of inertia slows the response.
Roll subsidence is therefore a purely stable, non-oscillatory mode. Its frequency content is essentially zero, and it is strongly damped for most airplanes. Pilots usually do not consciously perceive this mode, since the airplane “settles” out of a roll when the ailerons are released. Nevertheless, roll damping is essential for flying qualities, because if is too small, the airplane may feel sluggish or unresponsive in roll.
While roll subsidence describes how an initial roll rate decays through damping, static lateral stability is also determined by how the airplane responds to a steady bank angle or a sideslip disturbance. These effects introduce additional rolling-moment derivatives that play an essential role in overall lateral stability.
In the state-space formulation, this mode appears directly in the lateral-directional system matrix. With the state vector , the second row of
is
(97)
so that the element of
is
. The corresponding eigenvalue is therefore
(98)
which represents the roll subsidence mode.
Dihedral Effects
It is well known that using dihedral on the wings is a powerful means of increasing an airplane’s lateral stability, as shown in the figure below. Just a few degrees of dihedral can make a marked improvement in lateral stability. The horizontal tail may also exhibit some dihedral, contributing somewhat to lateral stability, as illustrated in the figure below.
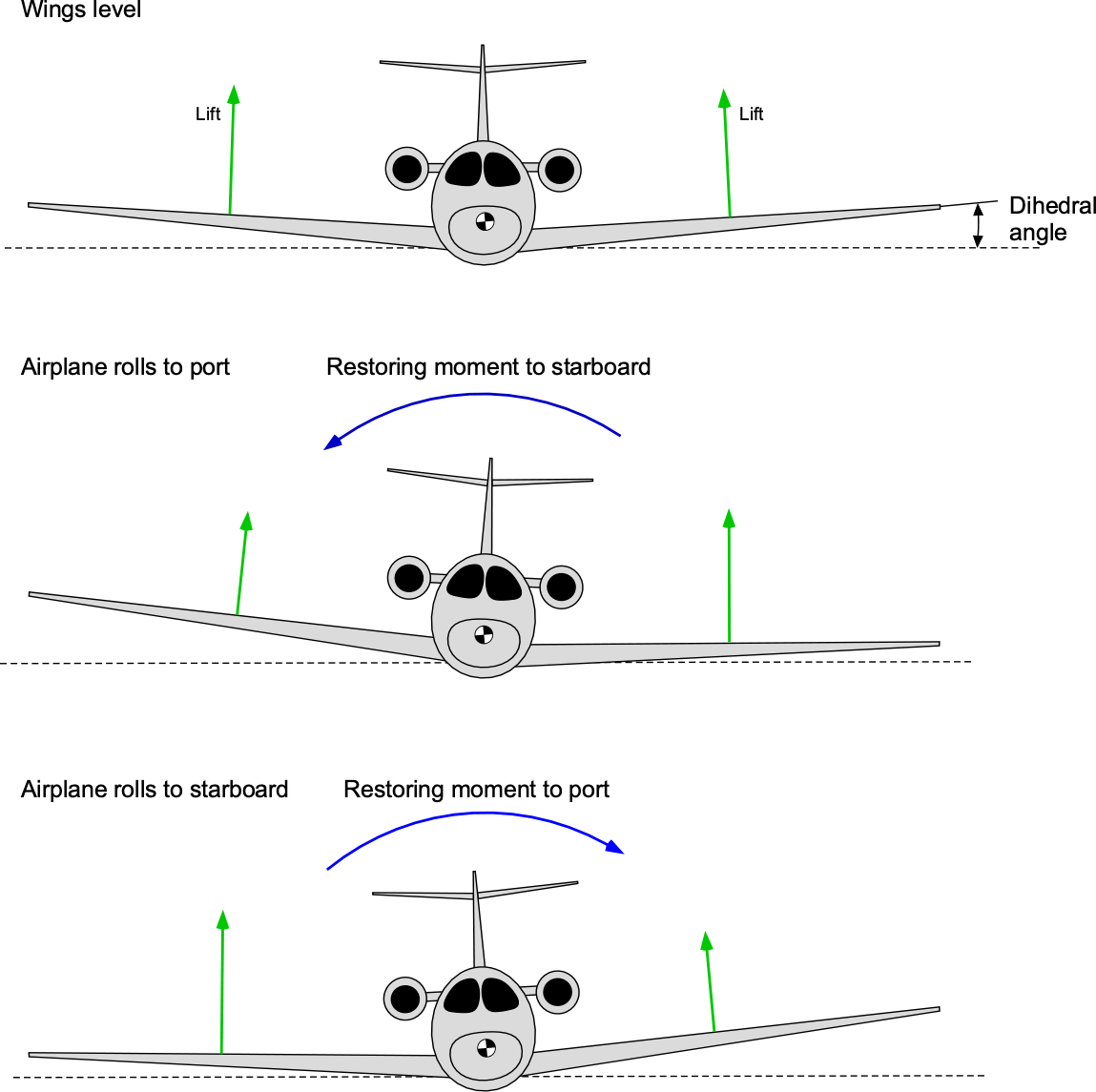
The rolling moment coefficient, , can be expressed as a function of the roll angle
, roll rate
, sideslip angle
, and other contributing factors as
(99)
where is the static roll stiffness (restoring moment with bank angle),
is the roll damping (resists roll rate), and
is the dihedral effect (rolling moment due to sideslip angle). The dihedral effect is significant because it determines how the airplane responds to a steady sideslip disturbance. A positive geometric dihedral angle produces a rolling moment that tends to raise the lower wing in a sideslip, giving
. This contribution is often called the “dihedral effect,” even though it arises not only from wing dihedral but also from wing placement, sweep, and other design features.
The corresponding rolling moment about the -axis is
(100)
so that the dimensional derivative is
(101)
In the state-space formulation, this term appears in the second row of the lateral-directional system matrix. With the state vector , recall that sideslip is related to lateral velocity by
. Therefore,
(102)
where . Therefore, the
element of
corresponds directly to the dihedral effect. A positive
gives a positive contribution, rolling the airplane away from the sideslip, and plays a central role in the overall lateral-directional stability. Using dihedral, however, tends to enhance the coupling between yaw and roll control inputs, i.e., rudder and aileron, respectively.
Besides wing dihedral, other geometric features also influence lateral stability. Wing position relative to the fuselage, wing sweep, and even fuselage and tail aerodynamics can increase or reduce roll stability. These factors often interact, so designers sometimes need to counterbalance one source of stability with another, for example, by adding anhedral to highly swept or high-mounted wings.
The vertical position of the wing relative to the aircraft’s c.g. also affects lateral stability, such as in airplanes with a high-mounted wing versus a low wing. A high-wing airplane design naturally tends to have better lateral stability than a low-mounted wing because the c.g. is below the wing’s center of pressure, giving a form of pendular stability. This behavior is why dihedral is not a common design feature on high-wing airplanes. Some airplanes with high-mounted wings may use partial dihedral only on the outer wing panels, but this feature is rare.
Wing sweep is used on high-speed airplanes to reduce compressibility drag; however, it also significantly increases lateral stability. A combination of wing dihedral and wing sweep often gives an airplane too much lateral stability. Therefore, airplanes with highly swept wings may use anhedral to negate the inherent lateral stability caused by wing sweep. Furthermore, on a large/heavy airplane with a high-mounted wing configuration, e.g., the C-5 Galaxy, there is usually excess pendular roll stability because the c.g. lies below the center of the lift, as shown in the figure below. The center of lift can be assumed to be the aerodynamic “pivot” point. In this case, anhedral on the wing is necessary to prevent lateral stability from being too pronounced, thereby making the aircraft easier to turn and maneuver.

An anhedral angle on a fighter airplane, as shown in the photo below, is necessary to provide both agility and maneuverability. Fuselage and vertical tail effects may contribute to or detract from the airplane’s lateral stability, depending on the shape of the fuselage and the position of the vertical tail. In this context, it is important to distinguish between maneuverability and agility.

On the one hand, maneuverability refers to the ability of an aircraft to achieve and sustain significant changes in flight path or attitude under pilot command, such as entering a steep climb, rolling rapidly into a bank, or sustaining high load factors in a turn. Agility, on the other hand, emphasizes how quickly and responsively the aircraft can react to short-duration control inputs or disturbances, reflecting its immediate dynamic behavior. While maneuverability is most often associated with structural capability and aerodynamic limits, agility is tied directly to the aircraft’s stability and control characteristics. The need for high agility is particularly crucial for modern fighter airplanes, where rapid responses to pilot inputs are essential.
Maneuverability and agility can also be connected to the mathematical descriptions of stability and control. Maneuverability is often characterized by the maximum load factor an airplane can sustain, which directly relates to how tightly it can turn, climb, or produce a load factor. A wing with a higher maximum lift coefficient and/or a higher overall thrust-to-weight ratio leads to greater maneuverability.
Agility, by contrast, refers to the rate at which an airplane responds to control inputs or disturbances. One measure of roll agility is the roll acceleration produced by an aileron deflection, i.e.,
(103)
where is the rolling-moment derivative with respect to aileron deflection,
is the roll moment of inertia, and
is the aileron input. This equation indicates that greater control effectiveness or lower inertia results in a more agile roll response.
In pitch, agility is often linked to the frequency of the short-period mode. From the reduced state-space form, the undamped natural frequency is , as previously discussed. A larger value of
corresponds to a crisper, more responsive pitch feel. Together, these measures highlight the differences between maneuverability, a sustained capability, and agility, an immediate and dynamic response, as summarized in the table below.
| Characteristic | Maneuverability | Agility |
|---|---|---|
| Definition | Ability to achieve and sustain large changes in flight path or attitude | Ability to respond quickly and precisely to short-duration inputs or disturbances |
| Typical examples | Sustaining a steep climb, executing a high-g turn, rolling to a large bank angle | Rapid pitch response, quick roll acceleration, sharp yaw correction |
| Primary emphasis | Structural strength, aerodynamic performance, and available thrust | Stability derivatives, control effectiveness, and dynamic response |
| Time scale | Seconds to tens of seconds (sustained motion) | Fractions of a second to a few seconds (immediate reaction) |
| Pilot perception | How well the aircraft can be pushed to and held at its performance limits | How “crisp,” “snappy,” or responsive the aircraft feels to quick inputs |
| Relevance | Important for transport aircraft, heavy military aircraft, and sustained maneuvers | Critical for fighters, aerobatic aircraft, and situations demanding rapid response |
Directional Stability
Dynamic flight responses are also associated with an airplane’s directional (yaw) or weathercock motion. However, as already mentioned, an airplane’s static lateral (roll) and directional (yaw) stability characteristics are intrinsically coupled; i.e., a roll response causes a yaw response, and vice versa. This coupling also affects the dynamic response, i.e., what happens to the airplane at longer times after a disturbance in roll or yaw. This so-called cross-coupling between the directional and lateral static stability can give rise to three critical dynamic responses: a directional divergence mode, spiral divergence mode, and the oscillatory “Dutch roll” mode.
Directional Divergence
The directional divergent response results from a directionally unstable airplane, as explained in the figure below. When the airplane yaws or rolls into a sideslip, side forces are generated, and the resulting yawing moments can continue to increase the sideslip, leading to significant yaw angles. Recovery is accomplished by the regular use of flight controls. However, the concern is that the vertical tail can stall at steep angles, reducing its aerodynamic effectiveness in response to pilot rudder inputs and making recovery difficult. For this reason, not only is the sizing of the vertical tail essential to give sufficient directional stability, i.e., in providing adequate surface area, but also in controlling its higher yaw angle of attack behavior.
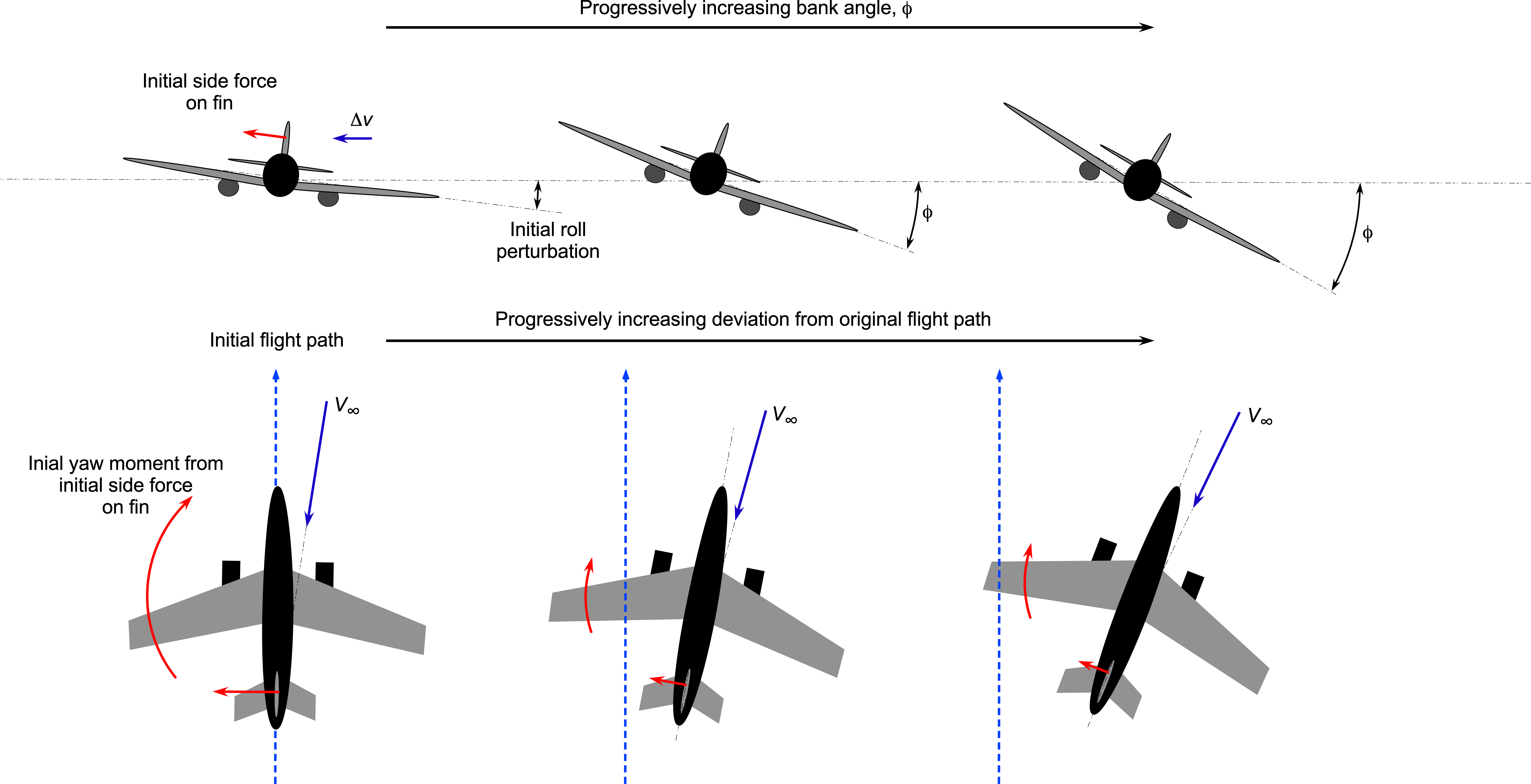
Quantifying the directional divergence requires the evaluation of the stability derivatives with respect to yaw, particularly the yawing moment coefficient derivative with respect to sideslip angle, . The yawing moment coefficient can be expressed as a function of the sideslip angle
, yaw rate
, and possibly other contributing factors, as
(104)
where is the yawing moment coefficient at zero sideslip,
is the yawing moment coefficient derivative with respect to sideslip angle, and
is the yawing moment coefficient derivative with respect to yaw rate. A disturbance in yaw should result in a restoring yawing moment for an aircraft to be considered directionally stable, which is indicated by a negative value of
. Mathematically, this condition can be stated as
(105)
For directional stability, then
(106)
However, if , then the airplane will be directionally divergent, which is an undesirable flight characteristic.
In the state-space formulation, the directional stability derivative appears in the third row of the lateral-directional system matrix. With the state vector , note that
. The dimensional derivative is
(107)
so that the yaw equation includes
(108)
where . Therefore, the
element of
corresponds directly to
, and the sign of this derivative determines whether the yaw motion is restoring (stable) or divergent.
Dutch Roll
The “Dutch roll”[14] response of an airplane is a weaving dynamic response mode coupled with both the directional and spiral divergence modes. For most airplanes, the lateral stability is always fairly good, whereas the directional stability can be weaker. This behavior is especially pronounced if the tail is slightly undersized during design, a relatively standard approach to save airframe weight. Airplane designs typically become tail-heavy when stability requirements are fully met.
If a sideslip disturbance occurs, the airplane yaws in one direction, and the airplane rolls the other way in the form of a weaving motion, as illustrated in the figure below. While this motion is relatively low in frequency and usually well-damped, it can be incredibly annoying for the crew and passengers during flight and may even be uncomfortable. In addition, on some airplanes, the Dutch roll mode can become weakly divergent, which is always cause for concern. In this case, a yaw damper, which is part of the flight control system (autopilot), is used to damp out the Dutch roll mode and improve the flying qualities; the damper is switched on soon after takeoff and switched off again just before landing. Most swept-wing jet aircraft require a yaw damper to prevent excessive Dutch roll.
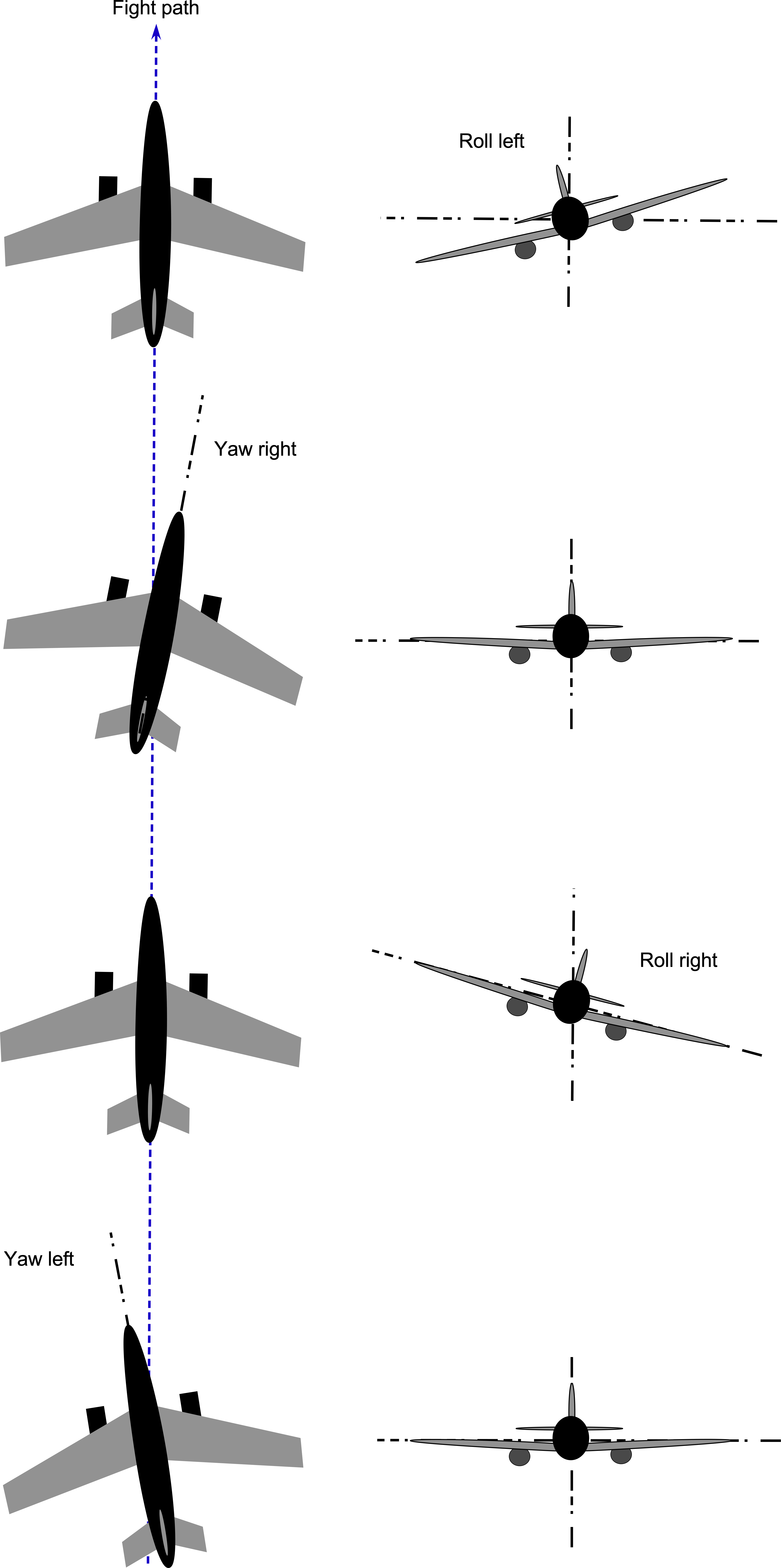
Analysis of the Dutch Roll Response
The Dutch roll motion can be described using the linearized equations of motion for small perturbations around a steady flight condition. For the sideslip angle, the equation of motion may be written in approximate form as
(109)
where is the sideslip angle,
is the yaw rate,
is the moment of inertia about the
-axis, and
and
are the yawing-moment stability derivatives. The corresponding equation of motion for the roll rate is
(110)
where is the roll moment of inertia, and
and
are rolling-moment stability derivatives. These equations highlight the coupling between sideslip, yaw, and roll, which is the essence of the Dutch roll motion.
Collecting these terms into state-space form with gives
(111)
The parameters and
represent effective yaw- and roll-damping time constants, respectively, while
represents the cross-coupling between yaw and roll. These terms combine the effects of the underlying dimensional stability derivatives into a compact state-space form, making the Dutch roll dynamics transparent.
Because the Dutch roll is a lightly damped, oscillatory mode, the eigenvalues of this reduced system appear as a complex conjugate pair, which can be written in the familiar second-order form
(112)
where is the natural frequency and
is the damping ratio of the Dutch roll oscillation. Typical values of
lie between 0.05 and 0.2, so the oscillations often persist for many cycles. For this reason, many airplanes rely on yaw dampers to increase effective yaw damping (to reduce
) and improve Dutch roll handling qualities.
Design Factors Influencing Dutch Roll
The vertical tail provides most of an airplane’s static directional stability, significantly affecting the Dutch roll response. An airplane is said to possess lateral directional or yaw stability if the aircraft yaws after a disturbance is applied, but simultaneously generates new aerodynamic forces and moments that tend to dampen out the yaw displacement. However, the combined size and depth of the fuselage, as well as the vertical tail’s height, area, and shape, ultimately affect an airplane’s directional stability characteristics.
For example, suppose an airplane experiences a sideslip angle, . In this case, the fuselage produces a side force that tends to increase that angle, similar to what the fuselage does for the pitch response. Deep fuselages with boxy or deep elliptical cross-sections tend to be much worse in terms of directional stability than fuselages with circular cross-sections. During the design process, such issues are often explored by wind tunnel testing. A design goal is to shape the fuselage to minimize static instability, thereby reducing the tail size and saving airframe weight.
Fuselages with a larger area forward of the airplane’s c.g. tend to have less directional stability. Examples include the Boeing 747 and the C-5 Galaxy, which feature large vertical tails to compensate for the large “hump” on the forward fuselage. The Airbus A380 had similar design issues, so it has a large vertical tail. The somewhat disproportionately large vertical fin and horizontal tail sizes of the A380, as well as the shorter fuselage of the Boeing 747SP (SP = Special Performance), are also distinctive, as shown in the photograph below. These features are necessary to provide sufficient static and dynamic stability while minimizing Dutch roll.

Ventral and/or dorsal fins are used on some airplanes to augment the directional stability and/or reduce the tendency to develop a Dutch roll, especially at high airspeeds. Adding more vertical tail area, such as through a dorsal fin extension or a ventral tail extension, as shown in the figure below, provides increased directional stability but at the cost of a minor increase in structural weight.
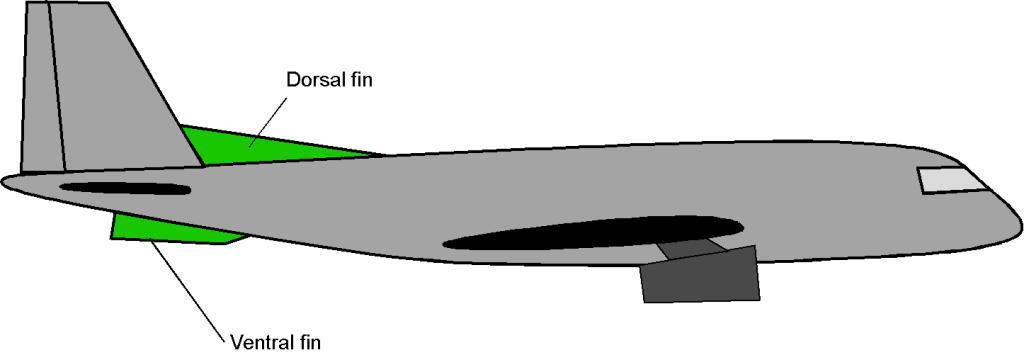
Indeed, dorsal or ventral fins are simple, lightweight structures that can be resized quickly and inexpensively during flight testing. They are often helpful in achieving the necessary levels of directional stability for the airplane without requiring a complete redesign of the vertical tail to resolve deficiencies in flight dynamics. The airplane in the photograph below, for example, suggests that additions were made after the first flights to improve its flight stability characteristics. In this case, adding so many separate vertical tail surfaces seems almost a design afterthought.

Spiral Divergence
Spiral divergence occurs if the coupling between roll and yaw leads to an unstable spiral motion. The spiral divergence mode tends to be pronounced on an airplane that is very stable directionally (about the yaw axis) but is not as stable laterally. This behavior is related to the size of the vertical fin in comparison to the amount of dihedral on the main wing. The tendency to exhibit spiral divergence is reduced by increasing the dihedral angle on the wing. When the airplane is in a bank, the aerodynamic forces tend to deepen the bank, causing the nose to drop, resulting in an ever-tightening downward spiral with increasing airspeed, as shown in the figure below.
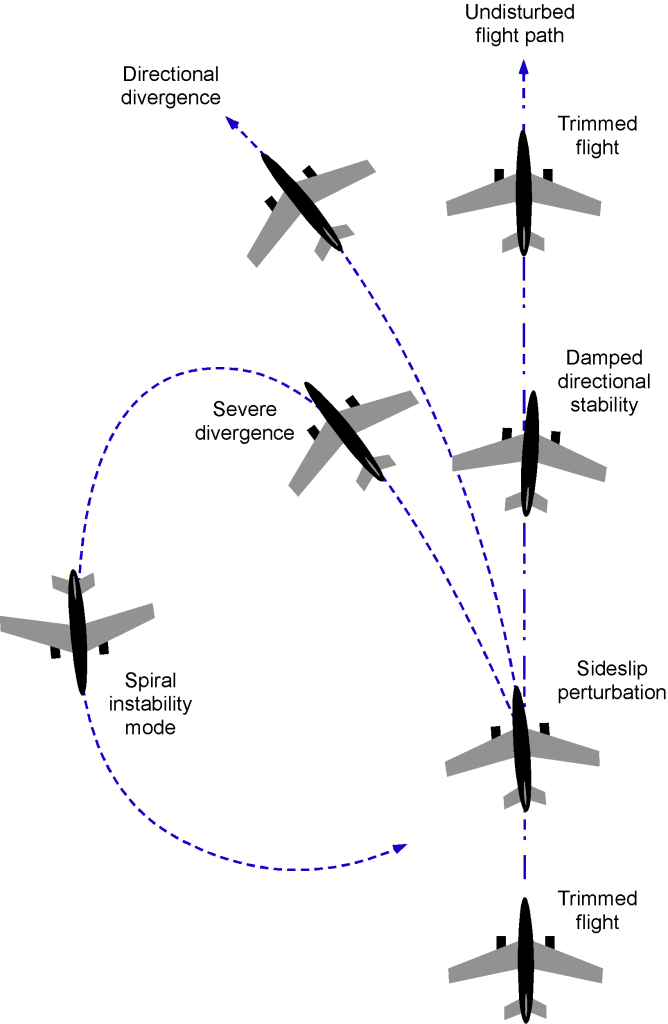
This instability can be analyzed by examining the specific stability derivatives ,
,
,
,
, and
. Generally, for spiral instability to develop,
must be positive and large, while the lateral stability or dihedral effect,
, must be small or negative. The interaction of these stability derivatives can lead to a situation where an initial roll disturbance produces a yaw response that further increases the roll angle, resulting in an ever-tightening spiral.
In the state-space formulation, the spiral mode arises from the coupled dynamics of roll rate , yaw rate
, and sideslip
. With the state vector
and using
, the approximate spiral eigenvalue is obtained by combining the
and
entries of
(the roll and yaw equations driven by sideslip), along with the roll- and yaw-rate couplings
and
. The result is that the sign of the spiral mode eigenvalue depends directly on the combination
(113)
so that a negative value produces an unstable (divergent) spiral. Therefore, the and
elements of
, associated with
and
, play a central role in determining whether the airplane exhibits spiral stability or divergence.
Most airplanes exhibit a spiral instability mode, but it typically develops very slowly. The airplane can be quickly recovered to a level flight attitude through appropriate flight control inputs, such as leveling the wings using ailerons and the elevator to regain a level pitch attitude. Of course, this assumes that the pilot has visual references to the horizon and the ground, or equivalent instrument readings. Unfortunately, if a spiral divergence occurs in the clouds without a clear reference to the horizon, and the pilot cannot interpret (or does not believe) the instruments correctly, then the divergence can continue with increasing airspeed and bank angle into what pilots know as a Graveyard spiral.
A contributing human factor in the case of a graveyard spiral is the possibility of spatial disorientation resulting from the vestibular response in the pilot’s ears (which tells the brain about balance and orientation) that the forces on the aircraft are in equilibrium, even though airspeed and bank angle are increasing. Corrective control inputs, in this case, by pulling back on the controls to decrease airspeed, serve only to tighten the spiral’s radius and increase the rate of descent. If this characteristic continues, the airplane will eventually crash into the ground.
Adverse Yaw & Adverse Roll
As previously discussed, when the ailerons or rudder are applied to control an airplane, they often produce secondary effects in addition to the intended motion. These arise from a cross-coupling between the control inputs and the aircraft response. The two most important secondary effects are adverse yaw and adverse roll. Both are present to some degree on most airplanes, but their significance depends strongly on the wing geometry and the tail design.
Adverse Yaw
When a pilot applies the ailerons to roll the airplane, the downward-deflected aileron increases both lift and drag on one wing, while the upward-deflected aileron decreases lift and drag on the opposite wing. This drag differential produces a yawing moment in the direction opposite the intended turn, a phenomenon known as adverse yaw . To the pilot, the airplane may appear to “hesitate” or “skid” into the turn, the nose initially yawing away from the direction of roll after aileron inputs rather than toward it. The tendency to develop adverse yaw can be eliminated with the use of the rudder. For this reason, basic flight training emphasizes the need for coordinated rudder use with aileron inputs, especially in airplanes with long wings or pronounced dihedral effects. The use of differential aileron deflections or Frise ailerons[15] can reduce adverse yaw effects but cannot eliminate them.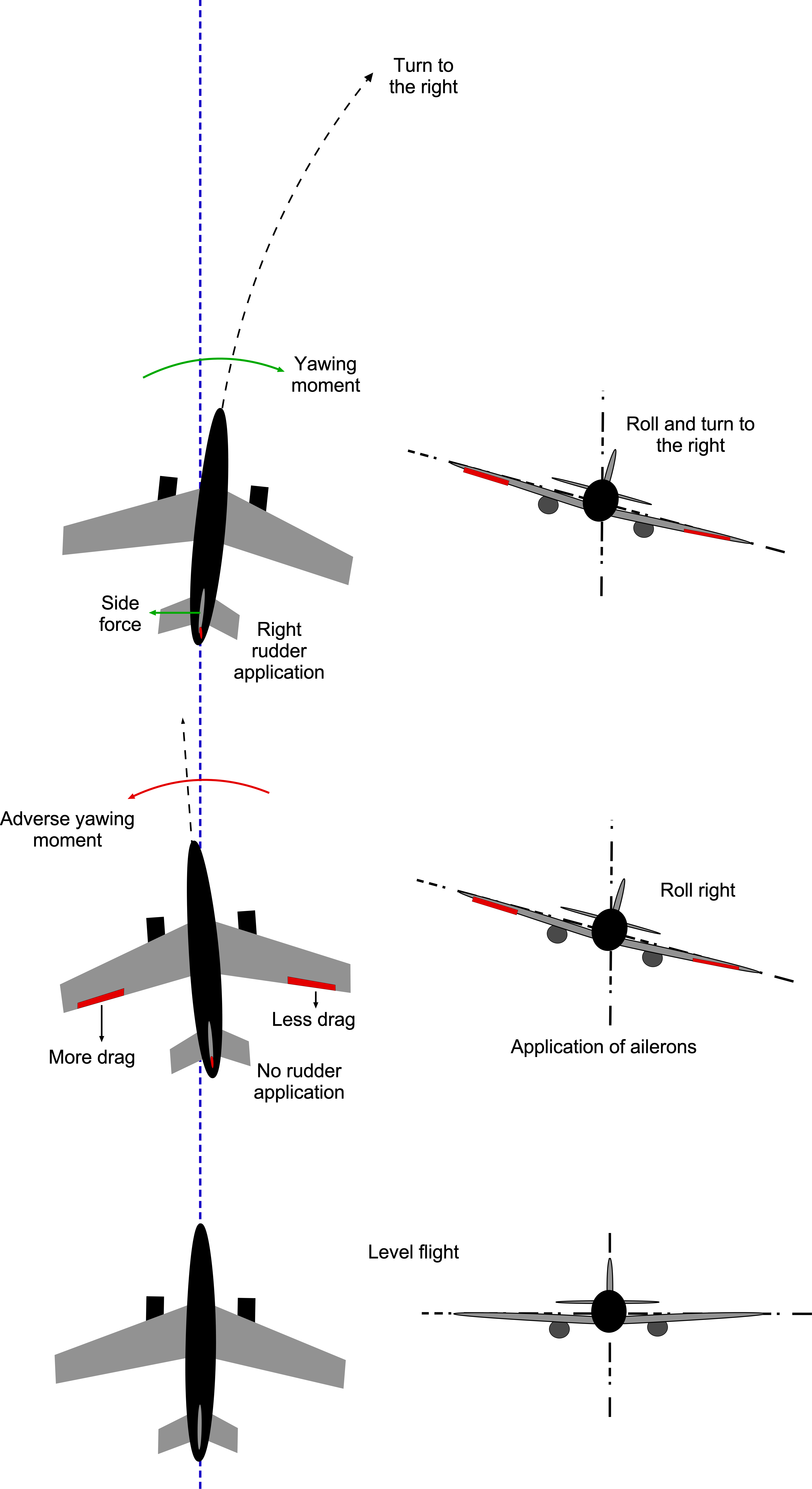
In terms of stability and control derivatives, adverse yaw appears in the yawing moment derivative with respect to aileron deflection, . In nondimensional form, then
(114)
so the dimensional yawing moment is
(115)
For most airplanes, , meaning a positive aileron deflection (rolling right) produces a yawing moment to the left.
In the state-space formulation of the lateral-directional dynamics, this effect shows up in the input matrix . With the state vector
(116)
the yaw rate equation includes
(117)
so that the aileron column of is
(118)
The third entry, , is the adverse yaw term. This shows how an aileron deflection produces not just roll acceleration (through
) but also an unwanted yaw acceleration.
Notice that adverse yaw is fundamentally a static aerodynamic effect because it originates from the derivative . However, the pilot perceives it dynamically because it enters the state-space equations through the input matrix and affects the time evolution of yaw rate and sideslip. It is, therefore, best regarded as a static coupling with dynamic consequences.
Adverse yaw can be rather pronounced on sailplanes and other airplanes with high-aspect ratio wings. Drag changes from aileron deflections, combined with the long moment arm along the wing, create a significant adverse yawing moment. At the same time, sailplanes have relatively small vertical tails, so the yaw stability and damping are weak. Combined with their relatively slow roll response, the result is that adverse yaw on a sailplane is very noticeable, and every aileron input must be carefully coordinated with rudder inputs. Leading the roll using the rudder becomes instinctive to sailplane pilots.
Adverse Roll
Just as ailerons produce a yawing moment through the term, rudder deflections also produce a rolling moment through the
term. This coupling is called adverse roll. When the rudder is deflected, it generates a yawing moment by changing the side force on the vertical tail. Because the tail is usually located above or below the airplane’s center of gravity, the same side force also produces a rolling moment. The result is that a rudder input intended to control yaw may simultaneously induce roll.
In nondimensional form, then
(119)
so the dimensional rolling moment is
(120)
For most airplanes, , so a rudder deflection introduces a rolling moment in addition to the desired yawing moment.
In the state-space formulation, this coupling appears in the roll-rate equation. With the state vector
(121)
the roll-rate equation includes
(122)
so the rudder column of contains the term
. This is the adverse roll contribution, showing how a rudder deflection produces not only yaw acceleration but also an unwanted roll acceleration.
In practice, adverse roll is usually less pronounced than adverse yaw, but it can still influence coordinated flight. Pilots quickly notice that rudder inputs produce a rolling tendency, and in some cases, this effect is used deliberately. For instance, in trimmed cruising flight in most small general aviation airplanes, many of which have pronounced dihedral for roll stability, the wings can be kept level with minor rudder corrections. This is handy when there is no autopilot, freeing one’s hands for other tasks. Similarly, roll-yaw cross-coupling is routinely exploited during strong crosswind landings, where rudder and aileron inputs are combined to align the airplane with the runway while maintaining lateral control.
Summary of Lateral-Directional Dynamics
The airplane’s lateral-directional dynamics consist of three primary modes: roll subsidence, spiral divergence, and Dutch roll. Unlike the longitudinal modes, these motions are coupled between roll and yaw through aerodynamic cross-derivatives such as dihedral effect, weathercock stability, and damping in roll and yaw. The table below summarizes their main characteristics for easy reference, including cross-coupling effects.
| Characteristic | Roll Subsidence (Mode) |
Spiral Mode (Mode) |
Dutch Roll (Mode) |
Adverse Yaw (Control effect) |
Adverse Roll (Control effect) |
|---|---|---|---|---|---|
| Typical frequency | Aperiodic, time constant of a few seconds | Very low, period of tens of seconds to minutes | Moderate, typically 0.2–2 Hz | Not a mode; occurs immediately with aileron input | Not a mode; occurs immediately with rudder input |
| Typical damping ratio | Strongly damped (fast decay) | Often weakly stable or unstable | Light to moderate (ζ ≈ 0.05–0.2) | Static derivative |
Static derivative |
| Dominant motion | Pure roll decay | Slow divergence/convergence in bank and heading | Coupled roll-yaw oscillation | Yaw opposite to commanded roll | Unwanted roll with rudder input |
| Appearance in state-space | Real pole from |
Near-real pole from |
Complex conjugate pair | ||
| Pilot perception | Wings leveling naturally | Slow uncommanded bank/heading change | Noticeable “wobble” in yaw/roll | Nose yaws outward in an aileron roll | Rudder input also banks the airplane |
| Control requirement | None (self-damping) | Aileron/rudder input often required | Yaw damper often used | Rudder coordination, differential/Frise ailerons | Pilot awareness; exploited in crosswind landings |
| Primary stability factor | Negative |
Cross-coupling derivative |
Cross-coupling derivative |
Evaluating Stability & Control Characteristics
The FAA’s regulations (and EASA’s Certification Specifications) outline comprehensive requirements to ensure an aircraft remains stable and controllable under all flight conditions within its operational flight envelope. Stability and control standards include static and dynamic stability requirements, control surface effectiveness, and overall aircraft handling qualities. Aircraft must demonstrate positive static stability about all flight axes, ensuring they return to a steady state after disturbances. They must also show adequate dynamic stability, with pitch or other attitude oscillations damping out over time or being damped with the regular use of flight controls. Control surfaces, such as ailerons, elevators, and rudders, must be effective throughout the entire flight envelope, providing sufficient authority for attitude and flight path management. Additionally, handling qualities must be predictable and manageable, with control forces and responses well-balanced and coordinated to provide pleasing and safe flight characteristics.
The stability and control certification process involves rigorous design and testing phases. Aircraft manufacturers conduct computational simulations, simulator tests, wind tunnel tests, and in-flight testing to ensure that the airplane’s stability and control characteristics comply with regulatory standards. They must also provide comprehensive documentation of the results, including detailed test reports, data, and analysis, to the relevant aviation authority to demonstrate adherence to stability and control requirements. Continuous monitoring and periodic re-evaluation ensure that aircraft maintain compliance with these standards throughout their operational life.
Flight Testing
Flight testing is essential for validating design assumptions and ensuring the aircraft meets stringent safety and performance criteria. Flight testing to validate stability and control is a crucial phase in aircraft development and certification. It aims to ensure safe, predictable flight characteristics throughout the entire flight envelope. It involves a systematic approach to performing maneuvers and analyzing data to validate the aircraft’s performance against regulatory standards and design requirements. It is a lengthy and expensive part of the aircraft’s certification process.
Maneuvers conducted during flight testing include trim and static stability tests to assess how the aircraft responds to pitch, roll, and yaw changes, and to confirm that it returns to its original state after disturbances. Dynamic stability tests involve inducing disturbances to excite short- and long-period oscillations and evaluating the aircraft’s damping and characteristics as a function of speed (Mach number) and altitude. Control effectiveness tests assess the responsiveness of the ailerons, elevators, and rudders to ensure they provide sufficient control authority and operate normally and in the correct sense throughout the flight envelope.
Data analysis techniques during flight testing involve comprehensive instrumentation to record parameters such as airspeed, altitude, control surface positions, and aircraft accelerations. Time-history analysis examines how these variables evolve during maneuvers, providing quantitative estimates of the aircraft’s stability characteristics. As previously discussed, frequency-domain analysis evaluates the aircraft’s response to control inputs in terms of damping ratios and the natural frequencies of oscillatory modes. Parameter estimation and statistical analysis refine the mathematical models used in the simulator, validating flight-test values against theoretical predictions.
Control Effectiveness & Harmony
Control effectiveness refers to the ability of an aircraft’s control surfaces, including the ailerons, elevators, rudder, and flaps, to produce the desired changes in the flight path. Effectiveness is influenced by factors such as the size and shape of the control surfaces, the deflection angle, airflow, speed, and the overall aircraft configuration. Larger control surfaces generally provide greater control authority, allowing for more pronounced changes in attitude. Additionally, higher speeds improve control effectiveness due to the greater dynamic pressure, whereas lower speeds require additional systems, such as spoilers, flaps, or other high-lift devices, to maintain control.
Control harmony concerns the balance and coordination of different control inputs, ensuring the aircraft responds predictably and smoothly to pilot commands. Achieving control harmony involves ensuring that the forces needed to operate all control surfaces are well-balanced and that the aircraft responds proportionally to control inputs. For example, the effort required to move the ailerons, elevator, and rudder should be consistent to avoid excessive force requirements during maneuvers. Additionally, when rolling the aircraft with ailerons, coordinated rudder use helps prevent adverse yaw, resulting in smoother turns.
Overall, good control harmony means the effort and displacement required for the various control inputs are proportional and intuitive to the pilots. This proportionality reduces the likelihood of over-controlling in one flight axis. Balanced control forces and intuitive coordination among controls are essential for maintaining smooth and predictable aircraft behavior, and test pilots approach this using formal assessments. Poor control effectiveness or disharmony can lead to unpredictable aircraft behavior, increased pilot workload, and potentially hazardous flight conditions. For airliners, control harmony also plays a crucial role in delivering a smooth ride, which is a vital aspect of passenger comfort and satisfaction.
Handling Qualities Assessments
As part of the flight testing process, handling or flying qualities is used in the study and evaluation of an aircraft’s stability and control characteristics. It is a field where aircraft design, aerodynamics, physiology, psychology, and ergonomics intersect.[16] Assessments of handling qualities are critical to the flight of the aircraft. They relate to the ease of controlling an airplane in steady flight and during various types of maneuvers. The ease of controlling the aircraft will include measurements of the forces required to move or otherwise actuate the various controls the pilot must use during flight.
Poor handling qualities can lead to pilot error, loss of control, and mishaps or accidents. Therefore, aircraft manufacturers and regulatory bodies place a great emphasis on an aircraft’s handling qualities during its certification and operational phases. Test pilots and flight test engineers use the Cooper-Harper handling qualities rating scale to assess aircraft handling and flying qualities. The numerical scale ranges from 1 to 10, with 1 indicating the best handling characteristics and 10 indicating the worst (i.e., the aircraft is unflyable).

The scale is subjective, so several test pilots and engineers are usually used to evaluate aircraft handling qualities. Specific mission task elements (MTEs) are generally defined for the aircraft in question (based on its intended purpose), which are a set of “role-relatable” or representative flight tasks. The test pilots and flight test engineers then evaluate the aircraft’s handling qualities against these MTEs, amongst other criteria.
The handling qualities are judged not just by reference to the aircraft’s role but also by the MTE and the skill level expected of an average pilot. Typically, handling qualities assessments rated below Level 3 are considered unacceptable for a modern aircraft, and changes to the aircraft and/or the flight control system are likely to be required. Particular attention is usually focused on exploring deficient handling qualities in the form of pilot-induced oscillations (PIO) or, in general, the possibility of any Aircraft-Pilot Coupling (APC) effects. Additionally, there are derivative MTEs used for specialized military flight operations, such as air-to-air refueling and ship-based operations.
Check Your Understanding #4 – Handling qualities exercise: yaw/roll coupling
During a test flight evaluation, a light airplane is trimmed in level flight at an airspeed of 90 kts. The test pilot then applies small rudder doublets (i.e., left-right pulses) without using ailerons. The tests are repeated several times. The average responses are measured from the onboard instrumentation giving and
.
- Describe what these measurements reveal about the rudder-roll coupling of the airplane.
- From a handling qualities perspective, discuss whether this coupling is likely to help or hinder pilot workload in trimmed cruise and crosswind landings.
- Assign a tentative Cooper-Harper rating for a moderate crosswind landing task, explaining your reasoning in terms of expected pilot workload and controllability of the airplane.
Show solution/hide solution.
- The measurements show a notable yaw-roll coupling: a rudder doublet producing
yields
, i.e.,
This result indicates a predictable roll response to small-amplitude rudder inputs. The sign is consistent with a dihedral effect, i.e., a positive sideslip produces a rolling moment that banks the airplane.
- In a trimmed cruise, the coupling will be beneficial because small rudder inputs can be used to maintain wings level with low workload. In crosswind landings, the coupling is also helpful; i.e., rudder inputs naturally help generate the bank needed to track the runway centerline, thereby limiting pilot workload. At the measured sensitivity, the task will likely pose no concerns for pilots with average skill.
- In regard to a precision landing in moderate crosswinds, the rudder-roll coupling would be viewed positively. The pilot will likely be able to perform the task with a low workload and only minor coordination required. A tentative Cooper-Harper rating of 3 (“satisfactory, minor but no significant deficiencies”) is likely to be appropriate. If it is subsequently found that an occasional over-bank or slightly higher pilot workload is observed during a gusty landing approach, a rating of 4 (“adequate performance, some pilot compensation required”) would also be considered acceptable.
Stability Augmentation Systems
Stability Augmentation Systems (SAS) are sophisticated systems comprising avionics and computers that are designed to enhance an aircraft’s stability and handling characteristics, particularly in adverse conditions or during critical phases of flight. These systems are integrated into the normal flight control system and use automatic adjustments to the flight control surfaces to maintain acceptable margins of stability and performance during flight. Autopilot systems, which are not the same as a SAS, manage the aircraft’s flight path, including altitude, heading, and airspeed. Autopilots reduce the need for constant manual inputs from the pilot, enabling more balanced and safer flight operations, particularly in turbulent air.
Key components of a SAS include air data sensors to provide critical information about airspeed, altitude, temperature, static pressure, and angle of attack. Other components may include accelerometers, rate gyros, yaw dampers, pitch and roll stabilization systems, and other components, depending on the aircraft type. For example, yaw dampers are crucial on higher-performance airplanes to prevent Dutch roll by automatically making small corrective rudder inputs. Pitch stabilization systems maintain the desired pitch attitude, while roll stabilization systems prevent unwanted roll movements by controlling ailerons or spoilers. With the advent of fly-by-wire technologies, SAS has become highly sophisticated, enabling greater control and automation in aircraft flight.
Despite their advantages, SAS introduces specific challenges. The complexity and safety-critical nature of these systems require preventative maintenance and regular verification of proper functionality. Because these systems operate as part of the primary flight control architecture, any malfunction can have significant consequences for aircraft stability and controllability. Common failure scenarios include sensor faults and actuator malfunctions. Pilots must also receive thorough training to understand the behavior of SAS-equipped aircraft, which varies depending on the make and model. In airline operations, there is an additional concern that reliance on automation may lead to a gradual decline in manual flying proficiency. However, with proper training protocols and regular practice, pilot competency can be maintained. Many airline pilots make a point of flying manually when conditions allow, or maintain their proficiency by flying other types of aircraft.
Yaw Damper
A yaw damper is a common type of SAS that can be used to illustrate the basic system-level concepts. At higher altitudes, where air density is lower, the Dutch roll characteristics of many airplanes tend to become more pronounced, resulting in a more noticeable oscillatory behavior that may be only lightly damped and difficult to control with pilot inputs alone. Recall from the previous exposition in this chapter that the Dutch roll is a coupled lateral-directional mode involving both yawing and rolling motions.
Yaw damping is governed primarily by the yaw rate derivative, , which quantifies the change in aerodynamic yawing moment in response to a yaw rate disturbance,
. For dynamic directional stability,
must be negative, providing a damping moment that resists continued yawing motion. The magnitude of
depends on the dynamic pressure, the vertical tail volume, and the moment arm from the vertical tail to the aircraft’s center of gravity. To reduce structural weight and minimize parasite drag, the vertical tail is typically sized just large enough to ensure adequate directional stability through the sideslip derivative,
. However, while
may ensure sufficient static stability, the damping contribution from
can become inadequate at high altitudes, where air density is lower, leading to degraded yaw damping.
Therefore, to compensate for this deficiency, a SAS in the form of a yaw damper is employed. The yaw damper is a closed-loop feedback control system that senses the aircraft’s yaw rate and commands the rudder to produce an opposing yawing moment, thereby increasing the effective damping of the Dutch roll mode. A schematic representation of a yaw damper system is shown in the figure below. The system typically consists of a yaw-rate gyro and a yaw-damper controller, which feed corrective signals into the control loop.

Let denote the measured yaw rate from the gyro. In a basic damping-only implementation, the desired yaw rate
is set to zero, indicating that no yaw motion is commanded. The yaw damper computes the error signal
(123)
This error is passed through a proportional gain to generate a corrective signal, i.e.,
(124)
This signal is sent to the rudder servo, producing the rudder deflection, i.e.,
(125)
The negative sign ensures that the rudder deflects in opposition to the sensed yaw rate, generating a stabilizing aerodynamic side force and yawing moment. This feedback action increases the effective yaw damping and raises the damping ratio of the Dutch roll mode. In more advanced implementations, the characteristics of the yaw damper may include additional features to improve stability and handling qualities.
A simplified second-order model for the yaw-rate dynamics that captures the Dutch roll oscillation is
(126)
where is the yaw moment of inertia. The coefficient
represents the total aerodynamic damping in yaw, and
is an effective restoring coefficient that, together with
, sets the oscillation frequency. Without control,
is typically small, so oscillations decay slowly. To augment the damping, the yaw damper measures the yaw rate and commands the rudder in proportion to
(127)
The rudder generates a yawing moment . The control moment primarily contributes to the term that multiplies
, i.e., it behaves like added damping. Substituting the control law into the moment balance gives the closed-loop equation
(128)
This result shows how feedback control increases the effective damping from to
. The natural frequency follows from the inertia and restoring terms, i.e.,
(129)
The closed-loop damping ratio is the damping coefficient normalized by the critical damping level, i.e.,
(130)
Because and
, increasing
increases
while
is essentially unchanged, so oscillations die out faster without a significant shift in their fundamental frequency. For underdamped motion where
, increasing
directly steepens that envelope, which is the essence of yaw-damper action in the Dutch roll mode. The response is shown in the figure below, which shows the time history of the yaw rate for the Dutch roll mode with and without the yaw damper. Both cases start from the same initial yaw rate disturbance of 5 degrees per second. Activating the yaw damper increases the effective damping ratio, so the oscillations decay much more rapidly than in the undamped case.

Check Your Understanding #5 – Dutch roll and yaw damper
During a flight test, rudder doublet inputs are used to excite the lateral directional response oscillations of an airplane. The doublet is a short but deliberate, equal-and-opposite rudder input that briefly disturbs the aircraft’s yaw characteristics and excites its natural dynamic behavior without changing the trim condition. A post-test modal analysis of the results identifies the Dutch-roll poles as follows:
- Yaw damper OFF: poles at
- Yaw damper ON: poles at
For each case, determine the natural frequency , damping ratio
, damped frequency
, peak time
, and the 2% settling time
. Then use the results to interpret the change in the airplane’s flying qualities with the yaw damper engaged.
Show solution/hide solution.
A refresher on the mathematics to solve this problem must recognize that a complex-conjugate pole pair has the following characteristics:
(real part) sets the decay rate; more negative
means faster decay.
(imaginary part) is the damped oscillation frequency.
- The undamped natural frequency and damping ratio follow from
,
.
- The time constants are:
(first peak) and
(2% criterion).
(a) Yaw damper OFF case. From the poles , take
and
. Then the natural frequency between
,
, and
can be computed to get
(131)
Compute the damping ratio by normalizing the decay rate by , i.e.,
(132)
Now the results can be translated into time constants using the standard second-order relations, i.e.,
(133)
This is a lightly damped () Dutch roll, which will result in noticeable airplane sway after the doublet input, persisting for many cycles. This is not a very pleasant flight characteristic to have.
(b) Yaw damper ON case. When the yaw damper is switched ON, it senses the yaw rate and commands rudder inputs to oppose it. In modal terms, this makes the yaw damping derivative more negative, effectively increasing the value of the aerodynamic force , which reduces the yaw-rate time constant. From the poles
, take
and
, so the natural frequency in this case is
(134)
and the damping ratio is
(135)
The corresponding time constants are
(136)
Therefore, the yaw damper increases directional damping (a more negative real part), roughly doubling with minimal frequency change, and moves the Dutch-roll poles leftward on the pole plot (greater decay), while the coupling keeps the oscillation frequency nearly the same. Therefore, the sway from the Dutch roll feels similar but dies out much more quickly. The upshot is that the aircraft’s normal ride comfort improves significantly, with little to no Dutch roll.
Fly-By-Wire (FBW) Flight Control Systems
A fly-by-wire (FBW) flight control system replaces conventional mechanical linkages between the cockpit controls and the flight control surfaces with an electronic system. The introduction of FBW flight control systems has fundamentally transformed modern aircraft. FBW enables the implementation of high-authority automatic control functions, reduces overall system weight and mechanical complexity, and improves handling qualities across the entire flight envelope. These systems are now standard in both civil and military aviation and are considered essential to the design and operation of advanced aircraft.
The architecture of a FBW flight control system is shown in the figure below. Control inputs from the pilot are sensed electrically and interpreted by flight control computers, which generate corresponding signals to drive the surface actuators. These signals may be modified or augmented by programmed control laws that enable functions such as automatic trimming, stability augmentation, flight envelope protection, and command input shaping. FBW systems also provide the framework for implementing a SAS. These systems apply feedback based on measured motion states, and SAS functionality is usually essential for achieving acceptable flight handling qualities.

Unlike mechanical systems, in which the pilot physically moves the control surfaces through rods or cables, often with hydraulic assistance, a FBW system decouples the pilot’s control inputs from the direct mechanical response of the surfaces. The pilot issues a control input, and the system interprets it as a request for a specific aircraft response, such as a change in attitude or flight path. The necessary control surface deflections are then computed and applied automatically. This type of system allows the flight control system to be optimized for both performance and safety across the entire flight envelope.
FBW systems operate as closed-loop feedback systems. Aircraft state variables, such as pitch rate, roll rate, airspeed, angle of attack, sideslip angle, and load factor, are continuously measured using inertial and air-data sensors. These signals are processed in real time and compared against reference values. The control laws determine the actuator commands needed to minimize the error between the commanded and measured responses. This feedback loop provides precise, high-bandwidth control that cannot be achieved solely through manual inputs.
One significant consequence of using a FBW system, particularly in modern military fighter aircraft, is the ability to design the airframe to be statically unstable or only marginally stable. This configuration improves maneuverability and agility. By embedding the required stabilizing feedback into the flight control logic, the aircraft’s overall aerodynamic and structural design can be optimized for performance and efficiency rather than constrained by the need for natural stability.
To meet the reliability requirements of flight-critical systems, modern FBW implementations incorporate high levels of redundancy. Triplex and quadruplex architectures are commonly used, with multiple independent computing channels operating in parallel. Each channel typically contains its own processor, sensor interface, and actuator command path. The outputs of these channels are continuously compared using mid-value selection or majority-voting schemes. If a channel exhibits anomalous behavior or fails consistency checks, it is automatically isolated from the system to maintain continued safe operation. The design philosophy emphasizes fault tolerance, ensuring aircraft control is maintained even in the presence of multiple failures.
Summary & Closure
Adequate stability and control are essential design requirements for any flight vehicle. Aerospace engineers must understand the fundamental principles of both to ensure safe and efficient flight throughout the operational envelope. Stability is initially considered in terms of static stability, which refers to the aircraft’s initial tendency to return to its original equilibrium state following a disturbance, such as a gust of wind. If the aircraft generates a restoring moment that opposes the disturbance, it is considered statically stable. Static stability in all three axes (longitudinal, lateral, and directional) is typically required to ensure safe flight and acceptable handling.
Dynamic stability refers to the aircraft’s response over time after a disturbance. If the aircraft oscillates about its trimmed flight condition and eventually returns to equilibrium, it is said to be dynamically stable. Dynamic characteristics are investigated during flight testing, and modifications may be introduced if necessary to improve damping or time response. For example, aerodynamic surfaces such as dorsal or ventral fins may be added to increase stability margins and improve damping. Tied to the principles of stability and control is the concept of handling qualities, which describes the ease and precision with which a pilot can control the aircraft to perform specific tasks, such as maintaining a heading, conducting an approach, or executing a maneuver. Good handling qualities are essential for both safety and mission effectiveness, enabling the pilot to maintain precise, predictable control under all expected flight conditions.
An understanding of stability and control lies at the heart of aircraft design and performance. As flight vehicles become more complex and capable, the need for engineers who can analyze, model, and refine their behavior becomes increasingly important. For students entering the field, mastering these foundational concepts opens the door to a wide range of exciting opportunities, from designing cutting-edge military aircraft to developing the next generation of autonomous aerial systems. At the same time, there is great value for engineers in learning to fly themselves. Experiencing flight firsthand provides an intuitive sense of stability, control, and handling qualities that no textbook or simulator can fully convey, deepening both technical insight and professional judgment.
5-Question Self-Assessment Quickquiz
For Further Thought or Discussion
- Review and comment on the tail design for the Beech 1900 turboprop airplane.
- Can you fly a statically unstable aircraft? Explain carefully.
- During flight testing, it was found that a new military fighter airplane has a very pronounced spiral instability mode. Consider the options as to whether this is a problem and whether it should be mitigated.
- It is found during flight testing of an airplane that, under some conditions, the phugoid mode is mildly divergent. Discuss whether this is a problem or not.
- Besides PIO, do some research to learn more about Aircraft-Pilot Coupling (APC) events.
- If the yaw damper on a jet aircraft fails during flight, are there likely any issues of concern?
- Consider some types of handling qualities assessments that might be needed for an uncrewed aerial vehicle.
Other Useful Online Resources
To dive further into the stability and control of aircraft, visit the following websites:
- A great website covering many aspects of aircraft stability and control.
- A fantastic educational old film on the Secret of Flight 5: Stability and Control
- A nice set of course notes on stability and control published by Cornell University.
- A good website on aspects of stability and control from the piloting perspective.
- The author acknowledges his teacher, Arthur W. Babister. Dr. Babister was a flight dynamics engineer at the Blackburn Aircraft Company and contributed to the design of the Buccaneer fighter-bomber and the Beverley transport airplane. He became a professor of aeronautical engineering at the University of Glasgow in 1965. Drawing on his well-known book, Aircraft Dynamic Stability and Response , he taught countless student engineers the intricacies of flight dynamics, always appreciating that it was not the most straightforward subject to master. ↵
- Anderson, J. D., A History of Aerodynamics, Cambridge University Press, 1999. ↵
- Lilienthal, O., "Birdflight as the Basis of Aviation, '' 1889; transl. U.S. War Dept., 1911. ↵
- Anderson, J. D., The Airplane: A History of Its Technology, Published by AIAA, 2002. ↵
- Wright, O., and W. Wright, Flying-Machine, Patent No. 821,393, filed 1903, granted 1906. ↵
- Jakab, P. L., "Visions of a Flying Machine,'' Smithsonian Institution Press, 1990. ↵
- Lanchester, F. W., Aerodynamics, Vol. 1, Archibald Constable, 1907. ↵
- Prandtl, L., “Applications of Modern Hydrodynamics to Aeronautics,” NACA Report 116, 1921. ↵
- Bryant, W. C., Stability and Control of Airplanes, McGraw-Hill, 1934. ↵
- Perkins, C. D., and R. E. Hage, Airplane Performance, Stability and Control, John Wiley, New York, 1949. ↵
- Etkin, B., Dynamics of Flight: Stability and Control, Wiley, 1959. ↵
- U.S. Air Force, MIL-F-8785B: Flying Qualities of Piloted Airplanes, 1969. ↵
- Hallion, R. P., On the Frontier: Flight Research at Dryden, 1946–1981, NASA SP-4303, 1990; Etkin, B., and L. D. Reid, Dynamics of Flight: Stability and Control, 3rd ed., Wiley, 1996. ↵
- The term “Dutch roll,” describing this particular dynamic response of an airplane in analogy with ice skating, was coined by Jerome C. Hunsaker in 1916. ↵
- This is a type of aileron having a nose portion projecting ahead of the hinge axis and a lower surface in line with the lower surface of the wing, which is explicitly designed to reduce adverse drag. ↵
- Micael Carley, "Aircraft Stability and Control,'' University of Bath. ↵

