Chapter 5 Time Value of Money

Overview and Background

Chapter 5 deals with cash flows. In chapter 3, we analyzed the financial statements of a firm, while in chapter 4, we discussed financial ratios. We studied the details of balance sheet and the intricacies involved in creating a market value balance sheet and common size balance sheet. We observed how to create common size income statement and learnt how to analyze cash flows of a company with respect to change in different assets and liabilities. This chapter deals with cash flows in detail. It begins with an analysis of simple and compound interest rates, the concept of discounting and dealing with multiple cash flows and discounting of multiple cash flows. This chapter also discusses cash flows that are well defined (such as in a loan or from a bond) and cash flows that are infinite (such as dividends from shares of a stock). Finally, this chapter will deal with inflation: the analysis of how growth in investments is brought down in real terms by inflation adjustments.

In Chapter 2, we have studied that borrowing and lending are a part of balance sheet expansion in firms. This can be done either by issuing bonds (debentures) or short-term commercial papers or through term loans from banks. We have also intuitively seen why debt is an important component of liabilities in a firm’s balance sheet. The fundamental question associated with debt and borrowing is — is $1 today the same as $ 1 after a certain period of time? In other words, if we borrow $ 1 today, will it grow/ shrink with time? We are aware that inflation erodes the purchasing power of an individual. We are also aware that usually loans carry a rate of interest. How does this rate of interest connect the value of loan being borrowed today with the final value being repaid at a later point in time? This chapter answers that question and more. Not only will we determine if a dollar today is the same as a dollar in future, but also, we will determine if a dollar today is better than 50 cents received in one year as well as 50 cents received in two years. Broadly speaking, we will discuss in this chapter the meaning of interest rates and using the concept to connect present value (value of something today) with a future value (value of that thing in the future). We will discuss single and multiple cash flows and discuss annual percentage rates to compare and contrast them with effective annual rates. Finally, we will study the erosion of money due to inflation and how to account for it in our calculations.

What we discussed in the previous paragraph can be called time value of money or TVM as it is popularly known in finance. Time value of money is important for an individual or a corporation because in most situations, a dollar borrowed today is returned with interest. We will define interest in two ways: in terms of the percentage of the borrowed amount as well as in terms of a dollar value. To keep things simple, let us assume that Ms. Cici borrowed $ 100 today and was asked to return $ 110 in one year. Assuming for now no compounding, we can state that Ms. Cici will pay $ 110:

$ 110 – $ 100 = $ 10 in interest, that is, 10/100 = 10% in interest.

5.1 Simple interest

The 10% interest mentioned above is actually simple interest: meaning it accrues at a flat rate of 10%. Let us look at this interest accumulated over different intervals of time. For simplicity, let us assume that interest is applied every year. In practice, with this method it does not matter how often interest is applied. Table 5.1 below describes the accumulation of interest every year with this method.

Time	Principal	Periodic interest	Amount
0	100	N/A	N/A
1	100	10	110
2	100	10	120
3	100	10	130
4	100	10	140
5	100	10	150

In Table 5.1, the principal amount identified in column 2 is defined as the starting value or present value. Present value is defined as the value of money that we have today (at time t=0). In this chapter, we will define these terms (time, principle, interest, and amount) as components of time value of money (TVM) equation. As discussed above, the value of interest can be measured in dollars or in percent (in this case, a flat 10% on the starting $ 100 for every period). Lastly, the final column called amount is also called future value because this value will be available after the time period.

These details of table 5.1 are also explained in this video

In reality, TVM equation defines the relative value of a certain amount as it progresses through time. So, it is not inappropriate to call “past value”, “present value” and “future value.” The basic concept is that money grows as it progresses in time assuming a non-negative interest rate. If we consider a certain time as today, then the relative value held today is called present value and the subsequent values are called future values. Table 5.1 above represents progression of dollar value accumulating simple interest. This is akin to the investor who lent money to Ms. Cici receiving payment of interest regularly. What happens if the investor wants to reinvest the dollar value of interest received as well? This can be measured with the help of compound interest.

5.2 Compound interest

In the previous section, we mentioned that the interest is calculated by multiplying rate of interest and starting value of $ 100. However, in reality this is not the case. In the real world, value of interest in dollars is calculated using the starting balance at the beginning of that period. Since interest accumulates with time, with every period the beginning value resets to a higher starting value. Therefore, interest owed grows with time. This is the idea of compound interest. Using compound interest, the periodic rate of interest is applied to a value that accumulates previous period’s interest in addition to the beginning value. Consequently, nominal interest owed in a future compounding period grows with time. Let us see the progression of compound interest and the final value with time. Table 5.2 below represents this. Unlike Table 5.1, Table 5.2 assumes that the 10% interest each year is recalculated annually based on the new principal: while in year 1 this interest is $ 10, in year 2 the new interest is 10% of the year 2 principal amount, or $ 11 and so on. While in table 5.1, interest was $ 10 (calculated on the initial principal) no matter what the time period is.

Time	Principal (Present value)	Periodic Interest	Amount (Future Value)	Compound Interest Formula
Annotation →	PV	FV – PV	FV
0	100	N/A	N/A
1	100	10	110	[latex]\small=100(1+0.1)^1[/latex]
2	110	11	121	[latex]\small=110(1+0.1)^1 = 100(1+0.1)^2[/latex]
3	121	12.1	133.1	[latex]\small=121(1+0.1)^1=110(1+0.1)^2 = 100(1+0.1)^3[/latex]
4	133.1	13.31	146.41	[latex]\small=133.1(1+0.1)^1=121(1+0.1)^2=110(1+0.1)^3 =100(1+0.1)^4[/latex]
5	146.41	14.64	161.05	[latex]\small=146.41(1+0.1)^1=133.1(1+0.1)^2 =121(1+0.1)^3=110(1+0.1)^4=100(1+0.1)^5[/latex]
‘t’	…	…	…	[latex]\small100(1+0.1)^t[/latex]

As can be seen from Table 5.2a, the principal increases with time, creating a rise in interest accrued even though it is at the same rate (10%). In this case, we call 10% as the compound interest rate with t=1 (year) being the reset period for the principal. This reset period can be lower than 1 year. In case of many loans such as mortgages and car loans, this reset period is actually 1-day. However, for the sake of theory, we can drill this down into ½ year (2 compounding periods per year) or ¼ year (4 compounding periods per year) and so on. In fact, we can set this to limit as the time period becomes continuous (infinite compounding periods per year). We will be discussing this further in the final section of this chapter when discussing periodic rate and effective annual rate.

In the “formula” column of Table 5.2, we can see that

[latex]future \; value = present \; value \times (1+rate)^{time}[/latex]     …(1)

Conversely, we can also state that

[latex]present \; value = \frac {future \; value}{(1+rate)^{time}}[/latex]            …(2)

Conversely, we can demonstrate the connection between future value at the end of one period and present value prior to that period, prior to two period and so on in table 5.2b1 below. Here the assumption is that we want to have a beginning value of $ 100 i.e. we want to have a starting value or initial present value of $ 100. All we need to do is that we need to divide the future value (amount at that period in table 5.2a) by the term (1+r) to the appropriate power (difference of the current period in time and the period where we want to discount it). For example, to discount from period 5 to 4, i.e. from 161.05 by 1 period, as seen in the row titled time = 5, we simply divide by 1.1 to the power 1. On the other hand, to reach time = 1, as in the row with title = 1, we have to divide this by 1.1 to the power 4.

This is also explained in this video

Time	Principal (Present value) or value as at that time	Discounting needed	Amount for 1-period compounding (Future value)	Periodic Interest (1 – period)	Compound Interest Formula to convert it to a past period by 1, 2, 3, 4, 5…t periods
‘t’	PV	t -> 0 (t-periods)	FV	FV-PV	[latex]\small PV={FV}/{(1+0.1)^t}[/latex]
4	146.41	5-> 4 (1-period)	161.05	14.64	[latex]\small ={161.05}/{(1+0.1)^1}[/latex]
3	133.1	5 -> 4 -> 3 (1, 2-periods)	146.41 or 161.05	13.31 or 27.951	[latex]\small ={146.41}/{(1+0.1)^1}={161.05}{(1+0.1)^2}[/latex]
2	121	5 -> 4 ->3 -> 2 (1, 2, 3-periods)	133.1 or 146.41 or 161.05	12.1	[latex]\small =133.1/(1+0.1)^1 = 146.41/(1+0.1)^2 = 161.05/ (1+0.1)^3[/latex]
1	110	5 -> 4 ->3 -> 2 -> 1 (1, 2, 3, 4-periods)	121 or 133.1 or 146.41 or 161.05	11	[latex]\small =121/(1+0.1)^1 = 133.1/(1+0.1)^2 = 146.41/(1+0.1)^3 = 161.05/ (1+0.1)^4[/latex]
0	100		110 or 121 or 133.1 or 146.41 or 161.05	10	[latex]\small =110/(1+0.1)^1 = 121/(1+0.1)^2 = 133.1/(1+0.1)^3 = 146.41/(1+0.1)^4 = 161.05/ (1+0.1)^5[/latex]
0	100	Zero periods	100	Zero	[latex]\small =100/(1+0.1)^0[/latex]

The intricacies of Table 5.2b1 are discussed through MS Excel in this video.

Notice how the phrase present value has become relative in this table. To illustrate the depth of this table further, we can split it into two parts. The first part summarizes starting values (present values), as they are called in Corporate Finance as seen in table 5.2b2-1 below:

t	Future value	Present value (1 period prior)	Present value (2 periods prior)	Present value (3 periods prior)	Present value (4 periods prior)	Present value (5 periods prior)
5	161.051	146.41	133.1	121	110	100
4	146.41	133.1	121	110	100
3	133.1	121	110	100
2	121	110	100
1	110	100
0	100	100

In table 5.2b2-1 above, in the row with time labelled t=2, for example, we want to have a final value of $ 121. At 10% interest (compounding rate), we will need 1-period prior balance of $ 110 and 2-period prior balance of $ 100 to achieve this. These calculations are as explained in table 5.2b2-2 below.

Table 5.2b2-2: calculating 1, 2, 3, 4 and 5-period prior values needed to reach a final value or future value as seen in the appropriate column

t	Future value	Present value (1 period prior)	Present value (2 periods prior)	Present value (3 periods prior)	Present value (4 periods prior)	Present value (5 periods prior)
5	161.051	[latex]\small161.05/(1.1)^1=146.41[/latex]	[latex]\small161.05/(1.1)^2 = 133.1[/latex]	[latex]\small161.05/(1.1)^3 = 121[/latex]	[latex]\small161.05/(1.1)^4 = 110[/latex]	[latex]\small161.05/(1.1)^5 = 100[/latex]
4	146.41	[latex]\small146.41/(1.1)^1=133.1[/latex]	[latex]\small146.41/(1.1)^2=121[/latex]	[latex]\small146.41/(1.1)^3=110[/latex]	[latex]\small146.41/(1.1)^4=100[/latex]
3	133.1	[latex]\small133.1/(1.1)^1=121[/latex]	[latex]\small133.1/(1.1)^2=110[/latex]	[latex]\small133.1/(1.1)^3=100[/latex]
2	121	[latex]\small121/(1.1)^1=110[/latex]	[latex]\small121/(1.1)^2=100[/latex]
1	110	[latex]\small110/(1.1)^1=100[/latex]
0	100	[latex]\small100[/latex]

Calculations in the above tables (5.2b2-1 and 5.2b2-2) are discussed and elaborated in this video.

We can also calculate the interest accumulated over 1 – 5 periods if the starting point was $ 100 and the ending points were 1 – 5 years as seen in table 5.2b3 below. For example, in the row with t=3, the ending value desired is $ 133.1. To reach there, per table 5.2b2, we will need a value of 121 1-period prior, 110 2-periods prior and 100 3-periods prior. Accordingly, interest accumulated for these starting values are shown as 133.1-121 = 12.1 for 1-period; 133.1 – 110 = 23.1 for 2-periods and 133.1 – 100 = 33.1 for 3-periods respectively as shown in the appropriate columns below.

t	Future Value	Interest 1 – period	Interest 2 – periods	Interest 3 – periods	Interest 4 – periods	Interest 5 – periods
5	161.051	161.051-146.41 = 14.641	161.051-133.1 = 27.951	161.051-121 =40.051	161.051-110 =51.051	161.051-100 =61.051
4	146.41	146.41-133.1 =13.31	146.41-121 =25.41	146.41-110 =36.41	146.41-100 =46.41
3	133.1	133.1-121 =12.1	133.1-110 =23.1	133.1-100 =33.1
2	121	121-110 =11	121-100 =21
1	110	110-100 =10
0	100	100-100 =0

The intricacies of Table 5.2b1 are discussed through MS Excel in this video.

5.3 Connecting simple and compound interest

We will now replace the word “principal” with “present value” and “amount” with “future value.” Table 5.3 below lists the progression of future value with time for both simple and compound interest. For the rest of this book, we will only be dealing with compound interest from this point. In table 5.3, we are now merging what we learned in table 5.1 as well as table 5.2a. The column “simple interest” simply refers to the difference between future value (SI or simple interest) and present value (at time=0). The column present value (CI) refers to the starting value at each period, that was the pending or future value at the previous period that will now accumulate 1-period interest defined here as compound interest. In short, values in the column compound interest (CI) are calculated as 10% of the present value (CI). Adding the corresponding entries in the columns Present value (CI) and compound interest (CI) yield value in the column titled future value (CI). What is noticeable in this is as seen in the graph of figure 5.1 below. How future value obtained with compound interest diverges from that obtained from simple interest is because of growing interest accrued from compound interest (column titled compound interest (CI) versus column titled simple interest (SI)).

Time	Present value (SI)	Simple interest (SI)	Future value (SI)	Present value (CI)	Compound interest (CI)	Future value (CI)
0	100	N/A	N/A	100	N/A	N/A
1	100	10	110	100	10	110
2	100	10	120	110	11	121
3	100	10	130	121	12.1	133.1
4	100	10	140	133.1	13.31	146.41
5	100	10	150	146.41	14.64	161.05

Calculations in the above table (along with figures 5.1 and 5.2 below) are discussed comprehensively in this video

Present value and future value progression shows that as interest accumulates (compound interest), the future value grows faster. This can also be seen from Figure 5.1 below.

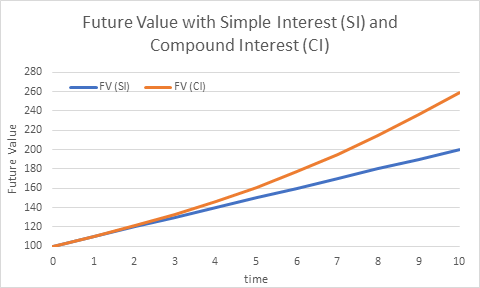
The reason why amount in compound interest grows with time is because payment of interest is not made as they are earned rather the earned interest is added to the principal. Therefore, amount grows as straight line when investors are paid simple interest. However, growth is non-linear when investors are paid compound interest. This is also seen in figure 5.2 below. Interest paid to investors if simple is linear. That interest if compounded grows non-linearly because of this accumulation of interest on interest as seen in table 5.2a

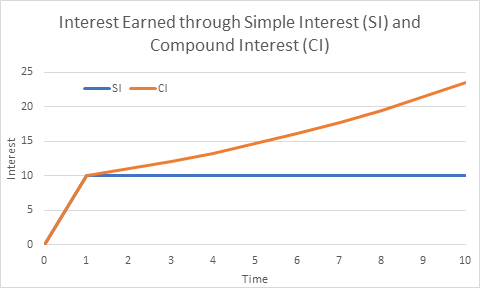
Calculations from the figures 5.1 and 5.2 above are discussed in this video.

5.4 Multiple cash flows – annuity and annuity due

5.4.1 Annuity

In section 5.3 above we have demonstrated through examples the temporal progression of a single value of cash flow i.e. how it changes over time given a certain interest rate. In other words, we have found final or future values of $ 100 after period 1…5. In the real world however, multiple cash flows are associated with for example a loan (loan repayment) or a bond (coupon payments) or a share of a stock (dividend payments). How can we analyze these staggered cash flows separated over different points in time and come up with a single equivalent cash flow that if given to an investor makes the investor indifferent between receiving the single and multiple cash flows. Therefore, the objective of this section is that when there are multiple cash flows, we need to find an equivalent value that would make an investor indifferent between attaining a single cash flow versus attaining the staggered multiple cash flows over different points in time. Table 5.4 below describes those future cash flows and the method to find a present equivalent value at a single interest rate that makes an investor indifferent between the present value and the future cash flows. In table 5.4 below, we have multiple cash flows of $ 100 listed in the column with title CF_t (notation for cash flow available at time t). In the column PV_CF_t, we calculate the present value (taken back across ‘t’ periods). The notation PV_CF_t stands for the present value of CF_t. In the column with title “formula”, we describe how the present value of that single cash flow available at time ‘t’ is obtained.

For example, in the row where the value of time (t) is 4, the value available after 4 periods is $ 100 (Cash flow at time ‘4’, CF_4). To find its value today (4-periods prior), i.e. Present Value of CF_4, we simple discount it by 4 periods. In other words, we divide $ 100 by (1+rate)^t or (1+0.1)^4 to obtain $ 68.30. When we look at the entire table 5.4, we notice that there are 6 cash flows of $ 100 each being received at time 1, 2, 3, 4, 5 and 6 respectively. This is an example of a 6-period annuity. Note that while the annuity starts today (i.e. the contract starts today), cash flows do not start until 1-year from today. Examples of annuity are loan payments, lease payments etc.

Time (t)	[latex]CF_t[/latex]	[latex]PV_{CF_t}[/latex]	Formula
0
1	100	90.91	[latex]\small 100/(1.1)^1[/latex]
2	100	82.64	[latex]\small 100/(1.1)^2[/latex]
3	100	75.13	[latex]\small 100/(1.1)^3[/latex]
4	100	68.30	[latex]\small 100/(1.1)^4[/latex]
5	100	62.09	[latex]\small 100/(1.1)^5[/latex]
6	100	56.45	[latex]\small 100/(1.1)^6[/latex]
	Total PV	435.53	[latex]\small Sum \; of \; PV_{CF_{t}}[/latex]

Notice that the sum of all present values is 435.53. In other words, if we received $ 90.90 today for the first cash flow of $ 100 available after 1 year (entry in column titled [latex]PV_{CF_t}[/latex] for time = 1), we would be okay not receiving that $ 100 after 1 year. Similarly, if we received $ 82.64 today for the second cash flow of $ 100 to be received after 2-years (entry in column titled [latex]PV_{CF_t}[/latex] for time t=2), we would be okay not receiving that $ 100 after 2 years. We can keep extrapolating this argument for all 6 cash flows. So if we receive the sum total of all those present values (435.53) we would be happy to not receive any of those $ 100s available at different points in time. In other words, we can state from Table 5.4 above, that an investor is indifferent between receiving $ 100 per year for 6 years and receiving $ 435.53 today, as long as the rate of interest (which we will start calling discount rate from now) is 10%.

This stream of constant cash flows is called annuity. In Table 5.4, $ 435.53 is the sum of present value of all cash flows and is called present value of annuity. The present value of annuity is used to determine the amount that can be traded at a given discount rate to an investor for receiving future cash flows. For example, when someone is retiring with a large lumpsum from their 401K, they may not like to receive the whole amount in one single payment. They may instead prefer if this was spread out over a certain number of years through equal payments. This is an example of annuity. If we use this same example, if they invested $ 435.53 today, they would receive 6-equal annual payments of $ 100 each. The nominal sum of these $ 100 payments (i.e. $ 600) far exceeds the value of present investment ($ 435.53). This is a small illustration of the power of compounding for investors/ lenders. Similarly, we can find the future value of this annuity by compounding the present value as: [latex]Future \; value = present \; value(1+rate)^t[/latex]

Calculations in table 5.4 are discussed in this video illustration.

To understand the application of future value of annuity is also fairly straightforward. Our 401K retirement savings account usually has a constant cash flow of investment over a period of time. We only make a single lumpsum withdrawal at the end of the investment period, i.e. at retirement.

We can also take the future value of each cash flow individually as in Table 5.5 below.

Time (t)	Investment Period	[latex]CF_t[/latex]	[latex]FV_{CF_t}[/latex]	Formula for Future Value or Cash Flow
0	6 – 0 = 6
1	6 – 1 = 5	100	161.05	[latex]\small 100 (1.1)^{(6-1)}[/latex]
2	6 – 2 = 4	100	146.41	[latex]\small 100 (1.1)^{(6-2)}[/latex]
3	6 – 3 = 3	100	133.10	[latex]\small 100 (1.1)^{(6-3)}[/latex]
4	6 – 4 = 2	100	121.00	[latex]\small 100 (1.1)^{(6-4)}[/latex]
5	6 – 5 = 1	100	110.00	[latex]\small 100 (1.1)^{(6-5)}[/latex]
6	6 – 6 = 0	100	100.00	[latex]\small 100 (1.1)^{(6-6)}[/latex]
Method 1		Total FV	771.56	[latex]\small Sum \; of \; FV_{CF_t}[/latex]
Method 2		Total FV	771.56	[latex]\small Sum \; of  \; PV_{CF_t}(1.1)^6=435.53(1.1)^6[/latex]

The column formula (for future value) on the right side of table 5.5 above describes the nuts and bolts of how to calculate the future value of each individual cash flow. This future value is obtained by compounding that cash flow and investing it for the difference of 6 and the time it was invested. For example, in the row where time = 4, cash flow invested is $ 100, It is invested for 6 minus 4 = 2 periods as shown in column “investment period”. This investment period is the exponent of the term 1+r. At the bottom of the column is just a future value computed using the single value of present value obtained from the result of Table 5.5.

These calculations are also demonstrated in this video.

Practical Implication of compounding with relation to the future value 771.56: The nominal sum of 6 cash flows of $ 100 invested over 6-periods is $ 600. However, when we invest it at a compound rate of 10%, we notice that we end up with $ 771.56, which is a lot more. Again, as we saw in figure 5.1 for a single cash flow of $ 100, this growth is now available for 5 more cash flows added at different periods of time. Notice also in table 5.5 that ending values (future value) of cash flows invested at later points in time such as t=2, 3… start to decline. This is because the growth afforded by compound interest is not as great due to time under investment being smaller.

There are two important implications of investing with compound interest: time horizon of the investment and the rate of interest of the investment itself.

5.4.2 Annuity Due

Annuity due is similar to annuity in which there are a certain number of cash flows but different in when the cash flows begin. In an annuity, when the dotted line is signed today, cash flows do not begin until t=1 from today (i.e. one period later). In annuity due, however, cash flows start as soon as the contract begins. Examples of annuity due are insurance premia payments, rent payments etc.

Table 5.6 below represents the present value of 6-period annuity at 10%. This is a modification of table 5.5 above. As usual, column on the left titled ‘t’ defines the time at which cash flow (CF_t) is received/ paid. PV_CF_t represents an equivalent value today of that cash flow, obtained by discounting (i.e. dividing cash flow i.e. future value by 1+rate to the power of appropriate exponent of time). The column PV_CF_t represents the value obtained after such operation. The operation itself is described in the column titled “formula”.

Time (t)	[latex]CF_t[/latex]	[latex]PV_{CF_t}[/latex]	Formula
0	100	100.00	[latex]\small \frac{100}{(1.1)^0}[/latex]
1	100	90.91	[latex]\small \frac{100}{(1.1)^1}[/latex]
2	100	82.64	[latex]\small \frac{100}{(1.1)^2}[/latex]
3	100	75.13	[latex]\small \frac{100}{(1.1)^3}[/latex]
4	100	68.30	[latex]\small \frac{100}{(1.1)^4}[/latex]
5	100	62.09	[latex]\small \frac{100}{(1.1)^5}[/latex]
6
	Total PV	479.08	[latex]\small Sum \; of  \; PV_{CF_t}[/latex]

Calculations in table 5.6 are discussed in this video.

The operation in each row is same that is performed in table 5.4 for an annuity. The only difference is how cash flows are available. In table 5.4, first cash flow of $ 100 was available at time t=1. In case of annuity due it is available at time t = 0. This, however, does not change how we discount our cash flows. For example, if we go to the row which reads t=2, this cash flow of $ 100 is available at the end of second period. Its present value is calculated exactly the same way in which we calculated the present value of cash flow available at t=2 in table 5.4, as we discussed previously i.e. [latex]100/(1.1)^2 = 82.64[/latex].

All these present values are added to calculate a single value of $ 479.08. If an investor who received a cash flow stream of $ 100 per year starting now through t=5, they would be indifferent between receiving $ 479.08 and $ 100 per year starting now through t= 5 as long as the perceived rate of interest is 10% (used to calculate the present value). Overall, how an annuity due connects with annuity is that if we compare tables 5.4 and 5.6, we notice that every cash flow in annuity has become available sooner by 1 period in annuity due. Therefore, if we do not discount every cash flow in annuity by 1.1^1, we will obtain the present value of annuity due instead.

Therefore, the relation between present value of 6-period annuity and 6-period annuity due is 1.1 times. We can extend this discussion to annuity of any period. It is just the timing of every cash flow has shifted one period prior, thus making annuity due more valuable by 10% or 1.1 times. Let us do this by actually placing tables 5.4 and 5.6 adjacent to each other in table 5.7 below.

Annuity				Annuity Due
Time (t)	[latex]CF_t[/latex]	[latex]PV_{CF_t}[/latex]	Formula	Time (t)	[latex]CF_t[/latex]	[latex]PV_{CF_t}[/latex]	Formula
0				0	100	100.00	[latex]\small \frac{100}{(1.1)^0}[/latex]
1	100	90.91	[latex]\small \frac{100}{(1.1)^1}[/latex]	1	100	90.91	[latex]\small \frac{100}{(1.1)^1}[/latex]
2	100	82.64	[latex]\small \frac{100}{(1.1)^2}[/latex]	2	100	82.64	[latex]\small \frac{100}{(1.1)^2}[/latex]
3	100	75.13	[latex]\small \frac{100}{(1.1)^3}[/latex]	3	100	75.13	[latex]\small \frac{100}{(1.1)^3}[/latex]
4	100	68.30	[latex]\small \frac{100}{(1.1)^4}[/latex]	4	100	68.30	[latex]\small \frac{100}{(1.1)^4}[/latex]
5	100	62.09	[latex]\small \frac{100}{(1.1)^5}[/latex]	5	100	62.09	[latex]\small \frac{100}{(1.1)^5}[/latex]
6	100	56.45	[latex]\small \frac{100}{(1.1)^5}[/latex]	6
	Total PV	435.53	[latex]\small Sum \; of  \; PV_{CF_t}[/latex]		Total PV	479.08	[latex]\small Sum \; of  \; PV_{CF_t}[/latex]

Calculations in table 5.7 are illustrated in this video.

As we can notice from table 5.7, at t=0, we have already received a cash flow in annuity due. Since money today is more valuable than money in the future (as long as interest rates are greater than zero), we prefer annuity due intuitively. This intuition is verified by look at the values of total PV. [latex]PV_{annuity \; due} = 479.08 > PV_{annuity} = 435.53[/latex]

We can also observe that [latex]PV_{annuity} \times 1.1 = 435.53 \times 1.1 = 479.08 = PV_{annuity \; due}[/latex]

Finally, if we look at the present value of any intermediate cash flow, we notice that they have the same present value whether they were received in annuity or annuity due. This comes from the principle of discounting, which leads us to a major conclusion.

It does not matter what the name or nature of an instrument is. Its value is always determined by the nature of its cash flows, the timing of these cash flows and the discount rate used.

We can translate this into a mathematical equation. Let a stream of cash flows for simplicity have a constant cash flow “C” available at every period ‘t’ starting at t=1…n. Let the discount rate be ‘r’.

Then at time ‘t’, each cash flow will have a present value [latex]\frac{C}{(1+r)^t}[/latex]. We can represent each cash flow and its present value as in table 5.8 below.

Time (t)	[latex]CF_t[/latex]	Formula for [latex]PV_{CF_t}[/latex]
0
1	C	[latex]\small \frac{C}{(1+r)^1}[/latex]
2	C	[latex]\small \frac{C}{(1+r)^2}[/latex]
3	C	[latex]\small \frac{C}{(1+r)^3}[/latex]
4	C	[latex]\small \frac{C}{(1+r)^4}[/latex]
5	C	[latex]\small \frac{C}{(1+r)^5}[/latex]
t	C	[latex]\small \frac{C}{(1+r)^t}[/latex]
	Total PV	[latex]\small Sum \; of  \; PV_{CF_t}[/latex]

5.5 Infinite cash flows Perpetuity and perpetuity due

The concept of annuity is also applied to perpetuity except that in a perpetuity, each cash flow has the same nominal value as previous cash flow (therefore we call these constant cash flows) just like in an annuity. Similarly, these cash flows are also periodic. However, these cash flows never stop (i.e., these are not finite). An example of a perpetuity could be coupon payments of a bond that does not mature. In other words, the issuer would never repay the face value of the bond (because there is no maturity) but would keep paying constant coupon payments forever. It is not difficult to find the present value of perpetuity.

Let the present value of a perpetuity be PV for the remainder of this section. Then for equal cash flows of C and at a discount rate of ‘r’ at a time ‘t’, the present value of the period ‘t’ cash flow is [latex]\frac{C}{(1+r)^t}[/latex] as we saw in table 5.8 above.

Let [latex]\frac{1}{(1+r)} = R[/latex]

Since [latex]r > 0, R = \frac{1} {(1+r)} < 1[/latex]

Also,

[latex]1-R = 1 -\frac{1}{(1+r)} = \frac{(1+r)-1}{(1+r)} =  \frac {r} {(1+r)}[/latex], and

[latex]\frac{R}{(1-R)} = R\times \frac{1}{(1-R)} = \frac{1}{(1+r)} \times \frac{(1+r)}{r} = \frac{1}{r}[/latex] …(3)

Therefore the present value of perpetuity (PV) will be sum of present value of all cash flows.

[latex]PV(1-R)=CR[/latex]  …(12)

Using equation (3), [latex]PV = \frac{C}{r}[/latex] …(15)

The intuition behind simplicity of equation 15 is not unobvious. All it tells us is that the present value of infinite cash flows converges to a single number. We can notice from table 5.7 that for the same cash flow of $ 100, as we progressed further in time, its present value equivalent was lower. For example, the present value of $ 100 available after 2 periods was 82.64 at 10% rate of discount. Similarly, present value of $ 100 available after 6 periods is only 56.45. If this cash flow was available after 36 periods, its present value would be 3.23. If it was available after 96 periods; its present value would be a meagre 0.01. In other words, once we pass a certain threshold of time, incremental cash flows add no noticeable benefit to the present value of the overall cash flow stream. This is particularly applicable to cash flow streams that are large such as 100-period annuity or a perpetuity. In other words, as ‘t’ increases, the present value becomes smaller and smaller until the incremental value of present value of a cash flow does not make any significant impact on the increment in the present value of the perpetuity. In other words, the present value of perpetuity asymptotically reaches [latex]\frac{C}{r}[/latex] as t[latex]\rightarrow \infty[/latex]

Table 5.9 below shows how the present value of equal cash flow at a hypothetical rate of 75% progresses as we progress in time (over time periods). Columns 1 through 3 are the same as what we saw in Table 5.4 above. What changes here is we have added column 4, which contains a rolling sum of the present value of cash flows until that point. For example, at period two, we would have received two cash flows and the sum of those is the rolling sum of annuity for those two periods. For example, the present value of a two-period annuity of $ 100 at 75% discount rate would be 89.8. Similarly, the present value of an 8-period annuity would be 131.82. What we notice is that even as cash flows increase, the present value does not increase significantly. This is particularly true if either the time period is too far out or if the rate of discount is high. Therefore, we can notice that the cumulative (total) present value is approximately 133 and change even as we add cash flows 12, 13 …

Table 5.9 Present value and cumulative present value of cash flow of $ 100 at the discount rate of 75% for periods 1…15 for annuity.

Time (t)	[latex]CF_t[/latex]	[latex]PV_{CF_t}[/latex]	[latex]PV_t[/latex] (cumulative)
0
1	100	57.14	57.14
2	100	32.65	89.80
3	100	18.66	108.45
4	100	10.66	119.12
5	100	6.09	125.21
6	100	3.48	128.69
7	100	1.99	130.68
8	100	1.14	131.82
9	100	0.65	132.47
10	100	0.37	132.84
11	100	0.21	133.05
12	100	0.12	133.17
13	100	0.07	133.24
14	100	0.04	133.28
15	100	0.02	133.30
	Total PV	24.85

We can extend this discussion further to see that if we make infinite cash flows of $ 100, the cumulative present value will taper off to 133.33333… or cash flow/ rate of discount = 100/0.75.

To summarize:

• If interest rates are sufficiently high, distant cash flows have no residual effect on present value today.
• Present value of perpetuity of cash flow = C at a discount rate ‘r’ is [latex]\frac{C}{r}[/latex]

Calculations of Table 5.9 are discussed in this video.

We can also find the present value of perpetuity due. Using the same connection that exists between annuity and annuity due, we can find the connection between perpetuity and perpetuity due.

[latex]PV_{perpetuity \; due} = (1+r) \times PV_{perpetuity}[/latex]

The present value of annuity and perpetuity can vary depending on the compounding periods. So far, we have discussed present value and future value if the compounding period conforms to the rate of interest. In other words, if the rate of interest is annual, our compounding periods were 1 year. If the compounding periods were semi-annual, then the rate of interest given was for 6-months. Next, we will see what happens when the compounding period and the rate of interest are for different durations.

5.6 Effective Annual Rate and Annual Percentage Rate

Let us consider a simple example of a future value of $ 100 at 5% (annual rate) in 1 year. We will either use the FV function in Excel or simply use the formula 100(1.05) to calculate the value as 105. However, we had assumed that the number of compounding periods in this calculation were consistent with the rate of interest given. What if the rate of interest was still 5% (annual) but the number of compounding periods were 2, instead of 1? In other words, what if the compounding occurred semi-annually?

Then we will have to break down the rate of interest to semi-annual as [latex]\frac{5%}{2} = 2.5%[/latex]

Our future value would then be [latex]100(1.025)^2 = 105.0625[/latex]

So, the borrower would have to pay 6.25 cents extra per $ 100 borrowed.

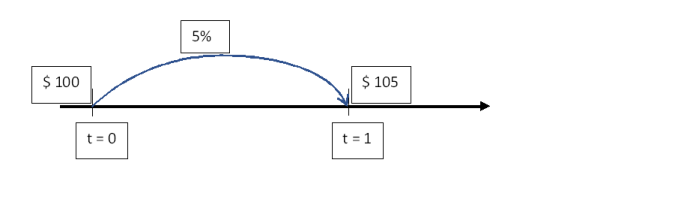
To illustrate this through a timeline, in Figure 5.3, the $ 100 just travels through 1 period at a given rate of 5% to become $ 105 in a year.

If the number of compounding periods increases to 2, or semi-annual compounding periods, then the number of times $ 100 has to travel would be over 2 periods. However, the rate at which it travels per compounding period would be ½ the annual rate = 5%/2 = 2.5%.

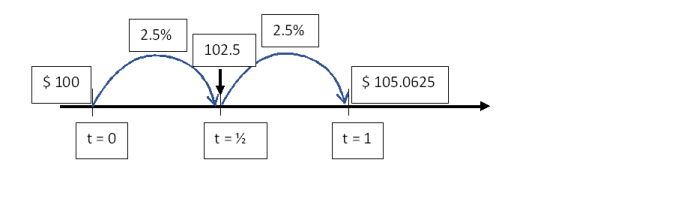
From Figure 5.4, it can be seen that after 6-months, the value increases to 102.5 and that increases to 105.0625, which is greater than the future value obtained with just one compounding period.

The  5% rate that we have used above is also called annual percentage rate or APR. It is the annual rate which is used to find rates associated with compounding periods (such as semi-annual in the above case). The amount 105.0625 is based on an effective rate of 5.0625/100 = 5.0625%. Another observation that we make  from the above figures is that as the number of compounding periods increases from 1 to 2, the effective rate increases.

Table 5.10 below explains how different compounding periods are related to the same annual rate (which we call annual percentage rate). In the first column, we have number of compounding periods per year. In the next column, we have to apportion the annual rate ‘r’ into those compounding periods by dividing by the number of compounding periods per year. In the final column on the right, we can find the future value using our compound interest formula.

Number of compounding periods/ year	Periodic rate	Future value
1	[latex]\small r[/latex]	[latex]\small PV(1+r)[/latex]
2	[latex]\small \frac{r}{2}[/latex]	[latex]\small PV(1+\frac{r}{2})^2[/latex]
3	[latex]\small \frac{r}{3}[/latex]	[latex]\small PV(1+\frac{r}{3})^3[/latex]
4	[latex]\small \frac{r}{4}[/latex]	[latex]\small PV(1+\frac{r}{4})^4[/latex]

In our example of 5%, we illustrate the future value with the increase in number of compounding periods in table 5.11 below. We use an annual rate of 5% and a starting value of $ 100.

Table 5.11: Connection between periodic rate, number of compounding periods and future value for $ 100 at 5% APR

Number of compounding periods/ year	Periodic rate	Future value
1	5%	105
2	2.5%	105.0625
3	1.667%	105.0838
4	1.25%	105.0945

On one hand, an increase in the number of compounding periods increases the future value, while on the other, it is well known that inflation erodes into the future value. The rate of inflation is used as a discounting rate. Let us illustrate this concept with a small example below.

Let us say our APR is 5% with annual compounding. Then $ 100 becomes $ 105 in one year.

However, for that year if the rate of inflation is 0.5%, then we can conclude that the final amount of 105 is eroded (or discounted) by 0.5%. In other words, with a rate of ‘r’ and an annual rate of inflation of [latex]‘\pi’[/latex], then the value today (PV) becomes [latex]\frac{PV \times (1+r)}{(1+\pi)}[/latex] as future value.

In other words, the effective rate is [latex]\frac{(1+r)}{(1+\pi)}[/latex].

If the rate of inflation is infinitesimally small, then the effective rate is [latex](1+r)(1-\pi) \approxeq (1+r-\pi)[/latex]. This is because ‘r’ times ‘[latex]\pi[/latex]’ is  infinitesimally small as well.

So, the effective rate is [latex]r-\pi[/latex].

In our case, the effective rate is 5-0.5% = 4.5%

We can see this as [latex]\frac{100\times(1.05)}{(1.005)} = 104.48[/latex], which works out to 4.5% (approx.)

Summary

In this chapter we learnt how to interpret and analyze simple and compound interest. We computed the present values of cash flows.

An investment of $ 1 after ‘t’ years at a rate ‘r’ will be 1+rt with simple interest and [latex](1+r)^t[/latex] with compound interest. The present value of $ 1 due after ‘t’ years, at a discount rate ‘r’ is [latex]\frac{1}{(1+r)^t}[/latex]. This expression is also called discount factor. Notice that this discount factor is based on compound interest rate.

Annuity is cash payment at a regular intervals, that lasts a finite number of periods; while perpetuity involves cash payments that never end. This chapter involves computing present values of both annuities and perpetuities.

Interest rate for a given period (less than 1 year) is multiplied with the number of periods in the year to achieve the annual percentage rate. However, with compounding, the effective annual rate would be higher. The effective annual rate equals the rate of interest per period compounded for those number of periods per year.

A dollar today is not the same as a dollar after a year, thanks to interest rates. However, if the interest rate is zero, and in the presence of inflation, a dollar after one year cannot buy the same quantity of goods as a dollar today. Thus, we need to compute real interest rates, which are a difference of actual (or nominal) interest rates and inflation.

In Chapter 6, we will apply the concept of cash flows in understanding the price of bonds, using the present value approach.