Chapter 10: Return and Risk in Finance

Overview/ Background

After going through the concept of rate of return on different investments, it is natural to turn our attention to one of the riskier investments in financial markets, that is stocks. The natural question to ask is, “What is the meaning of riskiness of stocks? If we identify stocks of two different companies, can we assess which stock is riskier and by how much?” This chapter seeks to answer those questions. We also discuss quantitatively, the benefits of investing in multiple securities at the same time, also known as diversification. In summary, this module defines risk and measures it in the context of single and multiple investments.

10.1 Introduction

Investments are synonymous with Finance. Without the thrill associated with investing, finance would not be as popular as it is. Often, we hear about the trading profits of large investment banks being very high. For example, Reuters reports that, in 2022, investment banks made around $20 billion profit by trading commodities such as oil, gas and metals.² We also hear about the listing of new initial public offerings (IPOs) through price discovery in when-issued markets bringing the lenders of funds to the borrowers, as we saw in earlier chapters.³ Dealing with these fluctuations are some of the most important functions of finance. In the aviation sector, airlines have active treasuries that deal with oil price volatility. In this chapter, we define these fluctuations as risk, quantify these fluctuations and discuss how measuring risk will help companies manage their risk.

10.2 Returns

10.2.1: Capital gains yield and Dividend Yield

We define returns on any investment as a ratio of what we earn as a proportion of the original sum invested. In case of stocks with dividends, we can easily predict that there are two types of earnings. One is the capital gains we make from selling the stock at a (hopefully) higher price than we bought it. The other is the dividend we receive because we are shareholders in a company while we are holding the stock. To simplify our calculations, let us assume that we hold our investment for 1 year. The period for which we hold any investment is the holding period. Another way to look at holding period is that it is the time period between when we purchased the stock and sold it. If we did not make this assumption, then we would have to normalize our returns to annualize them. We will see this later. Formally,

Here P₀ is the purchase price of the stock and P₁ is the selling price of the stock.

The second component of returns is dividend yield.

[latex]dividend\;yield=\frac{D_1}{P_0}[/latex] …(10.2)

D₁ is the dividend received at the end of the year.

Capital gains signifies the profits made on sale of stock as compared to the purchase price and dividend yield is the earning made by investors: thanks to dividends received.

Return or rate of return is therefore a very important benchmark to compare different stocks. When return is calculated for 1-year, it is called annual return. However, most often, investors hold their investments for either shorter or longer durations. Returns for any such durations are called holding period returns. So holding period returns imply the returns for entire period of investment. The higher the return is, the better the investment.

[latex]Holding \; period \; returns = h = \frac{(End \; Value – Beginning \; Value + Dividends)}{Beginning \; Value}[/latex] …(10.3)

All these yields/ returns can either be expressed in ratio or a percentage. They are equivalent. For example 20% \equiv 0.2; 1% \equiv 0.01 and so on. Now, let us look at calculation of returns in example 10.1.

10.2.2: Holding Period Returns and Annualized Returns

As mentioned earlier, holding period returns are defined as profits earned including any dividends received over the period of investment. Note that we can also annualize these returns as needed.

[latex]Holding \; period \; returns = h = \frac{(End \; Value – Beginning \; Value + Dividends)}{Beginning \; Value}[/latex] …(10.3)

If the holding period return is over a time period ‘t’ > 1 year, then we can annualize it using compound interest formula annualized return ‘r’.

[latex](1+r)^t = (1+h)[/latex] …(10.4)

[latex]r = (1+h)^{\frac{1}{t}}-1[/latex] …(10.5)

As with capital gains yield and dividend yield, holding period returns can also be expressed as either a fraction or as a percentage.

One intuitive way to look at the relationship between holding period return and annualized return is that holding period return will accrue compound interest on annualized return ‘r’. Therefore, in Example 10.3, approximately 14.4% times 2 and some more will be the holding period return.

In previous chapters, we have studied different financial instruments: bonds, stocks and treasury bills. Historically, the stock markets have always outperformed bonds and treasury bills.

In figure 10.1 we look at the stock returns of Treasury Bills (SHV), long-term Bonds (TLT), and stock market indices (S&P 500 (GSPC) and the Dow Jones Industrial Average (DJIA) from May 8, 2007 through July 8, 2023⁵ We observe the performance of several exchange traded funds (ETFs).⁶ S & P 500 index (GSPC) represents  the performance of more risky stocks compared to  the Dow Jones Industrial Average (DJIA). Recall that a corporation is not liable to pay anything to its owners but owes all the residual profits to them. In other words, if a company is liquidated then on one hand, shareholders may get nothing back (as in the case of bankrupt companies) while on the other hand, shareholders’ wealth may multiply exponentially (as in the case of giant corporations such as Apple, Google, Microsoft, Exxon, Tesla etc.). The figure above also represents ETFs that include longer duration bonds (i.e. that have a ttm > 20 years) such as seen in investment in TLT. It may be recalled from chapter 6 that for the same change in interest rates (i.e. YTM) longer maturity bonds tend to fluctuate more in prices as compared to short-term bonds. In figure 10.1 above, we represent short-term bonds through SHV (which essentially deals with investment in treasury-bills). Since stocks are the riskiest, they have produced the most returns. SPY and DJIA yielded 173% and 152% respectively whereas, TLT yielded 19.17% and SHV 0.79%. If we include their dividends, these yields would be higher, but returns would stay in relatively same proportions.

10.3 Choice of financing

It is important to understand returns from a firm’s perspective because it is the rate on returns that determines what type of capital must be used to generate these returns. This is particularly important if the firm is borrowing directly from financial markets in the form of loans or debentures or commercial paper. As an example, during the COVID pandemic, a number of airlines received loans from the government. This so called “line of credit” of $ 25 billion for passenger airlines and $ 4 billion for cargo air carriers was not without strings. As a part of loan covenant (conditions), airlines were required to keep their employees on payroll until 1 year after totally repaying the loan. These airlines were also not permitted to pay dividends to shareholders, buy back stocks, or pay special dividends. These restrictions were meant to ensure it was not shareholders but employees and business associates that benefited from such a facility. All these aspects are important: if a company is sure it is not going to generate profits, such as in the early part of the pandemic, it must be necessary to access funds that have low cost (i.e. rate of interest) attached to them. Hence the need to focus on return is important because a company must look at the cost (that is, return paid) on debt (bonds and commercial paper) and stock (return on equity). As we saw in the graph above and in the previous chapters, the greatest returns are expected by shareholders (recall that return on equity we saw in chapter 4 on ratio analysis was in double digit percentages), while bond investors i.e. debenture holders and holders of commercial papers are more interested in safety and stability of their returns. Hence the yields on these debt instruments are lower than return on equity.

Risk management deals with the dispersion of returns. In particular, if a company is generating profits, these profits are intricately linked with the business cycle. Hence, understanding how profits and returns to shareholders will fluctuate over a period of time will determine whether funds can be raised via debt or equity or hybrid or not at all. Conventionally, risk management applies to bond and stock returns and the variability of these returns over periods of time. Typically, using concepts from math one way we could measure risk attached to a security is by measuring the volatility through dispersion of returns. This is calculated from variance (or standard deviation) of returns about their mean.

10.4 Measure of Risk

Let’s detour for a quick review of average (expected value/ mean) and standard deviation.

Assume an event is associated with three possible outcomes. A good outcome 1, a normal outcome 2, and a bad outcome 3. In each situation, we expect stocks to produce certain returns (1, 2, and 3). Then if the probabilities associated with each of these are p₁, p₂ , and p₃ respectively, we can find out the expected value of the return. Table 10.1 lists these.

r_e = p₁r₁+ p₂r₂+ p₃r₃ …(10.6)

where (p₁ + p₂ + p₃ = 1) …(10.7)

[latex]r_e = p_1r_1+p_2r_2+p_3r_3[/latex], where [latex](p_1+p_2+p_3 = 1)[/latex]

We can show: Expected value of deviation is zero.

This is because

Rearranging terms,

[latex]p_1r_1+p_2r_2+p_3r_3 – (p_1+p_2+p_3)\times r_e = r_e – r_e = 0[/latex]

Expected value of squared deviation is

variance = squared standard deviation = [latex]p_1(r_1-r_e)^2 + p_2(r_2-r_e)^2 + p_3(r_3-r_e)^2[/latex] …(10.8)

Intuition: Deviations are both positive and negative. Taking expectations (average) of deviations produces outcomes that are close to zero since positive and negative values tend to cancel out each other. Therefore, taking average of deviations does not tell us anything about the extent of dispersion (and hence volatility) of our data. Since obtaining deviation does not tell us anything about the volatility around the mean (expected value), if we square the deviation, this neutralizes the negative values of deviation and makes all deviations positive. After taking the weighted average of that and taking square root, (i.e. obtaining standard deviation), we are obtaining a monotonic function of the deviation, which does not cancel out negative and positive deviations. This number so obtained then gives us an estimate of the magnitude of the overall deviations around the average.

Returns from financial instruments are forecasted by using our knowledge from the past and expectations of future events. Let us see this in an example below.

Now let us simulate this a little bit. What happens if we change the extreme values and make them more extreme (i.e. make returns during boom times to 30% and recession -10%)? Let us see this in table 10.3 below.

From Table 10.3, the expected value of returns increases because of greater increase in the positive extreme value (20% to 30%) as compared to the negative extreme value (-4% to -10%). The expected value therefore increases from 7.43% to 9.05%. However, since both the extreme values increase, the variance now increases to 0.0195 and the standard deviation increases to 13.98%.

What we imply from this is that increase in dispersion/ spread increases the variance and hence standard deviation of returns.

What if the extreme values did not change? Suppose the returns during boom times remain at 20% and recession remain at -4%. However, if we double the returns from 5% to 10% during normal times, this should increase the variance, but by how much? Let us see that in Table 10.4 below.

From Table 10.4, the expected value of returns increases to 10.18% because of huge increase in the positive value during normal times (5% to 10%). The expected value therefore increases from 7.43% to 10.18%. However, since neither extreme value have increased, the variance has only marginally increased to 0.013 (as compared to 0.019 in table 10.3) and the standard deviation increases very slightly to 8.36% (from 8.33% in Table 10.2 and compare with 13.98% in Table 10.3).

What all the above examples suggest is that standard deviation is a measure of risk. When extreme values increase, standard deviation increases. Or conversely, greater standard deviation is a measure of extreme volatility or greater change in extreme values of returns for a security.

Summary: greater standard deviation is a feature of greater volatility in returns.

10.5 Risk Management and Portfolio Creation

10.5.1 Portfolio and risk

From the above discussion on riskiness of securities, one might be tempted to think that it is not appropriate to invest in risky securities because of greater expectation of loss. However, as we have learned from legendary investor Warren Buffet,⁸ if we can ride out the losses in bad times, and as long as we have faith in our investment, we can also expect greater than normal returns for investments with a larger standard deviation.

But how can we be relatively insulated from bad times? The answer to that question is hidden behind the fact that not all securities move extremely low during a recession. Examples of utilities, commodities (to some extent), consumer staples, bonds can show us that these investments are not affected as greatly by business cycles as are “regular stocks” such as industrials or transportation. It is expected that industrial or transportation activity decreases as the business cycle goes from normal times to recessions. Therefore, these stocks are expected to yield less positive or even negative returns as the economy turns. However essential items such as hygiene products or household items do not see a massive decline in demand during such turns. This can help us create a portfolio, a collection of different securities that are not affected by business cycles in the same way in order to “hedge” or not face extreme returns during a recession. Let us see how that works in an example below.

From Table 10.7, we can see that now we have recession proofed our portfolio (i.e. designed it to get overall positive returns, even in a recession), but also managed to increase our returns from just holding Spirit airline (SAVE) stock in boom times. The best part is our volatility remains low at 1.64%. This is the benefit of creating a portfolio. It helps increase our returns at a modest loss of risk (i.e., increase in standard deviation).

10.5.2 From stock specific to market risk

We can create such portfolios with much more assured returns such as from treasury bills or commercial paper to decrease the volatility of our returns. However, the sacrifice we make is that our returns decrease as well. Thus, the key learning is that risk and returns are directly related to each other for normal investment instruments. Another important learning is that if two securities are better than one, then we can add away more stocks to lower our standard deviation of the portfolio. Thus, as we add more and more securities to our portfolio, the standard deviation decreases. However, the best we can do at the limit is to achieve market risk (standard deviation). This is seen in Figure 10.1 below. As the number of firms in our portfolio increase (along the x-axis), the portfolio standard deviation decreases to market levels (as seen by the levelling of the curve along an intercept on the y-axis). Market risk (also known as systematic risk) is the risk associated with holding a portfolio that reflects stock market indices and indicators such as Dow Jones Industrial Average (DJIA) and S&P 500 index. It is associated more with macroeconomic factors that cannot be diversified any further. Stock-specific risk that can be diversified away is called unsystematic risk. Unsystematic risk is associated with a portfolio that holds too few stocks or securities and therefore this portfolio will fluctuate with company specific idiosyncrasies.

Portfolio Standard Deviation as number of stocks increase in a portfolio

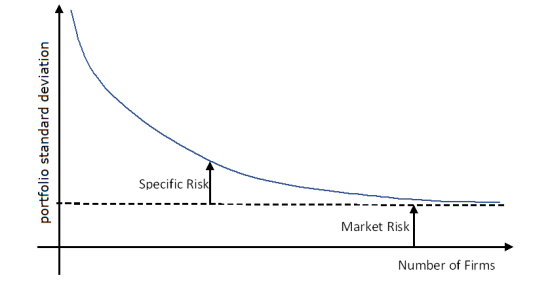
From Figure 10.2, there is some evidence that the forces that move overall markets also move individual stocks. Companies whose stocks move up when the overall market also goes up are called pro-cyclical stocks. Some stocks either do not move up when this happens or even move down. Similarly, when procyclical stocks go down in value, any investor who has invested in these stocks will lose investment value. Most stocks are procyclical. Examples are Boeing (BA), Delta (DAL), United (UAL), Deere (DE), Caterpillar (CAT), FedEx (FDX) etc. Can investors protect themselves from these shocks? In Figure 10.1, we saw that investors can diversify away by adding more stocks and reducing stock specific risks. However, we saw that we could not do anything about market risk, also known as systematic risk. However, by adding stocks that are either not correlated with the market (such as gold or bonds) or are inversely correlated with the market, investors can decrease the risk of their portfolio. In other words, when the overall market moves down, investors still lose value from their portfolio but not as much if they held only pro-cyclical stocks. The benefit of risk management is exactly this. With the help of risk management, investors can quantify how much their portfolio will fall in value when the market changes by a given amount. In order to understand this correlation, we need to develop the Capital Asset Pricing Model (also called CAPM). However, we will first discuss different types of risk and yield curve that we learned in the bond market chapter to apply it to risk management in case of portfolio in this chapter.

10.6 Some Types of Risk and the Yield Curve

In the previous section we discussed  the implications of holding a portfolio of stocks and the consequent reduction in risk due to portfolio creation. In other words, we realized that we can diversify unsystematic risk but not systematic risk. In this section we will analyze the correlation of stock returns with market returns through the capital asset pricing model (CAPM). However, before we explore CAPM, we need to revisit the implications of returns. Any investor makes an investment in different financial instruments for returns through capital gains or dividends or both. By investing, an investor is trading funds today for funds in the future. By doing so, they are taking a risk in terms of how long the funds would be invested (called maturity or term risk) and who the borrower of the funds is (credit risk).

Term (maturity) risk is simply a function of time. Greater the duration of investment, greater the risk carried. This is simply because of uncertainty associated with time. For example, if Delta Airlines issue bonds for 20-years and also commercial paper for 3 months, an investor who is considering these two investments is only worried about comparing the maturity risk, because the borrower is same. Intuitively, the investor wants to be paid more for holding on to a bond for a longer time. Additionally, they want an investment that generates a greater rate of return. This means, if the rate is 2%, an investment of $ 100 will produce 102 in 1 year, 104.04 in two, 106.12 in three years and so on. However, the uncertainties of time also imply that any investor who wants to invest for longer duration should be compensated additionally ( that is rate should be above the 2%). That is usually why the bond yields on longe- term bonds are greater than those on short-term bonds.

This relation between duration and yield is called the yield curve. The yield curve shows the interest rates of bonds at different points in their maturities. Figure 10.3 below shows the treasury yield curve on January 3, 2023, as compared to January 3, 2020. On January 3, 2020 (vertical axis on the left) the yield curve was steep, implying short-term yields were lower than long-term yields. For example, the 30-year yield was 2.26% — greater than the 3-year yield of 1.54%. However, due to aggressive rate hikes by the U.S. Federal Reserve on the shorter end as of October 2, 2023, yield for the 3-year bond increased to 4.2% (vertical axis on the right) but the yield on the 30-year bond only increased to 3.9%. Therefore, the yield curve is inverted, meaning investors on the shorter-end of the curve are paid higher due to greater inflation expectations than the investors on the longer-end.

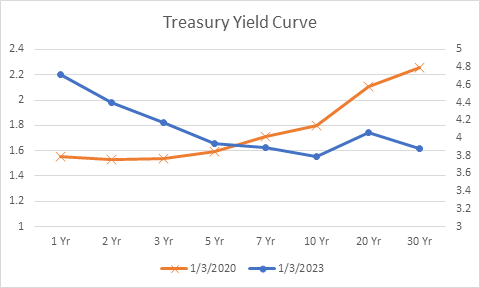
Figure 10.3 shows treasury bond yields for 1 to 30-year maturity bonds as of January 3, 2020 (left vertical axis) and January 3, 2023 (right vertical axis) Returns from the shortest treasury bill (the 1-month treasury bill or sometimes the 3-month treasury bill) is considered as the risk-free rate. The reason for this is that there is neither borrower risk nor term risk attached to this instrument. Difference of returns between a stock and a treasury bill is called the risk premium (of stock over risk-free rate). Risk premia can be calculated for any pair of securities using the Capital Asset Pricing Model (CAPM).

10.7 Capital Asset Pricing Model

According to the Capital Asset Pricing Model (CAPM), the risk premium of a stock (over the risk-free rate) is beta times the risk premium of the overall market. In other words, mathematically:

[latex]r_i – r_f = \beta (r_m – r_f)[/latex] …(10.9)

Here,

[latex]r_i[/latex] : rate of return of a stock

[latex]r_f[/latex] : return on risk free security

[latex]r_m[/latex] : return on overall stock market (usually S&P 500 or Dow Jones industrial average or the NASADAQ 100)

If the value of beta is more than 1, then risk premium of a stock is highly volatile as compared to the risk premium of the overall market.

On the other hand, beta of zero means that the risk premium of the security does not have a correlation with the risk premium of the market.

Value of beta less than one implies the risk premium of the stock is not as volatile as the risk premium of the market.

Sometimes beta can be negative implying that the risk premium of the security is inversely correlated with the risk premium of the overall market.

If we simplify this discussion, then we can plot the returns of a stock against the returns of the overall market. We know that the equation of a straight line is

For our purposes, we can rewrite the equation of the straight line as

[latex]r_i = \beta_0 + \beta_i r_m + e[/latex] …(10.10)

Here

[latex]r_i[/latex] : rate of return of a stock

[latex]r_m[/latex] : return on overall stock market

[latex]\beta[/latex] : is the slope of the line (correlation of the stock with the overall market)

e: idiosyncratic error term, which represents noise part in the return that is associated with investor biases etc. that disappear over time

When we plot values of stock returns on the y-axis versus market returns (S & P 500) on the x-axis, we obtain a scatter plot. A scatter plot is just a collection of several points on a graph that are arranged by exactly how they occur and not a predetermined rule. For example, the difference between a scatter plot and a straight line (i.e. predetermined rule) is that when we plot straight line, there is a fixed correlation between values on y-axis and x-axis determined by a rule (y=mx + b). In a scatter plot, we just observe these values as they occur and not according to a predetermined rule. Then using, the relation in equation 10.10 above we obtain an approximate representation of a straight line to determine slope and intercept ([latex]\beta_0[/latex] and [latex]\beta_1[/latex]). All inaccuracies from this line for each point on the scatter plot (i.e. actual versus estimated r_i are estimated as the error value ‘e_i’ for that observation. This is known as regression line, which we observe in figures 10.4 and 10.5 below.

Summary: A regression line approximates the relation between ‘r_i’ and ‘r_m’ to estimate the values of slope and intercept.

From Figures 10.4 and 10.5 below, we can conclude that Delta Airline stock (DAL) is highly positively correlated with the stock market ([latex]\beta_1= 1.28[/latex]). as compared to Gold ([latex]\beta_1= 0.018[/latex]).

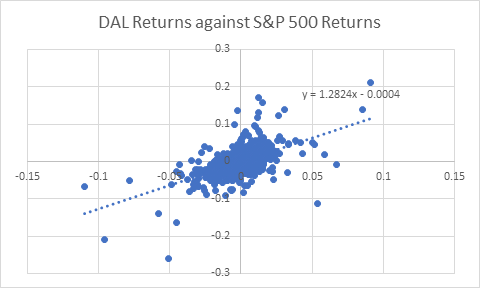
From figure 10.4, we notice that when daily returns from Delta airlines plotted against S&P 500 over a period of 5 years between 2015 and 2020 and the parameters of the dotted line (i.e. the trendline) are observed, the slope is observed to be 1.282 and intercept is observed to be almost zero. This means that when overall market jumps by 1%, DAL stock changes by 1.282%, all else constant.

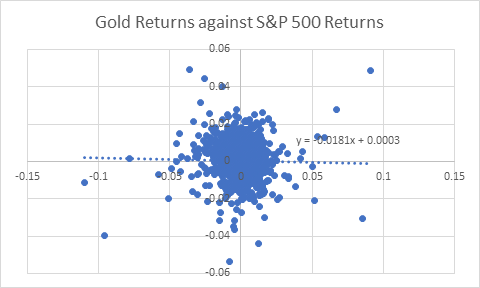
In figure 10.5, we make a similar plot as figure 10.4. However, we now use daily returns from Gold exchange traded fund (ETF), which are plotted against S&P 500 returns over a period of 5 years between 2015 and 2020. We again notice from the fitted dotted line that the slope of the trendline is 0.0181 and intercept is close to zero. From Figures 10.4 and 10.5, we can conclude that Delta airline stock behaved like a procyclical stock during the 5-year period as compared to Gold (positive ₁ for Delta as compared to that for Gold). The latter was almost uncorrelated with the overall market ([latex]\beta_1 = 0.018 \approxeq 0[/latex]).

Just a note on terminology: financial markets consider [latex]\beta_1[/latex] we discussed here as the [latex]\beta[/latex] of a stock. In other words, when finance specialists refer to [latex]\beta[/latex] of a stock, we infer the slope of the relationship expressed in equation 10.10

10.8 Behavior of returns against risk: Security Market Line

Every stock behaves differently because of the nature of business of the company. When the absolute value of beta of a stock is high, we call it risky. This is because if market moves up (down) by say 1%, the stock is expected to move up (down) by beta percentage. Since betas of different stocks are different, we can plot returns of these stocks (y-axis) on a graph against their betas (x-axis).

When we plot returns versus risk (as measured by [latex]\beta[/latex]), then we first notice that the relationship has a positive slope. This implies that greater the risk associated with a stock, greater the reward from that stock. This relationship is represented in figure 10.6 below. In the figure, we can see returns from treasury bills are at the lower end (to the left). However, for treasury bills [latex]\beta[/latex] is close to zero or uncorrelated with the market. At the other end of the spectrum, we have [latex]\beta[/latex] for market is 1, with a greater return from the overall market during normal times.

In between these we can have stocks that have [latex]\beta[/latex]s between zero and one or even greater than one.

When value of [latex]\beta =0[/latex]  (as in the case of risk-free rate), the rate of return is that from these risk-free investments (typically treasury bills).

When the value of [latex]\beta =1[/latex] (as in the case of any instrument that follows the overall market closely, such as the SPY exchange traded fund), then the return is that from overall market.

This positive correlation between risk ([latex]\beta[/latex]) and return is approximated through a straight-line (or linear) relationship called security market line as shown in Figure 10.6 below.

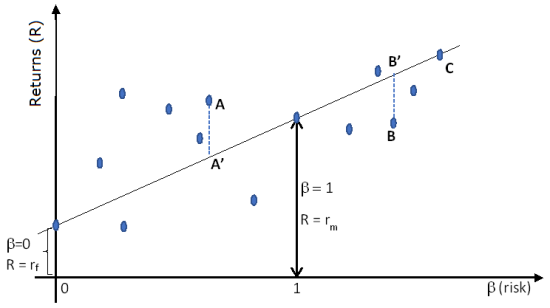
Now, let us analyze the security market line for some hypothetical stocks. Let us consider point A in Figure 10.6. As predicted by the security market line, this stock was expected to produce returns equivalent to that at point A’ because both have same [latex]\beta[/latex] (i.e. A’ is vertically below A, meaning they both are associated with the same value of [latex]\beta[/latex] on the x-axis. However, the stock actually produced greater returns than that, as can be observed from the fact that the returns at A are greater than the returns predicted at A’. If observed returns are greater, this implies that in future, more investors will buy this stock. Thus, its price will increase, and its expected future returns will decrease. On the other hand, the opposite logic applies to stock corresponding to point B. At point B, actual returns are less than expected (returns should be at B’ corresponding to that risk level according to the theoretical prediction of the security market line). Therefore, investors will sell this stock today. Its price will drop and for the same expected future price, its expected future returns will go up (due to lower price today). Lastly, point “C” is exactly as expected in terms of risk-return relationship.

To summarize: stocks that correspond to points that are above the security market line should produce greater returns and will be bought today. Therefore, their prices increase and expected returns will drop, thereby bringing them to the security market line. The opposite is true for stocks that correspond to points that are below the security market line. Notice that this is a theoretical prediction. As we saw in the chapter on stock markets, due to market inefficiencies, sometimes such bubbles may persist for longer durations of time.

10.9 Summary/Conclusion

Conclusion:

• Profits are dollars gained on investments. A return is the ratio of profit to the cost of the investment.
• Returns are typically stated on an annual basis, not according to holding period basis.
• When there is an absence of knowledge, uncertainty exists, as measured by risk.
• Looking at historical data, we find that stocks were riskiest and had the largest variance, while Treasury Bills were the least risky.
• Probability is used to measure likelihood of favorable and adverse events. This helps us compute variance and standard deviation.
• Variance is a probability weighted sum of squared deviation from the expected (average) value. Standard deviation is the square root of variance.
• Higher value of the expected return is generally associated with higher risk as measured by variance.
  • [latex]\uparrow[/latex] expected return [latex]\rightarrow \uparrow[/latex] risk
  • Generally, stocks > bonds > bills (in terms of risk and return).
• Risk and return:
  • Variance and standard deviation are measures of risk
  • For the same risk, we prefer higher return.
  • For the same return, we prefer lower risk.
• Diversification helps alleviate individual stock risk.
• Adding more stocks to a portfolio creates diversification, particularly if stocks are from unrelated sectors.
• We cannot diversify the risk of the overall market, called systematic risk.
• [latex]\beta[/latex]: is another measure of risk.
• Covariance of asset return with risk adjusted expected returns from market.
• Security market line (SML) is a locus of points that represent the best return corresponding to each risk level.
• SML can be used to determine the expected returns of an asset from its beta.

In this chapter, we discussed various types of returns, defined and quantified risk of an individual asset and of the portfolios. We also distinguished between different types of risk, and developed a model called Capital Asset Pricing Model (CAPM) relating risk and return.