MKZ airlines is planning a project investment: the purchase of 3 Cessna aircraft to fly a specific route. The cost of acquisition of aircraft (including all charges) is $ 2,000,000. It is expected that annual net revenue from operations will be $ 1,500,000 and thereafter the aircraft will be sold for $ 1.2 million. This yields a total net cash flow of $ 2.7 million from operations.

The alternative opportunity MKZ is considering is to invest the money in non-risky bonds at 3.5%. Please calculate and/ or report:

• the opportunity cost of capital
• present value of investment in real project
• net present value of investment in real project

Answer:

• The opportunity cost of capital is the alternate return on investment obtained = 3.5%
• The present value from investing in the project is
• [latex]PV = \frac{2,700,000}{1.035} \approxeq $ 2,608,696[/latex]
• Since this value is now equivalent to the period zero, we can compare this with initial cash (out) flow. Comparing generates the net present value of $608,696 (2,608,696 – 2,000,000).

Video demonstration of this example in MS Excel here.

Consider the purchase of Cessna aircraft by MKZ airlines in Example 8.1 above. The opportunity cost of capital is 3.5% from investing in the best alternate option – government bond for 1 year. The investment in Cessna for 1 year, and resale of the used aircraft thereafter produces a cash flow of $ 2.7 million net of operating and other expenses. Is this a better investment than investing in bonds?

Answer:

Investing in bonds yields

When we compare 2,070,000 with 2,700,000, investing in bond is inferior as compared to the Cessna project. Therefore, investing in bonds is not a better investment than investing in the aircraft, and MKZ should invest in the project investment. One aspect to note about real projects being evaluated at the opportunity cost of capital is that real projects are risky.

Video demonstration of this example in MS Excel here.

KMZ airlines, a competitor of MKZ airlines, considers entering the same market. Their marketing manager estimates the same initial cost of $ 2 million. However, since the market is getting saturated, the manager estimates that cash flow thus produced is $ 800,000 from operations (net revenue) and $ 1.25 million from resale. A financial analyst at the company estimates that the opportunity cost of capital is 3.5% obtained by investing in safe bonds. Calculate the net present value at the opportunity cost of capital of 3.5%. Also compare the future value of the two investments.

Answer:

Cash flow at the end of 1-year is 2,050,000.

The present value of this at 3.5% is

[latex]PV = \frac{2,050,000}{1.035} \approxeq 1,981,000[/latex]

When we compare it with initial cost, we get a net present value of -19,000 (1,981,000 – 2,000,000).

Thus, we should not purchase the aircraft needed to operate in this market.

Looking at future values, the future net cash flow from operations would be 2,050,000.

However, the future cash flow from bond investment would be

MKZ airlines is planning a project investment: the purchase of 3 Cessna aircraft to fly at a specific route. The cost of acquisition of aircraft (including all charges) is $ 2,000,000. It is expected that one year net revenue from operations will be $ 1,500,000 and thereafter the aircraft will be sold for $ 1.2 million. This yields a total net cash flow of $ 2.7 million from operations.

The alternative opportunity MKZ is considering is to invest the money in more risky and longer duration bonds at 4.5%. Please calculate and/ or report:

• the opportunity cost of capital
• present value of investment in real project
• net present value of investment in real project

Answer:

• The opportunity cost of capital is the alternate return on investment obtained = 4.5%
• The present value from investing in the project is[latex]PV = \frac{2,700,000}{1.045} \approxeq 2,584,000[/latex]
• Comparing generates the net present value of $584,000, which is lower than $608,696.in example 8.1. Thus, as opportunity cost increased, the net present value decreased. That is, the project investment became less valuable.

Video demonstration of this example in MS Excel here.

MKZ airlines is planning a project investment: the purchase of 3 Cessna aircraft to fly at a specific route. The cost of acquisition of aircraft (including all charges) is $ 2,000,000. It is expected that one year net revenue from operations will be $ 650,000 for three years (always end of the year) and the aircraft will be sold for $ 800,000 at the end of the third year. The alternative opportunity with MKZ is to invest the money in safe bonds at 3.5%. Please show/ calculate and/ or report:

• cash flows in a diagram
• present value of positive cash flows
• net present value of the investment

Answer:

• Cash flow diagram is as in Figure 8.1 below. Numbers at the top are dollar values (with appropriate signs) and represent cash flows from the Cessna project.

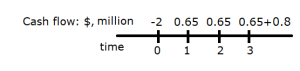
• [latex]PV_{inflows} = \frac{650,000}{1.035^1}+\frac{650,000}{1.035^2}+\frac{1,450,000}{1.035^3} \approxeq $ 2,540,000[/latex]
• Net present value is $ 540,000 and is positive, which implies that the company should go ahead with the project.

Video demonstration of this example in MS Excel here.

MKZ airlines can either invest in the Cessna project now for $ 2 million or any time in the next five years. The CFO of company estimates that the cost of investment increases by 10% every year from now for 2 years due to high inflation currently. The subsequent increase would be 7%, 5% and 3% for years 3, 4 and 5 respectively. The present value of cash inflows is 2.54 million now. This value after 1 year would be 2.48 million due to expected recession, 2.69 million after year 2, 3.12 million after year 3, 3.45 million after year 4 and 3.55 million after year 5. When should MKZ airlines invest in the project if the discount rate is 3.5%?

Answer:

To solve this, refer to Table 8.1 below:

As seen in Table 8.1, the present value of net present value at each point in time is in column titles PV_NPV at the right. The greatest value is in year 4 and therefore MKZ should launch the project at the end of year 4.

Video demonstration of this example in MS Excel here.

Let us compare Example 8.1 with exact cash flows in Example 8.5.

In Example 8.1, MKZ airlines is planning to purchase 3 Cessna aircraft for 1 year before reselling them. The cost of acquisition of aircraft is $ 2,000,000. The cash inflows would be $ 1,500,000 (net revenues) and $ 1.2 million (resale). This yields a total net cash flow of $ 2.7 million at the end of one year.

In Example 8.5, MKZ airlines is planning to purchase 3 Cessna aircraft for 3 years. The cost of acquisition of aircraft is the same ($ 2,000,000). However, now for the sake of comparison, let us modify that the cash flows will be $ 1,500,000 every year for three years and $ 1,200,000 at the end of the third year (resale). The opportunity cost of capital is 3.5%.

Using the regular procedure, please compute the NPV and compare them.

Answer:

We have modified Example 8.5 to match up with cash flows of example 8.1. This yields interesting results as seen in Table 8.2 below:

Video demonstration of this example in MS Excel here.

Let us still compare Example 8.1 with Example 8.5. In Example 8.1, MKZ airlines is planning to purchase 3 Cessna aircraft for 1 year before reselling them. The cost of acquisition of aircraft is $ 2,000,000. The cash inflows would be $ 1,500,000 (net revenues) and $ 1.2 million (resale). This yields a total net cash flow of $ 2.7 million at the end of one year.

In Example 8.5, MKZ airlines is planning to purchase 3 Cessna aircraft for 3 years. The cost of acquisition of aircraft is the same ($ 2,000,000). However, now for the sake of comparison, let us modify the cash flows will to $ 650,000 every year for three years and $ 1,200,000 at the end of the third year (resale). The opportunity cost of capital is 3.5%.

Using the regular procedure, please compute the NPV and compare them.

Answer:

We have modified Example 8.5 to match up with cash flows of Example 8.1. This yields interesting results as seen in Table 8.3 below:

Video demonstration of this example in MS Excel here.

Let us compare projects in Example 8.8 using equivalent annual annuity method. What is the net cost/ benefit of cash flows from Examples 8.1 and 8.5 at 3.5%. Based on this, which project would be recommended?

We find that the two projects have unequal lives. Hence NPV does not provide a clear picture of which project is superior per year. Therefore, we use the method of equivalent annual annuity corresponding to the period for which the project is carried out in Table 8.4 below.

Video demonstration of this example in MS Excel here.

MKZ airlines currently has A220s on their fleet that need $ 16 million to maintain per year.^{2 3}

Their general manager Mr. Aykan is wondering whether he can replace these aircraft with more energy efficient models which cost $ 34 million⁴ upfront and $ 11.75 million per year for maintenance. For simplicity, his maintenance manager Ms. Doshi estimates that both existing and new aircraft will be used for the next 10 years.

Please use our going discount rate of 3.5% to answer the following questions:

• Is it better to purchase new aircraft or continue with the existing ones?
• If the existing aircraft only had a useful life of 5 years, how does the comparison change now?
• If the discount rate increases, what is that discount rate that makes us indifferent between the two options? What happens if the discount rate increases further?

Answer:

Part a: Is it better to purchase new aircraft or continue with the existing ones?

Let us set up a cash flow table and find the net present values first. The existing project has no cash outflow at t=0. However, the new one has -$3 million. The existing project has annual outflows of $ 16 million but the new one has $ 11.75 million. Let us observe that and its NPV in Table 8.5a below:

As seen from Table 8.5a above, we can see that existing project has a greater (negative) NPV of maintenance. Therefore, its equivalent annual annuity (or net annual cost including discount rate) is also more expensive. But we also notice that (not so) weirdly, the EAA for existing project is $16 million, which is the annual maintenance cost. This is because the NPV and EAA are calculated on an annuity using the same discount rate.

Part b: If the existing aircraft only had a useful life of 5 years, how does the comparison change now?

Now, we modify the cash flows for existing project in Table 8.5a to only 5 years. This is seen in Table 8.5b below:

As seen from Table 8.5b above, we can see that the existing project now has a lower (negative) NPV of maintenance. But its equivalent annual annuity (or net annual cost including discount rate) is still more expensive. This is because, as noticed above that NPV and EAA are calculated on an annuity using the same discount rate. But now, we can see clear benefits of proceeding with the new project because of its lower annual equivalent cost despite higher set-up cost.

Part c: If the discount rate increases, what is that discount rate that makes us indifferent between the two options? What happens if the discount rate increases further?

Now we change the rate to make the two cash flows have the same EAA. This is straightforward in MS Excel®. We create a cell in which we find the difference between the two EAA’s and set it to zero using goal seek by changing the interest rate which is in another cell. Doing so gives us a rate of 4.28%

Table 8.5d represents the NPV and EAA at different discount rates

As we can see, beyond a rate of 4.28%, the equivalent annual cost of new project becomes more expensive. This demonstrates the moving parts that need to be handled in new project management.

Video demonstration of this example in MS Excel here.

MKZ airlines is planning to purchase 3 Cessna aircraft to fly at a specific route. The cost of acquisition of aircraft (including all charges) is $ 2,000,000. It is expected that annual net revenue from operations will be $ 650,000 for three years (always end of the year) and the aircraft will be sold for $ 800,000 at the end of the third year. Please calculate the payback period for this project.

In column 3, we just keep adding each cash flow to the previous remaining value. Accordingly, in cell that corresponds to time = 0, the value of cumulative cash flow is minus 2 million. Similarly, as we proceed to the cell that corresponds to time = 1, we add the cash flow of 650,000 to -2,000,000 to get -1,350,000. Then, as we proceed to next cells (time = 2 and time = 3) we repeat this calculation to discover that the cash flows become positive for the first time between 2 and 3 years. Since we had to cover -700,000 but actually covered 1,850,000, we can divide 700/1850 to obtain 0.38 years.

Consequently, the project payback period is 2.38 years.

Video demonstration of this example in MS Excel here.

MKZ airlines is planning to purchase 3 Cessna aircraft to fly at a specific route. The cost of acquisition of aircraft (including all charges) is $ 2,000,000. It is expected that annual net revenue from operations will be $ 650,000 for three years (always end of the year) and thereafter the aircraft will be sold for $ 800,000 at the end of the third year. Assume the discount rate is 3.5%. Please calculate the discounted payback period for this project.

Same as before, in column 4, we just keep adding present value of each cash flow to the previous remaining value. Accordingly, in cell that corresponds to time = 0, the value of cumulative cash flow is minus 2 million. Similarly, as we proceed to the cell that corresponds to time = 1, we add the present value of cash flow of 650,000 i.e. 628019 to -2,000,000 to get -1,371,981. Then as we proceed to next cells (time = 2 and time = 3), we repeat this calculation to discover that the cash flows become positive for the first time between 2 and 3 years. Since we had to cover -765,199 but actually covered 1,668,594, we can divide 765199/1668594 to obtain 0.46 years.

Consequently, the project discounted payback period is 2.46 years.

Video demonstration of this example in MS Excel here.

Let us find some internal rates of return for our projects in the previous solved examples. In Table 8.3c below, we list out the cash flows of the three projects we have discussed extensively so far in this chapter, and using Microsoft® Excel, we calculate the IRR.

Video demonstration of this example in MS Excel here.

Consider the cash flow sequence in Table 8.9 below.

Find out the IRR and create the NPV profile at different rates of discount.

Consider the same project as discussed above. Now, the set-up cost is $ 2,000,000. The project produces consistent cash flows of $ 1,000,000 from periods 1 – 7. However, MKZ airlines decides to invest further in the project. It invests $ 9 million more and gets $ 2,000,000 cash inflow. Thereafter, it determines that the project is likely to be infeasible and sells it for $ 1,700,000.

The project net present values are shown in Table 8.10 below:

Figure 8.2 below depicts these net present values at different discount rates.

Video demonstration of this example in MS Excel here.

Please compare projects 1, 2, 3 and 4 below with respect to PI and make a recommendation

As can be seen in Table 8.11, project 4 is the most expensive project and is also not as profitable as project 2.

Video demonstration of this example in MS Excel here.