Chapter 7 Stock Markets

Background and Overview

In this chapter we discuss another application of the concept of discounted cash flows learnt in Chapter 5: in a Stock Market set-up. We start by looking how to read different finance websites such as Yahoo! Finance. Then we will discuss what determines stock prices looking at the cash flows available from these stocks. Listing shares of a corporation sometimes turns their founders into millionaires (and billionaires). The case in point can be seen with the listing of numerous companies such as Google, Facebook, Twitter, LinkedIn, GoPro, Fitbit etc. At the same time the entrepreneur must know when to list the shares on an exchange. This Chapter provides an insight into some of these issues.

7.1 Introduction

As we discussed in chapter 2, a share is a part ownership of a company. When we invest in stocks of companies, we usually look at their nominal price per share. Is this a right way to understand stocks? Do prices reflect the value of stocks? Is there something else we need to look at when buying shares of a company? What about profits? What about dividends? This chapter discusses various aspects of stock markets and valuation of shares of a company. A sneak preview: one important concept to realize by the end of this chapter is reached is that a $5 nominal price of a stock may actually be more expensive than a nominal price of $ 2,000 of another stock. From the bond pricing equation in previous chapters, we have learned that discounting the cash flows of a security provides its present value (price). Can we use something similar for stocks? This chapter provides all these answers. Stocks are at the heart of capitalism. Stock markets provide different job opportunities and may also provide rewards as owners of company stock.

There are several types of finance and aviation finance jobs in stock markets. Such jobs include underwriting and determination of stock IPOs, mergers; roadshows for new issues; determining loan versus lease agreements for aircraft; determining new fuel hedging strategies, issue of commercial papers or debentures; negotiating term loan conditions; and comparing new loan/ debenture with an equity issue. Understanding stocks, stock prices, and stock markets will benefit readers who hope to be in any of these positions. Thus, a financial manager has several functions, even in the aviation and aerospace sector.

This chapter discusses stocks and stock markets. We discuss how to read the quotes available for stocks at any given point of time, and valuation of stocks assuming constant dividends as well as growth.

Companies offer stocks to public and institutional investors through initial public offering. Firms can buy back as well as reissue stocks. We will discuss buyback and reissuance when we discuss the capital structure of an organization in a subsequent chapter. For now, it is sufficient to note that the number of shares outstanding of a company may not remain constant. By outstanding number of shares, we mean the maximum total number of shares that can theoretically be purchased by an investor.

Stocks are traded on a stock exchange such as NYSE or NASDAQ. Unlike bonds, stocks do not mature. Unlike coupon bonds, stocks do not assure investors of dividends. Unlike bonds, stockholders may or may not get anything if a company is liquidated. Still, investors prefer to invest in stocks. That is because, as we will study in risk management, stocks, on average, deliver very high returns. Stocks do not have maturity, so they need not be held for a set period. Therefore, all stocks have very active secondary markets for trading except those that are illiquid due to the company not performing well or being relatively small. For this reason, startups do not go to the initial public offering (IPO) stage in a hurry to list their stock for the first time on a stock exchange. Facebook (now META) waited several years before deciding to proceed with an IPO, as did Twitter.²

Every stock has buyers (on the bid side) and sellers (on the offer side) listed according to the best purchaser (highest price) and the best seller (lowest price). If offer price matches with bid price, a sale takes place. The difference between best bid price and the best offer price is called bid-offer spread or bid-ask spread. Typically, most liquid stocks have very small bid-offer spreads as they are traded during the market hours.³

Table 7.1 below lists the bid and ask prices for a hypothetical stock listed on a hypothetical exchange.

We can see that the difference between the best buyer (at the highest price of 24.50) and the best seller (at the lowest price of 24.51) is 1 cent. In other words, the bid ask spread is 1 penny. If these are all the buyers and sellers of the stock, then the total bid size is 455 shares and the total offer size is 275 shares. Just looking at the bid and ask listings, one may be tempted to say that the market is currently biased towards the “buy” side because the demand for number of shares on the buy side seems to be more than number of shares supplied on the sell side, at least at this point in time. However, we must take this with a caveat: just because shares on the buy side are more, may not mean anything. There may be some traders “lurking” that wait for an opportunity to pounce on the best possible price.

However, the most important driver of price fluctuations is news, particularly economic news. For example, if there is a news release that crude oil prices have jumped due to supply disruption, and the above stock is an airline stock, ceteris paribus the stock price will go down. In other words, the bidders will either remove their willingness to purchase prices and/ or will sell the shares at their desired price and sellers will lower their offer prices even further. This phenomenon that the market incorporates all available information is known as efficient markets hypothesis. Thus, according to this hypothesis, any new information is immediately priced in the stock’s value.

Interestingly, traders can place their bets in two ways. One of them could be as in Table 7.1 above, in which they express their reservation price and quantity of shares they will buy at the reservation price. Such market participation is called limit order. For example, in Table 7.1, if we assume all orders are from different traders, then the trader who placed the best bid has a limit order of 125 shares at the price of $ 24.50.

The other way traders could place a bet would be to directly buy from or sell to traders who have placed their market orders. Let us assume that the news item we just discussed was indeed released, and we have to sell 200 shares. Assuming that we want to sell at the market order, we will sell at the best possible prices available on the bid side. So, we will sell 125 shares at a price of 24.50 and remaining 75 shares at a price of 24.49, thus receiving a weighted average price on sale of 200 shares of $ 24.4963 ().⁴ This is an illustration of market order, in which we do not wait for our best price to be hit, instead proactively get out of our positions. If this psychology of waiting to buy but not waiting to sell and getting out of position is witnessed, then stock markets move up slowly (grind higher) but sell off precipitously (fall off a cliff). This behavior of markets was largely observed in the US stock markets during the period 2010 to 2020.

7.2 How to read stock quote and market data

Scanning a website such as Yahoo! Finance, MarketWatch, Morningstar, or NYSE/ NASDAQ for a quote on a stock not only provides its current price, but also some relevant data and information about the stock itself. For example, one might learn about its chart (how the stock price has moved), its 52-week price history, its earnings data, its dividend information, and some details on trading volume. Figure 7.1 below shows a quote for Delta Airlines accessed on business close of September 19, 2022, from NYSE and NASDAQ.

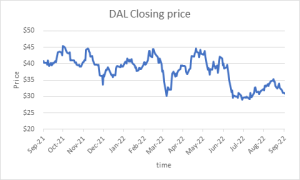
Hovering over the graph on the NASDAQ website gives accurate information on price at which the stock was first traded (open price), the price at which the stock was last traded (closing price), the highest price, the lowest price as well as the total number of shares traded (volume) on a given trading day.

Detailed quote and information are available from screenshot obtained from Yahoo & NASDAQ.com and is seen in Figure 7.2 as follows:

Looking at the column on the left gives us information about the Delta airline company, where it is listed (NYSE), the sector it belongs to (consumer discretionary) and the related industry (aviation). The next part is what we will learn in this chapter (based on current expectations, what is the price likely to be after a certain time period — in this case a year). The next field is today’s high price and low price. High price is the maximum level at which the stock has traded so far. Low price is the minimum level at which the stock has traded so far. Next, the number of shares traded so far today (volume). Next field is average volume traded over the previous period (usually it is 90 days). This is calculated as the sum of number of shares traded divided by the count of number of trading days. Next is the high price traded over the last year (52 weeks) (52-week high) and the low price over same range (52-week low). The first entry in column on the right is the market capitalization (shares of the company outstanding times the price of one share). The next entry is ratio of price to earnings (P/E), which tells us how expensive the stock is with respect to the industry. We saw this ratio in the previous chapter. P/E ratio is simply the share price divided by earnings per share. Every company projects its revenues and earnings per share. So, the next entry is forward P/E ratio (1 year), which accounts for these projected earnings per share. The next entry is earnings per share which is the total profit (net income) available for shareholders either as dividends or for retaining in business operations divided by number of shares outstanding. Next, is annualized dividend, which is, generally, the quarterly dividend that was just paid out times four (four quarters in a year). There are two dates associated with dividend payments: the payment date and the ex-date or ex-dividend date. Payment date is the actual date on which dividend was/ would be paid out. The ex-date is that date on which anyone who held a share of DAL would be paid that dividend irrespective of whether they owned the shares on the payment date. The next is current yield, which is similar to current yields in bonds we discussed in the previous chapter. However, the only difference is that instead of the numerator being coupon in case of bonds, it is now dividend paid out by stock. So, current yield for a stock is divided by price. Last field is beta. The beta explains the volatility of the stock with respect to the overall market index.

7.3 Dividend discount models

So far, we have seen how information about stocks can be read and interpreted from stock markets. But there is a more crucial function of a financial analyst in equity division of a corporation: that is to determine the intrinsic value of stock. Intrinsic value of stock is the fundamental dollar value that can be attached to the stock that is directly attributable to its expected future profits and dividend distributions. Therefore, we need to create theoretical models that can define and quantify this intrinsic value. We again rely on the concepts of present value and discount rate that we learnt in the previous chapters to create dividend discount models.

Dividend discount models assume that the value of a stock is the present value of its all expected (future) dividends.

Let us assume that ‘D’ be the dividend paid out by a company every year forever.

Using the present value concept, if this dividend was paid 1-period from today and the periodic rate is ‘r’, then its present value would be = \frac{D}{(1+r)^1}.

If it was ‘t’ periods from today, the present value would be = \frac{D}{(1+r)^t}.

Now, let us extrapolate this. If there was a steady stream of constant dividends value “D” paid out every period, then we can state that the present value of all the dividends will be:

[latex]Price = PV = \frac{D}{(1+r)^1}+ \frac{D}{(1+r)^2}+\frac{D}{(1+r)^3}+…+ \frac{D}{(1+r)^t}+…[/latex] …(7.1)

Let us find the sum of Right-hand side:

Let [latex]A = \left( 1+ \frac{D}{(1+r)^1}+\frac{D}{(1+r)^2}+…+\frac{D}{(1+r)^{t-1}}+…\right)[/latex]

Then equation (7.2) becomes [latex]Price = PV = \frac{D}{(1+r)} \times A[/latex] …(7.3)

Also, [latex]A-1 = \frac{D}{(1+r)} \times \left( 1+ \frac{D}{(1+r)^1}+\frac{D}{(1+r)^2}+…+\frac{D}{(1+r)^{t-1}}+…\right)[/latex]

Then

[latex]\frac{r}{(1+r)} \times A = 1[/latex]

[latex]A = \frac{(1+r)}{r}[/latex]…(7.4)

Plugging back equation (7.4) in equation (7.3)

[latex]Price = PV = \frac{D}{r}[/latex]…(7.5)

This is the same as a perpetuity pricing equation we learnt in chapter 5.

We will be building more advanced dividend models from here. However, one drawback is that if a company does not pay dividends, we have to find other ways to get fundamental value of such stocks..

We discuss the following Dividend Discount Models: Constant dividend model, Constant growth model, and Non-constant growth model

7.3.1 Constant dividend model

7.3.1.1 One-period Dividend pricing

Let us assume that the stock of XYZ airline pays dividend D₁ for period 1. We buy the stock at price P₀ today, hold it for 1 year, collect the dividend and sell it at P₁ after one year. Let us assume that the opportunity cost of our investment is ‘r’. Then using the discounting equation, we get that:

[latex]Present \; value = \frac{(D_1+P_1)}{(1+r)}[/latex]…(7.6)

This present value should equal to the intrinsic value of the share ..

7.3.1.2 t-period dividend pricing, constant dividend

If we extend this to ‘t’ periods, then our present value equation becomes:

[latex]Price = Present \; value = P_0 = \frac{D_1}{(1+r)^1}+\frac{D_2}{(1+r)^2}+…+\frac{D_t}{(1+r)^t}+\frac{P_t}{(1+r)^t}[/latex]…(7.7)

We can simply write this as

[latex]P_0 = \sum_{j=1}^{t} \left(\frac{D_j}{(1+r)^j}+\frac{P_j}{(1+r)^j} \right)[/latex]…(7.8)

Now, let us extend this discussion one step further. Suppose that the company pays a constant dividend D and we decide to never sell it. In that case, the above equation reduces to

[latex]P_0 = \frac{D}{r}[/latex]…(7.9)

using the perpetuity pricing equation from chapter 5.

7.3.2 Constant growth model

t-period dividend pricing constant growth

From above, if the dividend also grows, at a constant rate of ‘g’

So, [latex]D_1 = D_0 \times (1+g)[/latex]…(7.10)

[latex]D_2 = D_1 \times (1+g) = D_0 \times (1+g)^2[/latex]…(7.11)

[latex]D_t = D_{t-1} \times (1+g) = D_{t-2} \times (1+g)^2=…=D_0 \times (1+g)^t[/latex]…(7.12)

[latex]Present \; Value = P_0 = \frac{D_1}{(1+r)^1}+ \frac{D_2}{(1+r)^2}+…+\frac{D_t}{(1+r)^t}+\frac{P_t}{(1+r)^t}[/latex]…(7.13)

[latex]P_0 = \frac{D_0(1+g)}{(1+r)}+ \frac{D_0(1+g)^2}{(1+r)^2}+…+\frac{D_0(1+g)^t}{(1+r)^t}+\frac{P_t}{(1+r)^t}[/latex]…(7.14)

If we decide to never sell it, then

[latex]P_0 = \frac{D_0(1+g)}{(1+r)}+ \frac{D_0(1+g)^2}{(1+r)^2}+…+\frac{D_0(1+g)^t}{(1+r)^t}+…[/latex] …(7.15)

[latex]P_0 = D_0(1+g) \times \left( \frac{1}{(1+r)}+ \frac{(1+g)}{(1+r)^2}+…+\frac{(1+g)^{t-1}}{(1+r)^t}+…\right)[/latex] …(7.16)

[latex]P_0 = \frac{D_1}{(1+r)} \times \left( 1+ \frac{(1+g)}{(1+r)}+ \frac{(1+g)^2}{(1+r)^2}+…+\frac{(1+g)^{t-1}}{(1+r)^{t-1}}+…\right)[/latex] …(7.17)

Let [latex]B = \frac{(1+g)}{(1+r)}[/latex]…(7.18)

[latex]P_0 = \frac{D_1}{(1+r)} \left( 1+B+B^2+… \right)[/latex]…(7.19)

If B < 1, then we can simplify this as:

[latex]P_0 = \frac{D_1}{(1+r)} \cdot \frac{1}{(1-B)}[/latex]…(7.20)

From equation (7.18) [latex]1-B = \frac{1+r-1-g}{1+r} = \left[\frac{r-g}{1+r} \right][/latex]…(7.21)

For equation (7.19), we need

[latex]\frac{1}{1-B} = \left[ \frac{1+r}{r-g} \right][/latex]…(7.22)

Plugging equation (7.22) for [latex]\frac{1}{1-B}[/latex] in equation (7.20), we get

[latex]P_0 = \left( \frac{D_1}{1+r} \right) \cdot \left( \frac{1+r}{r-g} \right) = \left( \frac{D_1}{r-g} \right)[/latex]…(7.23)

This model is called Gordon’s model or Gordon growth model.

Gordon’s model is important to look at pricing of stocks and is used by equity analysts either to determine intrinsic value or when enough publicly traded information is not available. This can be used for IPO pricing as we discussed in the introduction of this chapter. This can also be used for reissue of stock to determine the price at which fresh stock can be issued.

Some examples are as follows:

If this discount rate is lower than the market rate, the stock price is either overpriced (i.e. too high) or the expected growth rate is too low.  Similarly, If the discount rate is higher than the market rate, the stock price is either underpriced (i.e. too low) or the expected growth rate is too high.

7.4 Purpose of earnings

A corporation earns profits to increase shareholder wealth. There are several options that the finance department and the top management of the corporation have to use these profits.

• The Company can either reinvest the profits into expansion of business. This is known as plowback.
• The company can distribute the profits or a part of profits to shareholders. This is called dividend payout.
• The company can also buy back shares from the open market.

Each of the three methods have their own advantages and drawbacks. We will discuss the first two in this chapter and the third one in capital structure.

We have seen that when a corporation earns profits from its operations, this is reported in its books of accounts. The main question facing corporations under such situations is what to do with these profits. In this part of this chapter, we will observe what happens when this profit is plowed back and / or paid out as dividends to shareholders. This leads us to define the dividend payout ratio:

[latex]Dividend \; payout = \frac{Dividend\;paid}{Profits}[/latex]       …(7.24)

[latex]Plowback \; ratio = \frac{Profits \; Retained}{Profits}[/latex]     …(7.25)

Or

[latex]p=\frac{R}{E}[/latex]             …(7.26)

The connection between equations 7.24 and 7.25 is:

[latex]Dividend \; payout + plowback = \frac{Dividend \; paid + profit \; retained}{Profits} = 1[/latex]      …(7.27)

Or,

[latex]plowback=1-payout[/latex]          …(7.28)

Let the first period earnings be “E” and let there be no retained earnings prior to this.

Therefore, based on the plowback ratio ‘p’, retained earnings = R = pE             …(7.29)

We know that retained earnings R will belong to owners as owner’s equity because now it is invested in firm’s business.

Let the return on equity be = “e”

In the next period, the firm will have additional earnings of: e.R = epE              …(7.30)

So total earnings will be: E + epE = E(1+ep)        …(7.31)

Therefore, the growth in earnings ‘g’ = ep        .…(7.32)

Let us illustrate this with an example.

All these models imply that as soon as new information about future of a company is learned in terms of profits and/ or the opportunity cost of capital, share price immediately changes right away because calculations lead us to assume the stock has a new value. In other words, markets discount future information immediately in current stock price. This is called efficient markets hypothesis.

There is considerable discussion and debate around market inefficiency. The main contention comes from proponents of behavioral finance who state two things: first, there exist pockets of inefficiency. These pockets of inefficiency can cause stock prices to be overvalued or undervalued for considerable periods of time before markets realize this and correctly price the stocks. Second, transaction costs may prevent traders from utilizing the concept of arbitrage to even out inefficiencies. Arbitrage is defined as purchasing a security at a lower price and selling it at a higher price. For example, a trader who has access to cheap crude oil at an oil producing nation that does not have facility to process it may sell transport and this oil at a refining facility where oil coming in from other production facilities may be more expensive. However, the cost of transporting this oil may not justify this transaction. First, this transaction is called arbitrage. Second the cost of carrying out this transaction is called transaction cost. In the absence of transactions costs, markets can be more efficient.

To conclude, we started this chapter discussing the nuts and bolts of how stock prices are read from publicly available information, went through a discussion of pricing of stocks and used various discount models for this purpose and finally closed this chapter discussing how publicly available information may sometimes be too obvious for investors to not act on through market efficiency and behavioral finance.

7.5 Summary

Large Corporations stocks are traded on stock exchanges. Stocks provide an insight into companies’ value. With the help of stocks, two companies can be compared in terms of earnings potential and performance. Shareholders expect either cash dividends or better than market growth from companies. The price of a company’s stock is the discounted value of expected future cash flows. If companies do well (not well), investors may overestimate (underestimate) the future cash flows of the company. This leads to higher (lower) than rational stock prices of the companies. Behavioral Finance provides an insight into that.

Therefore, the top management of a company always strive to search for/ create new projects that yield better than expected rate of return for the company and hence help grow the stock prices further. Chapter 8 in the next module provides an insight into selection of such projects.