Cost of Capital: Effect of Capital Structure

Overview and Background

The Net Present Value and Internal Rate of Return are important tools in analyzing new projects. However, the biggest enigma is the context of the discount rate or the hurdle rate. How does the company and its top management know what is an appropriate rate ? Every company has different risk structure: even two companies which manufacture similar products and sell them to the same customers may not have the same capital structure. So, the cost of capital is very important. This chapter not only helps in the determination of the appropriate cost of capital, but also in the relation of the cost of capital with respect to the adoption of new projects.

11.1 Introduction

Every firm that needs to expand its business and operations needs capital. The challenge that firms face is where to get this capital from. One might think it is quite straightforward to approach a bank for a term loan and get it over with. However, in real life, the situation is not as simple. When borrowing, it is pertinent to know how long the funds would be needed. If it is for a short-term need, then firms can issue commercial paper/ short-term liabilities. If it is a new project where funds would be locked in over a longer period, then potentially longer term debt or equity or a hybrid pathway is more pertinent. Also important is the cost of the borrowed fund (loan/ equity) and the timing of the payments, that is, how much must be returned every period to investors. That is where the importance of this chapter comes.

In the chapter 8 on capital budgeting, we discussed the importance of the rate of discounting and how projects with seemingly large cash flows become unprofitable at a higher discount rates. As we saw it is  because of the inverse proportionality of present value and discount rates (recall that rate is in the denominator of the present value equation). In this chapter, we will get a perspective on which routes of raising capital are more pertinent and important from a firm’s point of view.

Debt is the common way of raising money needed to expand a corporation. As we saw in Chapter 5, there are different types of loans a corporation can avail of: (constant) interest only, constant principal and interest, constant payment and all at the end. Additionally, a firm can also borrow by issuing debt market instruments such as commercial papers (short-term), notes and debentures (medium- to long-term). All of these modes are useful for raising debt for a corporation. Debt can be raised to fund new projects or for ongoing projects. Existing debt terms can also be refinanced to change details such as the timing of repayment or the length of repayment, and/or the rate of interest (i.e. cost of debt). There is an attractive reason for raising funds through debt markets. Interest paid on debt is not taxed, and it is treated same as expenses in an income statement. However, if a company raises money through equity issue (or reissue), then dividends paid out to shareholders are actually less because they are based on net profits or profits after tax. Additionally, shareholders also have to pay taxes on dividend income. Therefore, there is a problem of double taxation for shareholders as compared to bondholders. Let us see this in example 11.1 below.

11.2 Debt versus Equity

A firm can raise capital through debt or through equity. Both options have their pros and cons. We will discuss them below.

This can be easily analyzed by connecting the interest received by investors with tax rate. Interest received by bondholders times (1-tax rate) is equivalent to dividend received by shareholders.

In other words, 75x (1-0.2) = 60 (we’ve connected returns to investors in Columns 3 and 4 in Table 11.1!)

What we learn from equation 11.1 is that a company pays out greater interest to investors ($ 75, Column 4) than it does to shareholders ($ 60, Column 3). This makes a compelling case for an organization to raise only debt to make investors happy. The other issue is returns, which we will see after we look at the overall capital structure of the company―bondholders are typically satisfied with a fixed rate of return that is linked with the (bond) markets. Stockholders typically demand much larger rates of return, particularly in the first part of the 21^st century when yields on bonds are low.

Together debt and equity make up for what is known as capital structure of a corporation. Capital structure of a corporation describes different sources of financing that have been used to fund its assets. Some corporations prefer to display their balance sheet as sources and uses of funds for this reason.

Let us assume MKZ airlines has a balance sheet and capital structure as in Table 11.2 below:

In the balance sheet above, we assume that MKZ airlines increased its balance sheet from $ 3,200 to $ 4,000. It has been utilized to fund both short- and long-term assets. Short-term assets have increased by $ 500 and long-term assets by $ 300. On the other hand, most of the assets’ increase has been funded by new equity issue, which is not very common. The reason new equity issuance is not very common is discussed in the next section. Also, it is pertinent to note that assets and liabilities are recorded at their book values, but if for example a company raises cash using bonds or invests in financial instruments by raising cash, it may be more relevant to use market value balance sheet to estimate the true capital structure of the company. This is especially important in the case of organizations such as investment banks, brokerages, insurance companies, hedge funds, and mutual funds whose significant assets are linked with the markets and investments.

11.3 Cost of Capital

In the sections above, we discussed the process of accounting for interest expenses and dividends — two common types of payments corporations make to their investors. We also noticed how debt and equity are used to fund the assets, particularly in the long run and expanded business operations. Now, we calculate the cost of these funds and analyze how different market conditions can force certain companies from retreating from their plans to expand business operations. Now let us look at the pricing of stocks that we studied in chapter on Stocks. We learnt that we use the present value formula to price the stock.

[latex]Price = PV = \frac{CF_1}{(1+r)} + \frac{CF_2}{(1+r)^2} + …+\frac{CF_t}{(1+r)^t} +…[/latex] …(11.2)

Here:

[latex]CF_t[/latex] is the cash flow at time ‘t’, and

‘r’ is the discount rate

Or, [latex]Price = PV = \sum_{t=1}^{\infty}\frac{CF_t}{(1+r)^t}[/latex]

From equation 11.2 we observe that as interest rates increase, the expected future cash flows for technology firms get discounted by a greater discount rate. This causes present value to decrease significantly compared to other stocks with more steady cash flows. Therefore, interest rate changes affect technology firms such as Microsoft, Google, Apple, Amazon and Meta platforms more compared to other firms.

11.3.1 Cost of Debt

Firms issue bonds with different considerations and conditions to account for their debt on balance sheet. Broadly, bonds have a face value that must be repaid and a yield to maturity (YTM) that may or may not be linked to market conditions. Since YTM changes frequently, it may be a consideration in market value balance sheet creation, which is beyond the scope of this discussion. For our purposes, it is sufficient to consider the coupon payments and the price at the time of issuance to calculate yield to maturity of coupon paying bonds or the interest cost (again yield to maturity) of zero-coupon bonds at the time of issuance as a percentage of face value as the cost of debt. In a nutshell, when considering the cost of debt, one needs to calculate the yield to maturity at the time of issuance as well as face value of the bond for cost and amount purposes.

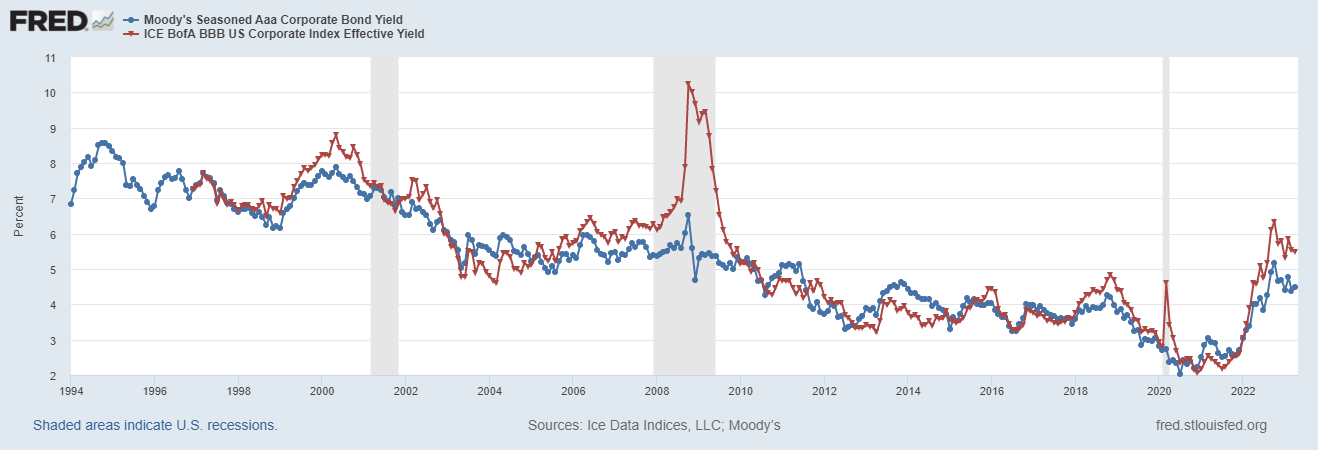
Cost of debt is historically cheapest among all external sources of funding ( that is, among borrowing,  issuing fresh stock or a hybrid of these two). Figure 11.1 below describes the cost of debt (y-axis) as a function of time axis (x-axis). There are two types of bonds whose yields are being plotted in this graph. AAA bonds (i.e. the best credit quality and hence cheapest borrowing cost) and BBB bonds (not the best credit quality i.e. just above the ‘junk’ status, junk implying greater risk of not being able to meet debt/ payment obligations). Shaded areas in the figure are periods of recession. Per Figure 11.1 below, cost of debt has been in a range of 2% and 11% during the time period 1995–2023.

Let us summarize some benefits and drawbacks of raising capital through debt.

Benefits of raising debt:

• Cheaper source of capital.
• After-tax benefits.
• Usually issuance of debt is quicker than equity, particularly when the debt issuance is through a bank or large institutional investors.

Disadvantages of raising debt:

• Debt has limited life but can go for multiple decades if the company is creditworthy.
• There is only so much debt a company can raise. Raising too much debt makes investors suspicious and credit usually dries off. Therefore, financial analysts look at the debt to equity ratio to measure the ‘leverage’ of a company. Moreover, as a company grows, generally its retained earnings grow as does the size of its balance sheet, which provides company more capacity to raise debt. Debt to equity ratio is critical in determining debt capacity.
• Debt payment is mandatory unless the company files for bankruptcy protection. Bond coupons and loan interest must be paid at scheduled intervals if the company does not want to risk being downgraded. Even during liquidation of a company, bond holders are paid first, before stockholders. Hence, if price of bonds issued by a company decreases significantly, shareholders should be aware. This characteristic of debt is one reason why bond markets are said to be better precursors of future events than stock markets.

We’ve learned from the previous section (equation 11.1) that

Here

Let us use an example of MKZ airlines above. Let us assume that MKZ airlines wants to raise $ 100. A natural answer based on discussion above would mean using the debt route. However, let us compare three possible options MKZ has—debt, preferred shares, and equity in Example 11.2 below. In part 1, we will use the debt route. Then as we discuss preferred shares, we will try to raise capital using preferred route. Lastly, as we discuss cost of equity, we will use the equity route—issuance of new shares. Le us see which of these options is the best.

11.3.2 Cost of Equity

Equity is another important method of raising capital. Firms issue shares to add more owners in the company. Adding new owners, particularly if they are block-holders (a block holder is an owner of a significant chunk of shares of a corporation), has benefits. These new owners generate new ideas or bring ideas from their other firms. These owners help manage the corporation and influence its decision-making process. These owners can help with new collaborations with other firms/ entities. They also monitor firms more closely. Overall, they can help grow the business.

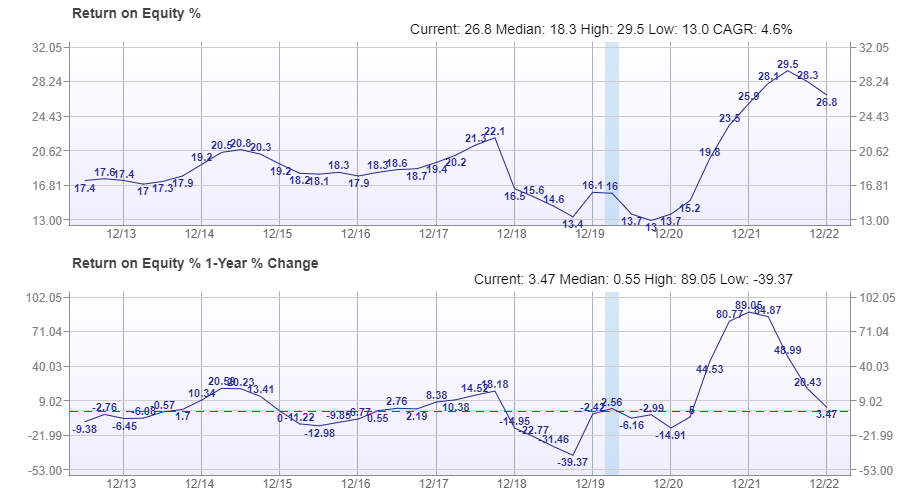
Equity is expensive. A corporation must make sure that it provides adequate returns to its owners, more than that for the bondholders. This is because shareholders are willing to wait and ride out challenging times with the corporation so that they can be compensated later. Figure 11.2 below shows return on equity for industrial firms listed in stock exchanges of the US. In figure 11.2, y-axis is the return on equity (percentage) and the x-axis is time. Shaded areas are periods of economic downturn (recessions).

Let us summarize some benefits and drawbacks of raising capital through equity.

There are two benefits of raising equity:

• During adversity, when there is a need for capital, equity provides a no-obligation way of bringing in funds. This is because corporations are not liable to pay dividends like they are to pay interest on debt or dividend on preferred shares.
• Equity has no maturity. By providing investors with equity option, a corporation also signs them up to be part-owners. Therefore, there is no need to consider repayment as part of cash flows, which lowers the financial obligations for the corporation.

There are three drawbacks of raising equity:

• When new shares are issued, the stake of existing shareholders is diluted. That can be a drawback, particularly if a group wants to remain in majority and control firm’s decisions. By issuing equity, the stake of all shareholders decreases as well as the controlling (voting) power in the firm. This may have adverse impact on the decision-making process within the firm.
• Equity is expensive. Although there is no obligation to pay dividends, a firm must earn profits (residual income left after payment of interest and taxes) that compensates shareholders to take the risk of owning the company.
• Equity has a problem of double taxation. Dividends that are distributed to shareholders are post tax. Hence, tax is charged to the corporation before dividends are paid out. However, shareholders have to pay their own taxes on dividends received. This is because dividends are considered shareholders’ income.

11.3.2.1 Equity Cost Estimation – Dividend Discount Model:

We can find the rate of return on equity using two methods. First is Gordon’s model.

In Gordon’s model, we know

[latex]P_0 = \frac{D_1}{(r-g)}[/latex] where

This can be rearranged as

[latex]r_e = r = g + \frac{D_1}{P_0} = g + \frac{D_0 \times (1+g)}{P_0}…[/latex] (11.3)

The second method is through the CAPM model. According to this model,

[latex]r_e = r_f + \beta(r_m-r_f)[/latex] …(11.4)

Here

Market risk premium is defined as the difference of [latex]r_m[/latex] the rate of return from overall market (typically an index such as the Standard and Poor’s 500 (S&P 500) Index) and the risk-free rate of return [latex]r_f[/latex].

Market risk premium [latex]RP_m = r_m - r_f[/latex]

This helps us rewrite equation 11.4 as: [latex]RP_e = \beta \times RP_m[/latex]

In our example of MKZ airlines, let us discuss another situation—this time with issuance of equity.

11.3.3 Cost of Hybrid Capital

Hybrid capital or preferred shares are issued by a company to compensate shareholders with guaranteed dividends for either infinite periods or for a fixed time horizon. Sometimes investors have the option to convert preferred shares into common stock in order to take advantage of capital gains associated with equity shares, typically if the company is doing really great financially. This is the reason why preferred stock is called hybrid. Now let us price preferred stock mathematically. Preferred stock is always treated as a perpetuity. Recall that in a perpetuity, price = PV = \frac{cash flow}{discount rate} or discount rate = yield = \frac{Dividend}{Price} Cost of preferred stock (either in percent or in decimal) is therefore dividend (cash flow) divided by either the book or market value (price) of preferred stock (depending on the valuation technique).

[latex]r_h = \frac{D}{P_0(1-r_u)}[/latex]…(11.5)

Here

Price of preferred stock P₀ will be paid by investors. However, not all of it is received by the company. Hence, we have to find the cost effective on what is received by the company. If r_u is the underwriting cost, we must pay r_u times P₀ dollars to the underwriters. Therefore, we are left with P₀ – P­₀r_u dollars after the underwriters are paid off. Factoring P₀, amount left for the corporation after underwriters are paid off is rewritten as [latex]P_0 \ times (1-r_u)[/latex], which is the denominator of equation 11.5 above¹.

If the price paid by investors is $ 100 and 3% is the underwriting fee, then the company received only $ 97. Hence, the cost of debt is adjusted by rate of underwriting fee, which we denote in this equation as r_h. Let us look at this through an example.

Let us summarize the three types of issues: debt, hybrid and equity and compare them side by side.

From Table 11.6 above, we can see that debt (either loan or bonds) is the cheapest route. In particular, cost of issue of bonds is cheaper than the cost of issue of term loan (although this could change with time). The reason bond issue is cheaper is particularly because of its association with bond markets (issuing directly to customers and not through intermediaries such as bank) and the US treasury yield curves, as well as the relief that is received because of tax. However, bonds come with an obligation to pay coupons/ interest at a predetermined frequency. This obligation applies to preferred stocks as well. The only benefit with preferred stock over bonds is that the company can defer preferred stock dividends. In case of equity or common stock, there is no obligation to pay dividends. However, if there are no returns to shareholders, the company’s stock gets punished in the stock markets. Also, with the new issues of preferred stock and common stock, there is the dilution of ownership to the existing shareholders. Companies typically issue stocks after skimming the markets with the help of underwriters. In case of bonds, there may be primary dealers associated or there may be private placement of bonds through direct issues. Sometimes, company may choose multiple options simultaneously. Hence understanding current balance sheet and costs associated with liabilities and equity is critical. This background helps us calculate the weighted average cost of capital as seen in the next section.

11.4 Weighted Average Cost of Capital (WACC)

11.4.1 Introduction to WACC

As discussed in the previous section (11.3), there are three sources of funding for a project. For simplicity, let us first consider two—debt and equity. As we discussed above, we can find the rate of return on debt and equity. Weighted average cost of capital is a measure of how expensive capital is for a project for that company. It is a useful yardstick in determining whether a new project would be incrementally successful for a company or if it would end up diluting return on capital for shareholders.

Weighted average cost of capital (WACC) is the average cost (weighted by each component of sources of funding) that is being paid by the company. It is calculated as the sum of percentage share of debt/preferred stock/equity on a company’s balance sheet (called its weight) times the cost of debt/preferred stock/equity.

11.4.2 Mathematical calculation and implications of WACC

Let us assume that total value of funds raised is $ V. V is composed of debt (D), Preferred stock (P) and Equity (E).

Mathematically, [latex]V=D+P+E[/latex] …(11.6)

[latex]WACC = \large( \frac{D}{V} \times r_d \times (1-t) \large) + \large( \frac{P}{V} \times r_p \large) + \large( \frac{E}{V} \times r_e \large)[/latex] …(11.7)

Let us illustrate an application of WACC for incremental funds in Example 11.6 below.

11.4.3 Caveats/ limitations while using WACC

There are a few important caveats in the above example. MKZ has a capital of $ 4,000 and is raising almost 8.7% new capital. Hence, investors need to know a good reason MKZ is raising funds. It could be for a new exciting subsidiary in a novel field or just expansion into a new territory or massive scaling up of business. Investors are always skeptical of this kind of stepping up of growth, whether it is organic (expansion of its existing business) or inorganic (merger or takeover of another company), both of which need capital.

Then, raising capital through multiple sources is relatively uncommon. It shows desperation for additional capital, which is never a good sign in financial markets. Finally, raising funds through multiple sources needs effort on three fronts. Bonds, preferred stocks, and common stocks all have different investors and different markets. Such fund raising may need use of too many internal resources of MKZ’s Treasury and capital markets division. This process requires pricing, underwriting, working with investors, carrying out roadshows and therefore drains too many resources. Smaller firms simply do not have those kinds of resources to spare.

11.4.4 Evaluating new projects with WACC

Funds raised through such issuances are always targeted to projects that have been evaluated by the corporation’s financial managers well in advance. This is carried out by capital budgeting methods.

Let us now assume that MKZ has a project to evaluate using these funds. Let us now explore that in Example 11.7.

This project looks good to go if we compare incremental funds with incremental costs. However, sometimes WACC is also evaluated by comparing with existing capital structure.

11.5 WACC and existing balance sheet

Let us now take another look at MKZ airlines’ balance sheet in Table 11.2 above. Let us add costs to its liabilities. MKZ currently does not have any preferred stocks issued. In addition, its shareholder’s equity is broken down into $ 400 of paid up capital (at the time of issue) and $ 900 in retained earnings brought forward over the years. Its balance sheet is $ 4,000, as seen in Table 11.9 below. In addition to contents in table 11.2, Table 11.9 also lists the weights (D/V and E/V) as well as existing costs of these sources of funds.

We can see that existing WACC for MKZ is 9.25% and the new project would become less favorable if evaluated using this WACC. Such different results are because [latex]company \; WACC \equiv 9.25% > 7.06% \equiv WACC \; of \; new \; funds[/latex] That is where the creativity, insightfulness, and experience of a top financial manager comes into play. In such situations, financial managers generally look at current financial market conditions and take a call on whether the project still looks good or not.

This is the reason why WACC and capital structure of corporations is so important for making those decisions. One can sense that the entire future of a firm is in the hands of a financial manager due to these reasons.

Summary

Cost of the new funds is very important for evaluating new projects of a company. Capital structure is regularly modified by a firm with issuance of new instruments. However, drastic changes to capital structure are seldom carried out without the approval of the board. Investors and analysts alike question new project adoption with respect to riskiness and firm’s capital structure which is reflected in  the weighted average cost of capital.

In essence, WACC is at the very core of what a firm achieves for its top management, its employees, its lenders, and its shareholders. That is the beauty of functions of corporate finance.