A-3: Basics of Aerodynamics
Fundamental Governing Equations of Aerodynamics
Shigeo Hayashibara
Conservation of mass (Continuity) Principle
Streamline and Stream Tube (Continuity)
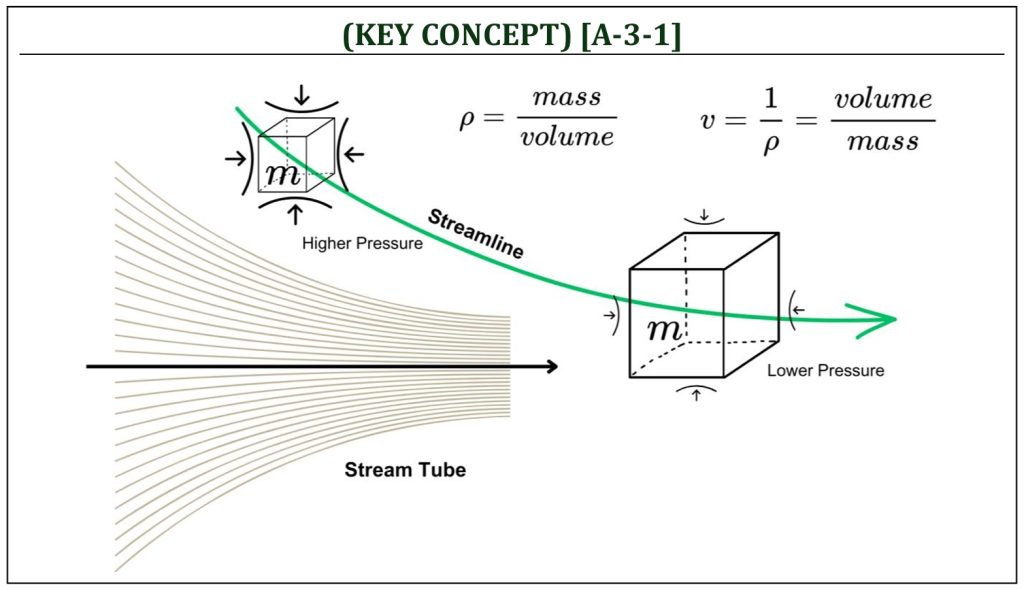
The principle of conservation of mass and Reynolds transport theorem can be combined, and the result is an important governing equation of aerodynamics: continuity equation. The principle of conservation mass, in Lagrangian description, can simply be “the substantial change of mass of a given system is zero.” A system usually refers to a single air particle in a continuum description of air. This is the first of three governing equations of aerodynamics (based on three conservation laws: mass, momentum, and energy).
Governing Equation of Continuity

Since air is a gas (fundamentally, it is compressible fluid), it is not appropriate to assume that the density of flow field is constant. If an element of air (a small mass) is closely observed, it is obvious that this element (control mass) changes volume as pressure changes. As a result, the density of this element changes. Pressure induced volume change is work (moving boundary work) and energy transfer will be involved (this is generally considered as compressibility effects of aerodynamics). It is often convenient to quantify the change of volume for a given unit mass (control mass) of an element of air (i.e., inverse of density). This is called specific volume of an element of air.
For a low-speed flow field (Mach number < 0.3), the compressibility effects can be negligible (small and can be ignored). This is often called incompressible subsonic flow. Since the density change can be ignored, it is possible to simplify the continuity equation further.
Simplified Equation of Continuity

It is important to understand “why” M < 0.3 can be considered as incompressible subsonic flow. This will be revealed later when details of energy principles are introduced. It is fundamentally important to understand that air (as a fluid substance) is not incompressible at all. This is called a material (fluid) property. However, if the flow field is low-speed (i.e., M < 0.3), we can ignore the effect of compressibility so that our analysis can be massively simplified. Under the assumption of M < 0.3 (we’ll discover the reasoning of this assumption later), we purposefully ignore the change in density within the flow field. This is, in fact, flow field (conditional) property (valid only under the condition of M < 0.3).
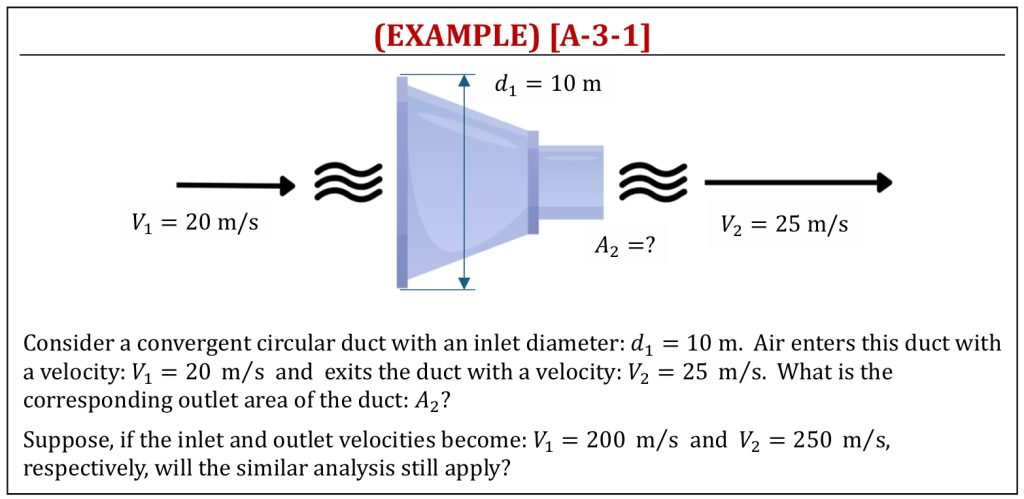
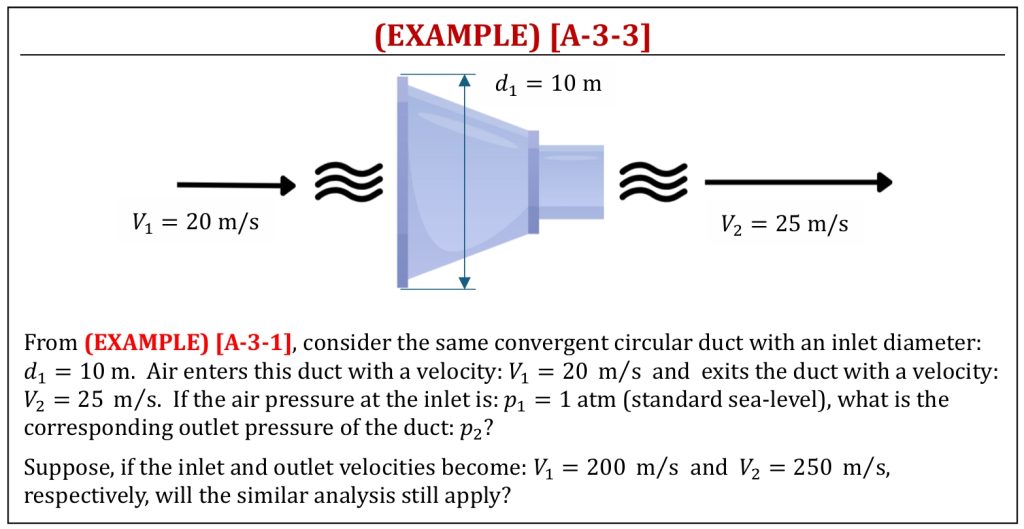
Simple Convergent Duct Air Flow (Continuity)
Conservation of (linear) momentum Principle
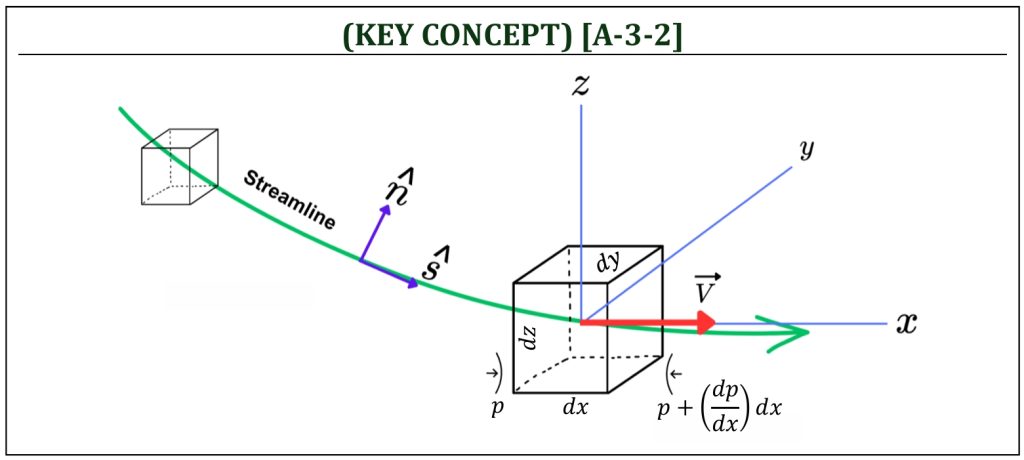
Equation of Motion along a Streamline (Momentum)
Known also as Newton’s second law of motion (or equation of motion), the conservation of momentum principle can be defined simply by “time rate of change of the system linear momentum is equal to the sum of all forces acting on the system.” This is the second of three governing equations of aerodynamics (based on three conservation laws: mass, momentum, and energy).
Governing Equation of Linear Momentum

From the governing equation of linear momentum, with assumptions of (i) steady and (ii) inviscid flow with (iii) zero body force, the integral form of Euler’s equation (based on Eulerian control volume approach) is obtained. In 3-D space, this can be expressed in three directional components (as linear momentum is essentially a vector equation). Often, it is more convenient to express Euler’s equation, as simply an equation of motion of a small element of air (a particle) steady moving along a specified streamline. If this streamline is chosen as a coordinate system (called, streamline coordinate system), an alternative form of Euler’s equation can be derived (i.e., Euler’s equation in differential form).
Euler’s Equation (1)

Euler’s equation in differential form (based on Lagrangian control mass type approach) can also alternatively be derived from the close observation of a small element of air (moving steadily along a given streamline). Let us consider a small cubic element of air (with the volume: dx dy dz) moving steadily along a given streamline. If we ignore body force and viscous force, the Newton’s second law (i.e., equation of motion) will simply become Euler’s equation.
Euler’s Equation (2)

Bernoulli’s Principle
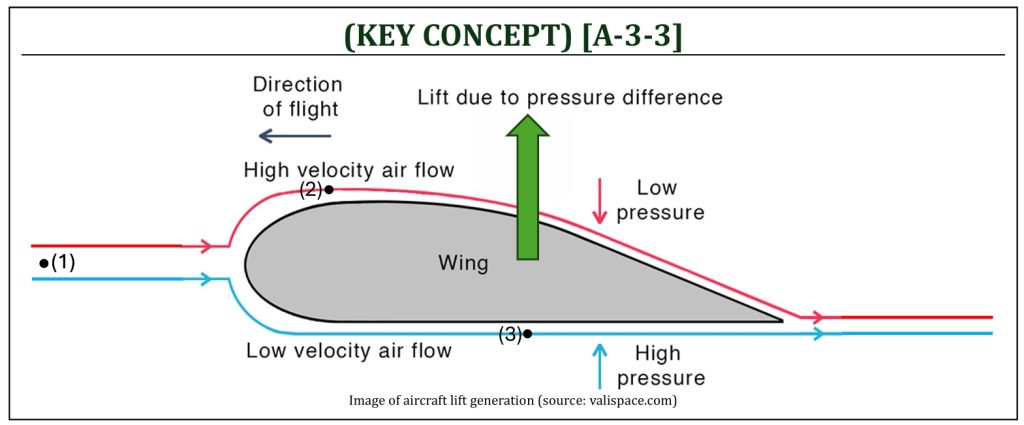
Bernoulli’s Principle for Aerodynamic Lift Generation
Recall that Euler’s equation is a governing equation for a steady and inviscid flow field with no body force involved. Also note that this is a differential equation and cannot be used for actual calculations of flow field properties. You must introduce another assumption incompressible (i.e., low-subsonic: M < 0.3) flow to further simplify this equation equation. The simplified Euler’s equation under the assumption of incompressible (M < 0.3) flow field is called Bernoulli’s equation.
Bernoulli’s Equation

Bernoulli’s equation is the most convenient (i.e., algebraic form of equation), but the most commonly abused (in other words, mistakenly used) equation in aerodynamics. Assumptions required for equation derivation (i.e., constraints) of the Bernoulli’s equation must carefully be reviewed, as follows:
Inherited from the Euler’s equation, the following assumptions are already included for Bernoulli’s equation:
(i) The flow is steady (streamline), (ii) the body force is ignored (no body force: common assumption in aerodynamics, but NOT in hydrodynamics), and (iii) the viscous force is ignored (inviscid).
Added onto the Euler’s equation, (iv) the assumption of the constant density is applied (incompressible). Note that this incompressible assumption is usually not true in aerodynamics . . . only if M < 0.3 (called incompressible subsonic flow). It is strictly prohibited to casually use Bernoulli’s equation without a series of careful pre-checking processes.
Careful observation of Bernoulli’s equation reveals that the equation relates pressure (static pressure) and velocity (dynamic pressure). In other words, the Bernoulli’s equation inversely relates pressure and velocity (often referred as pressure-velocity coupling equation). If the flow is accelerated, it is associated with lower pressure (and vise versa). If the Bernoulli’s equation is applied to an aircraft wing, upper surface of the wing (flow is accelerated) is lower pressure than lower surface of the wing. The result of upper and lower surface pressure difference will create an aircraft lift. This is one of the explanations of “how an aircraft generates lift” based on the Bernoulli’s principle.
Application of Bernoulli’s Equation (1)
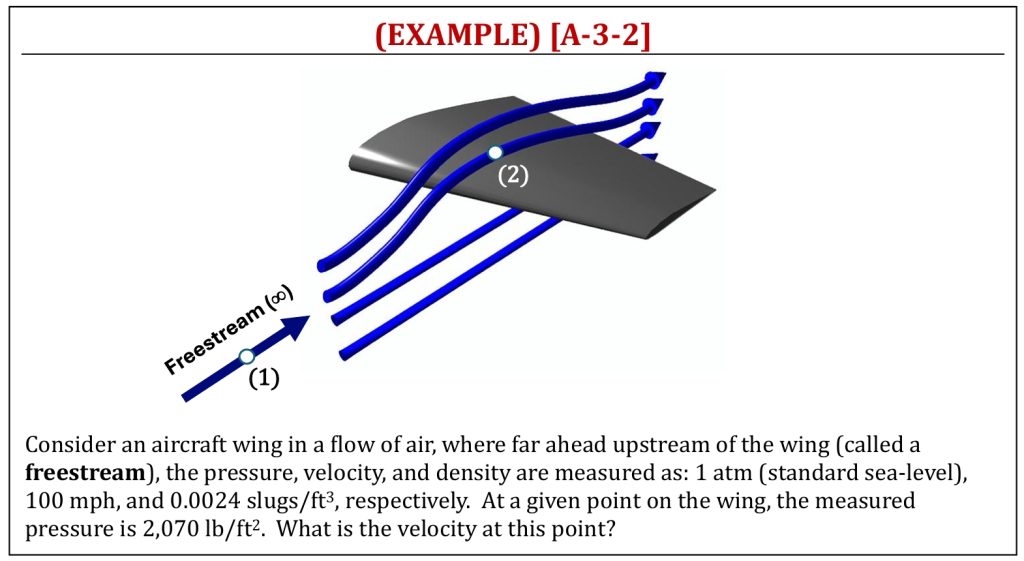
Application of Bernoulli’s Equation (2)
conservation of Energy Principle
Compressibility of High-Speed Flows (Energy Principle)
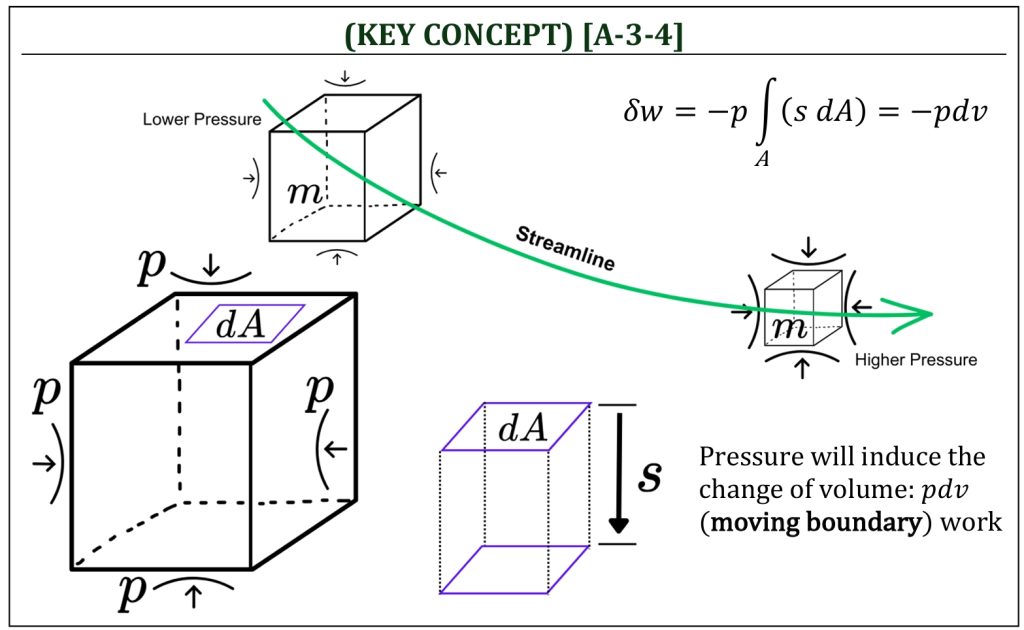
Known also as the 1st law of thermodynamics, the conservation of energy principle can be defined simply by “time rate of change of the system energy = sum of all energy transfer due to heat and/or work.” This is the third of three governing equations of aerodynamics (based on three conservation laws: mass, momentum, and energy).
Governing Equation of Energy

The energy equation (first law of thermodynamics) in differential form (Lagrangian control mass type approach) can also alternatively be derived from the close observation of a small element (energy per unit mass) of air in a steady flow field. The 1st law of thermodynamics says that “energy added or subtracted by heat and work is balanced against the change of internal energy” (i.e., energy must be balanced). This is the fundamental principle of the first law of thermodynamics. Before moving forward, however, it is crucially important that there are two distinctively different mathematical expressions: exact and inexact differentials.
Mathematical Expression: Exact and Inexact Differentials

Recall that, in aerodynamics, one important aspect of “high-speed” flow (M > 0.3) is the increased tendency of “compressibility” effects. A small element of air (unit mass of air) will be changing its volume as pressure changes in a high-speed flow. This is “moving boundary work” (often also called “pdV” work in thermodynamics.
Equation of the 1st Law of Thermodynamics

Specific Heats
Types of Specific Heats (Heat Energy Capacity)

A specific heat (c) is a material property that quantifies the amount of energy a unit mass of substance can contain within (often called the heat energy capacity). If the value of specific heat is known for air, it can mathematically define the relationship between temperature (T) and and either internal energy (u) or enthalpy (h) per unit mass. There are two different definitions of specific heat: (i) a specific heat defined under the condition of constant volume (cv) and (ii) a specific heat defined under the condition of constant pressure (cp).
Specific Heat (1): Constant Volume Heat Addition (cv)

Specific Heat (2): Constant Volume Heat Addition (cp)

There are two different models of air as an ideal gas: thermally perfect and calorically perfect ideal gas models. (i) Thermally perfect ideal gas is a model of flow field physics, based on the fact that the specific heats are not constant. The relationship between the flow field temperature and either internal energy or enthalpy are modeled as non-linear functions of temperature. This thermally perfect model can be used in a wide range of high-speed (M > 0.3) flows, as long as the air is considered as an ideal gas. This will certainly exclude hypersonic flow regime (M > 5), where air is no longer considered as an ideal gas. (ii) Under a certain (limited) temperature range (typically, room temperature or lower temperature range), the specific heats can be, further, assumed to be a constant property. This is called calorically perfect ideal gas. For a calorically perfect ideal gas, the ratio between two specific heats (cp and cv) is constant. This is called specific heat ratio (γ = cp/cv) and for the standard air (room temperature or lower temperature range): γ = 1.4.
Relations of Specific Heats cp and cv (Calorically Perfect Ideal Gas)

Modified Bernoulli’s Equation with Compressibility (Energy Equation)
(From thermodynamics) the assumption of isentropic flow is the flow, in which the process is both adiabatic and reversible. As you know well at this point, Bernoulli’s equation cannot be used for compressible flow, as the density is no longer constant due to the compressibility effects of high speed flow field (M > 0.3). This was a major issue (critically limits the application of Bernoulli’s equation, only for incompressible subsonic flow field: M < 0.3). Instead of assuming the constant density (which is limited only for M < 0.3), it is now required to modify the Bernoulli’s equation. Now, instead of invalid incompressible flow assumption, you may need to employ isentropic flow assumption. This means that, even though the flow field is no longer incompressible, still it is assumed to be isentropic. An isentropic flow field is an idealistic thermodynamic process that there will be no loss of energy throughout, so that the 1st law of thermodynamics can be applied as it is completely valid.
Suppose if the flow field is no longer incompressible (now, M > 0.3 flow field), you may no longer employ the assumption of constant density to simplify Euler’s equation (to arrive the resulting algebraic Bernoulli’s equation). Instead of incompressible assumption, however, you may (if the flow is assumed to be still isentropic) employ the 1st law of thermodynamics to simplify Euler’s equation. The resulting algebraic equation is called the energy equation (or “modified” Bernoulli’s equation with compressibility effects being included).
Isentropic flow assumption (adiabatic and reversible) is valid for a wide variety of flow regimes, even including supersonic flows. However, when either irreversibility (i.e., loss of energy due to friction) or heat transfer (i.e., combustion) is involved, the isentropic assumption will become unreasonable. Typical non-isentropic flows include (but not limited to): (i) high-speed flows across the shock waves (shock waves are non-isentropic compression), (ii) flows with combustions and/or significant chemical reactions (example: jet engines and rocket combustions), and (iii) flows under the significant viscous effects (i.e., frictions due to boundary layer formulations). For isentropic flows, it is possible to relate pressure, density, and temperature of the flow field in isentropic relations.
Energy Equation (Modified Bernoulli’s Equation)

Application of Energy Equation for High-Speed Flow Analysis

References
- NASA (www.nasa.gov)
- Valispace (www.valispace.com)
- EngineerExcel (www.engineerexcel.com)
- Fundamentals of Aerodynamics by J.D. Anderson, 5th ED, McGraw Hill, 2016
- Aerodynamics for Engineers by J. J. Bertin & M. L. Smith, 3rd ED, Cambridge University Press, 1997
- Aerodynamics for Engineering Students by E. L. Houghton & P. W. Carpenter, 4th ED, Edward Arnold, London, 1993
Media Attributions
If a citation and/or attribution to a media (images and/or videos) is not given, then it is originally created for this book by the author, and the media can be assumed to be under CC BY-NC 4.0 (Creative Commons Attribution-NonCommercial 4.0 International) license. Public domain materials have been included in these attributions whenever possible. Every reasonable effort has been made to ensure that the attributions are comprehensive, accurate, and up-to-date. The Copyright Disclaimer under Section 107 of the Copyright Act of 1976 states that allowance is made for purposes such as teaching, scholarship, and research. Fair use is a use permitted by copyright statute. For any request for corrections and/or updates, please contact the author.

