19 IPv4 Addressing – A Very Brief Review
Mathew J. Heath Van Horn, PhD
IPv4 subnetting can be confusing to many. These exercises are intended to emphasize the concept that IPv4 numbers are not numbers at all, but rather symbols of identification (i.e., names, e.g., Eileen =192.168.1.4, Hasan = 201.4.56.12, McDonalds = 10.14.67.12, etc.). When you see IP addresses, do not think numbers; think names.
Estimated time for completion: 10 minutes
learning Objectives
- Increase familiarity with using the GNS3 Environment
- Identify Ethernet packet traffic on Wireshark
- Convert Decimal to Binary
- Convert Binary to Decimal
- Given an IP address and netmask, determine:
- Network ID
- First Usable IPv4 Address
- Last Usable IPv4 Address
- Broadcast IPv4 Address
Prerequisites
Deliverables
- Complete the IPv4 Worksheet
Resources
- IP Subnet Calculator – https://www.calculator.net/ip-subnet-calculator.html
- Heath Van Horn, Mathew, “IP Refresh”, https://www.youtube.com/watch?v=Sr9gIYNpT4I
- Heath Van Horn, Mathew, “Calculating Subnet Mask”, https://www.youtube.com/watch?v=wIS8SLvAGkM
- Watchguard Articles:
- Nachreiner, Corey, “Understanding IP Addressing and Binary”, https://www.watchguard.com/wgrd-resource-center/security-fundamentals/understanding-ip-addresses-and-binary
- Farrow, Rik, “Understanding IPv4 Subnetting (Part 1)”, https://www.watchguard.com/wgrd-resource-center/security-fundamentals/understanding-ipv4-subnetting-part-one
- Farrow, Nachreiner, and Pinzon, “Understanding IPv4 Subnetting (Part 2)”, https://www.watchguard.com/wgrd-resource-center/security-fundamentals/understanding-ipv4-subnetting-part-two
Contributors and testers
- Alec Parish, Student, ERAU-Prescott
Phase I – A Very Brief Review
This instructional material is not designed to replace people’s favorite learning materials. We want to simply augment what already exists. However, it was pointed out by some of our testers that a very abbreviated review would be a helpful inclusion within the textbook.
Computers view the world in 1s and 0s. At the most fundamental level, Network Interface Cards (NICs) produce and receive streams of 1s and 0’s like ping-pong balls moving through a glass tube.
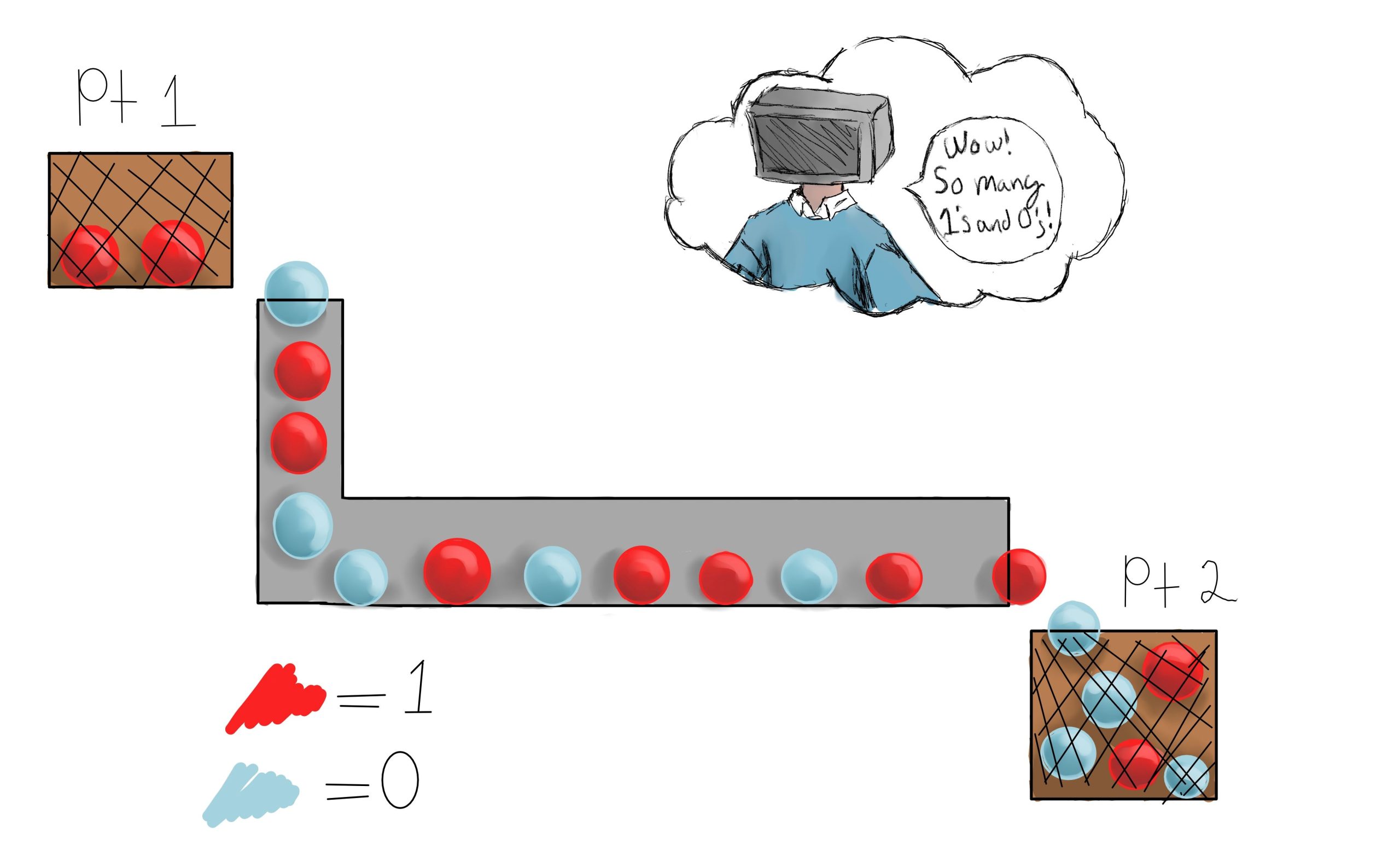
The NIC cannot see what data is coming; it can only see what has been received and has to make sense of the information. The Ethernet Protocol defines which combinations of 1s and 0s will result in commands for action. If the combination gets mixed up, the command is garbled, and the NIC has no idea what to do and will throw the data away.
IPv4 networks use two human-readable notations of 32 bits each to identify a NIC, such as 192.168.1.14 255.255.255.0. Back then, the first part, 192.168.1.14, was a sufficient identifier like a house number in a town. However, as the internet grew, just like towns, further identification was needed to handle the new NICs (new houses), and the existing identification system was still being used. Subnet masks (255.255.255.0) were introduced, acting like street names.
Each human-readable notation of 32 bits is broken into 4 octets (8 bits). This is for human readability; the NIC doesn’t care. Remember, the NIC only looks at 1s and 0s. Using these principles, we can look at our example (192.168.1.14). Generally, spaces are inserted every 4 bits to make things easier for humans to read.
| First Octet | Second Octet | Third Octet | Forth Octet |
| 192 | 168 | 1 | 14 |
| 1100 0000 | 1010 1000 | 0000 0001 | 0000 1110 |
The 192 is a decimal, human-readable notation of the binary value 1100 0000. If this were sent from one NIC to another, we would send a ‘ping-pong ball’ sequence of red, red, blue, blue, blue, blue, blue, blue.
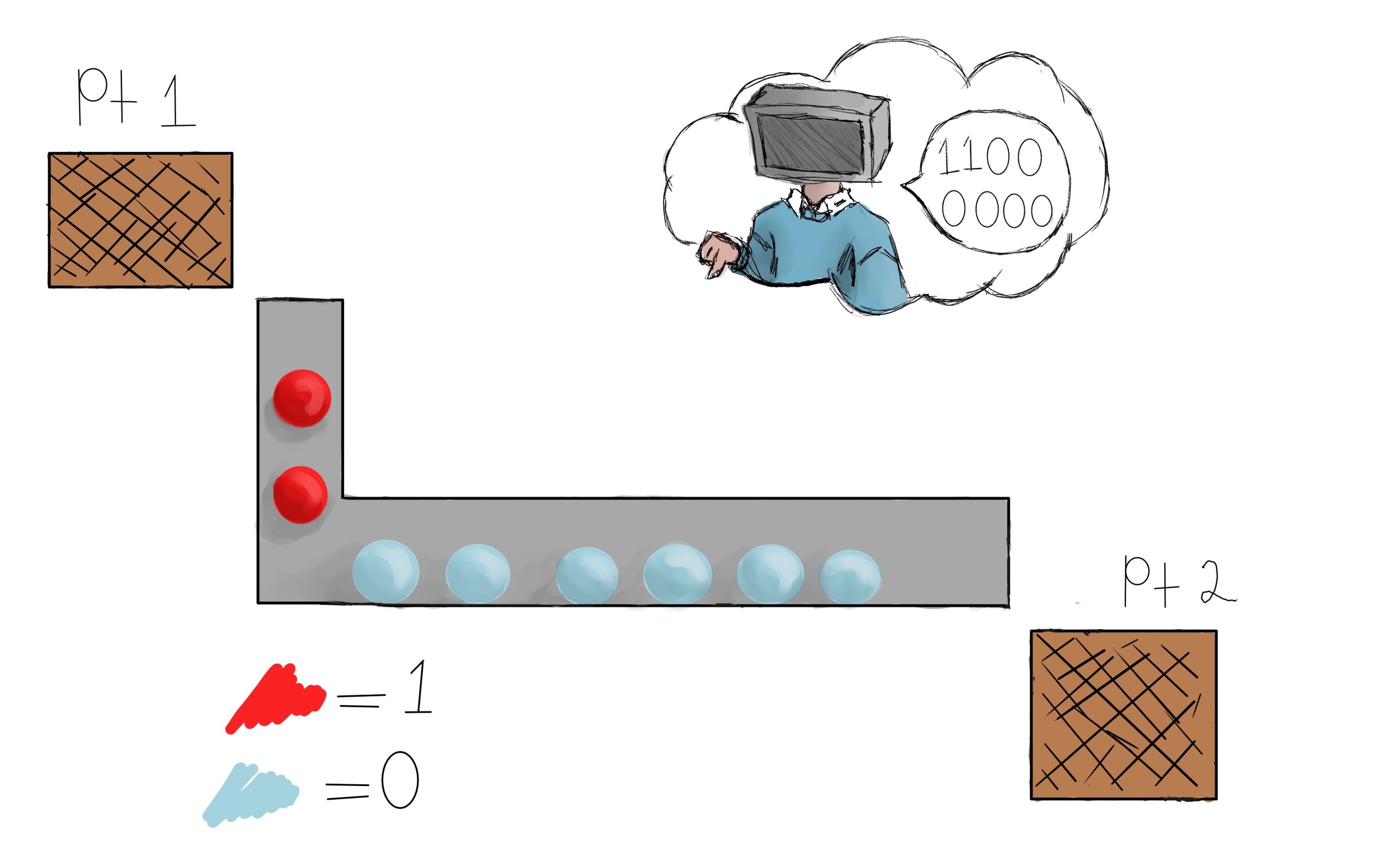
Converting between binary and decimal notation is beyond the scope of this lesson. Suffice it to say, most scientific calculators can make the conversion.
Looking at this, we can quickly run out of notational identifiers. Remember, the largest decimal notation we can have is 255 because the largest binary notation is 1111 1111.
| Decimal | Binary |
| 255 | 1111 1111 |
| 999 | 0011 1110 0111 (NO! larger than 8 bits) |
Subnet masks use a continuous string of 1s to identify which part of the IPv4 address is the “street name” and which part is the “house number”. A subnet mask means that the string of 1s is never interrupted. For example, if our subnet mask is 255.255.255.0, it represents a binary representation of 1111 1111.1111 1111.1111 1111.0000 0000. Notice there is no interruption of the sequence of 1s. Having a subnet mask of 255.192.16.14 is impossible because the sequence of 1s is interrupted.
| 255 | 255 | 255 | 0 | No interruption of bits |
| 1111 1111 | 1111 1111 | 1111 1111 | 0000 0000 | |
| 255 | 192 | 16 | 14 | Series of 1’s bits interrupted |
| 1111 1111 | 1100 0000 | 0001 0000 | 0000 1110 |
The final piece of the puzzle is called Logical AND addition. In this type of addition, any binary 1 added to another binary 1 will produce a binary 1 (1+1=1). Any use of zero will result in a zero. e.g. (1+0=0, 0+1=0, 0+0=0)
When we perform a Logical AND addition of our IP address with its associated network mask, it reveals both our device’s “street name” and “house number.”
In this example, our PC has an IP address of 192.168.1.65 with a network mask of 255.255.255.0. We will apply Logical AND addition and look at the results.
First, we convert the IP address and netmask to binary.
- 192.168.1.65 → 1100 0000 . 1010 1000 . 0000 0001 . 0100 0001
- 255.255.255.0 → 1111 1111 . 1111 1111 . 1111 1111 . 0000 0000
Second, apply Logical AND addition to the first octet of both
NOTE: The first octet in all instances is highlighted in red for illustrative purposes
| 192 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 255 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
| Logical AND Addition (1+1=1 with all other results being 0) | ||||||||
| Result | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Third, apply Logical AND addition to the remaining three octets
| 168.1.65 | 1010 1000 | 0000 0001 | 0100 0001 |
| 255.255.0 | +1111 1111 | +1111 1111 | +0000 0000 |
| Logical AND Addition (1+1=1 with all other results being 0) | |||
| Result | 1010 1000 | 0000 0001 | 0000 0000 |
| Results from Step 2 | Results from Step 3 | ||
| 1100 0000 | 1010 1000 | 0000 0001 | 0000 0000 |
NOTE: As you get more experienced, steps two and three will be done at the same time, so there will be no need for a fourth step.
Finally, convert the 32 bits into a decimal, human-readable form.
1100 0000 . 1010 1000 . 0000 0001 . 0000 0000 = 192.168.1.0
The result tells us that our “Street Address” is 192.168.1.0 and that we can use any decimal number from 1-254 instead of the 0 as our “House Number”. Yes, I see you in the back. “What happened to 255?” In this case, 255 is used as a shortcut that means “every house on the street”. Think junk mail. If a company wants to send snail mail to everyone on a street, it doesn’t look up every address; it just sends it to every house on the street.

At this time, we are going to abandon the street name and house number metaphor and use the proper names:
- Street Name = Network ID
- House Number = Host ID
- Every House = Broadcast ID
There are three more important identifiers we need to know:
- First Usable IP Address = Add 1 to the Network ID (e.g. 192.168.1.0 + 1 = 192.168.1.1)
- Last Usable IP Address = Subtract 1 from the Broadcast ID (e.g. 192.168.1.255 – 1 = 192.168.1.254)
- IP Address Range = The number of real numbers between the First Usable and Last Usable IP addresses, inclusive (e.g., 192.168.1.254 – 192.168.1.1 = 0.0.0.253, then include the 1 to increase the result to 0.0.0.254). This means 254 hosts can be joined to the network
‘Inclusion subtraction’ of large numbers is a handy means of quickly determining the number of options available from a set. This process can seem complicated, but when you look at a smaller set of options, your brain does the inclusion subtraction on its own.
Consider a series of numerical digits: 1, 2, 3, 4 (it could be a series of colors [blue, red, yellow, green], cars [Mustang, Pinto, Studebaker, Tundra], or whatever). Whatever the list is, if I asked how many options there are, you would respond with ‘four’. This is an easy task when we do it intuitively. However, doing it mathematically causes issues.
In this instance, we would write the last number and subtract the first number like 4 – 1 = 3. This is obviously the wrong answer. We need to include the original option of the number 1, so we add it back in for an ‘inclusive subtraction’ 4 – 1 + 1 = 4. It seems silly when he numbers are small, but when the numbers get large, we forget.
This is a lot of information, so let’s clean it up in a summary:
Given a PC with an IP address of 192.168.16.14 and a subnet mask of 255.255.255.0 find the resulting information:
| Given | ||||
| IP Address | 192 | 168 | 16 | 14 |
| Subnet Mask | 255 | 255 | 255 | 0 |
| Convert to binary | ||||
| IP Address | 1100 0000 | 1010 1000 | 0001 0000 | 0000 1110 |
| Subnet mask | 1111 1111 | 1111 1111 | 1111 1111 | 0000 0000 |
| Logical AND addition result | 1100 0000 | 1010 1000 | 0001 0000 | 0000 0000 |
| Convert back to human readable decimal form | ||||
| Network ID | 192 | 168 | 16 | 0 |
- Network ID = 192.168.16.0
- Host ID = 192.168.16.0
- Broadcast ID = 192.168.16.255
- First Usable IP = 192.168.16.1
- Last Usable IP = 192.168.16.254
- Address Range = 254 hosts
Another example: Given a PC with IP address of 58.213.107.5 and a subnet mask of 255.255.192.0 find the resulting information:
| Given | ||||
| IP Address | 58 | 213 | 107 | 5 |
| Subnet Mask | 255 | 255 | 192 | 0 |
| Convert to binary | ||||
| IP Address | 0011 1010 | 1101 0101 | 0110 1011 | 0000 0101 |
| Subnet mask | 1111 1111 | 1111 1111 | 1100 0000 | 0000 0000 |
| Logical AND addition result | 0011 1010 | 1101 0101 | 0100 0000 | 0000 0000 |
| Convert back to human readable decimal form | ||||
| Network ID | 58 | 213 | 64 | 0 |
- Network ID = 58.213.64.0
- Host ID = 58.213.64.0
- Broadcast ID = 58.213.127.255
- First Usable IP = 58.213.64.1
- Last Usable IP = 58.213.127.254 (remember, the third octet is 0100 0000 after the Logical AND, so the highest it can go is 0111 1111, which is 127 in decimal)
- Address Range = 16,382 hosts
Some will look at this and make some shortcut inferences. And some shortcuts can be made, but only under specific conditions. This is how cyber folks can impress laymen with their mental math skills. However, so long as you follow the above procedures every time, you will always get the correct answers, and your network will function because it is using the correct IP addresses.
A quick discussion on Classless Inter-Domain Routing (CIDR). Using network masks of 255.0.0.0, 255.255.0.0, or 255.255.255.0 leaves many unused Host IDs that other networks could use. Take our example earlier, 255.255.255.0 resulted in 254 Host IP addresses. However, if we are only connecting two devices (say 192.168.16.1 and 192.168.16.2), we are preventing the use of the remaining 253 Host IP addresses by other network parts.
CIDR allows us more flexibility. Using a netmask of 255.255.255.252 gives us two usable Host IDs and frees the remaining Host ID’s for other purposes. CIDR notation provides shortcut tools because it lists the number of continuous binary 1s in the netmask.
| Network Mask (netmask) | Number of 1’s | CIDR notation | ||||
| IP | 255 | 255 | 255 | 0 | ||
| Binary | 1111 1111 | 1111 1111 | 1111 1111 | 0000 0000 | 24 binary 1’s | /24 |
| IP | 255 | 255 | 255 | 252 | ||
| Binary | 1111 1111 | 1111 1111 | 1111 1111 | 1111 1100 | 30 binary 1’s | /30 |
Phase II – Practice Subnetting Principles
The following problems are self-graded. You can take as many attempts as necessary to ensure you understand the information.
End of Lab
Deliverables
Complete this worksheet and turn it in to receive credit for this exercise: Worksheet
Homeworks
Assignment 1 – Create your own GNS3 network
Generate a random IPv4 network ID and use it to build a GNS3 network using 4 PCs and a switch. Use a CIDR that would allow for the addition of 1,000 more hosts.
Assignment 2 – Create a GNS3 that doesn’t waste any IP addresses
Generate a random IPv4 network ID and use it to build a GNS3 network using 5 PCs and a switch. Use a CIDR that wastes as few IP addresses as possible.
Recommended binary grading criteria:
- Screenshot of the GNS3 Working environment where:
- All connections are made according to instructions
- All connections are labeled with the correct IP Address
- The correct CIDR is used
- Interface labels are turned on
- A screenshot of Wireshark packet captures taken from the PC1-switch link
- Any PC can successfully ping PC1
- A second PC can successfully ping PC2


