6 Bonds
Chapter 6 Bond Markets
Overview and Background
In the previous chapter, we studied how cash flows of different periods are compared using discounting. If there are two instruments[1] with different cash flows, all else equal, investors should choose the instrument which carries higher present value of cash flows. In this chapter, students are expected to look at the cash flows of bonds, analyze the cash flows to compute the price of the bond using the present value concept. In this chapter, we also compare and contrast pricing of long term versus short term bonds, discuss inflation, Treasury Inflation Protected Securities, the Treasury yield curve, and riskiness of bonds of corporations.
Learning Objectives
Following this Module, you should be able to:
- Analyze the cash flows of a bond
- Compare and contrast current yield, coupon and yield to maturity of bonds
- Analyze the riskiness of bonds
- Calculate the real returns from nominal returns
In order to open a new business or expand an existing business a firm has two options. Raise money or capital (meaning obtain new non-business generated cash) through either:
(1) equity markets or
(2) debt markets.
As seen in the previous chapters, equity markets involve shares of stock. These shares are listed on stock exchanges and are issued for the first time by companies that create owners of the company. Subsequently, these shares are traded in secondary markets. Both primary and secondary markets are a part of equity markets as long as the instruments are shares of stock. Shares can be issued either when a company goes public for the first time (Initial Public Offering, IPO) or when the company wants to expand its operations after reaching some maturity (issue of shares). The advantage of equity for a company is that once capital is raised using the equity route, the company does not have to return this capital. However, raising money through equity markets involves issue of new shares, a route some companies do not want to take. This is because issuing new shares makes the existing shareholders less powerful in terms of percentage of shares they hold.1
When a company does not want to issue shares, but at the same time wants to expand its operations, it can also choose to issue debt in bond markets or debt markets. This leads to the option of issue of debt. The common theme among all the debt market instruments is that money is “borrowed” from lenders. We have seen in chapter 2 that a corporation can participate in debt markets through several options. The company can borrow money: through term loans, through issue of debentures, or through short-term commercial papers. If the need is immediate, the corporation can also borrow money through a “line of credit” from a bank.
6.1 Operation of debt markets
Debt markets operate as follows:
First, there is a principal or sum borrowed against the company’s assets. We saw in the previous chapter that this principal borrowed is associated with present value in a loose sense.
Second, there is a sum returned, which we saw as future value in the previous chapter. Sometimes, there is a single lumpsum payment at the end or some other times, there are intermediate payments during the loan.
Third, there is a rate of interest, or the rate charged by lenders to borrowers, which when positive makes future values greater than the present value. This rate charged by lenders to borrowers compensates lenders for the intertemporal transfer of funds.
Let’s see the debt market in-action through an example. During the pandemic, large airlines such as Delta, went into action to protect themselves from drying up customer payments due to uncertainty surrounding passenger travel. Consequently, Delta airlines borrowed $3.5 billion on April 27th, 2020, through the bond market with a five-year deal secured against the company’s assets, including its aircraft routes and the slots it holds at airports such as Heathrow in London or John. F. Kennedy in New York. Delta also raised $1.5 billion through a three-year loan, secured against the same assets. The company drew down on a $3bn lending facility with a group of banks and received $5.4 bn to support its payroll from the US government’s giant stimulus package. All these sums of money were borrowed with certain rates of interest with the intent to return the money at a future point in time. Hence these sums of money are classified in Delta’s balance sheet as liabilities (meaning debt) and not owners’ equity. Furthermore, the duration of these loans would determine whether these are money or capital market instruments (i.e. short- or long-term instruments). This example illustrates two facts:
One: even a large airline such as Delta needs to borrow money.
Two: Debt market instruments are issued relatively more frequently (than equity). Sometimes they are issued privately (such as in the above case with government or consortium of banks) and money is received quickly.
6.2 Debt vs. Equity Markets
For corporations, debt instruments such as lines of credit, term loans, direct issuance debentures, and commercial papers provide quicker access to funds. In contrast, instruments such as public issuance of debentures and shares are time-consuming as they need approval from regulatory bodies, need the service of underwriters, and also need to go through roadshows and marketing activities. Corporations can also raise capital through equity market instruments such as shares and preferred stocks. However, corporations typically must return more on equity markets than debt.
Typical values of return on equity for investors range between 10 and 35%, meaning corporations raising capital through equity issues are expected to pay this percentage to their shareholders as a proportion of new capital raised. According to a study by the federal deposit insurance commission in 2017, the return on equity for companies in the S&P 500 index ranged between 5% and 30%. The weighted average (by market capitalization) return on equity of the top 10 companies was 18.6%, and the median was 14.75%. These statistics imply that if a corporation issued shares, it would be obliged to return an excess of 14% to shareholders for every dollar of stock issued.
In contrast, the debt market interest rates are significantly lower. The average 10-year treasury yield has been in the range of 2 – 3%. Adding a 1 to 1.5% spread on top of that (for the riskiness of firms as compared to the government)2, the cost of issuing a 10-year debenture for a corporation would work out to a maximum of 4.5%. This lower debt cost makes debt issuance more attractive to companies. The other benefit of issuing debt is that on the income statement, corporate profits are calculated after the interest cost on debt is subtracted. In other words, the interest obligations of a company are deducted before tax obligations are calculated. However, profits are distributed to equity holders after tax is deducted from pre-tax income. Thus, a bondholder would be paid before taxes are calculated on a company’s income statement, while a shareholder would be paid after taxes are paid. Theoretically, this before tax deduction of interest in debts allows a corporation greater “post expense” income to distribute to shareholders as compared to if there were no debt and everything else same. This greater reduction through interest payment on debt also enables corporations to pay lower taxes for an equal amount of income. We will illustrate this concept in subsequent chapters, but for now, it is sufficient to know that there are tax benefits for issuing debt market instruments.
Another caveat to bear in mind when issuing debt is that if a company is liquidated, it does not owe anything to shareholders. However, it still owes all the debt borrowed from its lenders. It is not just corporations who go through times of distress, but also countries (i.e., their governments) that potentially default on their sovereign debt. The famous case of Greece, Italy, Spain and other governments coming close to the brink between 2010 and 2020.The most common way to avoid default on debt is to pledge more assets as security and renew larger debt. In the case of most countries and corporations, this is one way of sustenance, particularly during adverse times. This is called bailout and bailouts are commonly sponsored by large financial organizations such as banks. In the case of countries, bailouts are typically sponsored by the International Monetary Fund (IMF).
6.3 Bonds and bond terminology
A bond is a debt market instrument that promises investors agreed sum(s) of future payments in return for a certain amount borrowed during its issue. Every bond is associated with a face value (which is not necessarily the principal or present value or price), a coupon and a yield to maturity. We will attempt to discuss these facets of a bond next.
6.3.1 Price
Price or bond price is the value of a single bond that is exchanged in return for its ownership. Bond’s price is always calculated as present value in the time value of money equation we saw in the previous chapter. In other words, the technical term for price is present value (of future cash flows). Interest rates fluctuate a lot, almost every fraction of a second as bonds are bought and sold. Since present value (and hence price) is a function of discount rate (interest rate), bond price changes very frequently.
6.3.2 Face value
Face value, par value, or simply par, is the value associated with a bond at its maturity for the bondholder. Face value also determines calculated coupon interest payments for the borrower. In simple terms, face value is the nominal value of the loan promised to the bondholder per unit bond. In reality, the issuer may or may not borrow the par value at the time of issuance because interest rates are extremely dynamic. We will see the connection between price and interest rates in this chapter. Corporations issue bonds with par values of $ 100 or $ 500 or $ 1,000. The US government typically issues bonds with a par value of $ 1,000. As we discuss the bond terminology, let us consider an example of a 10-year bond with a par value of $ 1,000. The bond is 10-year because it will mature to be worth $1,000 (and any other final promised payments due when the bond’s life is over) to the bondholder ten years from today.
6.3.3 Coupon
A coupon is expressed in the associated dollar value that the bondholder receives periodically based on the coupon rate. This dollar value is determined as a percent of the par value. The issuer (or borrower) of a bond promises to pay coupons as intermediate payments to the bondholder while the bond is yet to mature (or expire or complete its life). For example, let us assume our ten-year government bond, as discussed above, has a coupon of 3%. That implies that on a par value of $ 1000, the coupon payment will be 3% of 1000 or $ 30 per year. The above payment assumes annual coupons. If the coupons are semiannual, the 3% will be considered equivalent to an APR, and $ 15 (or 3%/2 = 1.5%) will be paid every six months to the bondholder until maturity.
6.3.4 Maturity date and period
Maturity date is the date on which the bond expires or matures. Final cash flows of the bond occur at maturity date. Usually, it is the face value of the bond that is paid out to the bondholder along with any coupons. Maturity period and term to maturity is the life of the bond that remains from the current date. All bonds are measured according to maturity period. Maturity period is also called term to maturity (ttm). So, a 10-year bond has 10 years left to maturity from the date of issue. Finally, bonds are not measured according to their residual life from when they were issued, but according to their residual life or maturity period or ttm from the current date.
6.3.5 Yield to maturity
Yield to maturity is a rate at which future cash flows associated with a bond are discounted. As we saw in the previous chapter, when there are future cash flows, we need to discount these cash flows using a discount factor. While a coupon rate is constant, it does not reflect the market interest rates. Market interest rates govern the present value of cash flows, and the coupon rates govern the coupon dollars as a percent of face value. Put differently, the bondholder will receive the coupon rate from the bond issuer regardless of what the market is doing. Since coupons are promised, coupon rates do not change.3 On the other hand, market interest rates change in real time. These interest rates are used as discounting factor in calculating present value of the bond (also referred to as the ‘price’ of the bond). As price changes, so do market interest rates (yield to maturity).4
To reiterate the difference between coupon rate and yield to maturity: Coupon rate determine coupon dollars, which go into the numerator of the present value equation for bond pricing because these determine cash flows. Yield to maturity is used as the discount rate in the denominator of the present value equation of bond pricing. Coupon rate is usually invariant. Yield to maturity changes very quickly as bond is traded and its price changes.
Next, we will see how bonds are priced using the bond pricing equation, which we saw in the previous chapter as the present value equation.
6.4 Issuing and trading a bond – basics of bond pricing
As we noted earlier, a bond has cash flows associated with it. At the time of borrowing, the issuer issues (writes) the bond with the help of an underwriter. An underwriter looks at companies similar to the issuer and considers the yields of those bonds.5 For example, if Apple wants to issue bonds, the underwriter will look around for similar companies such as Microsoft, Amazon, Oracle, IBM, etc. to see what price and yield these companies’ bonds for similar ttm are trading for. Once the market making exercise is done, then in case of some securities such as government bonds, trading takes place even before the bonds are officially issued. This is called when-issued market and is very helpful to identify actual prices of bonds when they are issued. We also note that US government bonds are typically issued through weekly auctions.
The price of a bond is valued the same way as the present value of irregular cash flows. Even though coupon payments are constant, cash flows from a bond are not regular because of the final (or terminal) cash flow. The terminal cash flow includes a coupon payment and payment of the face value. For our 10-year bond with coupon of 3% on face value of $ 1,000, the cash flows would look as in Figure 6.1 below.

In Figure 6.1, we can see that price = present value of cash flows which are 10 coupons plus the final cash flow of par value at t=10. In this case, the cash flows are negative because we are looking at them from the perspective of the issuer/ borrower. Both the coupons and final cash flow or terminal value are paid out to investors/bondholders by the issuer/borrower over time (t). These signs can be easily inverted without any loss of accuracy in pricing of this bond if we want to see them from an investor’s point of view. In other words, from an investor’s perspective price is paid now (negative cash flow at t=0) and subsequently cash flows are received (hence +30 for periods t=1…9 and +1030 for t=10)
Next, we will use the same concept as present value of multiple cash flows in order to find the present value/ price of bond that will be charged to investors/bondholders.
[latex]Price = PV = \frac{CF_1}{(1+r)}+\frac{CF_2}{(1+r)^2}+…+\frac{CF_t}{(1+r)^t}+…+\frac{CF_n}{(1+r)^n}[/latex]…(1)
Where,
is a cash flow for period ‘i’.
When i = t, we consider it as an intermediate cash flow.
When i = n, we consider it as a terminal cash flow.
‘r’ is the discount rate or present interest rate for time = ‘n’ or yield to maturity as we discussed in the previous section. (‘r’ should not be confused with the coupon rate, which is coupon percent times the face value)
The difference between
In our example of the ten-year bond above, the price is
As ‘r’ changes in the above equation, so does PV = price.
For example, if r = 1%, then
[latex]Price=PV=\frac{30}{1.01^1}+\frac{30}{1.01^2}+…+\frac{30}{1.01^t}+…+\frac{1030}{1.01^{10}}= 1189.43[/latex]
If r = 4%, then
[latex]Price=PV=\frac{30}{1.04^1}+\frac{30}{1.04^2}+…+\frac{30}{1.04^t}+…+\frac{1030}{1.04^{10}}= 918.89[/latex]
Notice that as the interest increases from 1% to 4%, price decreases. Interestingly, price went from above par to below par. This is because of the fulcrum point: the price will be par when the rate of interest or discount rate is equal to the coupon rate of 3%. Let us see that:
[latex]Price=PV=\frac{30}{1.03^1}+\frac{30}{1.03^2}+…+\frac{30}{1.03^t}+…+\frac{1030}{1.03^{10}}= 1000[/latex]
Note that we saw above that when interest rate (YTM) changes from 1% to 4%, price changes from 1189.4 to 918.9 (decrease of $ 270.5)
We can do similar calculations for a 30-year bond. The only difference is that we have to add 20-more discounted cash flows, which is easily done in Excel in two ways: either lay out cash flows and discount and add them or use the PV function.
For example, if r = 1%, then
[latex]Price=PV=\frac{30}{1.01^1}+\frac{30}{1.01^2}+…+\frac{30}{1.01^t}+…+\frac{1030}{1.01^{30}}= 1516.15[/latex]
Note, that for same coupon rate and same par, as ttm increases, price increases. This is because more coupons are received over time increasing the present value. In this case, as the ttm increases from 10 years to 30 years, price increases from 1189.43 to 1516.15.
For our 30-year bond, if r = 4%, then
[latex]Price=PV=\frac{30}{1.04^1}+\frac{30}{1.04^2}+…+\frac{30}{1.04^t}+…+\frac{1030}{1.04^{10}} = 827.10[/latex]
[latex]Change \; in \; price = \Delta{Price}=1516.15 – 827.10 = 689.05[/latex]
Notice that as the interest increases from 1% to 4%, price decreases by $ 689.05 (which is more than the $ 270.5 we noticed for the 10-year bond). Interestingly, price again went from above par to below par. This is because the fulcrum point remains par and YTM = coupon = 3%. When the interest rate was below 3%, i.e. at 1%, price was above $ 1000 (par) and vice versa.
Let us see what happens (at the fulcrum point) i.e. when the interest rate equals the coupon rate of 3%.
[latex]Price=PV=\frac{30}{1.03^1}+\frac{30}{1.03^2}+…+\frac{30}{1.03^t}+…+\frac{1030}{1.03^{30}}= 1000[/latex]
It is not surprising that even though we moved from 10-year bond to 30-year bond, the fulcrum point remains at YTM = coupon rate. This is because face value and coupon rate (hence coupon dollars) are fixed for the life of a bond.
Moving on from these “coupon-paying” bonds to zero coupon bonds, we notice that as the name suggests, zero coupon bonds have no coupon. Let us now see the pricing of zero-coupon bonds.
Let’s price a 10-year zero coupon bond using what we learned about coupon paying bonds at YTMs of 1%, 4% and 3% respectively:
[latex]Price = PV = \frac{0}{(1.01)} + \frac{0}{(1.01)^2}+…+\frac{0}{(1.01)^t}+…+\frac{1000}{(1.01)^{10}}= \frac{1000}{1.01^{10}} = 905.30[/latex]
[latex]Price=PV=\frac{1000}{1.04^{10}}=675.60[/latex]
Notice that all the bonds are now priced below par due to a lack of coupon payment. Being priced below par compensates investors for not getting paid coupons. As interest rates (discounting rates) go up from 1% to 3% to 4%, price decreases from 905.3 to 744.1 to 675.6. In order to compensate investors for not receiving coupon payments, as yield to maturity increases, price today (i.e. present value invested by investors) decreases.
To summarize:
- When coupon rate = YTM, price = Face Value.
- When YTM > coupon, price < Face Value, and the bond trades at discount.
- Price and YTM are inversely related.
- Long-term bonds are more volatile than short-term bonds because for the same change in interest rates, there are more cash flows to discount. Even if there are no more cash flows to discount, the time duration over which discounting is applied is greater (than short-term bonds).
- The relationship between ttm and ytm is defined as the term structure of interest rates and when interest rates are plotted against time to maturity, this representation is called as the yield curve.
The above concepts are discussed in these videos:
- Pricing of a coupon paying bond 10-30 year with different yields. Video
- Pricing of a zero coupon bond. Video
6.5 Term Structure of interest rates
Usually short-term rates (we have defined them in equation (1) above as discount rate ‘r’ and elsewhere as yield to maturity YTM) are smaller than long-term interest rates. The yield curve is a representation of interest rates against the term to maturity of a bond at a given point of time on a graph. These interest rates are plotted against term to maturity. For example, in February 2019, right before the pandemic began, yield curve looked as in Figure 6.2 below:
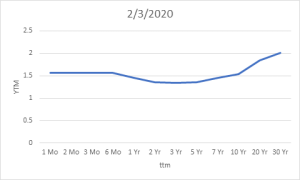
In figure 6.1, interest rates or yield to maturity are represented on y-axis and are plotted against term to maturity, which is represented on the x-axis. What we can read from figure 6.1 is that yield on 1 month through 6-month treasury bills is about 1.5 to 1.6%. This yield drops as ttm increases to 5-years, and then after reaching a ttm of 5 years, YTM tends to increase with ttm.
Notice how the slope of the yield curve is “inverted”, meaning short-term interest rates are slightly higher than long-term interest rates (in this case the < 1 year T-Bill rates are greater than 3-year and 5-year YTMs). This kind of yield curve is semi-inverted, in which not all short-term interest rates are higher than their longer-term counterparts. In this case, the YTM on 7-year, 10-year and 30-year bonds increase as ttm increase. This is illustrated further in table 6.1 below.
|
TTM |
YTM |
|
1 Mo |
1.56 |
|
2 Mo |
1.57 |
|
3 Mo |
1.57 |
|
6 Mo |
1.56 |
|
1 Yr |
1.46 |
|
2 Yr |
1.36 |
|
3 Yr |
1.34 |
|
5 Yr |
1.35 |
|
7 Yr |
1.45 |
|
10 Yr |
1.54 |
|
20 Yr |
1.84 |
|
30 Yr |
2.01 |
In table 6.1, we notice that yields on 1-, 2-, 3-, and 5-month treasury bills are almost the same at around 1.56-1.57%. As the ttm increases to 1 year, yields drop by 0.1% from 1.56% to 1.46%. We also call this a drop of 10 basis points. One basis point is 0.01%. As we move from ttm of 1 year to 2 years, yields drop to 1.36%, another drop of 10 basis points. As we move from 2-years to 3-years, 4-years and 5-years, there is very little change in yields (1-2 basis points). As we move from ttm of 5-years to 7-years and 10-years, yields move up by 10 basis points (bps) and 9 bps respectively. Moving from 10-years to 20-years makes yields jump by another 30 bps. Moving from ttm of 20-years to 30-years makes yields jump by another 17 bps from 1.84% to 2.01%
Let us now observe the yield curve for February 2022 and August 2022 as in Figure 6.3 below.
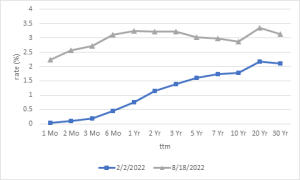
Notice that in February 2022 (the blue line), the yield curve was mostly steep, but that in August (the gray line) was inverted between 3 year and 10-year maturities.
6.6 Bond price nomenclature
In the US, bonds are quoted in 32nd increments to calculate the bid price. This is somewhat similar to the hour being split into 60 minutes and a minute being split into 60 seconds. The bid price of a bond is measured as a proportion of the par value. For example, if a dealer quotes the price of a bond as 103:05 (bid) and 103:06 (offer) of the par value, they are willing to buy the bond from us at a price (103+5/32)% of par value and are willing to sell the bond for (103 + 6/32)% of par value.
If the par value is $ 1000, then let us find the actual bid price.
Step 1: convert [latex]\frac{5}{32}[/latex] into a decimal = 0.15625
Step 2: combine the first and second part of the quote [latex]= 103+0.15625 = 103.15625 %[/latex] of par
Step 3: now convert it into actual number by translation. [latex]\frac{103.15625}{100}\times1000 = $ 1031.56[/latex]
To convert a price into 32nds, we go in the opposite direction. Let us use the offer price for this.
Step 1: convert the price into percentage [latex]\frac{1031.875}{1000}\times100 = 103.1875%[/latex] of par
Step 2: keep the part before decimal and multiply the second part by 32. So [latex]0.1875\times32 = 6[/latex]
Step 3: Express into the quote: 103:06
6.7 Some more types of rates
So far, we have seen coupon rate and YTM (discount rate). However, there are two more rates associated with a bond: Current yield and rate of return. These are often used for back-of-the-envelope calculations or “what is in it for me” calculations.
6.7.1 Current Yield
The first type of rate is called current yield. It is the coupon divided by price. (Current yield = Coupon/ Current Price) Very loosely, it is the yield produced by coupon payments of a bond on today’s price. Let us revisit the bond pricing calculation we carried out in section 6.4. Recall that it is a ten-year bond 3% coupon, $ 1000 par at YTM of 1%, 3% and 4% in table 6.2 below. There is no new information in the table below. We are just summarizing details from section 6.4 above.
| YTM | Price |
| 1.0% | $ 1,189.43 |
| 3.0% | $ 1,000 |
| 4.0% | $ 918.89 |
For this bond, the current yield is 2.52% (30/1189.43) if the price corresponds to a YTM of 1%; is 3.26% (30/918.89) if YTM is 4% and 3% (30/1000) if the price is par.
We summarize this in table 6.3 below:
| YTM | Price | Current Yield |
| 1.0% | $ 1,189.43 | 2.52% |
| 3.0% | $ 1,000 | 3.00% |
| 4.0% | % 918.89 | 3.26% |
6.7.2 Rate of Return
The second type of rate is called rate of return. Rate of return is defined as the [latex]\frac{selling \; price \; – \; purchase \; price \; + \; coupons}{purchase \; price}[/latex]. So, rate of return signifies the gains made through capital gains and coupons as a percent of the purchase price. This rate is particularly relevant if an investor holds the bond for less than the maturity date, which is often the case. Let us consider a simple example:
Suppose an investor bought the 10-year bond today (i.e. when 10-cash flows are left) at a YTM of 1% at a price of 1189.43. Assuming for simplicity, the investor holds the bond for 1-year and sells it after 1 year. Luckily the YTM is now 0.75% for 9-years (notice there are only 9-cash flows left). The price of the bond now (after 1 year) is 1195.1 (using the same present value equation we learnt before).
So, the rate of return = (selling price – purchase price + coupons)/purchase price
[latex]\frac{(1195.1-1189.43+30)}{1189.43} = 3%.[/latex]
6.8 Riskiness and bond yields
The meaning of the word risk is associated with the inability of a borrower to make payment in time. Sometimes borrowers pay either partial payment or no payment at all due to a variety of conditions. For corporations, the main condition that makes them unable to fulfill their commitments is bankruptcy. So, it is important to determine whether some firms are more likely to repay their debt in time as compared to others. This process involves evaluating the quality of bonds and creating bond ratings.
In the US, there are mainly three bond rating agencies: Standard & Poors (S&P), Moody’s and Fitch. These ratings assign grades to companies’ kind of like professors attach a grade to students at the end of the semester. So, if a company has a grade similar to “A,” it is more credit worthy or able to repay its debt with better probability than a company which has a grade of say “BB.” Similarly, bonds that have a rating of “BAA” or below are called “junk bonds” because these borrowers are “risky.” In order to compensate a lender for assuming more risk, the issuer of lower quality bond must pay a higher rate than the less risky corporations. This way, raising debt is more expensive for lower rated corporations compared to higher rated firms. This difference in rate (spread) is called a default premium and the associated risk is called default risk.
Longer the term of the bonds, there is a higher possibility that the value of the bond is impacted. So, everything else same, longer-term bonds are riskier than shorter term bonds. This risk is called maturity risk or term risk or duration risk. We studied the term structure of interest rates earlier. Generally speaking, a 30-year bond has a greater coupon (hence yield) as compared to a bond with lower ttm issued by the same company. Consequently, the premium that needs to be paid by corporations to compensate investors for holding their bonds longer is called term or maturity premium. This provides the underlying “steepness” to the yield curve.
6.9 Bonds and inflation
We have seen that the world economy has seen historic inflation shock in 2022. In order to curtail that inflation, central banks around the world are raising interest rates. When interest rates rise, we have seen that due to inverse relationship of present value and discount rate, when bond yields (discount rate) rise prices (present value) drops.
Investors in bonds do not like this. They ask the issuers to compensate them for this inflation risk. Otherwise, investors would rather invest in commodities rather than government bonds in search for higher returns. Recall that from chapter 5, real interest rate approximately equals nominal interest rate – inflation. If inflation > nominal interest rate, real interest is negative. The US Federal government (treasury) issues inflation protected bonds to compensate investors for high inflation.
In case of inflation protected bonds, the face value is floating. In other words, the government may start with a face value of $ 1000. This amount is used for paying coupons. But if inflation rate increases, then the principle also gets reset after 1 year to a higher value, depending on the rate of inflation. Thus, coupon payments are paid out on the higher face value. For example, for a bond with par value of $ 1000, if inflation for year 1 is 2.5%, the coupon calculated for bond next year would be on a base of 1.025 times $1.000 = $1,025.
Finally, some issuers like to reset the coupon itself in response to market interest rates. Such bonds with variable coupons are called floating rate bonds.
Some companies issue bonds that give an option to investors to convert these bonds into either shares or reinvest into bonds of same tenure at maturity. Such flexible options enable these bonds to be called as convertible bonds.
Summary and Conclusion
This chapter discusses pricing of bonds. The face value of a bond is the price at which the bond was first issued. The coupon of a bond is the percent of the face value that the issuer promises to pay every fixed period. The yield to maturity is the rate at which the present value of all cash flows from the bond equals its price. The US Government borrows money by issuing bonds of different maturities. Tracking the yields of different bonds maturing on different days on a single graph at a point of time gives us a yield curve. Risky corporations usually have to pay higher coupons than less risky firms.
To Conclude:
- Bonds are priced using the present value equation, where discount rate is YTM and present value is price.
- As interest rates increase, prices decrease. When interest rate = coupon rate, then price = par value.
- Zero coupon bonds do not pay coupons. Therefore, their price is below par as long as ttm > 0 and interest rate > 0.
- Bonds are quoted in 32nds instead of decimals.
- Current yield is the percentage of initial investment made by investor through coupon payments.
- Yield to maturity is the interest rate (discounting rate) at which if the coupons of the bond are discounted, the present value will equal the price at which the bond is trading.
- Rate of return is the percentage of initial investment made by investor by holding the bond.
- Yield curve is a representation of interest rates as a function of term to maturity.
- Real rate offered by bonds becomes significant if inflation increases in an economy.
- Investors can ask to be compensated if real rates become negative.
- Bonds have risks associated with them: these are default risk and term risk.
- Consequently, bonds of corporations need to be rated.
- Better the rating, lower the default risk and better is the credit quality and lower is the borrowing cost of the corporation
Bonds are a very important component of an investor’s portfolio. Corporations issue bonds to borrow money directly from capital markets. The primary advantage of issuing own bonds for corporations is lower coupons (or fixed payments on the borrowed money) as compared to bank loans. However, too much borrowing by a corporation can lead to suspicion in investors. Then corporations either have to increase coupons or raise money by issuing (sometimes additional) equity or shares. An analysis of shares and price and dividend of shares is carried out in chapter 7 on stocks.
Resources
Self Assessment
This self assessment can help you check your growing knowledge from this chapter. You can take the self-assessment as many times as you would like to check your understanding.
Short Answers and Activities
These activities will help you begin applying concepts in this chapter:
- Activity 6.1
- Instructions for Activity 6.1
- File for practicing the activity Activity 6.1 blank
- Activity 6.2
- Instructions for Activity 6.2
- File for practicing the activity Activity 6.2 blank
- Activity 6.3
- Instructions for Activity 6.3
- File for practicing the activity Activity 6.3 blank
- The word instrument is used for financial instrument can be interchangeably used for a security as in a financial security which is a more general form of any financial asset such as bond or stock or even a contract that represents derivatives or commodities or certificate of deposit etc. ↵
Market in which shares of stock are traded.
State of owing money.
Representation of interest rates against the term to maturity of a bond at a given point of time on a graph.
The current yield is the coupon divided by the current price.
The net gain or loss of an investment over a specified time period, expressed as a percentage of the investment's initial cost.
Inability of a borrower to make payment in time.
Bonds with variable coupons.
Bonds that allow investors to either convert these bonds into shares or reinvest them into bonds of the same tenure at maturity.

