Compressibility Effects

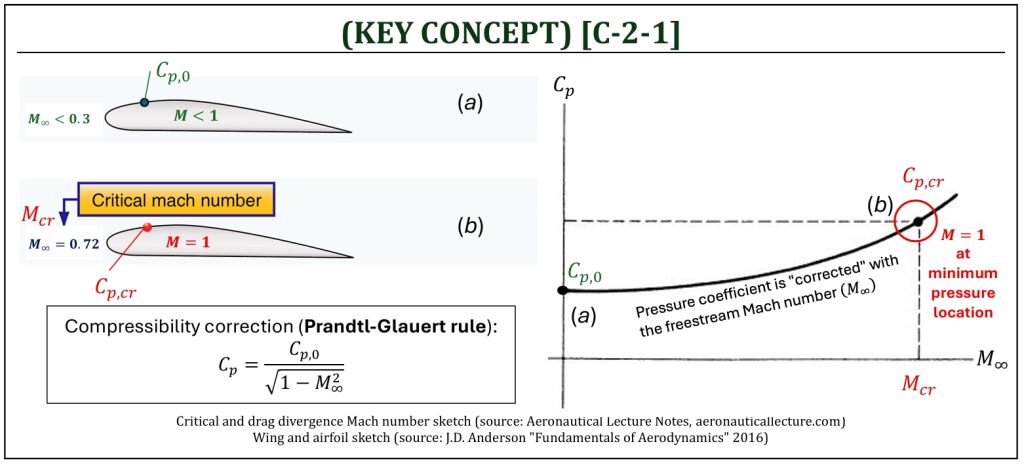
Recalling from EQUATION [C-1-3], the definition of pressure coefficient is defined under the condition of low-speed subsonic (i.e., incompressible) condition without any consideration of variation of density within the flow field.  From A-4, the valid condition of this pressure coefficient is obviously “incompressible subsonic” (M < 0.3) flow field only.  That would significantly limit the use of this pressure coefficient definition.  We are hereby redefine this incompressible subsonic pressure coefficient as C_p,0.

Recalling also from A-4, the variation of density within the flow field is less than 5 percent, if the freestream Mach number is less than 0.3 (incompressible subsonic).   As the freestream Mach number (M_∞) is becoming more than 0.3 and continue increasing, however, the variation of density within the flow field becomes more and more significant.  A commonly known empirical equation for the compressibility correction to be applied for pressure coefficient (for “compressible subsonic” flow field: 0.3 < M_∞ < 1) is called, “Prandtl-Glauert” rule.

As the freestream Mach number becomes more than 0.3 and continues increasing, the flow on the surface of a given airfoil accelerates and becomes close to the speed of sound.  An airfoil naturally accelerates the flow on the upper surface, creating the “minimum pressure point” on the upper (i.e., suction) surface.  The minimum pressure point is, essentially, the location of most accelerated (i.e., highest velocity, or “critical” point) on the surface of a given airfoil.

Even though the “flight Mach number” (freestream Mach number M_∞) is still subsonic, the “local” Mach number (M) at this critical point can become sonic (M = 1).  Then, the corresponding freestream Mach number of this special condition is called, the “critical Mach number” (M_cr).  The critical Mach number is a design parameter that actually specifies an important design parameter of aircraft’s high-speed capability.  This is the highest flight Mach number that aircraft can achieve without developing any local sonic flow on the surface.  The low value of critical Mach number means that the aircraft is NOT quite capable for high-speed flight.  Any design of high-speed aircraft should be associated with the critical Mach number value as high as possible.  The choice of airfoil shape (i.e., thickness) will have a significant impact on the critical Mach number.

Critical mach number

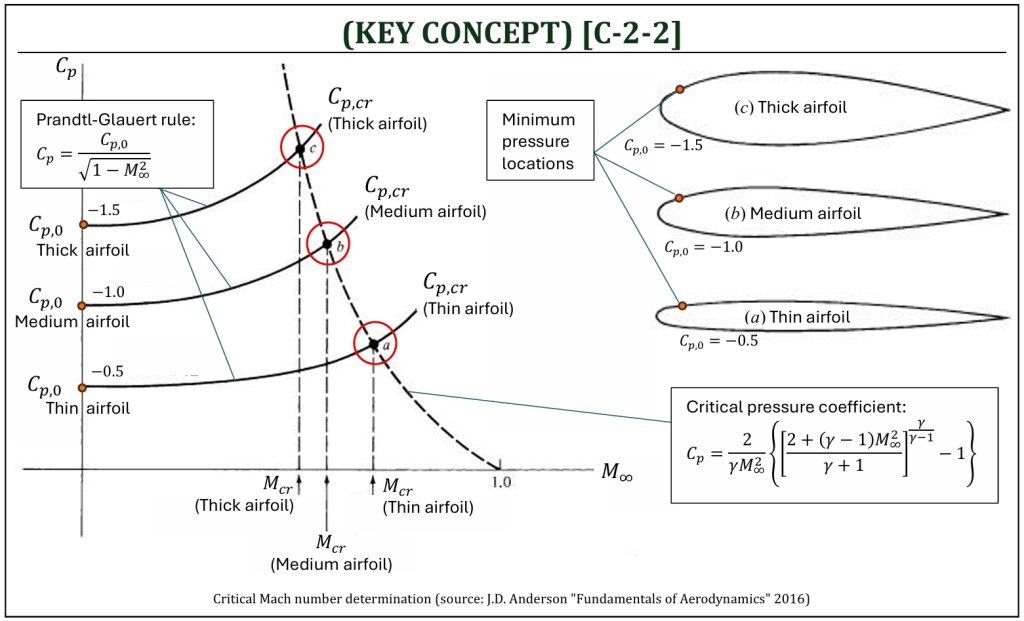
If the given airfoil is thick, the pressure at the minimum pressure (i.e., critical) point on the surface of the airfoil becomes lower.  As a result, the sonic flow begins to appear at much lower Mach number.  Therefore, the critical Mach number is lower.  Obviously, it is better not to accelerate “too much” the flow field to avoid lower critical Mach number.  The airfoil thickness has a strong negative impact on the critical Mach number.  The actual value of the critical Mach number, unfortunately, cannot be easily determined (at least in a direct mathematical computation).  We need to usually trace out two mathematical relations and determine where these mathematical relations have common solution, that is the critical Mach number of a given airfoil choice.

Assuming that the flow field is compressible subsonic (0.3 < M < 1), but still isentropic, we can apply energy equation.  The pressure coefficient at the location of the critical point (where, the flow is most accelerated and becoming sonic: M = 1) is called the “critical pressure coefficient” (C_p,cr).  Similar to the Prandtl-Glauert rule, this can be represented as a mathematical function of the freestream Mach number (M_∞).

Drag divergence

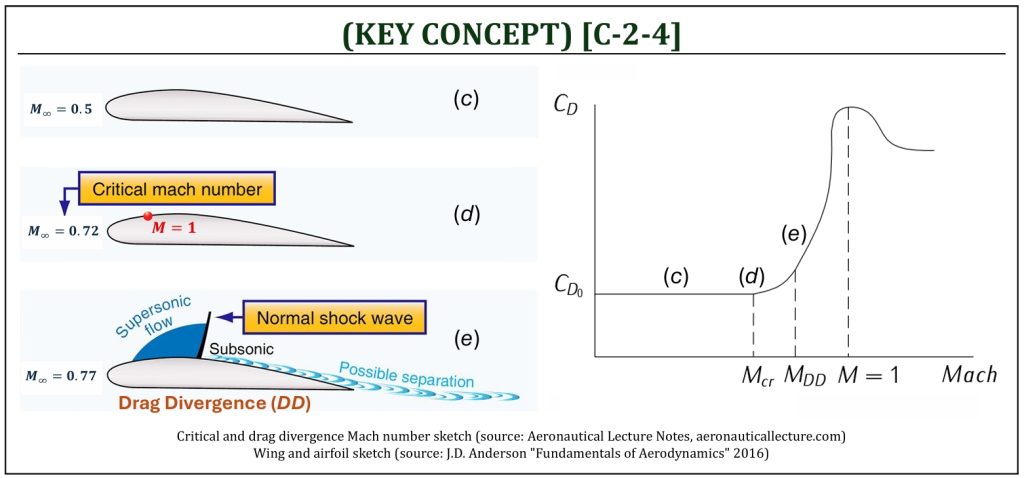
Drag divergence Mach number (M_DD) is the flight Mach number (freestream Mach number) at which drag coefficient begins to “diverge” (i.e., increase rapidly) toward the flight Mach number of 1 (sonic).  This is commonly observed beyond the critical Mach number (M_cr), close to the sonic speed, but still subsonic range (this is usually called, the “transonic” flow regime): M_cr < M_DD < 1.

Drag divergence is based mainly on the formation of strong normal shock wave at the minimum pressure point on the (typically) upper surface of the airfoil.  The formation of surface shock wave induces massive flow separation behind the shock wave, commonly called the shock-induced flow separation.  Due to the drag divergence, the early attempts of supersonic flight (NASA / Bell X-1) faced tremendous difficulties of achieving the successful supersonic flight: this is commonly known as the “SONIC BARRIER.”  Today, there are several effective solutions to avoid this drag divergence at transonic flight.

• In 2-D airfoil, one can choose a “supercritical” (NASA-SC) type airfoil to effectively delay the onset of drag divergence.

• For 3-D wing design, one can apply “wing sweep” to increase the critical Mach number and, consequently, delay  the onset of drag divergence.

Supercritical Airfoil

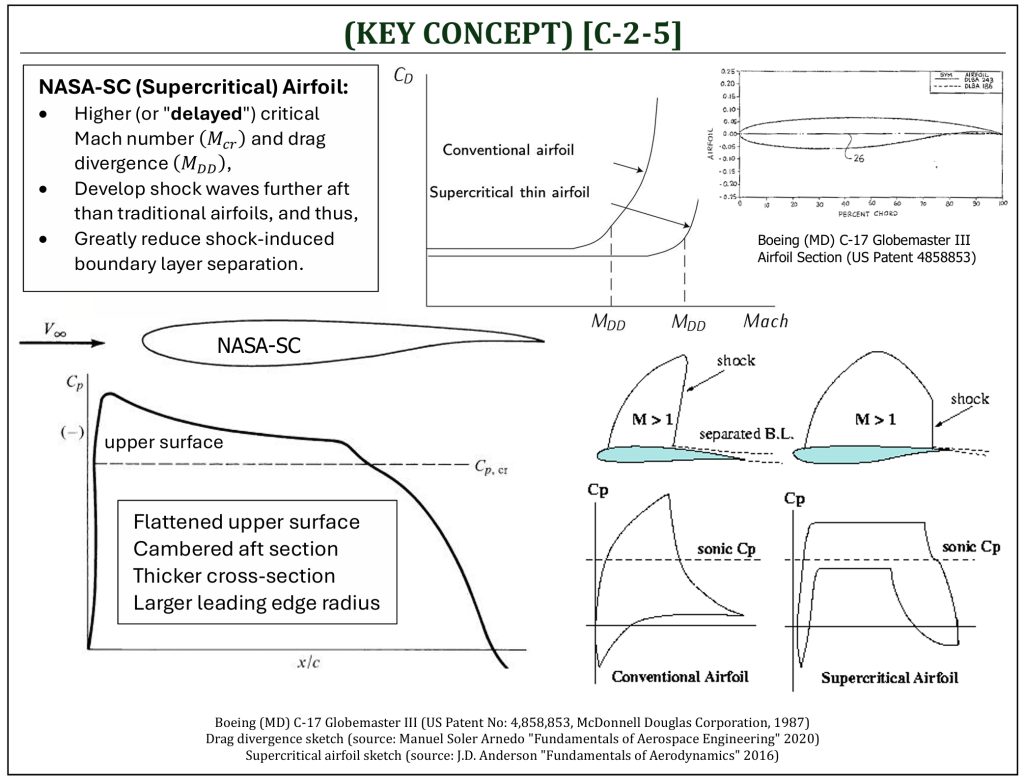
A supercritical (SC) airfoil (NASA-SC or NACA 8-series) is an airfoil designed, primarily, to delay the onset of drag divergence in the transonic flight regime.  The supercritical airfoil was created in the 1960s, by NASA scientist Richard Whitcomb.  While the design was initially developed as part of the supersonic transport (SST) project at NASA, it has since been mainly applied to increase the fuel efficiency of many high subsonic (transonic) jet transport aircraft.  Supercritical airfoils have three main benefits:

• Higher (or “delayed“) critical Mach number,

• Develop shock waves further aft than traditional airfoils, and thus,

• Greatly reduce shock-induced boundary layer separation.

NASA-SC airfoil is relatively thick airfoil and not suitable for supersonic flight.  The design purpose is to delay formation of “shock-induced flow separation” to avoid drag divergence at the high-end of transonic flight.

wave drag

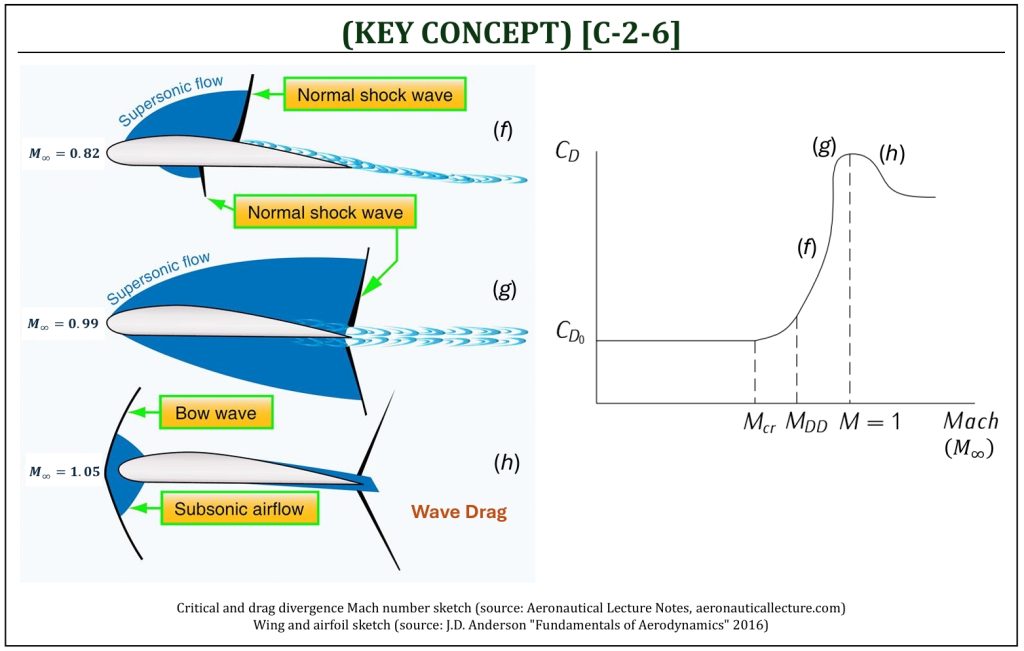
Wave drag is essentially the pressure drag due to the formation of shock waves.  In supersonic flight (M_∞ > 1), the entire vehicle is placed behind the shockwave.  Under this condition, the flow behind the shockwave is not the same condition as freestream: it is the condition of much higher pressure, density, and temperature.

Wave drag is typically the order of magnitude higher than other drag components (such as skin friction & pressure drags in subsonic flight).  Super-cruising of a high-speed aircraft (cruising at supersonic speed without afterburner) is technically very challenging, due to the massive increase of drag (due to the formation of shock waves, called wave drag), usually requires higher thrust to compensate the higher drag (wave drag) for supersonic cruising.

References

• NASA (www.nasa.gov)
• Aeronautical Lecture Note (https://aeronauticallecture.blogspot.com)
• AirfoilTools (https://airfoiltools.com)
• Google Patents (https://www.patents.google.com)
• Fundamentals of Aerospace Engineering by Manual Soler Arnedo, 2020
• Fundamentals of Aerodynamics by J.D. Anderson, 5th ED, McGraw Hill, 2016
• Aerodynamics for Engineers by J. J. Bertin & M. L. Smith, 3rd ED, Cambridge University Press, 1997
• Aerodynamics for Engineering Students by E. L. Houghton & P. W. Carpenter, 4th ED, Edward Arnold, London, 1993

Media Attributions

If a citation and/or attribution to a media (images and/or videos) is not given, then it is originally created for this book by the author, and the media can be assumed to be under CC BY-NC 4.0 (Creative Commons Attribution-NonCommercial 4.0 International) license.  Public domain materials have been included in these attributions whenever possible.  Every reasonable effort has been made to ensure that the attributions are comprehensive, accurate, and up-to-date. The Copyright Disclaimer under Section 107 of the Copyright Act of 1976 states that allowance is made for purposes such as teaching, scholarship, and research.  Fair use is a use permitted by copyright statute.  For any request for corrections and/or updates, please contact the author.